An Experimental Investigation of Passive Jet Control Method on Bridge Tower Wake
Abstract
:1. Introduction
2. Experimental Setup
2.1. Bridge Tower Model
2.2. Passive Jet Rings
2.3. Experiment Details and Measurement Point Arrangement
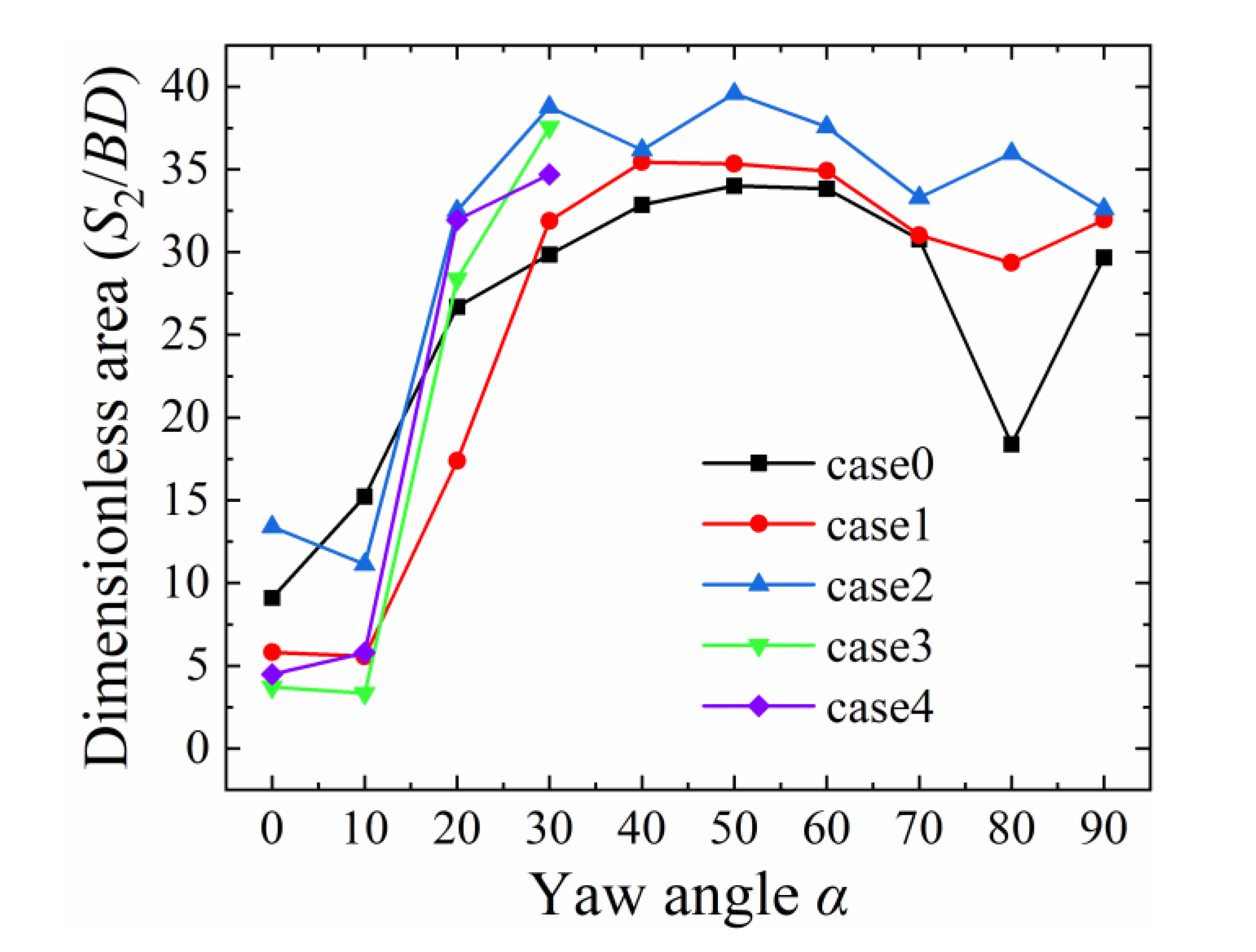
3. Results and Discussions
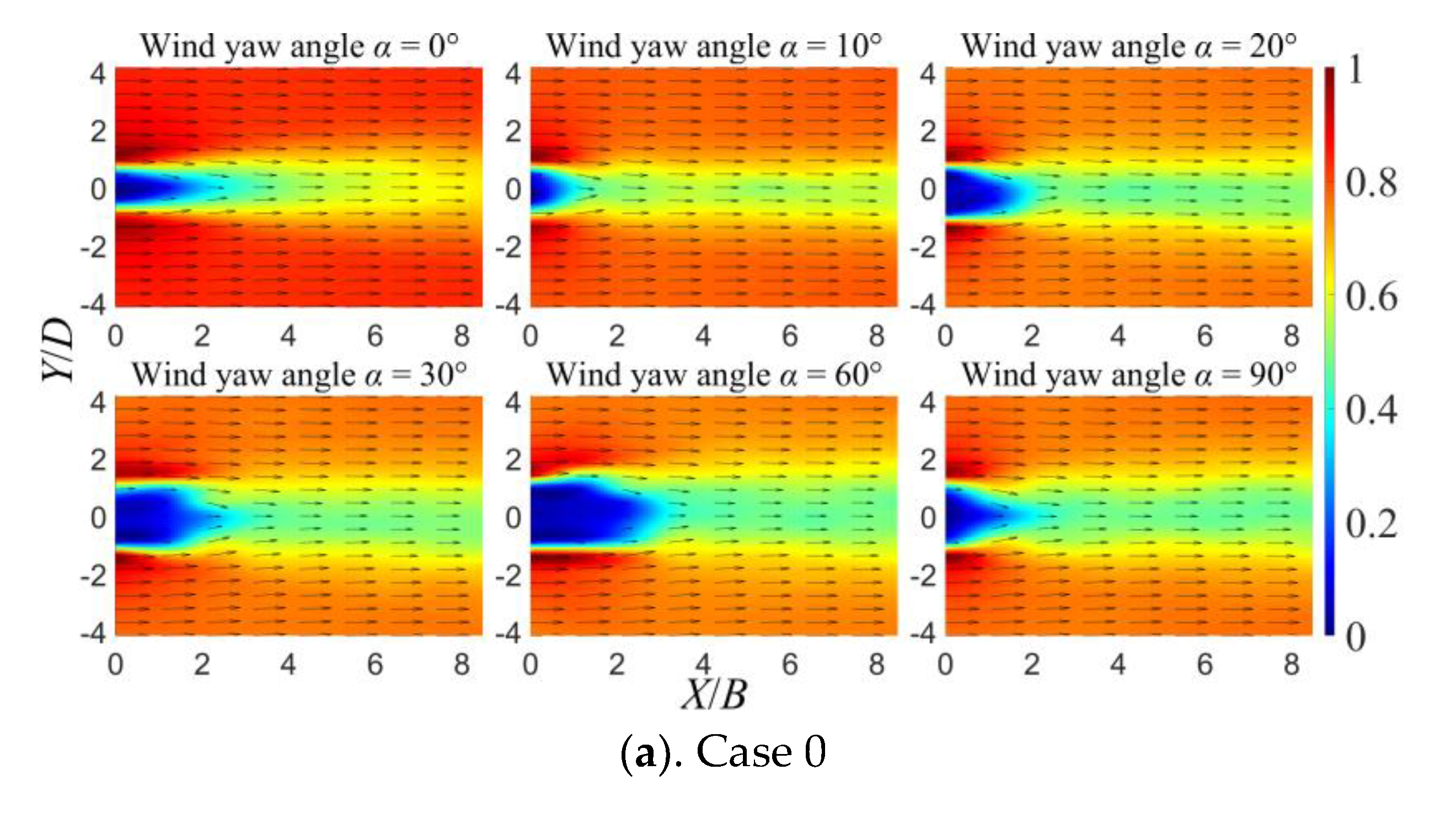
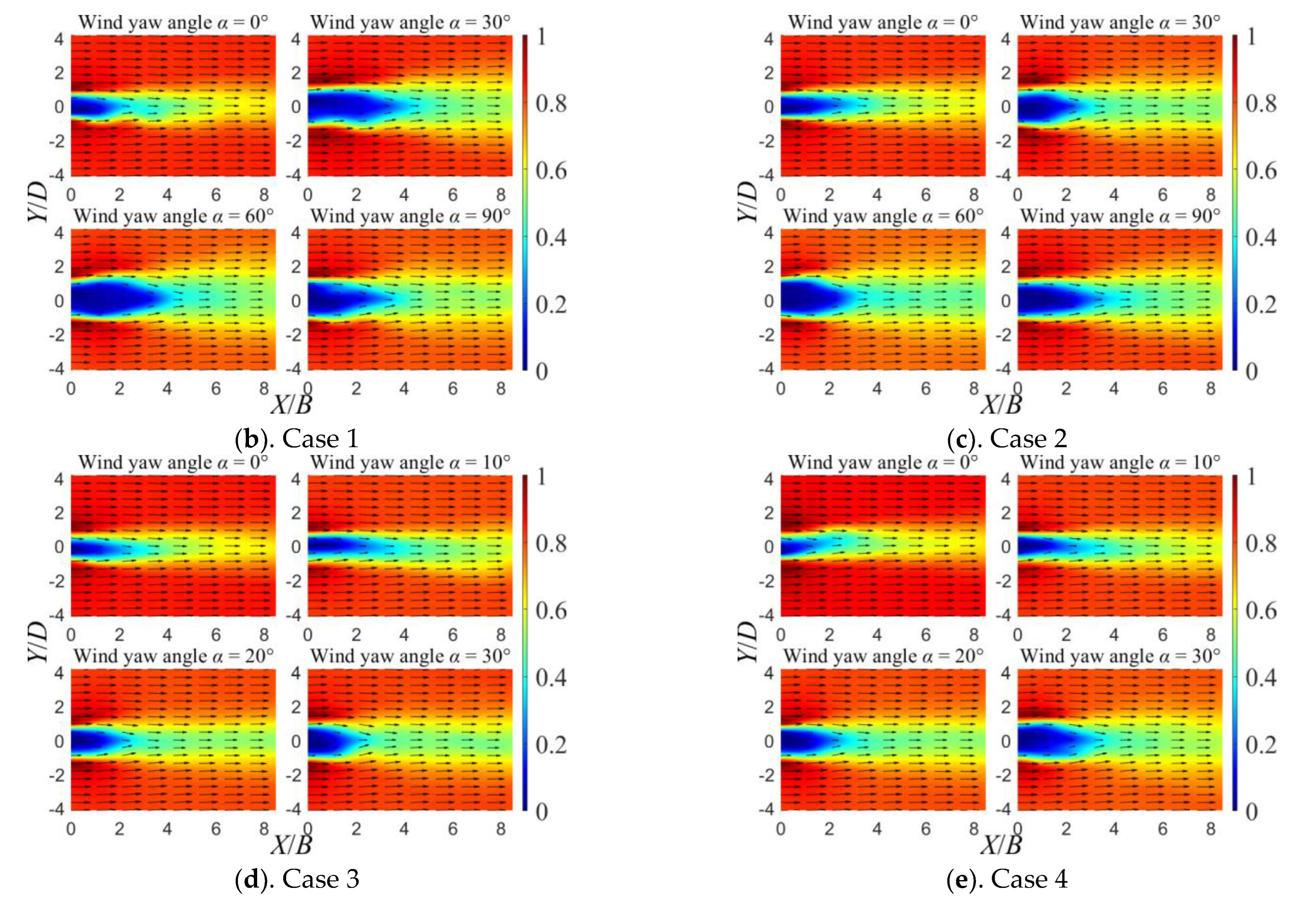
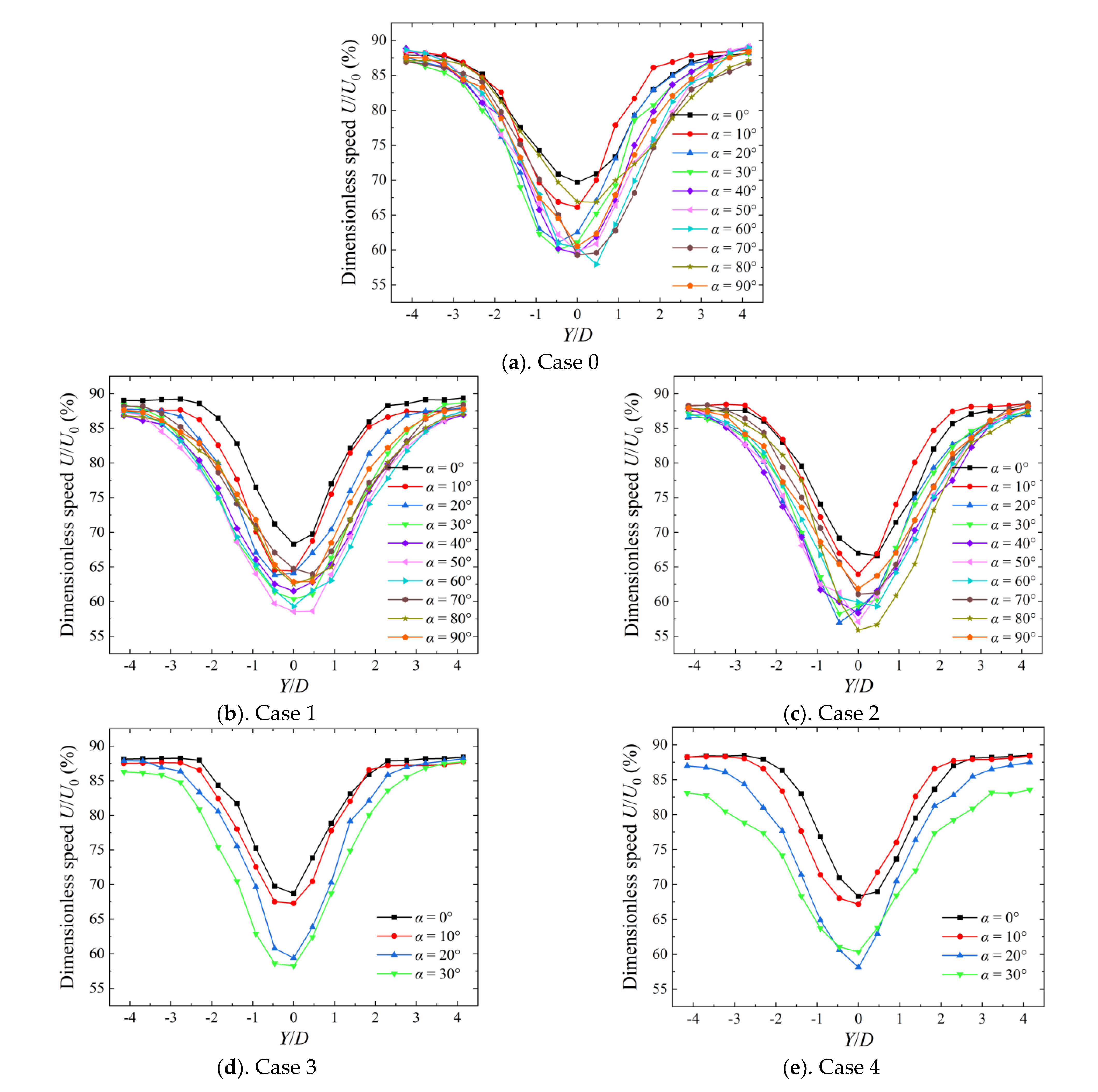
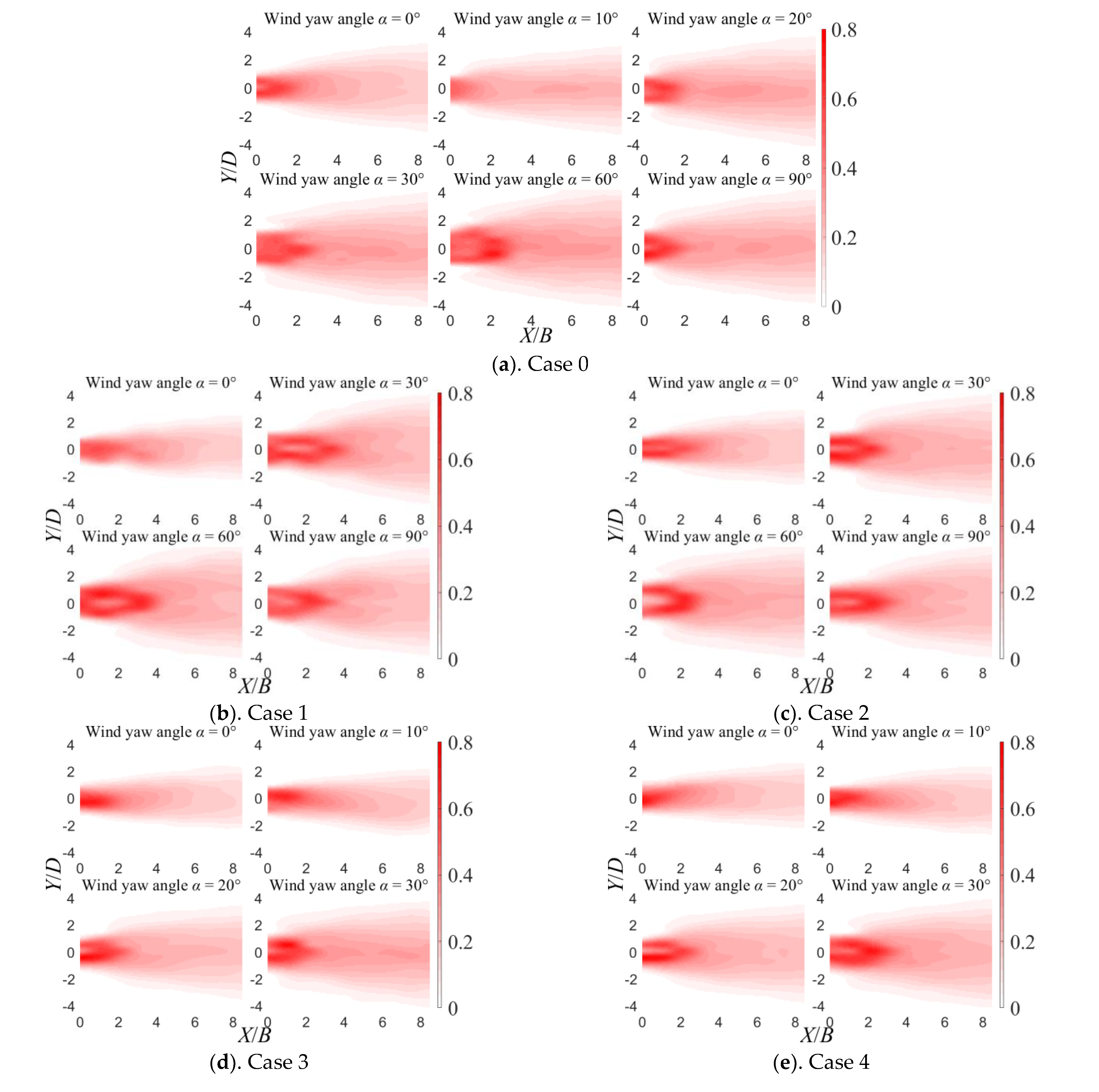
3.1. Mean Velocity Distribution
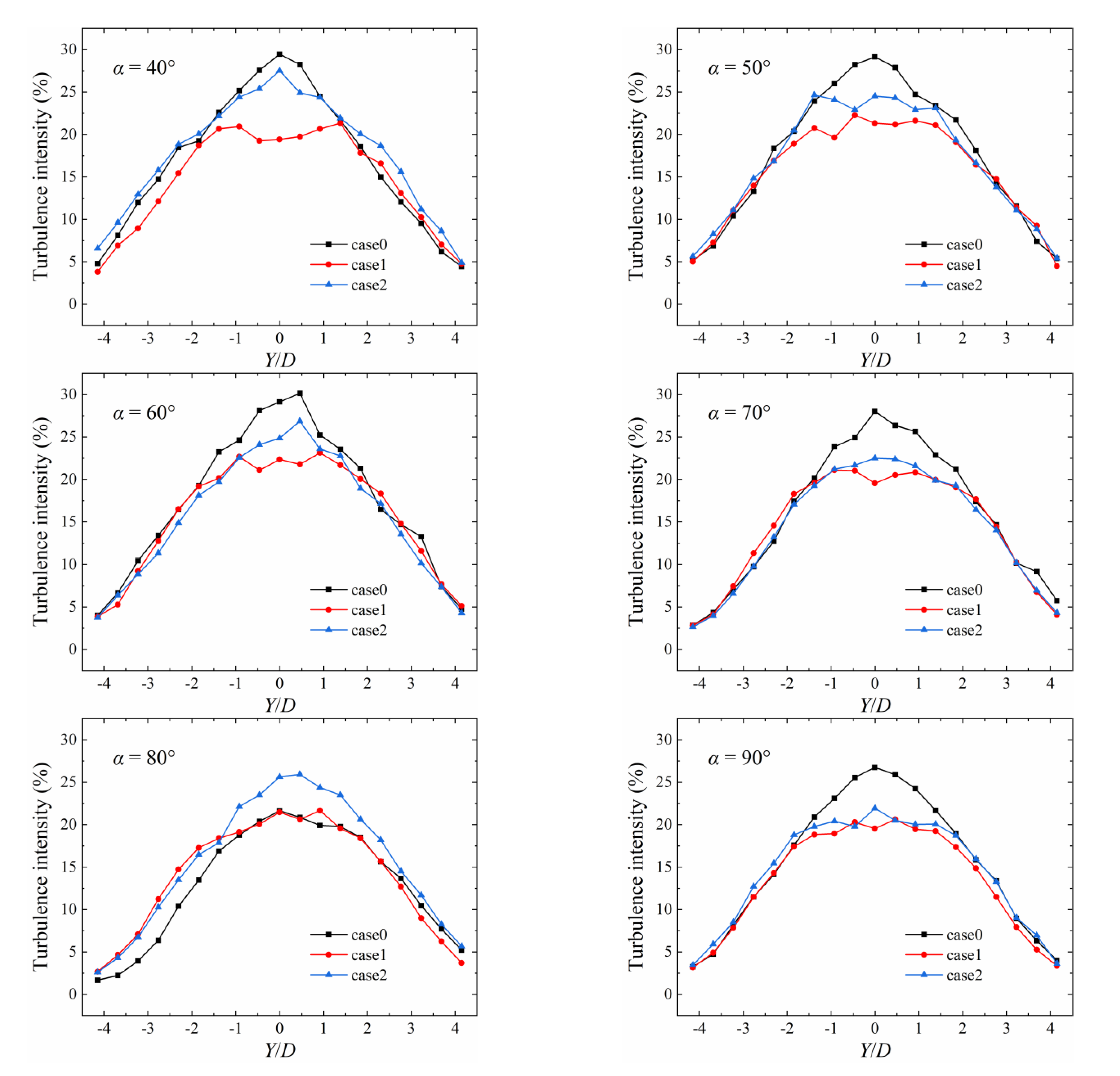
3.2. Turbulence Intensity Distribution
3.3. Dominant Frequency Distribution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knisely, C.W. Strouhal Numbers of Rectangular Cylinders at Incidence: A Review and New Data. J. Fluids Struct. 1990, 4, 371–393. [Google Scholar] [CrossRef]
- Norberg, C. Flow around Rectangular Cylinders: Pressure Forces and Wake Frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Shimada, K.; Ishihara, T. Application of a Modified K-ε Model to the Prediction of Aerodynamic Characteristics of Rectangular Cross-Section Cylinders. J. Fluids Struct. 2002, 16, 465–485. [Google Scholar] [CrossRef]
- Assi, G.R.S.; Bearman, P.W.; Meneghini, J.R. On the Wake-Induced Vibration of Tandem Circular Cylinders: The Vortex Interaction Excitation Mechanism. J. Fluid Mech. 2010, 661, 365–401. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. REVIEW—Review of Flow Interference Between Two Circular Cylinders in Various Arrangements. J. Fluids Eng. 1977, 99, 618. [Google Scholar] [CrossRef]
- Carmo, B.S.; Sherwin, S.J.; Bearman, P.W.; Willden, R.H.J. Flow-Induced Vibration of a Circular Cylinder Subjected to Wake Interference at Low Reynolds Number. J. Fluids Struct. 2011, 27, 503–522. [Google Scholar] [CrossRef]
- Bearman, P.W. Circular Cylinder Wakes and Vortex-Induced Vibrations. J. Fluids Struct. 2011, 27, 648–658. [Google Scholar] [CrossRef]
- Wang, H.; Yang, W.; Nguyen, K.D.; Yu, G. Wake-Induced Vibrations of an Elastically Mounted Cylinder Located Downstream of a Stationary Larger Cylinder at Low Reynolds Numbers. J. Fluids Struct. 2014, 50, 479–496. [Google Scholar] [CrossRef]
- Li, Y.; Tang, H.; Lin, Q.; Chen, X. Vortex-Induced Vibration of Suspenders in the Wake of Bridge Tower by Numerical Simulation and Wind Tunnel Test. J. Wind Eng. Ind. Aerodyn. 2017, 164, 164–173. [Google Scholar] [CrossRef]
- Amitay, M.; Smith, B.; Glezer, A. Aerodynamic Flow Control Using Synthetic Jet Technology. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Amitay, M.; Honohan, A.; Trautman, M.; Glezer, A.; Amitay, M.; Honohan, A.; Trautman, M.; Glezer, A. Modification of the Aerodynamic Characteristics of Bluff Bodies Using Fluidic Actuators. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar] [CrossRef]
- Crook, A.; Sadri, A.M.; Wood, N.J. The Development and Implementation of Synthetic Jets for the Control of Separated Flow. In Proceedings of the 17th Applied Aerodynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999; Volume 99, p. 3176. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Konieczny, P.; Alfredsson, P.H. Flow around a Porous Cylinder Subject to Continuous Suction or Blowing. J. Fluids Struct. 2004, 19, 1031–1048. [Google Scholar] [CrossRef]
- Wang, J.; Feng, L.; Xu, C. Experimental Investigations on Separation Control and Flow Structure around a Circular Cylinder with Synthetic Jet. Sci. China Ser. E Technol. Sci. 2007, 50, 550–559. [Google Scholar] [CrossRef]
- Dong, S.; Triantafyllou, G.S.; Karniadakis, G.E. Elimination of Vortex Streets in Bluff-Body Flows. Phys. Rev. Lett. 2008, 100, 204501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, L.H.; Wang, J.J. Synthetic Jet Control of Separation in the Flow over a Circular Cylinder. Exp. Fluids 2012, 53, 467–480. [Google Scholar] [CrossRef]
- Feng, L.-H.; Wang, J.-J.; Pan, C. Proper Orthogonal Decomposition Analysis of Vortex Dynamics of a Circular Cylinder under Synthetic Jet Control. Phys. Fluids 2011, 23, 014106. [Google Scholar] [CrossRef]
- Chen, W.-L.; Xin, D.-B.; Xu, F.; Li, H.; Ou, J.-P.; Hu, H. Suppression of Vortex-Induced Vibration of a Circular Cylinder Using Suction-Based Flow Control. J. Fluids Struct. 2013, 42, 25–39. [Google Scholar] [CrossRef]
- Chen, W.-L.; Li, H.; Hu, H. An Experimental Study on a Suction Flow Control Method to Reduce the Unsteadiness of the Wind Loads Acting on a Circular Cylinder. Exp. Fluids 2014, 55, 1707. [Google Scholar] [CrossRef]
- Chen, W.-L.; Wang, X.; Xu, F.; Li, H.; Hu, H. Passive Jet Flow Control Method for Suppressing Unsteady Vortex Shedding from a Circular Cylinder. J. Aerosp. Eng. 2017, 30, 04016063. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-L.; Gao, D.-L.; Yuan, W.-Y.; Li, H.; Hu, H. Passive Jet Control of Flow around a Circular Cylinder. Exp. Fluids 2015, 56, 201. [Google Scholar] [CrossRef]
- Zhang, L.-Q.; Chen, G.-B.; Chen, W.-L.; Gao, D.-L. Separation Control on a Bridge Box Girder Using a Bypass Passive Jet Flow. Appl. Sci. 2017, 7, 501. [Google Scholar] [CrossRef]
- Chen, W.L.; Huang, Y.W.; Gao, D.L.; Meng, H.; Chen, G.B.; Li, H. Passive Suction Jet Control of Flow Regime around a Rectangular Column with a Low Side Ratio. Exp. Therm. Fluid Sci. 2019, 109, 109815. [Google Scholar] [CrossRef]
- Chen, W.L.; Huang, Y.W.; Meng, H. Wake-Induced Vibration of a Suspender Cable in the Rear of a Bridge Tower. J. Fluids Struct. 2020, 99, 103166. [Google Scholar] [CrossRef]
- Mallipudi, S.; Selig, M.; Long, K. Use of a Four Hole Cobra Pressure Probe to Determine the Unsteady Wake Characteristics of Rotating Objects. In Proceedings of the 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, OR, USA, 28 June–1 July 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004; pp. 1–9. [Google Scholar]

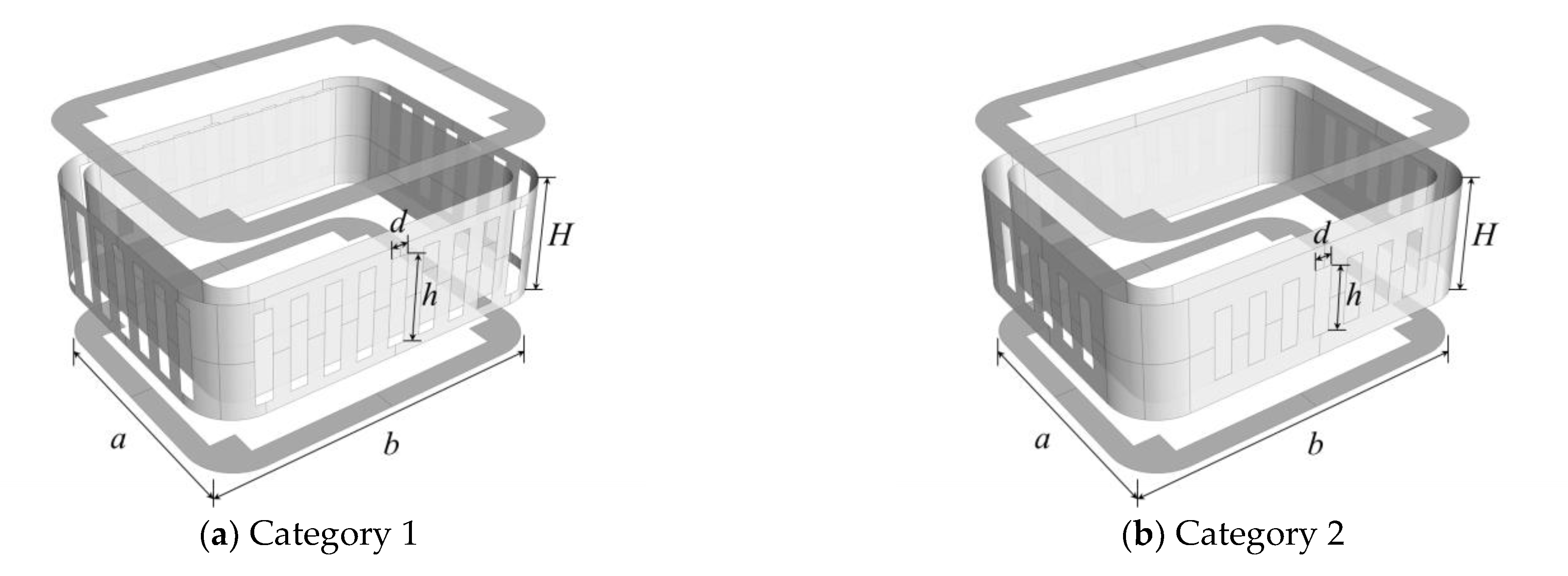
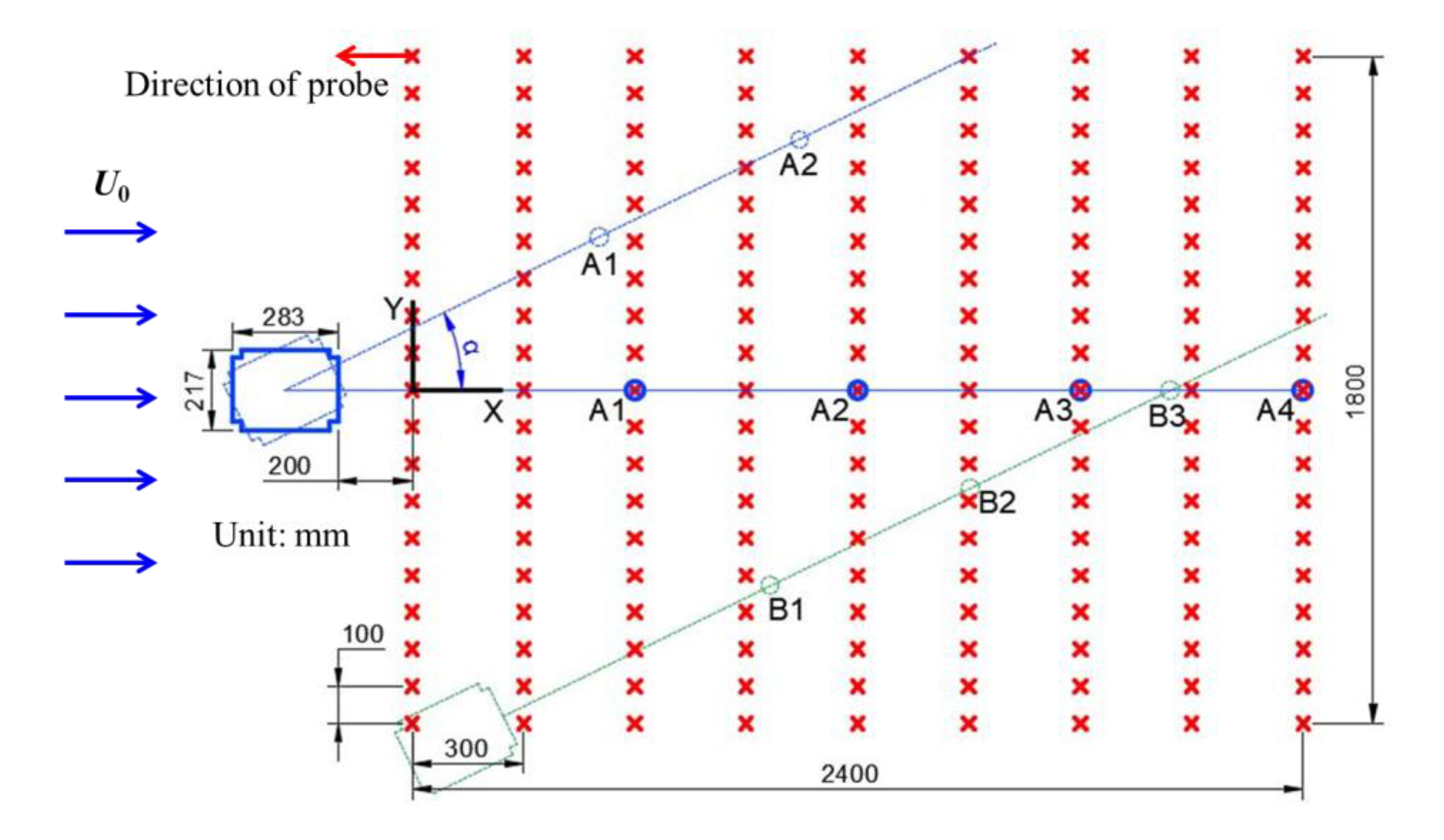



| Designation | Type of Passive Jet Ring | Slits Number at Long Side | Slits Number at Short Side | Length of Slits |
|---|---|---|---|---|
| Case 0 | without control | - | - | - |
| Case 1 | Category 1 | 9 | 7 | 80 mm |
| Case 2 | Category 2 | 7 | 5 | 60 mm |
| Case 3 | Category 3 | 0 | 7 | 80 mm |
| Case 4 | Category 4 | 0 | 5 | 60 mm |
| Yaw Angle | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 0.654 | 0.656 | 0.658 | 0.660 | 0.661 | 0.663 | 0.664 | 0.665 | 0.667 | 0.669 |
| Case 2 | 0.350 | 0.357 | 0.363 | 0.367 | 0.371 | 0.374 | 0.378 | 0.381 | 0.385 | 0.390 |
| Case 3 | 0.654 | 0.535 | 0.449 | 0.379 | - | - | - | - | - | - |
| Case 4 | 0.350 | 0.287 | 0.240 | 0.203 | - | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Chen, W. An Experimental Investigation of Passive Jet Control Method on Bridge Tower Wake. Appl. Sci. 2022, 12, 4691. https://doi.org/10.3390/app12094691
Huang Y, Chen W. An Experimental Investigation of Passive Jet Control Method on Bridge Tower Wake. Applied Sciences. 2022; 12(9):4691. https://doi.org/10.3390/app12094691
Chicago/Turabian StyleHuang, Yewei, and Wenli Chen. 2022. "An Experimental Investigation of Passive Jet Control Method on Bridge Tower Wake" Applied Sciences 12, no. 9: 4691. https://doi.org/10.3390/app12094691
APA StyleHuang, Y., & Chen, W. (2022). An Experimental Investigation of Passive Jet Control Method on Bridge Tower Wake. Applied Sciences, 12(9), 4691. https://doi.org/10.3390/app12094691







