The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint
Abstract
1. Introduction
1.1. Categories of Ankle–Foot Prostheses
1.2. Reasons to Design Multiaxial Ankle–Foot Prostheses
1.3. The Human Ankle Complex
1.4. State of the Art of Multiaxial Foot Prostheses
1.4.1. Commercial Devices and Patents
1.4.2. Academic Research
1.4.3. MyFlex- vs. Previous Technologies
1.5. Functionality Evaluation of Foot Prostheses
1.5.1. Mechanical Properties Testing
1.5.2. Human Subjects Testing
1.6. Summary
2. Materials and Methods
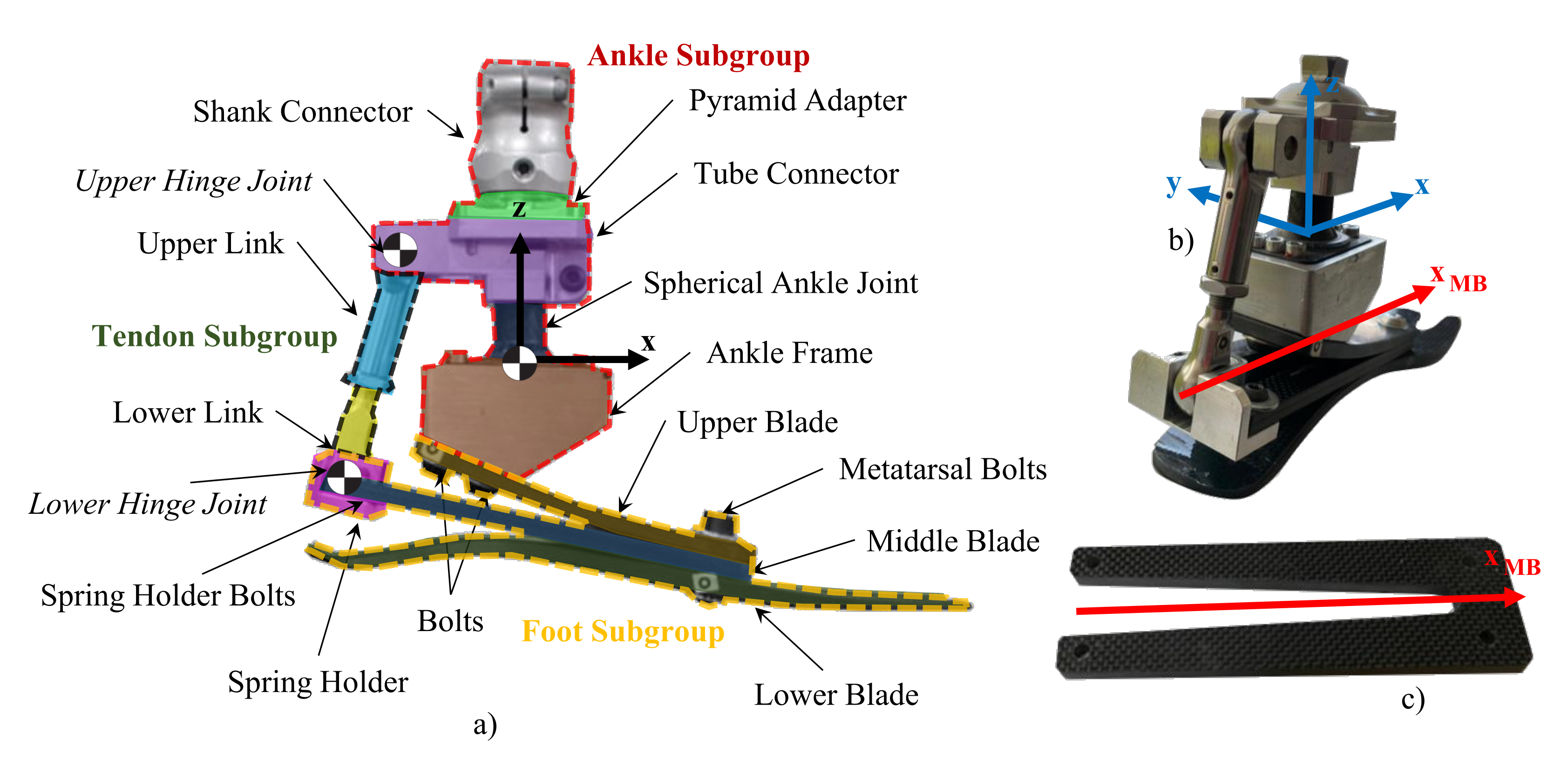
2.1. The Mechanical Design and Working Principle of MyFlex-
2.1.1. Mechanical Design of MyFlex-
2.1.2. Working Principle of MyFlex- in the Sagittal Plane
2.1.3. Elements Involved in the Torsional Stiffnesses of the Ankle Joint
2.2. The Design Methodology of MyFlex-
2.2.1. Design Phase
2.2.2. Validation Phase through ISO 10328-Equivalent Static Tests
2.2.3. Functionality Verification Phase
2.2.4. Elastic Energy Calculation
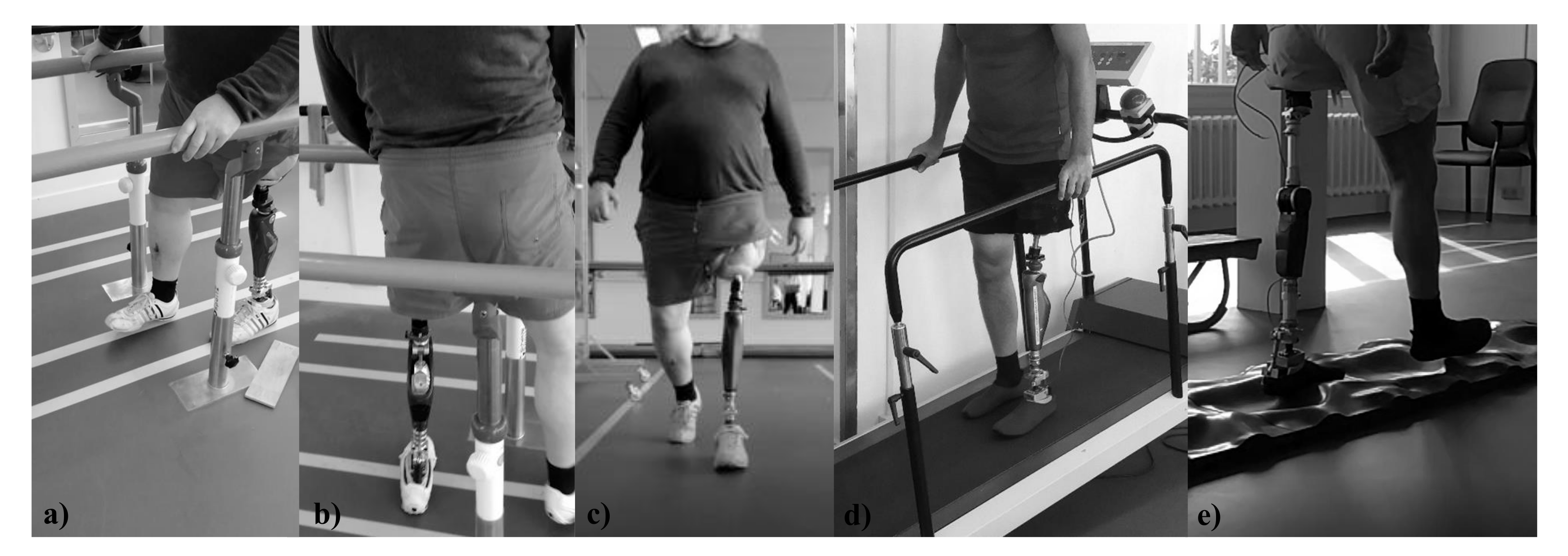
2.3. The Human Subjects Testing of MyFlex-
2.3.1. Procedure
2.3.2. Kinematics and Kinetics Data Collection
3. Results
3.1. Results from Design Phase and Validation Phase
3.1.1. Comparisons among 2D FEA and 3D FEA Mechanical Properties Testing
3.1.2. Calculated Stored Elastic Energy
3.2. Results from the Human Subjects Testing
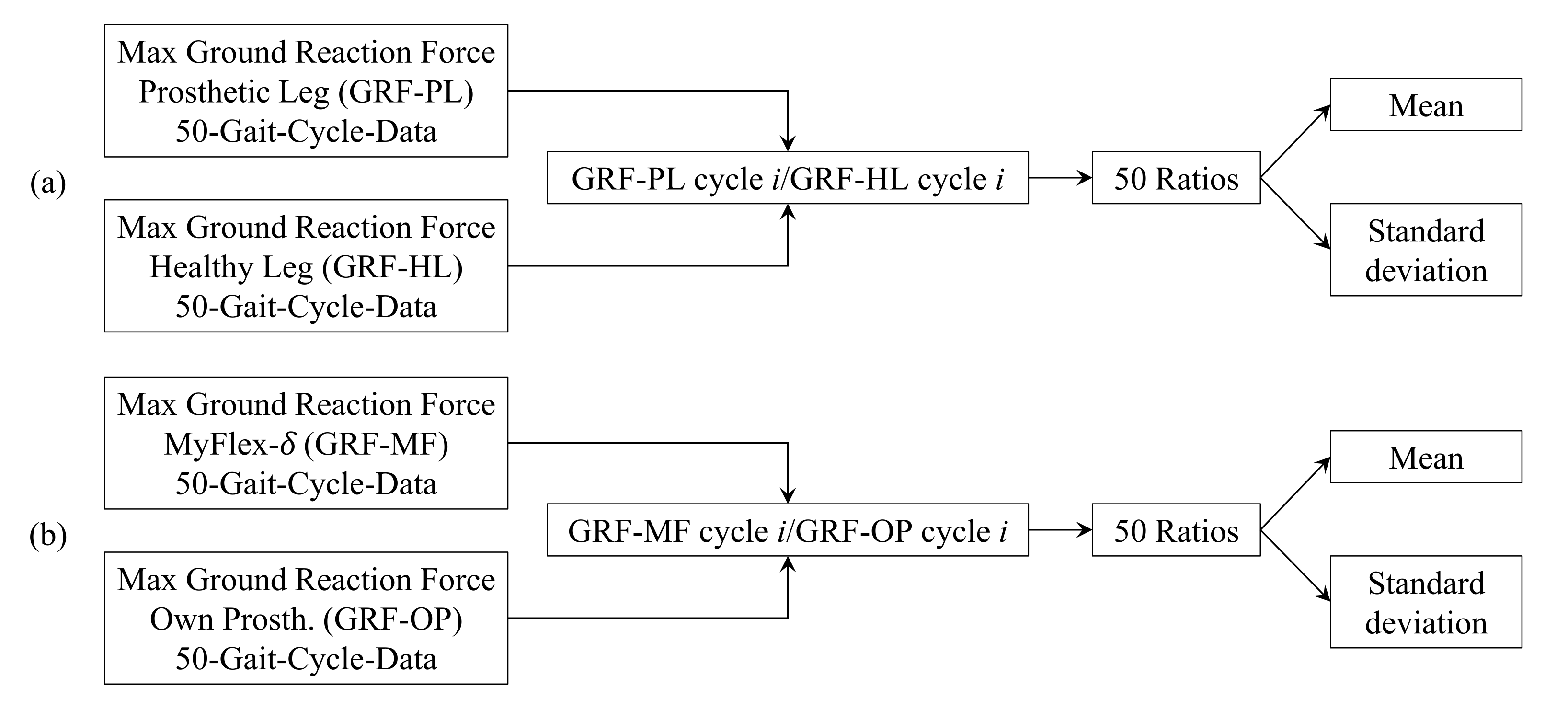
3.2.1. Ground Reaction Forces
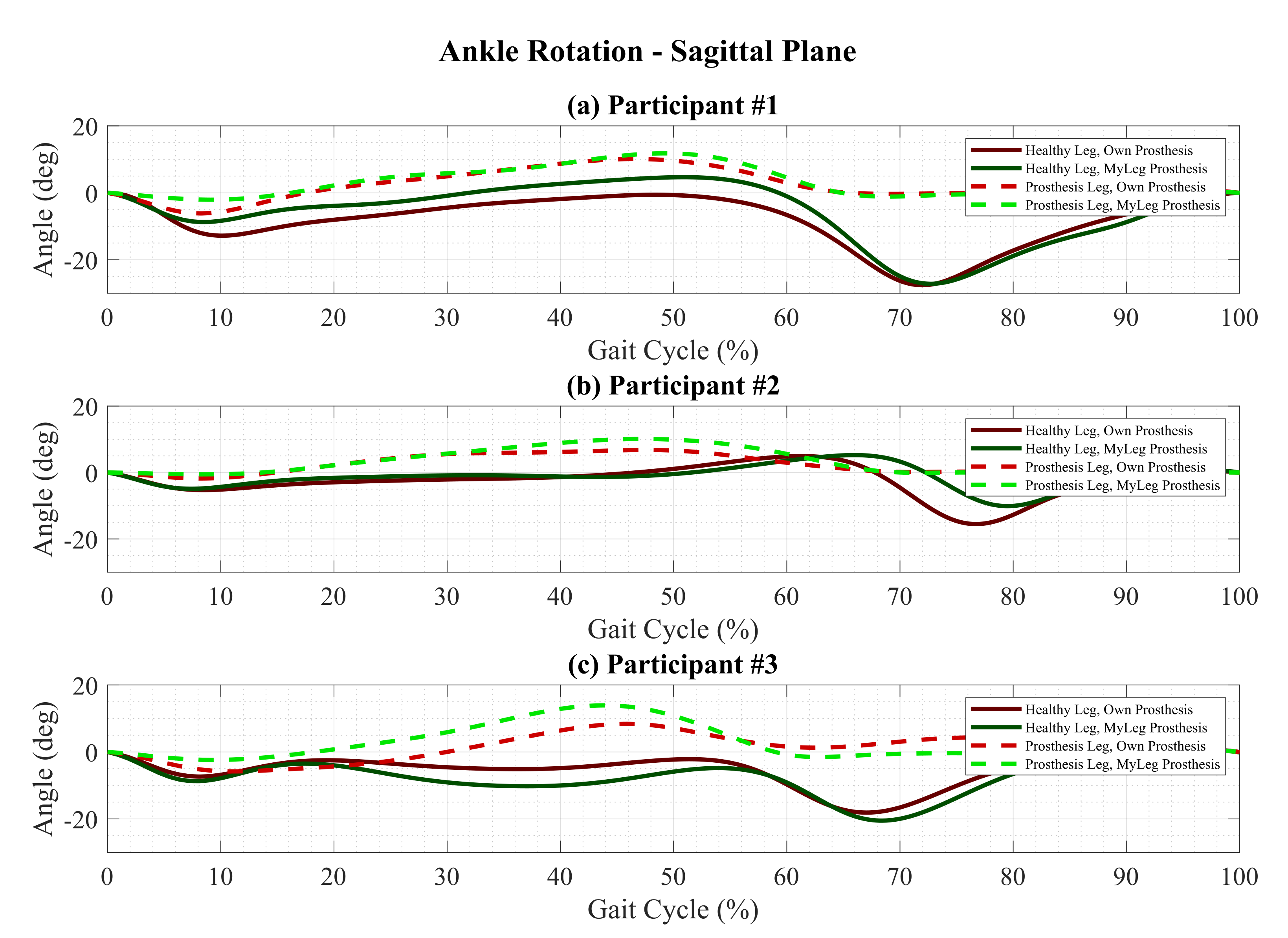
3.2.2. Sagittal Plane Kinematics
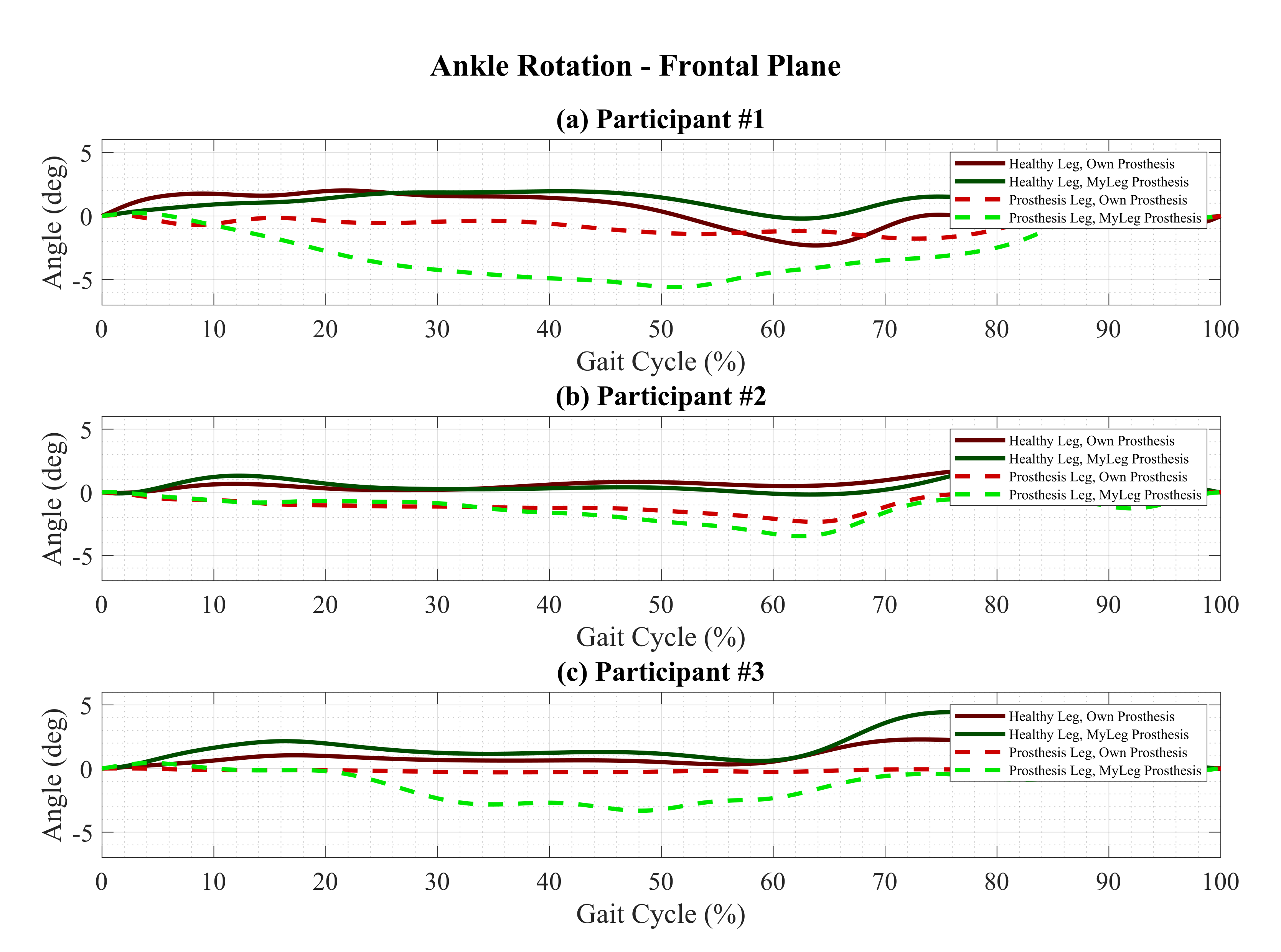
3.2.3. Frontal Plane Rotation
3.2.4. Step Length
3.2.5. Stance Phase
4. Discussion
4.1. MyFlex- vs. Their Own Prosthesis
4.1.1. Ground Reaction Forces
4.1.2. Sagittal Plane Kinematics
Plantarflexion at Toe Strike: Prosthetic Leg vs. Healthy Leg
Plantarflexion at Toe Strike: MyFlex-δ vs. Own Prosthesis
Dorsiflexion at Heel-Off: Prosthetic Leg vs. Healthy Leg
Dorsiflexion at Heel-Off: MyFlex-δ vs. Own Prosthesis
4.1.3. Step Length
Prosthetic Leg vs. Healthy Leg
MyFlex-δ vs. Own Prosthesis
4.1.4. Stance Phase
Early Stance
Midstance
Late Stance
4.2. Participants’ Feedback on MyFlex-
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shepherd, M.K.; Rouse, E.J. Design of a quasi-passive ankle-foot prosthesis with biomimetic, variable stiffness. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6672–6678. [Google Scholar]
- Shepherd, M.K.; Rouse, E.J. The VSPA foot: A quasi-passive ankle-foot prosthesis with continuously variable stiffness. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2375–2386. [Google Scholar] [CrossRef]
- Glanzer, E.M.; Adamczyk, P.G. Design and validation of a semi-active variable stiffness foot prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2351–2359. [Google Scholar] [CrossRef] [PubMed]
- Tryggvason, H.; Starker, F.; Lecomte, C.; Jonsdottir, F. Use of dynamic FEA for design modification and energy analysis of a variable stiffness prosthetic foot. Appl. Sci. 2020, 10, 650. [Google Scholar] [CrossRef]
- Tryggvason, H.; Starker, F.; Armannsdottir, A.L.; Lecomte, C.; Jonsdottir, F. Speed Adaptable Prosthetic Foot: Concept Description, Prototyping and Initial User Testing. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2978–2986. [Google Scholar] [CrossRef]
- Tryggvason, H.; Starker, F.; Lecomte, C.; Jonsdottir, F. Variable stiffness prosthetic foot based on rheology properties of shear thickening fluid. Smart Mater. Struct. 2020, 29, 095008. [Google Scholar] [CrossRef]
- Lecomte, C.; Ármannsdóttir, A.L.; Starker, F.; Tryggvason, H.; Briem, K.; Brynjolfsson, S. Variable stiffness foot design and validation. J. Biomech. 2021, 122, 110440. [Google Scholar] [CrossRef] [PubMed]
- Au, S.K.; Weber, J.; Herr, H. Biomechanical design of a powered ankle-foot prosthesis. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007; pp. 298–303. [Google Scholar]
- Au, S.K.; Herr, H.; Weber, J.; Martinez-Villalpando, E.C. Powered ankle-foot prosthesis for the improvement of amputee ambulation. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; pp. 3020–3026. [Google Scholar]
- Au, S.; Berniker, M.; Herr, H. Powered ankle-foot prosthesis to assist level-ground and stair-descent gaits. Neural Netw. 2008, 21, 654–666. [Google Scholar] [CrossRef] [PubMed]
- Au, S.K.; Herr, H.M. Powered ankle-foot prosthesis. IEEE Robot. Autom. Mag. 2008, 15, 52–59. [Google Scholar] [CrossRef]
- Au, S.K.; Weber, J.; Herr, H. Powered ankle–foot prosthesis improves walking metabolic economy. IEEE Trans. Robot. 2009, 25, 51–66. [Google Scholar] [CrossRef]
- Eilenberg, M.F.; Geyer, H.; Herr, H. Control of a powered ankle–foot prosthesis based on a neuromuscular model. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Herr, H.M.; Grabowski, A.M. Bionic ankle–foot prosthesis normalizes walking gait for persons with leg amputation. Proc. R. Soc. B Biol. Sci. 2012, 279, 457–464. [Google Scholar] [CrossRef]
- Grabowski, A.M.; D’Andrea, S. Effects of a powered ankle-foot prosthesis on kinetic loading of the unaffected leg during level-ground walking. J. Neuroeng. Rehabil. 2013, 10, 49. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, M.; Craig, K.; Kyberd, P.; Biden, E.; Bush, G. Design and development of ankle-foot prosthesis with delayed release of plantarflexion. J. Rehabil. Res. Dev. 2013, 50, 409–422. [Google Scholar] [CrossRef] [PubMed]
- Hitt, J.; Sugar, T.; Holgate, M.; Bellman, R.; Hollander, K. Robotic transtibial prosthesis with biomechanical energy regeneration. Ind. Robot. Int. J. 2009, 36, 441–447. [Google Scholar] [CrossRef]
- Hitt, J.K.; Sugar, T.G.; Holgate, M.; Bellman, R. An active foot-ankle prosthesis with biomechanical energy regeneration. J. Med. Devices 2010, 4, 011003. [Google Scholar] [CrossRef]
- Bellman, R.D.; Holgate, M.A.; Sugar, T.G. SPARKy 3: Design of an active robotic ankle prosthesis with two actuated degrees of freedom using regenerative kinetics. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 511–516. [Google Scholar]
- Sup, F.; Bohara, A.; Goldfarb, M. Design and control of a powered transfemoral prosthesis. Int. J. Robot. Res. 2008, 27, 263–273. [Google Scholar] [CrossRef]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.; Goldfarb, M. Design and control of an active electrical knee and ankle prosthesis. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 523–528. [Google Scholar]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.J.; Goldfarb, M. Preliminary evaluations of a self-contained anthropomorphic transfemoral prosthesis. IEEE/ASME Trans. Mechatronics 2009, 14, 667–676. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Wang, L. PANTOE 1: Biomechanical design of powered ankle-foot prosthesis with compliant joints and segmented foot. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 31–36. [Google Scholar]
- Zhu, J.; Wang, Q.; Wang, L. On the design of a powered transtibial prosthesis with stiffness adaptable ankle and toe joints. IEEE Trans. Ind. Electron. 2013, 61, 4797–4807. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Li, X.; Sun, W.; She, H.; Huang, Q. Importance of series elasticity in a powered transtibial prosthesis with ankle and toe joints. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 541–546. [Google Scholar]
- Zhu, J.; She, H.; Huang, Q. PANTOE II: Improved Version of a Powered Transtibial Prosthesis with Ankle and Toe Joints. Front. Biomed. Devices. Am. Soc. Mech. Eng. 2018, 40789, V001T03A015. [Google Scholar]
- She, H.; Zhu, J.; Tian, Y.; Wang, Y.; Huang, Q. Design of a powered ankle-foot prosthesis with an adjustable stiffness toe joint. Adv. Robot. 2020, 34, 689–697. [Google Scholar] [CrossRef]
- Cherelle, P.; Matthys, A.; Grosu, V.; Vanderborght, B.; Lefeber, D. The amp-foot 2.0: Mimicking intact ankle behavior with a powered transtibial prosthesis. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy,, 24–27 June 2012; pp. 544–549. [Google Scholar]
- Grosu, S.; Cherelle, P.; Verheul, C.; Vanderborght, B.; Lefeber, D. AMP-Foot 2.0 prosthesis dynamic behavior, preliminary computational multibody dynamics simulation results. In Proceedings of the ECCOMAS Thematic Conference on Multi-Body Dynamics, Zagreb, Croatia, 1–4 July 2013. [Google Scholar]
- Madusanka, D.; Wijayasingha, L.; Sanjeevan, K.; Ahamed, M.; Edirisooriya, J.; Gopura, R. A 3DOF transtibial robotic prosthetic limb. In Proceedings of the 7th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 22–24 December 2014; pp. 1–6. [Google Scholar]
- Masum, H.; Bhaumik, S.; Ray, R. Conceptual design of a powered ankle-foot prosthesis for walking with inversion and eversion. Procedia Technol. 2014, 14, 228–235. [Google Scholar] [CrossRef]
- Zheng, H.; Shen, X. Design and control of a pneumatically actuated transtibial prosthesis. J. Bionic Eng. 2015, 12, 217–226. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, K.; Zhu, J.; Wang, L. Walk the walk: A lightweight active transtibial prosthesis. IEEE Robot. Autom. Mag. 2015, 22, 80–89. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Q. Combining push-off power and nonlinear damping behaviors for a lightweight motor-driven transtibial prosthesis. IEEE/ASME Trans. Mechatronics 2017, 22, 2512–2523. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Y.; Liao, W.H. A new powered ankle-foot prosthesis with compact parallel spring mechanism. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 201; pp. 473–478.
- Gao, F.; Liu, Y.; Liao, W.H. Design of powered ankle-foot prosthesis with nonlinear parallel spring mechanism. J. Mech. Des. 2018, 140, 055001. [Google Scholar] [CrossRef]
- Rad, N.F.; Yousefi-Koma, A.; Tajdari, F.; Ayati, M. Design of a novel three degrees of freedom ankle prosthesis inspired by human anatomy. In Proceedings of the 2016 4th International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 26–28 October 2016; pp. 428–432. [Google Scholar]
- Agboola-Dobson, A.; Wei, G.; Ren, L. Biologically inspired design and development of a variable stiffness powered ankle-foot prosthesis. J. Mech. Robot. 2019, 11, 041012. [Google Scholar] [CrossRef]
- Tian, X.; Wang, S.; Wang, X.; Dong, D.; Zhang, Y. Design and Control of a Compliant Electro-Hydrostatic-Powered Ankle Prosthesis. IEEE/ASME Trans. Mechatronics 2021, 99, 1–11. [Google Scholar] [CrossRef]
- Gabert, L.; Hood, S.; Tran, M.; Cempini, M.; Lenzi, T. A compact, lightweight robotic ankle-foot prosthesis: Featuring a powered polycentric design. IEEE Robot. Autom. Mag. 2020, 27, 87–102. [Google Scholar] [CrossRef] [PubMed]
- Gabert, L.; Tran, M.; Lenzi, T. Design of an underactuated powered ankle and toe prosthesis. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Virtual, Mexico, 1–5 November 2021; pp. 4920–4923. [Google Scholar]
- Carney, M.E.; Shu, T.; Stolyarov, R.; Duval, J.F.; Herr, H.M. Design and preliminary results of a reaction force series elastic actuator for bionic knee and ankle prostheses. IEEE Trans. Med. Robot. Bionics 2021, 3, 542–553. [Google Scholar] [CrossRef]
- Jang, W.S.; Kim, D.Y.; Choi, Y.S.; Kim, Y.J. Self-Contained 2-DOF Ankle-Foot Prosthesis With Low-Inertia Extremity for Agile Walking on Uneven Terrain. IEEE Robot. Autom. Lett. 2021, 6, 8134–8141. [Google Scholar] [CrossRef]
- Laferrier, J.; Groff, A.; Hale, S.; Sprunger, N. A Review of Commonly Used Prosthetic Feet for Developing Countries: A Call for Research and Development. J. Nov. Physiother. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Hansen, A.; Starker, F. Prosthetic foot principles and their influence on gait. In Handbook of Human Motion; Springer: Cham, Switzerland, 2017; pp. 1–15. [Google Scholar]
- Grimmer, M. Powered Lower Limb Prostheses. Ph.D. Thesis, Johannes Kepler University Linz, Linz, Austria, 2015. [Google Scholar]
- Ficanha, E.M.; Rastgaar, M. Preliminary design and evaluation of a multi-axis ankle-foot prosthesis. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paolo, Brazil, 12 –15 August 2014; pp. 1033–1038. [Google Scholar]
- Stapleton, D.; Vardaxis, V. Evaluation of the subtalar joint during gait using 3-D motion analysis: Does the STJ achieve neutral position? Prosthetics Orthot. Int. 2017, 41, 157–163. [Google Scholar]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. A public dataset of overground and treadmill walking kinematics and kinetics in healthy individuals. PeerJ 2018, 6, e4640. [Google Scholar] [CrossRef] [PubMed]
- Glaister, B.C.; Bernatz, G.C.; Klute, G.K.; Orendurff, M.S. Video task analysis of turning during activities of daily living. Gait Posture 2007, 25, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Damavandi, M.; Dixon, P.C.; Pearsall, D.J. Kinematic adaptations of the hindfoot, forefoot, and hallux during cross-slope walking. Gait Posture 2010, 32, 411–415. [Google Scholar] [CrossRef]
- Gray, H. Gray’s Anatomy: With Original Illustrations by Henry Carter; Arcturus Publishing Ltd.: London, UK, 2015. [Google Scholar]
- Sarrafian, S.K. Biomechanics of the subtalar joint complex. Clin. Orthop. Relat. Res. 1993, 17–26. [Google Scholar] [CrossRef]
- Hicks, J. The mechanics of the foot: I. The joints. J. Anat. 1953, 87, 345. [Google Scholar]
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef]
- Michael, J.M.; Golshani, A.; Gargac, S.; Goswami, T. Biomechanics of the ankle joint and clinical outcomes of total ankle replacement. J. Mech. Behav. Biomed. Mater. 2008, 1, 276–294. [Google Scholar] [CrossRef] [PubMed]
- Merlette, J.B. Foot Prosthesis. U.S. Patent 6,261,324, 10 July 2001. [Google Scholar]
- Smith, N.; Rush, D.; Williams, N. Multi-Axial Prosthetic Foot. U.S. Patent 10/663,514, 11 July 2005. [Google Scholar]
- Clausen, A.V.; Ragnarsdottir, H.G.; Lecomte, C.; Thorhallsdottir, H. Foot Prosthesis with Resilient Multi-Axial Ankle. U.S. Patent 7,347,877, 23 July 2008. [Google Scholar]
- Lecomte, C.G.; Thorhallsdottir, H.; Ragnarsdottir, H.G.; Clausen, A.V. Foot Prosthesis with Resilient Multi-Axial Ankle. U.S. Patent 7,846,213, 2 August 2010. [Google Scholar]
- Lecomte, C.G.; Thorhallsdottir, H.; Ragnarsdottir, H.G.; Clausen, A.V. Foot Prosthesis with Resilient Multi-Axial Ankle. U.S. Patent 8,025,699, 15 August 2011. [Google Scholar]
- Harrison, N.F. Ankle-Joint. U.S. Patent 1,001,641, 29 August 1911. [Google Scholar]
- Kaiser, W.F. Artificial Ankle Joint. U.S. Patent 2,183,076, 13 March 1939. [Google Scholar]
- Georg, G. Artificial Foot with Ankle-joint. U.S. Patent 2,620,485, 12 September 1952. [Google Scholar]
- Carl, W. Ankle Joint for Artificial Limbs. U.S. Patent 2,731,645, 12 September 1956. [Google Scholar]
- Cornelius, C.J. Prosthetic Ankle Joint for Pivotally Connecting a Residual Limb to a Prosthetic Foot. U.S. Patent 5,571,212, 11 May 1996. [Google Scholar]
- Farneth, C.S. Ankle Joint for Artificial Limb. U.S. Patent 3,196,463, 27 July 1965. [Google Scholar]
- Mccoy, A.J. Articulated Ankle Joint with Inner and Outer Races for Universal Movement. U.S. Patent 5,405,411, 11 April 1995. [Google Scholar]
- Christensen, R.J. Multi-Axial Prosthetic Ankle. U.S. Patent 7,794,506, 14 September 2010. [Google Scholar]
- Hansen, A.H. Scientific methods to determine functional performance of prosthetic ankle-foot systems. J. Prosthetics Orthot. 2005, 17, S23–S29. [Google Scholar] [CrossRef]
- Lehmann, J.F.; Price, R.; Boswell-Bessette, S.; Dralle, A.; Questad, K. Comprehensive analysis of energy storing prosthetic feet: Flex Foot and Seattle Foot Versus Standard SACH foot. Arch. Phys. Med. Rehabil. 1993, 74, 1225–1231. [Google Scholar] [CrossRef]
- Lehmann, J.F.; Price, R.; Boswell-Bessette, S.; Dralle, A.; Questad, K. Comprehensive analysis of dynamic elastic response feet: Seattle Ankle/Lite Foot versus SACH foot. Arch. Phys. Med. Rehabil. 1993, 74, 853–861. [Google Scholar] [CrossRef]
- Knox, E.H. The Role of Prosthetic Feet in Walking; Northwestern University: Evanston, IL, USA, 1996. [Google Scholar]
- Tabucol, J.; Brugo, T.M.; Povolo, M.; Leopaldi, M.; Oddsson, M.; Carloni, R.; Zucchelli, A. Structural FEA-Based Design and Functionality Verification Methodology of Energy-Storing-and-Releasing Prosthetic Feet. Appl. Sci. 2022, 12, 97. [Google Scholar] [CrossRef]
- Postema, K.; Hermens, H.; De Vries, J.; Koopman, H.; Eisma, W. Energy storage and release of prosthetic feet Part 2: Subjective ratings of 2 energy storing and 2 conventional feet, user choice of foot and deciding factor. Prosthetics Orthot. Int. 1997, 21, 28–34. [Google Scholar] [CrossRef][Green Version]
- Huang, G.F.; Chou, Y.L.; Su, F.C. Erratum: Gait analysis and energy consumption of below-knee amputees wearing three different prosthetic feet (Gait and Posture (2000) 12 (162–168)). Gait Posture 2003, 18, 1. [Google Scholar] [CrossRef] [PubMed]
- Macfarlane, P.A.; Nielsen, D.H.; Shurr, D.G.; Meier, K. Perception of walking difficulty by below-knee amputees using a conventional foot versus the flex-foot. J. Prosthetics Orthot. 1991, 3, 114–119. [Google Scholar] [CrossRef]
- Menard, M.R.; Murray, D.D. Subjective and objective analysis of an energy-storing prosthetic foot. J. Prosthetics Orthot. 1989, 1, 220–230. [Google Scholar] [CrossRef]
- Mizuno, N.; Aoyama, T.; Nakajima, A.; Kasahara, T.; Takami, K. Functional evaluation by gait analysis of various ankle-foot assemblies used by below-knee amputees. Prosthetics Orthot. Int. 1992, 16, 174–182. [Google Scholar] [CrossRef][Green Version]
- Murray, D.; Hartvikson, W.; Anton, H.; Hommonay, E.; Russell, N. With a Spring in one’s step. Clin. Prosthetics Orthot. 1988, 12, 128–135. [Google Scholar]
- Alaranta, H.; Kinnunen, A.; Karkkainen, M.; Pohjolainen, T.; Heliovaara, M. Practical benefits of Flex-Foot in below-knee amputees. J. Prosthet. Orthot. 1991, 3, 179–181. [Google Scholar] [CrossRef]
- Day, H. The assessment and description of amputee activity. Prosthetics Orthot. Int. 1981, 5, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Gailey, R.S.; Roach, K.E.; Applegate, E.B.; Cho, B.; Cunniffe, B.; Licht, S.; Maguire, M.; Nash, M.S. The amputee mobility predictor: An instrument to assess determinants of the lower-limb amputee’s ability to ambulate. Arch. Phys. Med. Rehabil. 2002, 83, 613–627. [Google Scholar] [CrossRef] [PubMed]
- Barth, D.G.; Schumacher, L.; Thomas, S.S. Gait analysis and energy cost of below-knee amputees wearing six different prosthetic feet. J. Prosthetics Orthot. 1992, 4, 63–75. [Google Scholar] [CrossRef]
- Casillas, J.M.; Dulieu, V.; Cohen, M.; Marcer, I.; Didier, J.P. Bioenergetic comparison of a new energy-storing foot and SACH foot in traumatic below-knee vascular amputations. Arch. Phys. Med. Rehabil. 1995, 76, 39–44. [Google Scholar] [CrossRef]
- Cortes, A.; Viosca, E.; Hoyos, J.; Prat, J.; Sanchez-Lacuesta, J. Optimisation of the prescription for trans-tibial (TT) amputees. Prosthetics Orthot. Int. 1997, 21, 168–174. [Google Scholar] [CrossRef][Green Version]
- Culham, E.; Peat, M.; Newell, E. Analysis of gait following below-knee amputation: A comparison of the SACH and single-axis foot. Physiother. Can. 1984, 36, 237–242. [Google Scholar]
- Culham, E.; Peat, M.; Newell, E. Below-knee amputation: A comparison of the effect of the SACH foot and single axis foot on electromyographic patterns during locomotion. Prosthetics Orthot. Int. 1986, 10, 110301. [Google Scholar] [CrossRef] [PubMed]
- Doane, N.E.; Holt, L. A comparison of the SACH and single axis foot in the gait of unilateral below-knee amputees. Prosthetics Orthot. Int. 1983, 7, 33–36. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gitter, A.; Czerniecki, J.M.; DeGroot, D.M. Biomechanical analysis of the influence of prosthetic feet on below-knee amputee walking. Am. J. Phys. Med. Rehabil. 1991, 70, 142–148. [Google Scholar] [CrossRef]
- Goh, J.; Solomonidis, S.; Spence, W.; Paul, J. Biomechanical evaluation of SACH and uniaxial feet. Prosthetics Orthot. Int. 1984, 8, 147–154. [Google Scholar] [CrossRef]
- Hsu, M.J.; Nielsen, D.H.; Yack, H.J.; Shurr, D.G. Physiological measurements of walking and running in people with transtibial amputations with 3 different prostheses. J. Orthop. Sport. Phys. Ther. 1999, 29, 526–533. [Google Scholar] [CrossRef]
- Macfarlane, P.; Nielsen, D.; Shurr, D.; Meier, K. Gait comparisons for below-knee amputees using a Flex-Foot versus a conventional prosthetic foot. J. Prosthet. Orthot. 1991, 3, 150–161. [Google Scholar] [CrossRef]
- Macfarlane, P.A.; Nielsen, D.H.; Shurr, D.G. Mechanical gait analysis of transfemoral amputees: SACH foot versus the Flex-Foot. J. Prosthetics Orthot. 1997, 9, 144–151. [Google Scholar] [CrossRef]
- Menard, M.R.; McBride, M.E.; Sanderson, D.J.; Murray, D.D. Comparative biomechanical analysis of energy-storing prosthetic feet. Arch. Phys. Med. Rehabil. 1992, 73, 451–458. [Google Scholar]
- Nielsen, D.H.; Shurr, D.G.; Golden, J.C.; Meier, K. Comparison of energy cost and gait efficiency during ambulation in below-knee amputees using different prosthetic feet. Iowa Orthop. J. 1988, 8, 95. [Google Scholar] [CrossRef]
- Perry, J.; Boyd, L.A.; Rao, S.S.; Mulroy, S.J. Prosthetic weight acceptance mechanics in transtibial amputees wearing the Single Axis, Seattle Lite, and Flex Foot. IEEE Trans. Rehabil. Eng. 1997, 5, 283–289. [Google Scholar] [CrossRef]
- Perry, J.; Shanfield, S. Efficiency of dynamic elastic response prosthetic feet. J. Rehabil. Res. Dev. 1993, 30, 137–143. [Google Scholar]
- Postema, K.; Hermens, H.J.; De Vries, J.; Koopman, H.F.; Eisma, W. Energy storage and release of prosthetic feet Part 1: Biomechanical analysis related to user benefits. Prosthetics Orthot. Int. 1997, 21, 17–27. [Google Scholar] [CrossRef][Green Version]
- Powers, C.M.; Torburn, L.; Perry, J.; Ayyappa, E. Influence of prosthetic foot design on sound limb loading in adults with unilateral below-knee amputations. Arch. Phys. Med. Rehabil. 1994, 75, 825–829. [Google Scholar] [CrossRef]
- Rao, S.S.; Boyd, L.A.; Mulroy, S.J.; Bontrager, E.L.; Gronley, J.; Perry, J. Segment velocities in normal and transtibial amputees: Prosthetic design implications. IEEE Trans. Rehabil. Eng. 1998, 6, 219–226. [Google Scholar] [CrossRef]
- Schmalz, T.; Blumentritt, S.; Jarasch, R. Energy expenditure and biomechanical characteristics of lower limb amputee gait: The influence of prosthetic alignment and different prosthetic components. Gait Posture 2002, 16, 255–263. [Google Scholar] [CrossRef]
- Snyder, R.D.; Powers, C.M.; Fountain, C.; Perry, J. The effect of five prosthetic feet on the gait and loading of the sound limb in dysvascular below-knee amputees. J. Rehabil. Res. Dev. 1995, 32, 309–315. [Google Scholar]
- Torburn, L.; Perry, J.; Ayyappa, E.; Shanfield, S.L. Below-knee amputee gait with dynamic elastic response prosthetic feet: A pilot study. J. Rehabil. Res. Dev. 1990, 27, 369–384. [Google Scholar] [PubMed]
- Torburn, L.; Powers, C.M.; Guiterrez, R.; Perry, J. Energy expenditure during ambulation in dysvascular and traumatic below-knee amputees: A comparison of five prosthetic feet. J. Rehabil. Res. Dev. 1995, 32, 111. [Google Scholar] [PubMed]
- Wagner, J.; Sienko, S.; Supan, T.; Barth, D. Motion analysis of SACH vs. Flex-Foot in moderately active below-knee amputees. Clin. Prosthet. Orthot. 1987, 11, 55–62. [Google Scholar]
- Mentiplay, B.F.; Banky, M.; Clark, R.A.; Kahn, M.B.; Williams, G. Lower limb angular velocity during walking at various speeds. Gait Posture 2018, 65, 190–196. [Google Scholar] [CrossRef]
- Grimmer, M.; Seyfarth, A. Mimicking human-like leg function in prosthetic limbs. In Neuro-Robotics; Springer: Cham, Switzerland, 2014; pp. 105–155. [Google Scholar]
- Lipfert, S.W. Kinematic and Dynamic Similarities between Walking and Running; Kovač: Hamburg, Germany, 2010. [Google Scholar]
- Dong, D.; Convens, B.; Sun, Y.; Ge, W.; Cherelle, P.; Vanderborght, B. The effects of variable mechanical parameters on peak power and energy consumption of ankle-foot prostheses at different speeds. Adv. Robot. 2018, 32, 1229–1240. [Google Scholar] [CrossRef]
- Samson, W.; Dohin, B.; Desroches, G.; Chaverot, J.L.; Dumas, R.; Cheze, L. Foot mechanics during the first six years of independent walking. J. Biomech. 2011, 44, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Morais Filho, M.C.; Reis, R.A.d.; Kawamura, C.M. Evaluation of ankle and knee movement pattern during maturation of normal gait. Acta Ortop. Bras. 2010, 18, 23–25. [Google Scholar] [CrossRef][Green Version]
- Obrębska, P.; Skubich, J.; Piszczatowski, S. Gender differences in the knee joint loadings during gait. Gait Posture 2020, 79, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.Z.; Stanhope, S.J. Mechanical energy profiles of the combined ankle–foot system in normal gait: Insights for prosthetic designs. Gait Posture 2013, 38, 818–823. [Google Scholar] [CrossRef]
- Arvin, M.; van Dieën, J.H.; Bruijn, S.M. Effects of constrained trunk movement on frontal plane gait kinematics. J. Biomech. 2016, 49, 3085–3089. [Google Scholar] [CrossRef]
- Klute, G.K.; Kallfelz, C.F.; Czerniecki, J.M. Mechanical properties of prosthetic limbs: Adapting to the patient. J. Rehabil. Res. Dev. 2001, 38, 299–307. [Google Scholar] [PubMed]
- Lehmann, J.F. Push-off and propulsion of the body in normal and abnormal gait. Correction by ankle-foot orthoses. Clin. Orthop. Relat. Res. 1993, 97–108. [Google Scholar] [CrossRef]
- Silverman, A.K.; Neptune, R.R. Muscle and prosthesis contributions to amputee walking mechanics: A modeling study. J. Biomech. 2012, 45, 2271–2278. [Google Scholar] [CrossRef]
- Liu, M.Q.; Anderson, F.C.; Pandy, M.G.; Delp, S.L. Muscles that support the body also modulate forward progression during walking. J. Biomech. 2006, 39, 2623–2630. [Google Scholar] [CrossRef]
- Neptune, R.R.; Kautz, S.A.; Zajac, F.E. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. J. Biomech. 2001, 34, 1387–1398. [Google Scholar] [CrossRef]
- Neptune, R.; Zajac, F.; Kautz, S. Muscle force redistributes segmental power for body progression during walking. Gait Posture 2004, 19, 194–205. [Google Scholar] [CrossRef]
- Pandy, M.G.; Lin, Y.C.; Kim, H.J. Muscle coordination of mediolateral balance in normal walking. J. Biomech. 2010, 43, 2055–2064. [Google Scholar] [CrossRef] [PubMed]
- Zajac, F.E.; Neptune, R.R.; Kautz, S.A. Biomechanics and muscle coordination of human walking: Part II: Lessons from dynamical simulations and clinical implications. Gait Posture 2003, 17, 1–17. [Google Scholar] [CrossRef]
- Hafner, B.J.; Sanders, J.E.; Czerniecki, J.; Fergason, J. Energy storage and return prostheses: Does patient perception correlate with biomechanical analysis? Clin. Biomech. 2002, 17, 325–344. [Google Scholar] [CrossRef]
- Kulkarni, J.; Gaine, W.; Buckley, J.; Rankine, J.; Adams, J. Chronic low back pain in traumatic lower limb amputees. Clin. Rehabil. 2005, 19, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Arya, A.; Lees, A.; Nerula, H.; Klenerman, L. A biomechanical comparison of the SACH, Seattle and Jaipur feet using ground reaction forces. Prosthetics Orthot. Int. 1995, 19, 37–45. [Google Scholar] [CrossRef]
- Nolan, L.; Wit, A.; Dudziñski, K.; Lees, A.; Lake, M.; Wychowañski, M. Adjustments in gait symmetry with walking speed in trans-femoral and trans-tibial amputees. Gait Posture 2003, 17, 142–151. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Martin, P.E. Lower extremity kinematic and kinetic adaptations in unilateral below-knee amputees during walking. Gait Posture 1997, 6, 126–136. [Google Scholar] [CrossRef]





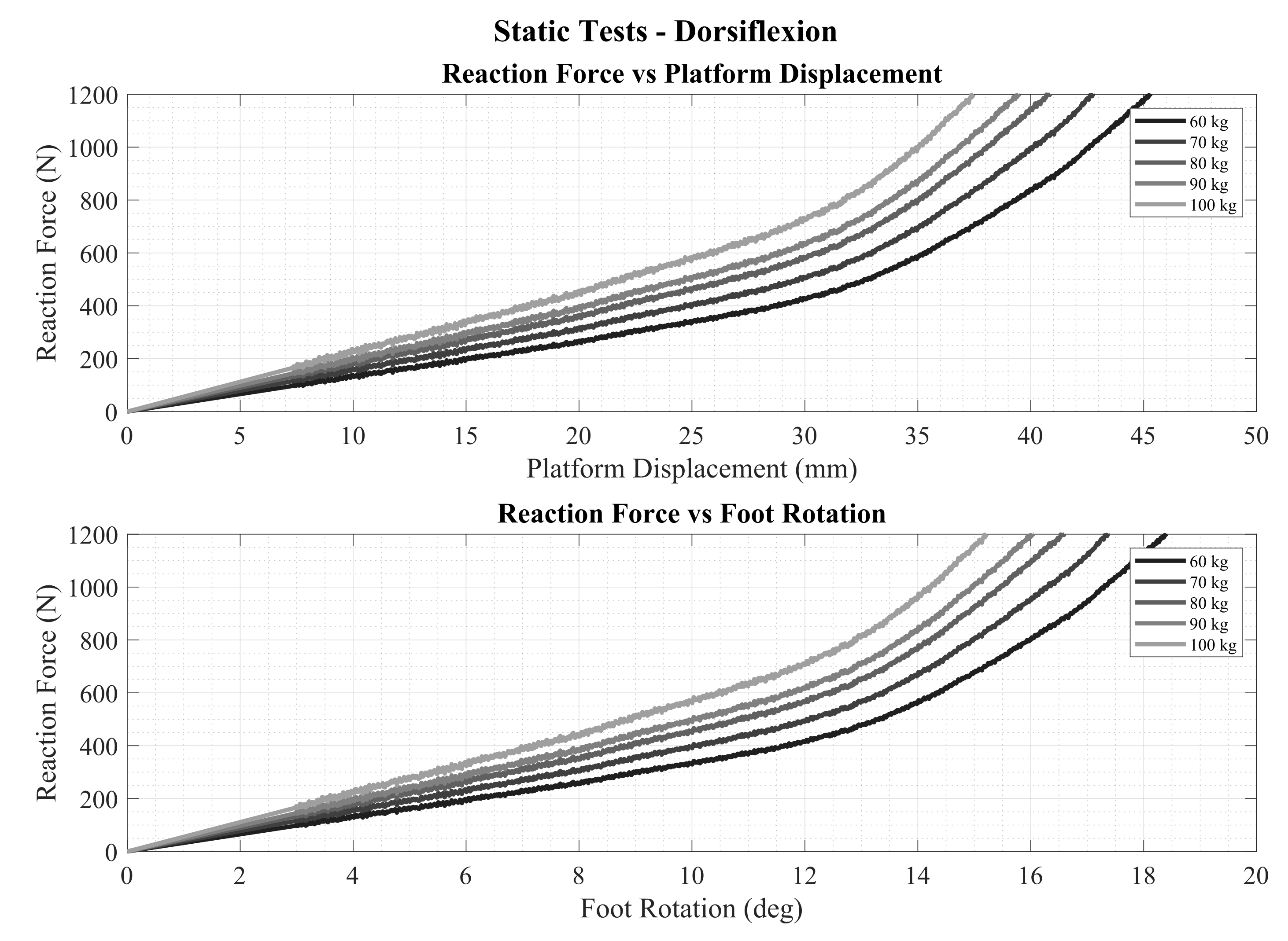


| Heel Load (Plantarflexion) | Toe Load (Dorsiflexion) | |||
|---|---|---|---|---|
| Weight Categories | 95% | 130% | 95% | 108% |
| 60 kg | 559 N | 765 N | 559 N | 636 N |
| 70 kg | 652 N | 893 N | 652 N | 742 N |
| 80 kg | 746 N | 1020 N | 746 N | 848 N |
| 90 kg | 839 N | 1148 N | 839 N | 954 N |
| 100 kg | 932 N | 1275 N | 932 N | 1059 N |
| Participant 1 | Participant 2 | Participant 3 | |
|---|---|---|---|
| Age (years) | 63 | 46 | 61 |
| Gender | M | M | M |
| Years of amputation (years) | 13 | 14 | 10 |
| Height (cm) | 171 | 184 | 181 |
| Weight with prosthesis (kg) | 103.3 | 80.6 | 73.3 |
| Weight of own prosthesis (kg) | 3.7 | 3.1 | 4 |
| Leg length (cm) | 78 | 84 | 86 |
| Prosthetic knee | Genium | C-Leg 4 | Rheo Knee |
| Prosthetic foot | Trias | Trias | Proprio Foot |
| MyFlex- tested | 90, 100 kg | 70–90 kg | 60–80 kg |
| K-Level | K4 | K4 | K4 |
| Weight Categories | |||||
|---|---|---|---|---|---|
| 60 kg | 70 kg | 80 kg | 90 kg | 100 kg | |
| Reaction force at 108% BW (N) | 636 | 742 | 848 | 954 | 1059 |
| Platform displ. at 108% BW (mm) | 36.04 | 35.83 | 35.79 | 36.18 | 35.79 |
| Rotation at 108% BW () | 14.64 | 14.55 | 14.54 | 14.69 | 14.54 |
| Stored energy at 108% BW (J) | 9.57 | 11.20 | 12.84 | 14.36 | 16.05 |
| Normalized stored energy at 108% BW (J/kg) | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Maximum Ground Reaction Forces | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 1088 N | 37 N | 809 N | 6 N | 820 N | 31 N |
| Healthy leg, MyLeg prosthesis | 1078 N | 27 N | 824 N | 14 N | 872 N | 30 N |
| Prosthetic leg, own prosthesis | 993 N | 18 N | 808 N | 9 N | 760 N | 50 N |
| Prosthetic leg, MyLeg prosthesis | 1014 N | 19 N | 814 N | 9 N | 751 N | 25 N |
| Maximum Ground Reaction Forces/Body Weight/9.81 m/s | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 107% | 4% | 103% | 1% | 114% | 4% |
| Healthy leg, MyLeg prosthesis | 106% | 3% | 104% | 2% | 121% | 4% |
| Prosthetic leg, own prosthesis | 98% | 2% | 102% | 1% | 106% | 7% |
| Prosthetic leg, MyLeg prosthesis | 100% | 2% | 103% | 1% | 104% | 3% |
| Prosthetic Leg Ground Reaction Forces/Healthy Leg Ground Reaction Forces | ||||||
| Prosthesis used | mean | std | mean | std | mean | std |
| Own prosthesis | 91.4% | 3.7% | 99.9% | 1.4% | 92.8% | 7.2% |
| MyFlex- | 94.0% | 3.0% | 98.8% | 1.6% | 86.3% | 4.5% |
| Ground Reaction Forces Using MyFlex-/Ground Reaction Forces Using their Own Prosthesis | ||||||
| Leg side | mean | std | mean | std | mean | std |
| Healthy leg | 99.2% | 3.9% | 101.9% | 1.8% | 106.4% | 4.7% |
| Prosthetic leg | 102.1% | 2.9% | 100.7% | 1.9% | 99.1% | 6.8% |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Plantarflexion at Toe Strike | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 13.0 | 1.2 | 5.8 | 1.0 | 8.0 | 1.0 |
| Healthy leg, MyLeg prosthesis | 8.8 | 1.4 | 5.3 | 1.1 | 9.1 | 1.8 |
| Prosthetic leg, own prosthesis | 6.3 | 0.7 | 1.8 | 0.2 | 6.0 | 0.6 |
| Prosthetic leg, MyLeg prosthesis | 2.1 | 0.1 | 0.5 | 0.1 | 2.4 | 0.4 |
| Prosthetic Leg Plantarflexion–Healthy Leg Plantarflexion | ||||||
| Prothesis used | mean | std | mean | std | mean | std |
| Own prosthesis | −6.8 | 1.2 | −3.9 | 1.0 | −2.0 | 1.3 |
| MyFlex- | −6.7 | 1.5 | −4.8 | 1.1 | −6.7 | 2.0 |
| Plantarflexion Using MyFlex-–Plantarflexion Using their Own Prosthesis | ||||||
| Leg side used | mean | std | mean | std | mean | std |
| Healthy Leg | −4.3 | 0.4 | −0.4 | 1.4 | +1.0 | 1.9 |
| Prosthetic Leg | −4.2 | 0.7 | −1.3 | 0.3 | −3.6 | 0.7 |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Dorsiflexion at Heel-Off | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | −0.8 | 1.7 | 5.0 | 1.8 | −1.8 | 2.9 |
| Healthy leg, MyLeg prosthesis | 4.7 | 1.4 | 4.6 | 1.9 | −3.7 | 2.0 |
| Prosthetic leg, own prosthesis | 10.2 | 0.4 | 6.9 | 0.2 | 8.3 | 0.8 |
| Prosthetic leg, MyLeg prosthesis | 11.9 | 0.3 | 10.2 | 0.3 | 14.0 | 0.5 |
| Prosthetic Leg Dorsiflexion–Healthy Leg Dorsiflexion | ||||||
| Prosthesis used | mean | std | mean | std | mean | std |
| Own prosthesis | +11.0 | 1.7 | +1.8 | 1.7 | +10.0 | 3.0 |
| MyFlex- | +7.1 | 1.5 | +5.6 | 2.0 | +17.7 | 2.0 |
| Dorsiflexion Using MyFlex-–Dorsiflexion Using their Own Prosthesis | ||||||
| Leg side | mean | std | mean | std | mean | std |
| Healthy Leg | +5.5 | 2.3 | −0.5 | 2.8 | −2.0 | 2.6 |
| Prosthetic Leg | +1.6 | 0.5 | +3.3 | 0.4 | +5.7 | 1.0 |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Step Length | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 0.534 m | 0.014 m | 0.357 m | 0.027 m | 0.554 m | 0.046 m |
| Healthy leg, MyFlex- | 0.535 m | 0.015 m | 0.358 m | 0.020 m | 0.562 m | 0.018 m |
| Prosthetic leg, own prosthesis | 0.478 m | 0.022 m | 0.256 m | 0.019 m | 0.646 m | 0.030 m |
| Prosthetic leg, MyFlex- | 0.471 m | 0.015 m | 0.242 m | 0.018 m | 0.624 m | 0.016 m |
| Prosthetic Leg Ankle Range of Motion/Healthy Leg Step Length | ||||||
| Prosthesis used | mean | std | mean | std | mean | std |
| Own prosthesis | 89.3% | 4.8% | 72.0% | 7.9% | 117.9% | 17.3% |
| MyFlex- | 88.1% | 3.2% | 67.7% | 6.6% | 111.2% | 4.7% |
| Step Length Using MyFlex-/Using their Own Prosthesis | ||||||
| Leg side | mean | std | mean | std | mean | std |
| Healthy leg | 100.2% | 3.7% | 100.9% | 10.0% | 102.5% | 15.3% |
| Prosthetic leg | 99.0% | 5.6% | 94.9% | 9.5% | 96.7% | 4.6% |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Toe Strike | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 10.3% | 0.6% | 9.3% | 1.9% | 8.5% | 0.6% |
| Healthy leg, MyFlex- | 8.6% | 0.5% | 8.0% | 1.2% | 8.0% | 0.5% |
| Prosthetic leg, own prosthesis | 8.4% | 0.8% | 8.4% | 0.9% | 11.2% | 0.7% |
| Prosthetic leg, MyFlex- | 9.3% | 0.5% | 8.6% | 1.5% | 9.6% | 0.9% |
| Heel-Off | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 48.5% | 1.8% | 61.4% | 2.1% | 51.4% | 1.8% |
| Healthy leg, MyFlex- | 51.0% | 1.3% | 66.1% | 1.7% | 54.2% | 1.0% |
| Prosthetic leg, own prosthesis | 46.9% | 0.9% | 48.3% | 1.6% | 45.7% | 1.0% |
| Prosthetic leg, MyFlex- | 49.4% | 1.0% | 47.4% | 1.6% | 43.9% | 0.9% |
| Toe-Off | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 74.3% | 7.4% | 77.6% | 1.8% | 67.1% | 1.6% |
| Healthy leg, MyFlex- | 73.6% | 2.2% | 79.1% | 2.0% | 70.6% | 5.0% |
| Prosthetic leg, own prosthesis | 63.3% | 1.0% | 69.2% | 1.4% | 61.0% | 7.3% |
| Prosthetic leg, MyFlex- | 64.2% | 1.3% | 68.6% | 1.7% | 58.4% | 1.0% |
| Participant 1 | Participant 2 | Participant 3 | ||||
|---|---|---|---|---|---|---|
| Early Stance Duration | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 10.3% | 0.6% | 9.3% | 1.9% | 8.5% | 0.6% |
| Healthy leg, MyFlex- | 8.6% | 0.5% | 8.0% | 1.2% | 8.0% | 0.5% |
| Prosthetic leg, own prosthesis | 8.4% | 0.8% | 8.4% | 0.9% | 11.2% | 0.7% |
| Prosthetic leg, MyFlex- | 9.3% | 0.5% | 8.6% | 1.5% | 9.6% | 0.9% |
| Mid Stance Duration | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 38.2% | 1.8% | 52.1% | 2.9% | 42.3% | 3.1% |
| Healthy leg, MyFlex- | 42.4% | 1.4% | 58.1% | 2.1% | 45.6% | 3.1% |
| Prosthetic leg, own prosthesis | 38.5% | 1.1% | 39.9% | 1.8% | 34.5% | 1.4% |
| Prosthetic leg, MyFlex- | 40.1% | 0.9% | 38.9% | 2.2% | 34.3% | 1.0% |
| Late Stance Duration | ||||||
| Leg and prosthesis used | mean | std | mean | std | mean | std |
| Healthy leg, own prosthesis | 25.8% | 6.6% | 16.2% | 1.7% | 15.7% | 1.4% |
| Healthy leg, MyFlex- | 22.6% | 1.9% | 13.6% | 1.8% | 16.4% | 5.0% |
| Prosthetic leg, own prosthesis | 16.4% | 0.8% | 20.9% | 1.4% | 15.4% | 7.2% |
| Prosthetic leg, MyFlex- | 14.8% | 0.6% | 21.2% | 1.0% | 14.5% | 0.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabucol, J.; Kooiman, V.G.M.; Leopaldi, M.; Brugo, T.M.; Leijendekkers, R.A.; Tagliabue, G.; Raveendranathan, V.; Sotgiu, E.; Benincasa, P.; Oddsson, M.; et al. The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Appl. Sci. 2022, 12, 4575. https://doi.org/10.3390/app12094575
Tabucol J, Kooiman VGM, Leopaldi M, Brugo TM, Leijendekkers RA, Tagliabue G, Raveendranathan V, Sotgiu E, Benincasa P, Oddsson M, et al. The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Applied Sciences. 2022; 12(9):4575. https://doi.org/10.3390/app12094575
Chicago/Turabian StyleTabucol, Johnnidel, Vera Geertruida Maria Kooiman, Marco Leopaldi, Tommaso Maria Brugo, Ruud Adrianus Leijendekkers, Gregorio Tagliabue, Vishal Raveendranathan, Eleonora Sotgiu, Pietro Benincasa, Magnus Oddsson, and et al. 2022. "The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint" Applied Sciences 12, no. 9: 4575. https://doi.org/10.3390/app12094575
APA StyleTabucol, J., Kooiman, V. G. M., Leopaldi, M., Brugo, T. M., Leijendekkers, R. A., Tagliabue, G., Raveendranathan, V., Sotgiu, E., Benincasa, P., Oddsson, M., Verdonschot, N., Carloni, R., & Zucchelli, A. (2022). The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Applied Sciences, 12(9), 4575. https://doi.org/10.3390/app12094575








