Thickness-Related Fault Diagnosis of Steel Strip Based on W-KPLS Method Considering Mechanism Weight Optimization
Abstract
:1. Introduction
2. Monitoring Model Based on Statistical Process Control
2.1. Offline Modeling Based on K-PLS Algorithm
- (1)
- Collect and standardize training sample data X and Y, initialize and set .
- (2)
- The projection direction of the process variable is calculated according to the given score vector of the quality matrix; the latent score vector is obtained; then invert the latent score vector of the quality matrix and iterate until the score vector converges.
- (3)
- Calculate the residual matrix of the process variable and quality variable.
- (4)
- The residual matrix is used to extract the next set of latent score vectors until the preset number of principal components is met: . The final linear data relationship model is as follows:
- (1)
- Initialize as any column of mass matrix and initialize .
- (2)
- The mapped input score is converted to an inner product by the kernel function:
- (3)
- Normalization processing: .
- (4)
- Find the latent variable of the output variable: , .
- (5)
- Normalization processing: .
- (6)
- Repeat steps (2)~(5) until converges.
- (7)
- Calculate the residual matrix:
- (8)
- Return to Step (2) and continue to extract the latent score vector until: .
2.2. Online Monitoring and Diagnosis
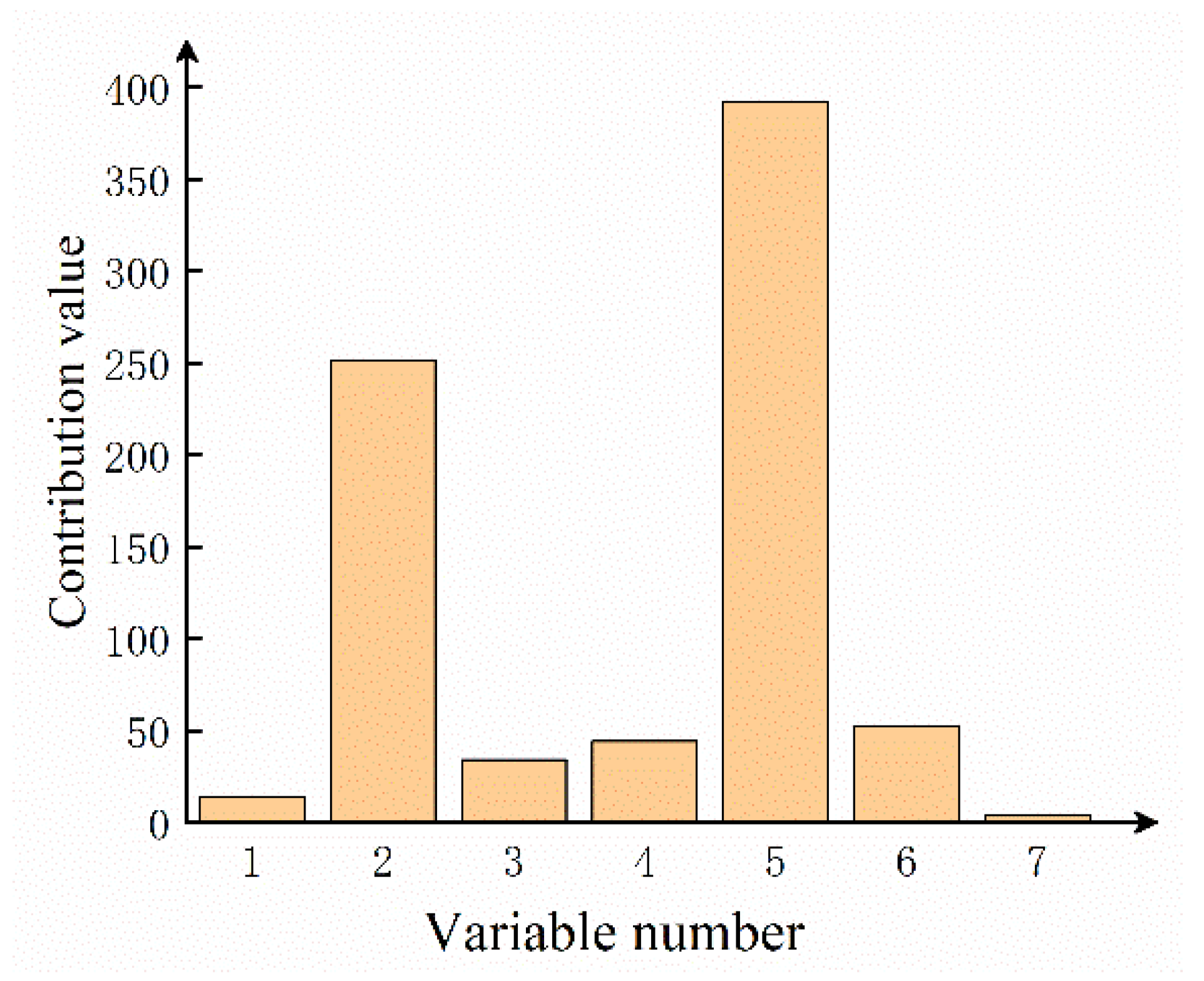
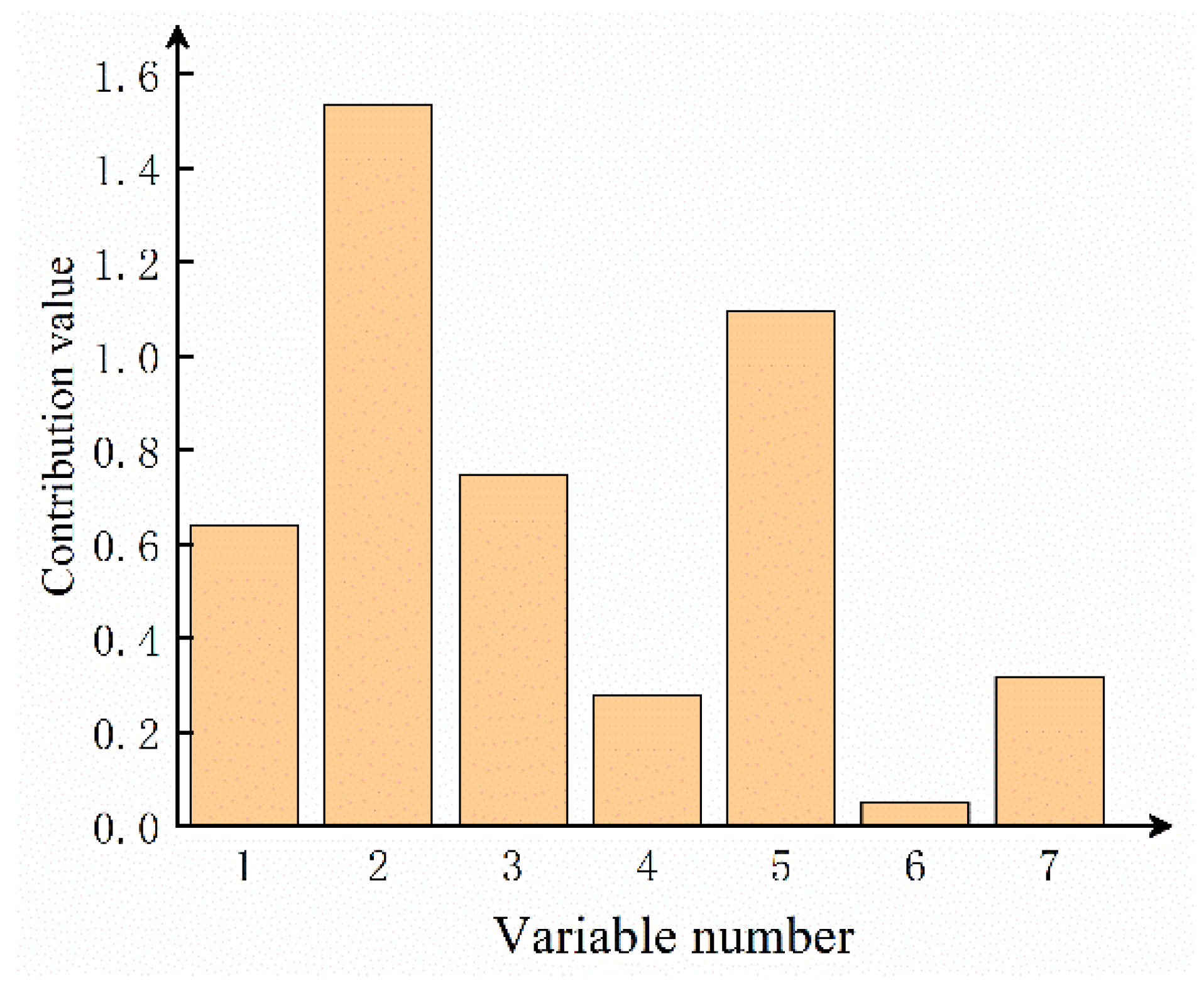
2.3. Fault Diagnosis Based on Nonlinear Contribution Plot
3. Thickness Control and Static Comprehensive Analysis of Rolling Process
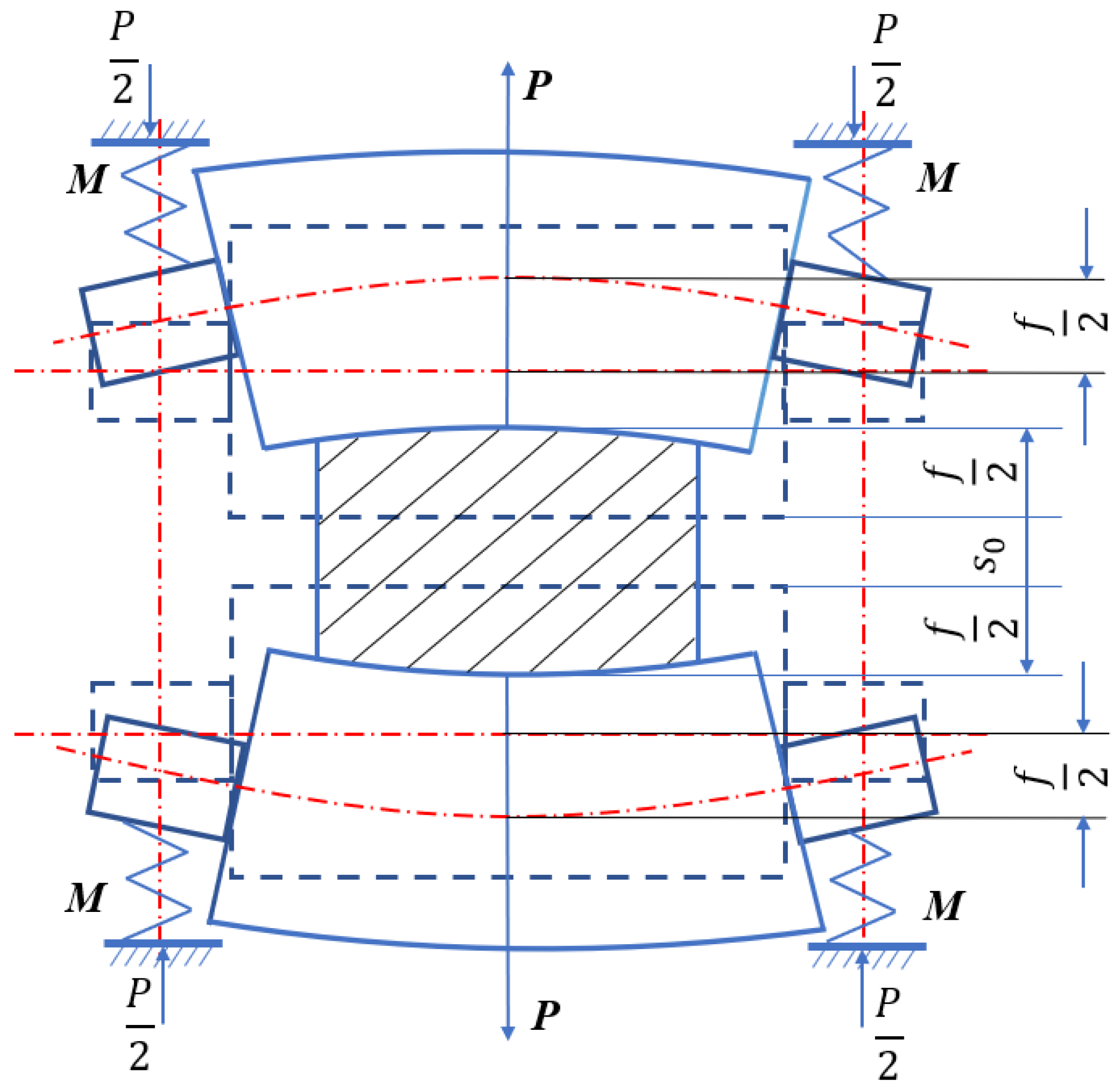
3.1. Mechanism Analysis of Aluminum Alloy Strip Rolling Process
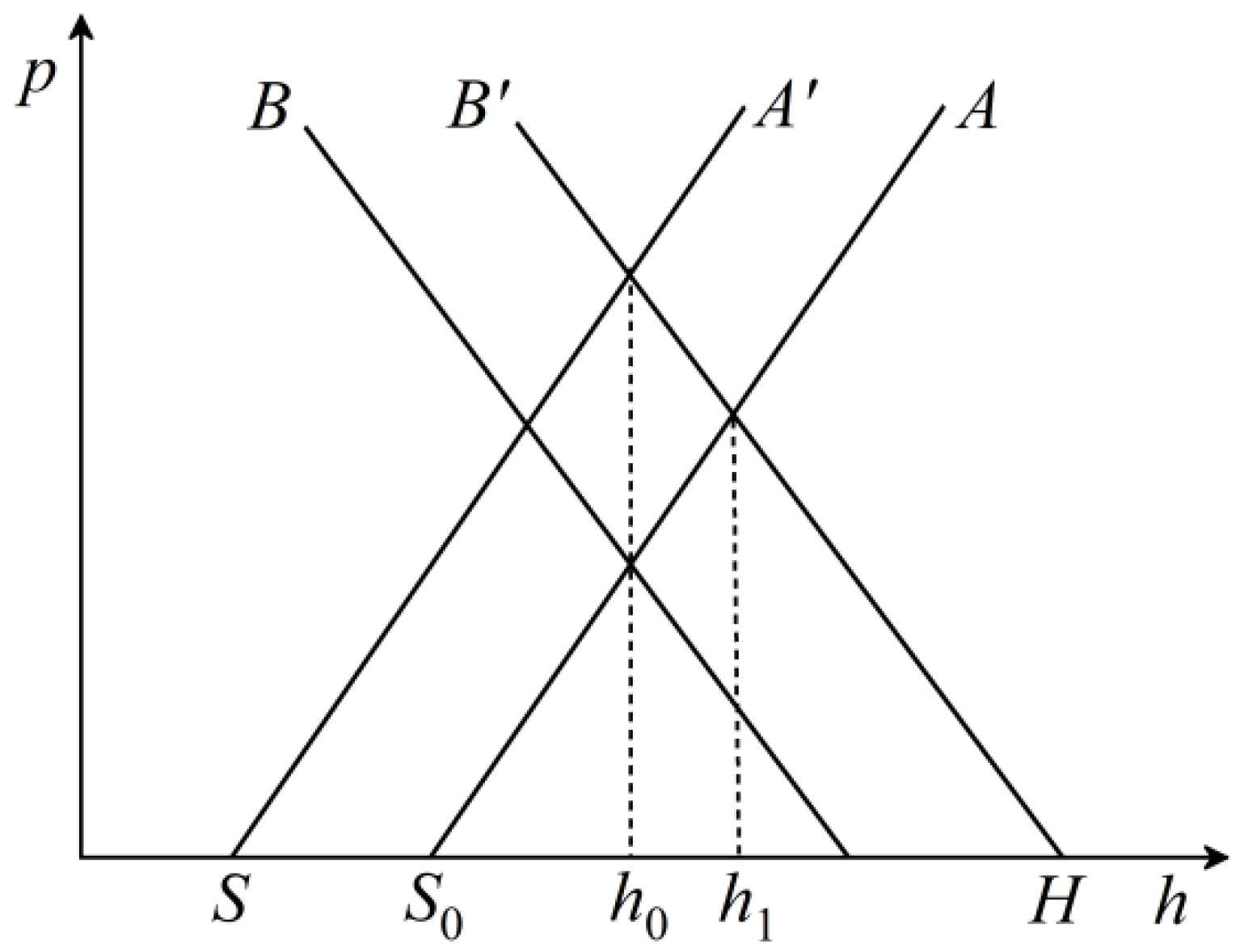
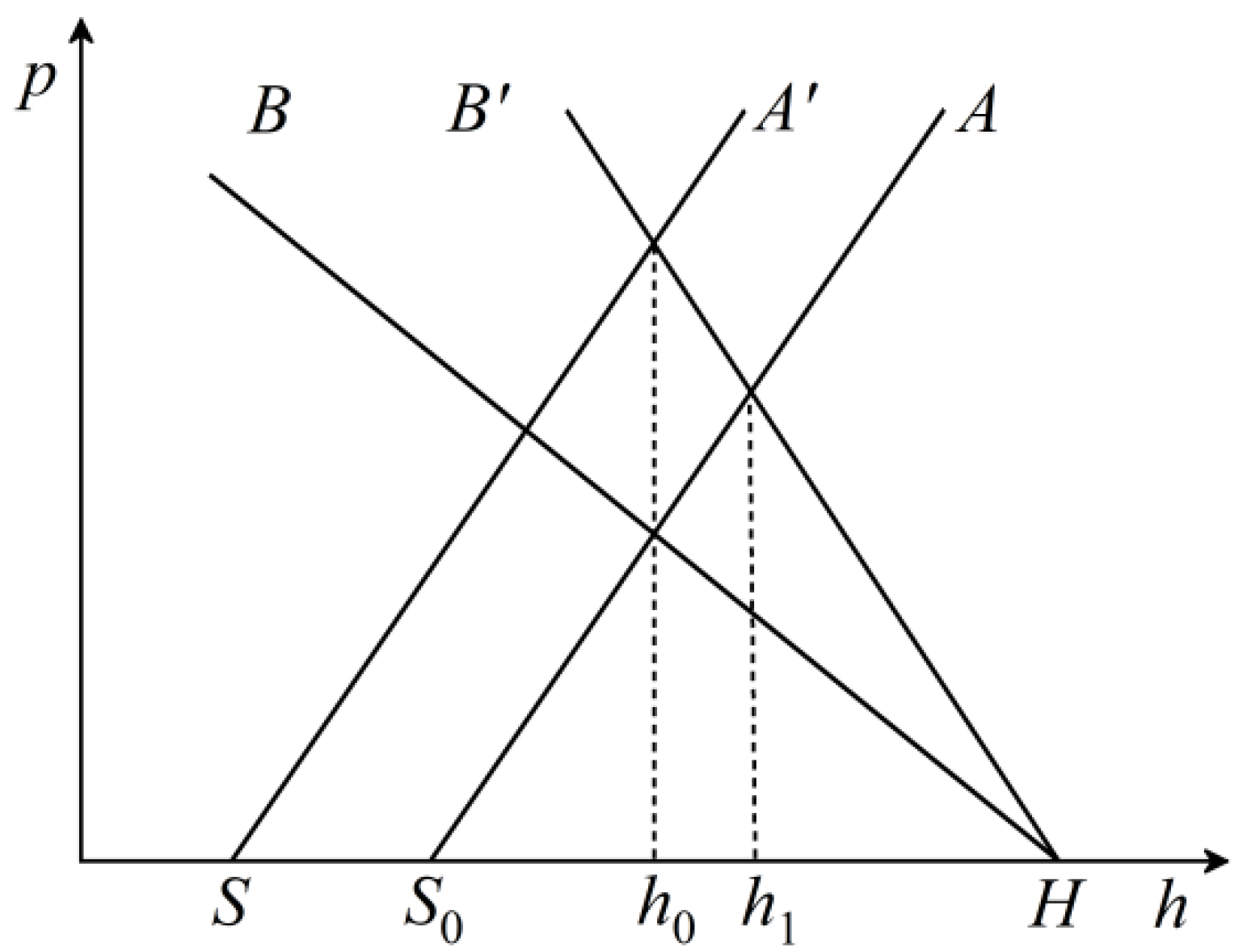
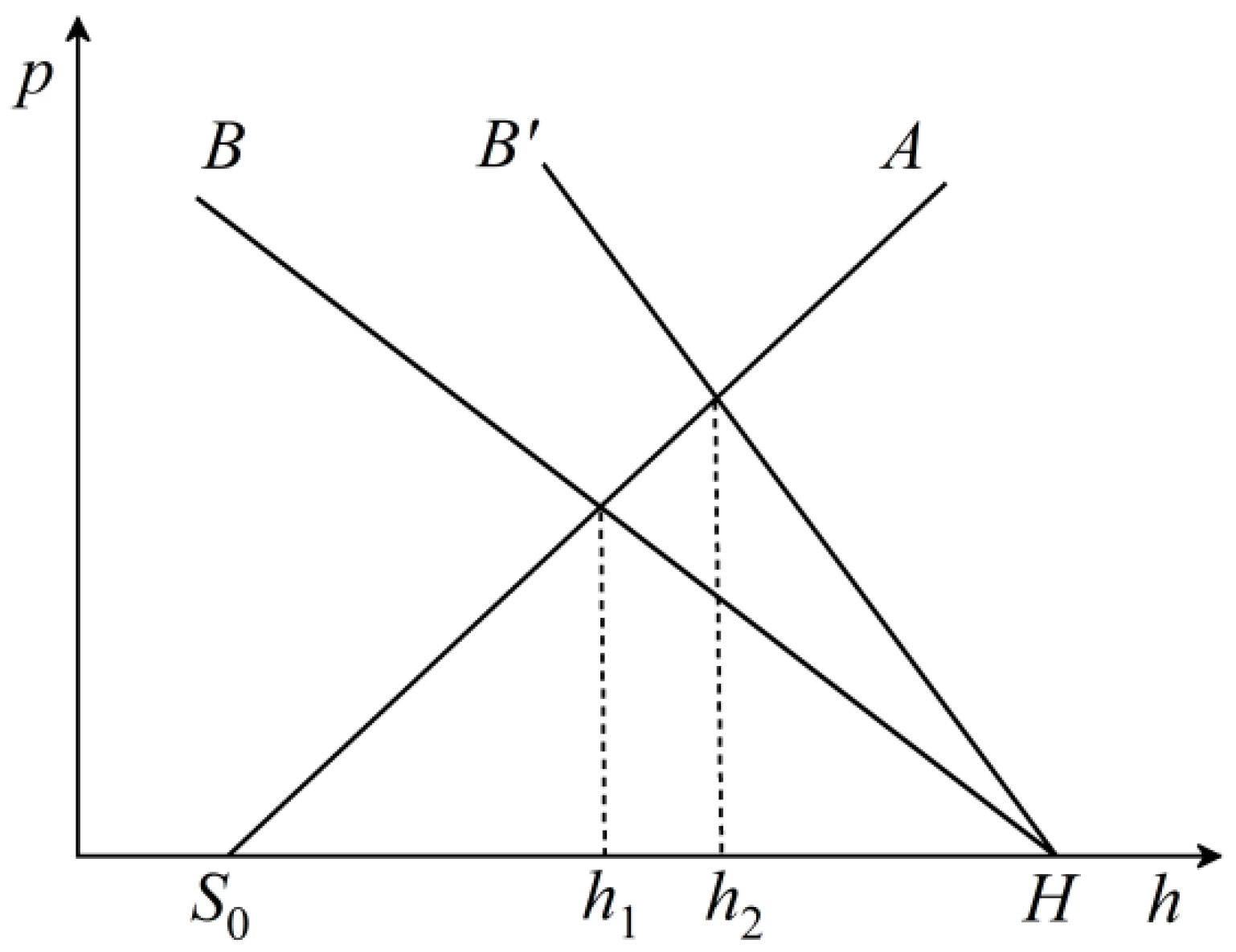
3.2. Static Synthesis Analysis of Steady-State Rolling
4. Monitoring Method Based on Influence Weight Optimization
4.1. Influence Coefficient Calculation of Data Set
4.2. KPLS Monitoring Method Based on Influence Weight W Optimization
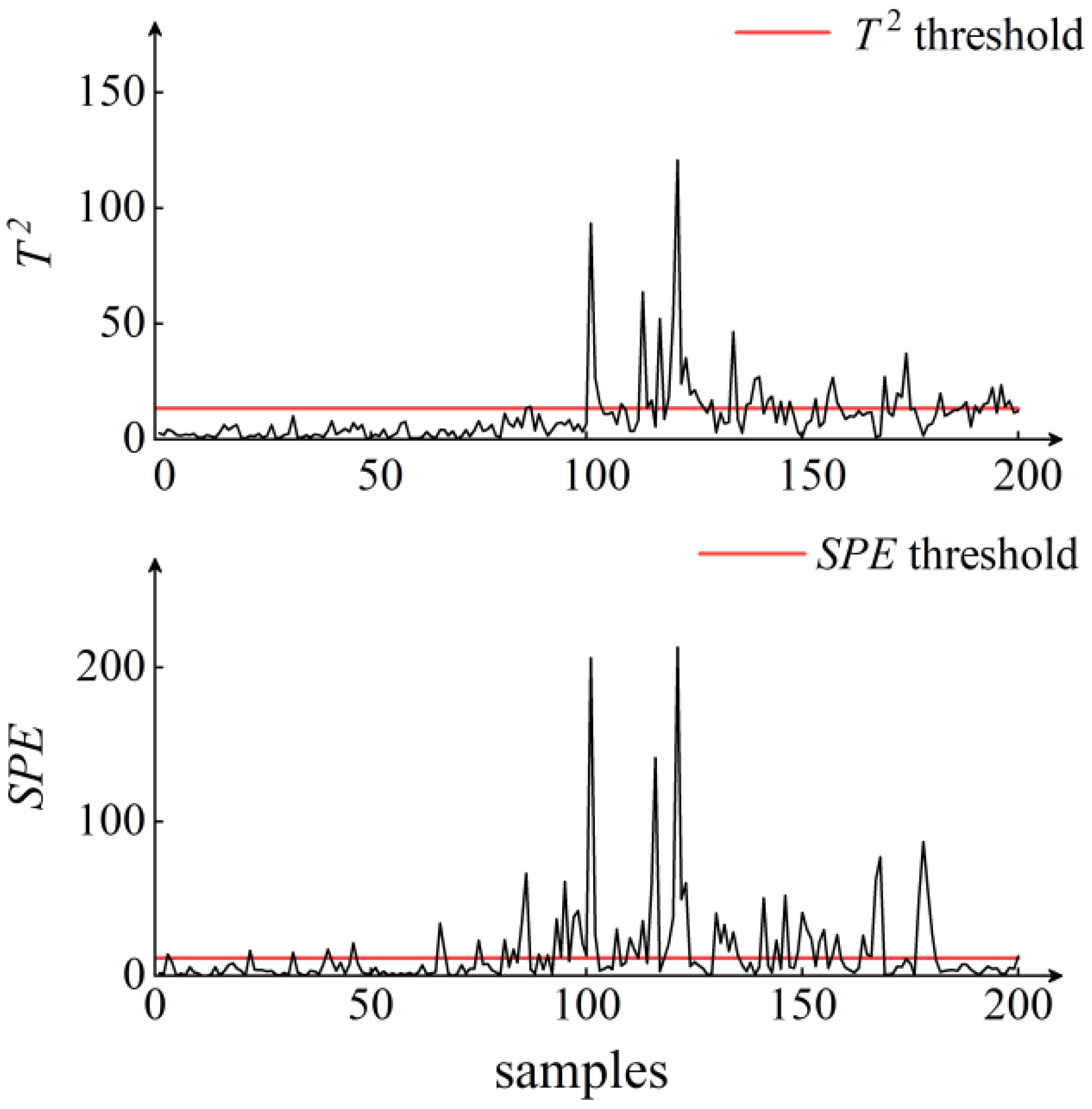
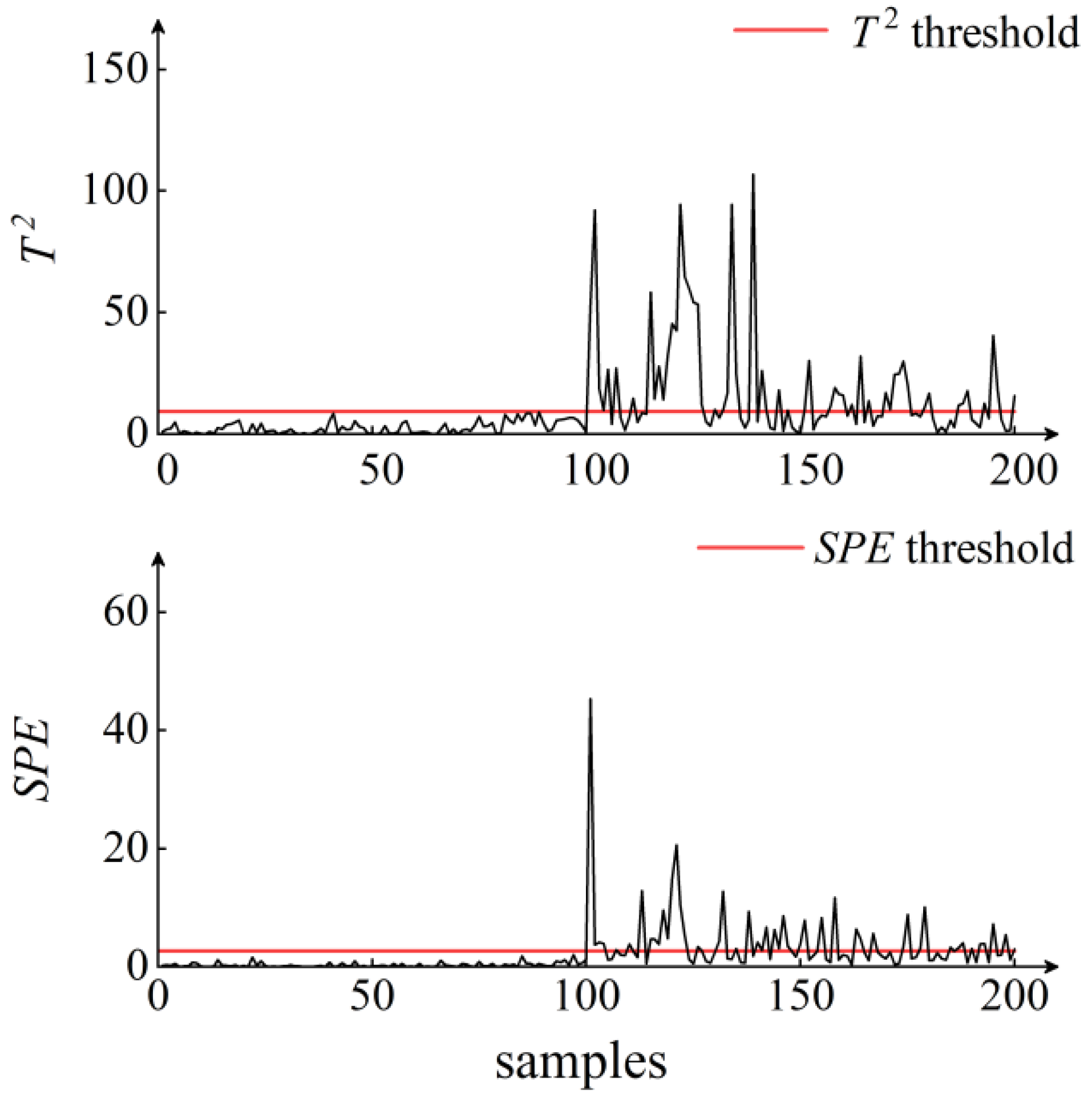
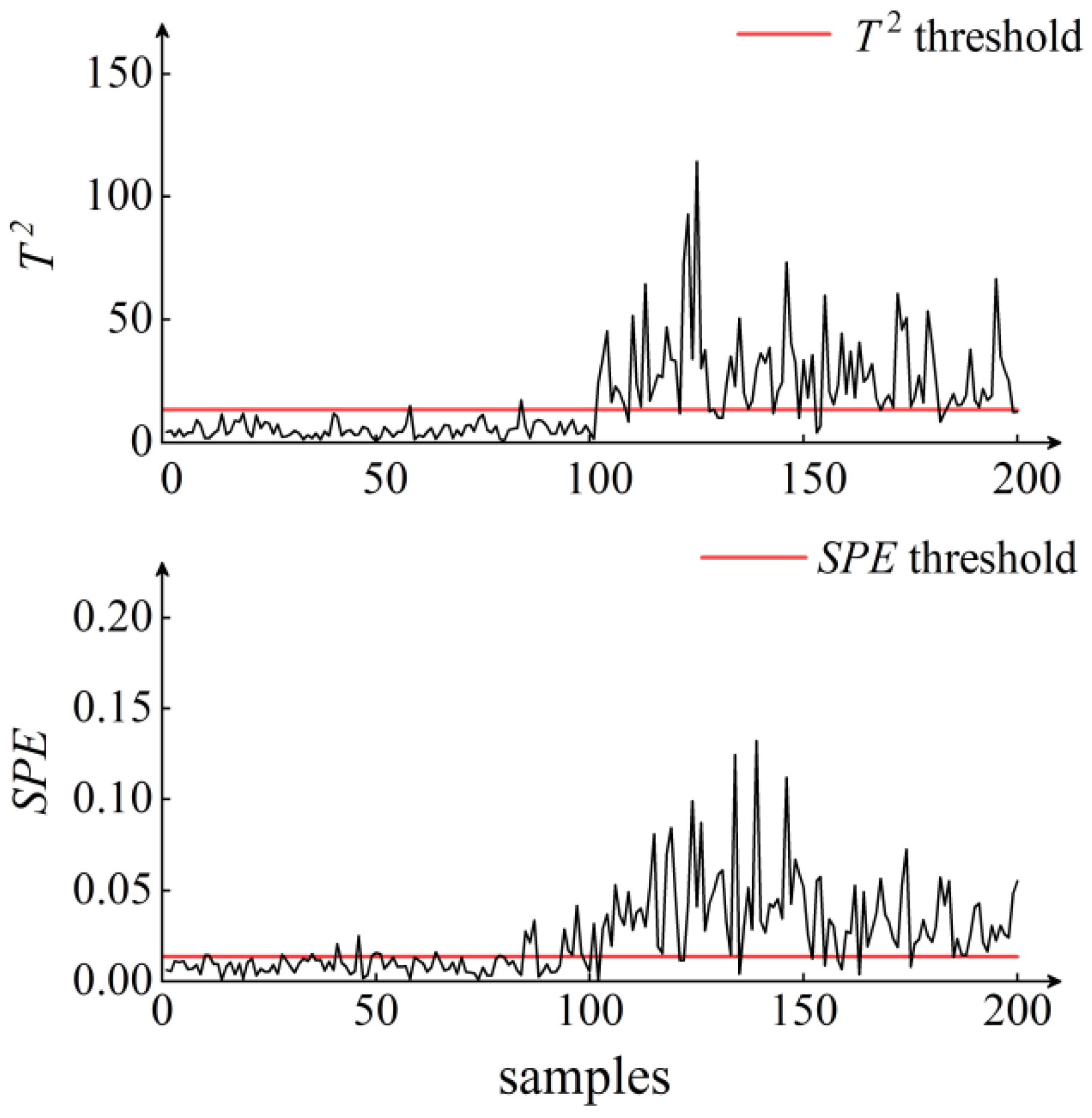
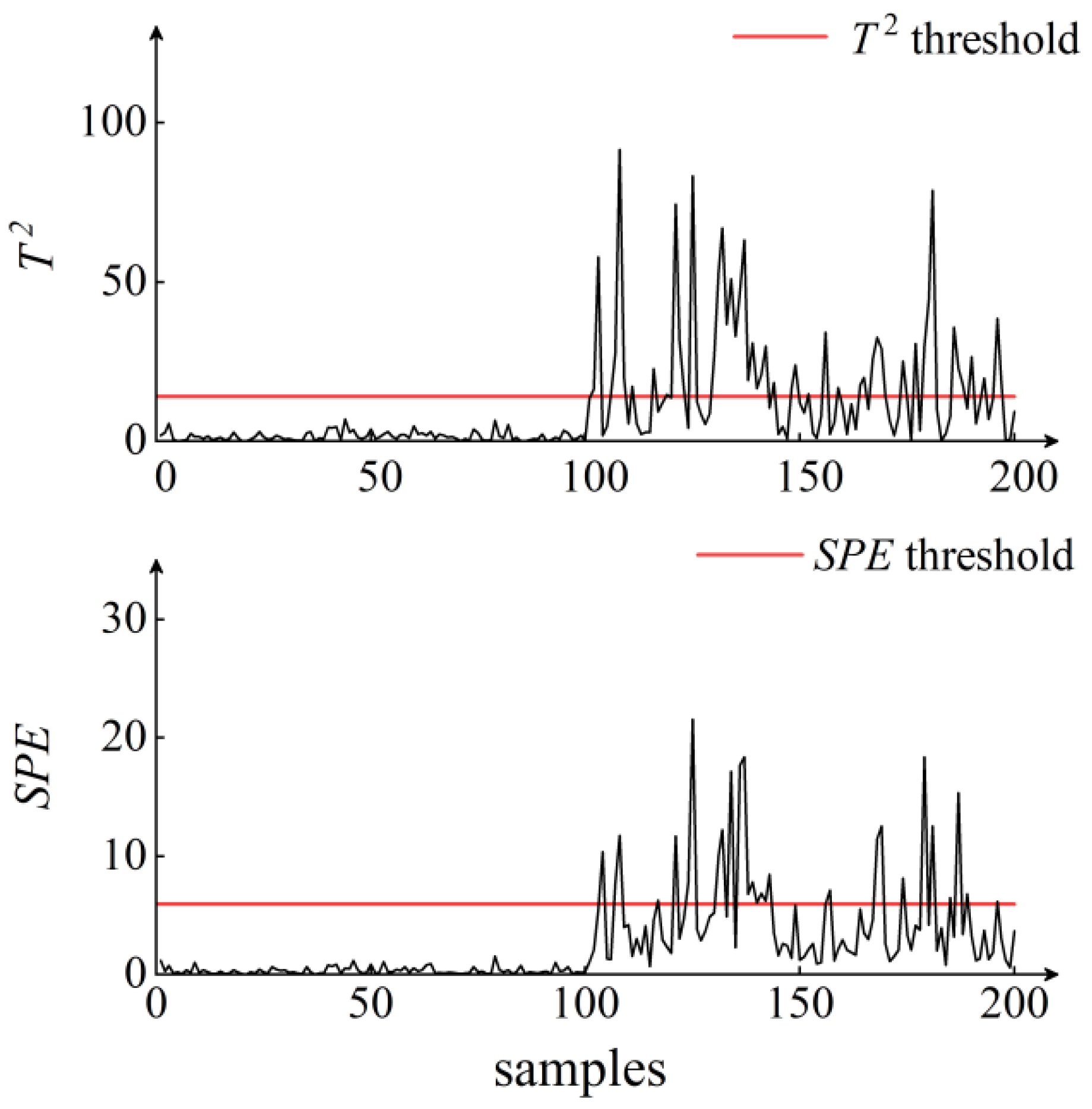
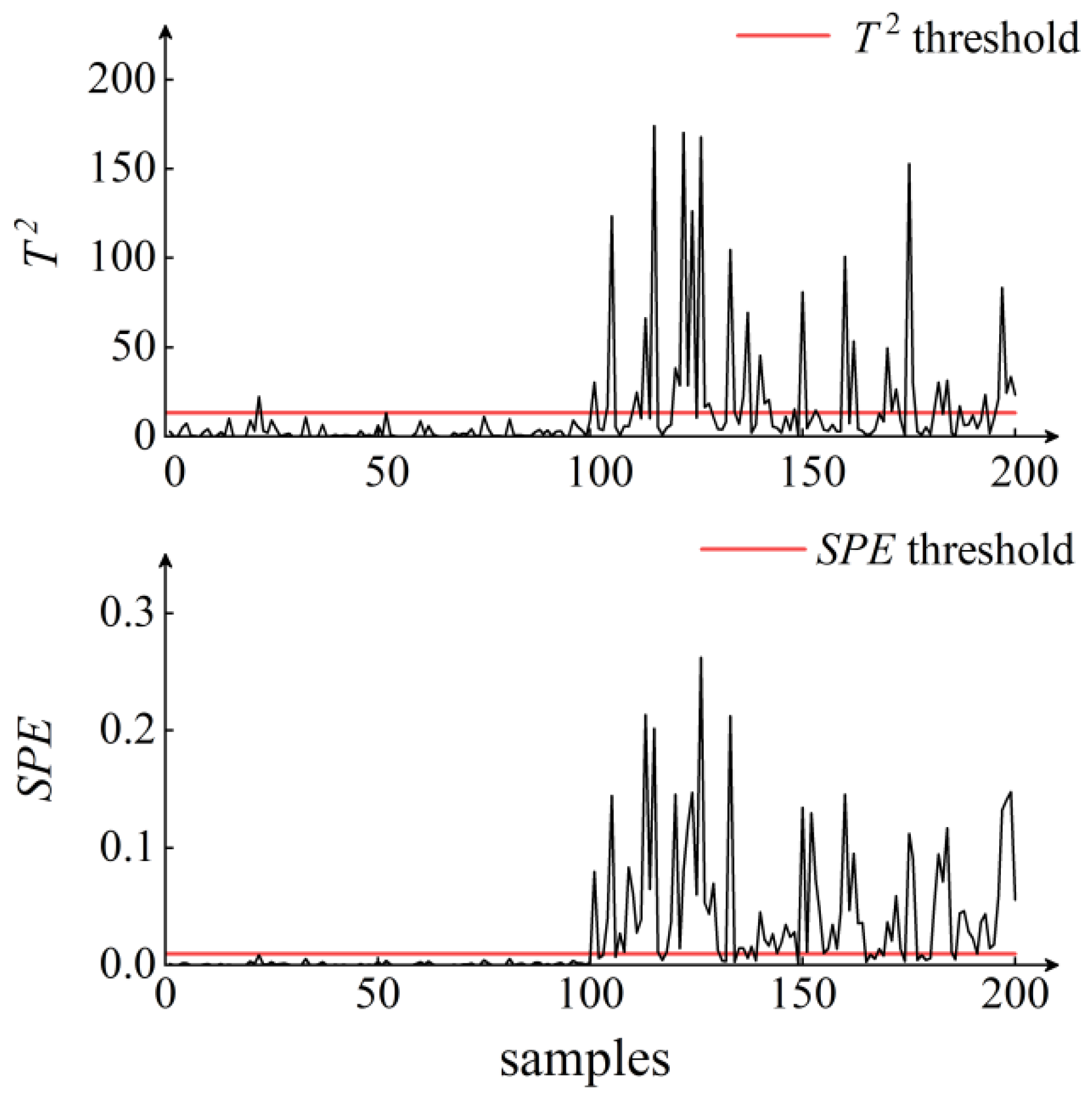
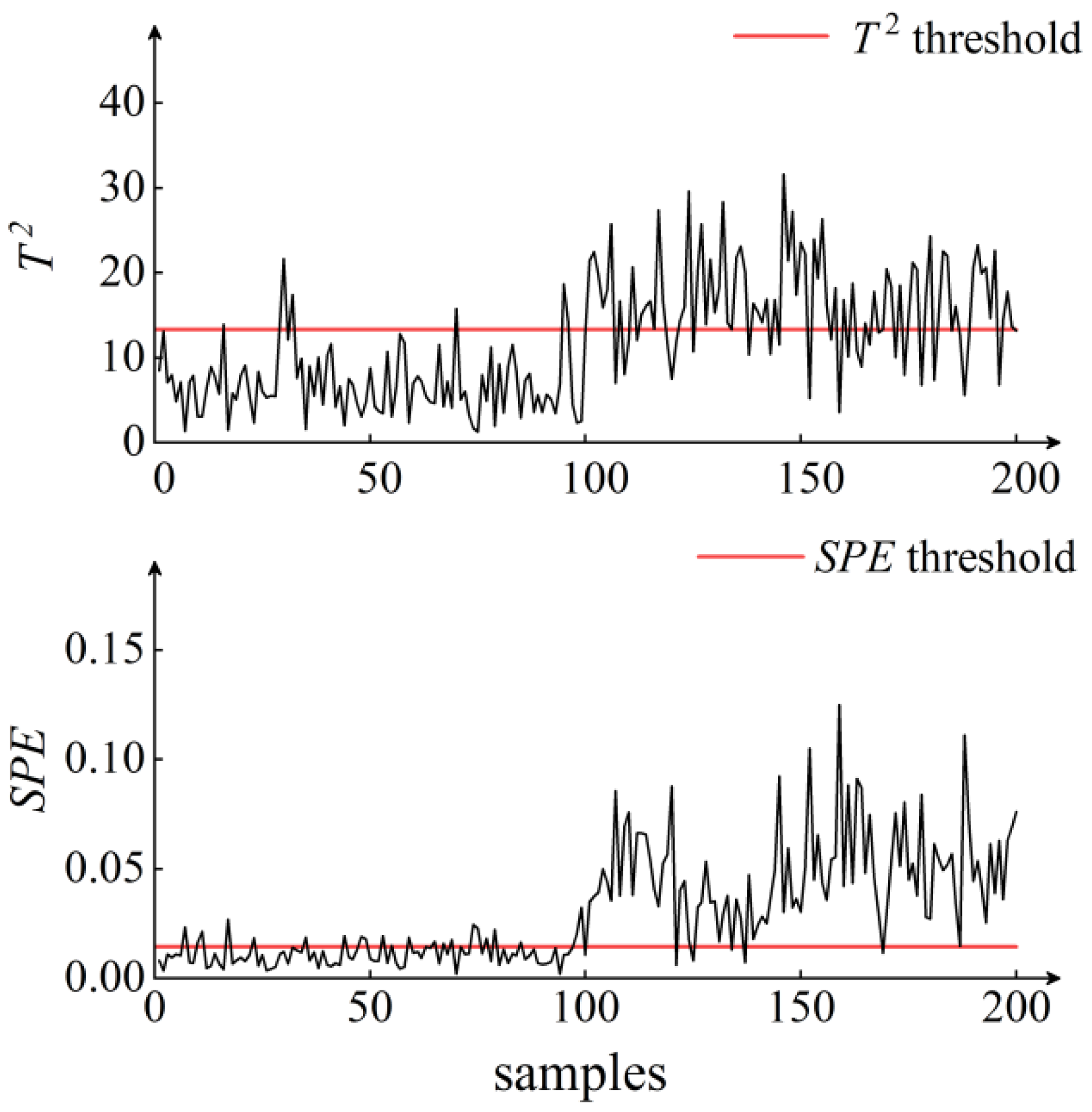
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, J.; He, A.; Dong, G.; Chen, B.; Chen, J. Whole process quality management and control system of iron and steel based on industrial interconnection. Metall. Ind. Autom. 2020, 44, 8–16. (In Chinese) [Google Scholar]
- Ma, L.; Dong, J.; Peng, K. A practical propagation path identification scheme for quality-related faults based on nonlinear dynamic latent variable model and partitioned Bayesian network. J. Frankl. Inst. 2018, 355, 7570–7594. [Google Scholar] [CrossRef]
- Si, Y.; Wang, Y.; Zhou, D. Key-Performance-Indicator-Related Process Monitoring Based on Improved Kernel Partial Least Squares. IEEE Trans. Ind. Electron. 2021, 68, 2626–2636. [Google Scholar] [CrossRef]
- Lan, T.; Tong, C.; Shi, X.; Luo, L. Dynamic statistical process monitoring based on generalized canonical variate analysis. J. Taiwan Inst. Chem. Eng. 2020, 112, 78–86. [Google Scholar] [CrossRef]
- Said, M.; Taouali, O. Improved Dynamic Optimized Kernel Partial Least Squares for Nonlinear Process Fault Detection. Math. Probl. Eng. 2021, 2021, 6677944. [Google Scholar] [CrossRef]
- Wang, G.; Li, J.D.; Sun, C.Y.; Jiao, J.F. Least Squares and Contribution Plot Based Approach for Quality-Related Process Monitoring. IEEE Access 2018, 6, 54158–54166. [Google Scholar] [CrossRef]
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Yan, P. Review on development of digital and intelligent metallurgical rolling equipment technology. J. Yanshan Univ. 2020, 44, 218–237. (In Chinese) [Google Scholar]
- Hu, Z.; Wei, Z.; Sun, H.; Yang, J.; Wei, L. Optimization of Metal Rolling Control Using Soft Computing Approaches: A Review. Arch. Comput. Methods Eng. 2021, 28, 405–421. [Google Scholar] [CrossRef]
- Kong, X.; Li, Q.; An, Q.; Xie, J. Quality-related fault detection based on the score reconstruction associated with partial least squares. Control. Theory Appl. 2020, 37, 2321–2332. (In Chinese) [Google Scholar]
- Jing, F.; Feng, Y.; Zhang, Y.; Li, W. Diagnostic study on based thickness deviation of hot rolled strip based on optimized RT-PLS. J. Iron Steel Res. 2021, 33, 593–599. [Google Scholar] [CrossRef]
- Zhang, K.; Hao, H.; Chen, Z.; Ding, S.X.; Peng, K. A comparison and evaluation of key performance indicator-based multivariate statistics process monitoring approaches. J. Process Control 2015, 33, 112–126. [Google Scholar] [CrossRef]
- Jiao, J.; Zhen, W.; Wang, G.; Wang, Y. KPLS–KSER based approach for quality-related monitoring of nonlinear process. ISA Trans. 2020, 108, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Zhang, R.; Liang, M.; Fu, J.; Wang, H.; Chai, T. Fault identification for quality monitoring of molten iron in blast furnace ironmaking based on KPLS with improved contribution rate. Control Eng. Pract. 2020, 97, 104354. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Quality-Driven Kernel Projection to Latent Structure Model for Nonlinear Process Monitoring. IEEE Access 2019, 7, 74450–74458. [Google Scholar] [CrossRef]
- Zhou, D.; Li, G.; Qin, S.J. Total projection to latent structures for process monitoring. AIChE J. 2009, 56, 168–178. [Google Scholar] [CrossRef]
- Qin, S.J.; Zheng, Y. Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures. AIChE J. 2013, 59, 496–504. [Google Scholar] [CrossRef]
- Peng, K.; Zhang, K.; You, B.; Dong, J. Quality-relevant fault monitoring based on efficient projection to latent structures with application to hot strip mill process. IET Control Theory Appl. 2015, 9, 1135–1145. [Google Scholar] [CrossRef]
- Kong, X.; Cao, Z.; An, Q.; Xu, Z.; Luo, J. Review of partial least squares linear models and their nonlinear dynamic expansion models. Control Decis. 2018, 33, 1537–1548. [Google Scholar] [CrossRef]
- Tang, Q.; Chai, Y.; Qu, J.; Fang, X. Industrial process monitoring based on Fisher discriminant global-local preserving projection. J. Process Control 2019, 81, 76–86. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, K.; Dong, J. A P-t-SNE and MMEMPM based quality-related process monitoring method for a variety of hot rolling processes. Control Eng. Pract. 2019, 89, 1–11. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Hierarchical monitoring for Multi-unit chemical processes based on Local-global correlation features. Acta Autom. Sin. 2020, 46, 1770–1782. [Google Scholar] [CrossRef]
- Odiowei, P.; Yi, C. Nonlinear Dynamic Process Monitoring Using Canonical Variate Analysis and Kernel Density Estimations. IEEE Trans. Ind. Inform. 2010, 6, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Pilario, K.; Cao, Y.; Shafiee, M. Mixed kernel canonical variate dissimilarity analysis for incipient fault monitoring in nonlinear dynamic processes. Comput. Chem. Eng. 2019, 123, 143–154. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Khan, F. Improved latent variable models for nonlinear and dynamic process monitoring. Chem. Eng. Sci. 2017, 168, 325–338. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, K.; Dong, J. A nonlinear full condition process monitoring method for hot rolling process with dynamic characteristic. ISA Trans. 2021, 112, 363–372. [Google Scholar] [CrossRef]
- Jiao, J.; Zhen, W.; Zhu, W.; Wang, G. Quality-Related Root Cause Diagnosis Based on Orthogonal Kernel Principal Component Regression and Transfer Entropy. IEEE Trans. Ind. Inform. 2021, 17, 6347–6356. [Google Scholar] [CrossRef]
- Tian, W.; Ren, Y.; Dong, Y.; Wang, S.; Bu, L. Fault monitoring based on mutual information feature engineering modeling in chemical process. Chin. J. Chem. Eng. 2019, 27, 2491–2497. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, J.; Ding, J.; Peng, W.; Li, X.; Wang, G. Intelligent control of hot strip rolling based on CPS architecture. Steel Roll. 2021, 38, 1–9. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, W.; Sun, J.; Ding, J.; Li, X. Key intelligent technologies of steel strip rolling process. J. Iron Steel Res. 2019, 31, 174–179. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z.; Wang, D.; Li, R.; Yu, H.; Zhang, Y. Mechanism-intelligent coordination shape control model of cold strip. Iron Steel 2017, 52, 52–57. [Google Scholar] [CrossRef]
- Li, W.; Yang, W.; Zhao, Y.; Hu, H. Mechanical property prediction model of hot-rolled strip via big data and metallurgical mechanism analysis. J. Iron Steel Res. 2018, 30, 302–308. [Google Scholar] [CrossRef]
- Tang, P.; Peng, K.; Dong, J. Nonlinear quality-related fault detection using combined deep variational information bottleneck and variational autoencoder. ISA Trans. 2021, 114, 444–454. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B. Design and optimization of thickness control system of tandem cold mill. South. Met. 2019, 231, 42–49. (In Chinese) [Google Scholar]
- Chen, E.; Zhang, S.; Xue, T. Study on shape and gauge control system of cold strip mill. J. Plast. Eng. 2016, 23, 92–95+118. (In Chinese) [Google Scholar]
- Ji, Y.; Yuan, H.; Song, L.; Li, H.; Peng, W.; Sun, J. Coordinate control of strip thickness-crown-tension based on inverse linear quadratic in tandem hot rolling mill. Int. J. Adv. Manuf. Technol. 2021, 118, 1213–1226. [Google Scholar] [CrossRef]






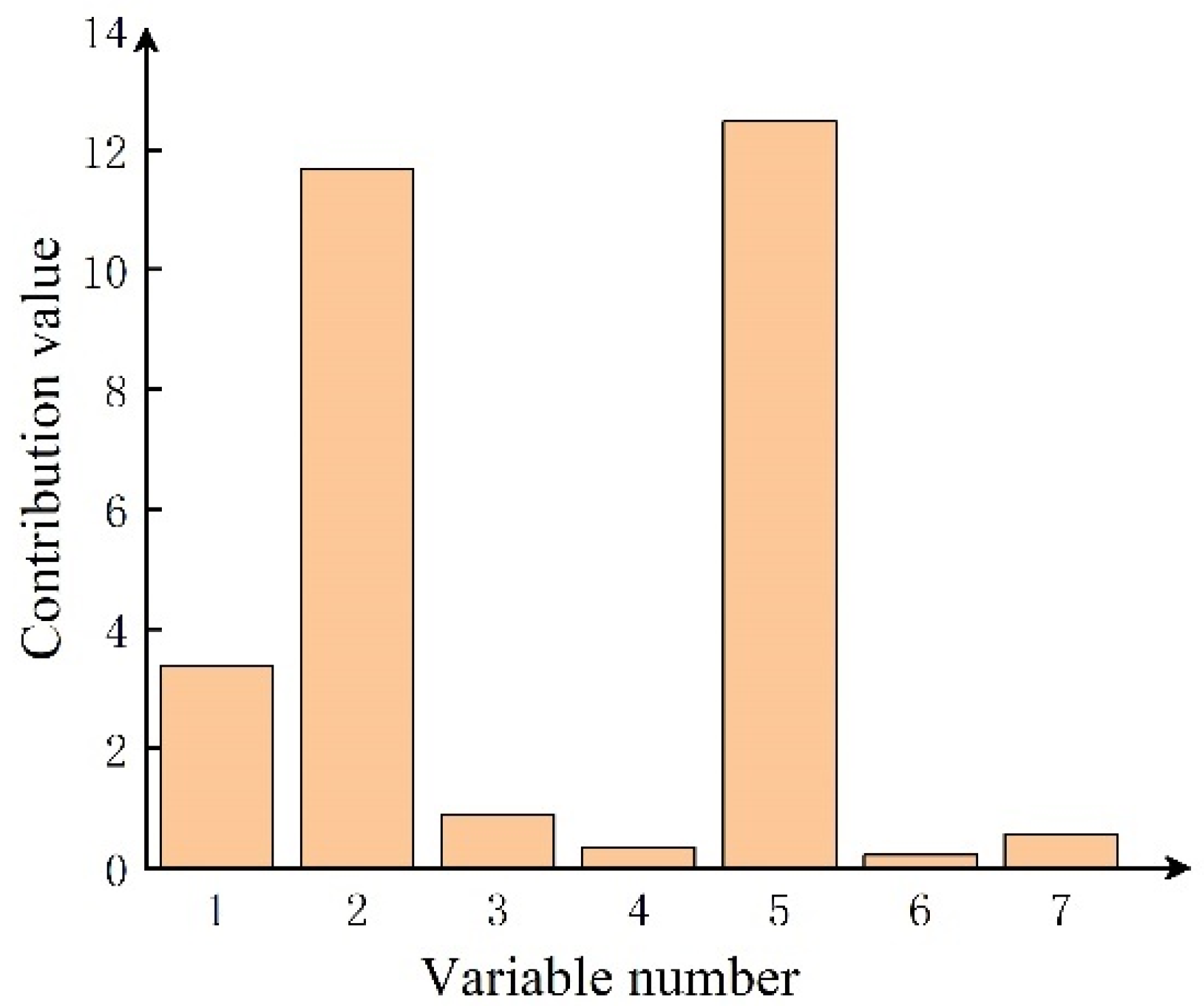
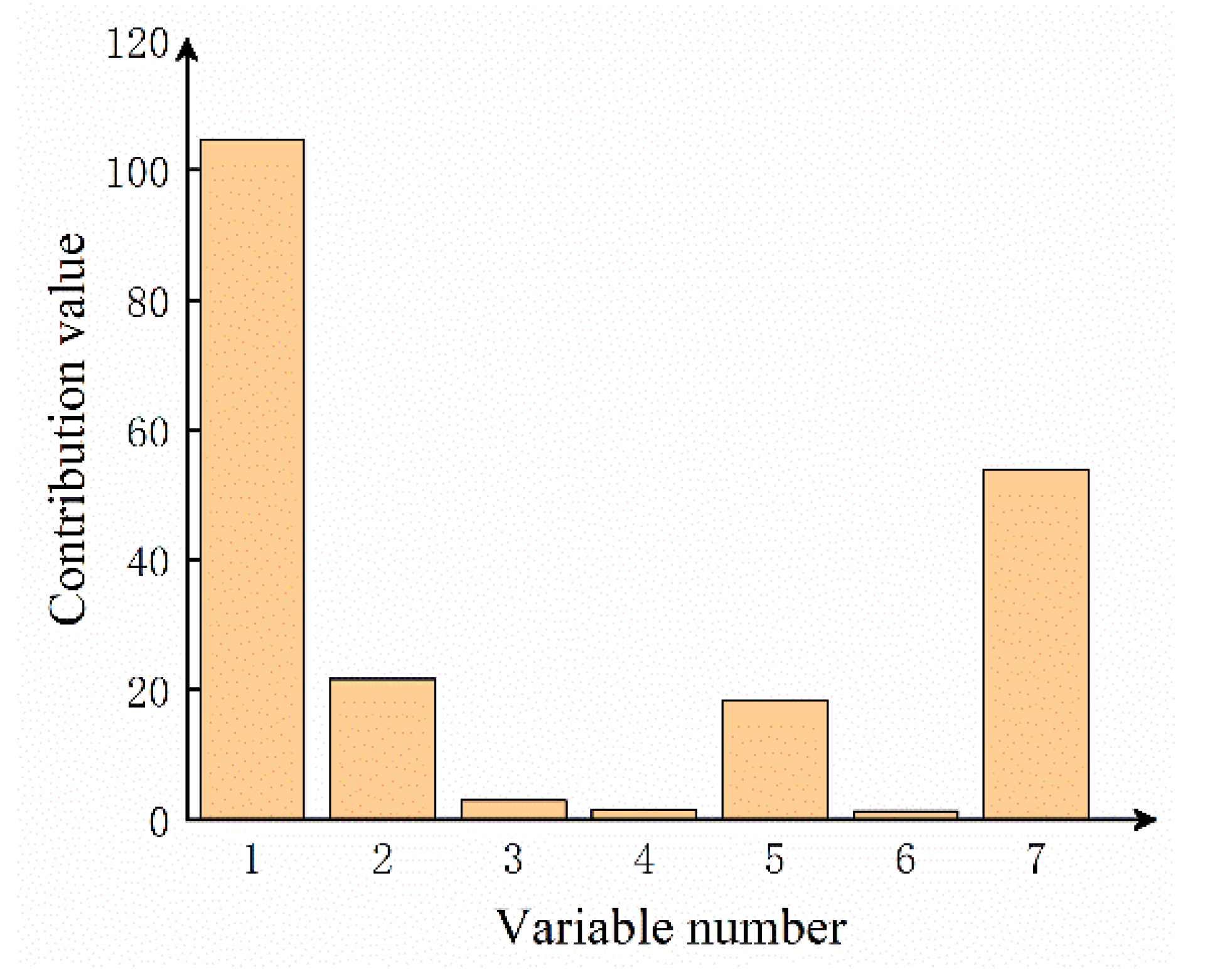

| Index | ||||||
|---|---|---|---|---|---|---|
| Expression |
| Index | Exit Velocity | Back Tension | Front Tension | Entry Thickness |
|---|---|---|---|---|
| Partial differential | 53,141.42 | 4.42 | 1.57 | 18,534.48 |
| Influence coefficient | 0.044 | 3.70 × 10−6 | 1.31 × 10−6 | 0.02 |
| Mean value | 5.78 | 18,829.54 | 15,846.74 | 0.28 |
| Influence weight | 0.254 | 0.070 | 0.021 | 0.004 |
| Component Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Variance contribution rate % | 39.02 | 61.87 | 80.67 | 89.93 | 95.69 | 99.38 | 100 |
| Index | Entry Velocity | Exit Velocity | Front Tension | Back Tension | Roll Gap | Roll Bending Force | Entry Thickness |
|---|---|---|---|---|---|---|---|
| Partial differential | 4494.08 | 7166.41 | 11.13 | 19.52 | - | - | 123,513.80 |
| Influence coefficient | 0.08 | 0.01 | 2.04 × 10−5 | 3.52 × 10−5 | 0.014 | 4.80 × 10−6 | 0.22 |
| Mean value | 10.58 | 13.57 | 15,828.13 | 18,820.76 | 0.72 | 146.36 | 0.28 |
| Influence weight | 0.85 | 0.14 | 0.32 | 0.66 | 0.01 | 0.007 | 0.06 |
| Monitoring Algorithms | PLS | W-PLS | KPLS | W-KPLS | |
|---|---|---|---|---|---|
| Sample 1 | Early warning rate % | 69 | 72 | 75 | 99 |
| Alarm rate % | 22 | 37 | 58 | 75 | |
| Sample 2 | Early warning rate % | 57 | 74 | 82 | 96 |
| Alarm rate % | 20 | 62 | 40 | 68 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Sun, J.; Luo, J.; Peng, Y.; Ye, C. Thickness-Related Fault Diagnosis of Steel Strip Based on W-KPLS Method Considering Mechanism Weight Optimization. Appl. Sci. 2022, 12, 4491. https://doi.org/10.3390/app12094491
Guo H, Sun J, Luo J, Peng Y, Ye C. Thickness-Related Fault Diagnosis of Steel Strip Based on W-KPLS Method Considering Mechanism Weight Optimization. Applied Sciences. 2022; 12(9):4491. https://doi.org/10.3390/app12094491
Chicago/Turabian StyleGuo, Hesong, Jianliang Sun, Jieyuan Luo, Yan Peng, and Chunlin Ye. 2022. "Thickness-Related Fault Diagnosis of Steel Strip Based on W-KPLS Method Considering Mechanism Weight Optimization" Applied Sciences 12, no. 9: 4491. https://doi.org/10.3390/app12094491
APA StyleGuo, H., Sun, J., Luo, J., Peng, Y., & Ye, C. (2022). Thickness-Related Fault Diagnosis of Steel Strip Based on W-KPLS Method Considering Mechanism Weight Optimization. Applied Sciences, 12(9), 4491. https://doi.org/10.3390/app12094491





