Integrated Framework for Bus Timetabling and Scheduling in Multi-Line Operation Mode
Abstract
:1. Introduction
- (1)
- A new multi-objective integrated framework for the M-TT/VS problem is proposed, which constructs a vehicle-based solution structure to facilitate simultaneous optimization.
- (2)
- A heuristic algorithm, including a feasible solution generation algorithm, CEG, and an optimization algorithm, HNS, is designed to find the Pareto frontier solutions. A heuristic method and a comprehensive tabu table are designed to improve optimization efficiency.
- (3)
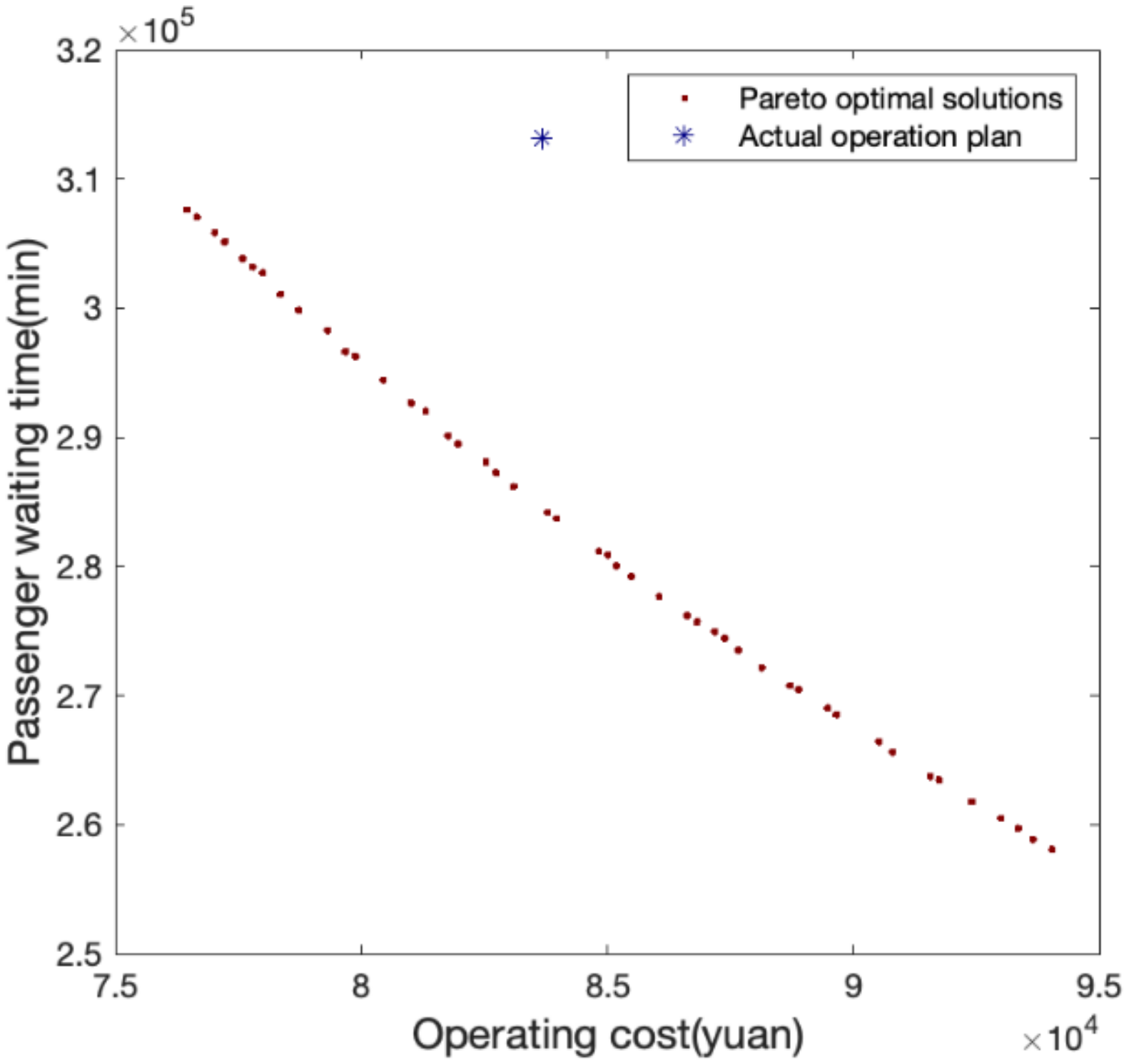
- A case study of Chongqing, China, is carried out to analyze and verify the effectiveness and efficiency of the framework. The Pareto frontier solutions are provided to bus operators as alternative operation schemes.
2. Problem Description
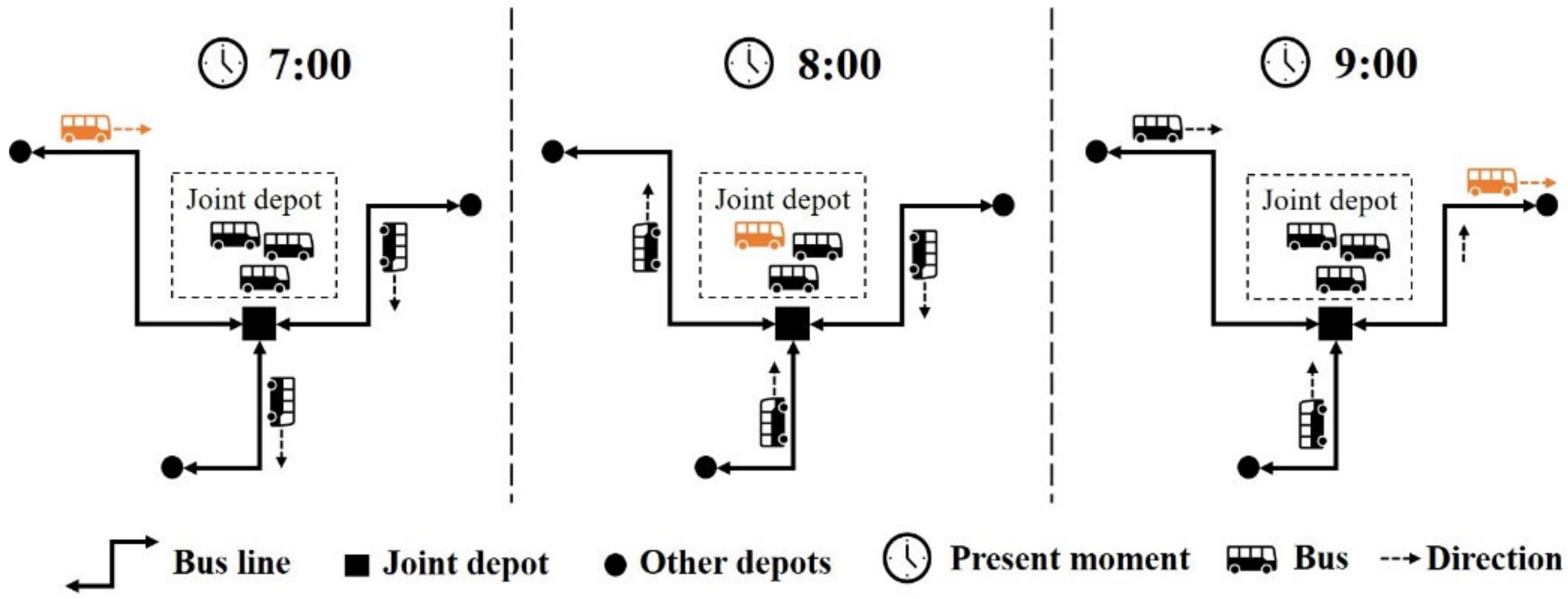
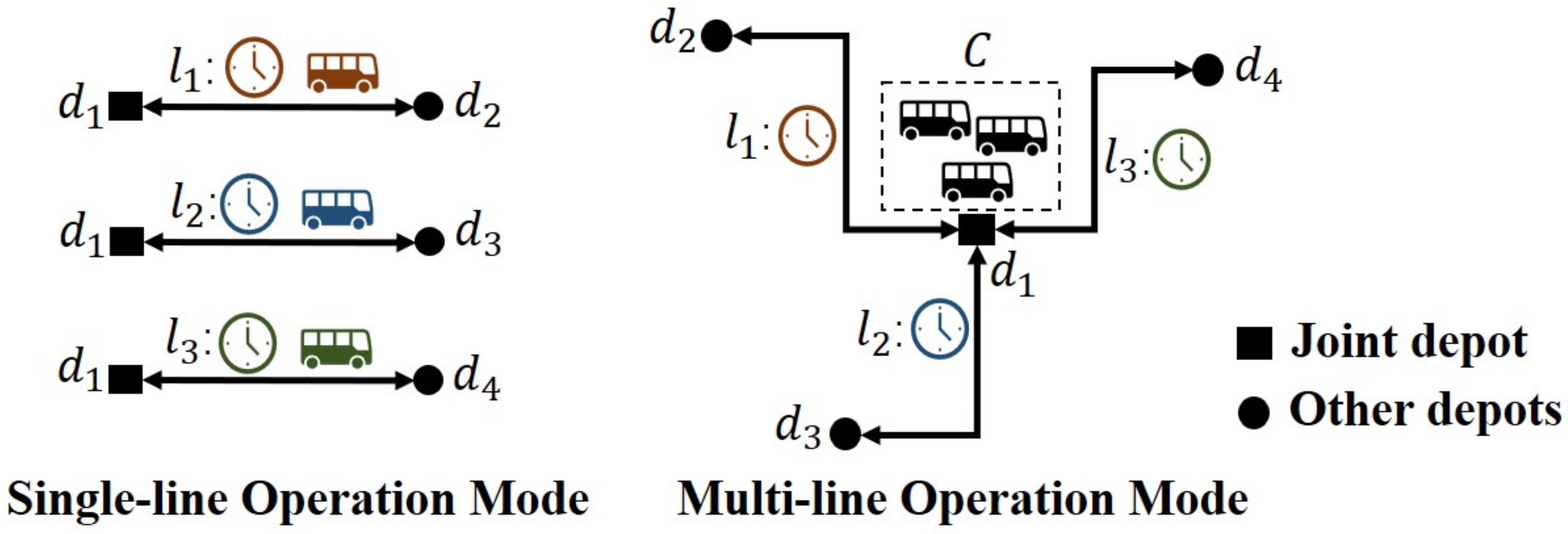
2.1. Description of the Multi-Line Operation Mode
2.2. Description of Input Data
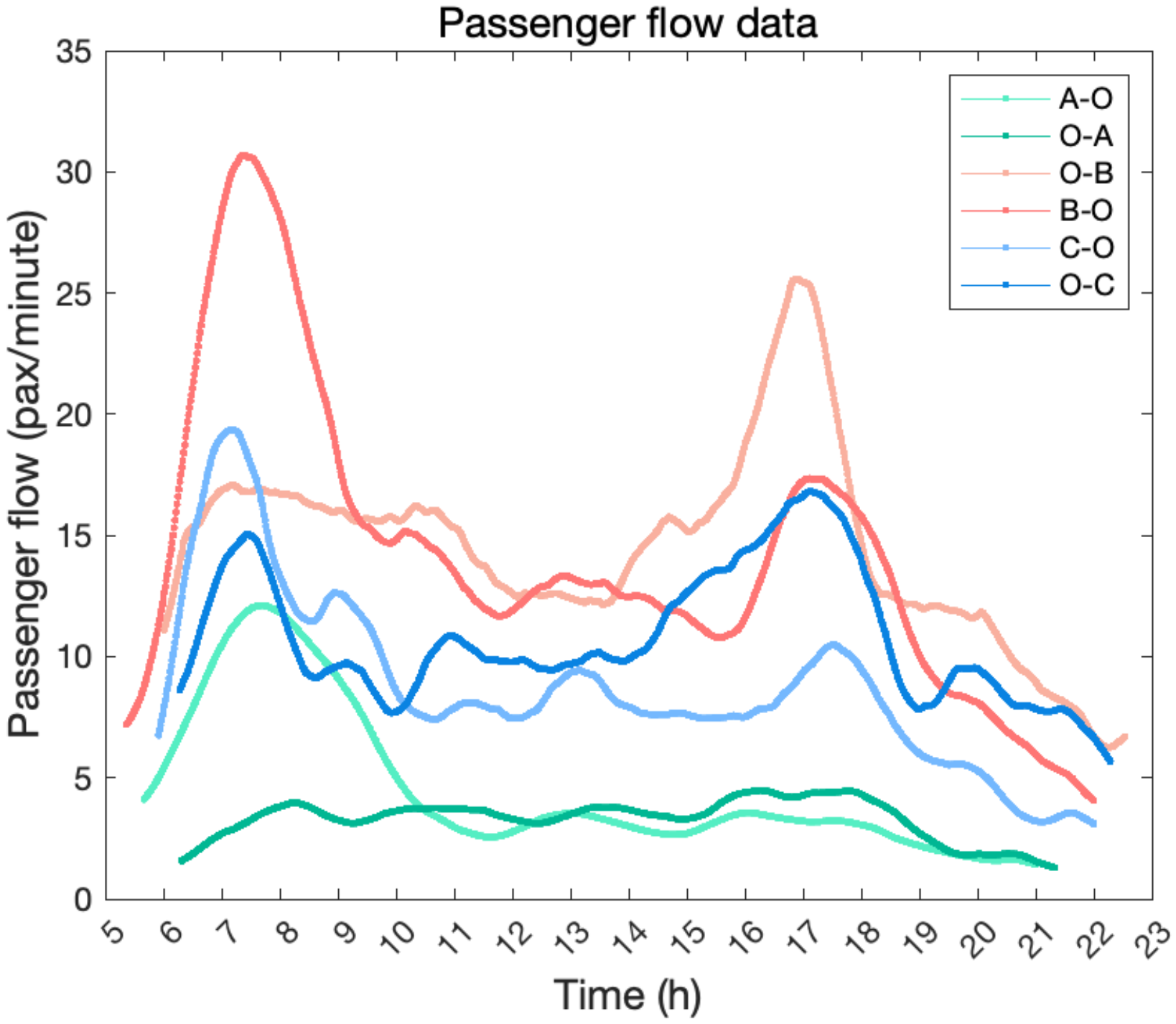
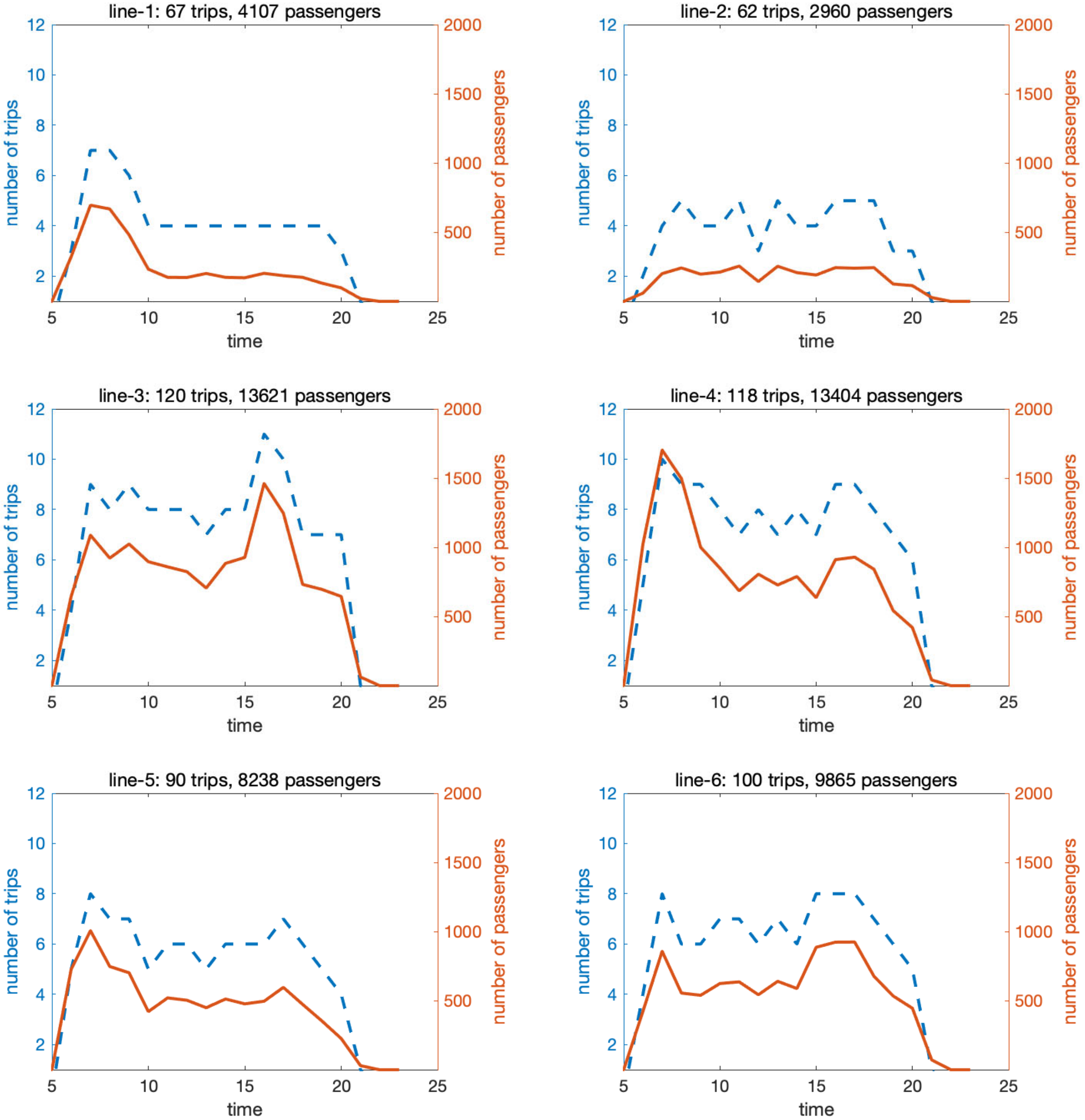
- Passenger flow data is obtained from historical IC card data. The IC card data enumerates passengers’ boarding times and trip numbers. At the same time, according to the operation data of vehicles, we can obtain the departure time and the line number of this trip. Therefore, we can count the total number of passengers carried on each trip. We assume that passengers are evenly distributed within the interval of two departure times. For example, suppose there is a trip carrying 100 passengers, and the departure time of this trip is 10 min apart from the previous trip. In this case, the arrival rate of passenger flow is 10 passengers/min. We have calculated the arrival rate of passenger flow of each line at time . In addition, we restore the passenger’s alighting station data from IC card data through an alight inference method. Based on the complete passenger on-and-off action, we can calculate the highest section flow of the trips. The highest section flow of each line at time is represented as .
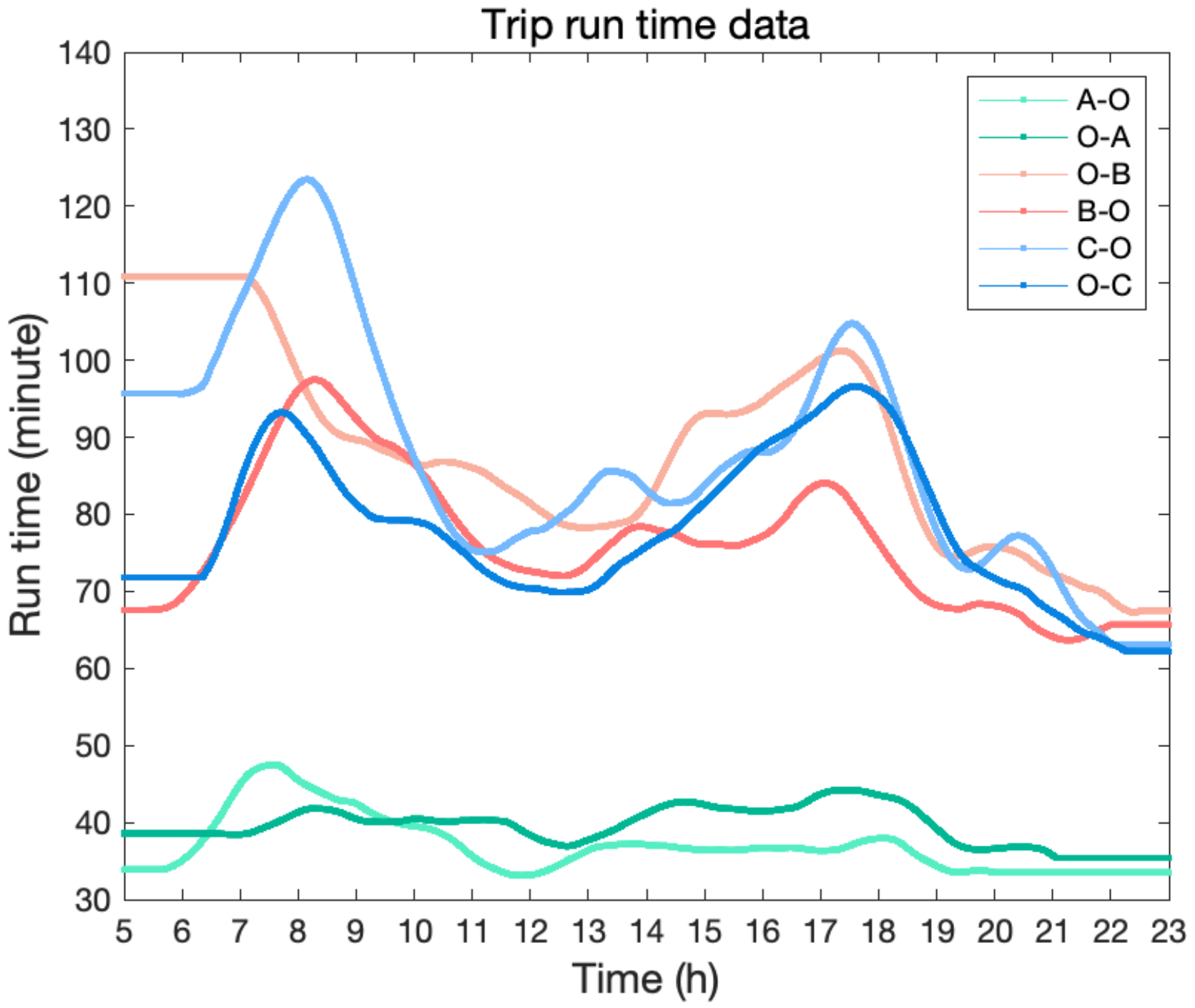
- Trip run time data is obtained from historical GPS data. For each line, we calculate the mean run time of the trips whose departure time is in a historical period. We also smooth the data and supplement the missing values, as shown in Equation (1).
- The operational parameters are determined based on actual operation scenarios. Part of these come from labor laws or regulations, and others from the experience of bus operators. The known operational parameters in this study include the set of all depots, set of all lines, number of standby vehicles, range of departure time, vehicle’s total operating time daily, minimum idle time between trips, and maximum departure time interval. These are listed in Table 1.
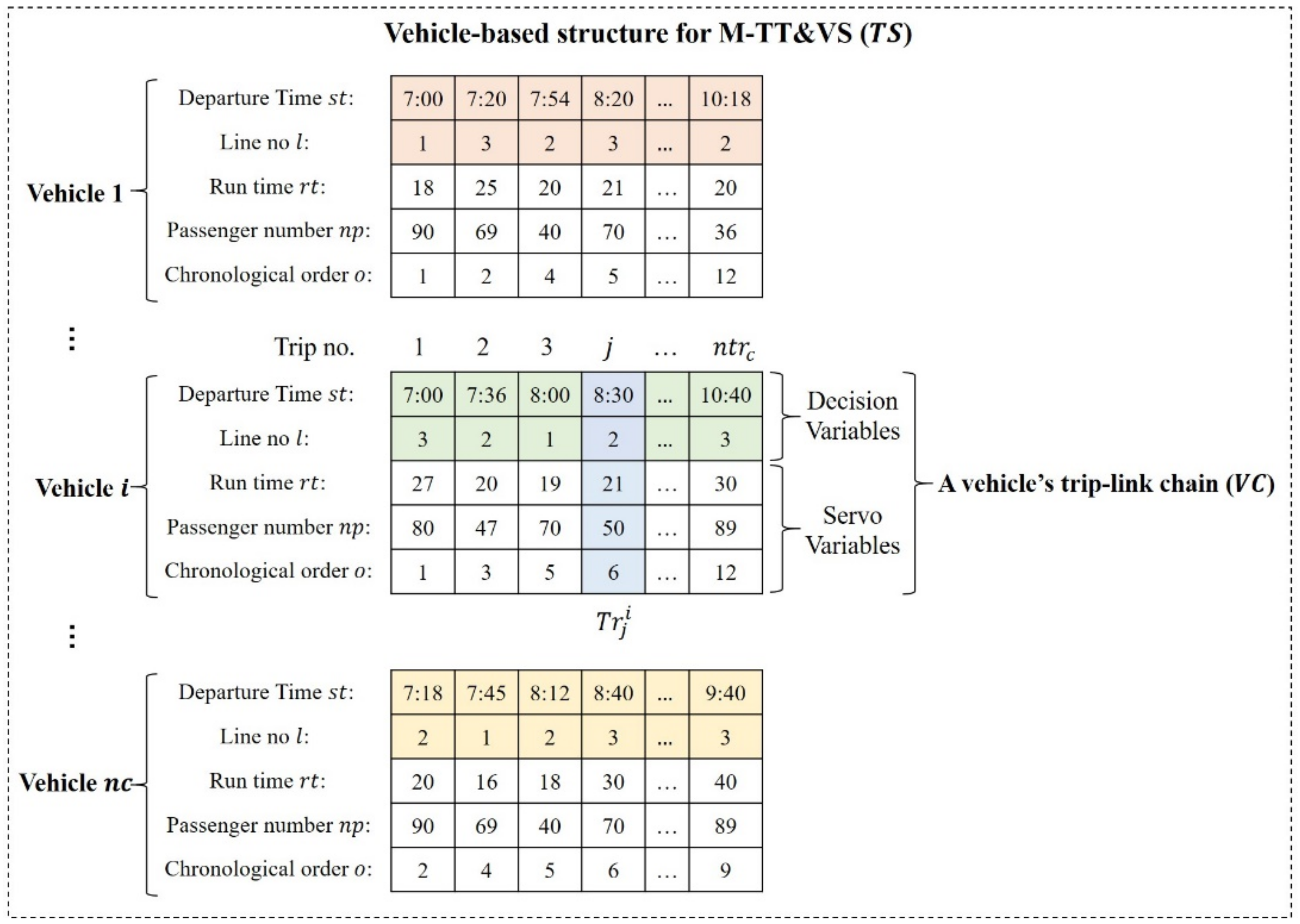
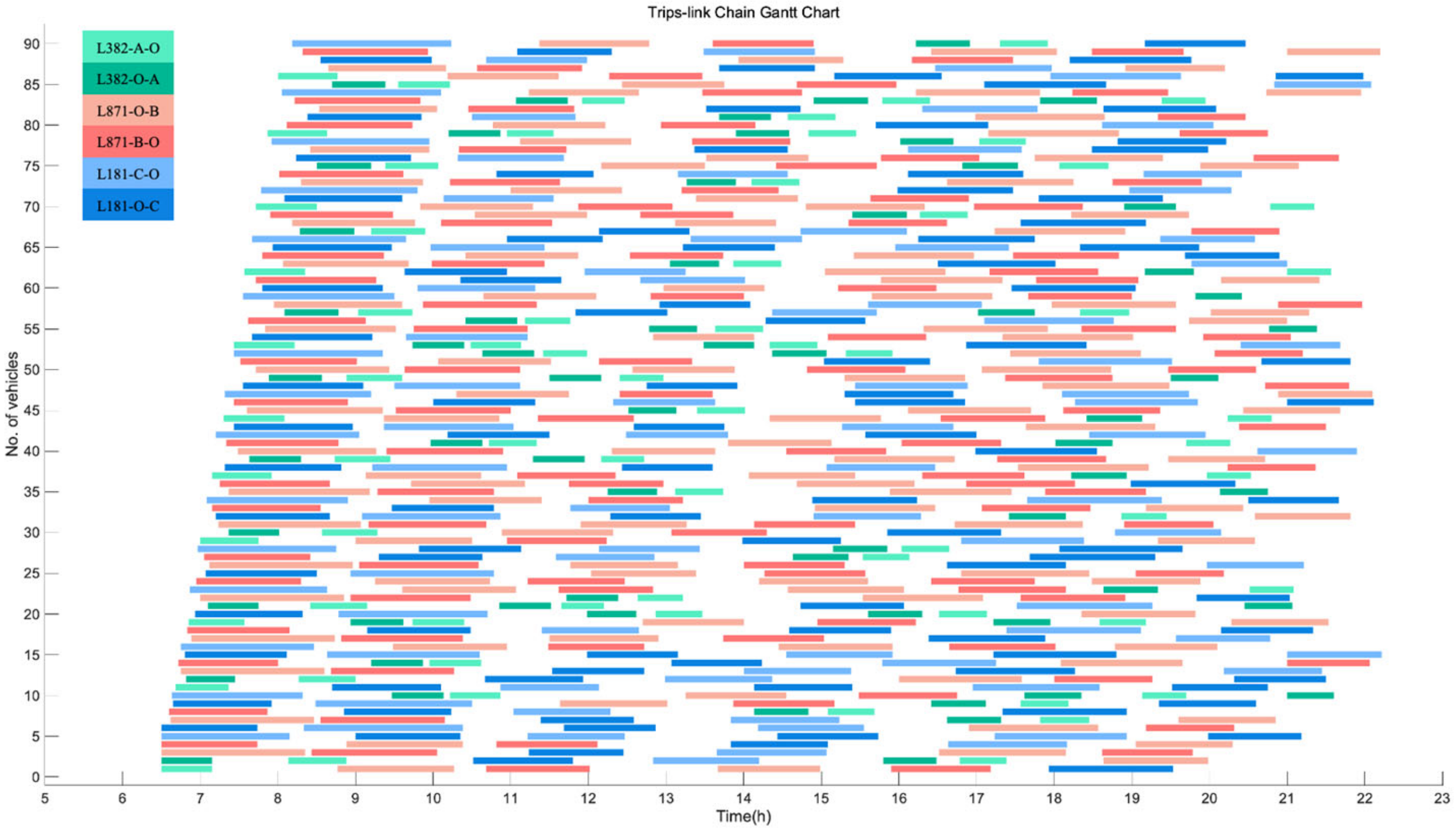
2.3. Solution Structure (Output)
3. Methodology
3.1. Optimization Model
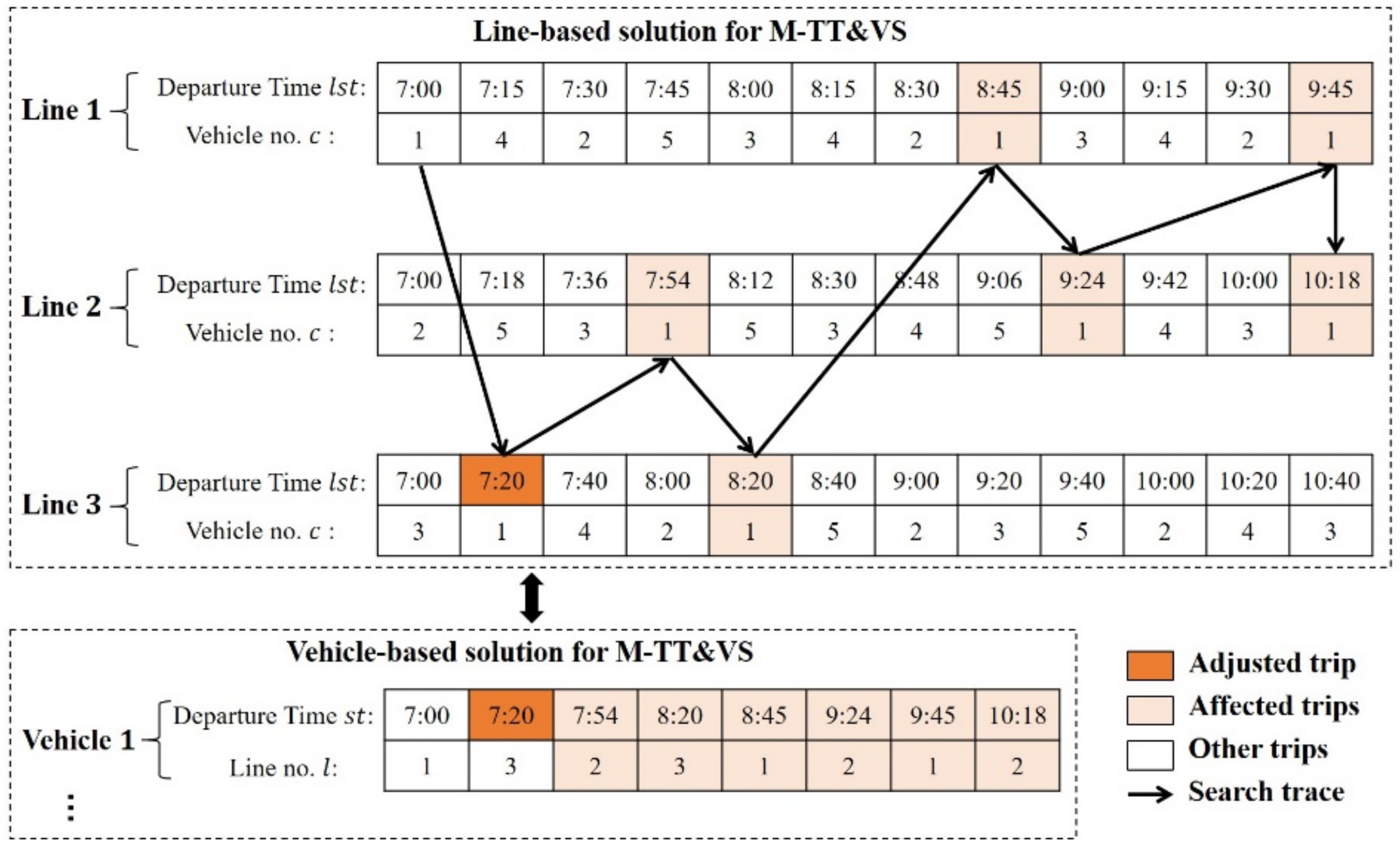
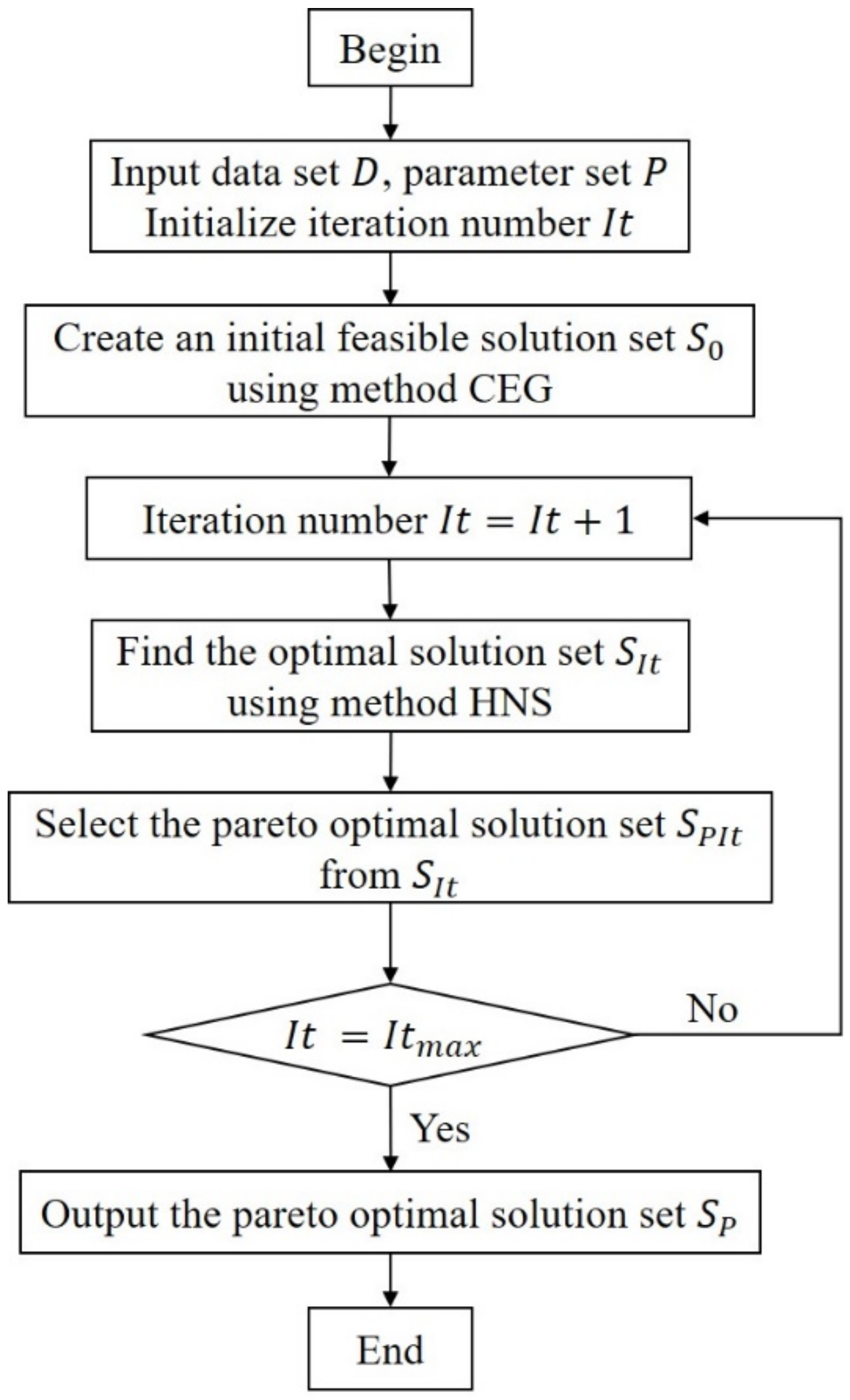
3.2. Solution Algorithm
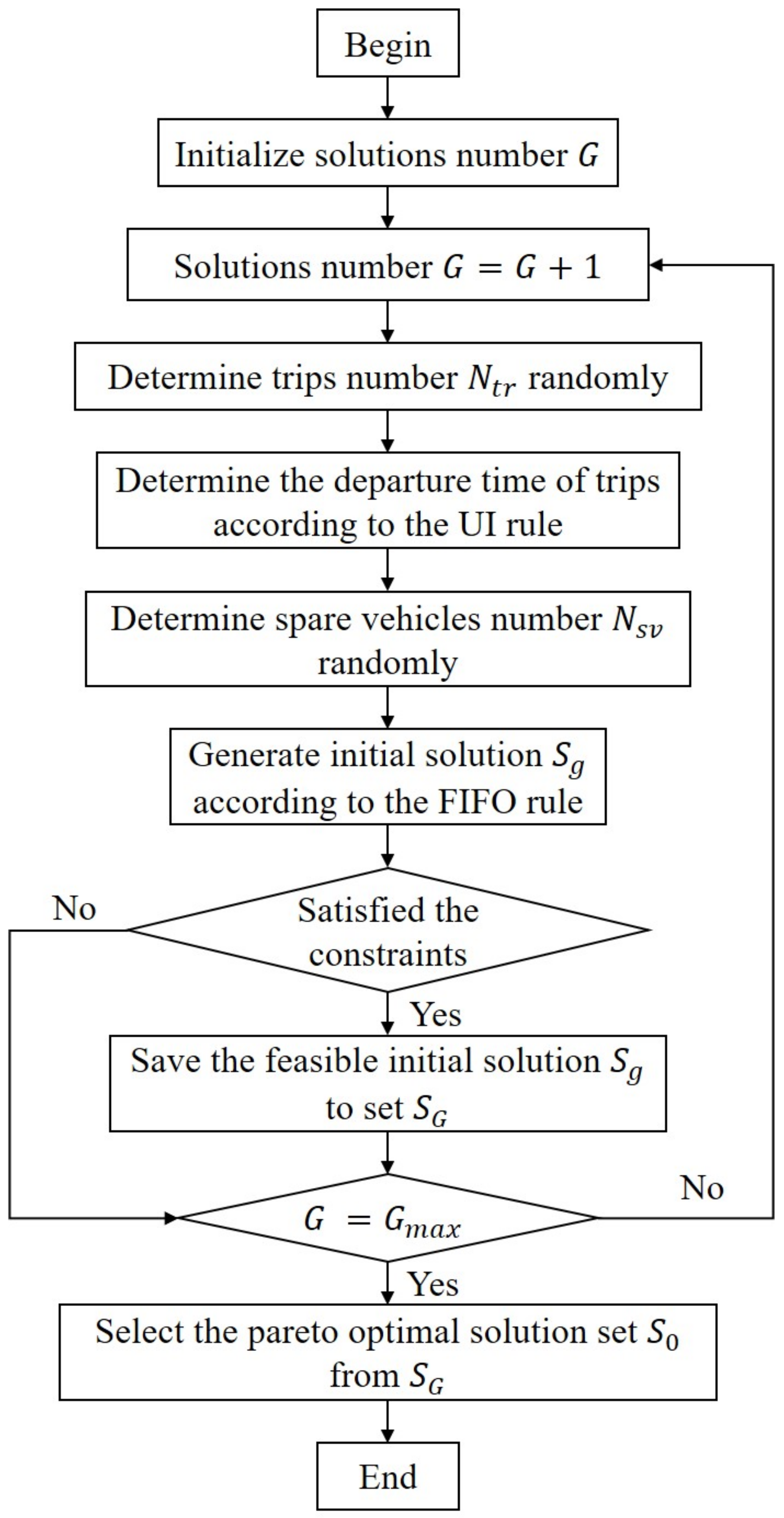
3.2.1. Phase 1: Generate Feasible Solutions
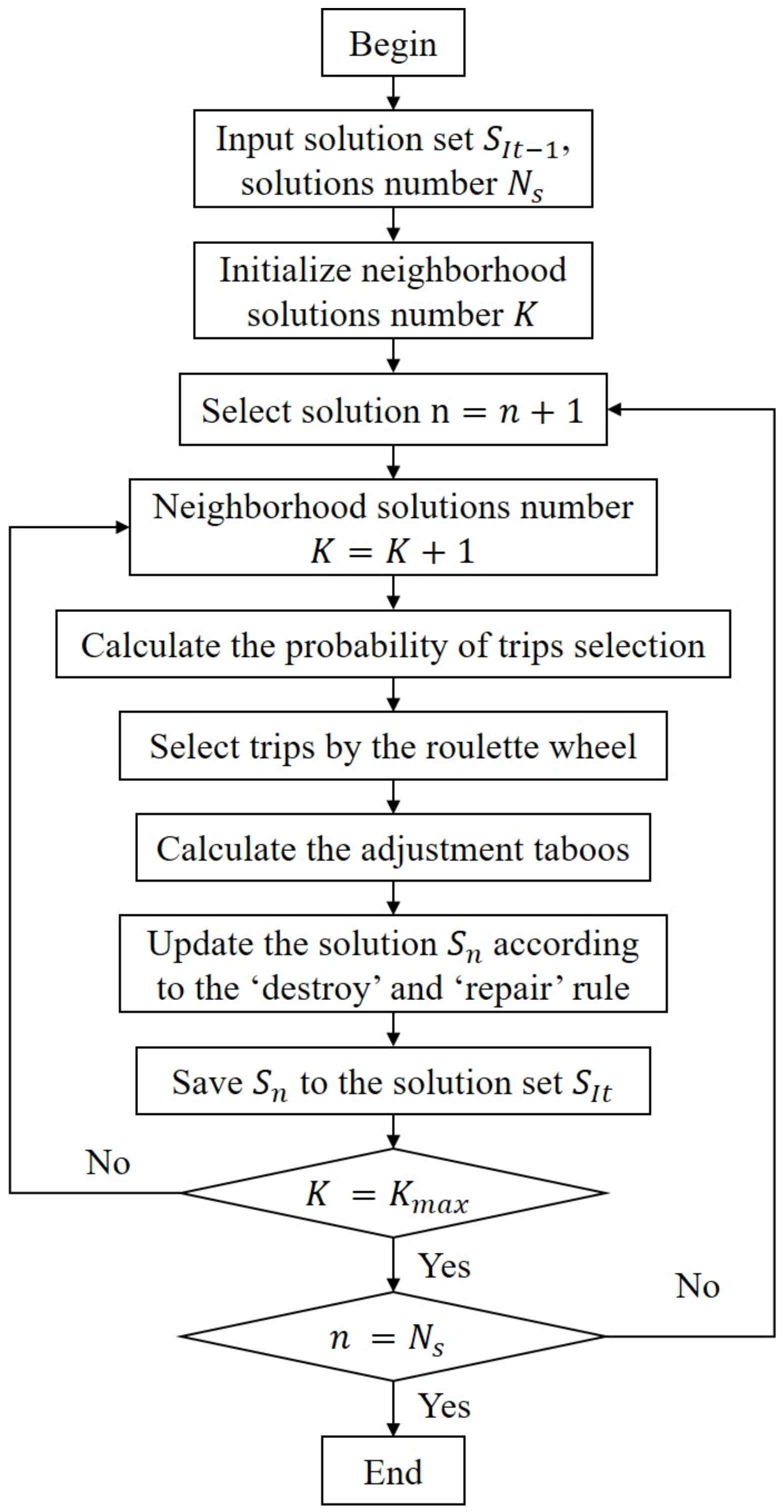
3.2.2. Phase 2: Optimize Solutions
4. Case Study and Discussion
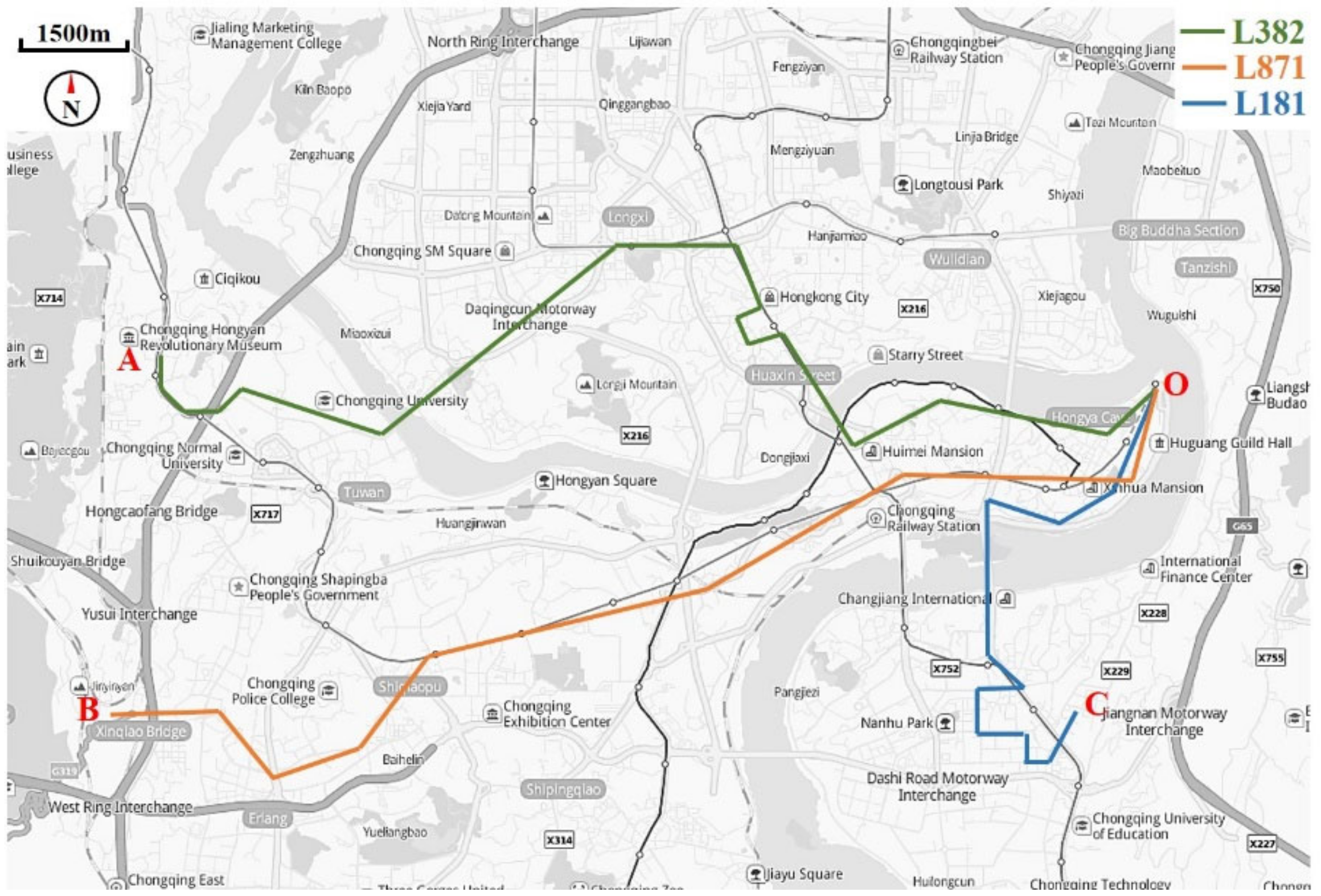
4.1. Case Description and Data Preparation
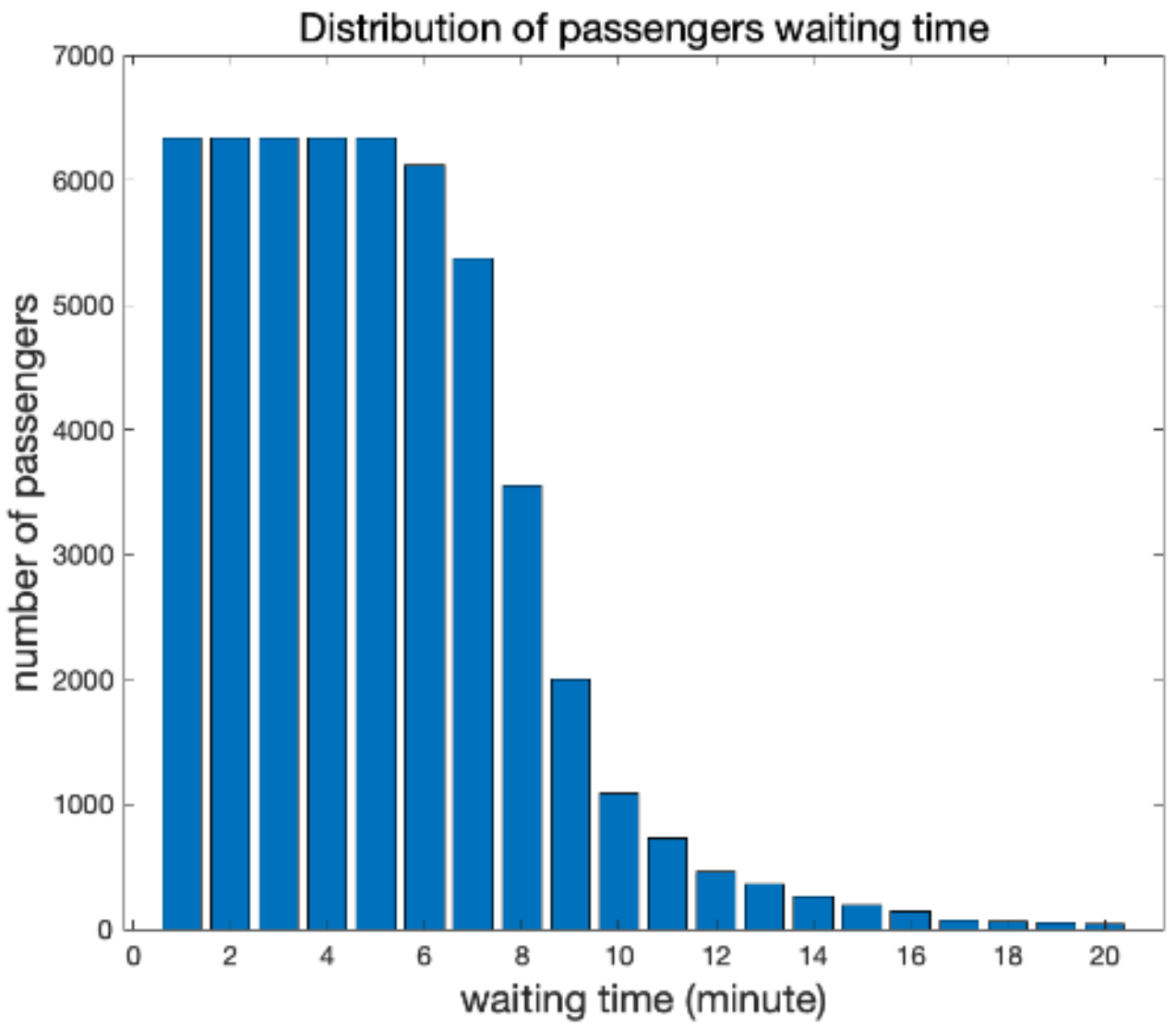
4.2. Results and Discussion
4.2.1. Description of Results
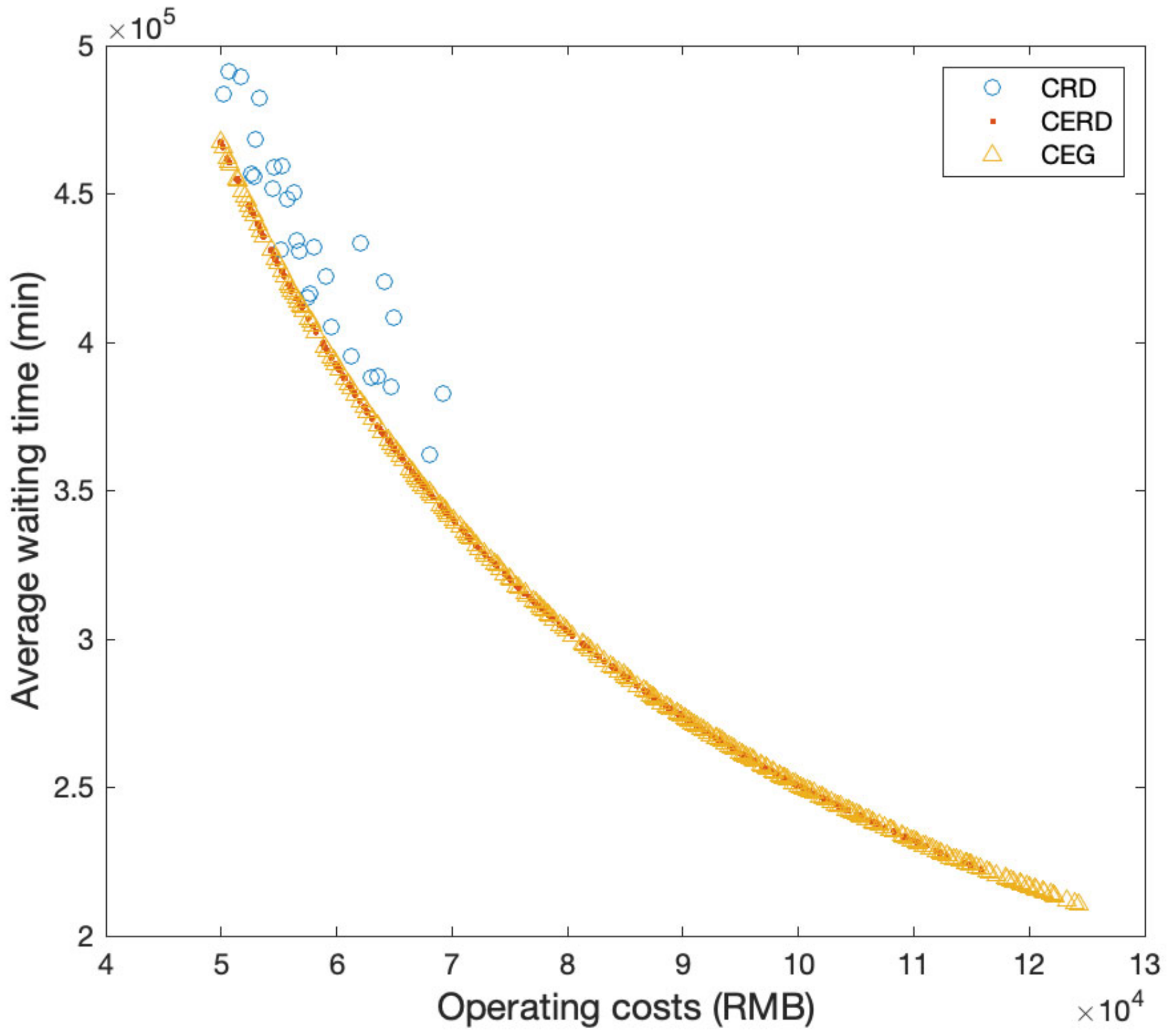
4.2.2. Contrast Experiment of Generation Algorithm
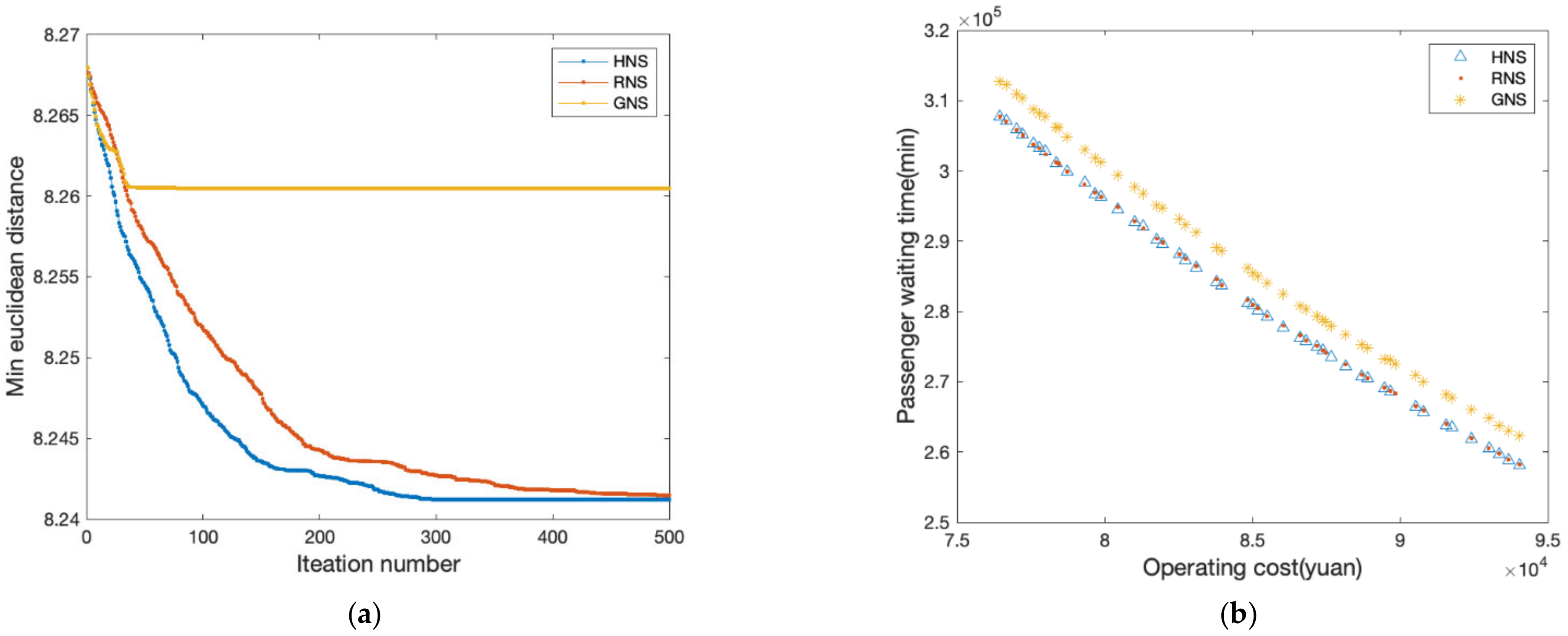
4.2.3. Contrast Experiment of Optimization Algorithm
4.2.4. Contrast Experiment of Operation Mode
4.2.5. Robustness Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xinchao, Z.; Hao, S.; Juan, L.; Zhiyu, L. DP-TABU: An algorithm to solve single-depot multi-line vehicle scheduling problem. Complex Intell. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Petit, A.; Lei, C.; Ouyang, Y. Multiline bus bunching control via vehicle substitution. Transp. Res. Part B Methodol. 2019, 126, 68–86. [Google Scholar] [CrossRef]
- Fouilhoux, P.; Ibarra-Rojas, O.J.; Kedad-Sidhoum, S.; Rios-Solis, Y.A. Valid inequalities for the synchronization bus timetabling problem. Eur. J. Oper. Res. 2016, 251, 442–450. [Google Scholar] [CrossRef]
- Seman, L.O.; Koehler, L.A.; Camponogara, E.; Zimmermann, L.; Kraus, W. Headway control in bus transit corridors served by multiple lines. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4680–4692. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Munoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part B 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Ceder, A. Public Transit Planning and Operation: Modeling, Practice and Behavior, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Yang, X.; Qi, Y. Research on Optimization of Multi-Objective Regional Public Transportation Scheduling. Algorithms 2021, 14, 108. [Google Scholar] [CrossRef]
- Nesmachnow, S.; Risso, C. Exact and Evolutionary Algorithms for Synchronization of Public Transportation Timetables Considering Extended Transfer Zones. Appl. Sci. 2021, 11, 7138. [Google Scholar] [CrossRef]
- Fonseca, J.P.; Evelien, V.; Roberti, R.; Larsen, A. A matheuristic for transfer synchronization through integrated timetabling and vehicle scheduling. Transp. Res. Part B Methodol. 2018, 109, 128–149. [Google Scholar] [CrossRef] [Green Version]
- Carosi, S.; Frangioni, A.; Galli, L.; Girardi, L.; Vallese, G. A matheuristic for integrated timetabling and vehicle scheduling. Transp. Res. Part B Methodol. 2019, 127, 99–124. [Google Scholar] [CrossRef] [Green Version]
- Schöbel, A. An eigenmodel for iterative line planning, timetabling and vehicle scheduling in public transportation. Transp. Res. Part C Emerg. Technol. 2017, 74, 348–365. [Google Scholar] [CrossRef]
- Qu, H.; Li, R.; Chien, S. Maximizing ridership through integrated bus service considering travel demand elasticity with genetic algorithm. J. Transp. Eng. Part A Syst. 2021, 147, 04021010. [Google Scholar] [CrossRef]
- Ciancio, C.; Laganà, D.; Musmanno, R.; Santoro, F. An integrated algorithm for shift scheduling problems for local public transport companies. Omega 2018, 75, 139–153. [Google Scholar] [CrossRef]
- Teng, J.; Chen, T.; Fan, W.D. Integrated approach to vehicle scheduling and bus timetabling for an electric bus line. J. Transp. Eng. 2020, 146, 04019073. [Google Scholar] [CrossRef]
- Shen, Y.; Xie, W.; Li, J. A MultiObjective Optimization Approach for Integrated Timetabling and Vehicle Scheduling with Uncertainty. J. Adv. Transp. 2021, 2021, 3529984. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Giesen, R.; Rios-Solis, Y.A. An integrated approach for timetabling and vehicle scheduling problems to analyze the trade-off between level of service and operating costs of transit networks. Transp. Res. Part B Methodol. 2014, 70, 35–46. [Google Scholar] [CrossRef]
- Schmid, V.; Ehmke, J.F. Integrated timetabling and vehicle scheduling with balanced departure times. OR Spectr. 2015, 37, 903–928. [Google Scholar] [CrossRef]
- Heidari, M.; Hosseini-Motlagh, S.M.; Nikoo, N. A subway planning bi-objective multi-period optimization model integrating timetabling and vehicle scheduling: A case study of tehran. Transportation 2020, 47, 417–443. [Google Scholar] [CrossRef]
- Jiang, X.H.; Guo, X.C.; Shen, H.X.; Gong, X.L. Integrated optimization for timetabling and vehicle scheduling of zone urban and rural bus. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 141–148. [Google Scholar] [CrossRef]
- Van Lieshout, R.N. Integrated periodic timetabling and vehicle circulation scheduling. Transp. Sci. 2021, 55, 768–790. [Google Scholar] [CrossRef]
- Wang, Y.; D’Ariano, A.; Yin, J.; Meng, L.; Tang, T.; Ning, B. Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transp. Res. Part B Methodol. 2018, 118, 193–227. [Google Scholar] [CrossRef]
- Moslem, S.; Alkharabsheh, A.; Ismael, K.; Duleba, S. An integrated decision support model for evaluating public transport quality. Appl. Sci. 2020, 10, 4158. [Google Scholar] [CrossRef]
- Ceder, A. Integrated smart feeder/shuttle transit service: Simulation of new routing strategies. J. Adv. Transp. 2013, 47, 595–618. [Google Scholar] [CrossRef]
- Gong, C.; Shi, J.; Wang, Y.; Zhou, H.; Yang, L.; Chen, D.; Pan, H. Train timetabling with dynamic and random passenger demand: A stochastic optimization method. Transp. Res. Part C Emerg. Technol. 2021, 123, 102963. [Google Scholar] [CrossRef]






| Parameters | Meaning |
|---|---|
| Set of all depots | |
| Set of all lines | |
| Number of vehicles | |
| Range of departure time | |
| Range of total operating time | |
| Minimum idle time between trips | |
| Maximum departure time interval |
| Time Complexity | ||
|---|---|---|
| 1 | ; | |
| 2 | For , Get union set ; | |
| 3 | ; | |
| 4 | ||
| Parameters | Meaning | Value |
|---|---|---|
| Set of all depots | ||
| Set of all lines | ||
| Number of vehicles | 90 | |
| Range of departure time | [6:30,21:00] | |
| Range of total operating time | [4 h,15 h] | |
| Minimum idle time between trips | 5 min | |
| Maximum departure time interval | 20 min | |
| Maximum seating capacity | 90 seats | |
| Operating cost per kilometer | 10 yuan/km |
| No. | CRD | CERD | CEG | ||||
|---|---|---|---|---|---|---|---|
| 1 | 500 | 17 | 3% | 267 | 53% | 332 | 66% |
| 2 | 700 | 33 | 5% | 370 | 53% | 447 | 64% |
| 3 | 1000 | 51 | 5% | 498 | 50% | 646 | 65% |
| 4 | 1500 | 49 | 3% | 765 | 51% | 1007 | 67% |
| 5 | 2000 | 77 | 4% | 978 | 49% | 1292 | 65% |
| 6 | 3000 | 100 | 3% | 1481 | 49% | 1987 | 66% |
| No. | CRD | CERD | CEG | ||||
|---|---|---|---|---|---|---|---|
| 1 | 500 | [5.08,7.18] | [3.68,4.78] | [5.05,11.23] | [2.28,4.62] | [5.07,12.43] | [2.11,4.61] |
| 2 | 700 | [5.06,7.02] | [3.56,4.81] | [4.99,11.25] | [2.28,4.67] | [5.01,12.33] | [2.12,4.66] |
| 3 | 1000 | [5.10,7.14] | [3.65,4.84] | [4.99,11.54] | [2.23,4.67] | [4.99,12.22] | [2.13,4.67] |
| 4 | 1500 | [5.09,8.66] | [3.06,4.72] | [4.99,11.66] | [2.21,4.67] | [4.99,12.43] | [2.11,4.67] |
| 5 | 2000 | [5.12,8.01] | [3.46,4.85] | [4.99,11.92] | [2.18,4.67] | [4.99,12.43] | [2.11,4.67] |
| 6 | 3000 | [4.99,7.91] | [3.25,5.02] | [4.99,11.54] | [2.23,4.67] | [4.99,12.43] | [2.11,4.67] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; He, Z.; Zhong, J. Integrated Framework for Bus Timetabling and Scheduling in Multi-Line Operation Mode. Appl. Sci. 2022, 12, 4210. https://doi.org/10.3390/app12094210
Chen S, He Z, Zhong J. Integrated Framework for Bus Timetabling and Scheduling in Multi-Line Operation Mode. Applied Sciences. 2022; 12(9):4210. https://doi.org/10.3390/app12094210
Chicago/Turabian StyleChen, Shengmei, Zhaocheng He, and Jiaming Zhong. 2022. "Integrated Framework for Bus Timetabling and Scheduling in Multi-Line Operation Mode" Applied Sciences 12, no. 9: 4210. https://doi.org/10.3390/app12094210
APA StyleChen, S., He, Z., & Zhong, J. (2022). Integrated Framework for Bus Timetabling and Scheduling in Multi-Line Operation Mode. Applied Sciences, 12(9), 4210. https://doi.org/10.3390/app12094210






