Abstract
Second harmonic generation has been widely applied in various fields. High second harmonic intensity can facilitate optical imaging, signal sensing, and detection. Thus, enhancing the intensity of the second harmonic is a significant work. However, changing the external character of crystal or increasing the pump light intensity to improve the intensity of the second harmonic is not always advisable in some applications, such as bioimaging, biopsies, etc. Here, we implemented a noninvasive method that constructs a specific spatial distribution field via a scattering medium to realize a high enhancement of second harmonic intensity. We studied that different scattering mediums exerted the influence on the optimal enhancement effect of second harmonic. It was found that choosing an appropriate scattering medium can greatly enhance the intensity of the second harmonic. The results can offer a helpful value for second harmonic applications such as bioimaging, sensing, and optical frequency conversion.
1. Introduction
Since the optical second harmonic generation (SHG) was discovered in 1961 [1], this nonlinear effect has been widely applied in imaging microscopy [2,3,4], laser frequency conversion [5,6], optical detection and sensing [7,8,9,10], etc. SHG is a parametric process without electron transitions, while two-photon fluorescence is a nonparametric process with electron transitions [11]. Due to lossless nonradiative energy, the signal and background of SHG are better than that of the two-photon fluorescence. Hence, instead of fluorescence markers, the SHG becomes the preference of biomedical imaging. The intensity of SHG has a significant influence on the applications, like that the stronger intensity of SHG can be sensitive to the variation of signal of optical detection and sensing.
Conversion efficiency of SHG is an important parameter. For all these years, enhancing the conversion efficiency of SHG has always been the focus of researchers [12,13,14]. From various perspectives, researchers have proposed many factors to affect the conversion efficiency of the second harmonic, such as crystal material [15,16], interaction length [17], crystal structure [18], and pump light intensity [19]. However, it is not always applicable to improve the signal quality of SHG via increasing the pump light intensity in bioimaging because of the phototoxicity that can damage the tissue and cells. In addition, most of above methods are related to the external crystal, which cannot be available to be applied in bioimaging applications where the second harmonic is generated by the protein molecule itself. Accordingly, a control and external method that is independent of the character of the medium is required in enhancing the second harmonic efficiency of biological tissue imaging.
Previous research has demonstrated that conversion efficiency of SHG is affected by phase and intensity of fundamental frequency light [13]. Therefore, modulating the wavefront of fundamental frequency light in front of the crystal can change the intensity distribution and conversion efficiency of the SHG signal. Further, we can improve the conversion efficiency of the SHG through a structured light field with spatial distribution: for example, wavefront shaping technique [13], facet functionalization of nonlinear crystals [20,21], and construction of structured light (i.e., vortex light) [22,23,24,25], etc. Furthermore, if multiple degrees of freedom are modulated simultaneously, such as wavefront phase and amplitude, higher conversion efficiency can be obtained. When a coherent light beam transmits the scattering medium, a speckle pattern with multiple random degrees of freedom is formed. Introducing a scattering process can simultaneously generate structured beams with specific phase and amplitude [26]. It has been demonstrated that the wavefront shaping technique is a noninvasive method to modulate the spatial distribution of a scattering light field in previous studies. Accordingly, we can control the scattering field to achieve high conversion efficiency enhancement of SHG based on wavefront shaping technique.
In this paper, we demonstrated experimentally that placing a scattering medium in front of the nonlinear crystal can greatly enhance the conversion efficiency of SHG using wavefront shaping technique. In the experiment, placing an appropriate scattering medium does not change the light intensity of fundamental frequency light, but changes the phase gradient and phase information of fundamental frequency light, which affect the intensity of SH. This method can be available in the applications for avoiding the phototoxicity. Meanwhile, we compared the impact of wavefront shaping on conversion efficiency of SHG with different scattering mediums (ground glass and zinc oxide film) mounted in front of nonlinear crystal. The results indicate that the enhancement effect of conversion efficiency is directly related to the character of the scattering medium. We show that high light intensity of the second harmonic with the scattering medium can be realized, comparing to the case of no scattering effect. These results can be valuable for applications such as optical frequency conversion, second harmonic sensing imaging, and bio-optical detection [4,7,27].
2. Methods and Experimental Setup
2.1. Methods
When a coherent light transmits through the scattering mediums, a speckle pattern with random phase and amplitude can be generated. Generally, the scattering process of light passing through a scattering medium is linear, which can be represented as follows [28]:
where tba describes the transmission matrix element of the scattering medium, Aa and φa are amplitude and phase of the incident light field, and Eb is the transmitted light field, which can be regarded as the linear superposition of N input elements of the incident light field. Therefore, the scattering medium can introduce a spatially distributed light field with a specific phase and amplitude.
Studies have shown in theory that the intensity of SHG has a dependence on the gradient of phase [13,29]. According to the Ref. [13], we can get the Equations (2) and (3), which are given as follows:
where n = 1 and 2 mean the fundamental and doubling frequency light, respectively. Δk = k1 − 2k2, Δφ = φ1 − 2φ2, and Fn is an interaction term related to the effective nonlinear coefficient of crystal and the amplitude of each wavelength. The above equations clearly explain the relationship between the complex field amplitude and transverse phase and amplitude. In other words, we only need to control the wavefront phase distribution (φa) in front of scattering medium to change the intensity of SHG.
It is possible to achieve the enhancement of SHG by modulating the transmitted light of the scattering medium. To our acknowledge, a speckle field has a random phase and amplitude distribution. The wavefront shaping technique was widely used in the modulation of the wavefront phase of incident light through the scattering medium [30,31,32]. Applying the wavefront shaping technique and spatial light modulator can obtain a spatial distribution of speckle field with specific phase and amplitude. In order to improve the light intensity of SHG, we used the wavefront shaping technique to control the wavefront phase distribution of the fundamental frequency light through the scattering medium. The optimization algorithm plays a key role in finding an optimal phase mask of wavefront shaping technique. In this paper, we adopted the genetic algorithm (GA) [33] as the feedback iterative algorithm, which can converge quickly and obtain the optimal phase.
2.2. Experimental Setup
The second harmonic generation (SHG) was enhanced experimentally by the combination of scattering medium and nonlinear crystal. The experiment setup is depicted in Figure 1. The femtosecond light with wavelength of 820 nm (Coherent, Santa Clara, VA, USA, 35 fs, 80 MHz) was expanded by a telescope system consisting of lenses L1 and L2. The expanded beam was reflected by a spatial light modulator (HAMAMATSU, Hamamatsu City, Japan, X13138-02) loaded with the optimal phase into the scattering medium. In addition, a half wave plate was used to control the polarization direction of the incident light of BBO crystal to maximize the efficiency of the crystal. The scattering light was incident on the barium borate crystal (BBO) to generate a second harmonic signal. After filtering by a set of filters, the second harmonic light was detected by CCD (AVT, München, Germany, PIKE F421B,). In order to better demonstrate the effect of enhancement of SHG during modulation, the spectrometer (Ocean Optics, Orlando, FL, USA, HR 2000) is used to detect the intensity of the second harmonic spectrum before and after optimization. In our experiment, instead of increasing the intensity on a small area, we improved the intensity of the whole second harmonic light field. The total intensity of the second harmonic signal is regarded as a feedback signal in the GA for achieving a desired phase mask on the SLM, which can change phase and phase gradient of speckle field. The objective function (the second harmonic intensity enhancement factor) of GA is defined as [28]:
where ηo and are optimized and initial conversion efficiency of SHG, respectively. IOS is optimized second harmonic light intensity, and IIS is initial intensity of second harmonic light. After iteration, the optimal phase was applied on SLM and the value of the feedback factor reached more than unity, indicating that the enhancement of the second harmonic conversion efficiency was realized.
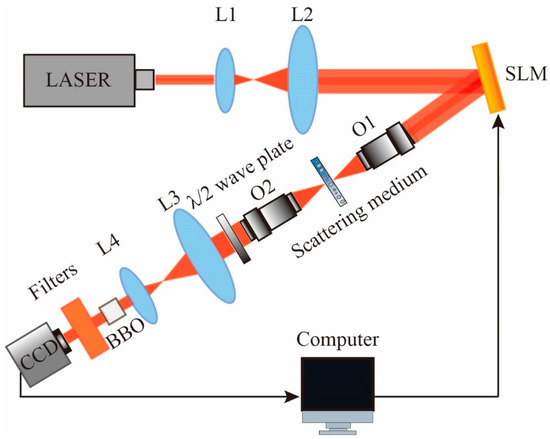
Figure 1.
Experimental setup. The focal lengths of lenses L1, L2, L3, and L4 are 50 mm, 100 mm, 50 mm, and 20 mm, respectively. Numerical apertures of the objective lenses (O1 and O2) are 0.25 and 0.4, respectively. BBO: type I, 10 × 10 × 0.2 mm, θ = 29.2°, φ = 0°.
3. Results and Discussion
3.1. Enhancement of SHG without Scattering Effect
It was proved experimentally that the optimization algorithm can indeed enhance the intensity of SHG without scattering, which can be shown in Figure 2. To ensure the credibility and repeatability of the experiment, we acquired multiple sets of experimental data of each experiment and used the statistical average as the comparison data. Figure 2a presents the calculated average values for each group of experimental data. In the experiment, the number of iterations of algorithm we uniformly used was 150 to strike a balance between calculation time and optimization effect, which can ensure the same time of each experiment for a contrast. Moreover, the spectrograms of optimized SHG without scattering were measured to visually show the optimization effect (Figure 2b), and the ten-fold intensity enhancement of 410 nm light was obtained.
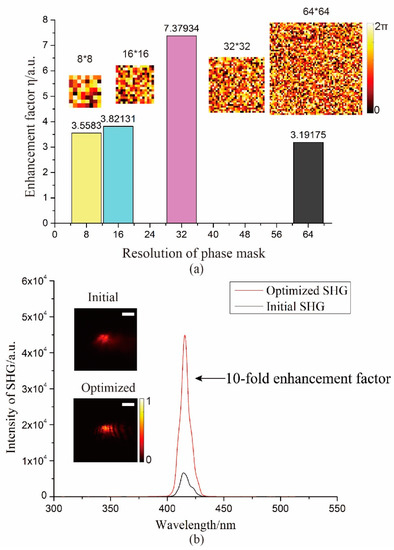
Figure 2.
The enhancement of SHG without scattering medium using wavefront shaping technique. (a) Comparison of enhancement effects of different phase mask resolutions (results from the statistical average values of multiple experimental data). (b) Comparison of the second harmonic spectrum before and after optimization (detecting the spectrum of the best results). Note: the optimized light field is collected after three times attenuation. Scale bar: 1.468 mm.
It was demonstrated that the optimized effect is related to the resolution of the phase mask loaded on the SLM [28]. In theory, the segments of SLM are positively correlated with the precision of modulation, which makes a high enhancement. However, we observed different results when applying different resolutions of phase in our experiment. It is not the case that the higher the resolution, the better the enhancement effect. On the one hand, we considered that it was limited by the number of iterations. Under the condition of a certain number of iterations, selecting an appropriate resolution of phase can allow it to converge quickly and achieve the best effect. Even increasing the resolution in this case, the optimization effect will not change. On the other hand, the optimization result is coordinated by the first-order phase gradient and the second-order phase gradient, which are affected by resolution. The best optimization effect can be achieved with a suitable phase gradient, but just increasing the resolution may lead to the destruction of the appropriate phase gradient. Therefore, enlarging the resolution only increases the calculation, but cannot make the optimization effect better.
3.2. Different Scattering Mediums
As mentioned above, it is possible to improve the light intensity of the SHG by introducing a structured light filed with a specific phase and amplitude. The degree of scattering of the scattering medium can affect the phase gradient, resulting in the change of second harmonic intensity. To explore the relationship between scattering medium and optimized effect, we used ground glass with different degrees of scattering and zinc oxide film (a thickness of 25 μm) to respectively construct such a structured light field. The different speckle patterns of the same size were generated in the same position after the light passed through the different scattering mediums, as shown in Figure 3. To intuitively distinguish the intensity gradient information of the speckle, the intensity of the same-row pixels (514th line) of different patterns were mapped. It can be seen from Figure 3 that the larger the grit of the ground glass, the finer the scattering particles of the speckle light field, and the speckle of zinc oxide film is more dense than that of ground glass.
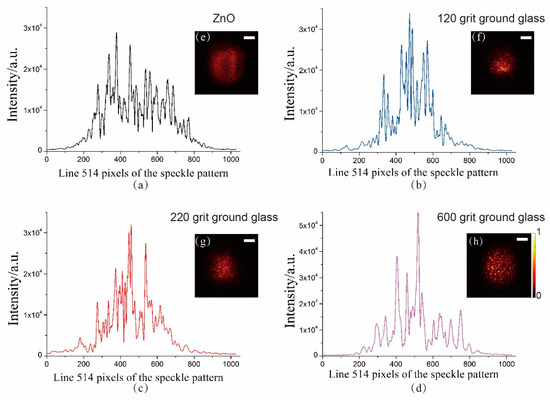
Figure 3.
Speckle pattern of different scattering mediums. (a–d) The light intensity distribution of the 514th line of the speckle pattern with different scattering mediums. (e–h) The speckle pattern of different scattering mediums. Scale bar: 1.063 mm.
3.3. Enhancement of SHG with Scattering Effect
Here, we studied the effect of different scattering mediums on the enhancement of SHG. Figure 4 demonstrated that the specific field distribution constructed by the medium of different scattering degrees has an impact on the modulation of the second harmonic signal. The coordination between the first and second order phases of the fundamental frequency light field reaches a preferable effect by wavefront modulation, which can obtain high intensity of SHG. Interestingly, compared with the case of no scattering medium, placing a 220-grit ground glass with 16 16 modulated phase map can achieve higher enhancement of SHG, and the enhancement factor was 25 times. However, it was not always that the results of adding scattering would be better than that without scattering mediums. Figure 4a described the origin and optimized second harmonic light filed with different scattering mediums. Furthermore, a statistical histogram of multiple sets of data was displayed to explicitly represent the optimized results with different resolutions for different scattering mediums (Figure 4b). Obviously, employing the 220-grit ground glass got the best enhancement of SHG (the average of 22 times). According to the intensity distribution information of scattering mediums from Figure 3, the different character of scattering mediums can generate different speckle intensity distribution. Therefore, choosing an appropriate scattering medium can effectively enhance the conversion efficiency.
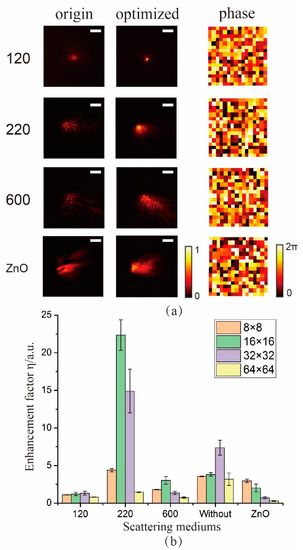
Figure 4.
The enhancement of SHG with different scattering mediums using wavefront shaping technique (results from the statistical average values of multiple experimental data). (a) The second harmonic light field before and after optimization of different scattering mediums. (b) Statistical histogram of the second harmonic intensity enhancement factor corresponding to different scattering mediums with different resolutions. Note: the optimized light field is collected after three times attenuation. Scale bar: 1.468 mm.
4. Conclusions
In this paper, a scattering medium to construct a speckle light field with a specific spatial distribution that can affect the intensity of SHG and increase the light intensity of SHG based on the wavefront shaping method was applied. Our experiment verified that modulation of phase and phase gradient of scattering field via genetic algorithm can achieve an effective enhancement of SHG. A higher enhancement can be realized when placing an appropriate scattering medium, compared to the case of no scattering medium. The 25-fold enhancement factor of SHG can be obtained when placing 220-grit ground glass in front of the BBO. The results have the potential to be applied in the fields of optical frequency conversion, second harmonic detection, and sensing. We envision that this experiment can be implemented in enhancement of higher harmonics.
Author Contributions
Conceptualization, L.W. and W.F.; methodology, L.W. and J.P.; software, L.W. and W.F.; validation, L.W.; formal analysis, L.W. and J.P.; writing—original draft preparation, L.W.; writing—review and editing, L.W., W.F., Z.C. and J.P.; project administration, Z.C. and J.P.; funding acquisition, Z.C. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC) under grant number 62005086, Graduate Student Research and Innovation Ability Training Program of Huaqiao University under grant number 18013082015.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.Y.; Nadiarynkh, O.; Plotnikov, S.; Campagnola, P.J. Second harmonic generation microscopy for quantitative analysis of collagen fibrillar structure. Nat. Protoc. 2012, 7, 654–669. [Google Scholar] [CrossRef] [PubMed]
- Campagnola, P.J.; Dong, C.Y. Second harmonic generation microscopy: Principles and applications to disease diagnosis. Laser Photon. Rev. 2011, 5, 13–26. [Google Scholar] [CrossRef]
- Keikhosravi, A.; Bredfeldt, J.S.; Sagar, A.K.; Eliceiri, K.W. Second-harmonic generation imaging of cancer. Method Cell Biol. 2014, 123, 531–546. [Google Scholar]
- Wang, C.; Zhang, M.; Yu, M.; Zhu, R.; Hu, H.; Loncar, M. Monolithic lithium niobate photonic circuits for Kerr frequency comb generation and modulation. Nat. Commun. 2019, 10, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Andrea, G.; Gorazd, P.; Daniele, R.; Degl′Innocenti, R.; Gunter, P. Electro–optically tunable microring resonators in lithium niobate. Nature. Photon. 2007, 1, 407–410. [Google Scholar]
- Abdelmonem, A.; Lützenkirchen, J.; Leisner, T. Probing ice-nucleation processes on the molecular level using second harmonic generation spectroscopy. Atmos. Meas. Tech. 2015, 8, 3519–3526. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.R. Surface properties probed by second-harmonic and sum-frequency generation. Nature 1989, 337, 519–525. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, H.; Miyauchi, Y.; Mizutani, G. Selective observation of local carrier dynamics at step bunches on vicinal TiO2 (110) by time-resolved pump-probe second harmonic generation method. Phy. Rev. B. 2012, 86, 045447. [Google Scholar] [CrossRef]
- Sun, Z.; Yi, Y.; Song, T. Giant nonreciprocal second-harmonic generation from antiferromagnetic bilayer CrI3. Nature 2019, 572, 497–501. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Padma, N.J.; Dhruba, J.B. Exploitation of an external unstable multi-pass cavity to enhance the second harmonic conversion efficiency. Opt. Commun. 2015, 341, 155–159. [Google Scholar] [CrossRef]
- Thompson, J.V.; Hokr, B.H.; Throckmorton, G.A.; Wang, D.W.; Scully, M.O.; Yakovlev, V.V. Enhanced second harmonic generation efficiency via wavefront shaping. ACS Photonics 2017, 4, 1790–1796. [Google Scholar] [CrossRef]
- Fan, W.R.; Chen, T.R.; Gil, E.; Zhu, S.Y.; Wang, D.W. Second harmonic imaging enhanced by deep learning decipher. ACS Photonics. 2021, 8, 1562–1568. [Google Scholar] [CrossRef]
- Nikolaev, N.A.; Yu, M.A.; Antsygin, V.D.; Bekker, T.B.; Ezhov, D.M.; Kokh, A.E.; Kokh, K.A.; Lanskii, G.V.; Mamrashev, A.A.; Svetlichnyi, V.A. Optical properties of β-BBO and potential for THz applications. J. Phys. Conf. Ser. 2018, 951, 012003. [Google Scholar] [CrossRef]
- Nguyen, D.T.T.; Lai, N.D. Deterministic Insertion of KTP Nanoparticles into Polymeric Structures for Efficient Second-Harmonic Generation. Crystals 2019, 9, 365. [Google Scholar] [CrossRef] [Green Version]
- Wei, D.; Wang, C.; Wang, H.; Hu, X.; Wei, D.; Fang, X.; Zhang, Y.; Wu, D.; Hu, Y.; Li, J.; et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal. Nat. Photon. 2018, 12, 596–600. [Google Scholar] [CrossRef]
- Reintjes, J.; Eckardt, R.C. Efficient harmonic generation from 532 to 266 nm in ADP and KD*P. Appl. Phys. Lett. 1977, 30, 91–93. [Google Scholar] [CrossRef]
- Chen, B.Q.; Ren, M.L.; Liu, R.J.; Zhang, C.; Sheng, Y.; Ma, B.; Li, Z. Simultaneous broadband generation of second and third harmonics from chirped nonlinear photonic crystals. Light Sci. Appl. 2014, 3, 189. [Google Scholar] [CrossRef]
- Lightman, S.; Gvishi, R.; Hurvitz, G.; Arie, A. Shaping of light beams by 3D direct laser writing on facets of nonlinear crystals. Opt. Lett. 2015, 40, 4460. [Google Scholar] [CrossRef]
- Shapira, A.; Libster, A.; Lilach, Y.; Arie, A. Functional facets for nonlinear crystals. Opt. Commun. 2013, 300, 244–248. [Google Scholar] [CrossRef]
- Liu, H.G.; Chen, X.F. The manipulation of second-order nonlinear harmonic wave by structured material and structured light. J. Nonlinear Opt. Phys. 2018, 27, 21. [Google Scholar] [CrossRef]
- Heinze, J.; Vahlbruch, H.; Willke, B. Frequency-doubling of continuous laser light in Laguerre-Gaussian modes LG(0,0) and LG(3,3). Opt. Lett. 2020, 45, 52–62. [Google Scholar]
- Wang, J.; Clementi, M.; Minkov, M.; Barone, A.; Carlin, J.-F.; Grandjean, N.; Gerace, D.; Fan, S.; Galli, M.; Houdré, R. Doubly resonant second-harmonic generation of a vortex beam from a bound state in the continuum. Optica 2020, 7, 1126–1132. [Google Scholar] [CrossRef]
- Zhang, L.; Qiu, X.; Li, F. Second harmonic generation with full Poincaré beams. Opt. Express. 2018, 26, 11678–11684. [Google Scholar] [CrossRef] [Green Version]
- Vellekoop, I.M. Feedback-based wavefront shaping. Opt. Express 2015, 23, 12189–12206. [Google Scholar] [CrossRef]
- Brown, E.; McKee, T.; DiTomaso, E.; Pluen, A.; Seed, B.; Boucher, Y.; Jain, R.K. Dynamic imaging of collagen and its modulation in tumors in vivo using second-harmonic generation. Nat. Med. 2003, 9, 796–800. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef]
- Sheng, S.C.; Siegman, A.E. Nonlinear-optical calculations using fast-transform methods: Second-harmonic generation with depletion and diffraction. Phys. Rev. A 1980, 21, 599–606. [Google Scholar] [CrossRef]
- Qiao, Y.; Peng, Y.; Zheng, Y. Second-harmonic focusing by a nonlinear turbid medium via feedback-based wavefront shaping. Opt. Lett. 2017, 42, 1895–1898. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.P.; Chen, Z.Y.; Huang, H.L.; Pu, J.X. Focusing light into desired patterns through turbid media by feedback-based wavefront shaping. Appl. Phys. B 2016, 122, 204. [Google Scholar] [CrossRef]
- Small, E.; Katz, O.; Guan, Y.; Silberberg, Y. Spectral control of broad-band light through random media by wavefront shaping. Opt. Lett. 2012, 37, 3429–3431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conkey, D.B.; Brown, A.N.; Caravaca-Aguirre, A.M.; Piestun, R. Genetic algorithm optimization for focusing through turbid media in noisy environments. Opt. Express 2012, 20, 4840–4849. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).