Uniform Accuracy Lifetime Principle and Optimal Design Methods for Measurement Systems
Abstract
:1. Introduction
2. The Principle of Uniform Accuracy Lifetime Design
2.1. The Principle
2.2. Definition of Uniformity of the Accuracy Lifetimes
2.3. Definition and Determination of the Accuracy Loss Weight
3. Optimization Modeling for the Uniformity Design of Accuracy Lifetimes
3.1. Determination of Design Variables
3.2. Selection of Objective Functions
- (1)
- The uniformity of lifetimes is the maximum:
- (2)
- The effective accuracy lifetime T′ of the measurement system is the maximum. Assuming that the effective lifetime of the system equals the minimum lifetime of all, the objective function is as follows:
- (3)
- The total improvement cost Cs is the minimum. Suppose that the relationship between the improvement cost Ci and the designed value of the i-th component is , the objective function can be derived:
3.3. Modeling of Constraint Conditions
3.4. Solution of the Optimization Model
4. An Optimal Design
4.1. Design Procedure Based on the Principle of Uniform Accuracy Lifetimes
- (1)
- Obtain the accuracy loss sequences of the measurement system and its components through experiences or experiments, and determine their accuracy loss allowable values.
- (2)
- Set up models for all accuracy loss sequences, obtain their mathematic functions, and then calculate their original accuracy lifetimes {T1, T2, …, Tn, Ts} according to their accuracy loss allowable values.
- (3)
- Calculate the uniformity ρ of the lifetime of the whole system, and judge whether it meets the requirement ρ ≥ ε. If ρ ≥ ε, the system does not need to be redesigned. If not, the system should be optimally designed.
- (4)
- Determine the accuracy loss weights of the components, and establish the optimal design model with an objective function, such as the longest lifetime, the lowest cost or the biggest uniformity (see Section 2).
- (5)
- Employ the method of combining uniform sampling technology with SQP to solve the optimization model, and then gain the optimal average accuracy loss velocities of the system and its components (see Section 3).
- (6)
- On the premise of mastering a large number of test data and accuracy loss laws of typical structures, gradually change some factors such as the structures, parameters, materials and working conditions of the original system according to the above designed results until the uniformity design target is achieved.
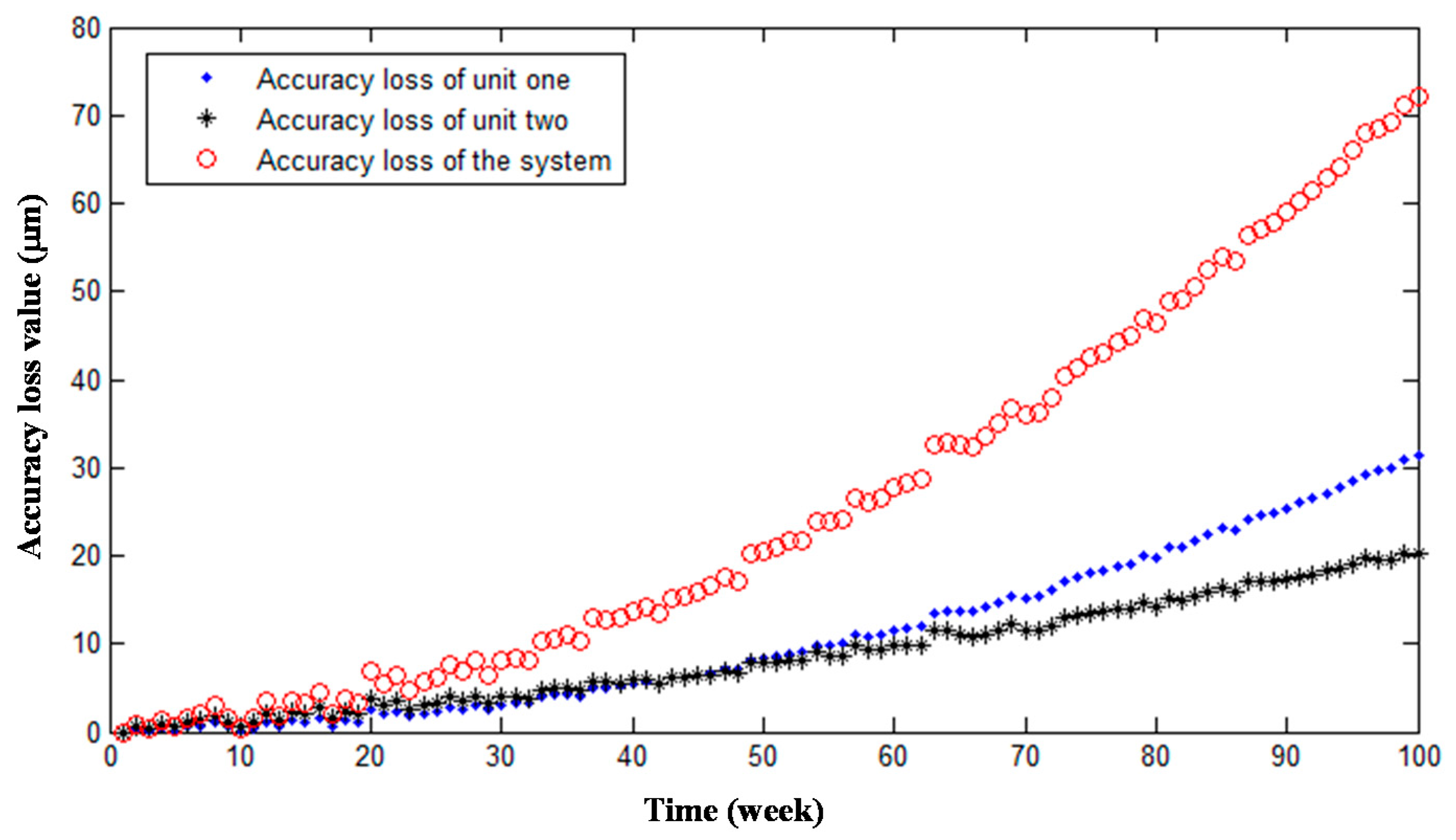
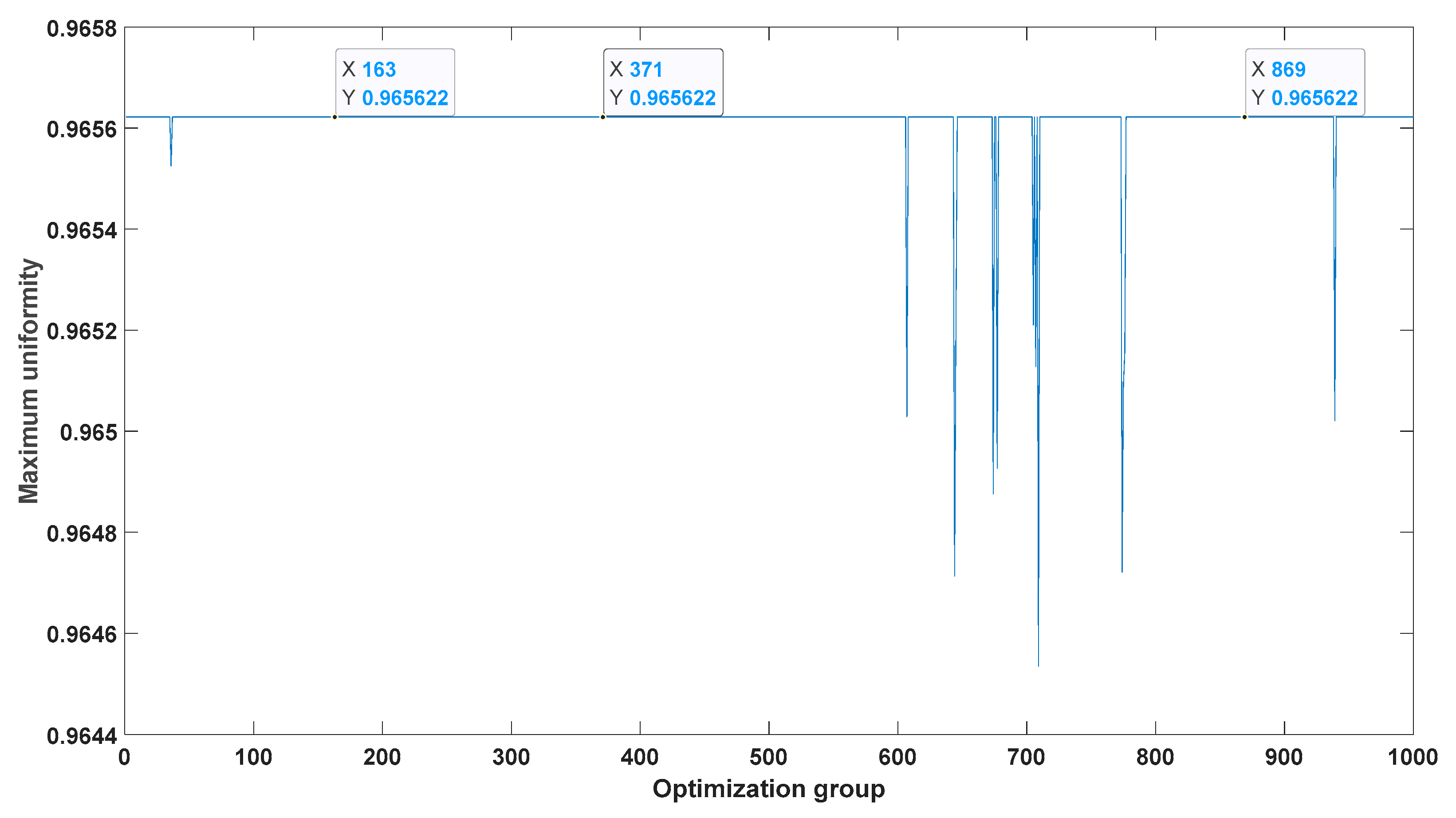
4.2. A Design Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, S.F.; Chen, X.H.; Zhang, Y.B.; Fei, Y.T. The Analysis of Uncertainty and Research of Dynamic Character on Measurement System. Acta Metrol. Sin. 2002, 3, 237–240. [Google Scholar]
- Liu, J.L.; Ma, C.; Wang, S.L. Precision loss modeling method of ball screw pair. Mech. Syst. Signal Process 2020, 135, 106397. [Google Scholar] [CrossRef]
- Zhao, J.J.; Lin, M.M.; Song, X.C.; Wei, N. A modeling method for predicting the precision loss of the preload double-nut ball screw induced by raceway wear based on fractal theory. Wear 2021, 486–487, 204065. [Google Scholar] [CrossRef]
- Qi, B.B.; Cheng, Q.; Li, S.L.; Liu, Z.F.; Yang, C.B. Precision loss of ball screw mechanism under sliding-rolling mixed motion behavior. J. Cent. South Univ. 2021, 28, 1357–1376. [Google Scholar] [CrossRef]
- Cheng, Q.; Qi, B.B.; Chu, H.Y.; Zhang, Z.L.; Liu, Z.F.; Zheng, J.G. The analysis on the influence of mixed sliding-rolling motion mode to precision degradation of ball screw. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2022, 236, 669–688. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen, H.M.; Kuo, T.H. Prediction of machining accuracy degradation of machine tools. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2012, 36, 288–298. [Google Scholar] [CrossRef]
- Ji, Z.Q.; Ou, Y.; Feng, H.T.; Zhang, Y. Measurement method and tests for precision-keeping of a linear rolling guide based on online measuring. J. Vib. Shock. 2016, 35, 56–61. [Google Scholar] [CrossRef]
- Zhong, Y.; Tao, W.J.; Han, J. Model Study of Precision Loss of Linear Ball Guide. Modul. Mach. Tool Autom. Manuf. Tech. 2013, 12, 33–36. [Google Scholar] [CrossRef]
- Jiang, M.L.; Fei, Y.T. The Accuracy Losing Diagnosis about Pressure Sensor System. J. Shanghai Jiaotong Univ. 2006, 12, 2063–2065. [Google Scholar] [CrossRef]
- Jiang, M.L. Accuracy losing diagnosis about measuring-system of differential mutual inductive displacement sensor. J. Heilongjiang Inst. Sci. Technol. 2005, 15, 371–373. [Google Scholar] [CrossRef]
- Jiang, M.L.; Li, F.P.; Wang, X.D. Dynamic Accuracy Loss Prediction model based on SVM. In Proceedings of the ETP/IITA Conference on System Science and Simulation in Engineering (SSSE 2010), Hong Kong, China, 29 June–1 July 2010. [Google Scholar]
- Jiang, M.L.; Wang, X.D.; He, X.H. Dynamic Accuracy Loss Prediction model based on BPNN. In Proceedings of the International Conference on Advanced Measurement and Test (AMT 2010), Sanya, China, 15–16 May 2010. [Google Scholar]
- Zhang, X.C.; Gao, H.L.; Huang, H.F.; Zhang, L.; Peng, Z.W. Screw lifetime prediction based on wavelet neural network and empirical mode decomposition. In Proceedings of the International Conference “Vibroengineering—2015”, Nanjing, China, 26–28 September 2015. [Google Scholar]
- Xu, Z.C.; Wang, L.J.; Liu, Y.; Cai, K.L.; Chen, Z.K.; Chen, B.J. A Prediction Method for Remaining Life of Rolling Bearing Using Improved Regression Support Vector Machine. J. Xi’an Jiaotong Univ. 2022, 56, 197–205. [Google Scholar] [CrossRef]
- Yoo, Y.; Baek, J.G. A Novel Image Feature for the Remaining Useful Lifetime Prediction of Bearings Based on Continuous Wavelet Transform and Convolutional Neural Network. Appl. Sci. 2018, 8, 1102. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.B.; Wang, X.H.; Wang, L.Z. Modeling of BN Lifetime Prediction of a System Based on Integrated Multi-Level Information. Sensors 2017, 17, 2123. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.Y.; Li, F.; Tang, B.P.; Tian, D.Q. Quantum gene chain coding bidirectional neural network for residual useful life prediction of rotating machinery. Chin. J. Sci. Instrum. 2020, 41, 164–174. [Google Scholar] [CrossRef]
- Wu, X.G.; Cui, Z.H.; Li, X.F.; Du, J.Y.; Liu, Y. Control Strategy for Active Hierarchical Equalization Circuits of Series Battery Packs. Energies 2019, 12, 2071. [Google Scholar] [CrossRef] [Green Version]
- Lewandowski, M.; Bernas, M.; Loska, P.; Szymala, P.; Placzek, B. Extending Lifetime of Wireless Sensor Network in Application to Road Traffic Monitoring. In Proceedings of the 26th International Conference on Computer Networks (CN), Kamien Slaski, Poland, 25–27 June 2019. [Google Scholar]
- Hung, L.L. A Smart Sensing and Routing Mechanism for Wireless Sensor Networks. Sensors 2020, 20, 5720. [Google Scholar] [CrossRef]
- Yetgin, H.; Cheung, K.T.K.; El-Hajjar, M.; Hanzo, L. A Survey of Network Lifetime Maximization Techniques in Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2017, 19, 828–854. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.Y.; Liu, Z.R.; Jia, J.H.; Bai, G.; Zhao, X.L. Mixed optimal control scheme based on capacity balance and voltage balance. Power Supply Technol. Its Appl. 2019, 45, 108–112. [Google Scholar] [CrossRef]
- Liu, X.H. Life Balance Evaluation System Development of Large Air Separation Compressor Unit. Master’s Thesis, Northeastern University, Shenyang, China, June 2014. [Google Scholar]
- Wang, Y.X.; Wei, X.Z.; Fang, Q.H.; Zhu, J.G.; Dai, H.F. Consistency Variation Law and Equalization Strategy of Electric Vehicle Battery for Maximizing the Life of the Battery Pack. J. Mech. Eng. 2020, 56, 176–183. [Google Scholar] [CrossRef]
- Wu, D.P. Study on Life Cycle Balancing Strategy of Lithium-ion Power Battery Pack. Master’s Thesis, Chongqing University, Chongqing, China, June 2019. [Google Scholar]
- Cheng, Z.Y.; Fei, Y.T.; Chen, X.H. Research on Uniform Design Theory for Dynamic Measurement Systems. China Mech. Eng. 2008, 19, 893–896. [Google Scholar]
- Jiang, M.L.; Lu, X.C.; Duan, M.J.; Wang, X.D. Weight function theory of dynamic accuracy loss. In Proceedings of the 7th International Symposium on Precision Engineering Measurements and Instrumentation (ISPEMI), Lijiang, China, 7–11 August 2011. [Google Scholar]
- Liu, F.F.; Fei, Y.T.; Jiang, M.L. Theoretical Model of Accuracy Loss Equality Design in Dynamic Measuring System. Trans. Chin. Soc. Agric. Mach. 2008, 39, 134–136. [Google Scholar]
- Liao, W.S. Experimental Study on Translucent Concrete Building Components and Indoor Environmental Performance. Master’s Thesis, Dalian University of Technology, Dalian, China, June 2019. [Google Scholar]
- Ma, C.F. Optimization Method and Its Matlab Program Design; National Defense Industry Press: Beijing, China, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Liu, L.; Li, R. Uniform Accuracy Lifetime Principle and Optimal Design Methods for Measurement Systems. Appl. Sci. 2022, 12, 3961. https://doi.org/10.3390/app12083961
Cheng Z, Liu L, Li R. Uniform Accuracy Lifetime Principle and Optimal Design Methods for Measurement Systems. Applied Sciences. 2022; 12(8):3961. https://doi.org/10.3390/app12083961
Chicago/Turabian StyleCheng, Zhenying, Liying Liu, and Ruijun Li. 2022. "Uniform Accuracy Lifetime Principle and Optimal Design Methods for Measurement Systems" Applied Sciences 12, no. 8: 3961. https://doi.org/10.3390/app12083961
APA StyleCheng, Z., Liu, L., & Li, R. (2022). Uniform Accuracy Lifetime Principle and Optimal Design Methods for Measurement Systems. Applied Sciences, 12(8), 3961. https://doi.org/10.3390/app12083961






