Tree Based Approaches for Predicting Concrete Carbonation Coefficient
Abstract
:1. Introduction
2. Tree Based Modelling Techniques
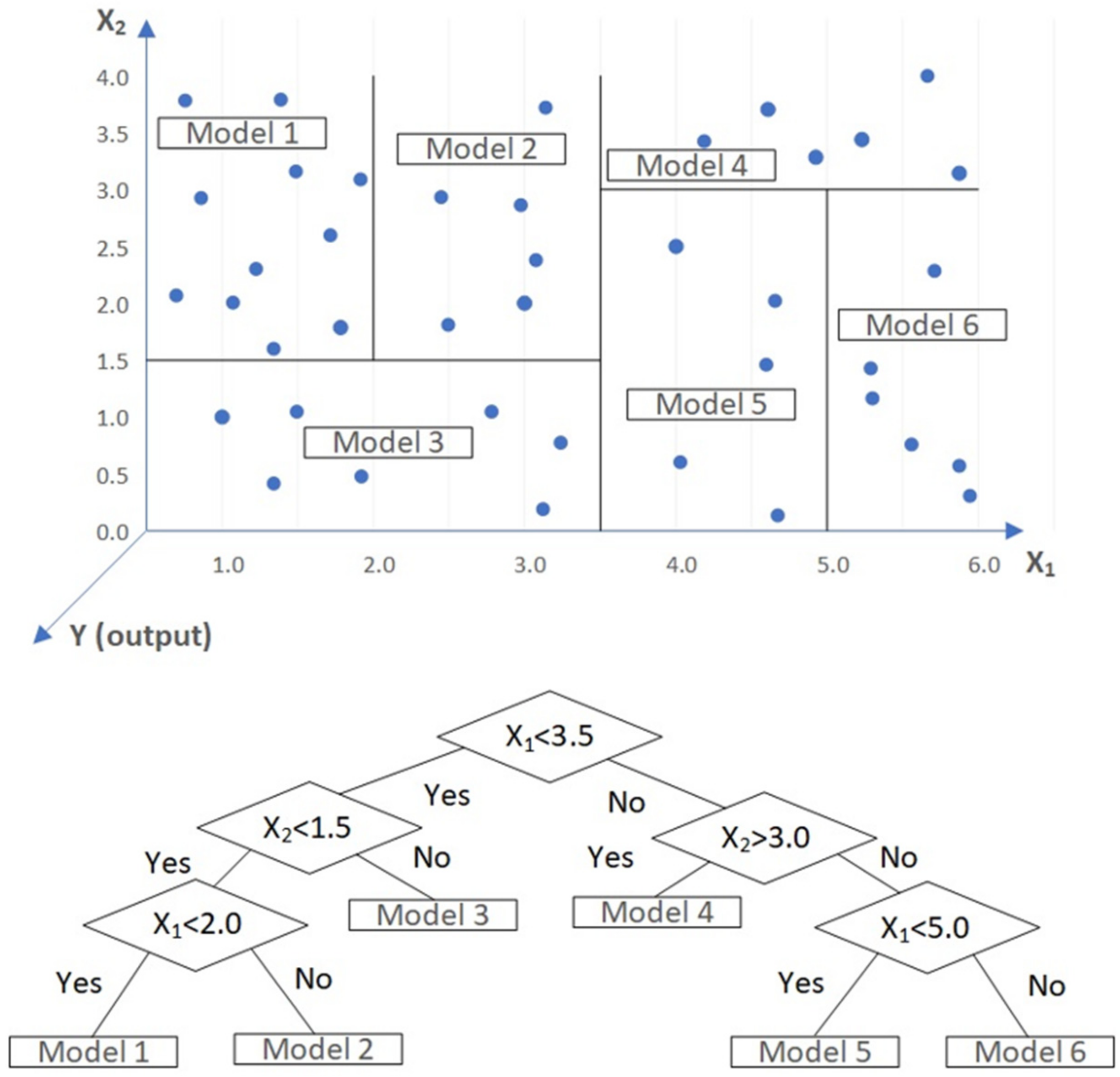
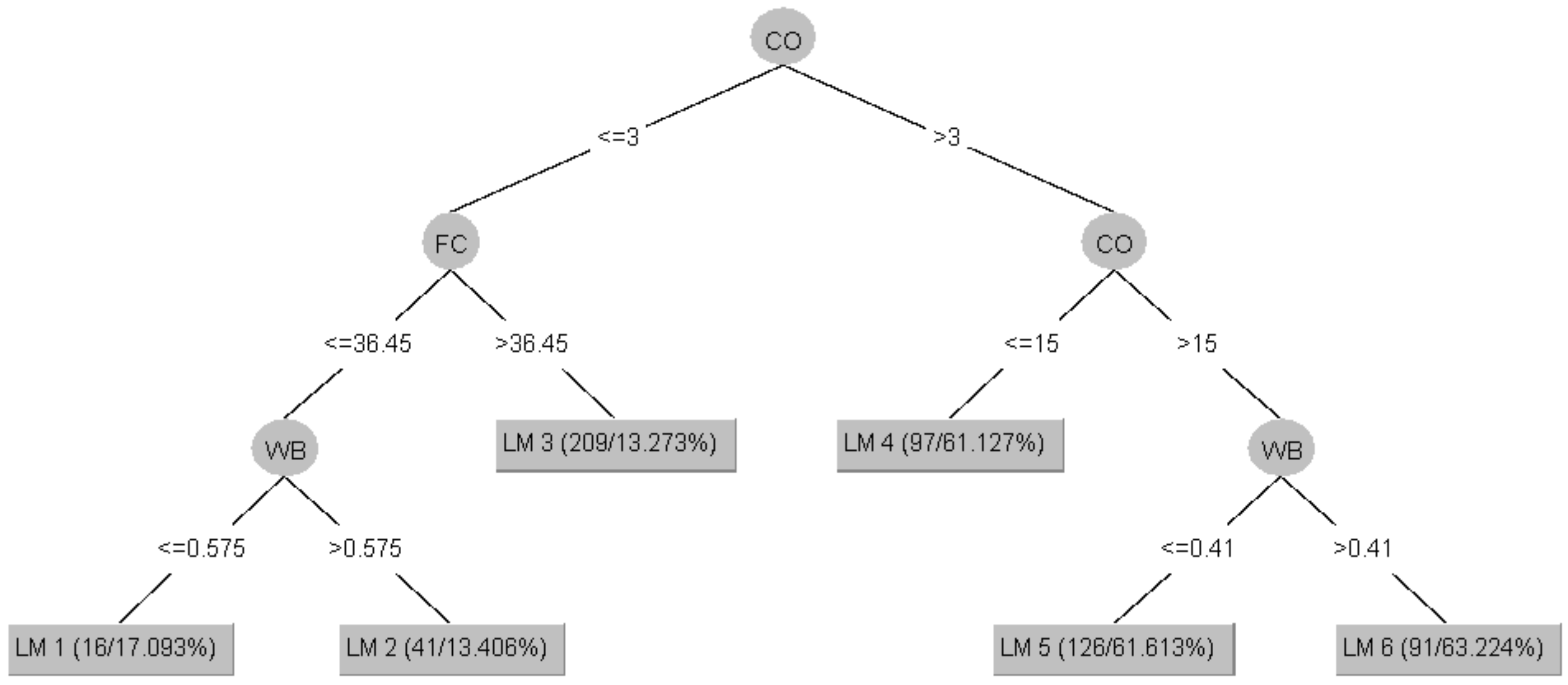
2.1. Model Tree (MT)
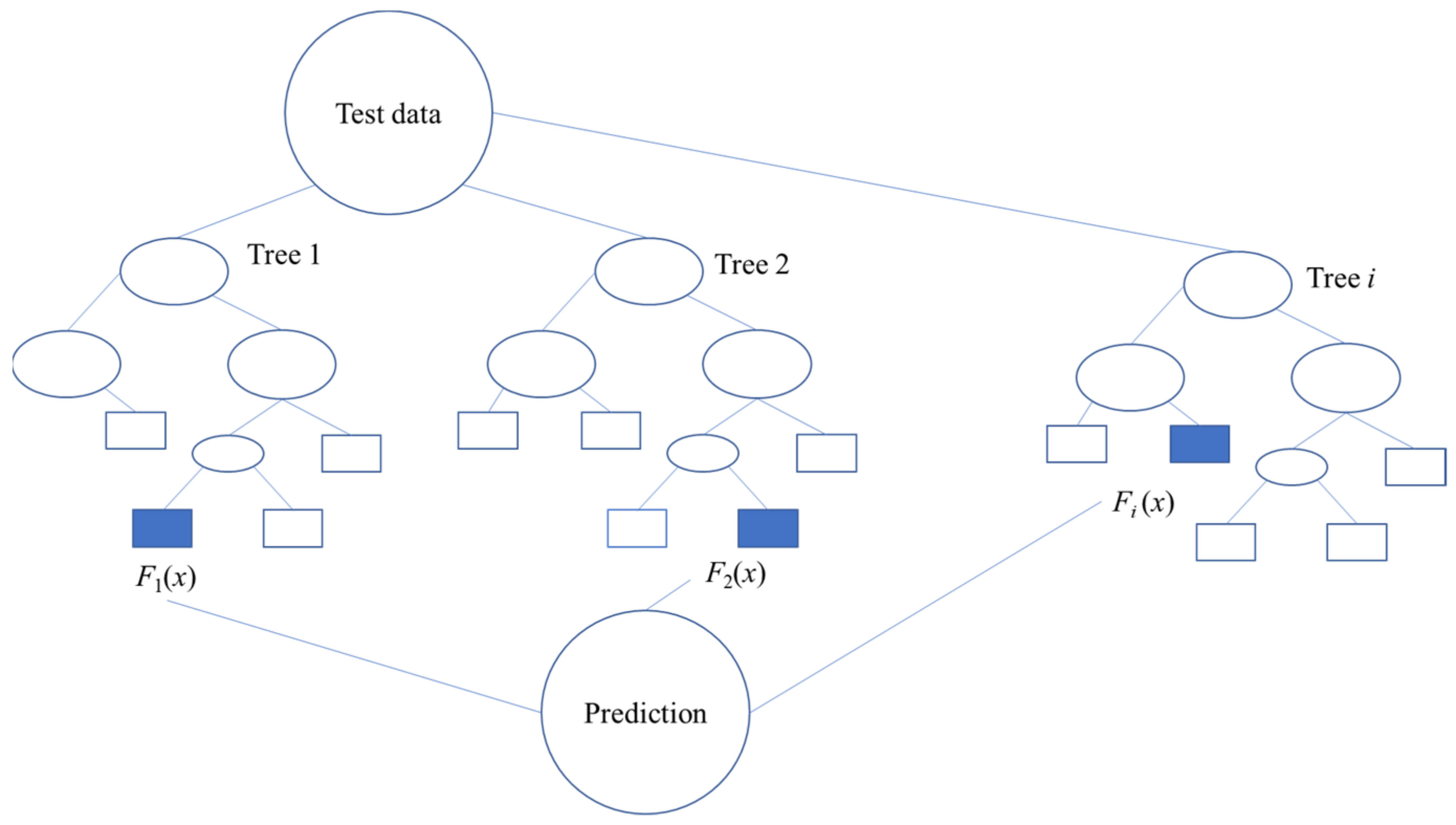
2.2. Random Forest (RF)
2.3. Multi-Gene Genetic Programming (MGGP)
3. Materials and Methods
3.1. Data Used in the Study
3.2. Methodology Adopted
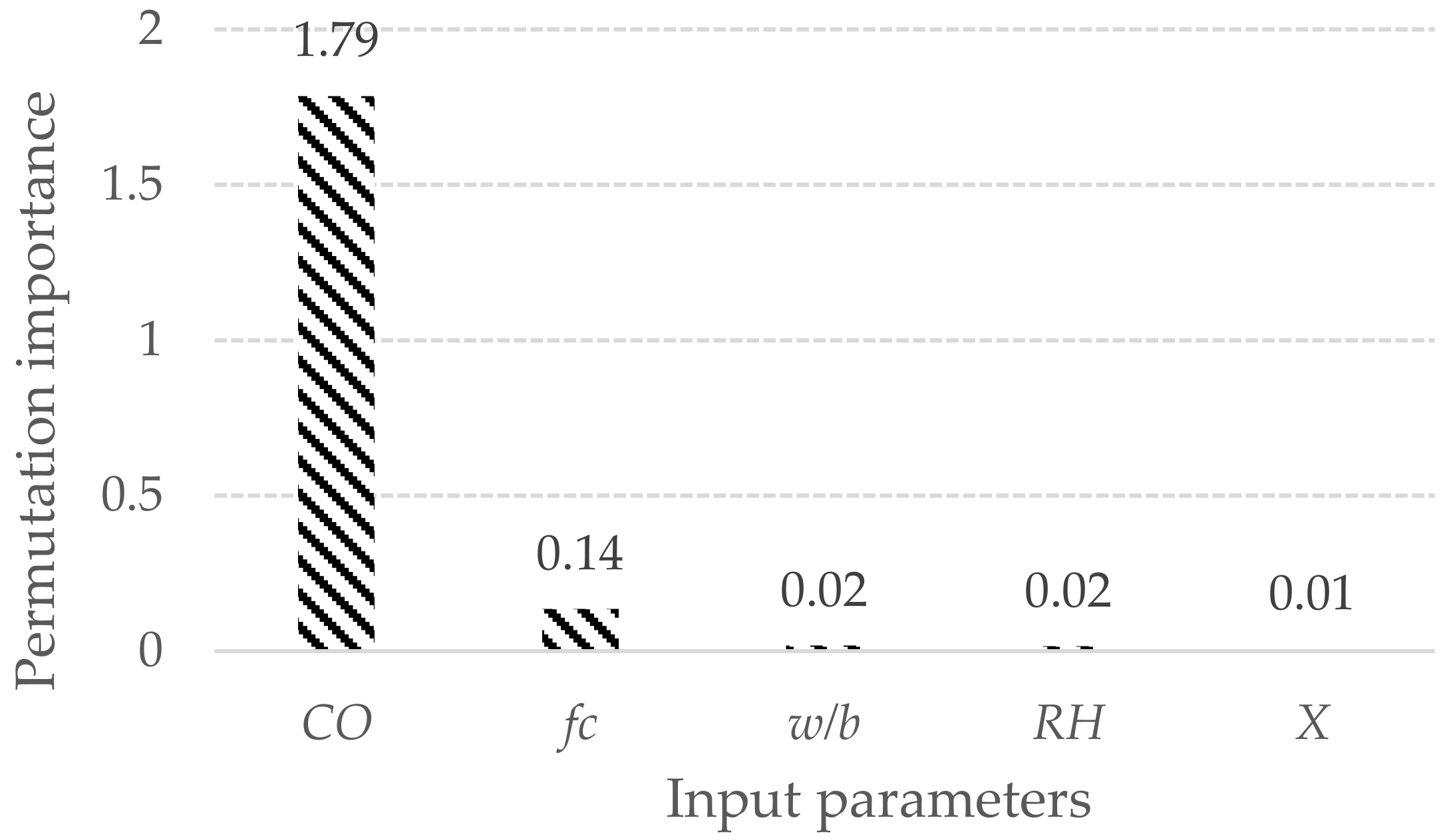
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ciampoli, M. Time dependent reliability of structural systems subject to deterioration. Comput. Struct. 1998, 67, 29–35. [Google Scholar] [CrossRef]
- Ann, K.Y.; Pack, S.W.; Hwang, J.P.; Song, H.W.; Kim, S.H. Service life prediction of a concrete bridge structure subjected to carbonation. Constr. Build. Mater. 2010, 24, 1494–1501. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, Z.; Zhang, W.; Gu, X.; Dou, X. Numerical analysis of the effect of coarse aggregate distribution on concrete carbonation. Constr. Build. Mater. 2012, 37, 27–35. [Google Scholar] [CrossRef]
- Taffese, W.Z.; Al-Neshawy, F.; Sistonen, E.; Ferreira, M. Optimized neural network-based carbonation prediction model. In Proceedings of the International Symposium Non-Destructive Testing in Civil Engineering (NDT-CE) 2015, Berlin, Germany, 15–17 September 2015. [Google Scholar]
- Neville, A.M. Properties of Concrete, 4th ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Neves, R. The Air Permeability and Concrete Carbonation of Concrete in Structures. Ph.D. Thesis, Instituto Superior Técnico, Technical University of Lisbon, Lisbon, Portugal, 2012. [Google Scholar]
- Chang, C.F.; Chen, J.W. The experimental investigation of concrete carbonation depth. Cem. Concr. Res. 2006, 36, 1760–1767. [Google Scholar] [CrossRef]
- Monteiro, I.; Branco, F.A.; de Brito, J.; Neves, R. Statistical analysis of the carbonation coefficient in open air concrete structures. Constr. Build. Mater. 2012, 29, 263–269. [Google Scholar] [CrossRef]
- Papadakis, V.G.; Vayenas, C.G.; Fardis, M.N. Fundamental modelling and experimental investigation of concrete carbonation. ACI Mater. J. 1991, 88, 363–373. [Google Scholar]
- Kwon, S.J.; Song, H.W. Analysis of carbonation behavior in concrete using neural network algorithm and carbonation modeling. Cem. Concr. Res. 2010, 40, 119–127. [Google Scholar] [CrossRef]
- Londhe, S.N.; Kulkarni, P.S.; Dixit, P.R.; Silva, A.; Neves, R.; de Brito, J. Predicting carbonation coefficient using Artificial neural networks and genetic programming. J. Build. Eng. 2021, 39, 1022–1058. [Google Scholar] [CrossRef]
- Parthiban, T.; Ravi, R.; Parthiban, G.T.; Srinivasan, S.; Ramakrishnan, K.R.; Raghavan, M. Neural network analysis for corrosion of steel in concrete. Corros. Sci. 2005, 47, 625–1642. [Google Scholar] [CrossRef]
- Peng, J.; Li, Z.; Ma, B. Neural network analysis of chloride diffusion in concrete. J. Mater. Civ. Eng. 2002, 14, 327–333. [Google Scholar] [CrossRef]
- Kewalramani, M.A.; Gupta, R. Concrete compressive strength prediction using ultrasonic pulse velocity through artificial neural networks. Autom. Constr. 2006, 15, 374–379. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architecture for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Brusaferria, A.; Matteuccib, M.; Portolania, P.; Vitalia, A. Bayesian deep learning based method for probabilistic forecast of day-ahead electricity prices. Appl. Energy 2019, 250, 1158–1175. [Google Scholar] [CrossRef]
- Daou, H.; Raphael, W. A Bayesian regression framework for concrete creep prediction improvement: Application to Eurocode 2 model. Res. Eng. Struct. Mater. 2021, 7, 393–411. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Martín-Pérez, B. Bayesian Belief Network to Assess Carbonation-Induced Corrosion in Reinforced Concrete. J. Mater. Civ. Eng. 2008, 20, 707–717. [Google Scholar] [CrossRef]
- Zewdu, W.T.; Sistonen, E.; Puttonen, J. Prediction of Concrete Carbonation Depth using Decision Trees. In Proceedings of the ESANN 2015 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 23–23 April 2015. [Google Scholar]
- Murad, Y.Z.; Tarawneh, B.K.; Ashteyat, A.M. Prediction model for concrete carbonation depth using gene expression programming. Comput. Concr. 2020, 26, 497–504. [Google Scholar]
- Londhe, S.N.; Kulkarni, P.S.; Dixit, P.R. A comparative study of concrete strength prediction using artificial neural network, multigene programming and model tree. Chall. J. Struct. Mech. 2019, 5, 1–42. [Google Scholar]
- Liu, P.; Wu, X.; Cheng, H.; Zheng, T. Prediction of compressive strength of High-Performance Concrete by Random Forest algorithm. IOP Conf. Ser. Earth Environ. Sci. 2020, 552, 012020. [Google Scholar]
- Silva, A.; Neves, R.; de Brito, J. Statistical modeling of carbonation in reinforced concrete. Cem. Concr. Compos. 2014, 50, 73–81. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings AI”92; Adams, A., Sterling, L., Eds.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations; Morgan Kaufmann: Los Altos, CA, USA, 2000. [Google Scholar]
- Granada, F.; Saroli, M.; de Marinis, G.; Gargano, R. Machine Learning Models for Spring Discharge Forecasting. Geofluids 2017, 2018, 8328167. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Tyralis, H.; Georgia, P.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Hai-Bang, L.; Tran, V.Q. Estimation of compressive strength of concrete containing manufactured sand by Random Forest. Int. J. Sci. Technol. Res. 2020, 9, 564–567. [Google Scholar]
- Londhe, S.N.; Dixit, P.R. Genetic programming: A novel computing approach in modeling water flows. In Genetic Programming—In New Approaches and Successful Applications; licensee InTech.16; IntechOpen: London, UK, 2012; Chapter 9. [Google Scholar]
- Searson, D.P.; Leahy, D.E.; Willis, M.J. GPTIPS: An Open-Source Genetic Programming Toolbox for Multigene Symbolic Regression. In Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010. [Google Scholar]
- Searson, D.P.; Willis, M.J.; Montague, G.A. Co-evolution of non-linear PLS model components. J. Chemom. 2007, 2, 592–603. [Google Scholar] [CrossRef]
- Pandey, D.S.; Pan, I.; Das, S.; Leahy, J.J.; Kwapinski, W. Multi-gene genetic programming based predictive models for municipal solid waste gasification in a fluidized bed gasifier. Bioresour. Technol. 2015, 179, 524–533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hii, C.; Searson, D.P.; Willis, M.J. Evolving toxicity models using multigene symbolic regression and multiple objectives. Int. J. Mach. Learn. Comput. 2011, 1, 30–35. [Google Scholar] [CrossRef] [Green Version]
- Hair, J.F.; Black, W.C.; Babin, B.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis, 6th ed.; Prentice-Hall Publishers: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- Helene, P.R.L. Contribution to the Study of Corrosion of Concrete Reinforcement. Ph.D. Thesis, Polytechnic School, University of São Paulo, São Paulo, Brazil, 1993. (In Portuguese). [Google Scholar]
- Available online: https://waikato.github.io/weka-wiki/downloading_weka/ (accessed on 24 November 2021).
- Jain, A.; KumarJha, S.; Misra, S. Modeling and analysis of concrete slump using Artificial Neural Networks. J. Mater. Civ. Eng. 2008, 20, 628–633. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness of fit” measures in hydrological and hydro climatic model validation. Water Resour. Res. 1991, 35, 233–241. [Google Scholar] [CrossRef]
- Londhe, S.N. Soft computing approach for real-time estimation of missing wave heights. Ocean. Eng. 2008, 35, 1080–1089. [Google Scholar] [CrossRef]
- Gandomia, A.H.; Mohammadzadeh, D.; Juan Luis Pérez-Ordóñez, S.B.; Alavid, A.H. Linear genetic programming for shear strength prediction of reinforced concrete beams without stirrups. Appl. Soft Comput. 2014, 19, 112–120. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Atefi, E. Software review: The GPTIPS platform. Genet. Program. Evolvable Mach. 2020, 21, 273–280. [Google Scholar] [CrossRef] [Green Version]
- Dang, S.; Peng, L.; Zhao, J.; Li, J.; Kong, Z. A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method. Energies 2022, 15, 663. [Google Scholar] [CrossRef]
- Meinshausen, N. Quantile Regression Forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Wang, H.; Zhang, Y.-M.; Mao, J.-X. Sparse Gaussian process regression for multi-step ahead forecasting of wind gusts combining numerical weather predictions and on-site measurements. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104873. [Google Scholar] [CrossRef]


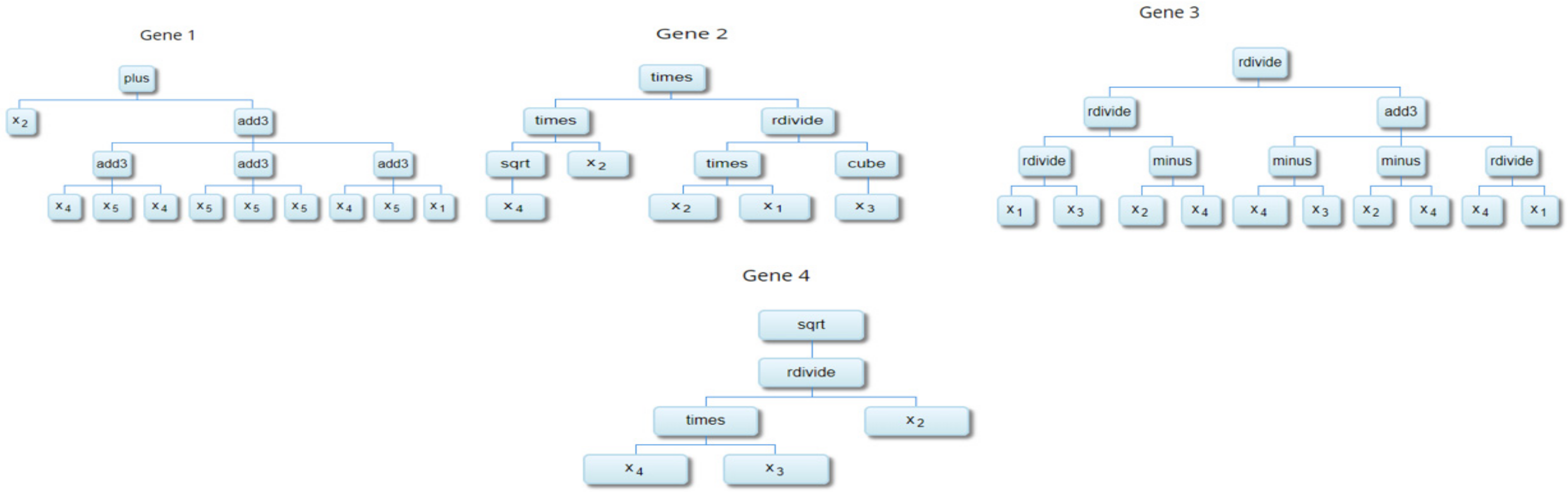

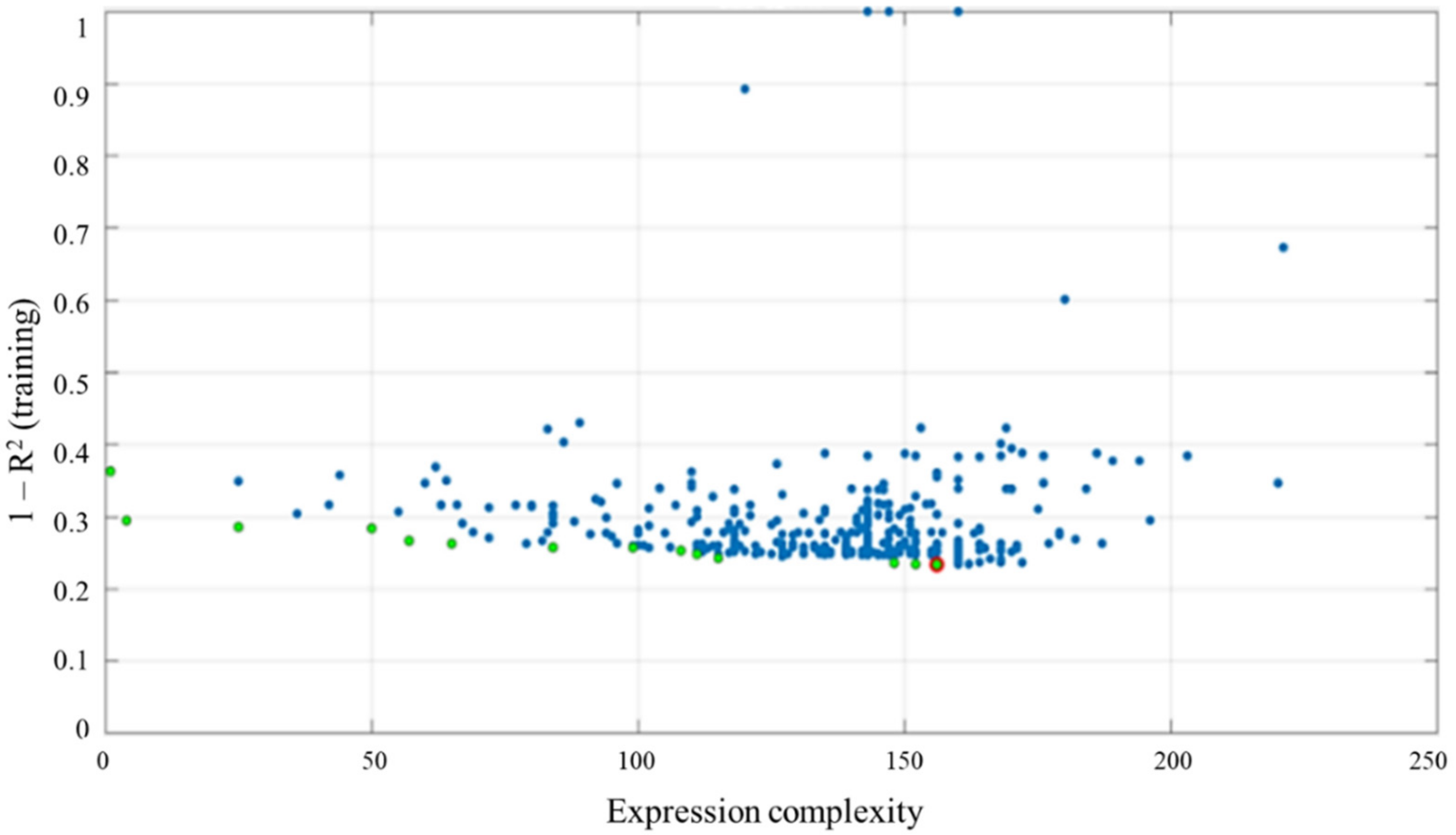
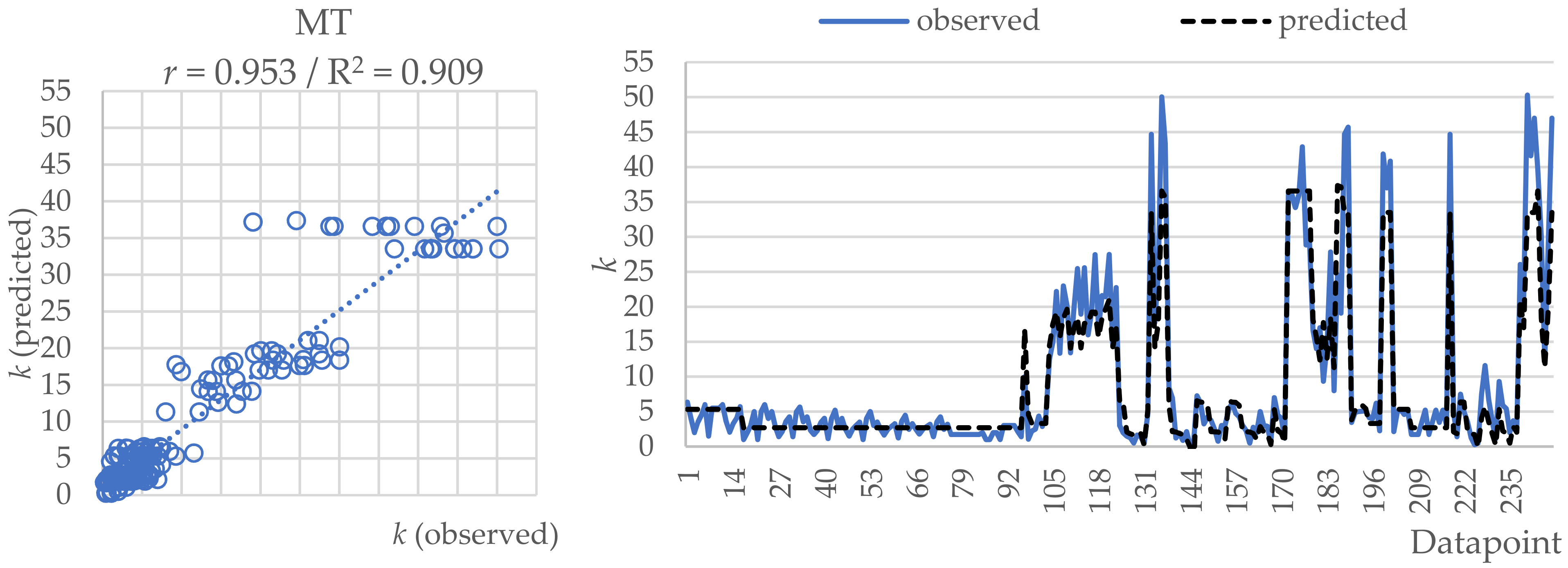
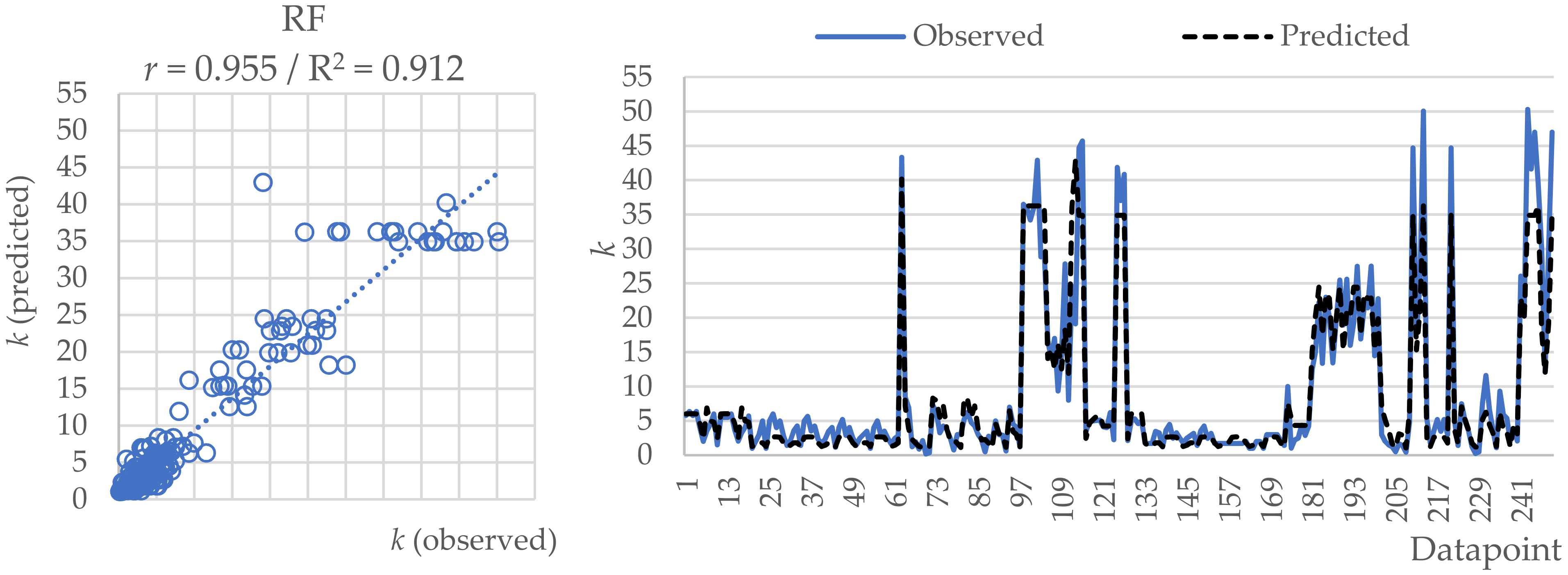

| Parameters | Min | Max | Mean | Mode |
|---|---|---|---|---|
| Clinker (kg/m3)—CC | 66.000 | 529.150 | 292.196 | 362.990 |
| Clinker/binder ratio (%)—CR | 20.000 | 100.000 | 80.228 | 95 |
| 28-day compressive strength in MPa—fc | 8.800 | 127.500 | 48.823 | 37.000 |
| CO2 content—CO | 0.020 | 50.000 | 15.490 | 0.040 |
| Number of curing days—d | 7 | 91 | - | 28 |
| Water/binder ratio—w/b | 0.240 | 1.000 | 0.501 | 0.370 |
| Relative humidity (%)—RH | 50 | 90 | - | 65 |
| Exposure class—X | 1 | 3 | - | 1 |
| Carbonation coefficient in (mm/year0.5)—k | 0.180 | 60.420 | 14.585 | 1.730 |
| MGGP Parameters | Parameter Settings |
|---|---|
| Population size | 500–900 |
| Number of generations | 200–500 |
| Selection method | Tournament |
| Tournament size | 13–15 |
| Cross-over rate | 0.78–0.84 |
| Mutation rate | 0.14–0.20 |
| Termination criteria | 500 generation or fitness value less than 0.00 whichever is earlier. |
| Maximum number of genes and tree depth | 4–5 |
| Mathematical operations | +, −, ×, /, sin, cos, exp, √, {} |
| Term | Value | Weight |
|---|---|---|
| Bias | 9.83 | 9.83 |
| Gene 1 | −0.138 | |
| Gene 2 | 451 | |
| Gene 3 | 83,300 | |
| Gene 4 | 4.39 |
| MT | RF | MGGP | |
|---|---|---|---|
| Time required for modelling | Building the model: 0.08 s Testing the models: 0.01 s | 40.5104 s | 14 min 88 s |
| r | 0.953 | 0.955 | 0.936 |
| RMSE | 3.871 | 3.584 | 4.453 |
| MAE | 2.341 | 2.032 | 2.546 |
| Artificial Neural Network (ANNs) | Genetic Programming (GP) | Multiple Linear Regression (MLR) | |
|---|---|---|---|
| Correlation coefficient—r | 0.940 | 0.937 | 0.917 |
| Root mean square error—RMSE | 4.554 | 4.510 | 5.019 |
| Mean Absolute Error | 2.991 | 2.598 | 3.371 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Londhe, S.; Kulkarni, P.; Dixit, P.; Silva, A.; Neves, R.; de Brito, J. Tree Based Approaches for Predicting Concrete Carbonation Coefficient. Appl. Sci. 2022, 12, 3874. https://doi.org/10.3390/app12083874
Londhe S, Kulkarni P, Dixit P, Silva A, Neves R, de Brito J. Tree Based Approaches for Predicting Concrete Carbonation Coefficient. Applied Sciences. 2022; 12(8):3874. https://doi.org/10.3390/app12083874
Chicago/Turabian StyleLondhe, Shreenivas, Preeti Kulkarni, Pradnya Dixit, Ana Silva, Rui Neves, and Jorge de Brito. 2022. "Tree Based Approaches for Predicting Concrete Carbonation Coefficient" Applied Sciences 12, no. 8: 3874. https://doi.org/10.3390/app12083874
APA StyleLondhe, S., Kulkarni, P., Dixit, P., Silva, A., Neves, R., & de Brito, J. (2022). Tree Based Approaches for Predicting Concrete Carbonation Coefficient. Applied Sciences, 12(8), 3874. https://doi.org/10.3390/app12083874









