Normalizing Flows for Out-of-Distribution Detection: Application to Coronary Artery Segmentation
Abstract
:1. Introduction
- Prior for variational inference: Instead of employing a fixed distribution (usually the normal distribution) in the KL term for ELBO maximization in variational inference, NF can be employed to model a much more expressive prior distribution. In a variational auto-encoder (VAE), this allows the encoder to better capture input patterns by not placing a fixed constraint on its computed embeddings. Ziegler and Rush [12] employed such a method for character-level language modeling and polyphonic music generation.
- Out-of-Distribution (OoD) detection: As log-likelihood values can be exactly and efficiently computed, NF may be good candidates in outlier detection [13].
2. Methods
2.1. Patients and Imaging Protocol
2.2. CCTA Annotations
2.3. Data Preparation for Convolutional Neural Networks
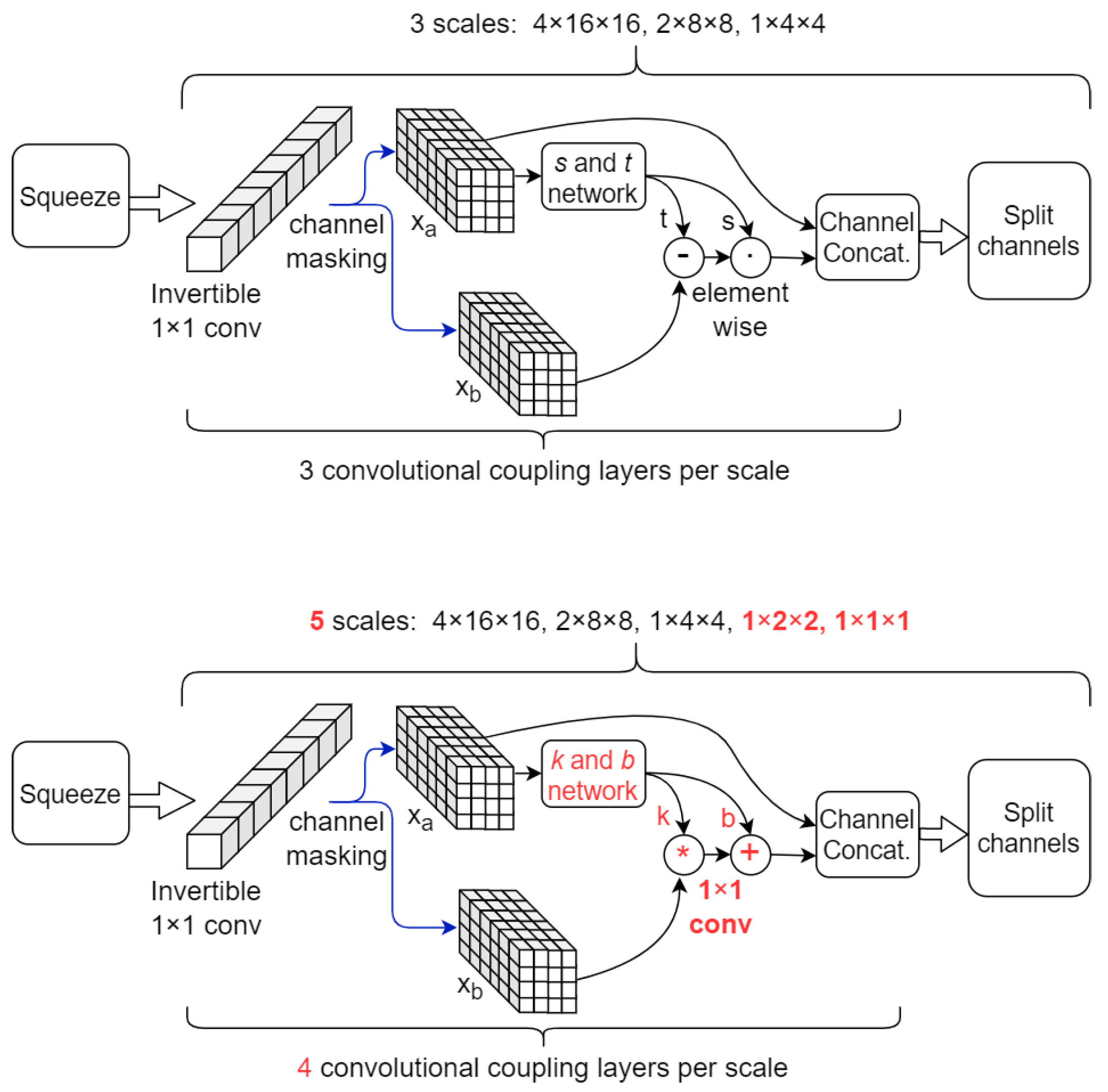
2.4. NF Architectures
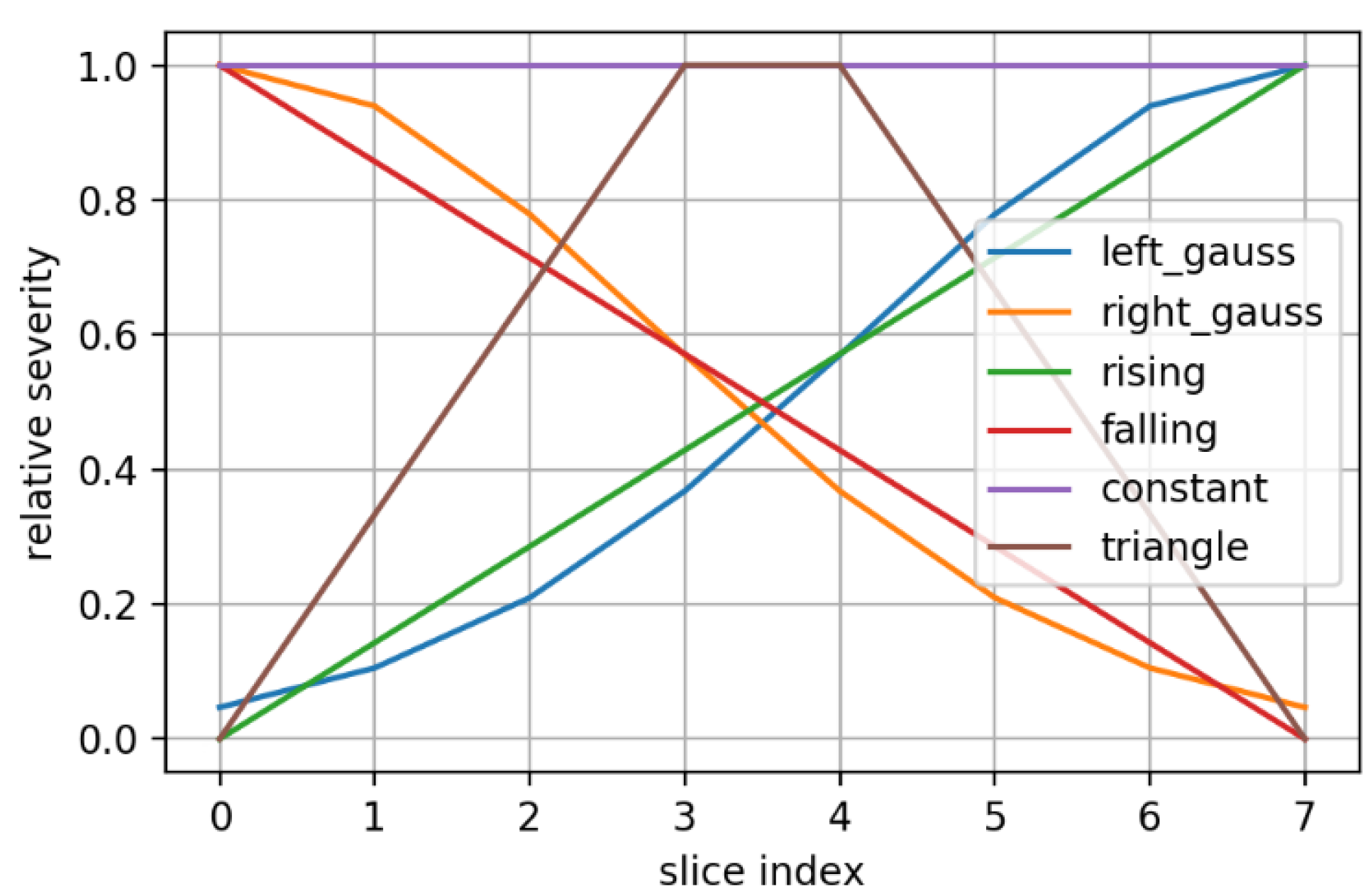
2.5. Synthetic Mask Perturbations
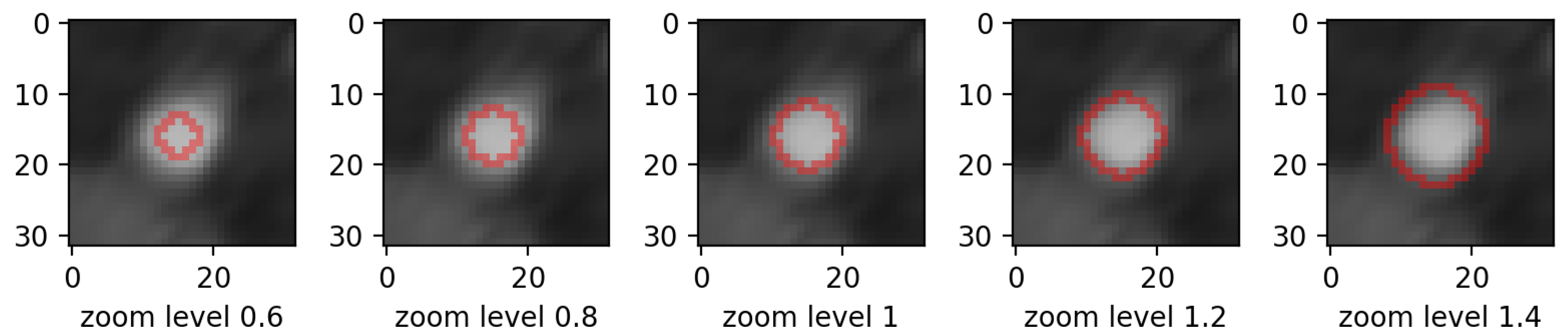
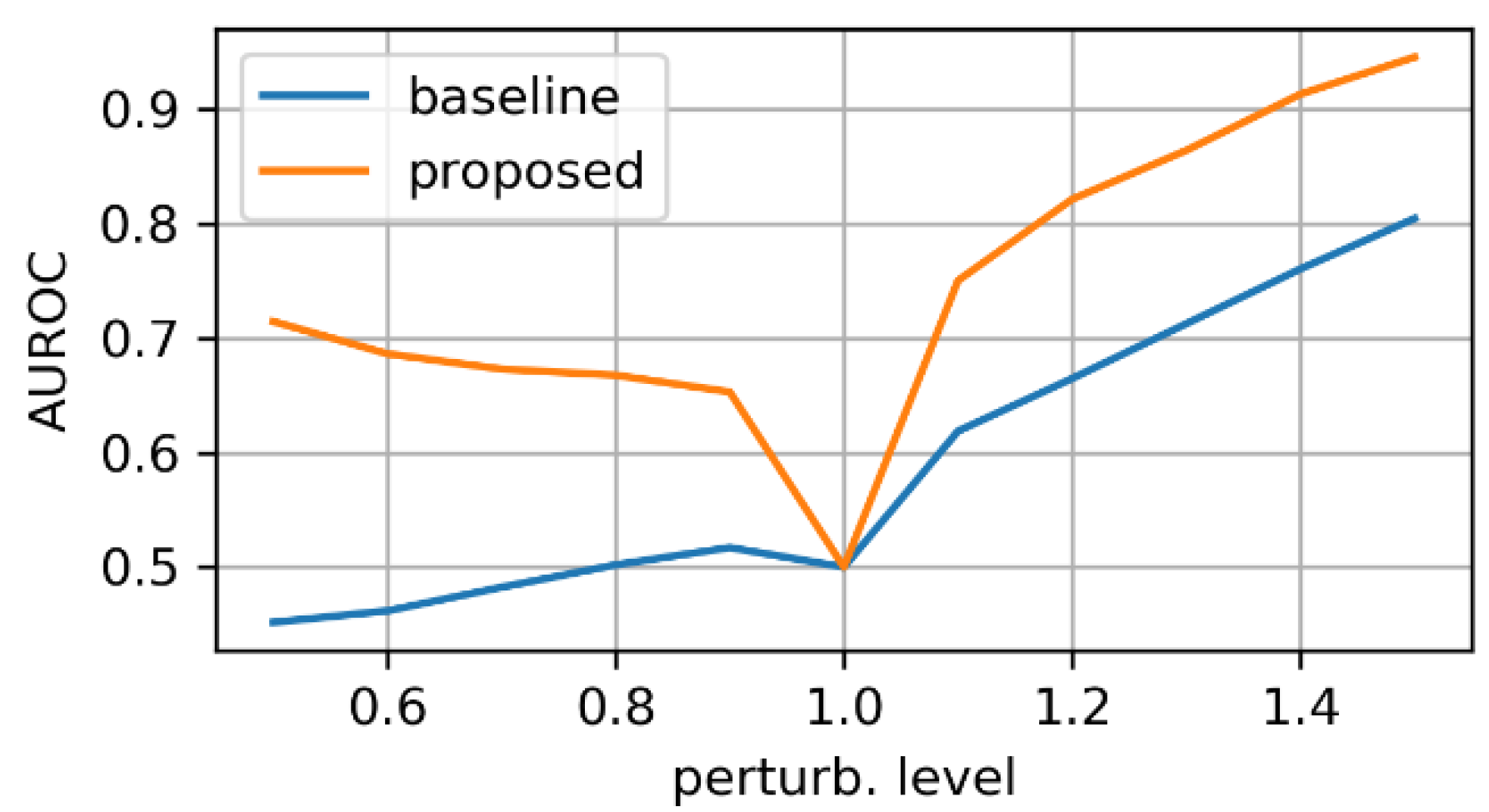
- zooming:we applied zoom in/out operations on the mask image with respect to the mask center, so that the resulting mask is still aligned with the angiography, but larger/smaller than before. Figure 3 displays an example for various levels of zoom.
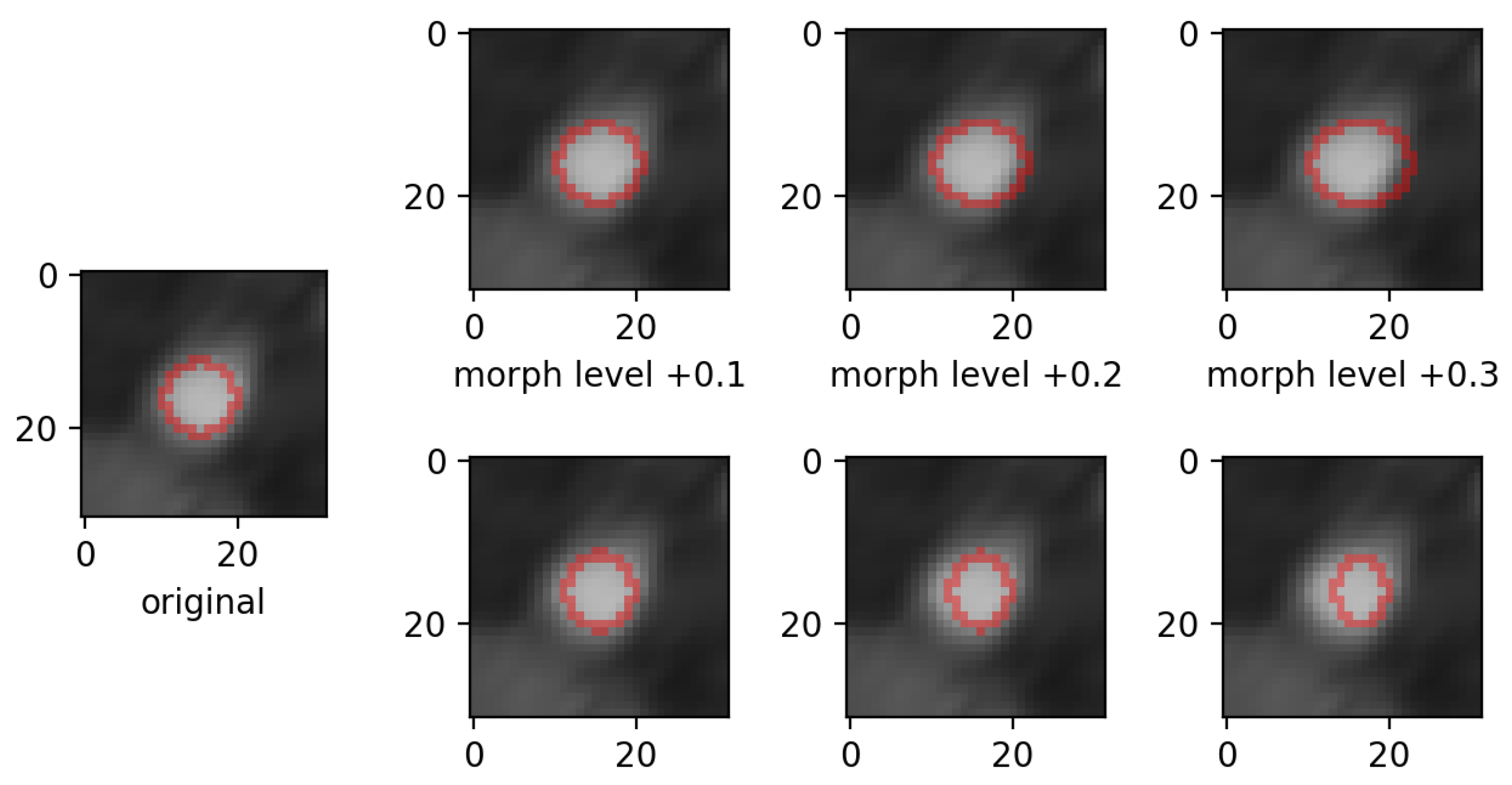
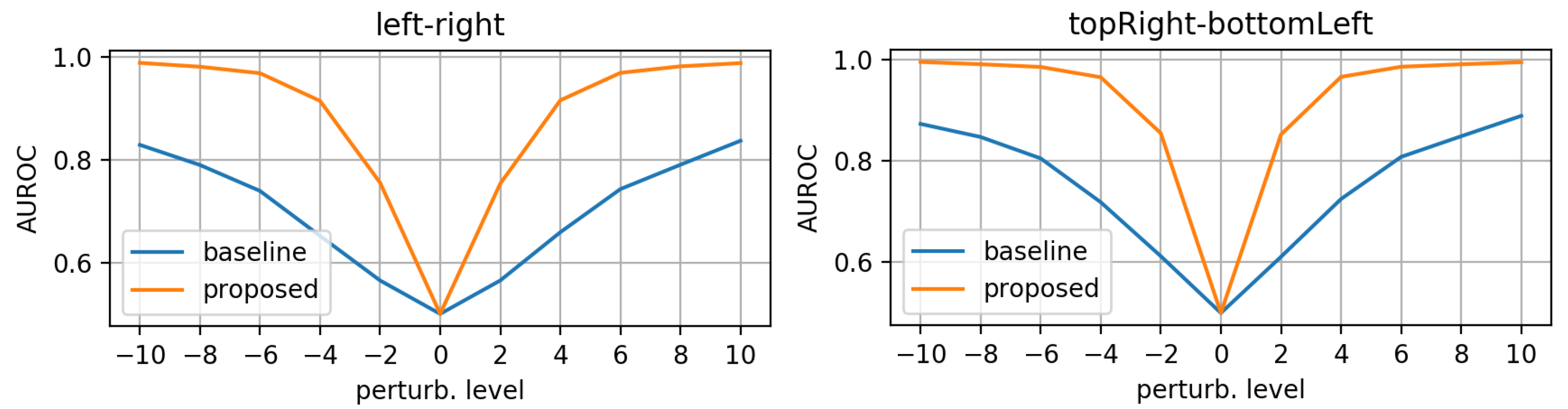
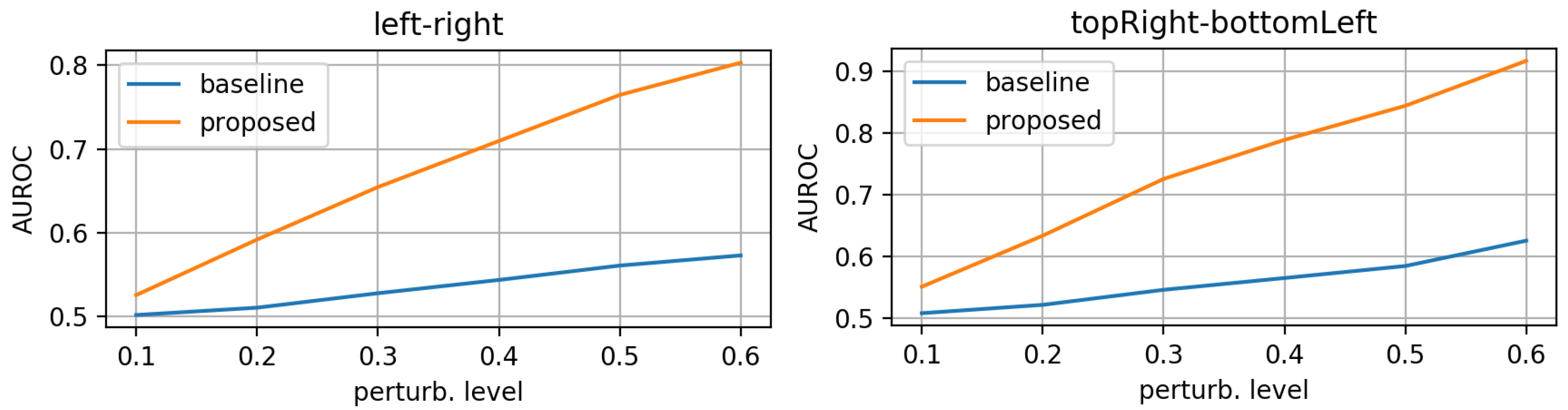
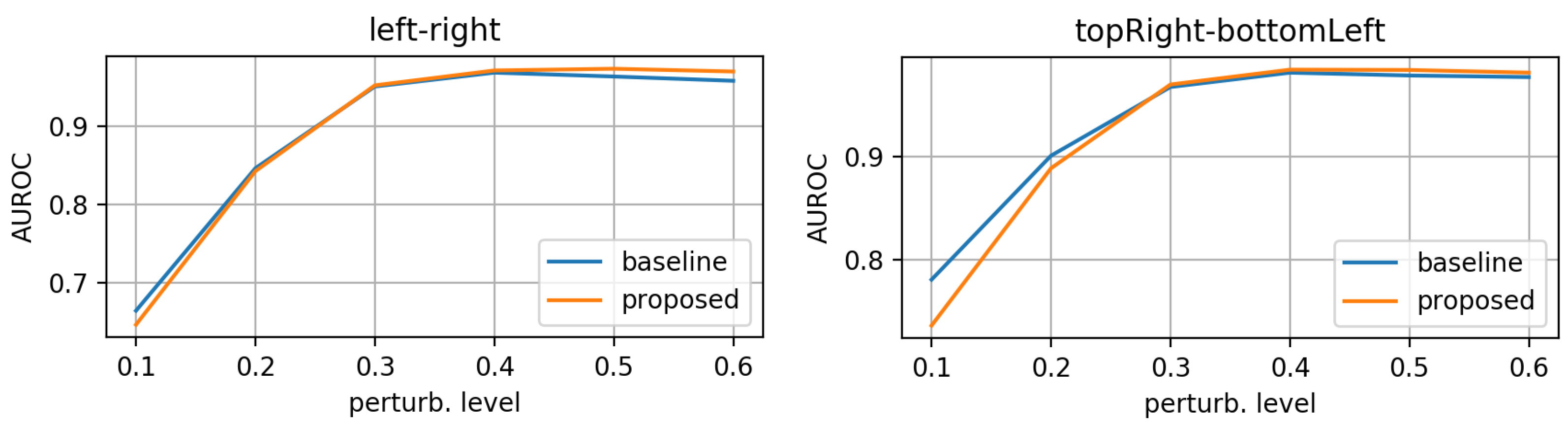
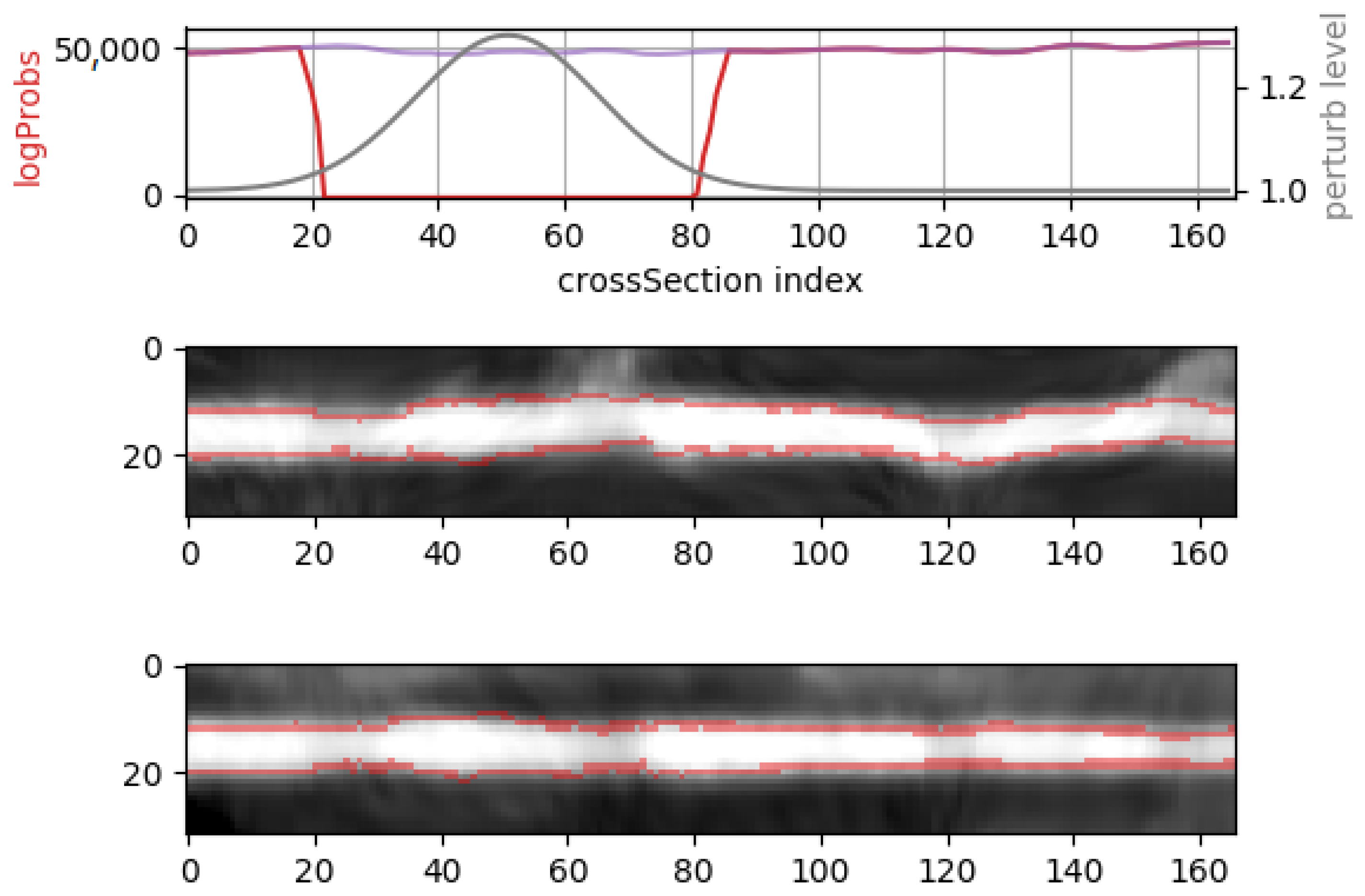
- morphing: we applied dilations or erosions along 4 directions on the height ∗ width plane: left-right, top-bottom, topLeft-bottomRight and topRight-bottomLeft. This perturbation only affects one part of the mask (the eroded or dilated part), while the other part is left untouched. Figure 4 displays an example for various levels of morphing. By convention, negative and positive levels refer to the two ways in the selected direction, with zero meaning original mask position (levels are expressed as ratios of the original mask size along the chosen direction). At every level, either dilation (resulting in prolonged masks) or erosion (resulting in shortened masks) can be applied.
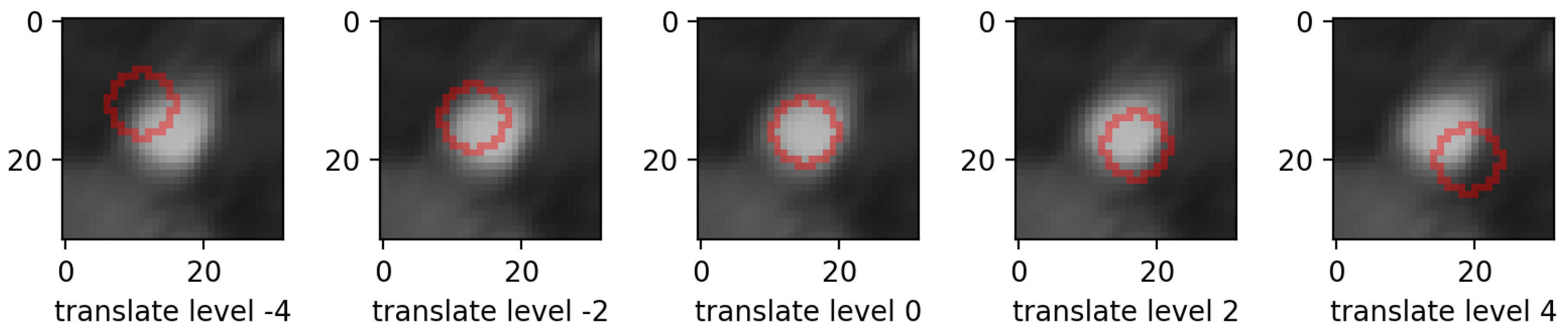
- translations: in the same 4 directions on the height * width plane, we translated whole mask images. Each level increment signifies a pixel shift. Figure 5 shows an example for various levels of translation.
3. Results and Discussion
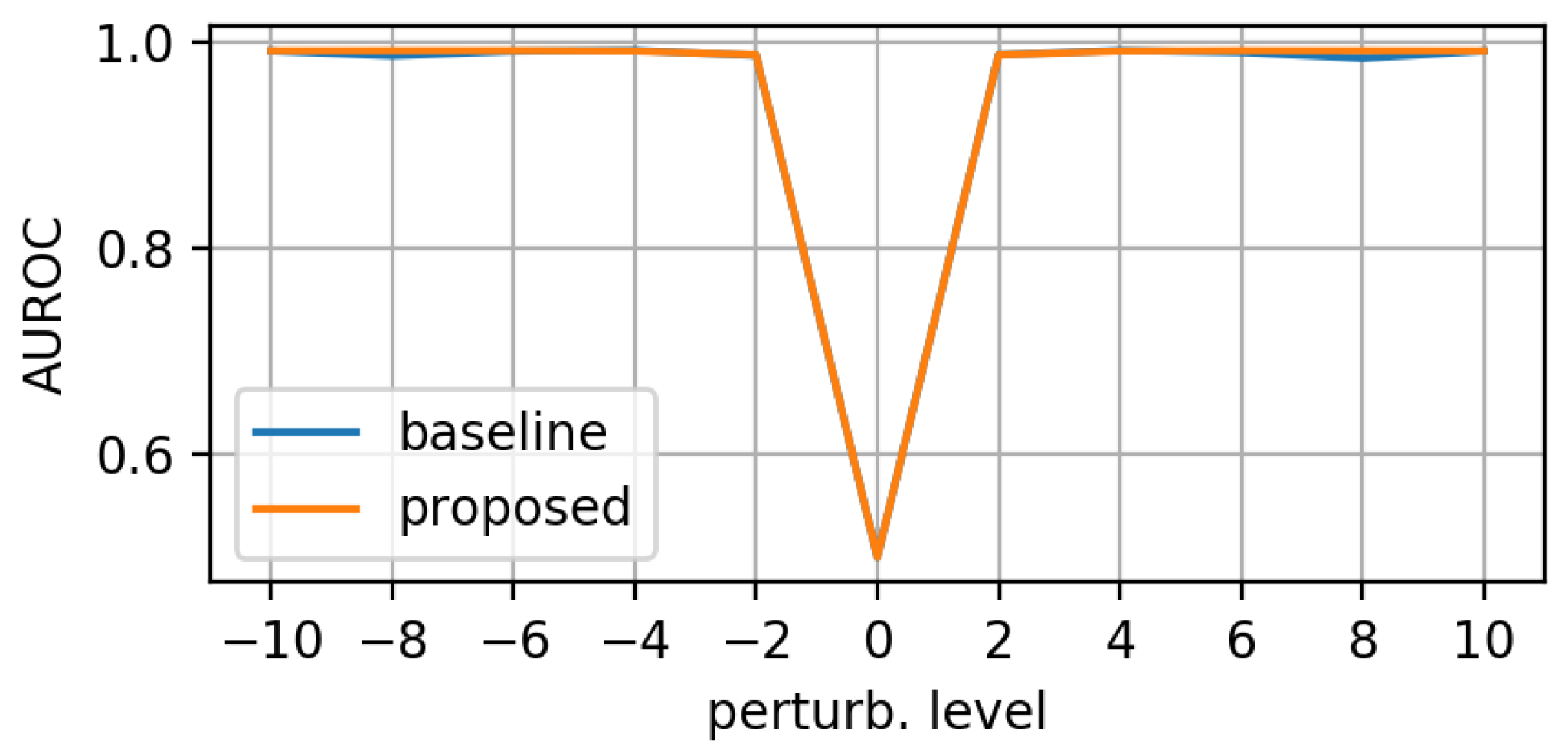
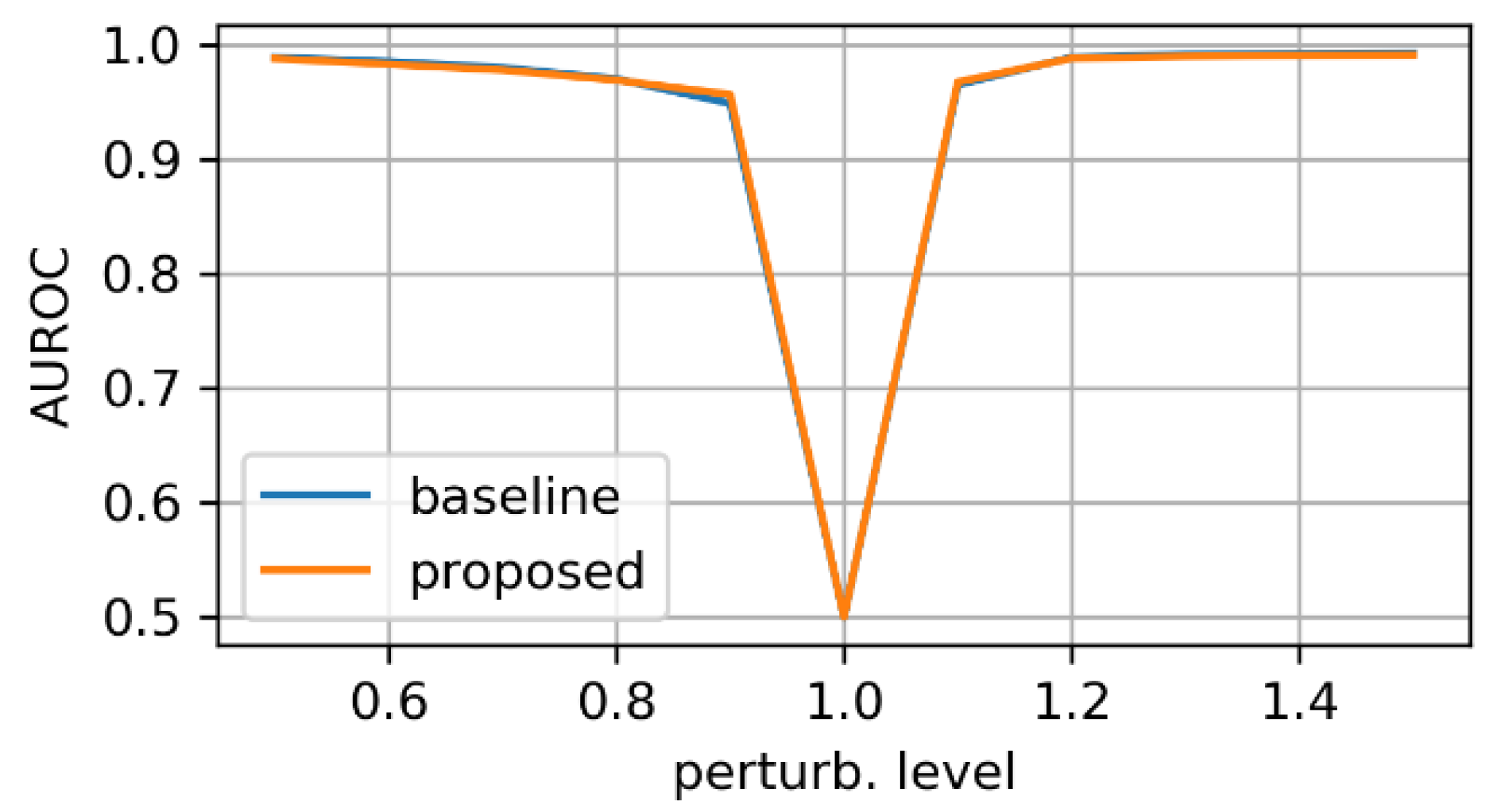
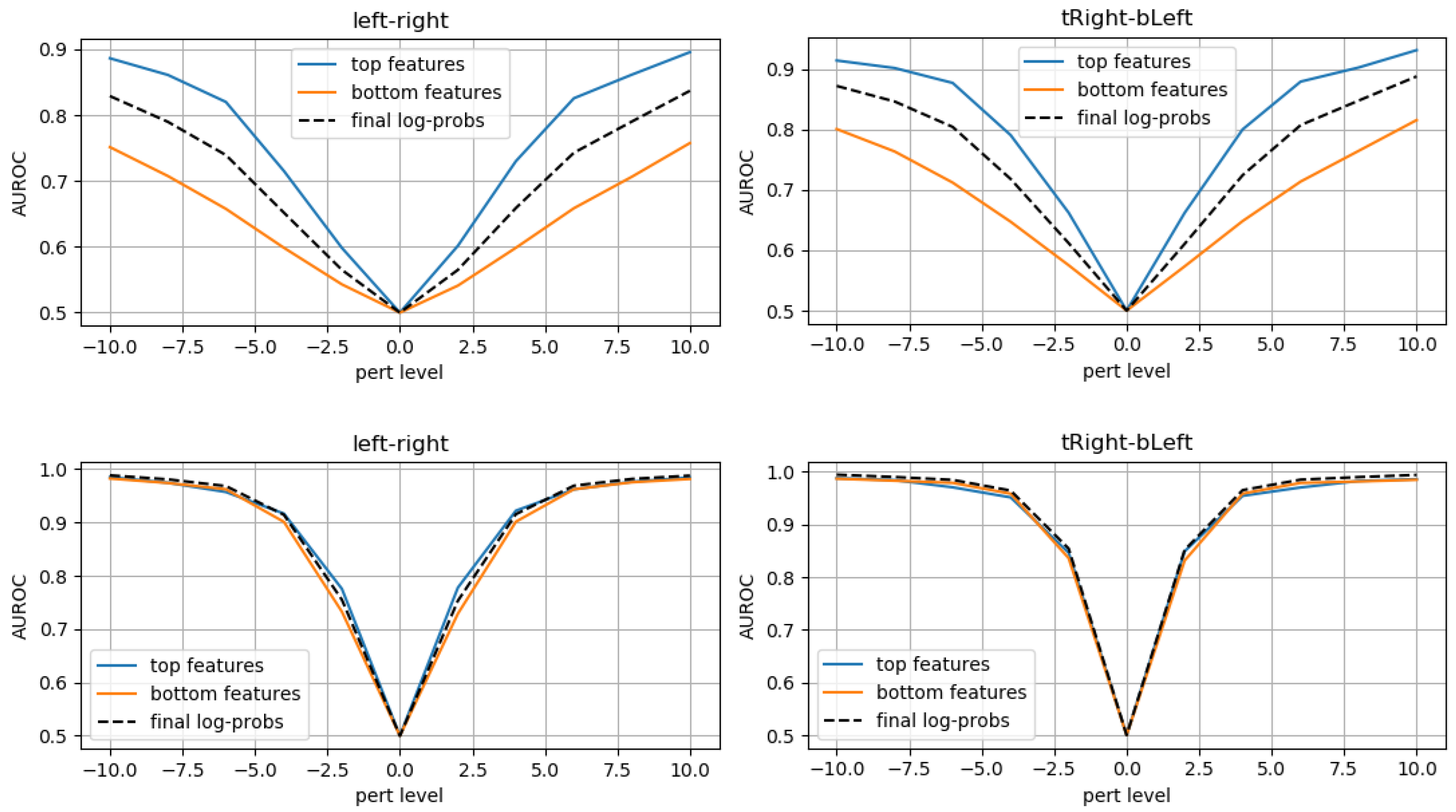
3.1. Evaluation on Synthetic Mask Perturbations
- translation (in all 4 directions) of ±3 or ±4 pixels;
- zooming levels of 0.65×, 0.8×, 1.2×, and 1.35×;
- morphing (in all 4 directions, erosions/dilations) levels of 0.2 and 0.35 (ratio of initial mask size).
3.2. Evaluation on Expert Annotations
3.3. Sampling from the Models
3.4. Inspecting the Flows
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCTA | Coronary computed tomography angiography |
| OoD | Out-of-Distribution |
| NF | Normalizing Flows |
| AI | Artificial Intelligence |
| CNN | Convolutional Neural Network |
| GT | Ground truth |
| CAD | Coronary artery disease |
| AuRoC | Area under the Receiver operating Characteristics |
| FFR | Fractional Flow Reserve |
| AHA | American Heart Association |
| CFD | Computational fluid dynamics |
| KL | Kullback–Leibler divergence |
| logDet | Logarithm of determinant |
| cMPR | curved Multiplanar Reconstruction |
| VAE | Variational Auto-Encoder |
References
- Mark, D.B.; Federspiel, J.J.; Cowper, P.A.; Anstrom, K.J.; Hoffmann, U.; Patel, M.R.; Davidson-Ray, L.; Daniels, M.R.; Cooper, L.S.; Knight, J.D.; et al. Economic Outcomes With Anatomical Versus Functional Diagnostic Testing for Coronary Artery Disease. Ann. Intern. Med. 2016, 165, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Levin, D.C.; Parker, L.; Halpern, E.J.; Rao, V.M. Coronary CT Angiography: Reversal of Earlier Utilization Trends. J. Am. Coll. Radiol. 2019, 16, 147–155. [Google Scholar] [CrossRef]
- Han, D.; Liu, J.; Sun, Z.; Cui, Y.; He, Y.; Yang, Z. Deep learning analysis in coronary computed tomographic angiography imaging for the assessment of patients with coronary artery stenosis. Comput. Methods Programs Biomed. 2020, 196, 105651. [Google Scholar] [CrossRef] [PubMed]
- Muscogiuri, G.; Van Assen, M.; Tesche, C.; De Cecco, C.N.; Chiesa, M.; Scafuri, S.; Guglielmo, M.; Baggiano, A.; Fusini, L.; Guaricci, A.I.; et al. Artificial Intelligence in Coronary Computed Tomography Angiography: From Anatomy to Prognosis. BioMed Res. Int. 2020, 2020, 6649410. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.C.; Earls, J.P.; Hecht, H. Quantitative assessment of atherosclerotic plaque, recent progress and current limitations. J. Cardiovasc. Comput. Tomogr. 2022, 16, 124–137. [Google Scholar] [CrossRef] [PubMed]
- Coenen, A.; Kim, Y.H.; Kruk, M.; Tesche, C.; Geer, J.D.; Kurata, A.; Lubbers, M.L.; Daemen, J.; Itu, L.; Rapaka, S.; et al. Diagnostic Accuracy of a Machine-Learning Approach to Coronary Computed Tomographic Angiography-Based Fractional Flow Reserve. Circ. Cardiovasc. Imaging 2018, 11, e007217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sankaran, S.; Grady, L.; Taylor, C.A. Fast Computation of Hemodynamic Sensitivity to Lumen Segmentation Uncertainty. IEEE Trans. Med Imaging 2015, 34, 2562–2571. [Google Scholar] [CrossRef] [PubMed]
- van Amersfoort, J.; Smith, L.; Jesson, A.; Key, O.; Gal, Y. Improving Deterministic Uncertainty Estimation in Deep Learning for Classification and Regression. arXiv 2021, arXiv:2102.11409. [Google Scholar]
- Liu, W.; Wang, X.; Owens, J.; Li, Y. Energy-based Out-of-distribution Detection. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 21464–21475. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. arXiv 2017, arXiv:1605.08803. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Ziegler, Z.; Rush, A. Latent Normalizing Flows for Discrete Sequences. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 7673–7682. [Google Scholar]
- Kirichenko, P.; Izmailov, P.; Wilson, A.G. Why Normalizing Flows Fail to Detect Out-of-Distribution Data. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 20578–20589. [Google Scholar]
- Papamakarios, G.; Nalisnick, E.; Rezende, D.J.; Mohamed, S.; Lakshminarayanan, B. Normalizing Flows for Probabilistic Modeling and Inference. J. Mach. Learn. Res. 2021, 22, 1–64. [Google Scholar]
- Kobyzev, I.; Prince, S.J.; Brubaker, M.A. Normalizing Flows: An Introduction and Review of Current Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3964–3979. [Google Scholar] [CrossRef] [PubMed]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Gorur, D.; Lakshminarayanan, B. Do Deep Generative Models Know What They Don’t Know? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zheng, Y.; Tek, H.; Funka-Lea, G. Robust and Accurate Coronary Artery Centerline Extraction in CTA by Combining Model-Driven and Data-Driven Approaches. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2013, Nagoya, Japan, 22–26 September 2013; Mori, K., Sakuma, I., Sato, Y., Barillot, C., Navab, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 74–81. [Google Scholar]
- Lugauer, F.; Zheng, Y.; Hornegger, J.; Kelm, B.M. Precise Lumen Segmentation in Coronary Computed Tomography Angiography. In Proceedings of the Medical Computer Vision: Algorithms for Big Data, Cambridge, MA, USA, 18 September 2014; Menze, B., Langs, G., Montillo, A., Kelm, M., Müller, H., Zhang, S., Cai, W.T., Metaxas, D., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 137–147. [Google Scholar]
- Leipsic, J.; Abbara, S.; Achenbach, S.; Cury, R.; Earls, J.P.; Mancini, G.J.; Nieman, K.; Pontone, G.; Raff, G.L. SCCT guidelines for the interpretation and reporting of coronary CT angiography: A report of the Society of Cardiovascular Computed Tomography Guidelines Committee. J. Cardiovasc. Comput. Tomogr. 2014, 8, 342–358. [Google Scholar] [CrossRef] [PubMed]
- Poston, T.; Fang, S.; Lawton, W. Computing and Approximating Sweeping Surfaces Based on Rotation Minimizing Frames. In Proceedings of the 4th International Conference on CAD/CG, Wuhan, China, 23–25 October 1995. [Google Scholar]
- Behrmann, J.; Grathwohl, W.; Chen, R.T.Q.; Duvenaud, D.; Jacobsen, J.H. Invertible Residual Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 573–582. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Sorkhei, M.; Henter, G.E.; Kjellström, H. Full-Glow: Fully Conditional Glow for More Realistic Image Generation. In Proceedings of the Pattern Recognition, Bonn, Germany, 28 September–1 October 2021; Bauckhage, C., Gall, J., Schwing, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 697–711. [Google Scholar]
- Lu, Y.; Huang, B. Structured Output Learning with Conditional Generative Flows. Proc. AAAI Conf. Artif. Intell. 2020, 34, 5005–5012. [Google Scholar] [CrossRef]
- Karami, M.; Schuurmans, D.; Sohl-Dickstein, J.; Dinh, L.; Duckworth, D. Invertible Convolutional Flow. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning—ICML’15, Lille, France, 7–9 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Zhang, L.; Goldstein, M.; Ranganath, R. Understanding Failures in Out-of-Distribution Detection with Deep Generative Models. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; Volume 139, pp. 12427–12436. [Google Scholar]
- Havtorn, J.D.; Frellsen, J.; Hauberg, S.; Maaløe, L. Hierarchical VAEs Know What They Don’t Know. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; Volume 139, pp. 4117–4128. [Google Scholar]
- van den Hoogen, I.J.; van Rosendael, A.R.; Lin, F.Y.; Bax, J.J.; Shaw, L.J.; Min, J.K. Coronary Computed Tomography Angiography as a Gatekeeper to Coronary Revascularization: Emphasizing Atherosclerosis Findings Beyond Stenosis. Curr. Cardiovasc. Imaging Rep. 2019, 12, 24. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.J.; Lin, F.Y.; Gebow, D.; An, H.Y.; Andreini, D.; Bathina, R.; Baggiano, A.; Beltrama, V.; Cerci, R.; Choi, E.Y.; et al. Selective Referral Using CCTA Versus Direct Referral for Individuals Referred to Invasive Coronary Angiography for Suspected CAD: A Randomized, Controlled, Open-Label Trial. JACC Cardiovasc. Imaging 2019, 12, 1303–1312. [Google Scholar] [CrossRef] [PubMed]
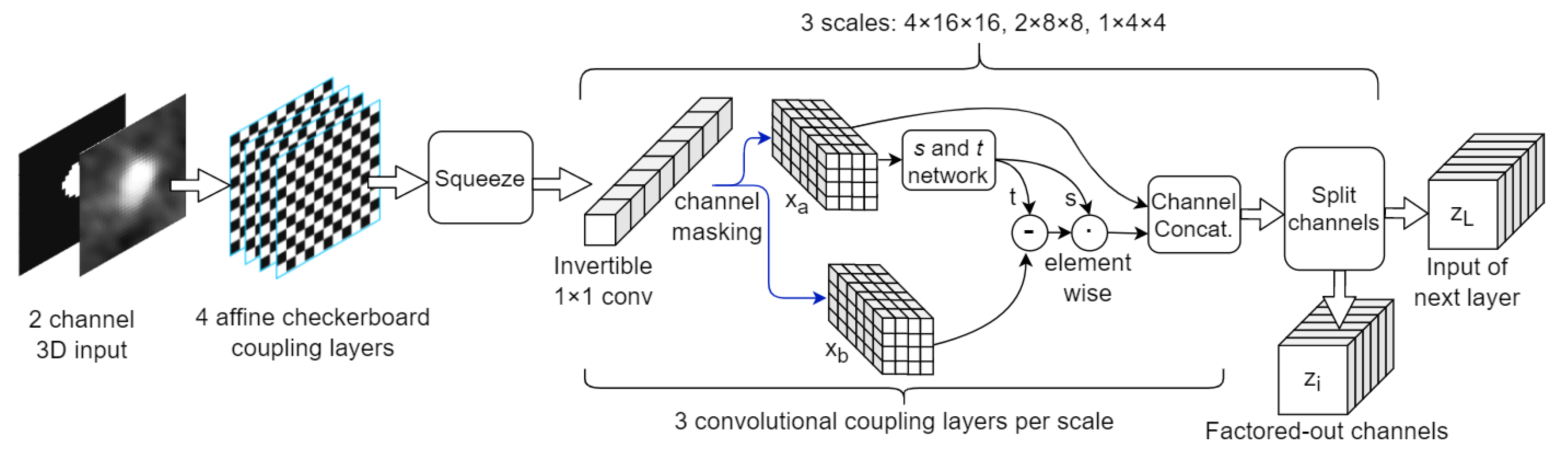


| Stage | No. Blocks | Block Description | Resolution | No. Channels | Total Number of Parameters |
|---|---|---|---|---|---|
| 1 | 4 | Affine coupling layer using checkerboard mask; Activation Norm (if not last block) | 8 × 32 × 32 | 2 | ∼2 millions |
| 2 3 4 | 1 | 3D Squeeze operation | Stage 2: 4 × 16 × 16 Stage 3: 2 × 8 × 8 Stage 4: 1 × 4 × 4 | Stage 2: 16 Stage 3: 64 Stage 4: 256 | |
| 3 | Activation Norm; Invertible 1 × 1 Convolution; Affine coupling layer using channel-wise masking | ||||
| 1 | Split channels | After stage 2: 8 After stage 3: 32 |
| Stage | Block | No. Filters | Cumulative Receptive Field |
|---|---|---|---|
| 1 | Conv3D with 3 × 3 × 3 kernel, stride 1, padding 1; BatchNorm; LeakyReLU | 64 | 3 × 3 × 3 |
| 2 | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0; BatchNorm; LeakyReLU; Dropout | 64 | 3 × 3 × 3 |
| 3 | Conv3D with 3 × 3 × 3 kernel, stride 1, padding 1; BatchNorm; LeakyReLU; Dropout | 64 | 5 × 5 × 5 |
| 4 − s | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0 | As many as x’s channels for checkerboard masking or half for channel masking | 5 × 5 × 5 |
| 4 − t | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0 |
| Stage | Block | No. Filters | Cumulative Receptive Field |
|---|---|---|---|
| 1 | Conv3D with 3 × 3 × 3 kernel, stride 1, padding 1; BatchNorm; LeakyReLU | 64 | 3 × 3 × 3 |
| 2 | MaxPool3D 2 × 2 × 2, stride 2 | 4 × 4 × 4 | |
| 3 | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0; BatchNorm; LeakyReLU; Dropout | 64 | 4 × 4 × 4 |
| 4 | Conv3D with 3 × 3 × 3 kernel, stride 1, padding 1; BatchNorm; LeakyReLU; Dropout | 64 | 8 × 8 × 8 |
| 5 − k | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0; Average pooling | full | |
| 5 − b | Conv3D with 1 × 1 × 1 kernel, stride 1, padding 0; Average pooling | full |
| Stage | No. Blocks | Block Description | Resolution | No. Channels | Total Number of Parameters |
|---|---|---|---|---|---|
| 1 | 4 | Additive coupling layer using checkerboard mask; BatchNorm (if not last block) | 8 × 32 × 32 | 2 | ∼8.7 millions |
| 2 3 4 5 6 | 1 | 3D Squeeze operation | Stage 2: 4 × 16 × 16 Stage 3: 2 × 8 × 8 Stage 4: 1 × 4 × 4 Stage 5: 1 × 2 × 2 Stage 6: 1 × 1 × 1 | Stage 2: 16 Stage 3: 64 Stage 4: 256 Stage 5: 512 Stage 6: 1024 | |
| 4 | BatchNorm; Invertible 1 × 1 Convolution; convolutional coupling layer using channel-wise masking | ||||
| 1 | Split channels | After stage 2: 8 After stage 3: 32 After stage 4: 128 After stage 5: 256 |
| Metric | Inter-Expert Agreement Average [Min, Max] | Baseline Model | Proposed Model |
|---|---|---|---|
| Accuracy | 0.81 [0.79, 0.86] | 0.64 | 0.79 |
| Sensitivity | 0.79 [0.70, 0.87] | 0.48 | 0.76 |
| Specificity | 0.83 [0.76, 0.90] | 0.77 | 0.81 |
| PPV | 0.79 [0.70, 0.87] | 0.63 | 0.76 |
| NPV | 0.83 [0.76, 0.90] | 0.65 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciușdel, C.F.; Itu, L.M.; Cimen, S.; Wels, M.; Schwemmer, C.; Fortner, P.; Seitz, S.; Andre, F.; Buß, S.J.; Sharma, P.; et al. Normalizing Flows for Out-of-Distribution Detection: Application to Coronary Artery Segmentation. Appl. Sci. 2022, 12, 3839. https://doi.org/10.3390/app12083839
Ciușdel CF, Itu LM, Cimen S, Wels M, Schwemmer C, Fortner P, Seitz S, Andre F, Buß SJ, Sharma P, et al. Normalizing Flows for Out-of-Distribution Detection: Application to Coronary Artery Segmentation. Applied Sciences. 2022; 12(8):3839. https://doi.org/10.3390/app12083839
Chicago/Turabian StyleCiușdel, Costin Florian, Lucian Mihai Itu, Serkan Cimen, Michael Wels, Chris Schwemmer, Philipp Fortner, Sebastian Seitz, Florian Andre, Sebastian Johannes Buß, Puneet Sharma, and et al. 2022. "Normalizing Flows for Out-of-Distribution Detection: Application to Coronary Artery Segmentation" Applied Sciences 12, no. 8: 3839. https://doi.org/10.3390/app12083839
APA StyleCiușdel, C. F., Itu, L. M., Cimen, S., Wels, M., Schwemmer, C., Fortner, P., Seitz, S., Andre, F., Buß, S. J., Sharma, P., & Rapaka, S. (2022). Normalizing Flows for Out-of-Distribution Detection: Application to Coronary Artery Segmentation. Applied Sciences, 12(8), 3839. https://doi.org/10.3390/app12083839






