Creating a Novel Mathematical Model of the Kv10.1 Ion Channel and Controlling Channel Activity with Nanoelectromechanical Systems
Abstract
Featured Application
Abstract
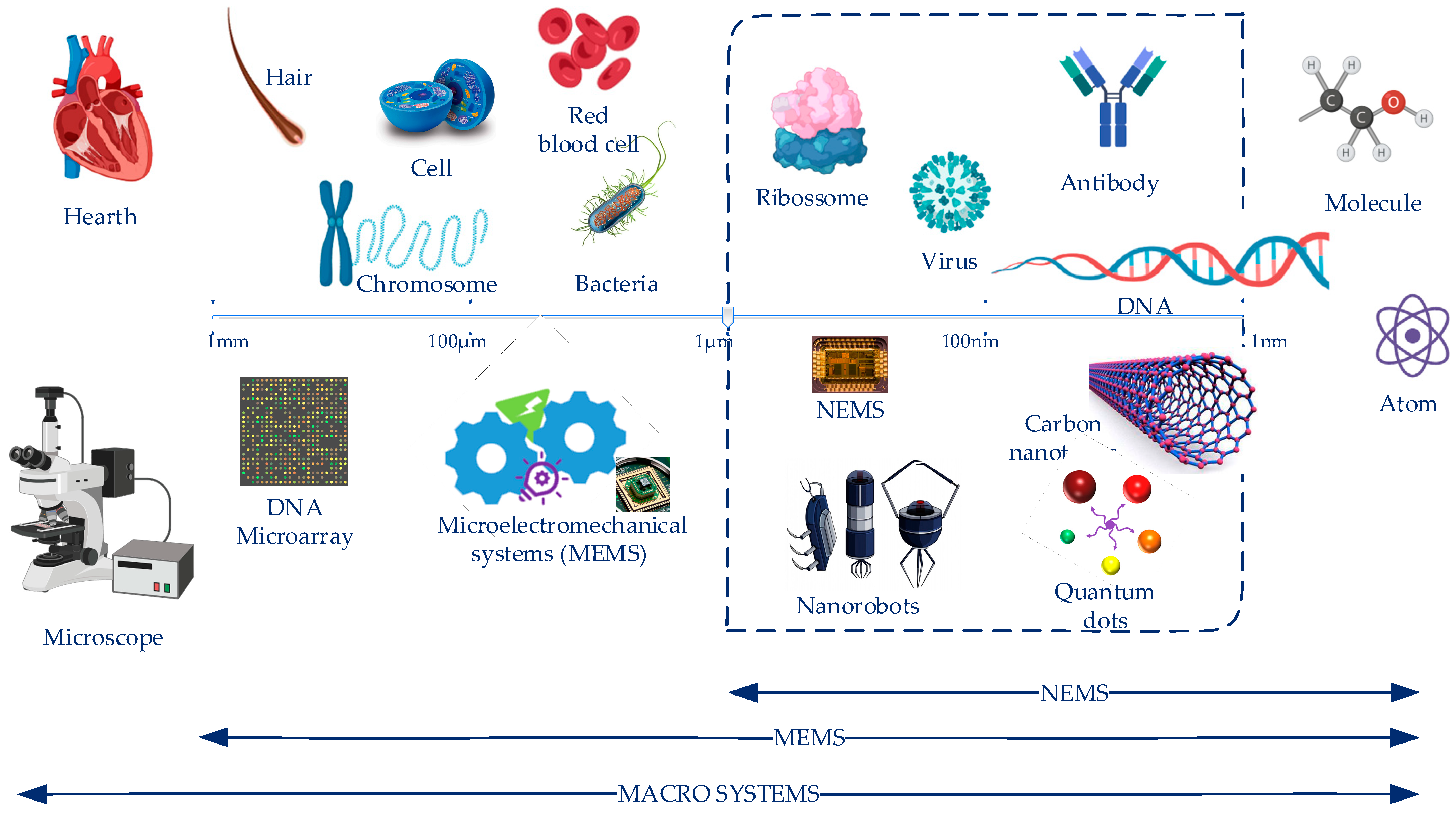
1. Introduction
2. Methods
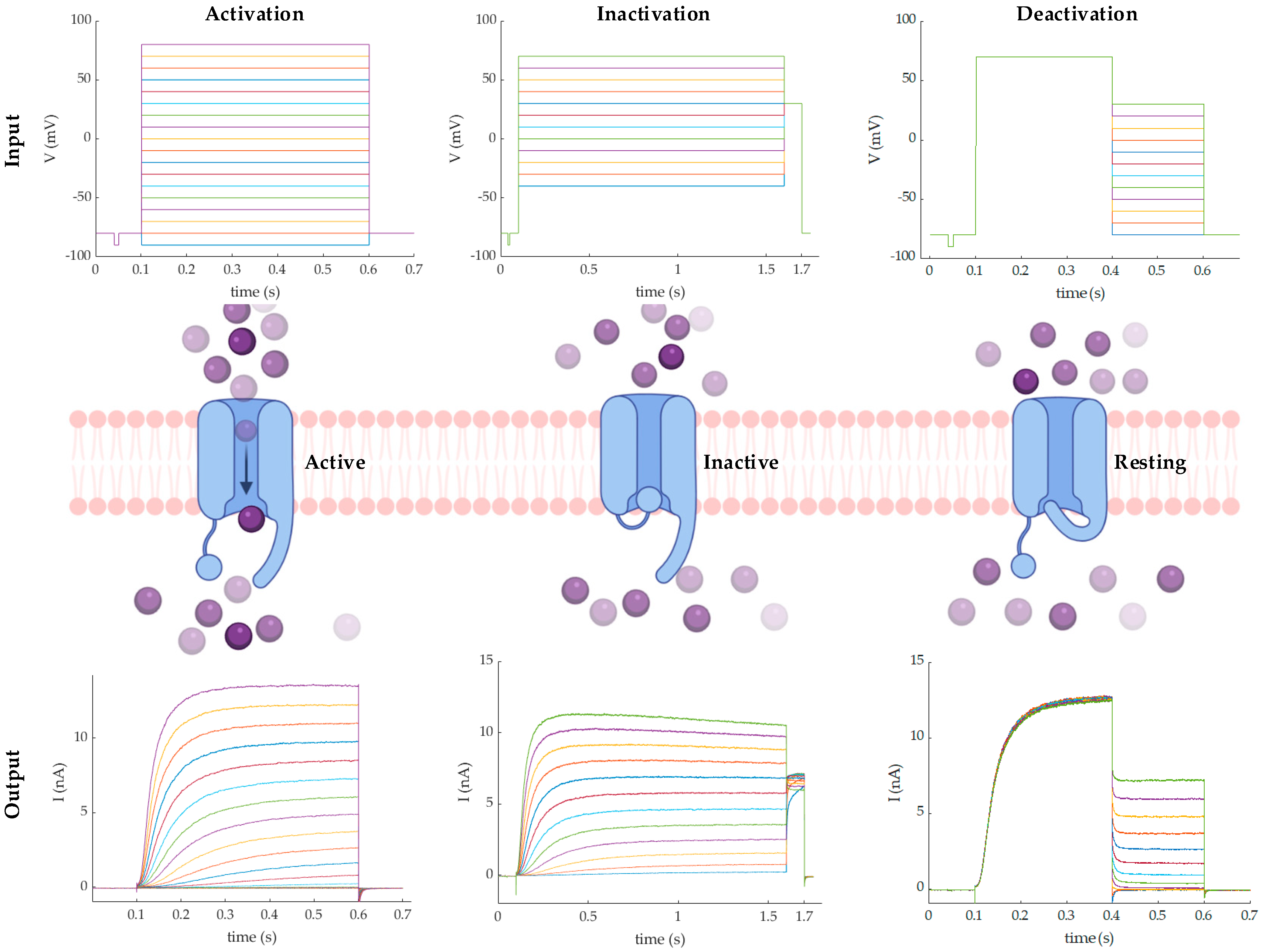
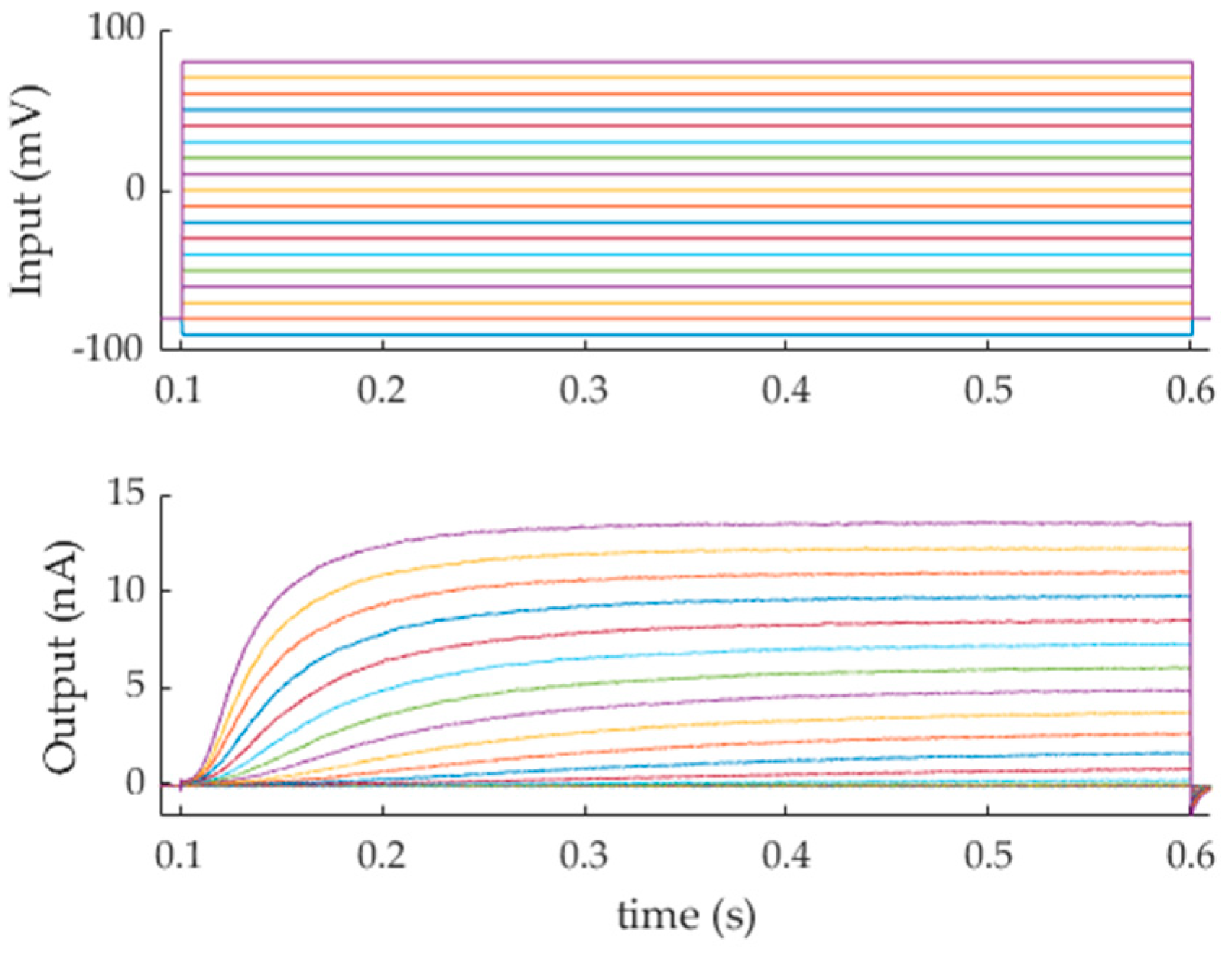
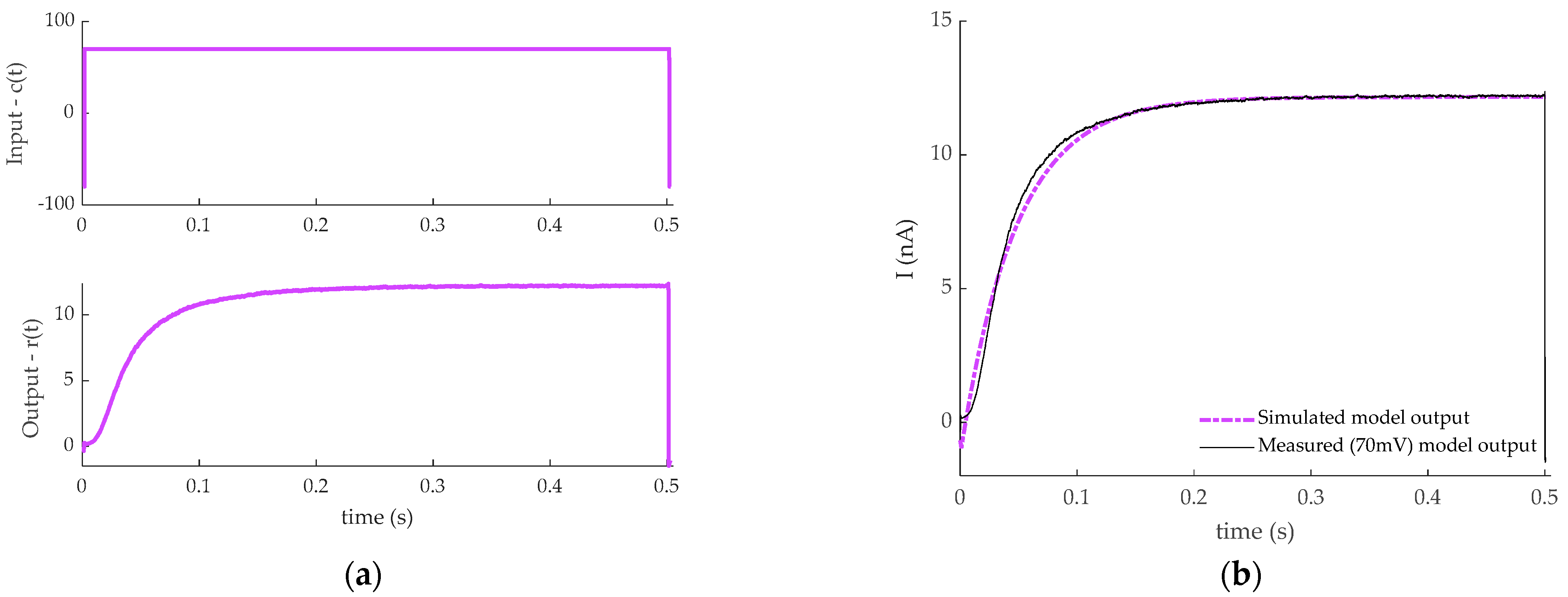
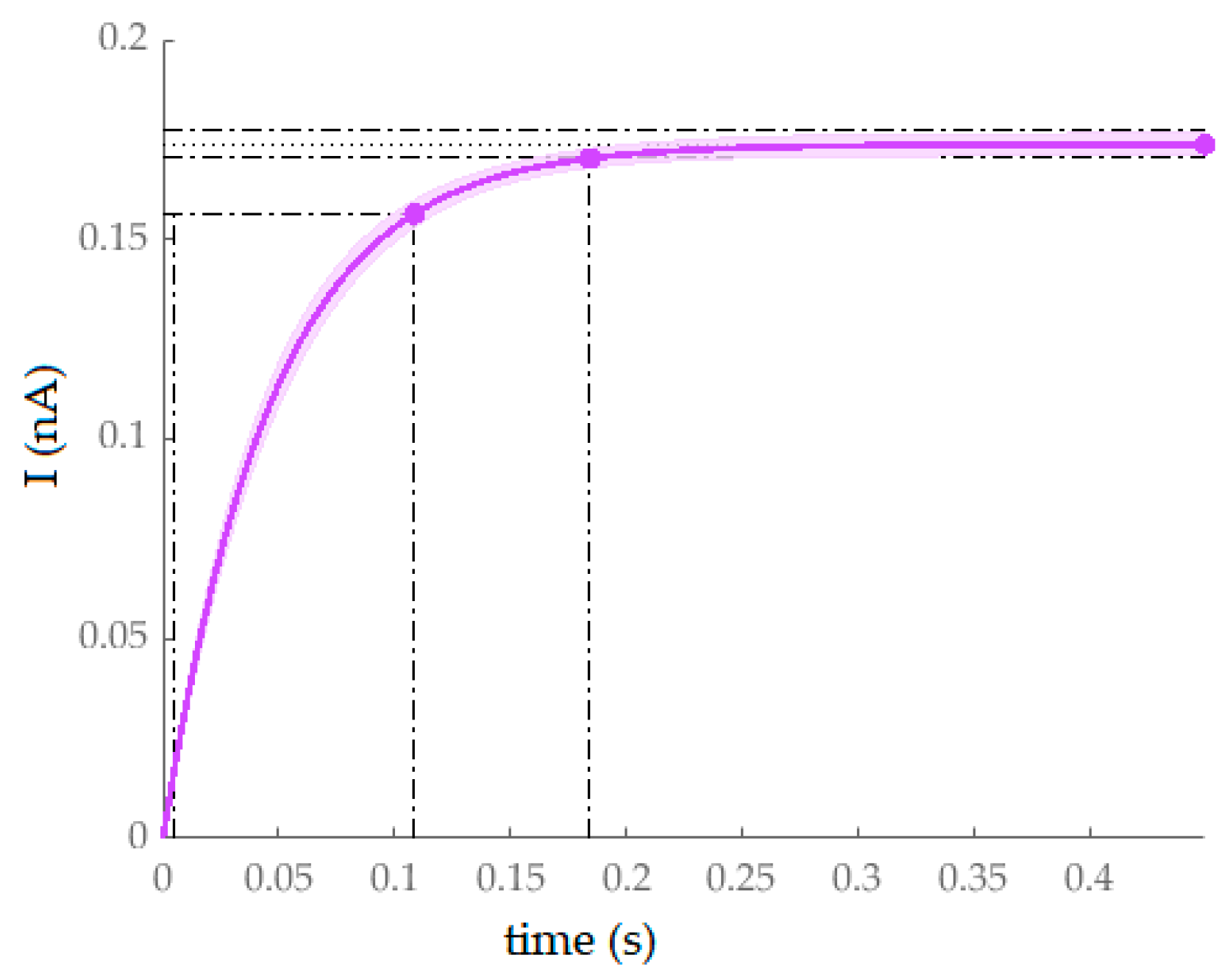
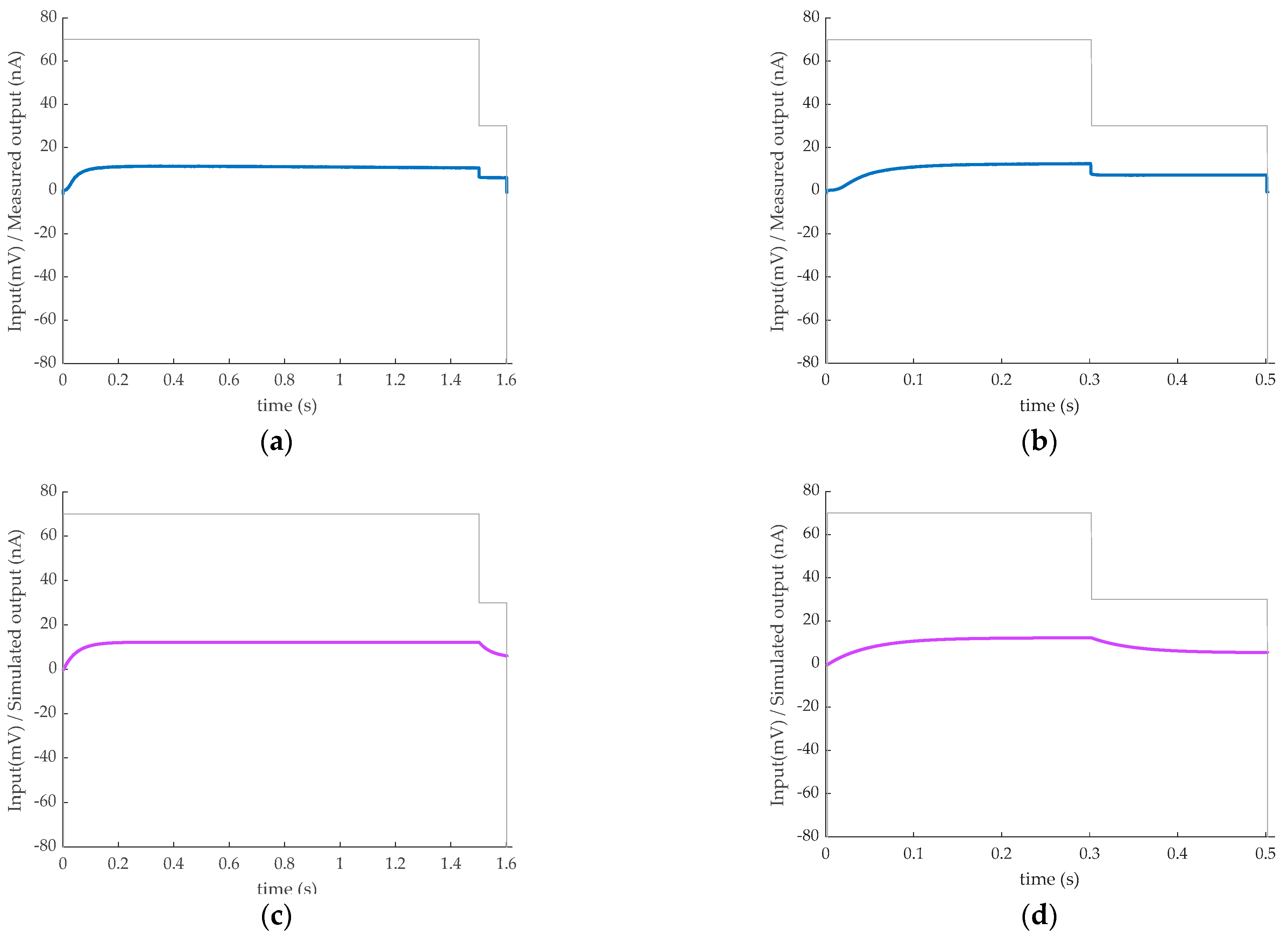
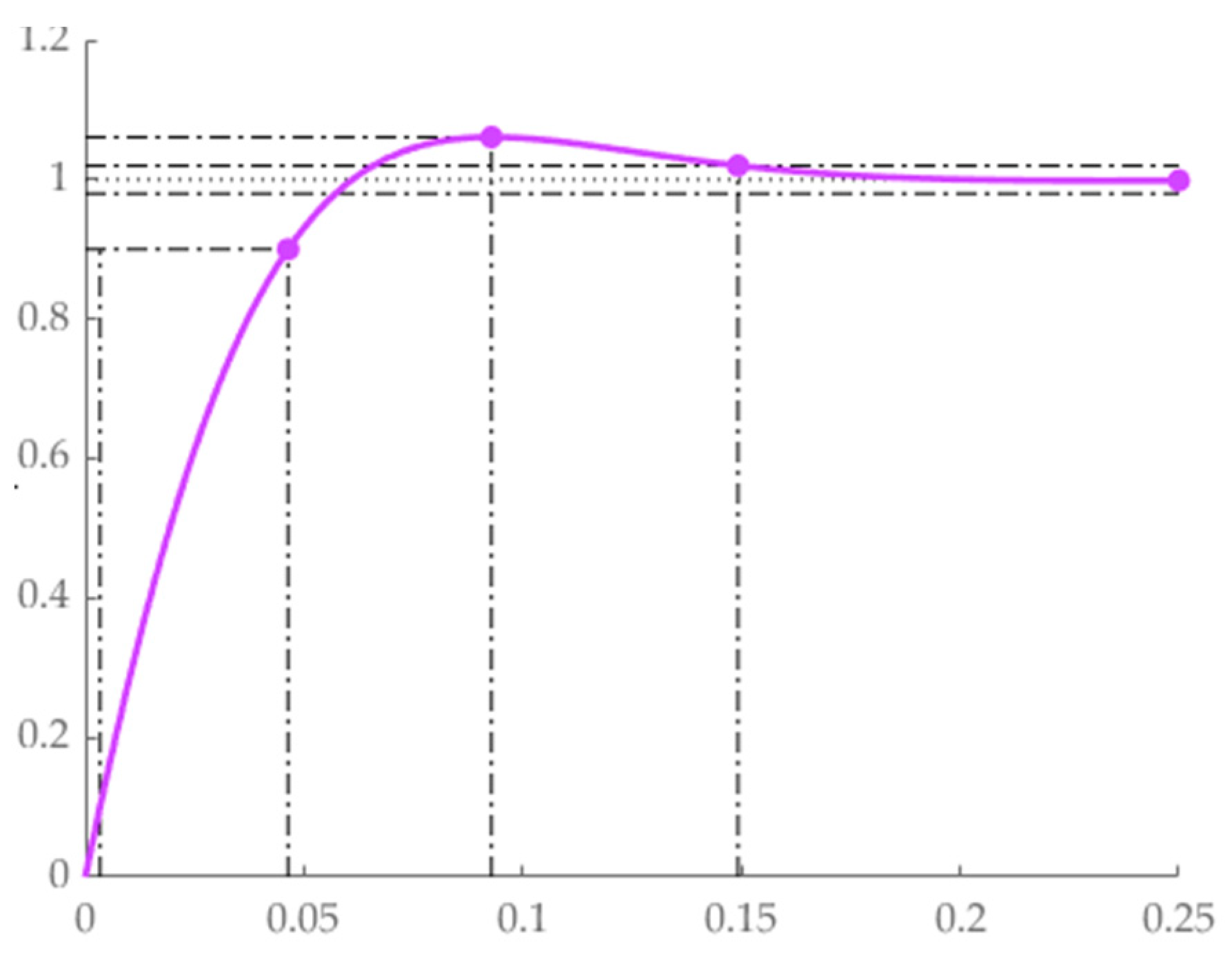
3. Results
4. Discussion
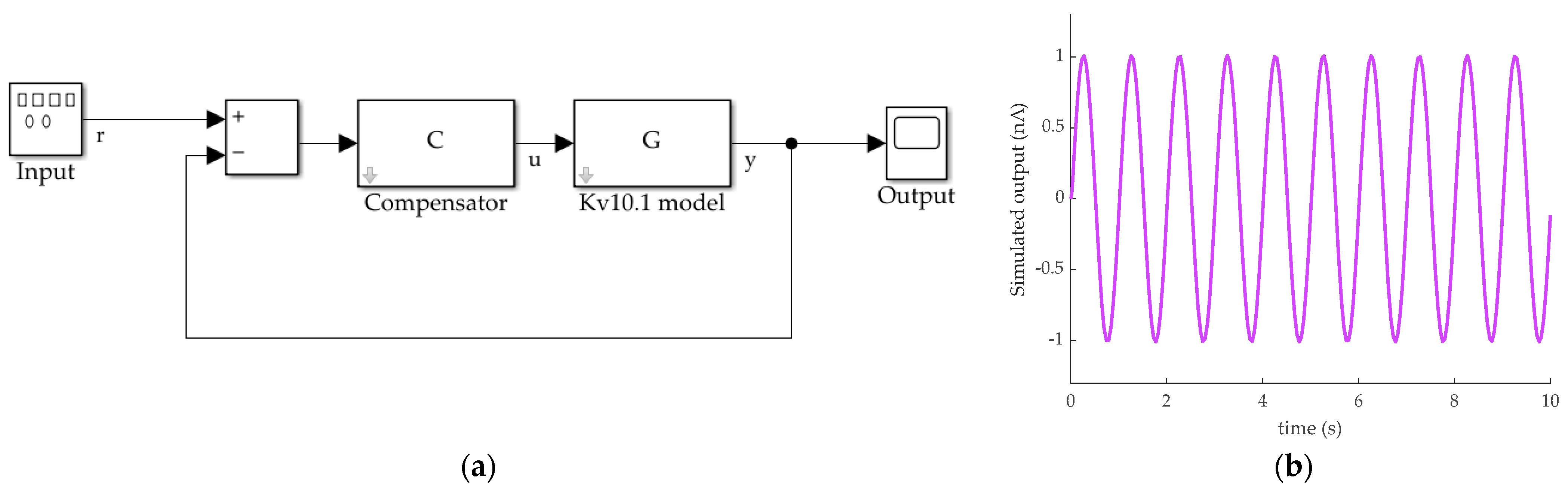
4.1. System Analysis
4.2. Control Algorithm
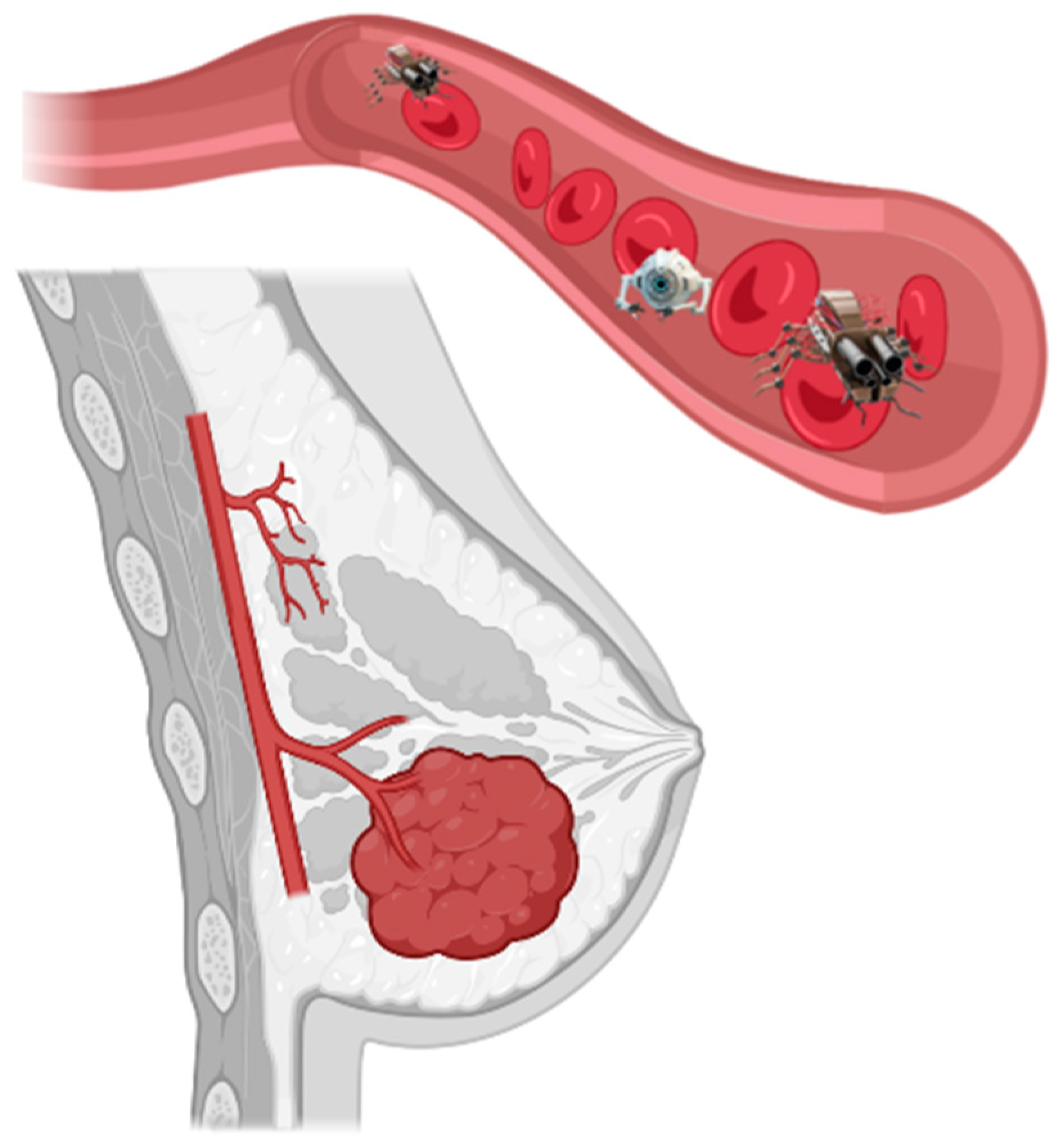
4.3. Potential Use Case for Treating Breast Cancer Using a Kv10.1 Controlled Nanorobot
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, A.; Jeyaraj, R.; De Lacey, S.F. Nanotechnology in Neurosurgical Oncology. In Nanotechnology in Cancer; Elsevier: Amsterdam, The Netherlands, 2017; pp. 139–170. ISBN 978-0-323-39080-4. [Google Scholar]
- Requicha, A.A.G. Nanorobots, NEMS, and Nanoassembly. Proc. IEEE 2003, 9, 1922–1933. [Google Scholar] [CrossRef]
- Simovic-Pavlovic, M.; Bokic, B.; Vasiljevic, D.; Kolaric, B. Bioinspired NEMS—Prospective of Collaboration with Nature. Appl. Sci. 2022, 12, 905. [Google Scholar] [CrossRef]
- Giri, G.; Maddahi, Y.; Zareinia, K. A Brief Review on Challenges in Design and Development of Nanorobots for Medical Applications. Appl. Sci. 2021, 11, 10385. [Google Scholar] [CrossRef]
- Asher, V.; Sowter, H.; Shaw, R.; Bali, A.; Khan, R. Eag and HERG Potassium Channels as Novel Therapeutic Targets in Cancer. World J. Surg. Oncol. 2010, 8, 113. [Google Scholar] [CrossRef]
- García-Becerra, R.; Díaz, L.; Camacho, J.; Barrera, D.; Ordaz-Rosado, D.; Morales, A.; Ortiz, C.S.; Avila, E.; Bargallo, E.; Arrecillas, M.; et al. Calcitriol Inhibits Ether-à Go-Go Potassium Channel Expression and Cell Proliferation in Human Breast Cancer Cells. Exp. Cell Res. 2010, 316, 433–442. [Google Scholar] [CrossRef]
- Wang, G.J.; Chen, C.L.; Hsu, S.H.; Chiang, Y.L. Bio-MEMS Fabricated Artificial Capillaries for Tissue Engineering. Microsyst. Technol. 2005, 12, 120–127. [Google Scholar] [CrossRef]
- Tsuda, S.; Zauner, K.-P.; Gunji, Y.-P. Robot Control with Biological Cells. Biosystems 2007, 87, 215–223. [Google Scholar] [CrossRef][Green Version]
- Mendonça Munhoz, A.; Santanelli di Pompeo, F.; De Mezerville, R. Nanotechnology, Nanosurfaces and Silicone Gel Breast Implants: Current Aspects. Case Rep. Plast. Surg. Hand Surg. 2017, 4, 99–113. [Google Scholar] [CrossRef]
- Ion Channel|Learn Science at Scitable. Available online: https://www.nature.com/scitable/topicpage/ion-channel-14047658/ (accessed on 7 April 2022).
- Marchesi, A.; Gao, X.; Adaixo, R.; Rheinberger, J.; Stahlberg, H.; Nimigean, C.; Scheuring, S. An Iris Diaphragm Mechanism to Gate a Cyclic Nucleotide-Gated Ion Channel. Nat. Commun. 2018, 9, 3978. [Google Scholar] [CrossRef]
- Shad, K.F.; Salman, S.; Afridi, S.; Tariq, M.; Asghar, S. Introductory Chapter: Ion Channels. In Ion Channels in Health and Sickness; Shad, K.F., Ed.; InTech: London, UK, 2018; ISBN 978-1-78984-227-2. [Google Scholar]
- Gabashvili, I.S.; Sokolowski, B.H.A.; Morton, C.C.; Giersch, A.B.S. Ion Channel Gene Expression in the Inner Ear. J. Assoc. Res. Otolaryngol. 2007, 8, 305–328. [Google Scholar] [CrossRef]
- Sands, Z.; Grottesi, A.; Sansom, M.S.P. Voltage-Gated Ion Channels. Curr. Biol. 2005, 15, R44–R47. [Google Scholar] [CrossRef] [PubMed]
- EPFL Blue Brain Project, Channelpedia. Available online: https://channelpedia.epfl.ch/ (accessed on 7 April 2022).
- Coetzee, W.A.; Amarillo, Y.; Chiu, J.; Chow, A.; Lau, D.; McCormack, T.; Morena, H.; Nadal, M.S.; Ozaita, A.; Pountney, D.; et al. Molecular Diversity of K+ Channels. Ann. N. Y. Acad. Sci. 1999, 868, 233–255. [Google Scholar] [CrossRef] [PubMed]
- Jan, L.Y.; Jan, Y.N. Voltage-Gated and Inwardly Rectifying Potassium Channels. J. Physiol. 1997, 505, 267–282. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Novillo, C.; Capera, J.; Colomer-Molera, M.; Condom, E.; Ferreres, J.; Felipe, A. Implication of Voltage-Gated Potassium Channels in Neoplastic Cell Proliferation. Cancers 2019, 11, 287. [Google Scholar] [CrossRef] [PubMed]
- Lastraioli, E.; Iorio, J.; Arcangeli, A. Ion Channel Expression as Promising Cancer Biomarker. Biochim. Biophys. Acta BBA-Biomembr. 2015, 1848, 2685–2702. [Google Scholar] [CrossRef]
- Asher, V.; Khan, R.; Warren, A.; Shaw, R.; Schalkwyk, G.V.; Bali, A.; Sowter, H.M. The Eag Potassium Channel as a New Prognostic Marker in Ovarian Cancer. Diagn. Pathol. 2010, 5, 78. [Google Scholar] [CrossRef]
- Langthaler, S.; Lozanović Šajić, J.; Rienmüller, T.; Weinberg, S.H.; Baumgartner, C. Ion Channel Modeling beyond State of the Art: A Comparison with a System Theory-Based Model of the Shaker-Related Voltage-Gated Potassium Channel Kv1.1. Cells 2022, 11, 239. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series; Prentice-Hall: Boston, MA, USA, 2010; ISBN 978-0-13-615673-4. [Google Scholar]
- Schoukens, J.; Pintelon, R.; Rolain, Y. Mastering System Identification in 100 Exercises; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-93698-6. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 13th ed.; Pearson: Hoboken, NJ, USA, 2016; ISBN 978-0-13-440762-3. [Google Scholar]
- Nise, N.S. Control Systems Engineering, 7th ed.; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-17051-9. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall Information and System Sciences Series; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999; ISBN 978-0-13-656695-3. [Google Scholar]
- Ljung, L. System Identification ToolboxTM User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2014. [Google Scholar]
- Option Set for Tfest-MATLAB-MathWorks Switzerland. Available online: https://ch.mathworks.com/help/ident/ref/tfestoptions.html (accessed on 7 April 2022).
- Delgado-Ramírez, M.; De Jesús-Pérez, J.J.; Aréchiga-Figueroa, I.A.; Arreola, J.; Adney, S.K.; Villalba-Galea, C.A.; Logothetis, D.E.; Rodríguez-Menchaca, A.A. Regulation of Kv2.1 Channel Inactivation by Phosphatidylinositol 4,5-Bisphosphate. Sci. Rep. 2018, 8, 1769. [Google Scholar] [CrossRef]
- Martínez, R.; Stühmer, W.; Martin, S.; Schell, J.; Reichmann, A.; Rohde, V.; Pardo, L. Analysis of the Expression of Kv10.1 Potassium Channel in Patients with Brain Metastases and Glioblastoma Multiforme: Impact on Survival. BMC Cancer 2015, 15, 839. [Google Scholar] [CrossRef]
- Lazic, D. Nelinearni Sistemi (Nonlinear Systems); Faculty of Mechanical Engineering, University of Belgrade: Belgrade, Serbia, 2005; ISBN 978-86-7083-530-6. [Google Scholar]
- Wang, W.; Wu, Z.; He, Q. Swimming Nanorobots for Opening a Cell Membrane Mechanically. View 2020, 1, 20200005. [Google Scholar] [CrossRef]
- Ouadid-Ahidouch, H.; Ahidouch, A.; Pardo, L.A. Kv10.1 K+ Channel: From Physiology to Cancer. Pflüg. Arch.-Eur. J. Physiol. 2016, 468, 751–762. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Xi, N.; Lai, K.W.C.; Patterson, K.C.; Chen, H.; Song, B.; Qu, C.; Zhong, B.; Wang, D.H. Cellular Biophysical Dynamics and Ion Channel Activities Detected by AFM-Based Nanorobotic Manipulator in Insulinoma β-Cells. Nanomed. Nanotechnol. Biol. Med. 2013, 9, 636–645. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pardo, L.A. Oncogenic Potential of EAG K+ Channels. EMBO J. 1999, 18, 5540–5547. [Google Scholar] [CrossRef] [PubMed]
- Cázares-Ordoñez, V.; Pardo, L.A. Kv10.1 Potassium Channel: From the Brain to the Tumors. Biochem. Cell Biol. 2017, 95, 531–536. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Q.; Ding, B.; Nie, G. Anticancer Activities of Tumor-Killing Nanorobots. Trends Biotechnol. 2019, 37, 573–577. [Google Scholar] [CrossRef]
- Hariharan, R.; Manohar, J. Nanorobotics as Medicament: (Perfect Solution for Cancer). In Proceedings of the INTERACT-2010, Chennai, India, 3–5 December 2010; IEEE: Chennai, India, 2010; pp. 4–7. [Google Scholar]
- Manjunath, A.; Kishore, V. The Promising Future in Medicine: Nanorobots. Biomed. Sci. Eng. 2014, 2, 42–47. [Google Scholar] [CrossRef]
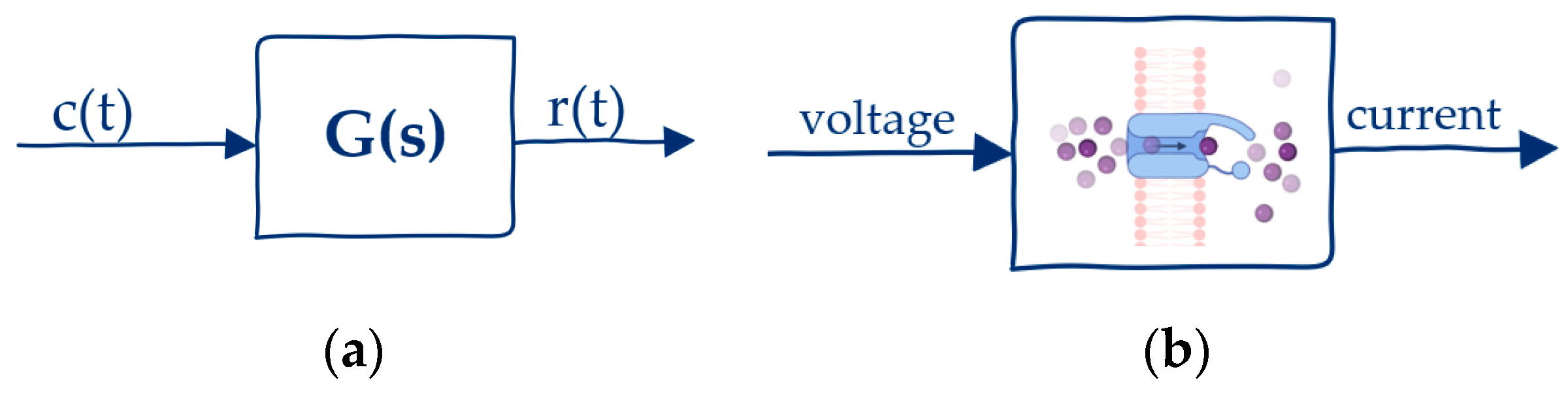
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozanović Šajić, J.; Langthaler, S.; Baumgartner, C. Creating a Novel Mathematical Model of the Kv10.1 Ion Channel and Controlling Channel Activity with Nanoelectromechanical Systems. Appl. Sci. 2022, 12, 3836. https://doi.org/10.3390/app12083836
Lozanović Šajić J, Langthaler S, Baumgartner C. Creating a Novel Mathematical Model of the Kv10.1 Ion Channel and Controlling Channel Activity with Nanoelectromechanical Systems. Applied Sciences. 2022; 12(8):3836. https://doi.org/10.3390/app12083836
Chicago/Turabian StyleLozanović Šajić, Jasmina, Sonja Langthaler, and Christian Baumgartner. 2022. "Creating a Novel Mathematical Model of the Kv10.1 Ion Channel and Controlling Channel Activity with Nanoelectromechanical Systems" Applied Sciences 12, no. 8: 3836. https://doi.org/10.3390/app12083836
APA StyleLozanović Šajić, J., Langthaler, S., & Baumgartner, C. (2022). Creating a Novel Mathematical Model of the Kv10.1 Ion Channel and Controlling Channel Activity with Nanoelectromechanical Systems. Applied Sciences, 12(8), 3836. https://doi.org/10.3390/app12083836






