Numerical Modeling of Flexible Net Panels under Steady Flow Using a Coupled Fluid–Structure Partitioned Scheme
Abstract
:1. Introduction
2. Governing Fluid–Structure Equations
2.1. Governing Equations for the Fluid
2.2. Governing Equations for the Structure
2.3. Governing Equations for the Fluid–Structure Interface
3. Numerical Solutions of Fluid–Structure Equations
3.1. Numerical Solutions of the Fluid Equations
3.2. Numerical Solutions of the Structural Dynamic Equations
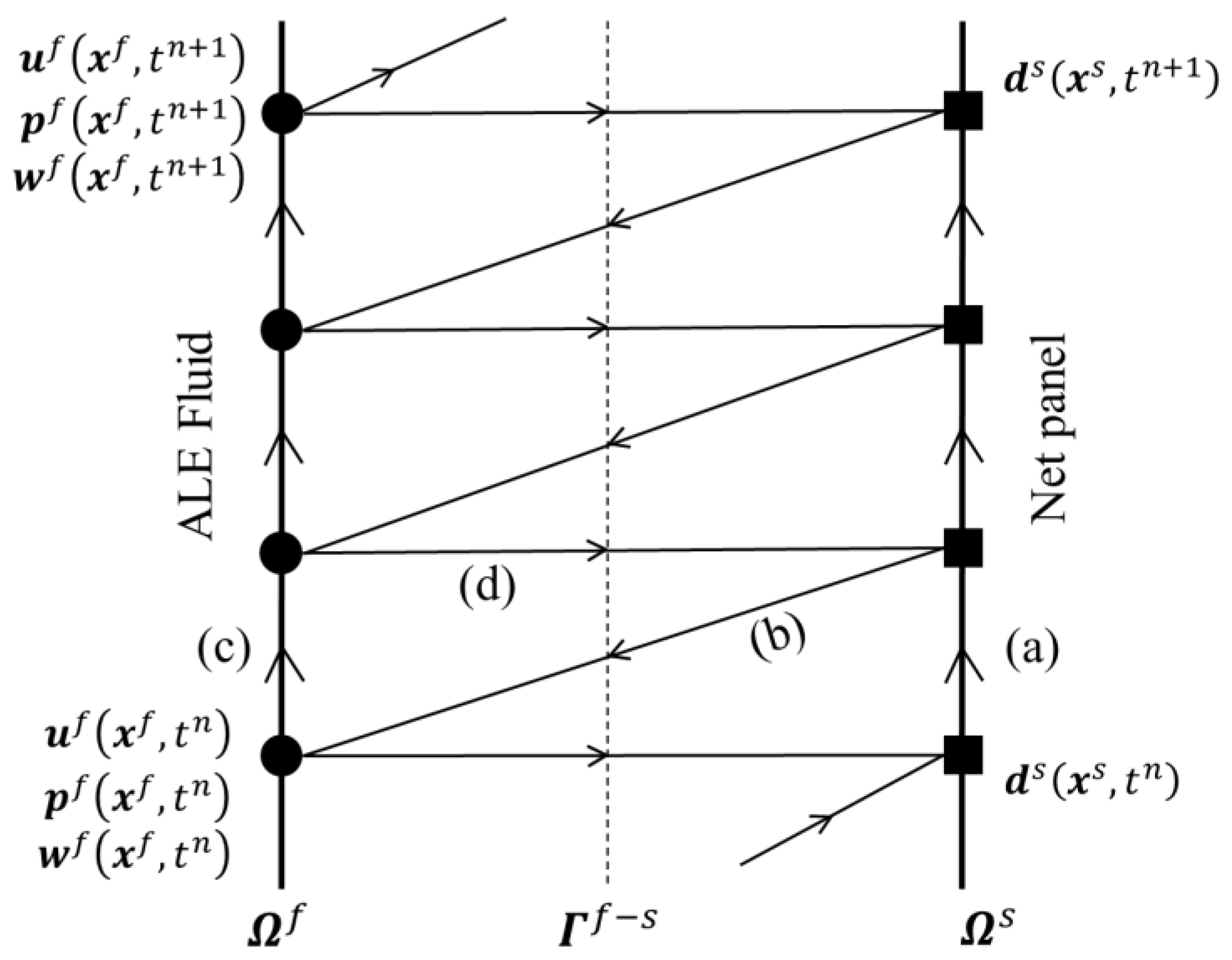
4. Partitioned Strong Coupling Formulation
| Algorithm 1. Partitioned coupling scheme. |
| 1. Perform the traction force predictor for interface traction pressure and velocity . |
| 2. Each FSI iteration between : |
| (a) Solve structural Eq. (15) using known interface traction ; |
| (b) Apply Dirichlet velocity continuity condition |
| on interface Γ; |
| (c) Set and update the fluid dynamic mesh; |
| (d) Solve ALE fluid Equation (10) for new interface traction and apply Neumann condition on interface Γ. |
5. Numerical Setup and Verification
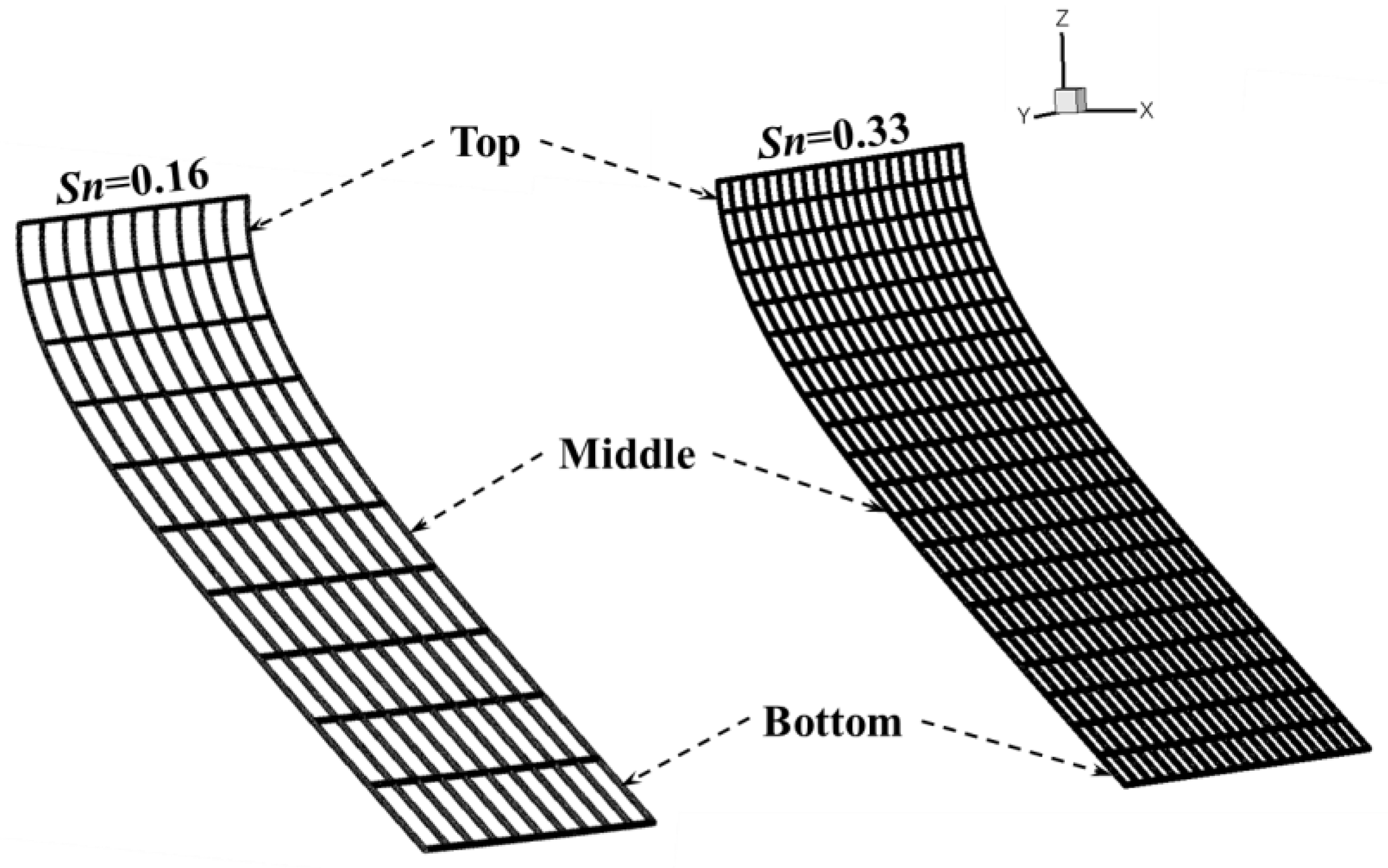
5.1. The Net Panel
5.2. Computational Domain and Boundary Conditions
5.3. Numerical Verification
6. Results and Discussion
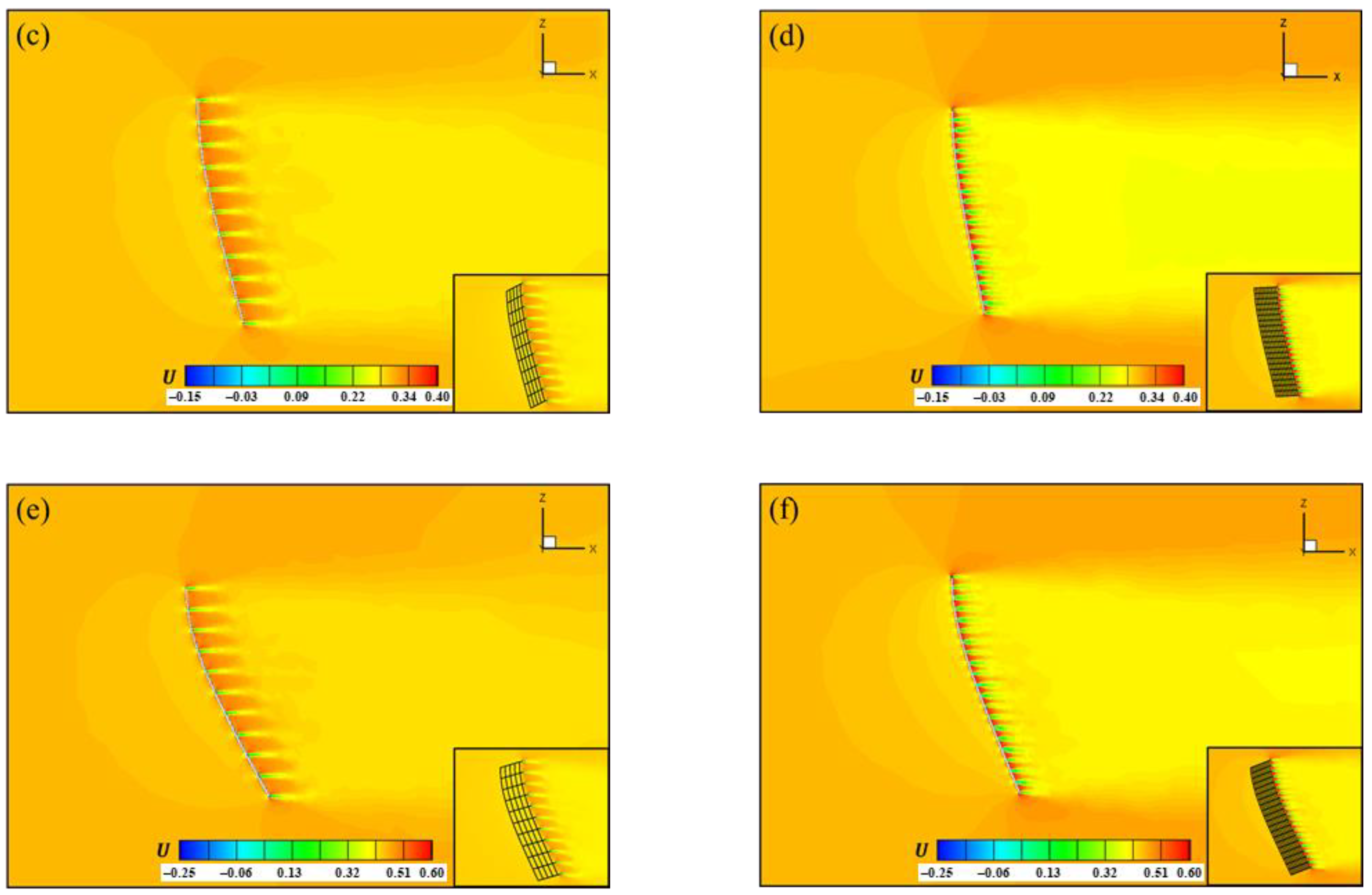
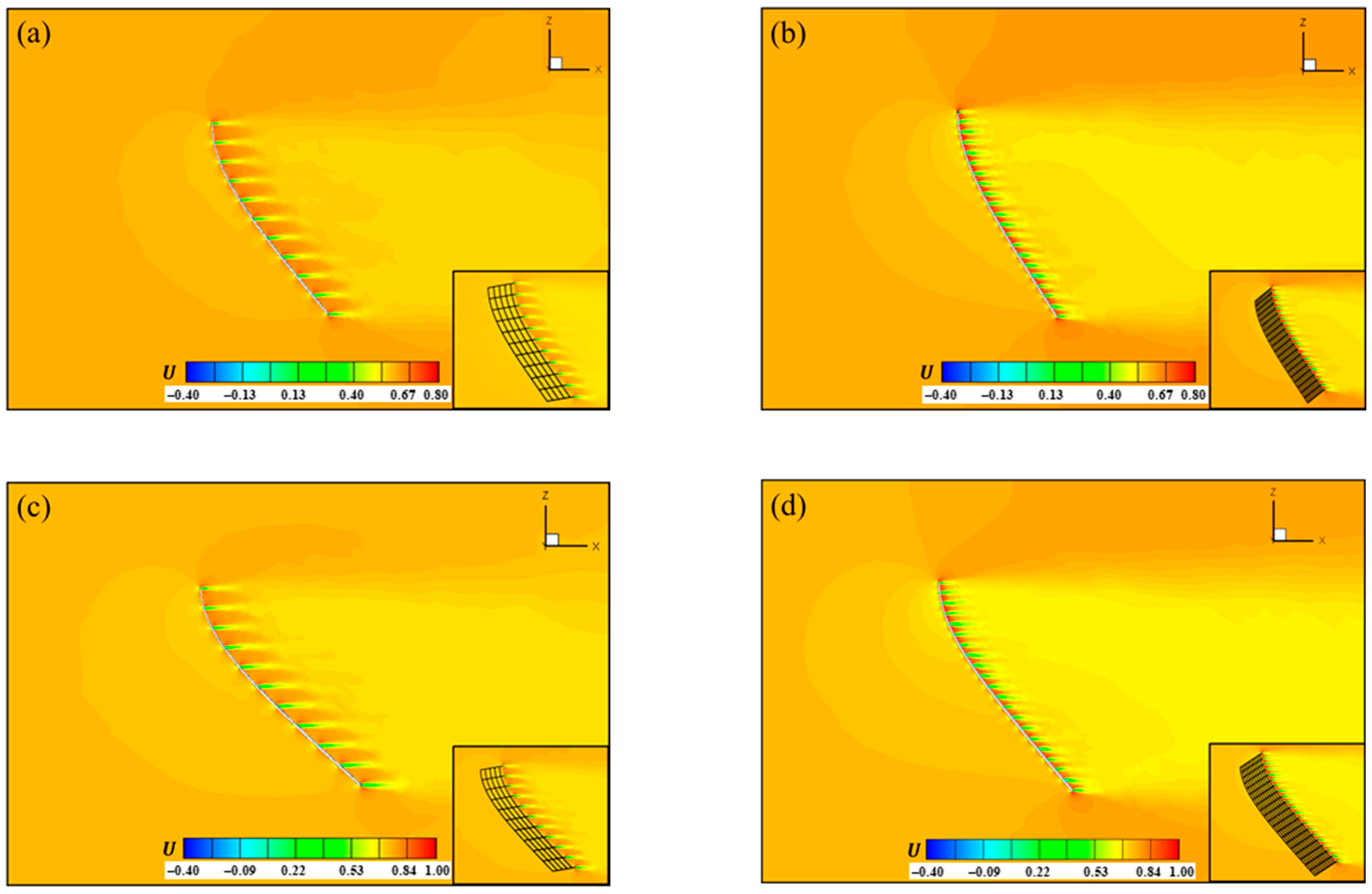
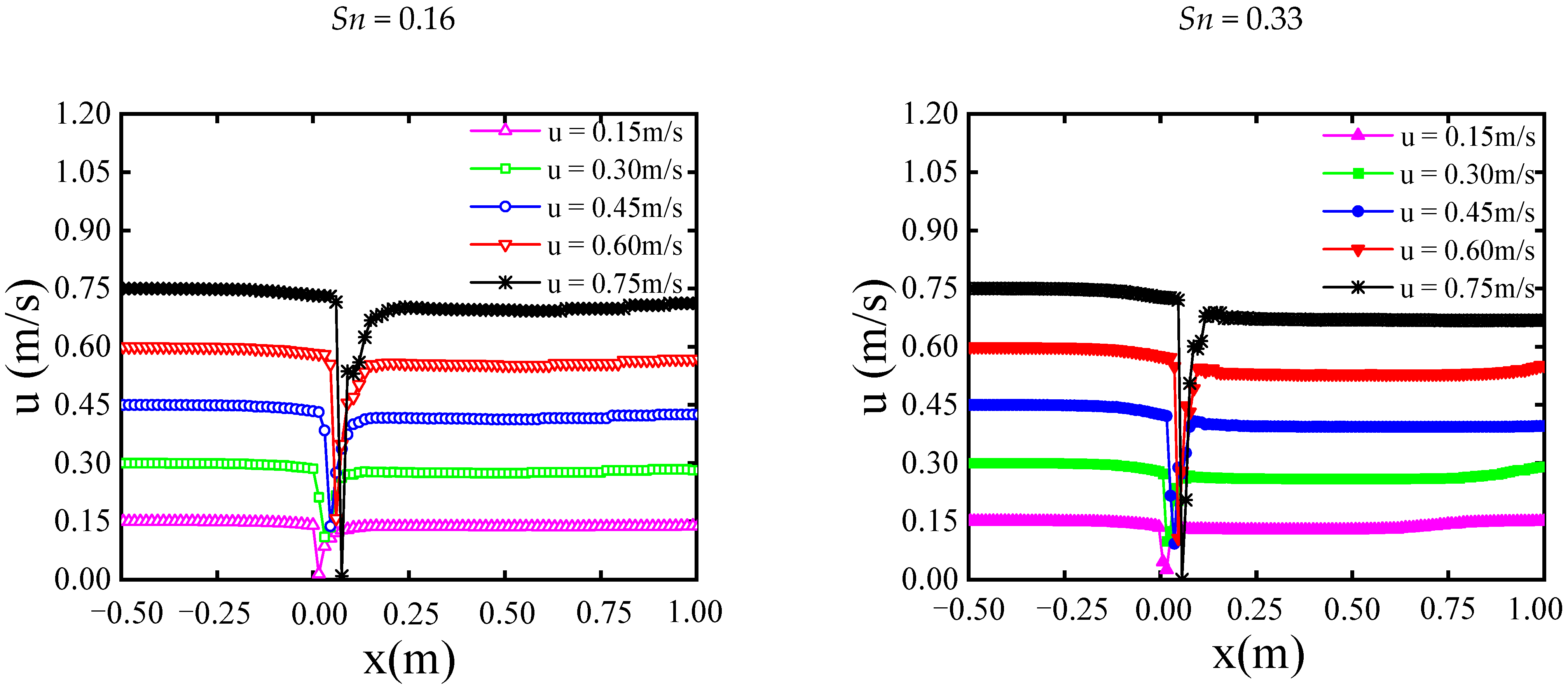
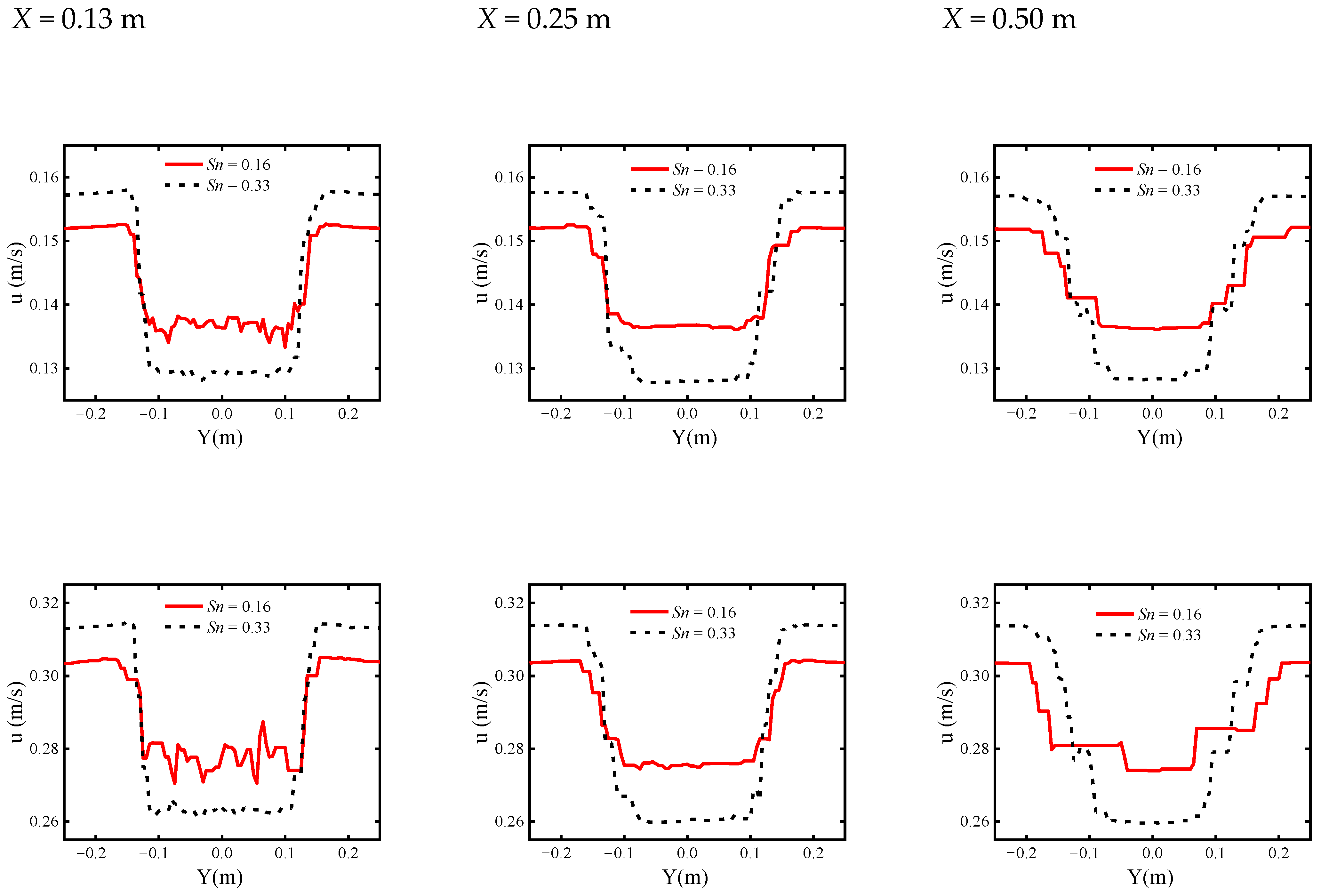
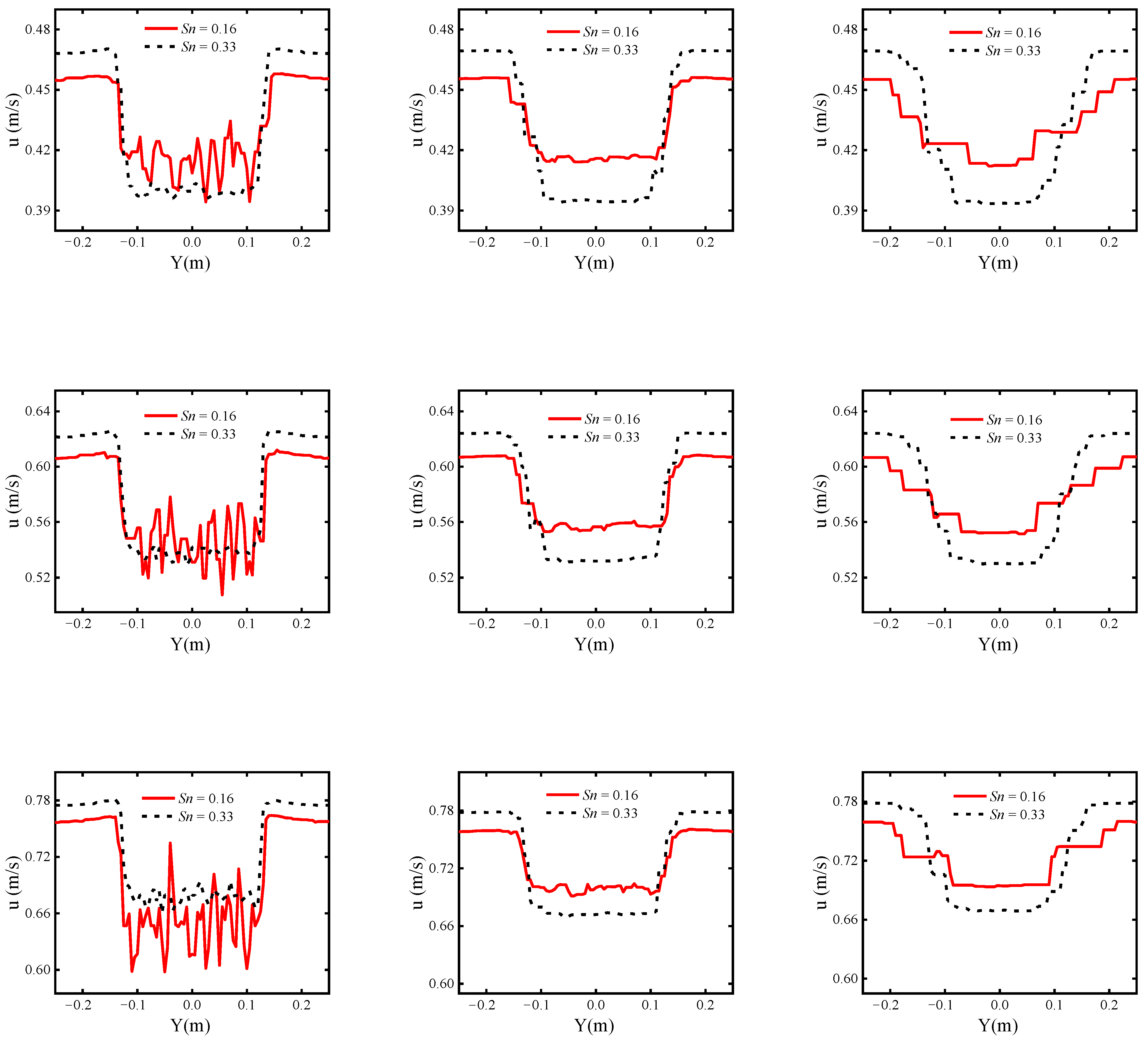
6.1. Velocity Distribution
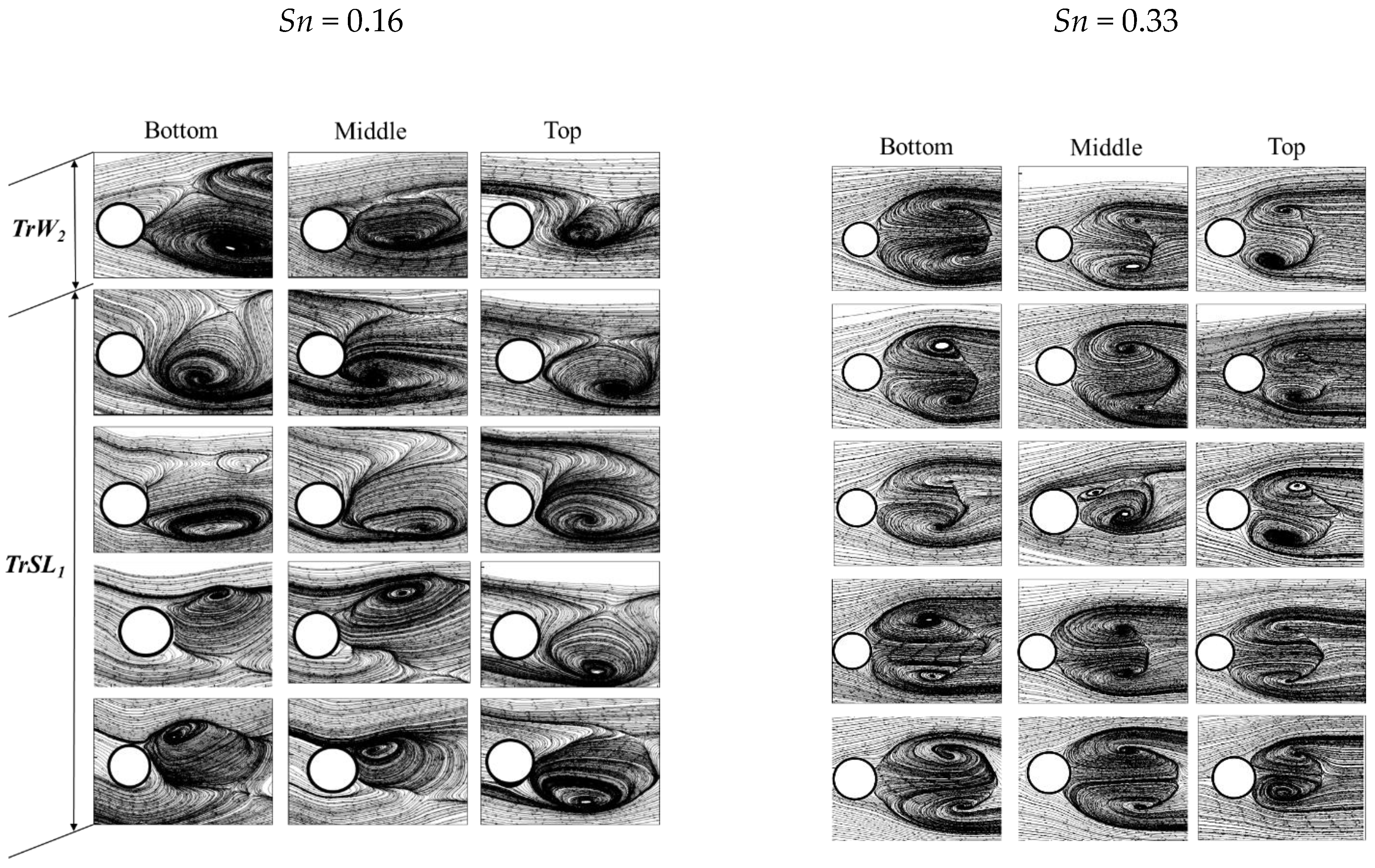
- (1)
- Transition-in-wake state of flow (TrW).
- (2)
- Transition-in-shear-layers state of flow (TrSL).
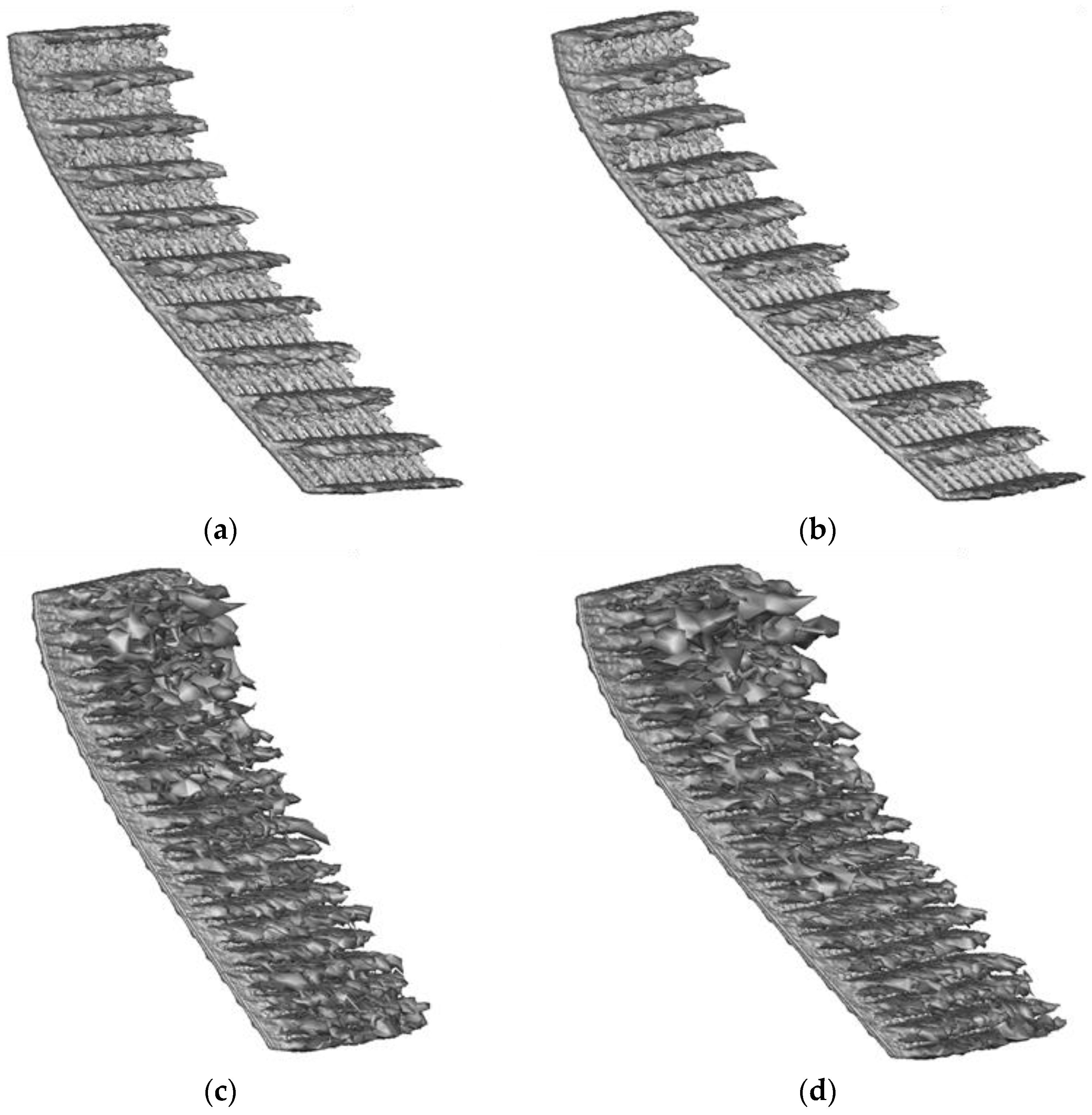
6.2. Recirculation and Vortex Formation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.; Qin, H. Fluid-structure interactions of cage based aquaculture: From structures to organisms. Ocean. Eng. 2020, 217, 107961. [Google Scholar] [CrossRef]
- He, Z.; Faltinsen, O.M.; Fredheim, A.; Kristiansen, T. The influence of fish on the mooring loads of a floating net cage. J. Fluids Struct. 2018, 76, 384–395. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.W.; Lee, J.H.; Cha, B.J.; Kim, H.Y.; Lee, J.H. Physical modeling for underwater flexible systems dynamic simulation. Ocean. Eng. 2005, 32, 331–347. [Google Scholar] [CrossRef]
- Li, L.; Fu, S.; Xu, Y. Nonlinear hydroelastic analysis of an aquaculture fish cage in irregular waves. Mar. Struct. 2013, 34, 56–73. [Google Scholar] [CrossRef]
- Li, L.; Fu, S.; Xu, Y.; Wang, J.; Yang, J. Dynamic responses of floating fish cage in waves and current. Ocean. Eng. 2013, 72, 297–303. [Google Scholar] [CrossRef]
- Tsukrov, I.; Eroshkin, O.; Fredriksson, D.; Robinson, M. Finite element modeling of net panels using a consistent net element. Ocean. Eng. 2003, 30, 251–270. [Google Scholar] [CrossRef]
- Tsukrov, I.; Eroshkin, O.; Paul, W.; Celikkol, B. Numerical modeling of nonlinear elastic components of mooring systems. IEEE J. Ocean. Eng. 2005, 30, 37–46. [Google Scholar] [CrossRef]
- Yang, R.-Y.; Tang, H.-J.; Huang, C.-C. Numerical Modeling of the Mooring System Failure of an Aquaculture Net Cage System Under Waves and Currents. IEEE J. Ocean. Eng. 2019, 45, 1396–1410. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Wu, Z.-M.; Zhang, Y.; Xu, T.-J. Drag on and flow through the hydroid-fouled nets in currents. Ocean. Eng. 2018, 161, 195–204. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Xu, T.-J.; Gui, F.-K. Numerical study on wave attenuation inside and around a square array of biofouled net cages. Aquac. Eng. 2017, 78, 180–189. [Google Scholar] [CrossRef]
- Chen, H.; Christensen, E.D. Investigations on the porous resistance coefficients for fishing net structures. J. Fluids Struct. 2016, 65, 76–107. [Google Scholar] [CrossRef] [Green Version]
- Patursson, Ø.; Swift, M.R.; Tsukrov, I.; Simonsen, K.; Baldwin, K.; Fredriksson, D.W.; Celikkol, B. Development of a porous media model with application to flow through and around a net panel. Ocean. Eng. 2010, 37, 314–324. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Bi, C.-W.; Dong, G.-H.; Gui, F.-K.; Cui, Y.; Guan, C.-T.; Xu, T.-J. Numerical simulation of the flow around fishing plane nets using the porous media model. Ocean. Eng. 2013, 62, 25–37. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Bi, C.-W.; Dong, G.-H.; Gui, F.-K.; Cui, Y.; Xu, T.-J. Numerical simulation of the flow field inside and around gravity cages. Aquac. Eng. 2013, 52, 1–13. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Xu, T.-J.; Gui, F.-K. Numerical simulation of the interaction between flow and flexible nets. J. Fluids Struct. 2014, 45, 180–201. [Google Scholar] [CrossRef]
- Chen, H.; Christensen, E.D. Development of a numerical model for fluid-structure interaction analysis of flow through and around an aquaculture net cage. Ocean. Eng. 2017, 142, 597–615. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Christensen, E.D. Simulating the hydrodynamic response of a floater–net system in current and waves. J. Fluids Struct. 2018, 79, 50–75. [Google Scholar] [CrossRef] [Green Version]
- Martin, T.; Tsarau, A.; Bihs, H. A numerical framework for modelling the dynamics of open ocean aquaculture structures in viscous fluids. Appl. Ocean. Res. 2021, 106, 102410. [Google Scholar] [CrossRef]
- Kristiansen, T.; Faltinsen, O.M. Modelling of current loads on aquaculture net cages. J. Fluids Struct. 2012, 34, 218–235. [Google Scholar] [CrossRef]
- Moe-Føre, H.; Endresen, P.C.; Aarsæther, K.G.; Jensen, J.; Føre, M.; Kristiansen, D.; Fredheim, A.; Lader, P.; Reite, K.-J. Structural analysis of aquaculture nets: Comparison and validation of different numerical modeling approaches. J. Offshore Mech. Arct. Eng. 2015, 137, 041201. [Google Scholar] [CrossRef]
- Martin, T.; Kamath, A.; Bihs, H. A Lagrangian approach for the coupled simulation of fixed net structures in a Eulerian fluid model. J. Fluids Struct. 2020, 94, 102962. [Google Scholar] [CrossRef]
- Martin, T.; Bihs, H. A non-linear implicit approach for modelling the dynamics of porous tensile structures interacting with fluids. J. Fluids Struct. 2021, 100, 103168. [Google Scholar] [CrossRef]
- Blom, F.J. A monolithical fluid-structure interaction algorithm applied to the piston problem. Comput. Methods Appl. Mech. Eng. 1998, 167, 369–391. [Google Scholar] [CrossRef]
- Dettmer, W.; Perić, D. A computational framework for fluid–rigid body interaction: Finite element formulation and applications. Comput. Methods Appl. Mech. Eng. 2006, 195, 1633–1666. [Google Scholar] [CrossRef]
- Dettmer, W.G.; Perić, D. A Fully Implicit Computational Strategy for Strongly Coupled Fluid–Solid Interaction. Arch. Comput. Methods Eng. 2007, 14, 205–247. [Google Scholar] [CrossRef]
- Hübner, B.; Walhorn, E.; Dinkler, D. A monolithic approach to fluid–structure interaction using space–time finite elements. Comput. Methods Appl. Mech. Eng. 2004, 193, 2087–2104. [Google Scholar] [CrossRef]
- Liu, J.; Jaiman, R.K.; Gurugubelli, P.S. A stable second-order scheme for fluid–structure interaction with strong added-mass effects. J. Comput. Phys. 2014, 270, 687–710. [Google Scholar] [CrossRef]
- Farhat, C.; Zee, K.G.V.D.; Geuzaine, P. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity. Comput. Methods Appl. Mech. Eng. 2006, 195, 1973–2001. [Google Scholar] [CrossRef]
- Piperno, S.; Charbel, F.; Bernard, L. Partitioned procedures for the transient solution of coupled aeroelastic problems. Part I: Model problem, theory, and two-dimensional apllication. Comput. Methods Appl. Mech. Eng. 1995, 124, 79–112. [Google Scholar] [CrossRef]
- Yenduri, A.; Ghoshal, R.; Jaiman, R.K. A new partitioned staggered scheme for flexible multibody interactions with strong inertial effects. Comput. Methods Appl. Mech. Eng. 2017, 315, 316–347. [Google Scholar] [CrossRef]
- Dettmer, W.G.; Perić, D. A new staggered scheme for fluid–structure interaction. Int. J. Numer. Methods Eng. 2012, 93, 1–22. [Google Scholar] [CrossRef]
- Jaiman, R.; Geubelle, P.; Loth, E.; Jiao, X. Combined interface boundary condition method for unsteady fluid–structure interaction. Comput. Methods Appl. Mech. Eng. 2011, 200, 27–39. [Google Scholar] [CrossRef]
- Jaiman, R.K.; Guan, M.Z.; Miyanawala, T.P. Partitioned Iterative and Dynamic Subgrid-Scale Methods for Freely Vibrating dSquare-Section Structures at High Reynolds Number. Comput. Fluids 2016, 133, 68–89. [Google Scholar] [CrossRef]
- Kadapa, C. A second-order accurate non-intrusive staggered scheme for the interaction of ultra-lightweight rigid bodies with fluid flow. Ocean. Eng. 2020, 217, 107940. [Google Scholar] [CrossRef]
- Donea, J.; Giuliani, S.; Halleux, J.-P. An arbitrary Lagrangian-Eulerian finite element method for transient dynamic fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 1982, 33, 689–723. [Google Scholar] [CrossRef]
- Hughes, T.J.; Liu, W.K.; Zimmermann, T.K. Lagrangian-Eulerian finite element formulation for incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 1981, 29, 329–349. [Google Scholar] [CrossRef]
- Huang, C.C.; Tang, H.J.; Pan, J.Y. Numerical Modeling of a Single-Point Mooring Cage With a Frontal Rigid Frame. IEEE J. Ocean. Eng. 2009, 34, 113–122. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Li, Y.-C.; Dong, G.-H.; Gui, F.-K.; Teng, B. Numerical simulation of the effects of structure size ratio and mesh type on three-dimensional deformation of the fishing-net gravity cage in current. Aquac. Eng. 2007, 36, 285–301. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Li, Y.-C.; Dong, G.-H.; Gui, F.-K.; Teng, B. A numerical study on dynamic properties of the gravity cage in combined wave-current flow. Ocean. Eng. 2007, 34, 2350–2363. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier–Stokes equation. Math. Comput. 1968, 22, 745. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Joosten, M.; Dettmer, W.; Perić, D. On the temporal stability and accuracy of coupled problems with reference to fluid–structure interaction. Int. J. Numer. Methods Fluids 2010, 64, 1363–1378. [Google Scholar] [CrossRef]
- Fredheim, A. Current Forces on Net Structure. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Noway, 2005. [Google Scholar]
- DeCew, J.; Tsukrov, I.; Risso, A.; Swift, M.; Celikkol, B. Modeling of dynamic behavior of a single-point moored submersible fish cage under currents. Aquac. Eng. 2010, 43, 38–45. [Google Scholar] [CrossRef]
- Lader, P.F.; Enerhaug, B. Experimental investigation of forces and geometry of a net cage in uniform flow. IEEE J. Ocean. Eng. 2005, 30, 79–84. [Google Scholar] [CrossRef]
- Aarsnes, J.; Rudi, H.; Løland, G. Current forces on cage, net deflection, Engineering for offshore fish farming. In Proceedings of the Conference Organised by the Institution of Civil Engineers, Glasgow, UK, 17–18 October 1990; Thomas Telford Publishing: London, UK, 1990; pp. 137–152. [Google Scholar]
- Løland, G. Current Forces on and Flow Through Fish Farms. Ph.D. Thesis, Norwegian University of Science and Technology, Institute for Hydrodynamics, Trondheim, Norway, 1993. [Google Scholar]
- Zdravkovich, M.M. Flow Around Circular Cylinders: Volume 1997, 2: Applications; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Xu, T.-J.; Gui, F.-K. Experimental investigation of the reduction in flow velocity downstream from a fishing net. Aquac. Eng. 2013, 57, 71–81. [Google Scholar] [CrossRef]
- Fredriksson, D.W. Open Ocean Fish Cage and Mooring System Dynamics. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 2001. [Google Scholar]
- Bai, H.; Alam, M.M. Dependence of square cylinder wake on Reynolds number. Phys. Fluids 2018, 30, 015102. [Google Scholar] [CrossRef]
- Hunt, J.; Wray, A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program; Center for Turbulence Research: Stanford, CA, USA, 1988; pp. 193–208. [Google Scholar]






| 0.16 | 2 | 25 |
| 0.33 | 2 | 12 |
| Researchers | Empirical Formulae |
|---|---|
| Aarsnes et al. [47] | |
| Kristiansen and Faltinsen [19] |
| Drag Coefficient/Relative Difference | ||||||
|---|---|---|---|---|---|---|
| Num. | Num. | Aarsnes et al. [47] | Kristiansen and Faltinsen [19] | |||
| Sn = 0.16 | Sn = 0.33 | Sn = 0.16 | Sn = 0.33 | Sn = 0.16 | Sn = 0.33 | |
| 300 | 0.221 | 0.747 | 0.184 −16.7% | 0.686 −8.2% | 0.250 13.1% | 0.719 3.7% |
| 600 | 0.209 | 0.682 | 0.181 −13.4% | 0.679 −0.4% | 0.235 12.4% | 0.680 0.2% |
| 900 | 0.199 | 0.640 | 0.174 −12.6% | 0.656 2.5% | 0.229 15.1% | 0.664 3.8% |
| 1200 | 0.192 | 0.601 | 0.162 −15.6% | 0.617 2.7% | 0.225 17.2% | 0.655 8.9% |
| 1500 | 0.188 | 0.476 | 0.151 −19.7% | 0.583 22.5% | 0.223 18.6% | 0.650 36.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Qin, H.; Li, P.; Xu, Z. Numerical Modeling of Flexible Net Panels under Steady Flow Using a Coupled Fluid–Structure Partitioned Scheme. Appl. Sci. 2022, 12, 3399. https://doi.org/10.3390/app12073399
Xu L, Qin H, Li P, Xu Z. Numerical Modeling of Flexible Net Panels under Steady Flow Using a Coupled Fluid–Structure Partitioned Scheme. Applied Sciences. 2022; 12(7):3399. https://doi.org/10.3390/app12073399
Chicago/Turabian StyleXu, Lingyun, Hongde Qin, Peng Li, and Zhijing Xu. 2022. "Numerical Modeling of Flexible Net Panels under Steady Flow Using a Coupled Fluid–Structure Partitioned Scheme" Applied Sciences 12, no. 7: 3399. https://doi.org/10.3390/app12073399
APA StyleXu, L., Qin, H., Li, P., & Xu, Z. (2022). Numerical Modeling of Flexible Net Panels under Steady Flow Using a Coupled Fluid–Structure Partitioned Scheme. Applied Sciences, 12(7), 3399. https://doi.org/10.3390/app12073399







