Numerical Evaluation of Fatigue Crack Growth of Structural Steels Using Energy Release Rate with VCCT
Abstract
:1. Introduction
2. Materials and Methods
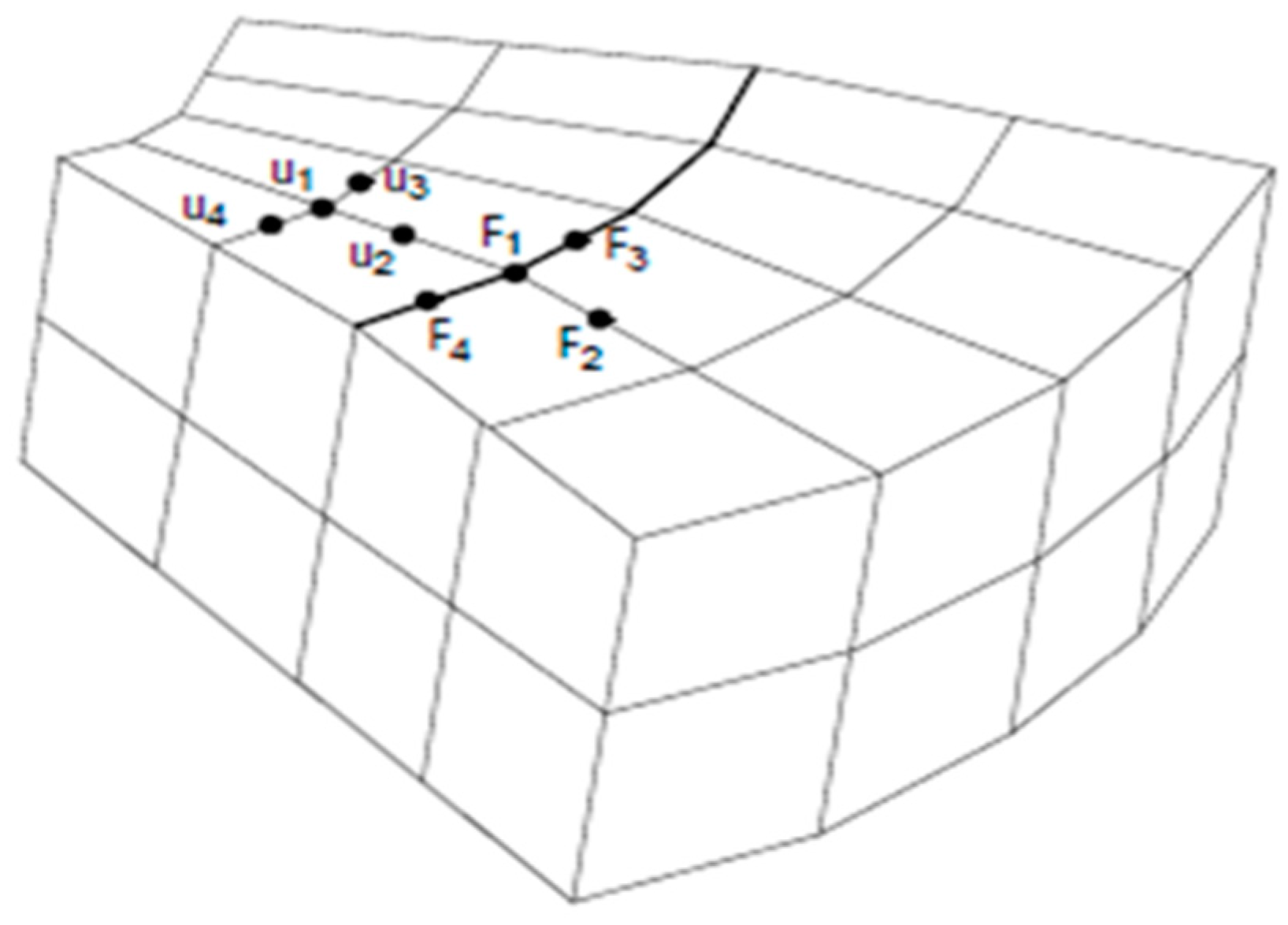
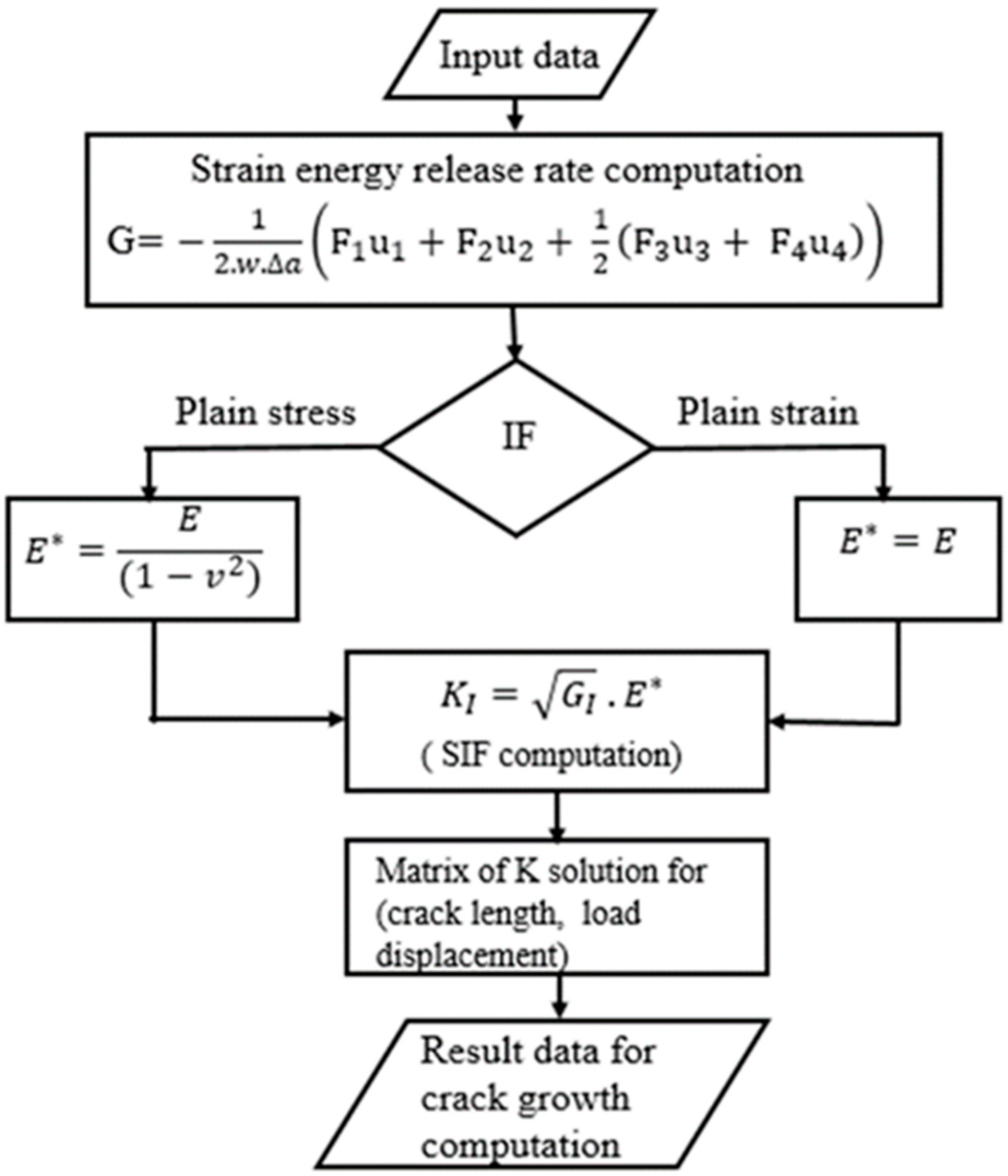
2.1. FCG Assessment of the Energy Release Rate with VCCT
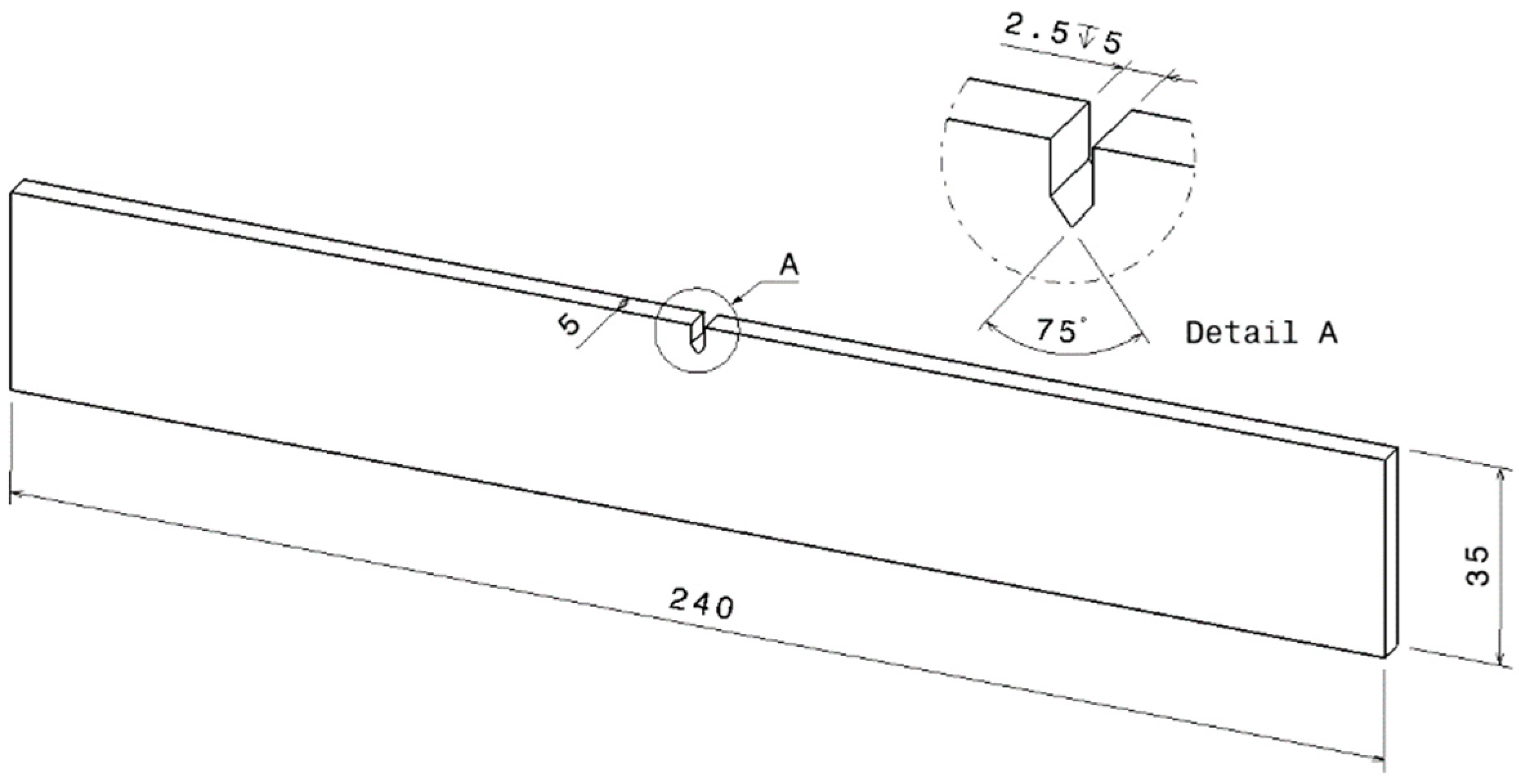
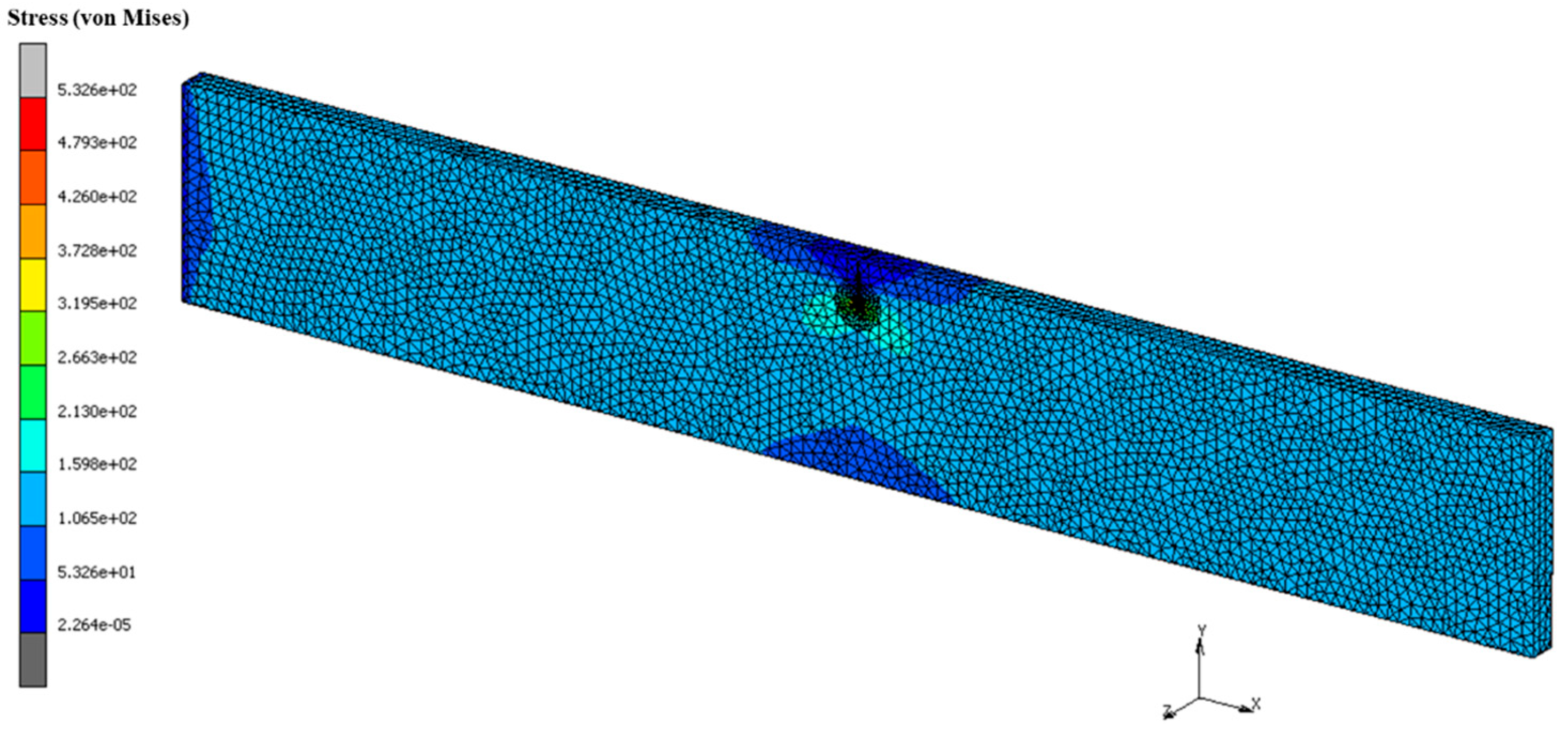
2.1.1. Geometrical Modelling
2.1.2. Boundary Condition
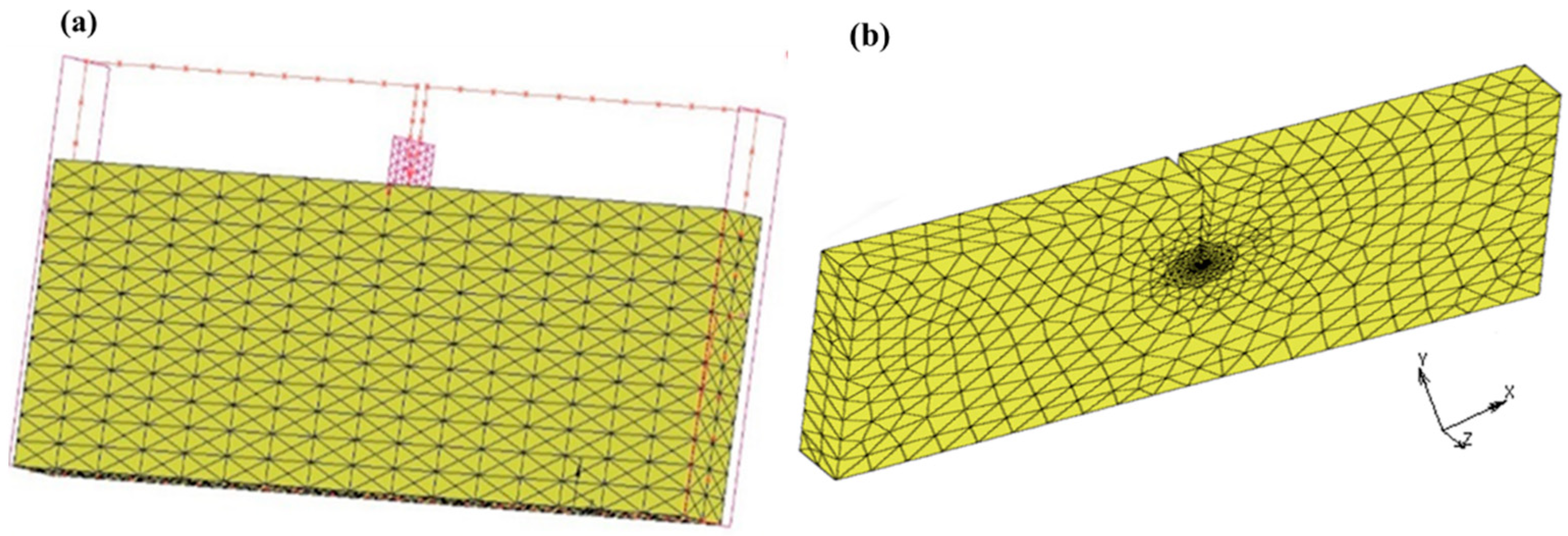
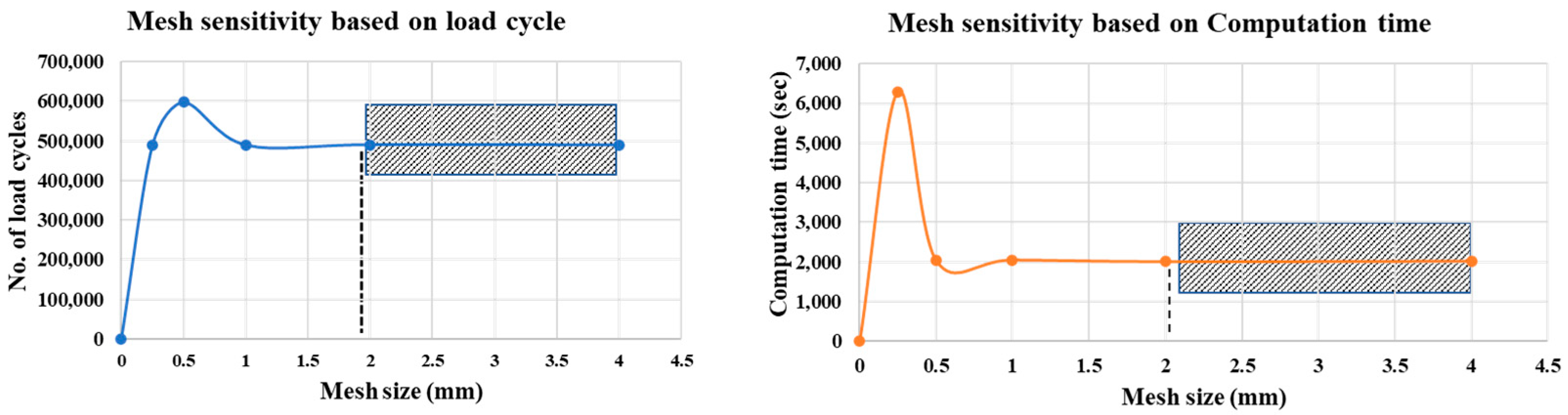
2.1.3. Mesh Sensitivity Analysis
3. Results and Discussion
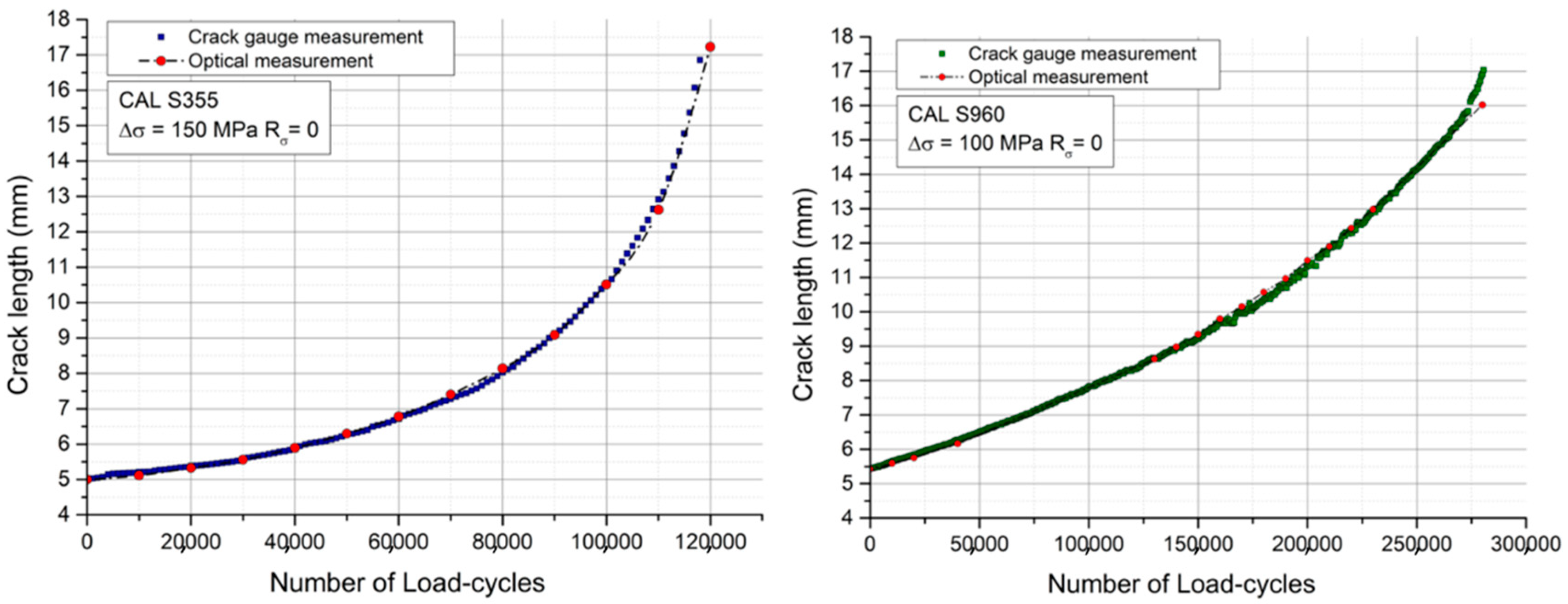
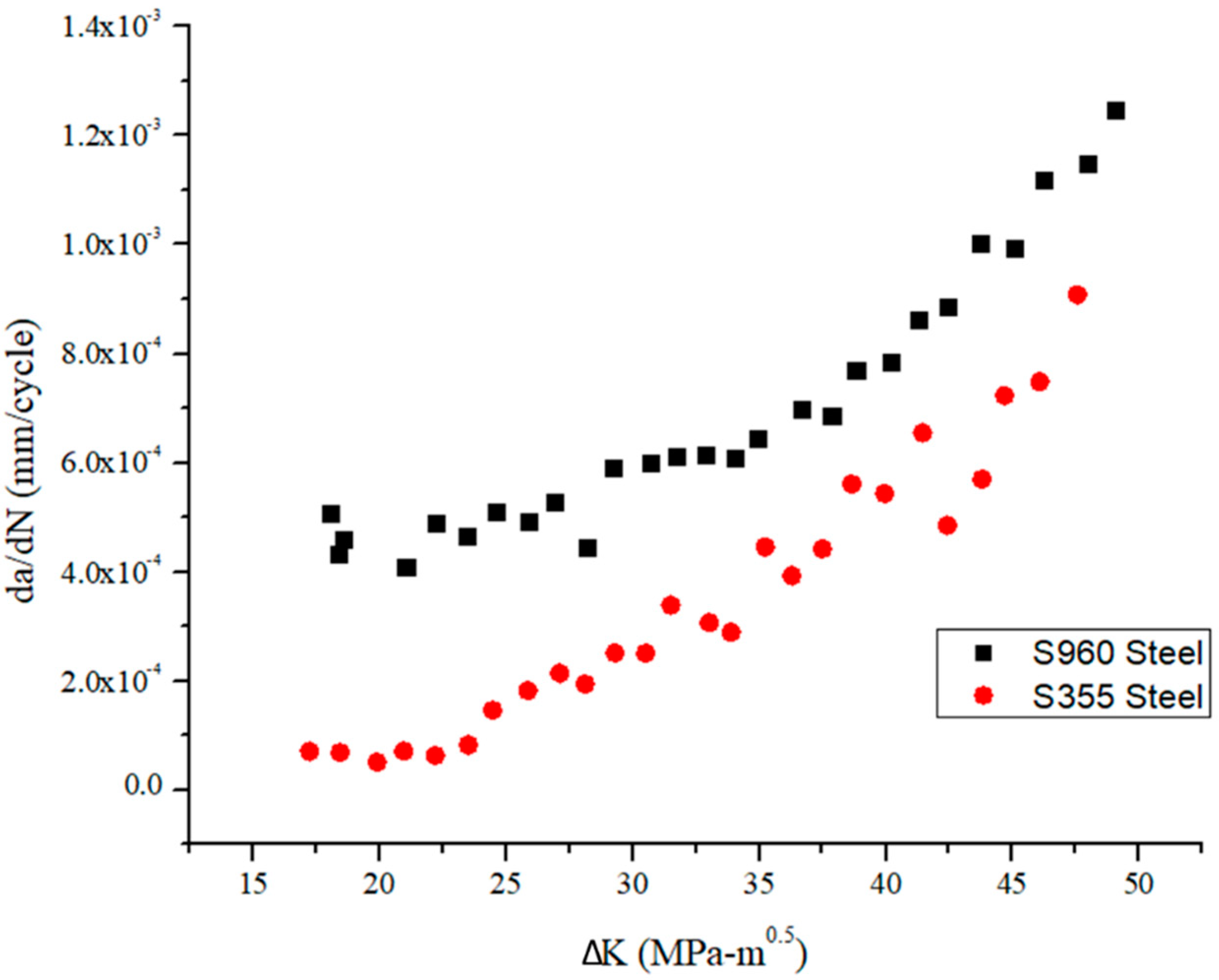
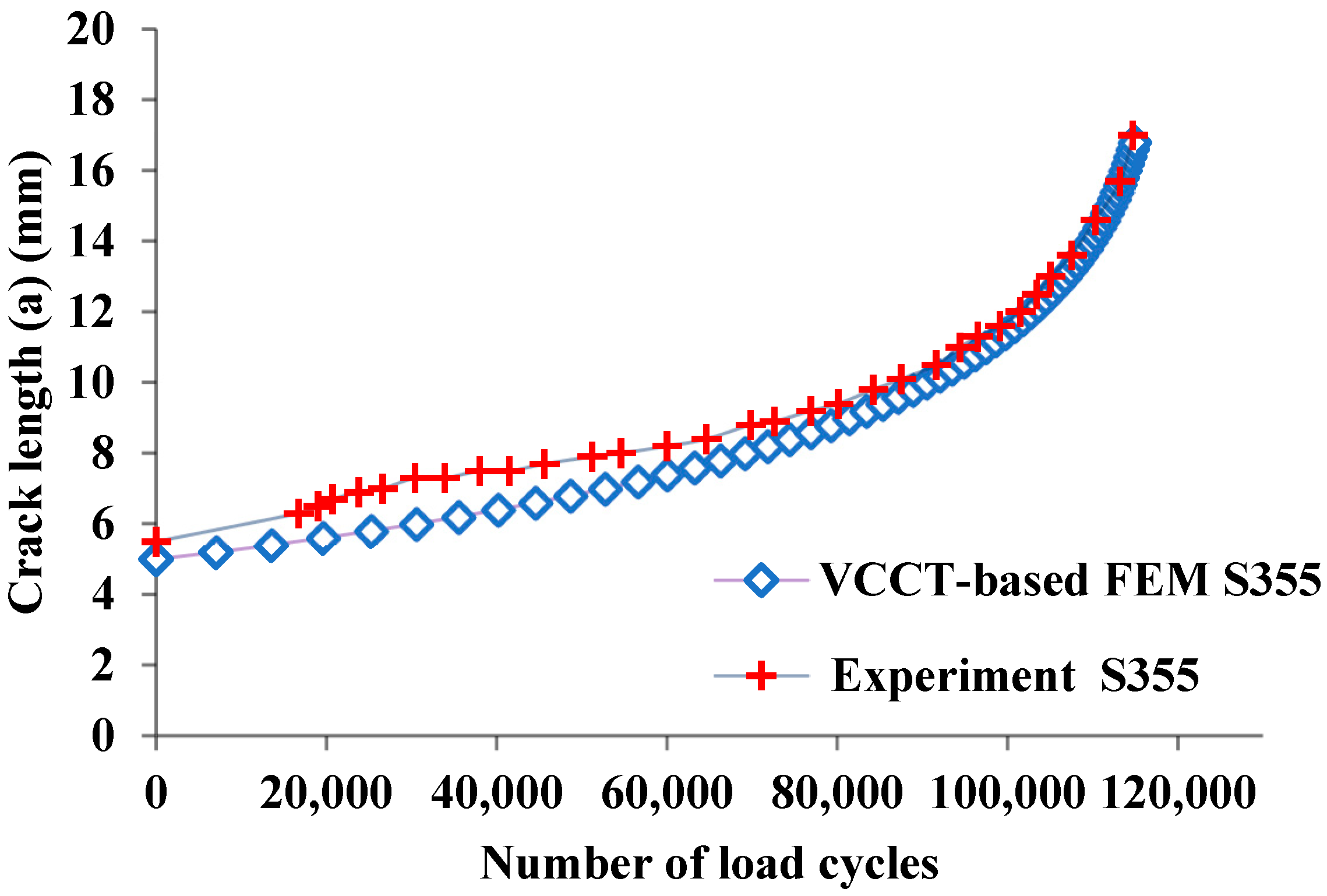
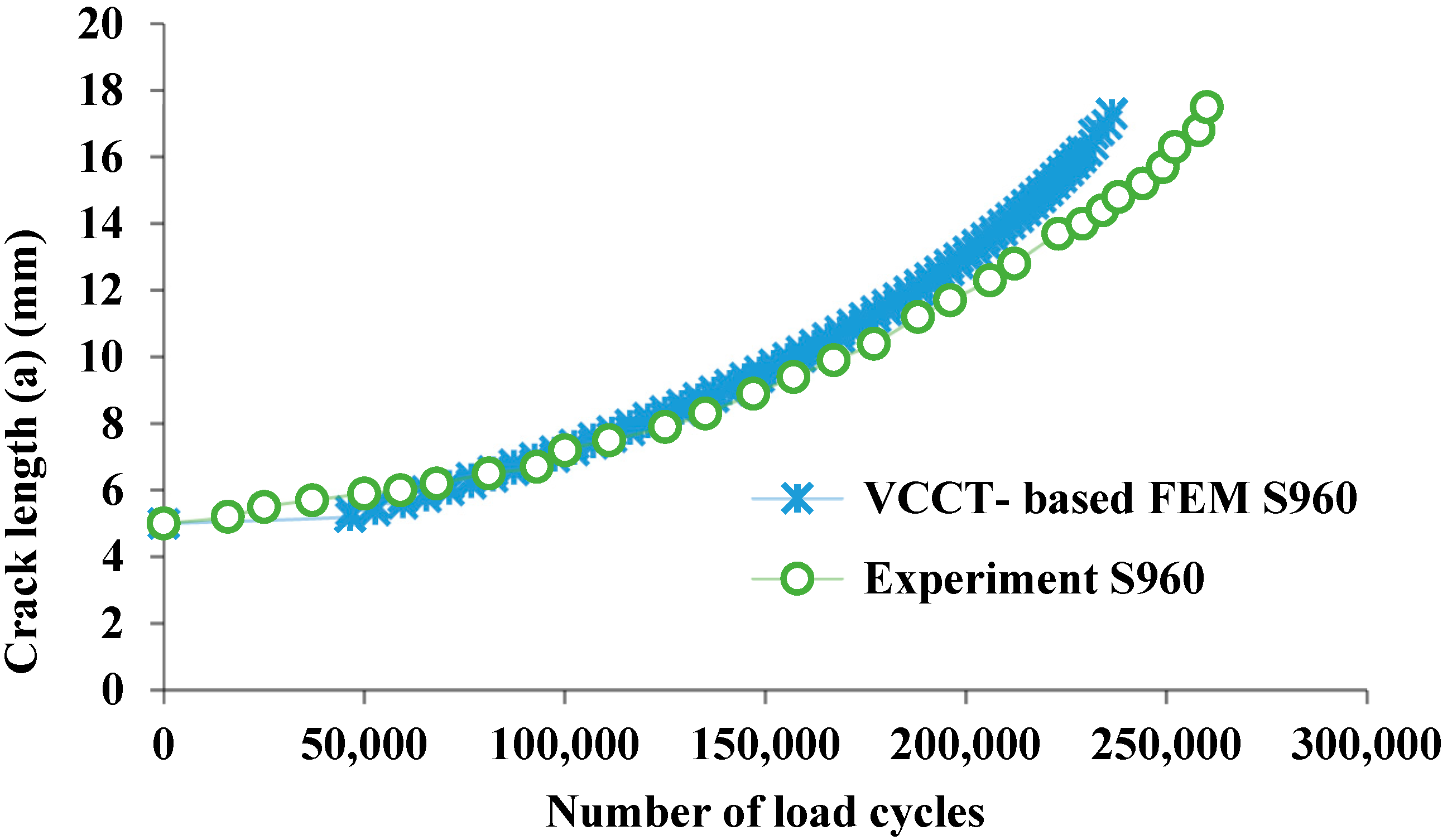
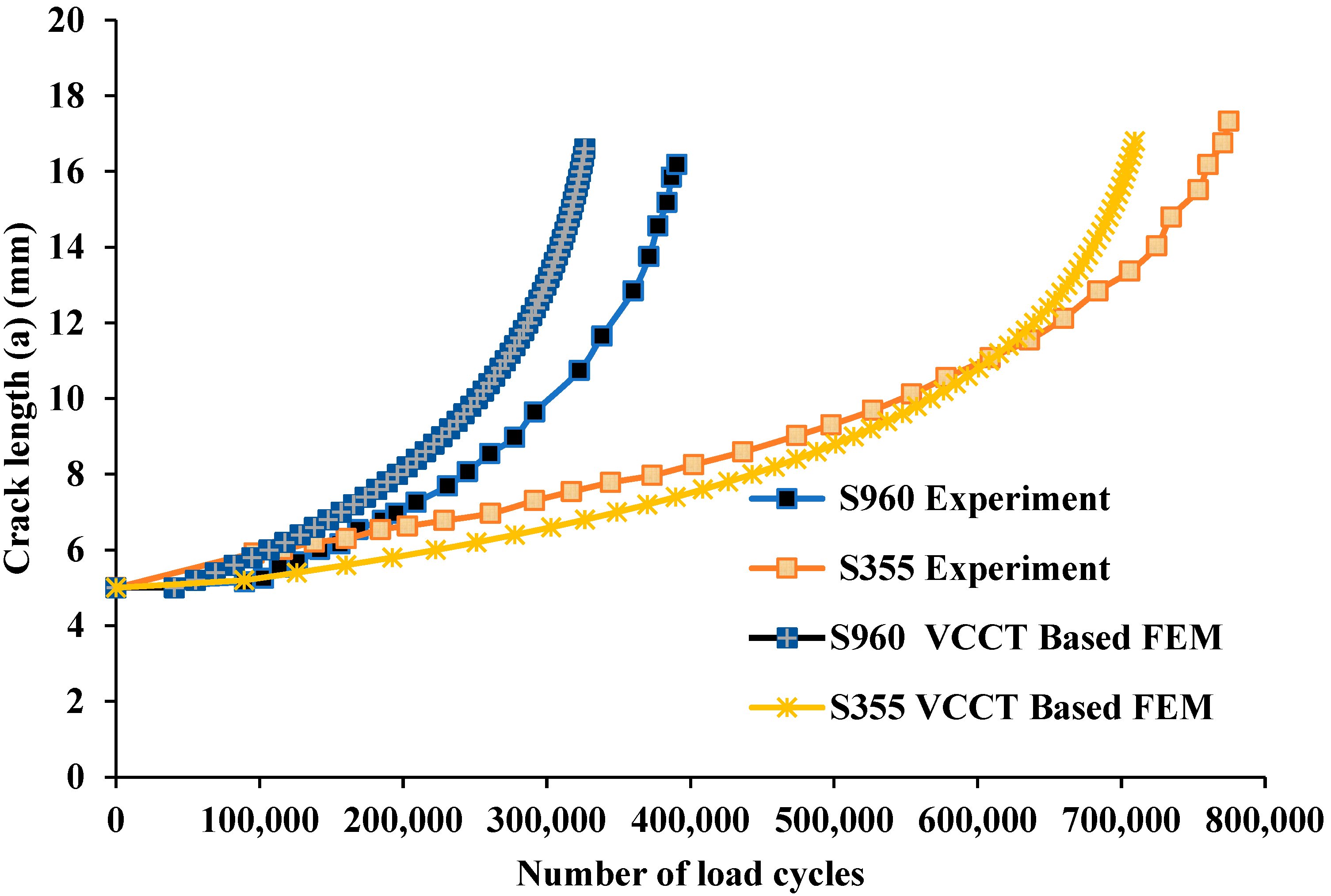
VCCT-Based Fatigue Crack Growth
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagoju, M.K.S.K.; Gopinath, V. Computation of Stress Intensity Factor and Critical crack length of ASTM A36 steel using Fracture Mechanics. Int. J. Eng. Res. Technol. (IJERT) 2013, 2, 2677–2683. [Google Scholar]
- Jones, R.; Chen, F.; Pitt, S.; Paggi, M.; Carpinteri, A. From NASGRO to fractals: Representing crack growth in metals. Int. J. Fatigue 2016, 82, 540–549. [Google Scholar] [CrossRef]
- Carpinteria, A.; Paggi, M. Are the paris law parameters dependenton each other? Frat. Ed Integrità Strutt. 2007, 1, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Irwin, G.R. Onset of Fast Crack Propagation in High Strength Steel and Aluminum Alloys; Naval Research Lab: Washington, DC, USA, 1956. [Google Scholar]
- Adak, D.; Pramod, A.L.N.; Ooi, E.T.; Natarajan, S. A combined virtual element method and the scaled boundary finite element method for linear elastic fracture mechanics. Eng. Anal. Bound. Elem. 2020, 113, 9–16. [Google Scholar] [CrossRef]
- Romlay, F.R.M.; Ouyang, H.; Ariffin, A.K.; Mohamed, N.A.N. Modeling of fatigue crack propagation using dual boundary element method and Gaussian Monte Carlo method. Eng. Anal. Bound. Elem. 2010, 34, 297–305. [Google Scholar] [CrossRef]
- Koenke, C.; Harte, R.; Krätzig, W.B.; Rosenstein, O. On adaptive remeshing techniques for crack simulation problems. Eng. Comput. 1998, 15, 74–88. [Google Scholar] [CrossRef]
- Aguirre-Mesa, A.M.; Ramirez-Tamayo, D.; Garcia, M.J.; Montoya, A.; Millwater, H. A stiffness derivative local hypercomplex-variable finite element method for computing the energy release rate. Eng. Fract. Mech. 2019, 218, 106581. [Google Scholar] [CrossRef]
- Krueger, R.; Shivakumar, K.; Raju, I.S. Fracture mechanics analyses for interface crack problems a review. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar] [CrossRef] [Green Version]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Shivakumar, K.N.; Tan, P.W.; Newman, J.C. A Virtual Crack-Closure Technique for Calculating Stress Intensity Factors for Cracked Three Dimensional Bodies. Int. J. Fract. 1988, 36, 43–50. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H.; Harari, I. Direct evaluation of stress intensity factors for curved cracks using Irwin’s integral and XFEM with high-order enrichment functions. Int. J. Numer. Methods Eng. 2017, 112, 629–654. [Google Scholar] [CrossRef]
- Barsoum, R.S. On the use of Isoparametric finite elements in linear elastic fracture mechanics. Int. J. Numer. Methods Eng. 1976, 10, 25–37. [Google Scholar] [CrossRef]
- Leski, A. Implementation of the virtual crack closure technique in engineering FE calculations. Finite Elem. Anal. Des. 2007, 43, 261–268. [Google Scholar] [CrossRef]
- Chang, Y.S.; Choi, J.B.; Kim, Y.J.; Yagawa, G. Numerical calculation of energy release rates by virtual crack closure technique. KSME Int. J. 2004, 18, 1996–2008. [Google Scholar] [CrossRef]
- Lin, X.B.; Smith, R.A. Finite element modelling of fatigue crack growth of surface cracked plates Part I: The numerical technique. Eng. Fract. Mech. 1999, 63, 503–522. [Google Scholar] [CrossRef]
- Liu, N.; Jeffers, A.E. Feature-preserving rational Bézier triangles for isogeometric analysis of higher-order gradient damage models. Comput. Methods Appl. Mech. Eng. 2019, 357, 112585. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Cyron, C.J.; Seleson, P.; Silling, S.A. A hybrid meshfree discretization to improve the numerical performance of peridynamic models. Comput. Methods Appl. Mech. Eng. 2022, 391, 114544. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Oterkus, S.; Oterkus, E. An energy-based peridynamic model for fatigue cracking. Eng. Fract. Mech. 2021, 241, 107373. [Google Scholar] [CrossRef]
- MSC Software Volume A: Theory and user information 2019.
- Areias, P.; Reinoso, J.; Camanho, P.P.; César de Sá, J.; Rabczuk, T. Effective 2D and 3D crack propagation with local mesh refinement and the screened Poisson equation. Eng. Fract. Mech. 2018, 189, 339–360. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T. Steiner-point free edge cutting of tetrahedral meshes with applications in fracture. Finite Elem. Anal. Des. 2017, 132, 27–41. [Google Scholar] [CrossRef] [Green Version]
- ASTM E 647–00. Method for Measurement of Fatigue Crack Growth Rates; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Gandossi, L.; Summers, S.A.; Taylor, N.G.; Hurst, R.C.; Hulm, B.J.; Parker, J.D. The potential drop method for monitoring crack growth in real components subjected to combined fatigue and creep conditions: Application of FE techniques for deriving calibration curves. Int. J. Press. Vessel. Pip. 2001, 78, 881–891. [Google Scholar] [CrossRef]
- Webster, G.A.; Ainsworth, R.A. Stress analysis of cracked bodies. In High Temperature Component Life Assessment; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Irwin, G.R. Analysis of stress and strain near the end of a crack traversing a plate. J. Appl. Mech. ASME 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, G.R.; Jiang, C.; Dong, X.W.; Chen, H.D.; Bao, Y.; Jiang, Y. An effective fracture analysis method based on the virtual crack closure-integral technique implemented in CS-FEM. Appl. Math. Model. 2016, 40, 3783–3800. [Google Scholar] [CrossRef]
- Narayana, K.B.; George, S.; Dattaguru, B.; Ramamurthy, T.S.; Vijayakumar, K. Modified crack closure integral (MCCI) for 3-d problems using 20-noded brick elements. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 145–157. [Google Scholar] [CrossRef]
- Fawaz, S.A. Application of the virtual crack closure technique to calculate stress intensity factors for through crack with an elliptical crack front. Eng. Fract. Mech. 1998, 59, 327–342. [Google Scholar] [CrossRef]
- Azimi, M.; Mirjavadi, S.S.; Asli, S.A. Investigation of Mesh Sensitivity Influence to Determine Crack Characteristic by Finite Element Methods. J. Fail. Anal. Prev. 2016, 16, 506–512. [Google Scholar] [CrossRef]
- González-Herrera, A.; Zapatero, J. Influence of minimum element size to determine crack closure stress by the finite element method. Eng. Fract. Mech. 2005, 72, 337–355. [Google Scholar] [CrossRef]
- Peng, X.; Atroshchenko, E.; Kerfriden, P.; Bordas, S.P.A. Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Comput. Methods Appl. Mech. Eng. 2017, 316, 151–185. [Google Scholar] [CrossRef] [Green Version]
- Hobbacher, A.F. The new IIW recommendations for fatigue assessment of welded joints and components—A comprehensive code recently updated. Int. J. Fatigue 2009, 31, 50–58. [Google Scholar] [CrossRef]
- Ślęzak, T. Fatigue examination of HSLA steel with yield strength of 960 MPa and its welded joints under strain mode. Metals 2020, 10, 228. [Google Scholar] [CrossRef] [Green Version]
- De Jesus, A.M.P.; Matos, R.; Fontoura, B.F.C.; Rebelo, C.; Simões Da Silva, L.; Veljkovic, M. A comparison of the fatigue behavior between S355 and S690 steel grades. J. Constr. Steel Res. 2012, 79, 140–150. [Google Scholar] [CrossRef]


| Properties | Young Modulus (GPa) | Yield Strength (MPa) | Poisson Ratio |
|---|---|---|---|
| S355 Steel | 213 | 355 | 0.3 |
| S960 Steel | 220 | 974 | 0.3 |
| S355 Steel | S960 Steel | |
|---|---|---|
| C (mm/cycle) | 1.67 × 10−12 | 4.71 × 10−11 |
| m | 2.51 | 2.09 |
| S960 Steel Load Cycle (N) | S355 Steel Load Cycle (N) | |
|---|---|---|
| Experiment | 120,000 | 275,000 |
| VCCT-based FEM | 114,873 | 239,679 |
| Percentage error | 4.3% | 12.8% |
| S355 Steel Load Cycle (N) | S960 Steel Load Cycle (N) | |
|---|---|---|
| Experiment | 770,000 | 375,000 |
| VCCT-based FEM | 709,260 | 351,422 |
| Percentage error | 7.9% | 6.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busari, Y.O.; Manurung, Y.H.P.; Leitner, M.; Shuaib-Babata, Y.L.; Mat, M.F.; Ibrahim, H.K.; Simunek, D.; Sulaiman, M.S. Numerical Evaluation of Fatigue Crack Growth of Structural Steels Using Energy Release Rate with VCCT. Appl. Sci. 2022, 12, 2641. https://doi.org/10.3390/app12052641
Busari YO, Manurung YHP, Leitner M, Shuaib-Babata YL, Mat MF, Ibrahim HK, Simunek D, Sulaiman MS. Numerical Evaluation of Fatigue Crack Growth of Structural Steels Using Energy Release Rate with VCCT. Applied Sciences. 2022; 12(5):2641. https://doi.org/10.3390/app12052641
Chicago/Turabian StyleBusari, Yusuf O., Yupiter H. P. Manurung, Martin Leitner, Yusuf L. Shuaib-Babata, Muhd F. Mat, Hassan K. Ibrahim, David Simunek, and Mohd Shahar Sulaiman. 2022. "Numerical Evaluation of Fatigue Crack Growth of Structural Steels Using Energy Release Rate with VCCT" Applied Sciences 12, no. 5: 2641. https://doi.org/10.3390/app12052641
APA StyleBusari, Y. O., Manurung, Y. H. P., Leitner, M., Shuaib-Babata, Y. L., Mat, M. F., Ibrahim, H. K., Simunek, D., & Sulaiman, M. S. (2022). Numerical Evaluation of Fatigue Crack Growth of Structural Steels Using Energy Release Rate with VCCT. Applied Sciences, 12(5), 2641. https://doi.org/10.3390/app12052641







