Analysis of the Acceleration Response Spectra of Single-Layer Spherical Reticulated Shell Structures

Abstract

In recent years, earthquake disasters have seriously damaged nonstructural components, so it is necessary to study their seismic performance. However, the existing scholarly research mainly concentrates on multistorey and high-rise buildings, and there are still deficiencies in the analysis of the seismic performance of the nonstructural components in large-span structures under seismic action. In this paper, the acceleration responses of a single-layer spherical reticulated shell structure are compared with those described in the current seismic design codes of the nonstructural components, and it is found that the current codes are not fully applicable to the seismic design of the nonstructural components in reticulated shell structures. The calculation formulas of the acceleration response spectra of single-layer spherical shell nodes are theoretically derived, and the shell node acceleration response spectra are affected by higher-order modes, orthogonal horizontal seismic input directions, and the membrane stiffness of the shell nodes. The variations in the acceleration responses of the shell nodes with node position and rise-to-span ratio are analysed, and a design method for the equivalent seismic action of the nonstructural components in a single-layer spherical reticulated shell with a roofing system is proposed.

1. Introduction

The single-layer spherical reticulated shell structure is a typical large-span space structure that is widely used in public buildings and densely populated places, shoulders the important functions of acting as temporary command centres, and provides rescue and rescue safety barriers for people after disasters. Scholars have carried out detailed research on the seismic performance of spherical reticulated shell structures. Fan et al. [1] studied the seismic response and seismic failure mechanism of reticulated shell structures and proposed the analysis methods for the seismic performance of different reticulated shell structures. Dominika et al. [2] analysed the seismic response of a geodesic reticulated shell structure simulated by two modelling methods under different seismic excitations and compared the influences of the different modelling methods on the seismic performance of geodesic reticulated shell structures. Li et al. [3] studied the dynamic elastic buckling of arch trusses under earthquake action and analysed the effects of different damping ratios and ground motions on the seismic failure modes of the structures. Qin et al. [4] studied the dynamic characteristics of the elliptical “suspen-dome” based on dynamic field test and analysed the spectral characteristics and seismic performance of the experimental model of elliptical suspen-domes. Li et al. [5] studied the stochastic dynamic stability of single-layer dome structures under stochastic seismic excitation based on the probability density evolution method. Deepshikha et al. [6] analysed the effects of higher modes of multistorey substructures on the seismic response of double-layered reticulated shells and proposed the equivalent static loads analysis method to quantify the interaction between the shell and the higher multistorey substructure modes. Based on the above-mentioned research, the seismic performance of large-span space structures has been significantly improved; however, with the increasing types of nonstructural components in public buildings, the seismic performance of the nonstructural components has become a key problem that cannot be ignored in the design and analysis. Figure 1a–c shows that many nonstructural components are arranged in public buildings, which ensures the normal operation of public building functions. However, under the action of an earthquake, the seismic damage of the nonstructural components is usually more serious than that of the main structure [7]. Kenichi et al. [8] performed a statistical analysis on the seismic damage of the nonstructural components in large-span space structures in the 1995 MS 7.3 Hanshin earthquake and the 2011 MS 9.0 East Japan earthquake and found that the economic losses caused by the seismic damage of the nonstructural components are relatively serious, causing serious injury and even death. Sun Dezhang et al. [9] investigated the seismic damage of various buildings under the 2017 Jiuzhaigo MS 7.0 earthquake and found that serious seismic damage of the nonstructural components occurred in the three local long-span buildings. Figure 2a–c shows that the seismic damage of the nonstructural components in a gymnasium, an airport terminal, and an opera house will cause serious economic losses in these public buildings. Therefore, the seismic performance of the nonstructural components is the key to ensuring the safety and sustainable operation of public buildings.

At present, the seismic design codes of the nonstructural components have been formulated in most counties, and calculation methods for the nonstructural components under the seismic action in the current main codes are summarized in

Table 1. Standards, building codes, and calculations of the seismic action for the nonstructural components.

No.	Codes and Standards	Calculation Formula
1	China: code for seismic design of non-structural components [10]	$F=\gamma \eta {\zeta }_1{\zeta }_2{\alpha }_{\max }G$
2	America: minimum design loads for buildings and other structures [11]	$F=\frac{0.4a_p{S}_{DC}{W}_p}{R_{\mathrm{p}}/I_{\mathrm{p}}}\left[1+2\frac{z}{h}\right]$
3	Europe: design of structures for earthquake resistance-Part 1 (general rules, seismic actions, and rules for buildings) [12]	$F_{EU}=M_{NC}\alpha \times S\left[\frac{3\times \left(1+\frac{z}{H}\right)}{1+{\left(1-\frac{T_a}{T_1}\right)}^2}-0.5\right]\times \frac{g{\gamma }_a}{q_a}$

. According to the above provisions on the seismic performance of the nonstructural components, the equations used to calculate the equivalent lateral forces on the nonstructural components are generally similar, and the seismic action is expressed in terms of the products of the equivalent seismic acceleration and the masses of the nonstructural components.

Scholars have simulated and tested the acceleration response spectra of different positions in various structures and proposed suggestions to improve the current codes. Miranda et al. [13,14] analysed the floor acceleration response of multistorey buildings, pointed out that the influence of high-order vibration modes of multistorey buildings was not fully considered in the seismic action calculation of the nonstructural components in ASCE 7-10, established the seismic response analysis model of multistorey buildings with frame-shear wall systems, and proposed the calculation method of floor acceleration response spectra, which takes the first three vibration modes of the structure into consideration. Miranda et al. verified the accuracy of the calculation method by comparing the floor acceleration response observed in actual earthquake. Singh et al. [15,16] further carried out research on the seismic equivalent lateral force of the nonstructural components in high-rise buildings, divided the nonstructural components into rigid and flexible members according to the natural vibration period of the nonstructural components, carried out seismic time history analysis for different high-rise buildings, compared the equivalent lateral force of the nonstructural components with ASCE 7-10, and proposed a seismic design method suitable for the nonstructural components in high-rise buildings, which considers the effects of high-order vibration modes of high-rise buildings. Wang et al. [17] analysed the floor acceleration response spectra of a high-rise reinforced concrete structure and compared them with those determined with the calculation method of the equivalent lateral force of the nonstructural components in ASCE 7-10, proposing a formula to calculate floor acceleration response spectra considering the plasticity of reinforced concrete structures. Fathali et al. [18] compared the measured floor acceleration data of 151 high-rise buildings with the results of the equivalent seismic action of the nonstructural components calculated based on ASCE 7-10 and corrected the position coefficient and dynamic amplification coefficient of the nonstructural components presented in ASCE 7-10; the modified equivalent lateral force formula considered the influence of the natural vibration period of high-rise buildings and the nonstructural components. Oropeza et al. [19] simplified the main structure into a single-degree-of-freedom simplified model, analysed the seismic response of the nonstructural components with the simplified model under 164 groups of ground motions, and pointed out that Eurocode 8 obviously underestimated the resonant response of the nonstructural components, proposing a modified calculation method on the basis of Eurocode 8, which can consider the influence of the main structure behaving plastically and the influence of the high-order vibration modes of the main structure. Sullivan et al. [20] analysed the main influencing factors of the floor acceleration response spectra of a main structure and proposed the calculation formula of the floor acceleration response spectra of the single-degree-of-freedom system based on the nonlinearity of the main structure and different damping ratios. Ioannis [21] further analysed the influence of the nonlinear behaviour of a multiple-degrees-of-freedom frame structure on the floor acceleration response spectra and found that the nonlinearity of the main structure can reduce the floor acceleration response and increase the influence of high-order vibration modes of the main structure. Calvi et al. [22,23] conducted an analysis of the floor acceleration response spectra of a system with multiple-degrees-of-freedom and proposed a modified calculation method for the nonstructural components in reinforced concrete high-rise buildings under seismic action based on Eurocode 8. Petrone et al. [24] analysed floor acceleration response spectra of reinforced concrete structures with different floors in Europe and further improved the calculation method of the equivalent seismic action of the nonstructural components in reinforced concrete structures presented in Eurocode 8. Samit et al. [25] carried out a time history analysis of steel structures with different heights, evaluated the horizontal floor acceleration response spectra of the nonlinear frames under the action of earthquakes, and studied the influence of the second and higher modes on the acceleration response spectra at different positions in the steel frames.

For the seismic design and analysis of the nonstructural components in complex structures that cannot be directly applied according to the current codes, the random vibration method and shaking table test are usually used to analyse the seismic performance of the nonstructural components. Qin et al. [26,27] established the floor response spectrum method of a main structure based on the random vibration method, developed a seismic action calculation program for the nonstructural components on the basis of multistorey buildings, and proposed design suggestions for seismic action calculations of the nonstructural components in the relevant Chinese code. Xiaolan Pan [28] proposed a multimode method for the estimation of floor response spectra on the basis of the seismic response analysis of multistorey steel frame buildings in Los Angeles. This method takes the coupling effect into consideration, establishes equivalent modal systems, and develops floor acceleration response spectra by incorporating the capacity spectrum method in conjunction with ductility-based floor response spectra for each modal system. Jiang et al. [29,30] derived calculation formulas of the floor acceleration response spectra in buildings in nuclear power plants; the formulas take into account the coupling effects of various modes of the main structures and the nonstructural components and establishes statistical relationships between the seismic response spectra of equipment and ground response spectra according to different site conditions. Hiram [31] studied the seismic fragility of a suspended ceiling system on the basis of the shaking table test, analysed the influence mechanism of each component in the seismic failure mechanism suspended ceiling system, and proposed an improvement suggestion for the seismic performance of the suspended ceiling system. Filiatrault et al. [32,33] studied the seismic performance of pressurized fire sprinkler piping systems and base-isolated pallet-type steel storage racks based on the shaking table tests, analysed the seismic failure mechanism of pipeline systems and steel storage racks, and proposed a seismic reinforcement scheme and suggestions for pipeline systems and steel storage racks based on the relevant American codes (NFPA-13 and FEMA 460).

The above scholars systematically studied the equivalent seismic action and seismic performance of the nonstructural components in buildings, but there are still some deficiencies that need to be further analysed. First, the above-mentioned analysis and design codes for the seismic performance of the nonstructural components are studied based on multistorey or high-rise buildings while there is little research on the large-span space structures, whose design method and dynamic characteristics are very different from those of multistorey or high-rise buildings. Second, in the current seismic design codes and analysis of the nonstructural components, more attention is given to the horizontal seismic action of the nonstructural components, and less attention is given to its vertical seismic action while large-span space structures, such as reticulated shells, are often more sensitive to vertical seismic excitation, and the vertical seismic action of the nonstructural components may be greater. Third, the dynamic performance of large-span space structures, such as reticulated shells, are more obviously affected by high-order vibration modes, and the vibration modes are more densely distributed, which is quite different from those of multistorey and high-rise buildings. Fourth, based on the existing studies [34,35], the roofing system has an obvious influence on the static bearing capacity and dynamic characteristics of such structures; however, most of studies and design codes generally ignore the influence of the roofing system, which will influence the seismic performance of the nonstructural components in the large-span space structures. Therefore, based on the above-mentioned shortcomings, it is necessary to carry out more targeted research on the calculation method of the equivalent seismic action of the nonstructural components in reticulated shell structures. In this paper, the acceleration response of single-layer spherical reticulated shell nodes under earthquake action is compared with that of the nonstructural components in the current seismic design codes, and the elastic acceleration response spectra of single-layer spherical reticulated shell nodes under earthquakes are studied. Additionally, the calculation formulas of acceleration response spectra in three directions of spherical reticulated shell nodes under three-dimensional earthquakes are derived, and a method is proposed for solving the equivalent seismic action calculations for the nonstructural components in a single-layer spherical reticulated shell with a bolted and welded purlin roofing system.

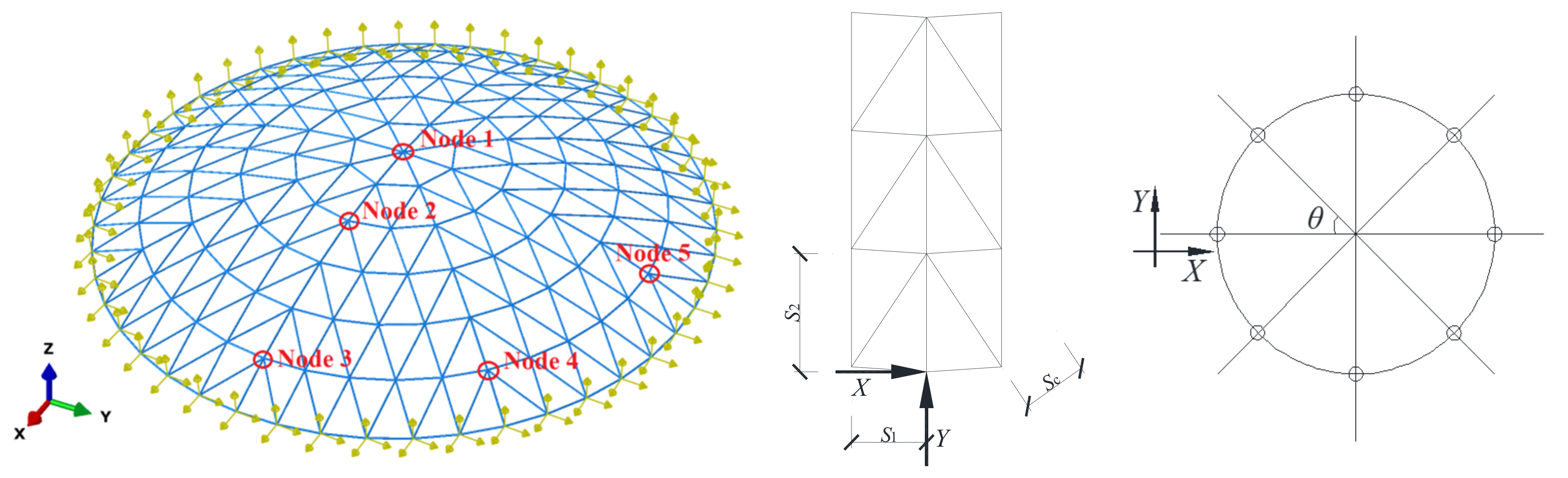
2. Methodology

2.1. The Reticulated Shell Structures without a Roofing System

In this paper, the single-layer spherical reticulated shell structures without a roofing system are taken as the main structure first, which is a K-8 Kewitt reticulated shell, with spans of 40 m, 60 m, and 80 m and rise-span-ratios of 1/7, 1/5, and 1/3. The material of shell members in the reticulated shell structure is Q235 steel, the elastic modulus is 206 GPa, the yield strength is 235 MPa, and the damping ratio is 0.02. The nomenclature for shell D4073-W, refers to the following: the 40-span of the shell, 7-span-to-rise ratio of the shell, 3-roof load (3 × 60 kg/m²), and W-the shell without a roofing system. The boundary condition of the finite element models is that the boundary shell nodes are directly connected with the ground and restrict the translational displacement (X, Y, Z) of the support nodes in three directions. To analyse the equivalent seismic action of the nonstructural components in reticulated shell structures, the acceleration response spectra of reticulated shell nodes are analysed. At present, the existing studies show that high-order modes can greatly affect the dynamic performance of the single-layer spherical reticulated shells; therefore, the complete quadratic combination (CQC) method is used to combine the effects of modes of each order, and the effects of coupling between different modes are considered. The single-layer spherical reticulated shell is a system with multiple degrees of freedom, and the equation of motion of the shell is shown in Equation (1):

$${\left\{\varphi \right\}}^{\mathrm{T}}\left\{M\right\}\left\{\varphi \right\}\left\{\ddot{U}\right\}+{\left\{\varphi \right\}}^{\mathrm{T}}\left\{C\right\}\left\{\varphi \right\}\left\{\stackrel{.}{U}\right\}+{\left\{\varphi \right\}}^{\mathrm{T}}K\left\{\varphi \right\}\left\{U\right\}=-{\left\{\varphi \right\}}^{\mathrm{T}}\left\{M\right\}\left\{I\right\}\left\{\ddot{U_{\mathrm{G}}}\right\}$$

(1)

where $\left\{M\right\}$ is the mass matrix of the shell, $\left\{C\right\}$ is the damping matrix of the shell, $\left\{K\right\}$ is the stiffness matrix of the shell, $\left\{U\right\}$ is the relative displacement matrix of the shell node, $\left\{\varphi \right\}$ is the modal matrix of the shell, and $\left\{U_g\right\}$ is the seismic displacement matrix.

Based on an accurate method [36], the j-direction velocity response and displacement response (${\stackrel{.}{q}}_{n,j,k}^i$ and ${\stackrel{}{q}}_{n,j,k}^i$) of the n-th node in the shell under the influence of the k-order mode and the i-direction earthquake are calculated, and then the j-direction absolute acceleration response and response spectra (${\ddot{Q}}_{n,j,k}^i$ and $S_{n,k,j}^i$) of the n-th node of the shell caused by the i-direction ground motion under the influence of the k-order mode are obtained, as shown in Equations (2) and (3) [29]:

$${\ddot{Q}}_{n,j,k}^i=-{\phi }_{n,j,k}{\lambda }_k^i\left(2{\zeta }_k{w}_k\stackrel{.}{q}{}_{n,j,k}{}^i+w_k^2{q}_{n,j,k}^i\right)$$

(2)

$$S_{n,k,j}^i=w_{d0}{\left|{\displaystyle \underset{0}{\overset{t}{\int }}{\ddot{Q}}_{n,j,k}^i{e}^{-\zeta w_0\left(t-\tau \right)}\left[\left(1-\frac{{\zeta }_0{}^2}{1-{\zeta }_0{}^2}\right)\sin w_{d0}\left(t-\tau \right)+\frac{2{\zeta }_0}{\sqrt{1-{\zeta }_0{}^2}}\cos w_{d0}\left(t-\tau \right)\right]d\tau }\right|}_{\max }$$

(3)

where ${\phi }_{n,j,k}$ is the j-th mode vector of the n-th node of the shell under the k-th mode, ${\lambda }_k^i$ is the i-direction mode participation coefficient of the shell under the k-th mode, w_k is the frequency of the k-th mode, and ζ_k is the damping ratio of the k-th mode. Additionally, Equation (4) is outlined below [37]:

$${\rho }_{ab}=\frac{2\sqrt{{\zeta }_a{\zeta }_b}\left[{\left(w_a+w_b\right)}^2\left({\zeta }_a+{\zeta }_b\right)+\left(w_a{}^2-w_b{}^2\right)\left({\zeta }_a-{\zeta }_b\right)\right]}{4{\left(w_a-w_b\right)}^2+{\left(w_a+w_b\right)}^2{\left({\zeta }_a+{\zeta }_b\right)}^2}$$

(4)

where ρ_ab is the correlation coefficient, w_a is the frequency of the a-th mode, and ζ_a is the damping ratio of the a-th mode.

$$\underset{q\to m}{{\displaystyle \lim }}\left|{\displaystyle \sum _{k=1}^q{\chi }_{n,j,k}^i-1}\right|\approx 0$$

(5)

The correlation coefficients between different vibration modes are obtained with Equation (4) [31]. The product of the participation coefficient (λⁱ_k) and the mode in the i-direction of the shell under the k-th mode (φ_n,j,k) is defined as the contribution coefficient of the k-th mode to the n-th node in the i-direction (${\chi }_{n,j,k}^i$). In this analysis, it is necessary to ensure that the sum of the contribution coefficients of the first m modes approaches 1.0, as shown in Equation (5) [29]. The j-direction absolute acceleration response spectra of the n-th node of the shell under the i-direction earthquake are obtained by the CQC method (Sⁱ_n,j), as shown in Equation (6). Furthermore, the absolute acceleration response spectra in the j-direction of the n-th node are obtained (S_n,j) with Equation (7) [38]:

$$S_{n,j}^i\left(T_0,{\zeta }_0\right)=\sqrt{{\displaystyle \sum _{a=1}^m{\displaystyle \sum _{b=1}^m{\rho }_{ab}{S}_{n,j,a}^i{S}_{n,j,b}^i}}}$$

(6)

$$S_{n,j}\left(T_0,{\zeta }_0\right)=\sqrt{{\left(S_{n,j}^1\right)}^2+{\left(S_{n,j}^2\right)}^2+{\left(S_{n,j}^3\right)}^2}$$

(7)

2.2. The Reticulated Shell Structures with a Roofing System

The roofing system is an essential part of the single-layer spherical reticulated shell structure. Scholars have generally ignored the influence of roofing systems in previous designs and analyses [39]. However, according to existing studies, the roofing system notably affects the static and dynamic performance of the reticulated shell structure [40,41,42]. Therefore, the influence of the roofing system should be considered in the analysis of the node acceleration response spectra of the shell. As shown in Figure 3, the finite element model (FEM) of a shell with a roofing system consists of an equivalent panel, a weakened area, a purlin hanger, a purlin, a pillar, and the shell. The FEM considers the semirigid character of the purlin joints, the orthotropic characteristics of the roofing panel, and the strength and stiffness of the self-tapping screw connections between the purlin and roof panel. The applicability of the FEM has been studied by experiments and finite element analysis in Ref. [41]. The nomenclature for the shells D6053-LSWM and D6053-HHWM refers to the following: the 60-span of the shell, 5-span-to-rise ratio of the shell, 3-roof load (3 × 60 kg/m²), LSWM-bolted purlin roofing system, and HHWM-welded purlin roofing system. The elastic modulus and the yield strength of the purlin members and pillars are 206 GPa and 235 MPa, respectively; the elastic modulus and the yield strength of the roof panel are 146 GPa and 460 MPa, respectively; the elastic modulus and the yield strength of weakened area are 160 MPa and 40 MPa, respectively. The boundary condition of the FEM is that the boundary shell nodes are directly connected with the ground. The degrees of freedom in three directions (X, Y, Z) of the support nodes are restricted, and the ground motions are input in three directions in the time history analysis.

In the modal analysis of the shell with a roofing system, the components such as the roof panel and purlin have obvious local vibrations in the high-order modes while the relative displacements of all nodes in the shell are very small. Thus, even if more modes are adopted in Equations (1)–(7), the sum of the contribution coefficients cannot approach 1.0, resulting in a large difference between the results of the calculations with the formulas and the simulation values. Therefore, the acceleration response spectra of nodes in the shell with a roofing system under seismic action are analysed by the time history analysis method. Seven Class II site ground motions [43] are used to analyse the acceleration response of nodes in the shell with a roofing system. The shell node in each ring with the maximum peak value of combined acceleration in three directions is defined as the representative node in each ring of the shell, as shown in Equation (8). The acceleration response spectra of the representative node of each ring are analysed in the shell with a roofing system. The information on the ground motions is shown in

Table 2. The information from the ground motion records.

No.	Name and Time	Station	Fault Distance (m)	PGA (g)
GM-1	San Fernando (1971)	LA-Hollywood Stor FF	22.77	0.17
GM-2	Imperial Valley-06 (1979)	Delta	22.03	0.33
GM-3	Parkfield (1966)	Cholame-Shandon Array #8	12.90	0.28
GM-4	Kobe (1995)	Shin-Osaka	19.15	0.08
GM-5	Duzce (1999)	Bolu	12.04	0.37
GM-6	Imperial Valley-06 (1979)	Compuertas	15.30	0.04
GM-7	Victoria Mexico (1980)	Chihuahua	18.96	0.04

.

$$\begin{gathered} A_n=\max \left\{A_{n,1},A_{n,1},A_{n,1}\dots A_{n,m}\right\} \\ {A}_{n,m}(t)=\sqrt{A^2{}_{n,m,x}(t)+A^2{}_{n,m,y}(t)+A^2{}_{n,m,z}(t)} \end{gathered}$$

(8)

where A_n is the maximum peak value of the combined acceleration for the representative node in the n-th ring, A_n,m is the combined acceleration of the m-th node of the n-th ring in the shell, and A_n,m,x is the acceleration of the m-th node of the n-th ring in the X-direction.

3. Results

The acceleration responses of single-layer reticulated shell nodes are compared with current codes in this section. The analysis examines examples of the horizontal and vertical acceleration responses of the shell nodes in the D6053-W, D6053-LSWM, and D6053-HHWM structures under three-dimensional ground motions. The Chinese code specifies the equivalent horizontal force (F_H) and vertical force (F_V) of the nonstructural components under earthquake action, as shown in Equation (9) [43]:

$$F_{\mathrm{H}}={\gamma }_{\mathrm{EH}}\gamma \eta {\xi }_1{\xi }_2{\alpha }_{\max }G, F_{\mathrm{V}}={\gamma }_{\mathrm{EV}}\gamma \eta {\xi }_1{\xi }_2{\alpha }_{\max ,\mathrm{v}}G$$

(9)

where γ_H and γ_V are the horizontal and vertical seismic action coefficients, taken as 0.5 and 1.0, respectively; α_max,v is the maximum vertical seismic influence coefficient; and G is the gravity of the nonstructural component.

Billboards, decorative connections, and fireproof ceilings are selected as common nonstructural components in large-span space structures. The relevant parameters of these nonstructural components are shown in

Table 3. Calculation parameters used to calculate the standard values of seismic action on the nonstructural components, according to the relevant Chinese code.

Nonstructural Component	Functional Coefficient (γ)	State Coefficient (ξ1)	Position Coefficient (ξ2)	Category Coefficient (η)	Maximum Horizontal Seismic Influence Coefficient (αmax)
Billboard	1.0	1.0	1.0–2.0	1.2	0.32
Decorative connection	1.0	1.0	1.0–2.0	1.0
Fireproof ceilings	1.0	1.0	1.0–2.0	0.9

.

As shown in Figure 4, the solid lines represent the design values according to the relevant Chinese code, and the red dots represent the results of finite analysis of the peak accelerations of the shell nodes. Figure 4a–c shows that the peak values of the horizontal acceleration of the shell nodes considerably exceed the specification, and the number of nodes exceeding specification requirements tends to decrease as the ring approaches the central node of the shell. As shown in Figure 5a–c, the vertical acceleration response of the shell nodes is more intense than the horizontal response, and the shell nodes in each ring exceed the requirements of the Chinese code. The peak vertical acceleration values of the shell nodes tend to increase as the ring approaches the central node of the shell, which indicates that the nonstructural components closer to the central node of the shell should agree with the more serious vertical seismic requirements. Figure 4b,c and Figure 5b,c show that the bolted and welded purlin roofing systems change the horizontal and vertical acceleration extremums of the shell nodes, indicating that it is necessary to consider the influence of the roofing system when analysing the acceleration response spectra of reticulated shell nodes. The above analysis shows that the current Chinese code is not applicable to the seismic design of the nonstructural components in single-layer spherical reticulated shells, and the same conclusion is also true for ASCE 7-10.

The current European code (Eurocode 8-1) considers the influence of different fundamental vibration periods of the nonstructural components, as shown in Equation (10):

$$F_{\mathrm{EU}}=M_{\mathrm{NC}}{A}_2,A_2=\alpha \times S\left[\frac{3\times \left(1+\frac{z}{H}\right)}{1+{\left(1-\frac{T_{\mathrm{a}}}{T_1}\right)}^2}-0.5\right]\times \frac{g{\gamma }_{\mathrm{a}}}{q_{\mathrm{a}}}$$

(10)

where α is the ratio of the design ground acceleration on type A ground; S is the soil factor, which is taken as 1.2; T_a is the fundamental vibration period of the nonstructural component; T₁ is the fundamental vibration period of the building; z is the height of the nonstructural component; H is the building height; γ_a is the importance factor, which is taken as 1.5; and q_a is the behaviour factor, which is taken as 1.0.

As shown in Figure 6 and Figure 7, the solid lines are the design values of the equivalent accelerations for the nonstructural components attached to the shell nodes, and the dotted lines are the finite element analysis results for the acceleration response spectra of the shell nodes. Eurocode 8 obviously underestimates the peak values of the horizontal acceleration response spectra of the shell nodes and cannot accurately predict the positions and sizes of the peak values of the vertical acceleration response spectra. Figure 6b,c and Figure 7b,c also show that the roofing systems notably change the acceleration response spectra of the shell nodes.

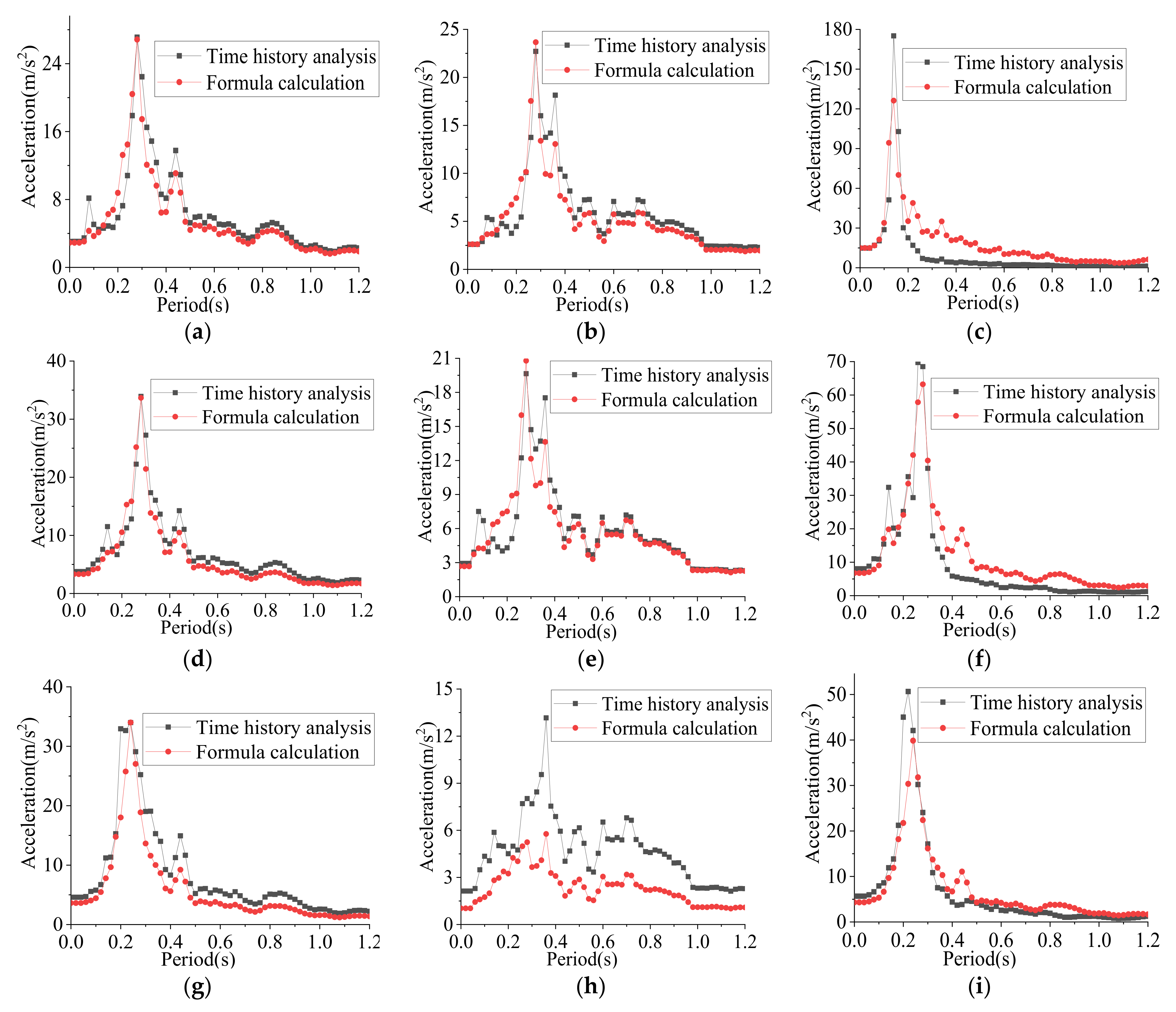
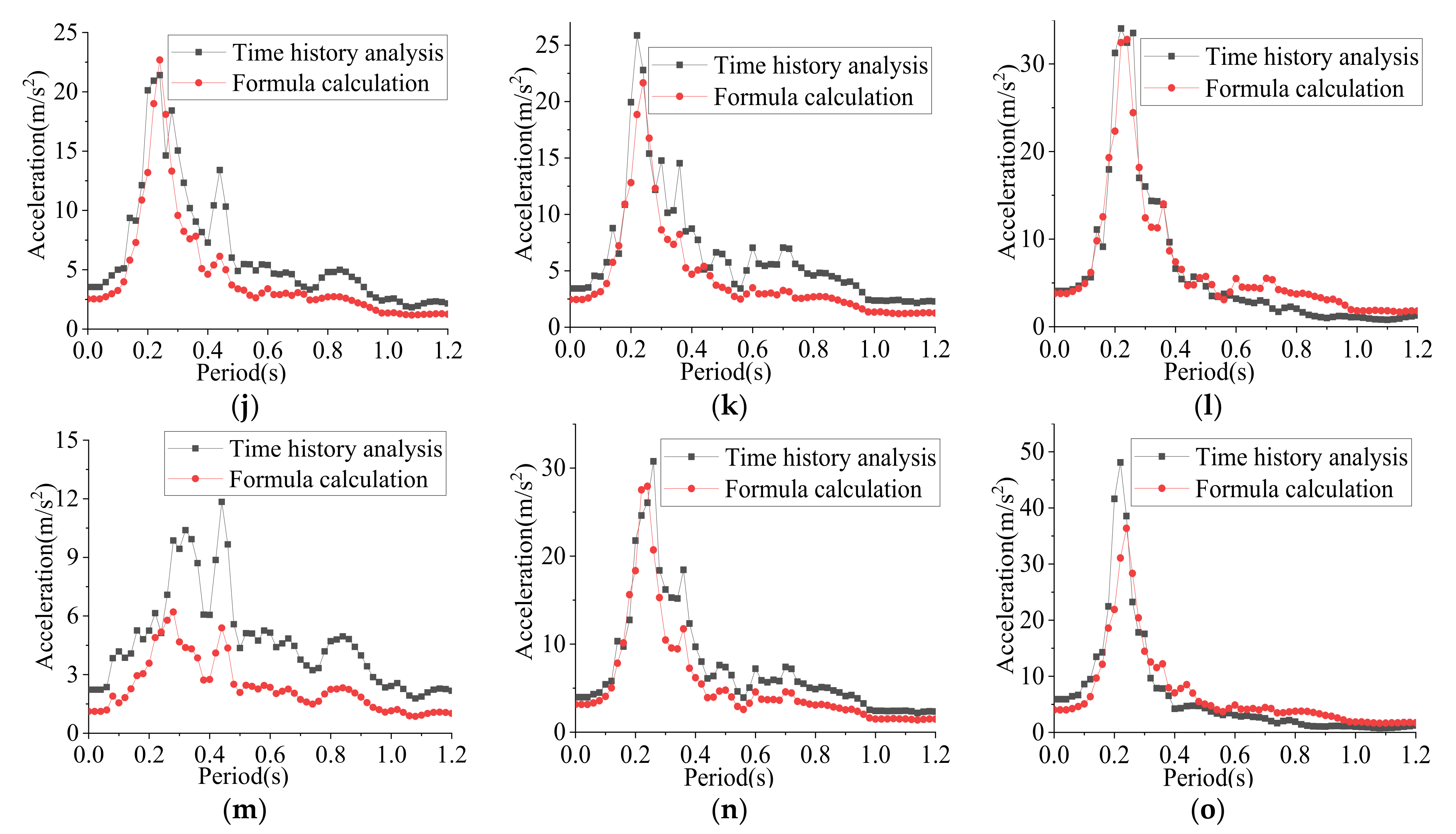
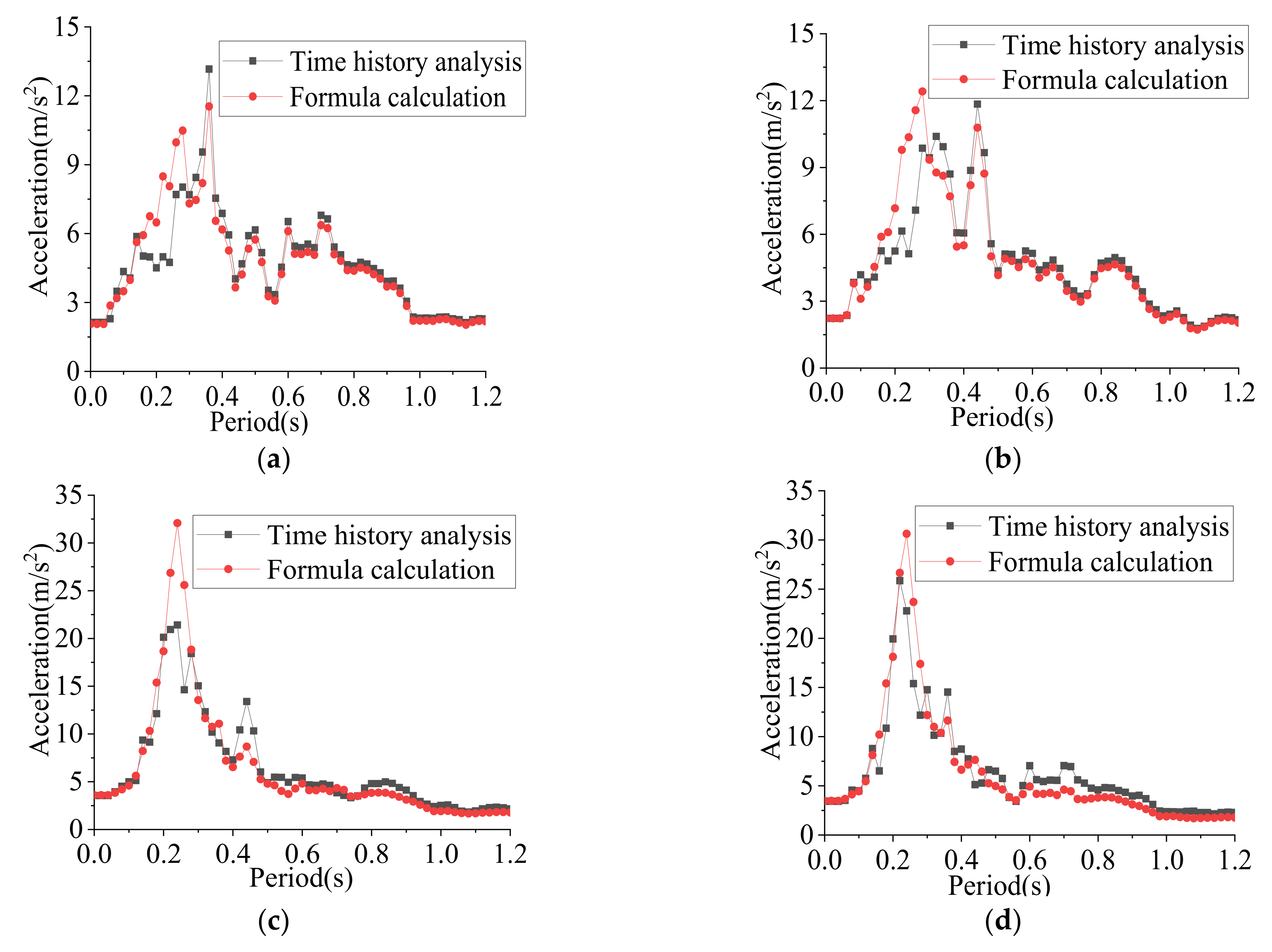
According to the above analysis, the current codes are not fully applicable to the seismic design of the nonstructural components in single-layer spherical reticulated shell structures, and it is necessary to study the equivalent seismic action of the nonstructural components in these shells.

4. Discussion

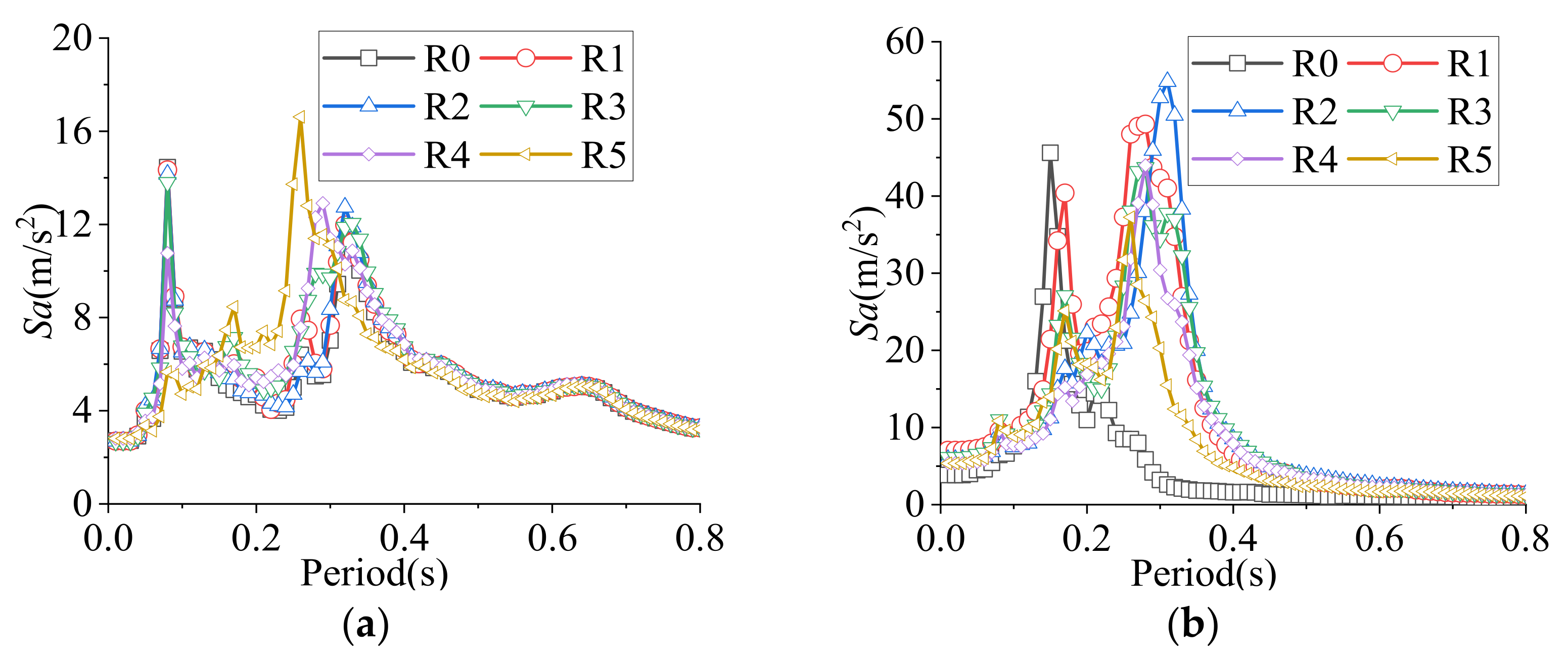
4.1. The Reticulated Shell Structures without a Roofing System

The shell of D4053-W is taken as an example to analyse the acceleration response of each ring node in the shell under the action of three-dimensional ground motions. The calculation model is shown in Figure 8. First, modal analysis of the spherical reticulated shell is carried out to calculate the frequency, participation coefficient, and mode vector of the shell. The acceleration response spectra of each ring node of the shell are calculated according to Equations (1)–(7). Additionally, a time history analysis of the shell under the earthquake action is carried out, and the finite element analysis results and the calculation results, determined with Equations (1)–(7), for the acceleration response spectra are compared.

Figure 9a–f shows that the peak position and size of the node response spectra of the shell can be accurately predicted by the formulas. Figure 9g–o shows that the calculation errors of the horizontal acceleration response spectra of Node 3 in the Y-direction and Node 5 in the X-direction on the first ring near the support are larger than the values from the time history analysis because the main rib directions of these two points coincide with the two orthogonal horizontal seismic input directions. As shown in Figure 8, taking Node 3 as an example, the difference in membrane stiffness in the two directions of the node has an obvious influence on the acceleration response. In the seismic time history analysis of the shells, the influences of the seismic input direction on the acceleration response of nodes near the support caused by the difference in membrane stiffness in different directions are considered. However, these differences cannot be accurately reflected in the modal analysis of the shells.

As shown in Equations (11) and (12), the influence of the membrane stiffness difference can be introduced into the calculation of the acceleration response spectra of nodes in the first ring near the support. As shown in Figure 10, the results of the modified calculation of the response spectra of the node in the first ring near the support are in agreement with the results of the time history analysis. Based on the above analysis, this approach can be applied in the analysis of the node acceleration response spectra of a single-layer spherical reticulated shell structure without a roofing system under the earthquake action.

$$B_1=\frac{E{A}_1}{S_1}+\frac{E{A}_{\mathrm{c}}}{S_{\mathrm{c}}}{\sin }^4\alpha , B_2=\frac{E{A}_2}{S_2}+\frac{E{A}_{\mathrm{c}}}{S_{\mathrm{c}}}{\cos }^4\alpha , R_0=\frac{B_1}{B_2}$$

(11)

where B₁ and B₂ are the membrane stiffnesses in the X-direction and Y-direction, respectively [39].

$$\left\{\begin{array}{l}{S}_{zn,x}\left(T_0,{\zeta }_0\right)=\frac{R_0\left(1+\cos \theta \right)}{2}\sqrt{{\left(S_{n,x}^1\right)}^2+{\left(S_{n,x}^2\right)}^2+{\left(S_{n,x}^3\right)}^2}\\ S_{zn,y}\left(T_0,{\zeta }_0\right)=\frac{R_0\left(1+\sin \theta \right)}{2}\sqrt{{\left(S_{n,y}^1\right)}^2+{\left(S_{n,y}^2\right)}^2+{\left(S_{n,y}^3\right)}^2}\\ S_{zn,z}\left(T_0,{\zeta }_0\right)=\sqrt{{\left(S_{n,z}^1\right)}^2+{\left(S_{n,z}^2\right)}^2+{\left(S_{n,z}^3\right)}^2}\end{array}\right.$$

(12)

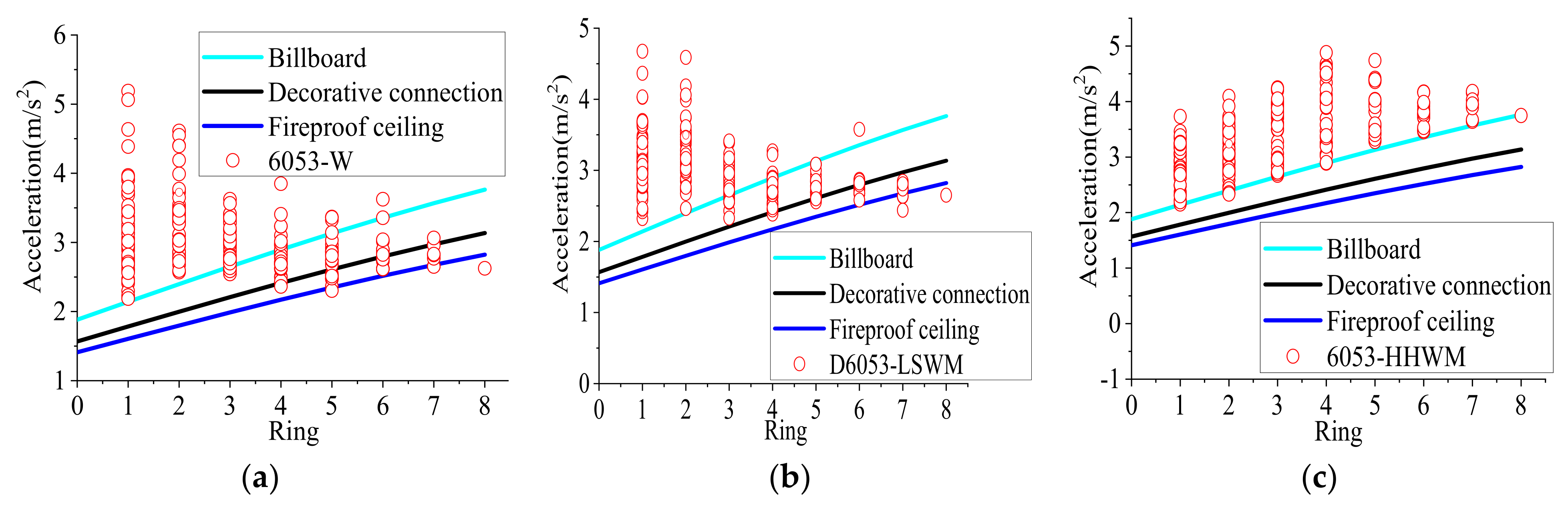
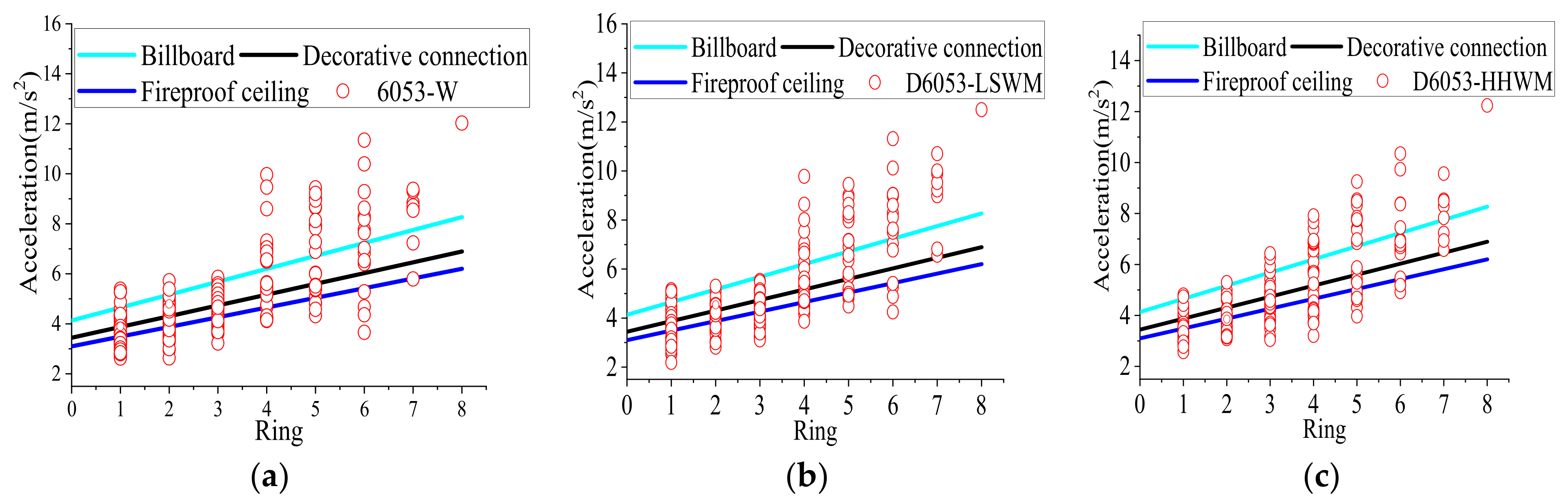
4.2. The Reticulated Shell Structures with a Roofing System

The acceleration response spectra of the representative node of each ring in the shell under the action of seven ground motions are calculated. Figure 11 shows that the acceleration response spectra of the representative node usually have two peaks corresponding to the basic period of the shell and the high-order sensitive period of the representative node, which are recorded as T_s and T_s1, respectively. By calculating the acceleration response spectra of the representative node under the action of seven ground motions, the ratios of the acceleration response spectra values of representative nodes at T_a = 0 s ($S_n\left(T_{\mathrm{a}}=0,{\zeta }_0\right)$) to the ground motion input amplitude ($S_{\mathrm{g}}\left(T=0,\zeta \right)$) are obtained and recorded as AF₀, as shown in Equation (13). The ratios of the peak values of the representative node acceleration response spectra ($\mathrm{MAX}\left(S_n\left(T_{\mathrm{a}},{\zeta }_0\right)\right)$) to $S_n\left(T_{\mathrm{a}}=0,{\zeta }_0\right)$ are recorded as AF_max, as shown in Equation (14). According to Figure 12, the combined distance between a node in the i-th ring and the nearest support node is defined as the effective distance D_i of the nodes in the i-th ring, and the distance between the central node of the shell and the nearest support node is defined as the maximum effective distance of the shell, which is recorded as D_max, as shown in Equation (15).

$$A{F}_0=\frac{S_n\left(T_{\mathrm{a}}=0,{\zeta }_0\right)}{S_{\mathrm{g}}\left(T=0,\zeta \right)}$$

(13)

$$A{F}_{\max }=\frac{\mathrm{MAX}\left(S_n\left(T_{\mathrm{a}},{\zeta }_0\right)\right)}{S_n\left(T_{\mathrm{a}}=0,{\zeta }_0\right)}$$

(14)

$$\left\{\begin{array}{l}{D}_i=\sqrt{D_{i,x}^2+D_{i,y}^2+D_{i,z}^2}\\ D_{\max }=\sqrt{D_{\mathrm{top},x}^2+D_{\mathrm{top},y}^2+D_{\mathrm{top},z}^2}\end{array}\right.$$

(15)

Based on the statistics of AF₀ and AF_max in the shell with the roofing system under different ground motions, both AF₀ and AF_max are described by a normal distribution. The AF₀ and AF_max values are obtained with 95% confidence, and their relationships with D_i/D_max are shown in Figure 13 and Figure 14. The horizontal AF₀ (AF_0,H) has no obvious increasing trend with the increasing D_i, and the AF_0,H of the shells, with three kinds of spans, increases with an increasing rise-to-span ratio. The overall trends of the vertical AF₀ (AF_0,V) and AF_max increase with the increasing D_i.

According to the above analysis, a calculation method for the equivalent seismic action of a nonstructural component in a shell with a roofing system is proposed. The acceleration response spectra curves of the shell nodes are divided into high-frequency response sections, peak sections, and low-frequency response sections. There are generally two peak values in the acceleration response spectra of the representative nodes, and the high-order sensitive period of the shell can be set as T_s1 = 0.5T_s. The design values of the acceleration response spectra in the shell can be calculated according to Equations (16)–(21). The calculation coefficients A_S1 and A_S2 are shown in Equation (20) and

Table 4. Calculation coefficients.

Roofing System	Fitting Coefficient	A1	B1	C1	D1	E1	F1	G1	H1
Bolted purlin roofing system	AS1	5.03	1.32	0.16	0.016	4.99	42.26	7.25	9.31
Welded purlin roofing system		8.74	1.48	0.16	0.024	0.056	41.82	3.84	13.04
Bolted purlin roofing system	AS2	11.38	−8.87	0.171	0.132	16.1	89.44	68.62	−18.1
Welded purlin roofing system		11.98	−10.38	0.116	0.093	16.2	44.52	55.26	−14.9

, and the horizontal and vertical AF_max values can be calculated by equation (21), according to

Table 5. Calculation coefficients (A and B) of the acceleration response spectra.

Coefficient	Bolted Purlin Roofing System Horizontal	Welded Purlin Roofing System Horizontal	Bolted Purlin Roofing System Vertical	Welded Purlin Roofing System Vertical
A	$3.75\times \frac{f}{L}-0.25$	$4.0\times \frac{f}{L}+0.30$	$3.5\times \frac{f}{L}+0.30$	$2.5\times \frac{f}{L}+0.30$
B	$1+2\times \frac{f}{L}$	$1+1.65\times \frac{f}{L}$	1.60	1.60

.

$$S_n{}_{,0}=A{F}_0{S}_{\mathrm{g},0}$$

(16)

$$S_{\mathrm{a}}(T_{\mathrm{a}})=\left\{\begin{array}{l}\frac{T_{\mathrm{a}}}{T_{\mathrm{s}1}}\left(A{F}_{\max }{S}_{n,0}-S_n{}_{,0}\right)+S_{n,0},T_{\mathrm{a}}\le T_{\mathrm{s}1}\\ S_n{}_{,0}A{F}_{\max },T_{\mathrm{s}1}\le T_{\mathrm{a}}\le T_{\mathrm{s}}\\ \frac{S_{n,0}A{F}_{\max }}{1+A{F}_0{\left(1-\raisebox{1ex}{$T_{\mathrm{a}}$}\!\left/ \!\raisebox{-1ex}{$T_{\mathrm{s}}$}\right.\right)}^2},T_{\mathrm{s}}\le T_{\mathrm{a}}\end{array}\right.$$

(17)

$$A{F}_{0,\mathrm{H}}=8.5\times \frac{f}{L}+1.7$$

(18)

$$A{F}_{0,\mathrm{V}}=A_{\mathrm{S}1}\frac{D_{\mathrm{i}}}{D_{\max }}+A_{\mathrm{S}2}$$

(19)

$$\begin{array}{l}{A}_{\mathrm{S}}=A_1+B_1\exp \left[-\exp \left(\frac{f/L-C_1}{D_1}\right)\right]+E_1\exp \left[-\exp \left(\frac{L-F_1}{G_1}\right)\right]\\ +H_1\exp \left[-\exp \left(\frac{f/L-C_1}{D_1}\right)-\exp \left(\frac{L-F_1}{G_1}\right)\right]\end{array}$$

(20)

$$A{F}_{\max }=\left(A\frac{0.02}{{\zeta }_0}\frac{D_i}{D_{\max }}+B\right)\frac{1}{\sqrt{{\zeta }_0}}$$

(21)

The design values of the node acceleration response spectra of the spherical reticulated shell with a roofing system are obtained according to Equations (16)–(21), which will be compared with the results of the time history analysis. The spherical reticulated shells D6053-1500 and D8031-1500 with bolted and welded roofing systems are selected as examples for analysis, and the acceleration response spectra of the representative nodes in each ring of the spherical reticulated shells are extracted and compared with the design values in this paper. As shown in Figure 15, it is found that the calculation method proposed in this paper can better envelope the peak values of the acceleration response spectra of the representative node in each ring of the shell, and the envelope lines are in agreement with the node acceleration response spectra curve shape and peak value positions. On the basis of the above analysis, it is found that the design method proposed in this paper can be used to calculate the equivalent seismic action of the nonstructural components in single-layer reticulated shell structures with bolted and welded purlin roofing systems.

5. Conclusions

In this paper, the applicability of the seismic provisions of the current codes for the nonstructural components of single-layer spherical reticulated shells was analysed. The acceleration response spectra of the nodes in the shell were studied, a seismic design method was proposed for the nonstructural components in a shell with a roofing system, and the following conclusions were obtained:

(1)

The applicability of Chinese, American, and European codes to the seismic design of the nonstructural components in single-layer spherical reticulated shells was analysed. The current codes are mostly based on the characteristics of horizontal floor response spectra of multistorey or high-rise buildings. The acceleration response characteristics of a node in a reticulated shell structure are significantly different from those suggested in the codes, so the current codes cannot be directly applied.

(2)

The roofing systems influence the dynamic performance of the shell and affect the seismic acceleration response of the shell node in each ring. The constraints of the bolted purlin roofing system are relatively weak, and the horizontal and vertical acceleration response characteristics of the shell with a bolted purlin roofing system are close to those of the shell without a roofing system. The seismic response of the shell nodes is obviously affected by the high-order vibration modes of the shell, which are not fully considered in the current codes. The phenomenon of the shell nodes near the support where the horizontal acceleration response exceeds the specification requirements is more serious. The reticulated shell structures are more sensitive to vertical seismic excitation, which leads to an increase in the vertical acceleration response as the ring approaches the central node of the shell. The strength and stiffness of the purlin joint in a welded purlin roofing system are larger, the dynamic characteristics of the shell will more obviously change, and the membrane stiffness and out-of-surface bending stiffness of the shell nodes will significantly improve. The seismic action can be transmitted more efficiently in the shell with a welded purlin roofing system, leading to the phenomenon that the horizontal and vertical acceleration response of the shell nodes tend to increase as the ring approaches the central node of the shell.

(3)

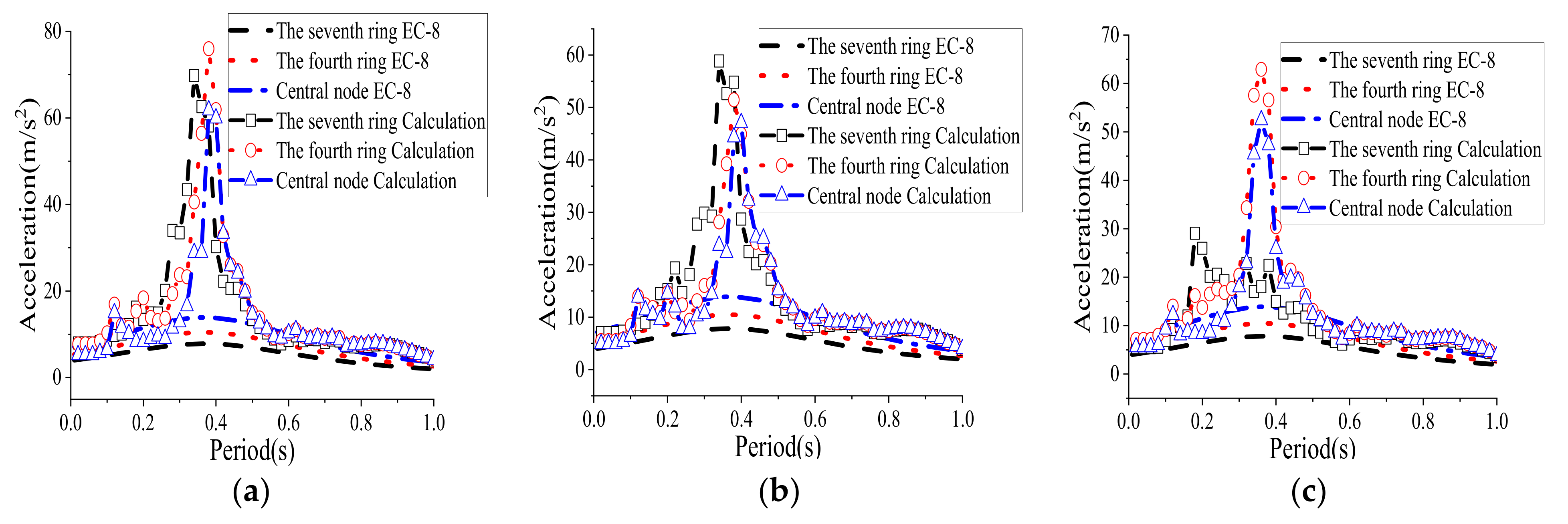
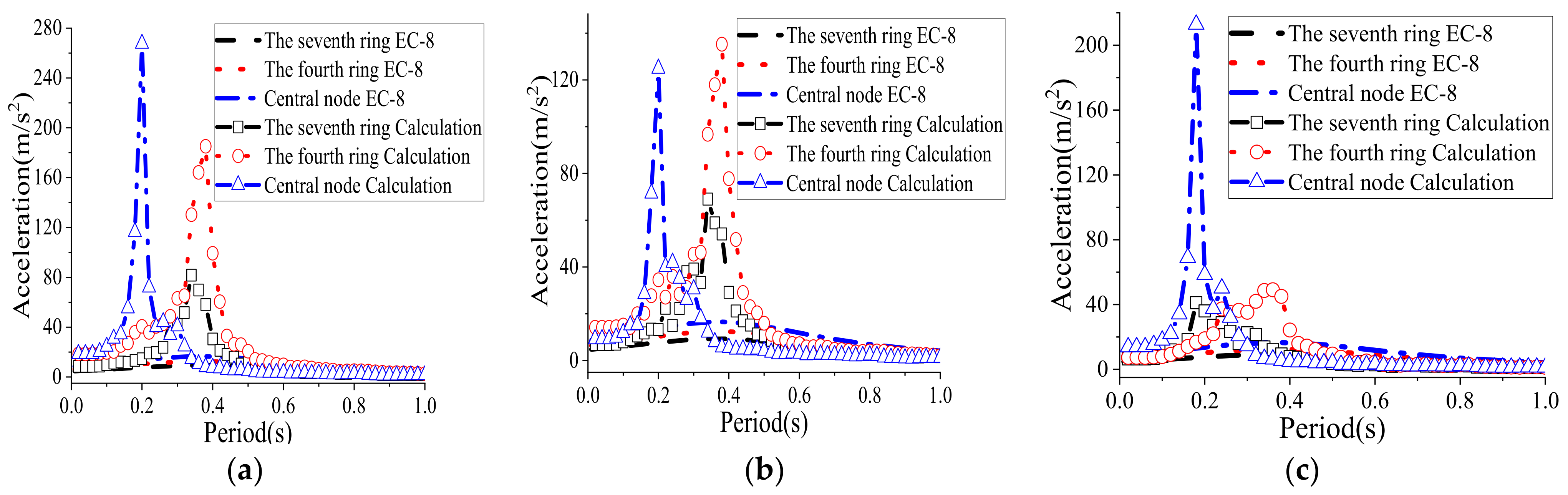
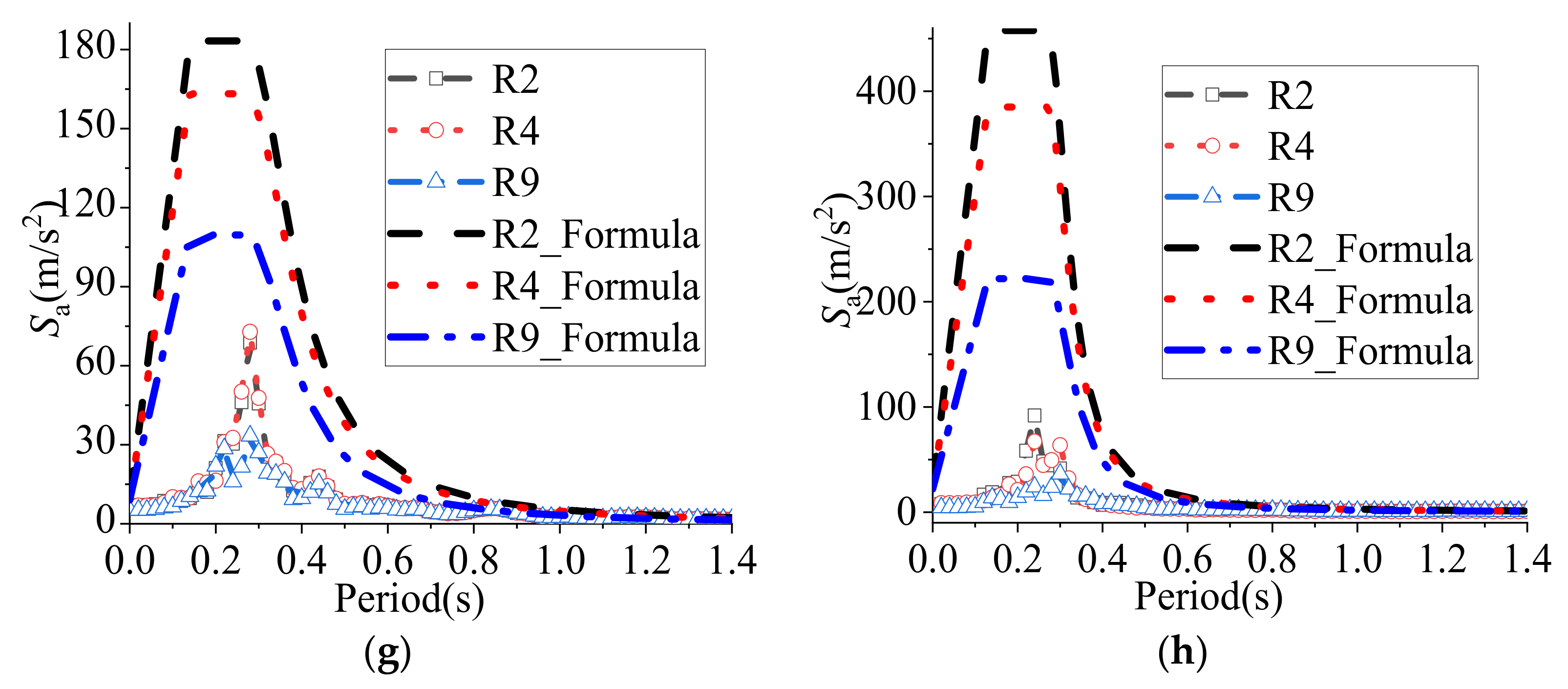
The acceleration response spectra of the shell node under three-dimensional ground motions were theoretically analysed based on the complete quadratic combination method. The difference in the membrane stiffness of the shell node in different directions will affect the seismic response of the shell node near the support, and the influence of the membrane stiffness of the shell nodes and the seismic input direction should be considered in the analysis of the acceleration response spectra of the shell nodes near the support. In this paper, the calculation method for the acceleration response spectra of the nodes in a single-layer spherical reticulated shell without a roofing system was proposed.

(4)

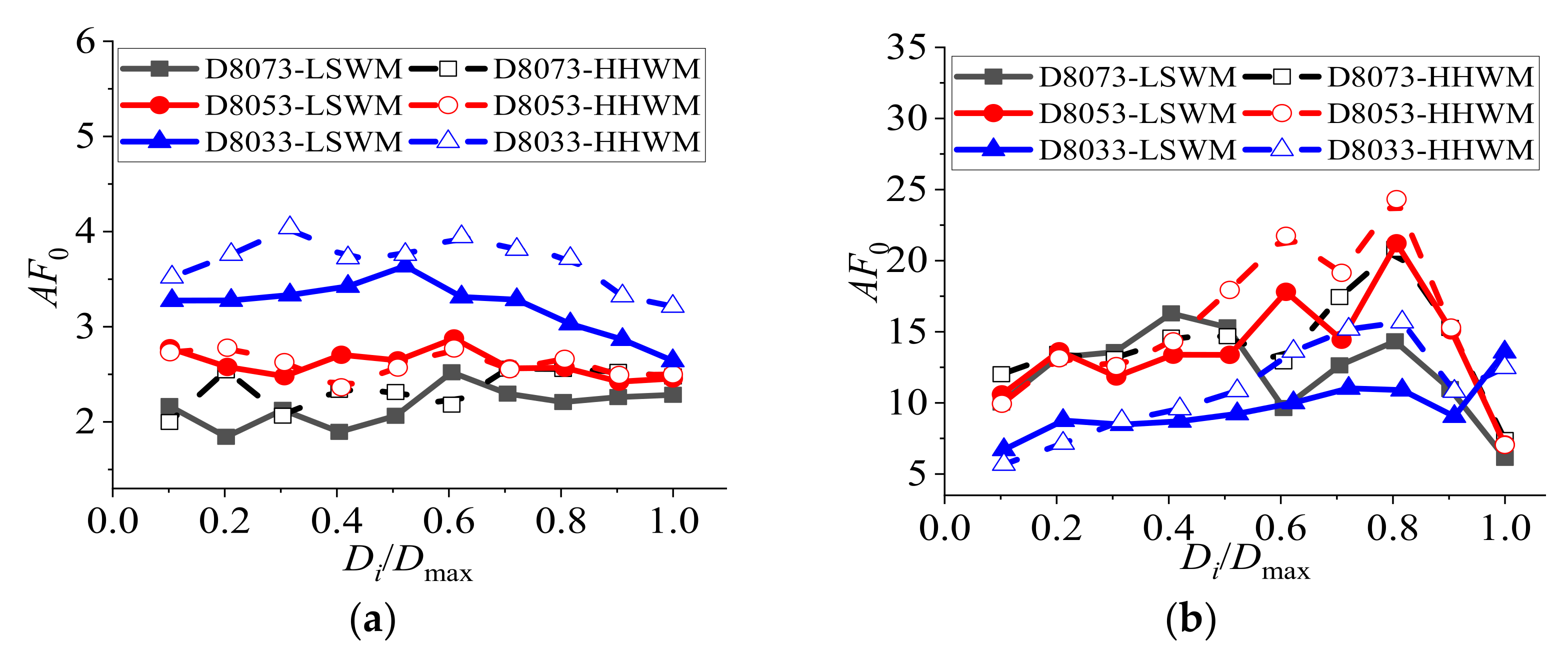
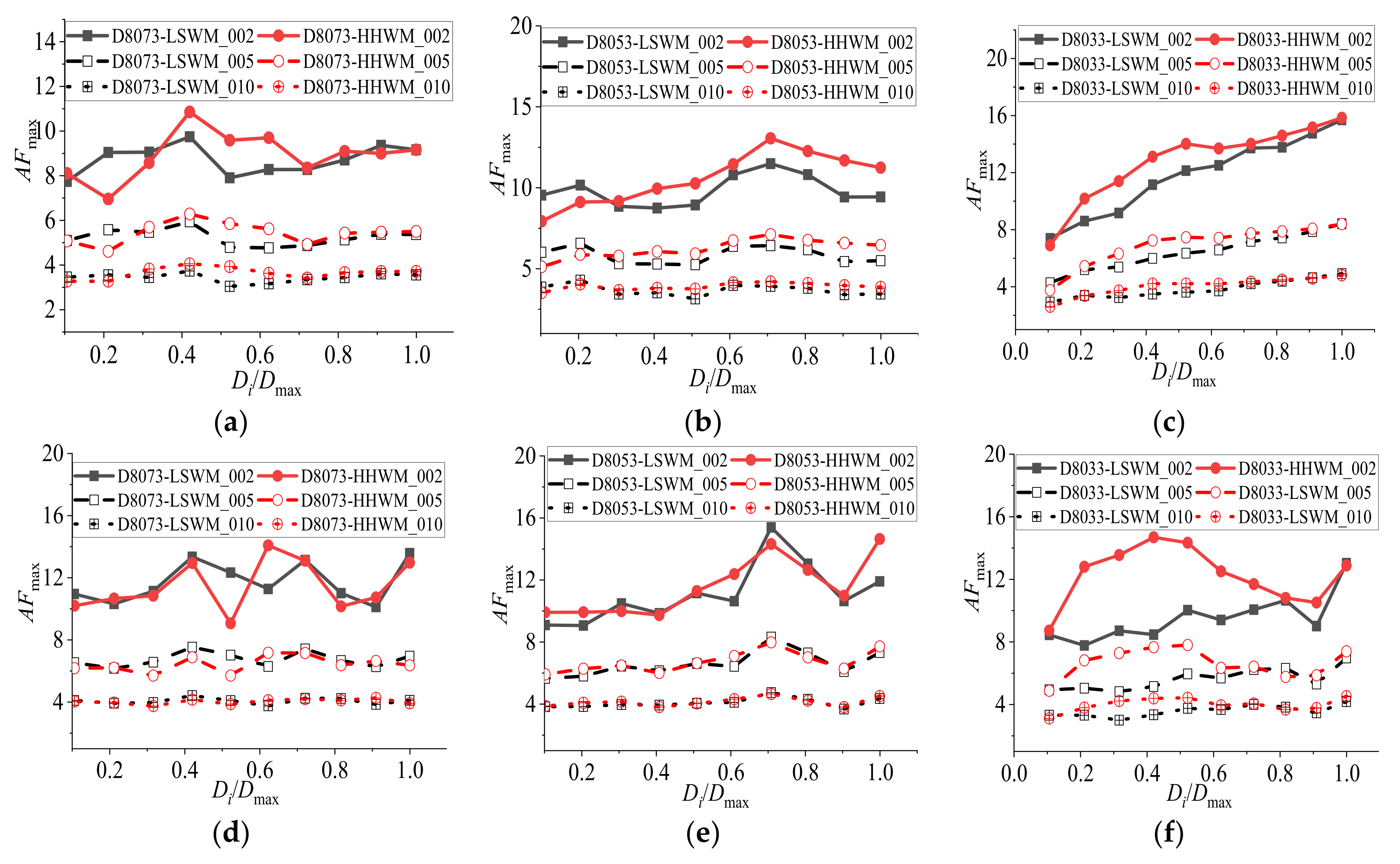
In the shell with a bolted and welded purlin roofing system, the larger the rise-to-span ratio of the shell with the same span, the higher the shell node height and shorter the horizontal distance in the same ring from the support. This leads to the phenomenon that the horizontal amplification coefficients (AF₀) of the seismic acceleration amplitude for the representative node in each ring of the shell tend to increase with the increase in the rise-to-span ratio and that the vertical amplification coefficients of a shell with a 1/3 rise-to-span ratio are smaller than those of the shells with other rise-to-span ratios. Generally, the horizontal and vertical amplification coefficients (AF_max) of the acceleration spectra peak value tend to increase with increasing effective distance (D_i).

(5)

The acceleration response spectra of the nodes in the shell with a roofing system were studied by the time history analysis method, and design methods were proposed for the horizontal and vertical seismic action of the nonstructural components in shells with bolted and welded purlin roofing systems.