Wavelet Model of Geomagnetic Field Variations and Its Application to Detect Short-Period Geomagnetic Anomalies
Abstract
:1. Introduction
2. Description of the Method
2.1. Identification of the Model Characteristic Component
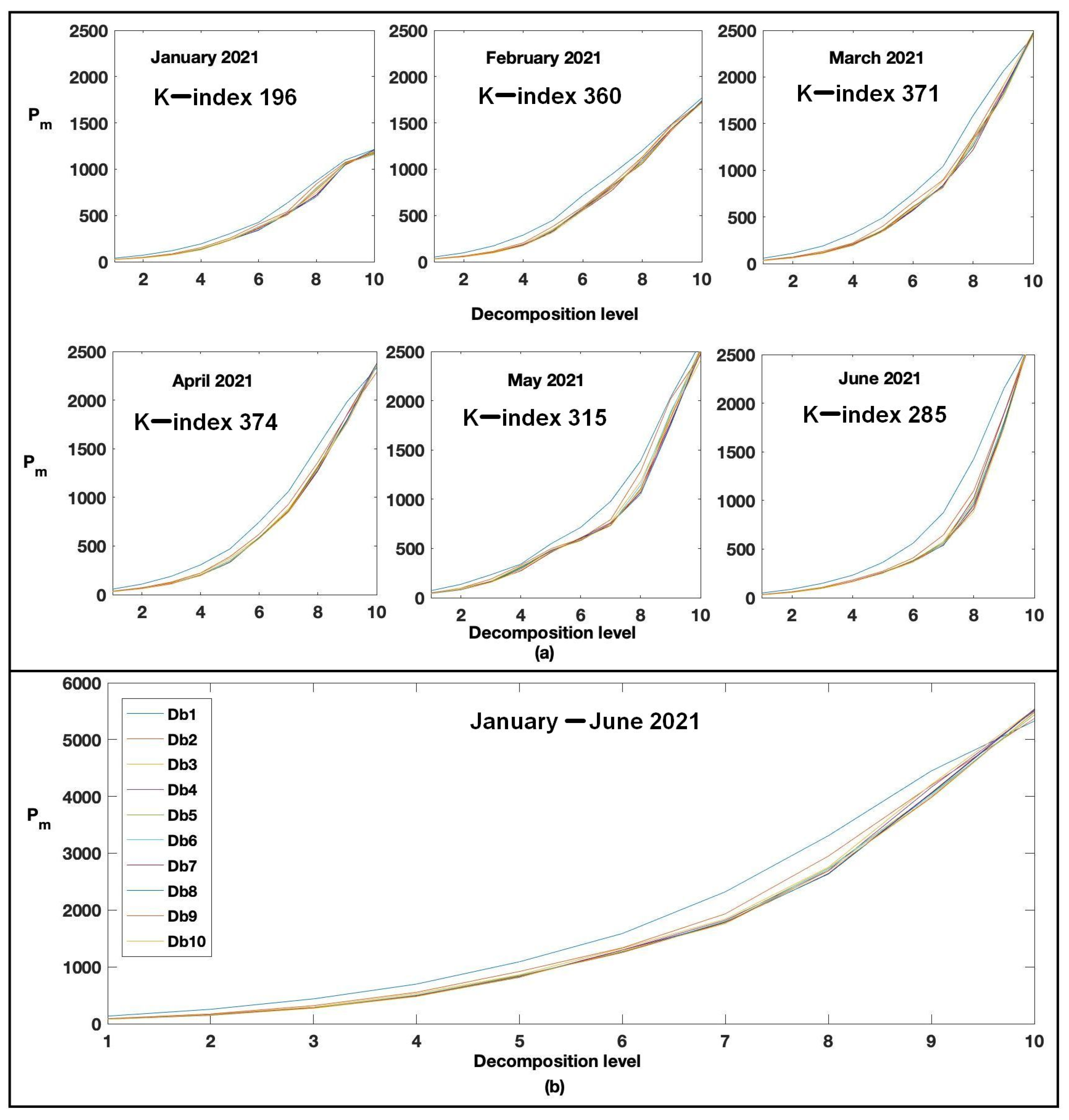
- We apply the MSA for the initial data estimated for each month of Sq-curves and obtain the representations , , , where ( is the signal length);
- For each decomposition level we carry out the reconstruction and and estimate the error and losses ;
- We determine the decomposition level providing the least error under admissible losses (conditions (5)).
2.2. Identification of the Model Disturbed Component
3. Calculation of Results and Discussion
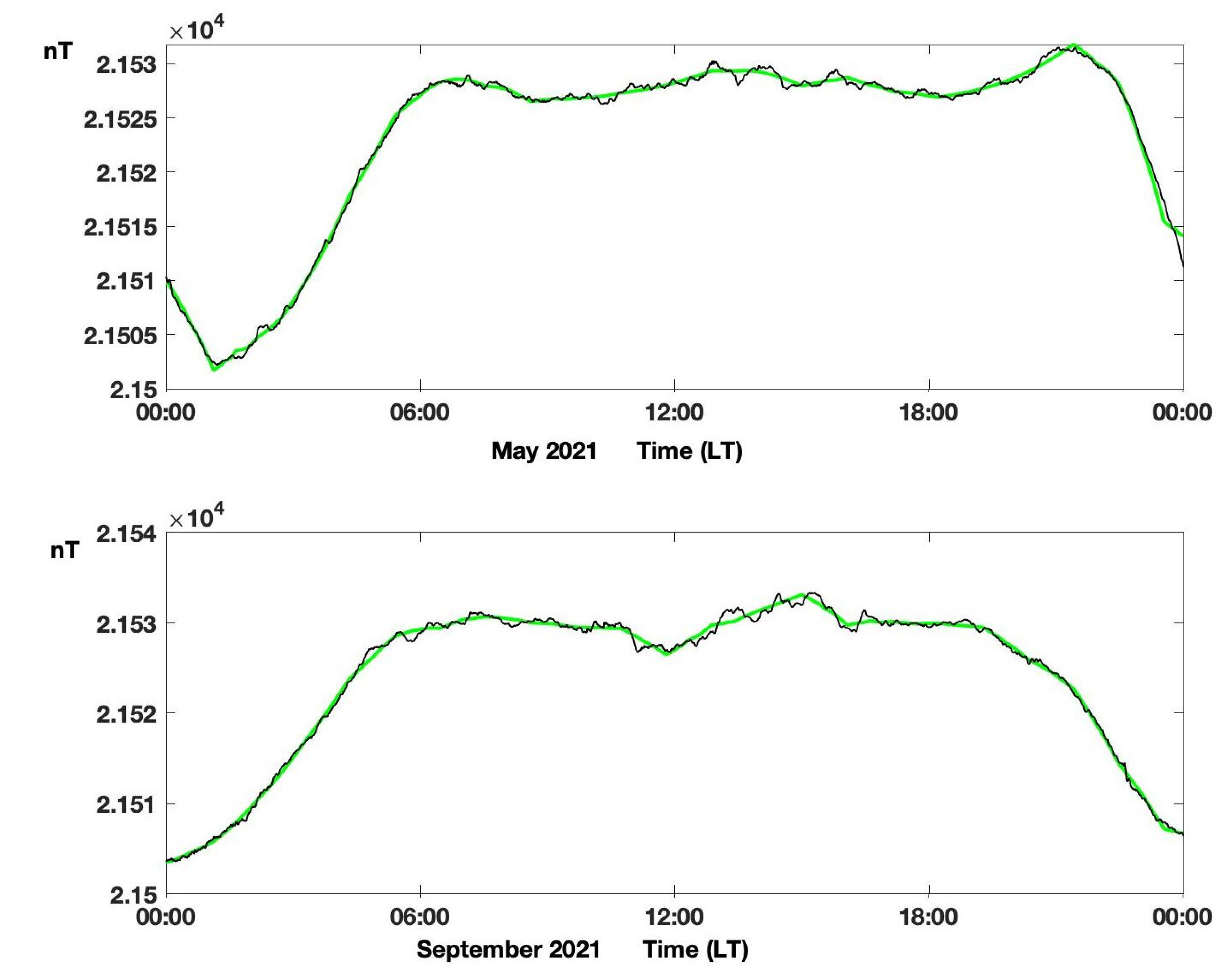
3.1. Approximation of Geomagnetic Field Quiet Variations
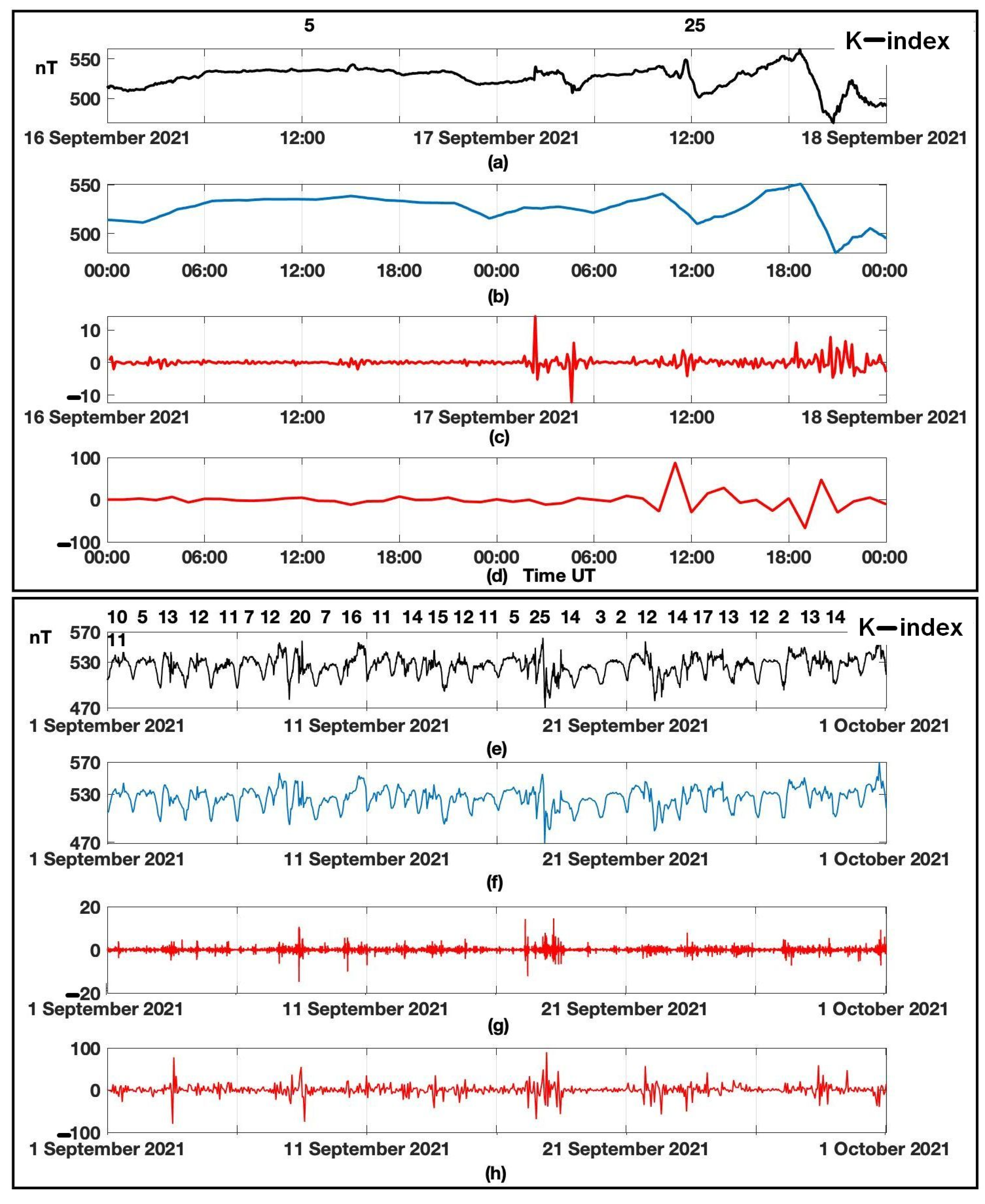
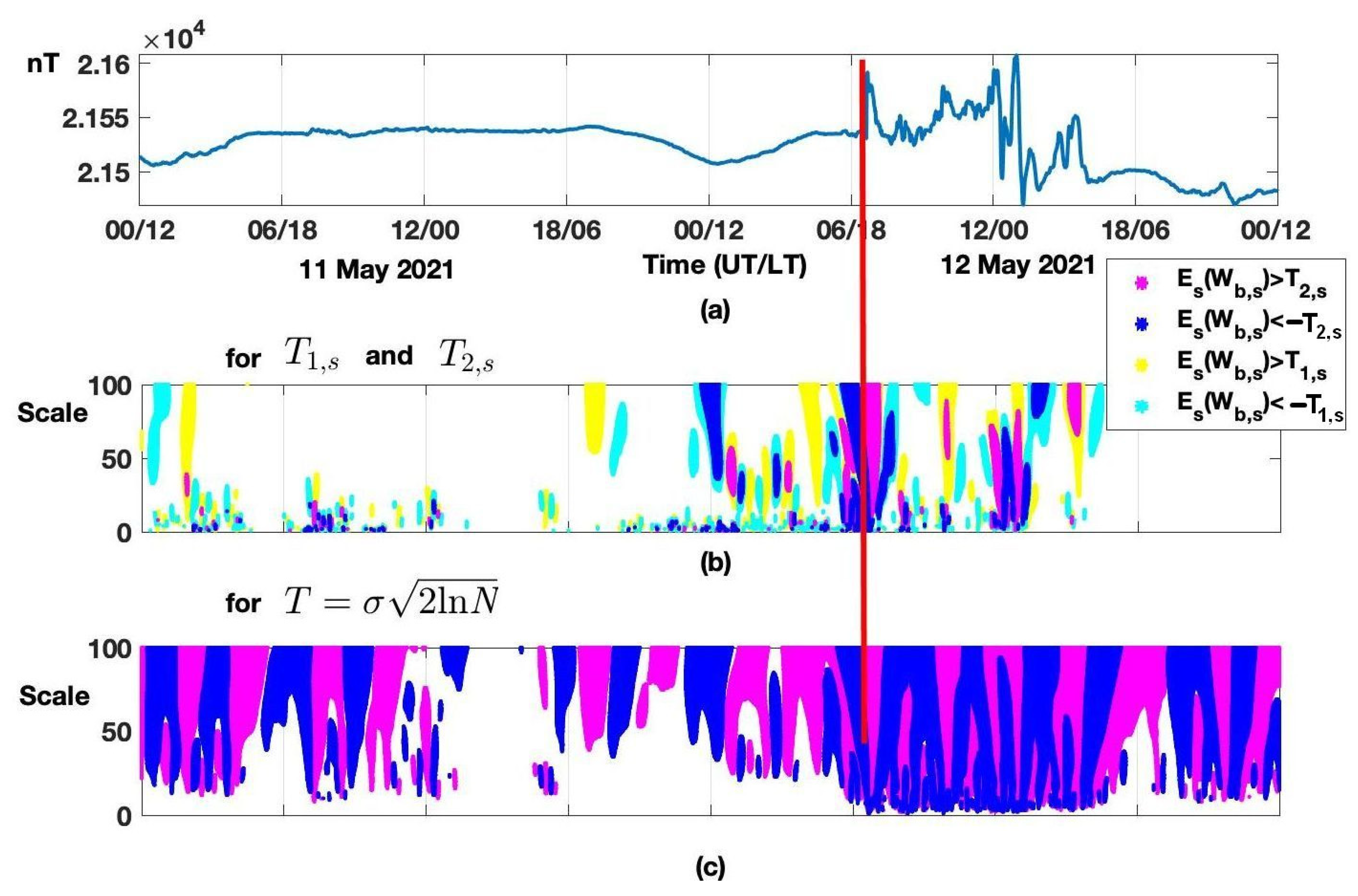
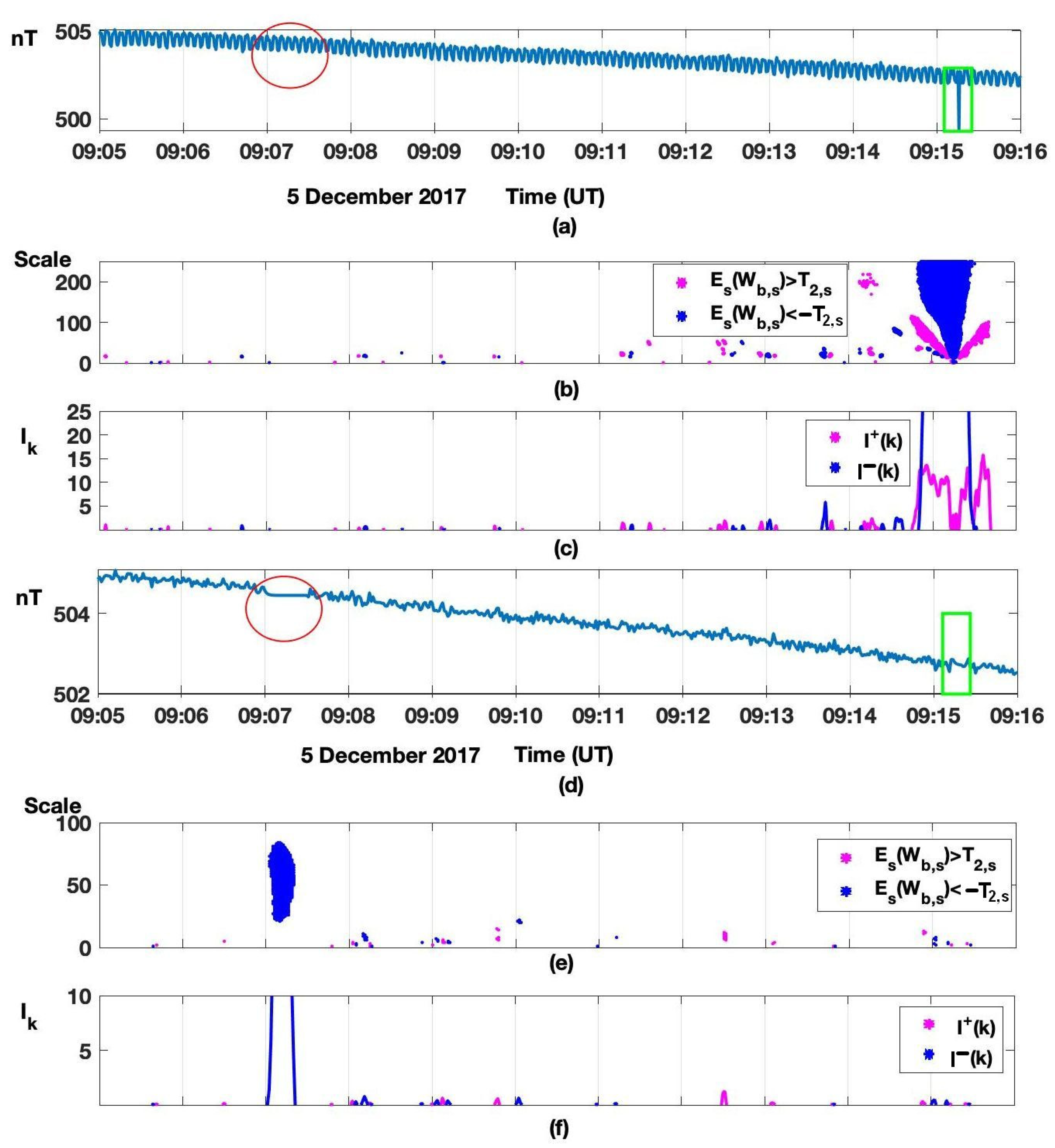
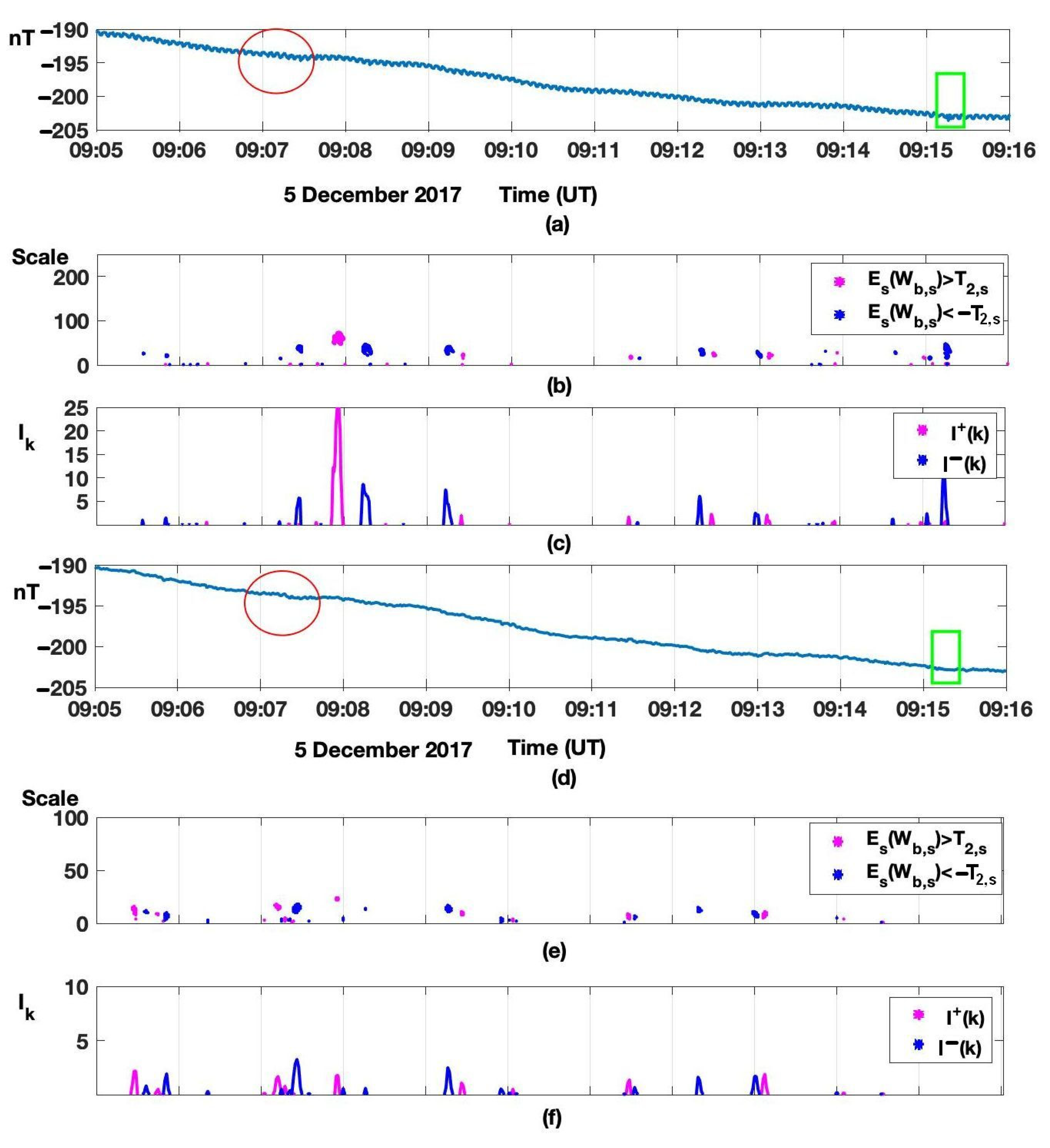
3.2. Detection of Short-Period Geomagnetic Disturbances, Second-Resolution Data Processing
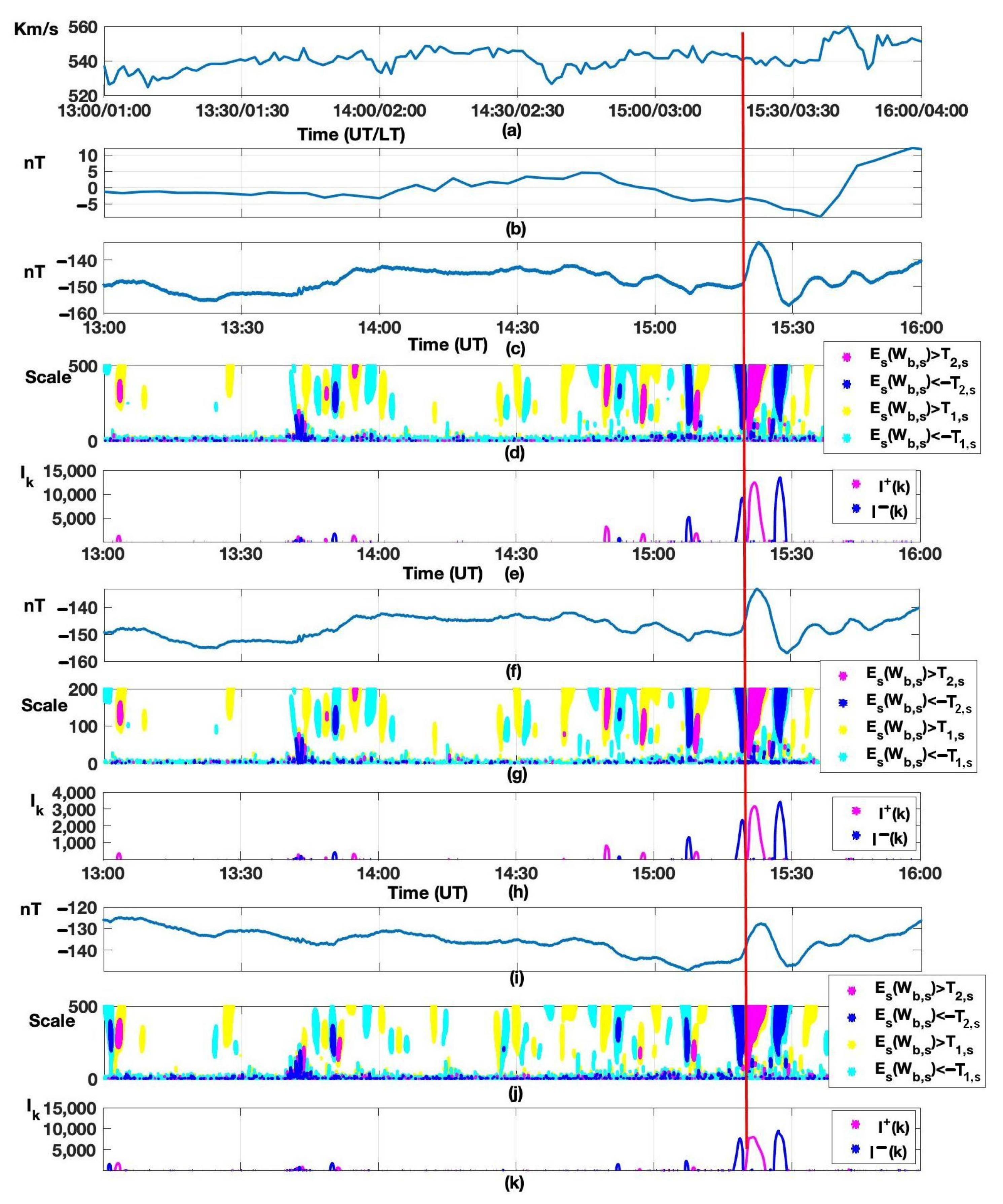
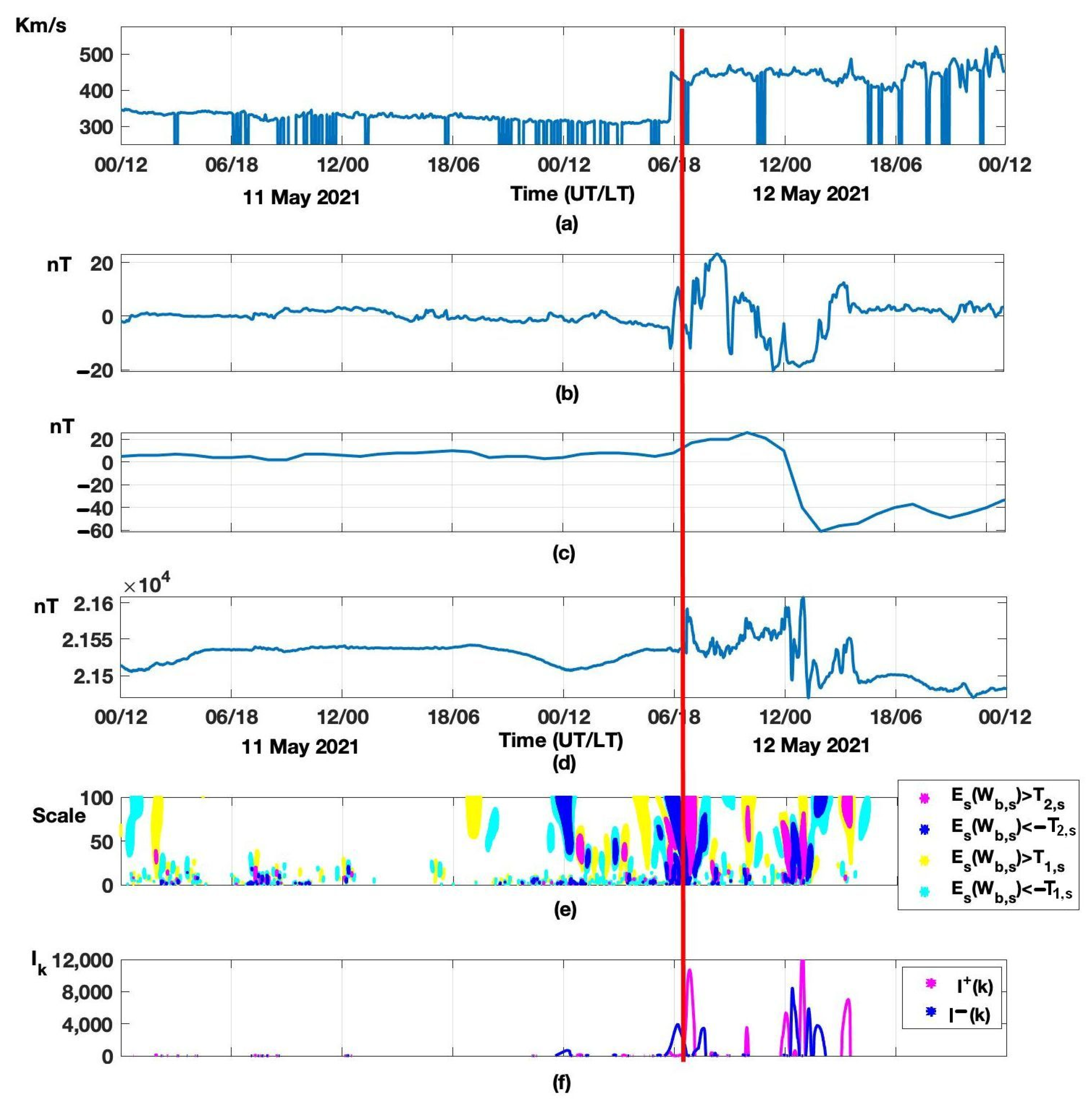
3.3. Detection of Short-Period Geomagnetic Disturbances, Minute-Resolution Data Processing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Real-Time Magnetic Observatory Network. Available online: https://intermagnet.github.io (accessed on 17 December 2021).
- Di Mauro, D.; Regi, M.; Lepidi, S.; Del Corpo, A.; Dominici, G.; Bagiacchi, P.; Benedetti, G.; Cafarella, L. Geomagnetic Activity at Lampedusa Island: Characterization and Comparison with the Other Italian Observatories, Also in Response to Space Weather Events. Remote Sens. 2021, 13, 3111. [Google Scholar] [CrossRef]
- Bailey, R.L.; Leonhardt, R. Automated Detection of Geomagnetic Storms with Heightened Risk of GIC. Earth Planets Space 2016, 68, 99. [Google Scholar] [CrossRef]
- Hafez, A.G.; Ghamry, E.; Yayama, H.; Yumoto, K. Wavelet Spectral Analysis Technique for Automatic Detection of Geomagnetic Sudden Commencements. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4503–4512. [Google Scholar] [CrossRef]
- Soloviev, A.; Agayan, S.; Bogoutdinov, S. Estimation of Geomagnetic Activity Using Measure of Anomalousness. Ann. Geophys. 2017, 59, 3. [Google Scholar] [CrossRef]
- Bogoutdinov, S.R.; Gvishiani, A.D.; Agayan, S.M.; Solovyev, A.A.; Kin, E. Recognition of Disturbances with Specified Morphology in Time Series. Part 1: Spikes on Magnetograms of the Worldwide INTERMAGNET Network. Izv. Phys. Solid Earth 2010, 46, 1004–1016. [Google Scholar] [CrossRef]
- Wahiduzzaman, M.; Yeasmin, A.; Luo, J.-J.; Ali, M.A.; Bilal, M.; Qiu, Z. Statistical Approach to Observe the Atmospheric Density Variations Using Swarm Satellite Data. Atmosphere 2020, 11, 897. [Google Scholar] [CrossRef]
- Fayemi, O.; Di, Q.; Zhen, Q.; Liang, P. Demodulation of EM Telemetry Data Using Fuzzy Wavelet Neural Network with Logistic Response. Appl. Sci. 2021, 11, 10877. [Google Scholar] [CrossRef]
- Zhou, R.; Han, J.; Guo, Z.; Li, T. De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition. Remote Sens. 2021, 13, 4932. [Google Scholar] [CrossRef]
- Singh, A.K.; Bhargawa, A.; Siingh, D.; Singh, R.P. Physics of Space Weather Phenomena: A Review. Geosciences 2021, 11, 286. [Google Scholar] [CrossRef]
- Despirak, I.V.; Kleimenova, N.G.; Gromova, L.I.; Gromov, S.V.; Malysheva, L.M. Supersubstorms during Storms of 7–8 September 2017. Geomagn. Aeron. 2020, 60, 292–300. [Google Scholar] [CrossRef]
- Gogatishvili, I.M. Geomagnetic precursors of intense earthquakes in the spectrum of geomagnetic pulsations with frequencies of 1–0.02 Hz. Geomagn. Aeron. 1984, 24, 697–700. [Google Scholar]
- Alabdulgader, A.; McCraty, R.; Atkinson, M.; Dobyns, Y.; Vainoras, A.; Ragulskis, M.; Stolc, V. Long-Term Study of Heart Rate Variability Responses to Changes in the Solar and Geomagnetic Environment. Sci. Rep. 2018, 8, 2663. [Google Scholar] [CrossRef] [Green Version]
- Hanzelka, M.; Dan, J.; Fiala, P.; Dohnal, P. Human Psychophysiology Is Influenced by Low-Level Magnetic Fields: Solar Activity as the Cause. Atmosphere 2021, 12, 1600. [Google Scholar] [CrossRef]
- Zenchenko, T.A.; Breus, T.K. The Possible Effect of Space Weather Factors on Various Physiological Systems of the Human Organism. Atmosphere 2021, 12, 346. [Google Scholar] [CrossRef]
- Stupishina, O.M.; Golovina, E.G.; Noskov, S.N.; Eremin, G.B.; Gorbanev, S.A. The Space and Terrestrial Weather Variations as Possible Factors for Ischemia Events in Saint Petersburg. Atmosphere 2022, 13, 8. [Google Scholar] [CrossRef]
- Zawawi, A.A.; Ab Aziz, N.F.; Ab Kadir, M.Z.A.; Hashim, H.; Mohammed, Z. Evaluation of Geomagnetic Induced Current on 275 kV Power Transformer for a Reliable and Sustainable Power System Operation in Malaysia. Sustainability 2020, 12, 9225. [Google Scholar] [CrossRef]
- Gil, A.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Wawrzynczak, A.; Pozoga, M.; Domijanski, S. Transmission Lines in Poland and Space Weather Effects. Energies 2020, 13, 2359. [Google Scholar] [CrossRef]
- Joo, B.-S.; Woo, J.-W.; Lee, J.-H.; Jeong, I.; Ha, J.; Lee, S.-H.; Kim, S. Assessment of the Impact of Geomagnetic Disturbances on Korean Electric Power Systems. Energies 2018, 11, 1920. [Google Scholar] [CrossRef] [Green Version]
- Kangas, J.; Guglielmi, A.; Pokhotelov, O. Morphology and Physics of Short-Period Magnetic Pulsations. Space Sci. Rev. 1998, 83, 435–512. [Google Scholar] [CrossRef]
- Ghamry, E.; Marchetti, D.; Yoshikawa, A.; Uozumi, T.; De Santis, A.; Perrone, L.; Shen, X.; Fathy, A. The First Pi2 Pulsation Observed by China Seismo-Electromagnetic Satellite. Remote Sens. 2020, 12, 2300. [Google Scholar] [CrossRef]
- Agayan, S.; Bogoutdinov, S.; Krasnoperov, R.; Sidorov, R. A Multiscale Approach to Geomagnetic Storm Morphology Analysis Based on DMA Activity Measures. Appl. Sci. 2021, 11, 12120. [Google Scholar] [CrossRef]
- Chinkin, V.E.; Soloviev, A.A.; Pilipenko, V.A.; Engebretson, M.J.; Sakharov, Y.A. Determination of Vortex Current Structure in the High-Latitude Ionosphere with Associated GIC Bursts from Ground Magnetic Data. J. Atmos. Sol. Terr. Phys. 2021, 212, 105514. [Google Scholar] [CrossRef]
- Zelinsky, N.R.; Kleimenova, N.G.; Gromova, L.I. Applying the New Method of Time-Frequency Transforms to the Analysis of the Characteristics of Geomagnetic Pc5 Pulsations. Geomagn. Aeron. 2017, 57, 559–565. [Google Scholar] [CrossRef]
- Agayan, S.; Bogoutdinov, S.; Soloviev, A.; Sidorov, R. The Study of Time Series Using the DMA Methods and Geophysical Applications. Data Sci. J. 2016, 15, 16. [Google Scholar] [CrossRef] [Green Version]
- Rabie, E.; Hafez, A.G.; Saad, O.M.; El-Sayed, A.-H.M.; Abdelrahman, K.; Al-Otaibi, N. Geomagnetic Micro-Pulsation Automatic Detection via Deep Leaning Approach Guided with Discrete Wavelet Transform. J. King Saud Univ. Sci. 2021, 33, 101263. [Google Scholar] [CrossRef]
- Gruet, M.A.; Chandorkar, M.; Sicard, A.; Camporeale, E. Multiple-Hour-Ahead Forecast of the Dst Index Using a Combination of Long Short-Term Memory Neural Network and Gaussian Process. Space Weather 2018, 16, 1882–1896. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.; Zheng, Y.; Ye, Y.; Feng, X.; Liu, C.; Ma, H. Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework. Remote Sens. 2021, 13, 1738. [Google Scholar] [CrossRef]
- Chui, C.K. An Introduction to Wavelets; Wavelet Analysis and Its Applications; Academic Press: Boston, MA, USA, 1992; ISBN 978-0-12-174584-4. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; CBMS-NSF Regional Conference Series in Applied Mathematics 61; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; ISBN 978-0-89871-274-2. [Google Scholar]
- Mandrikova, O.V.; Rodomanskaya, A.I.; Mandrikova, B.S. Application of the New Wavelet-Decomposition Method for the Analysis of Geomagnetic Data and Cosmic Ray Variations. Geomagn. Aeron. 2021, 61, 492–507. [Google Scholar] [CrossRef]
- Mandrikova, O.V.; Solovyev, I.S.; Khomutov, S.Y.; Geppener, V.V.; Klionskiy, D.M.; Bogachev, M.I. Multiscale Variation Model and Activity Level Estimation Algorithm of the Earth’s Magnetic Field Based on Wavelet Packets. Ann. Geophys. 2018, 36, 1207–1225. [Google Scholar] [CrossRef]
- Mandrikova, O.V.; Stepanenko, A.A. Automated method for calculating the Dst-index based on the wavelet model of geomagnetic field variations. Comput. Opt. 2020, 44, 797–808. [Google Scholar] [CrossRef]
- Nosé, M.; Iyemori, T.; Takeda, M.; Kamei, T.; Milling, D.K.; Orr, D.; Singer, H.J.; Worthington, E.W.; Sumitomo, N. Automated Detection of Pi 2 Pulsations Using Wavelet Analysis: 1. Method and an Application for Substorm Monitoring. Earth Planets Space 1998, 50, 773–783. [Google Scholar] [CrossRef] [Green Version]
- Nosé, M. Automated Detection of Pi 2 Pulsations Using Wavelet Analysis: 2. An Application for Dayside Pi 2 Pulsation Study. Earth Planets Space 1999, 51, 23–32. [Google Scholar] [CrossRef] [Green Version]
- Jach, A.; Kokoszka, P.; Sojka, J.; Zhu, L. Wavelet-Based Index of Magnetic Storm Activity. J. Geophys. Res. 2006, 111, A09215. [Google Scholar] [CrossRef] [Green Version]
- Mandrikova, O.; Fetisova, N.; Polozov, Y. Hybrid Model for Time Series of Complex Structure with ARIMA Components. Mathematics 2021, 9, 1122. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, L.; Sojka, J.; Kokoszka, P.; Jach, A. An Assessment Study of the Wavelet-Based Index of Magnetic Storm Activity (WISA) and Its Comparison to the Dst Index. J. Atmos. Sol. Terr. Phys. 2008, 70, 1579–1588. [Google Scholar] [CrossRef]
- Sugiura, M. Hourly values of equatorial Dst for the IGY. In Annals of the International Geophysical Year; Pergamon Press: Oxford, UK, 1964; Volume 35, pp. 7–45. [Google Scholar]
- Bartels, J.; Veldkamp, J. International Data on Magnetic Disturbances, Fourth Quarter, 1953. J. Geophys. Res. 1954, 59, 297–302. [Google Scholar] [CrossRef]
- Chapman, S.; Bartels, J. Geomagnetism; Oxford University Press: Oxford, UK, 1940. [Google Scholar]
- Mallat, S.G. A Wavelet Tour of Signal Processing; Academic Press: San Diego, CA, USA, 1999; ISBN 978-0-12-466606-1. [Google Scholar]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef] [Green Version]
- Bansal, A.K. Bayesian Parametric Inference; Narosa Publishing House Pvt. Ltd.: New Delhi, India, 2007. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Mandrikova, O.; Mandrikova, B.; Rodomanskay, A. Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition. Mathematics 2021, 9, 737. [Google Scholar] [CrossRef]
- Technical University of Denmark (Space). Available online: https://www.space.dtu.dk/english/Research/Research-Divisions/Geomagnetism-and-Geospace/Ground-based-magnetometry-instrumentation-infrastructure-and-data/3-axis_Fluxgate_Magnetometer_Model_FGM-FGE (accessed on 17 December 2021).
- Khomutov, S.Y.; Mandrikova, O.V.; Budilova, E.A.; Arora, K.; Manjula, L. Noise in Raw Data from Magnetic Observatories. Geosci. Instrum. Method. Data Syst. 2017, 6, 329–343. [Google Scholar] [CrossRef] [Green Version]
- Khomutov, S.Y. Methodological and Software Approaches to Processing of Magnetic Measurements of Observatories of IKIR FEB RAS, Russia. J. Ind. Geophys. Union 2016, 2, 54–61. [Google Scholar]
- Institute of Applied Geophysics. Available online: http://ipg.geospace.ru/ (accessed on 17 December 2021).
- St-Louis, B.; INTERMAGNET Operations Committee; INTERMAGNET Executive Council. INTERMAGNET Technical Reference Manual, Version 5.0.0; INTERMAGNET: Edinburgh, UK, 2020; 146p. [Google Scholar]
- Rastogi, R.G. Magnetic Storm Effects in H and D Components of the Geomagnetic Field at Low and Middle Latitudes. J. Atmos. Sol. Terr. Phys. 2005, 67, 665–675. [Google Scholar] [CrossRef]
- Chiaha, S.O.; Ugonabo, O.J.; Okpala, K.C. A study on the effects of solar wind and interplanetary magnetic field on geo-magnetic H-component during geomagnetic storms. Int. J. Phys. Sci. 2018, 13, 230–234. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Agayan, S.M.; Gvishiani, A.D.; Bogoutdinov, S.R.; Chulliat, A. Recognition of Disturbances with Specified Morphology in Time Series: Part 2. Spikes on 1-s Magnetograms. Izv. Phys. Solid Earth 2012, 48, 395–409. [Google Scholar] [CrossRef]
- Sheiner, O.A.; Fridman, V.M. The Features of Microwave Solar Radiation Observed in the Stage of Formation and Initial Propagation of Geoeffective Coronal Mass Ejections. Radiophys. Quantum Electron. 2012, 54, 655–666. [Google Scholar] [CrossRef]


| Wavelet | of the Optimal Basis | |||
|---|---|---|---|---|
| Db1 | 396.09 | 165.05 | 21.05 | 74.06 |
| Db2 | 349.63 | 141.32 | 21.37 | 53.99 |
| Db3 | 331.57 | 131.04 | 20.99 | 51.76 |
| Db4 | 330.26 | 130.85 | 21.26 | 50.54 |
| Db5 | 329.77 | 130.82 | 21.31 | 50.80 |
| Db6 | 327.42 | 130.91 | 21.06 | 51.55 |
| Db7 | 326.31 | 130.87 | 21.22 | 51.28 |
| Db8 | 329.35 | 131.02 | 21.32 | 50.06 |
| Db9 | 324.30 | 130.90 | 21.14 | 50.89 |
| Db10 | 324.20 | 130.96 | 21.17 | 51.20 |
| Wavelet | of the Optimal Basis | |||
|---|---|---|---|---|
| Db1 | 495.86 | 185.22 | 21.52 | 126.27 |
| Db2 | 459.81 | 170.22 | 21.34 | 68.39 |
| Db3 | 439.88 | 156.99 | 21.52 | 74.70 |
| Db4 | 438.27 | 155.61 | 21.57 | 63.92 |
| Db5 | 437.79 | 148.49 | 21.39 | 62.56 |
| Db6 | 437.09 | 146.00 | 21.51 | 61.23 |
| Db7 | 436.67 | 142.27 | 21.57 | 53.66 |
| Db8 | 336.82 | 145.82 | 21.41 | 61.57 |
| Db9 | 437.02 | 145.80 | 21.44 | 61.90 |
| Db10 | 436.73 | 140.62 | 21.57 | 52.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandrikova, O.; Polozov, Y.; Khomutov, S. Wavelet Model of Geomagnetic Field Variations and Its Application to Detect Short-Period Geomagnetic Anomalies. Appl. Sci. 2022, 12, 2072. https://doi.org/10.3390/app12042072
Mandrikova O, Polozov Y, Khomutov S. Wavelet Model of Geomagnetic Field Variations and Its Application to Detect Short-Period Geomagnetic Anomalies. Applied Sciences. 2022; 12(4):2072. https://doi.org/10.3390/app12042072
Chicago/Turabian StyleMandrikova, Oksana, Yuriy Polozov, and Sergey Khomutov. 2022. "Wavelet Model of Geomagnetic Field Variations and Its Application to Detect Short-Period Geomagnetic Anomalies" Applied Sciences 12, no. 4: 2072. https://doi.org/10.3390/app12042072
APA StyleMandrikova, O., Polozov, Y., & Khomutov, S. (2022). Wavelet Model of Geomagnetic Field Variations and Its Application to Detect Short-Period Geomagnetic Anomalies. Applied Sciences, 12(4), 2072. https://doi.org/10.3390/app12042072






