1. Introduction
The full-scale development of technical infrastructure in the Arctic zone of the Russian Federation is associated with risks arising from the negative influence of space weather (mainly through high-intensity geomagnetic disturbances) on technological systems. Thus, extreme geomagnetic disturbances (GMDs) observed in the auroral and subauroral zones are one of the factors, the neglect of which leads to an increase in the frequency of failures of technical systems in the high-latitude regions, a decrease in the overall level of technosphere safety, and, as a consequence, accidents of various scales. One of the most actively studied manifestations of GMD at high latitudes are geomagnetically induced currents (GICs) excited in spatially distributed conductive technical systems (pipelines, power lines, railway infrastructure facilities, etc.) due to geomagnetic disturbances with the variability dB/dt about several hundreds of nT/min and more.
GICs may cause malfunctions and failures of energy, transport, and telecommunication systems. For example, a magnetic storm on 13 March 1989 caused the failure of power transformers and a cascade shutdown (blackout) of electric power transmission lines for more than 9 h in the province of Quebec (Canada) [
1]. In the united power system in the northwest of Russia in November 2001, due to the GMA, there were two one-way disconnections of the electric power transmission line (330 kV) “Olenegorsk-Monchegorsk”, and consumers with a total capacity of more than 70 MW were disconnected [
2]. In October 2003, a similar reason caused the 20–50 min power outage in the power system in southern Sweden. The report of “Zurich Insurance Group” claims that only in the United States, as a result of electrical failures during the periods of magnetic storms from 2005 to 2015, the insurance payments exceeded
$1.9 billion [
3]. It was found that practically every strong magnetic storm produced anomalies in the signal automation of the northern branches of the railways “Oktyabrskaya” and “Severnaya” [
4,
5]. Additional information about the effects of the GMA on various technological systems can be found in the review [
6]. Besides a decrease in the reliability of terrestrial technical systems, due to a high level of ionospheric plasma turbulence in high-latitude regions, problems with the positioning accuracy and fault tolerance of the global navigation satellite systems (GNSS) GPS and GLONASS may occur [
7].
One of the few existing in the world system for the GIC monitoring and research was deployed in 2011 under the project “EURISGIC FP7-SPACE-2010”. It implements the registration of GIC parameters at four Russian (Vyhodnoy, Revda, Titan, Louhi, Kondopoga) and three Finnish (Pirttikoski, Rauma, Yllikkälä) transformer substations [
8] of electric power transmission 330/440 kV lines. The nearby magnetic stations of the IMAGE array make it possible to record the geomagnetic field variations simultaneously.
The prediction of GIC in a technological system during GMD is not a simple problem. For that, at least the knowledge of the GMD spectral and spatial characteristics, topology of the system, and distribution of surface impedances of the underlaying Earth’s crust are necessary. Therefore, a more simple and straightforward approach is developing—to construct from previous observational data a statistical model which would predict a probable GIC in a particular system from the data of nearby magnetic stations [
9,
10,
11,
12,
13].
However, such a goal has not yet been reached. It remains unclear what geomagnetic indices are most appropriate for the accurate diagnostics of GIC, and what the optimal number of parameters in the models should be taken into account. The choice of criteria based on which one or another source of reference data should be selected is not obvious. The GIC models proposed earlier for the northwest Russian power line [
12] provide the mean square error (MSE) of modeling at a level of ~0.91 A
2, which is not sufficient to provide effective diagnostics of GIC for objective reasons.
Thus, for the effective monitoring and nowcasting of GIC in high-latitude, spatially distributed technical systems, the elaboration of robust statistical models is an urgent task with practical applications. In this paper, we have applied machine learning (ML) methods, such as the regression approach and artificial neural networks (ANN), to find the best solution for the problem under consideration.
2. Initial Data, Their Preliminary Analysis and Preprocessing
The initial data in this research are 1-min values of the GIC recorded at the Vykhodnoy transformer substation (VKH) and 10-s data from the IMAGE magnetometers (
Figure 1,
Table 1). These observational data have been augmented by 1-min values of the geomagnetic IE index (regional proxy of the global AE index). The analysis of the samples was carried out for the period from 2015 close to the maximum activity of the 24th solar cycle (January 2009–May 2020).
Table 2 demonstrates the results of assessing the completeness of the raw time series, as well as of their reliability indicators. The gap occurrence is regarded as a failure of the data source, that is, its transition to an inoperative state [
14]:
where
TF is total downtime of the data source,
T is an operating time,
TW is number of informative values (total operating time) for the time period
T. In this example
T = 525,600 min (365 days).
The average time to restore the operating state (equivalent to the expectation of the size of the missing fragment) and the mean time between failures of the system (equivalent to the average size of the fragment without gaps) are determined by the following expressions:
here,
T2
Ri and
T2
Fi are the time until the
i-th system recovery after a failure and the time before the
i-th system failure, respectively;
NF and
NW are the number of system failures and the number of failover recoveries, respectively;
k = 1 or
k = 0, if at the time of the start of observation the system was in a working or inoperative state, respectively.
The magnetometer data have been downsampled to a common sampling step ∆
t = 1 min. The data detrending—exclusion of the baseline (daily component of the geomagnetic variations)—is carried out in accordance with the methodology described in [
15]. Further, using the two-sided difference method, the absolute values of the first derivative at each point of the time series are determined as follows: |
dB/
dt|
i = |
Bi+1−
Bi−1|/2Δ
t. At the final stage, to minimize the stochastic component, the time series are averaged over 15-min ranges. Thus, the size of the final sample includes ~35,040 values (including gaps) for each data source, which is enough to identify statistical relationships. In magnetometer data analysis, the main attention has been paid to the east–west component
Y, because this component corresponds to the north–south (
X) telluric electric field
Ex, driving GIC along the latitudinally extended power line [
16].
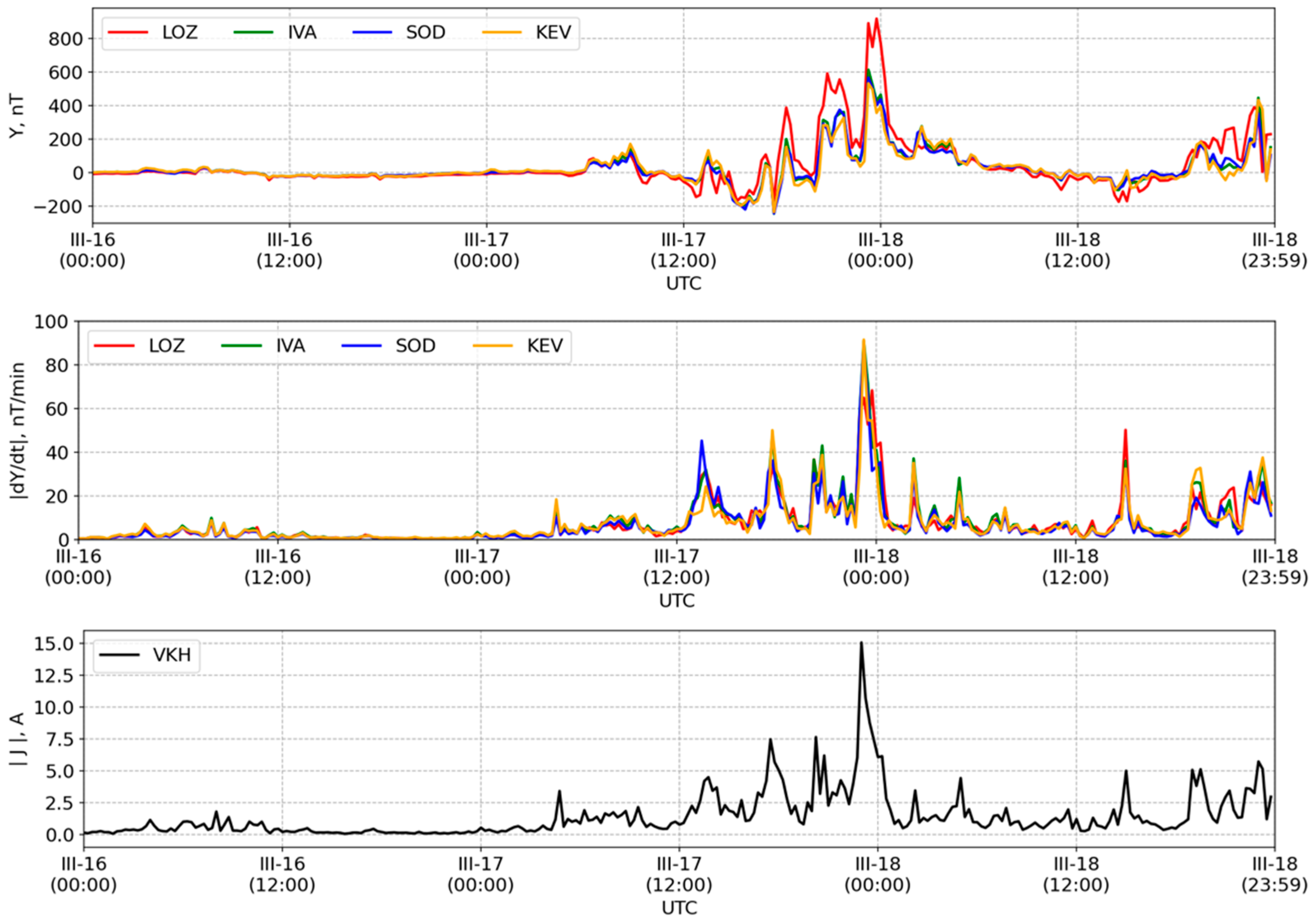
Figure 2 shows an example of variations of magnetic field (Y-component), field variability (|dY/dt|), and GIC during the period from 2015-03-16 00:00 (UT) to 2015-03-18 23:59 (UT). This time interval includes one of the powerful magnetic storms during recent years—St. Patrick’s Day Geomagnetic Storm (17 March 2015). Data are averaged over 15 min intervals.
3. Statistical and Correlation Analysis
The type and character of the statistical distribution, in addition to the homogeneity of the general samples, can indicate the physical mechanisms responsible for the appearance of one or another kind of disturbance [
17]. For example, a normal distribution is formed from the summing up effect of many random, weak independent impacts. In a closed system, the energy of its components is distributed according to the exponential law or the Laplace law. A random multiplicative set of several parameters leads to a log-normal distribution, etc.
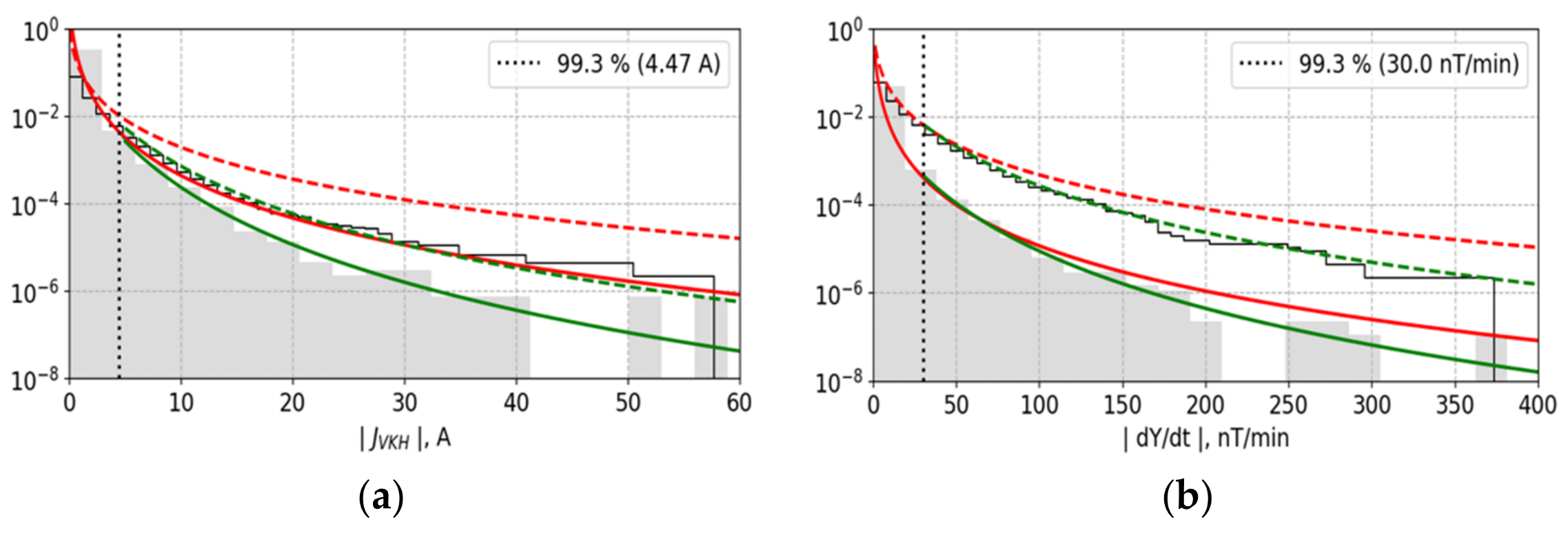
The results of the statistical analysis of the GIC values from VKH station |
J| and the geomagnetic field variability |
dY/
dt| are shown in
Figure 3a and
Figure 3b respectively. The calculated probability density function (PDF), the survival function (SF), and the empirical survival function (ESF) reveal that the distribution of both parameters is best described by the log-normal distribution. Starting from a ~99.3 percentile, a heavy tail can be traced, corresponding to generalized Pareto distribution law.
Analysis of the intensity of the geomagnetic variations of the Y-component from neighboring to VKH magnetic stations KEV, SOD, and LOZ (
Table 1) found a distribution of variability values |
dY/
dt| similar to that shown in
Figure 3. It indicates that fluctuations of both GIC amplitude and local geomagnetic field variability are determined mainly by rare intense deviations, probably due to substorm activity and geomagnetic pulsations in the Pc5-Pi3 range [
18]. At the same time, there are a number of research studies that have found that it is convective periods that generate the extremes, rather than pulsations [
19]. This situation may indicate the need for additional research in this area.
The analysis of the distribution of the regional IE-index characterizing the magnetic disturbance in the auroral zone [
20] demonstrates the structural similarity of the statistics. However, the distribution (not shown) predominantly corresponds to the exponential law with exponential tails.
Table 3 represents the results of assessing the Pearson correlation coefficient
r between the GIC values and the corresponding geomagnetic data. In order to reduce the influence of the stochastic component on the result, at this stage, the time series are averaged over 15-min intervals, taking into account that the duration of a substorm and the time interval between two following substorms are both usually at least 30 min.
The values of the Pearson correlation coefficient (
Table 3) correspond to the ranking of the statistical test for the compliance of heavy tails to the generalized Pareto law results. It eliminates the cases of the false correlation and is well explained by the spatial (km) and latitudinal (° N) separation of magnetic stations from the VKH station (
Table 1). The statistics obtained indicates the consistency of the results with physical laws and geostatistical principles.
4. Synthesis and Validation of ML Models for the GIC Diagnostics
The estimation of the coefficient of determination
R2 showed that, for the diagnostics of the GIC values |
JVKH|, the use of the geomagnetic field variability from nearby magnetic stations is reasonable. Here, we apply the methods based on multiple linear regression and an artificial neural network (ANN). The regression relationship is as follows:
here,
xT = (
x1, x2, …, xk) is a vector of regressors; β
T = (β
1, β
2, …, β
k) is a vector column of coefficients; and
k is a number of model input variables.
To increase the stability of the developed approach, the calculation of the values of the regression coefficients in expression (4) is performed by the Elastic Net method, which is a hybrid method of LASSO (λ
1 = λ, λ
2 = 0, where λ is a regularization parameter) and ridge regression (λ
2 = λ, λ
1 = 0) [
21]:
where
;
;
X is the
n×
k predictor matrix of standardized variables;
y is the response vector.
The analysis of the quality of the model’s feature objects by relief scoring method [
22] revealed that the input variable |
dYSOD/
dt| has the least quality at a sufficiently high correlation coefficient with the objective function (
Table 3). This may indicate the multicollinearity of the regressors and the necessity to exclude |
dY/
dt| from SOD analysis.
Finally, we have:
where β
0 = 0.1; β
1 = 90.56 × 10
−3; β
2 = 32.25 × 10
−3; β
3 = 32.36 × 10
−3; β
4 = 0.37 × 10
−3.
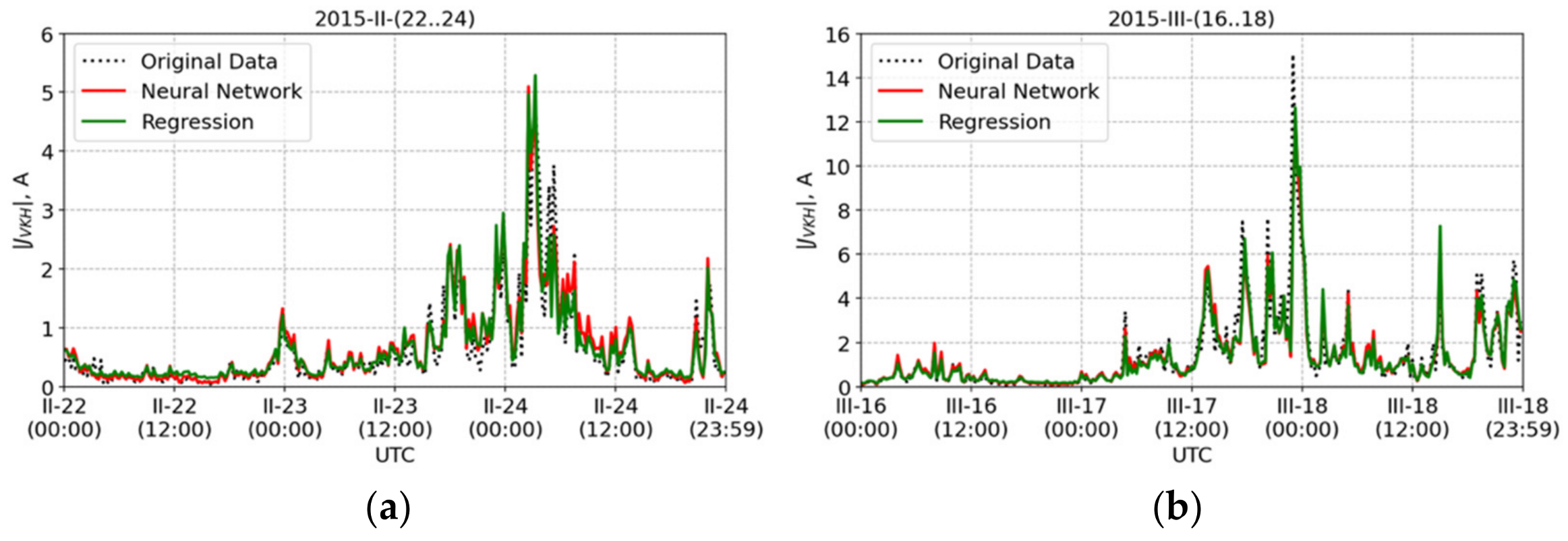
The result of GIC diagnostic based on expression (6) is shown in
Figure 4. The regression coefficients for Equation (6) were obtained for the year 2015 and tested on events from the same year. In the same plot, the results of the ANN with a similar set of input features, 20 neurons in the hidden layer, and the ReLu activation function are presented. For iterative updating of ANN weights, the Adam optimization algorithm has been used, which is an extension of the stochastic gradient descent method.
Table 4 shows the evaluation results of both approaches.
As follows from
Figure 4 and
Table 4, the diagnostics of the GIC by means of the ANN because of the quantity of neurons in the hidden layer is able to provide a slightly better result compared to the regression model (6). However, the ANN requires much more computational resources (computer time) and is less interpretable.
5. Discussion
The analysis of simultaneous GIC and magnetic field observations at Kola Peninsula has proved that a regression model can be a reliable tool for monitoring of the geomagnetic risks to electric power transmission lines. The regression method applied is somewhat similar to the transfer function approach [
23]. In the case of a change in the configuration of the power transmission line, the coefficients of this relationship require recalculation. With the advent of real-time magnetometer data access, such an approach can be applied to the nowcasting and short-term prediction of GIC in a system under control. The relative simplicity of the algorithm makes these methods of the space weather risk evaluation competitive with the current widely developing global modeling of the magnetosphere with supercomputers.
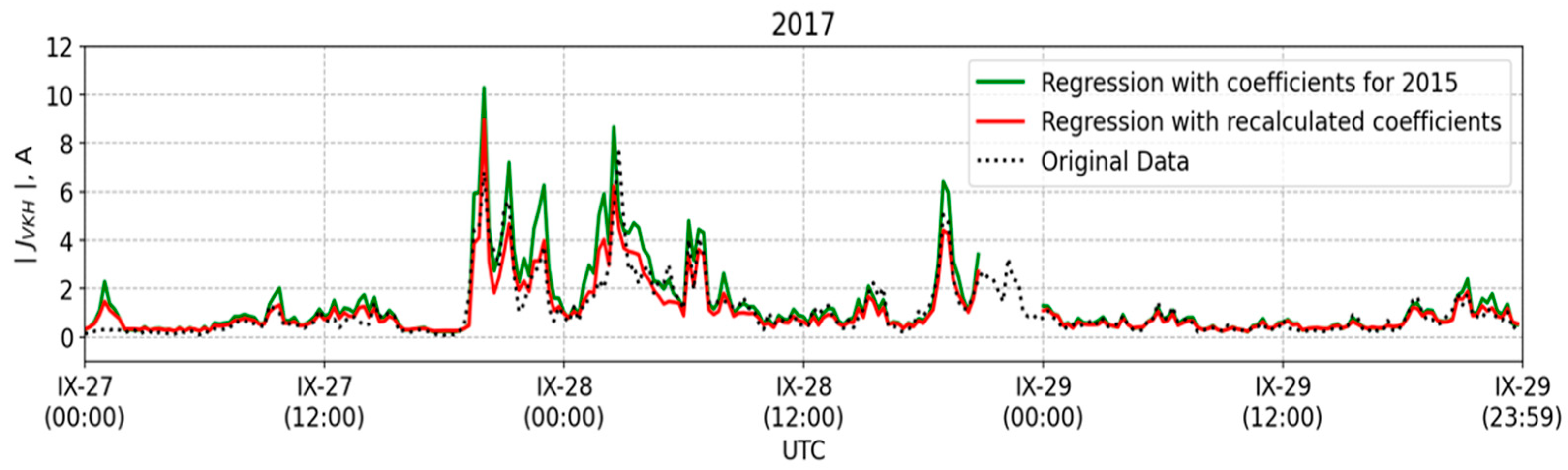
However, the application of expression (6) without recalculation of the regression coefficients to time intervals beyond 2015 may show a slightly worse quality of the GIC diagnostics (
Figure 5) as compared to the results presented in
Table 4. Thus, updating the regression coefficients would be necessary from time to time.
Another promising application of the proposed regression method is the monitoring of geomagnetic risk to pipelines in the oil/gas-producing high-latitude regions (e.g., Yamal, the Arctic shelf) [
24]. The development of GIC in pipelines results in an increased corrosion at grounding points or at points with insulation damage. GMD induce fluctuations in the pipe-to-soil potential, which take the pipeline voltage beyond the range of electrocorrosion protection. Thus, the influence of geomagnetic variations should be monitored regularly when maintaining the operation of the power transmission line and cathodic protection of pipelines, since the effect of GIC can manifest itself not only directly during the extreme GMD as failure of the equipment, but also has a long-term cumulative effect as pipeline electrocorrosion or the aging of industrial transformers [
25].
6. Conclusions
The best result of the GIC diagnostics from ground-based magnetometer data is provided by regression methods or ANN using the variability of the
Y-component of the geomagnetic field (d
Y/d
t). Verification tests showed that the ANN-based approaches provide a slightly higher diagnostic accuracy (MSE = 0.119 A
2) compared to the regression methods (MSE = 0.122 A
2). However, the ANN methods are less interpretable and require more computational power when implemented. The MSE of the obtained relationship for the GIC diagnostics is ~7.5 times lower than the MSE of similar expressions obtained previously in [
12]. This advancement has been achieved thanks to a detailed analysis and careful selection of feature objects, comprising statistical analysis of heavy tails, pairwise correlation analysis, and assessing the quality of the regression model’s feature objects, etc.
The proposed approach to the GIC monitoring can be used for the diagnostics of extreme GIC values at a transformer substation, when the results of direct GIC measurement in a given region are not available. This kind of GIC monitoring can significantly reduce the risks associated with failures of power transformers during periods of extreme geomagnetic activity. However, to maintain the high-quality metrics of the regression model, a periodic updating (recalculation) of the regression model coefficients is required.