Equivalent Electronic Circuit of a System of Oscillators Connected with Periodically Variable Stiffness
Abstract
:1. Introduction
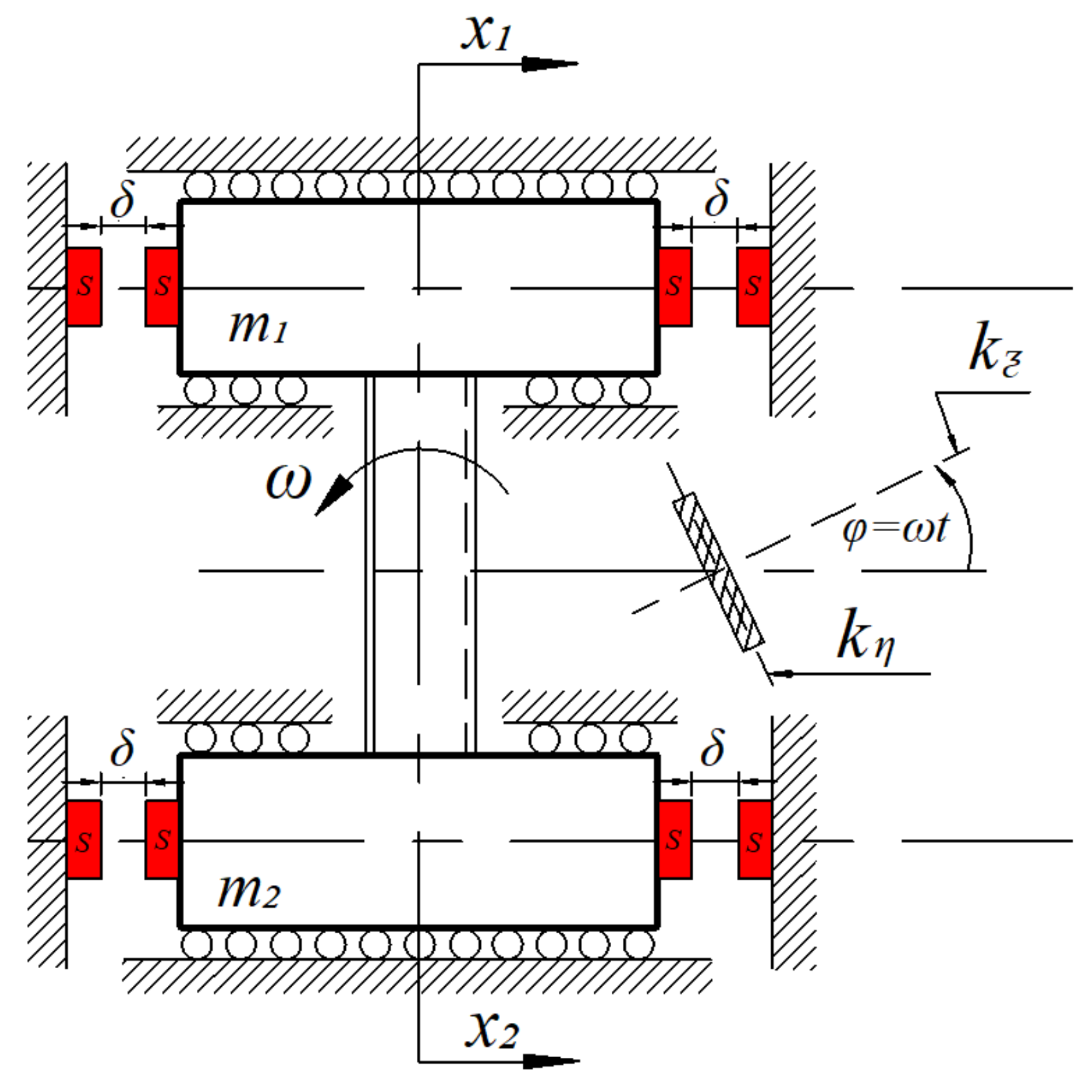
2. System Description
3. Mathematical Model
3.1. Dimensional Equations of the System
- 1
- ; . is the resistance force of the bearings and the term is the smooth approximation of the function sign().
- 2
- is the force due to the magnetic spring.= ; . The idea of the above formula is considered by the two assumptions: (i) the repulsive force between two magnets is defined by the simplest expression of the inverse square law, where the dipole expression has been considered. (ii) when = , the first term of the expression becomes the unity, when = , the second term becomes unity, and the expression becomes negative value.
- 3
- The stiffness coupling of the considered system, = . It varies periodically having the linear frequency, , where is the angular frequency of oscillation.
3.2. Non-Dimensional Equations of the System
4. Numerical Results
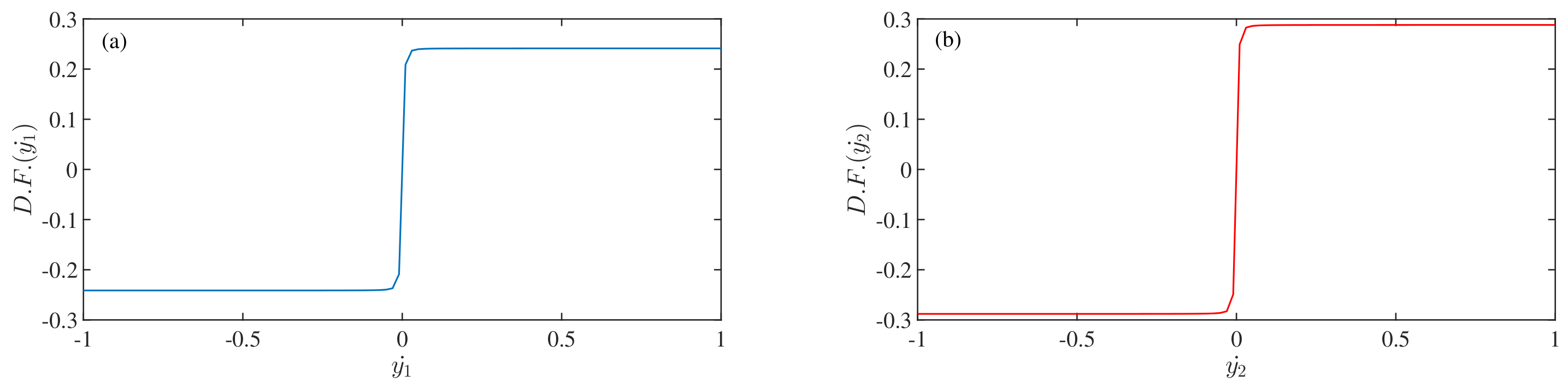
4.1. Behavior of the Dry-Friction and Resistance Force Terms
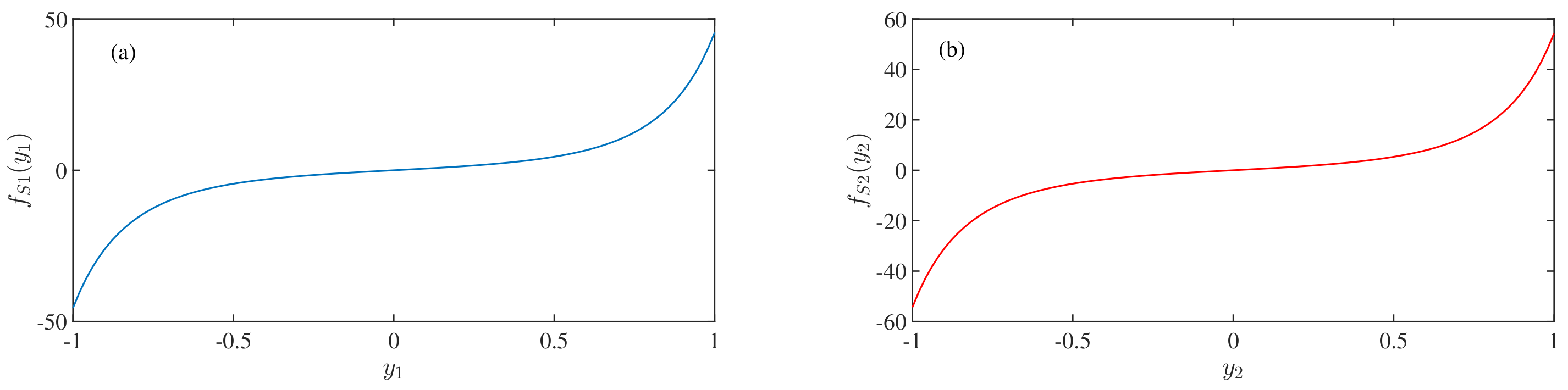
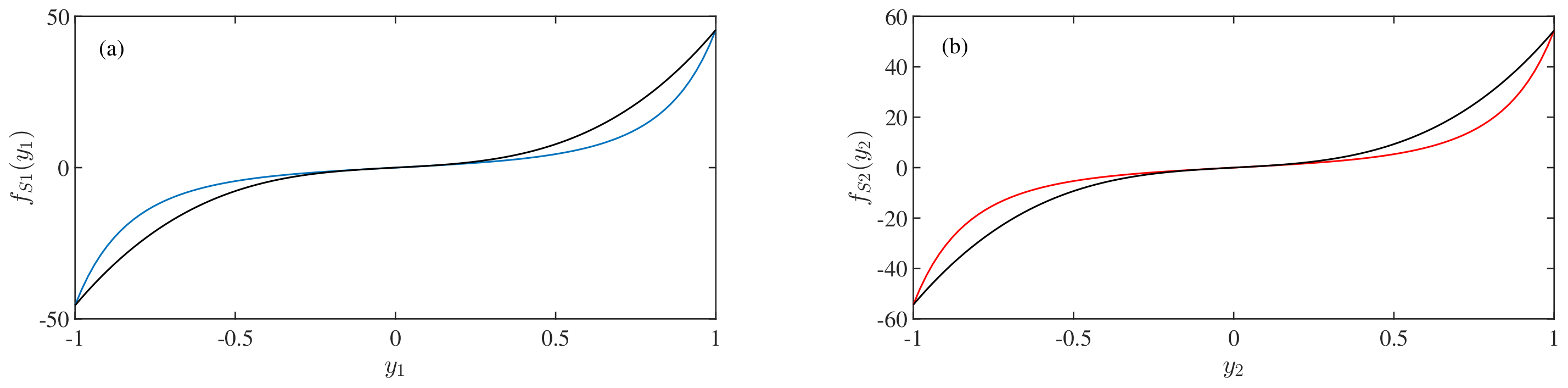
4.2. Behavior of Magnetic Spring Force Term
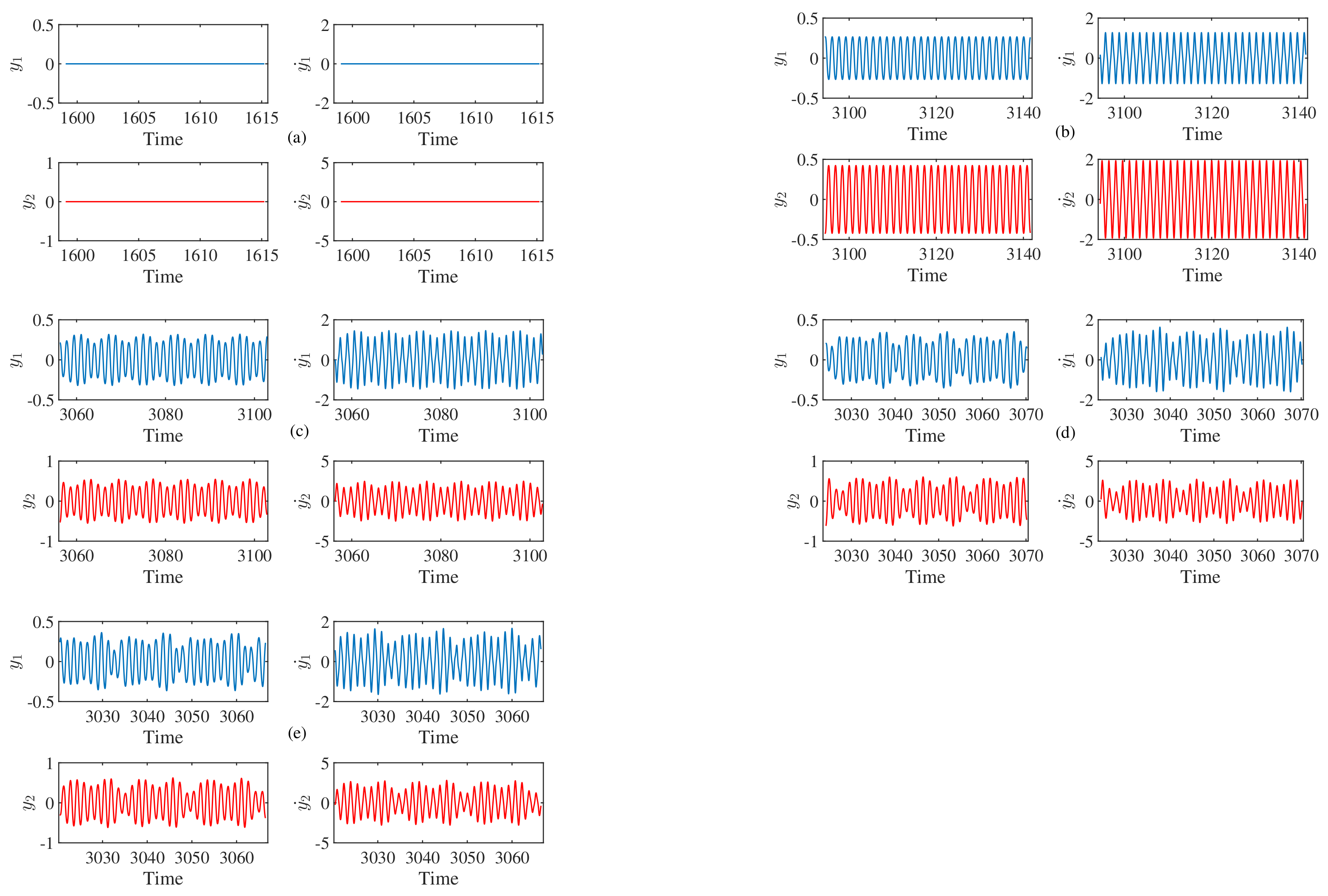
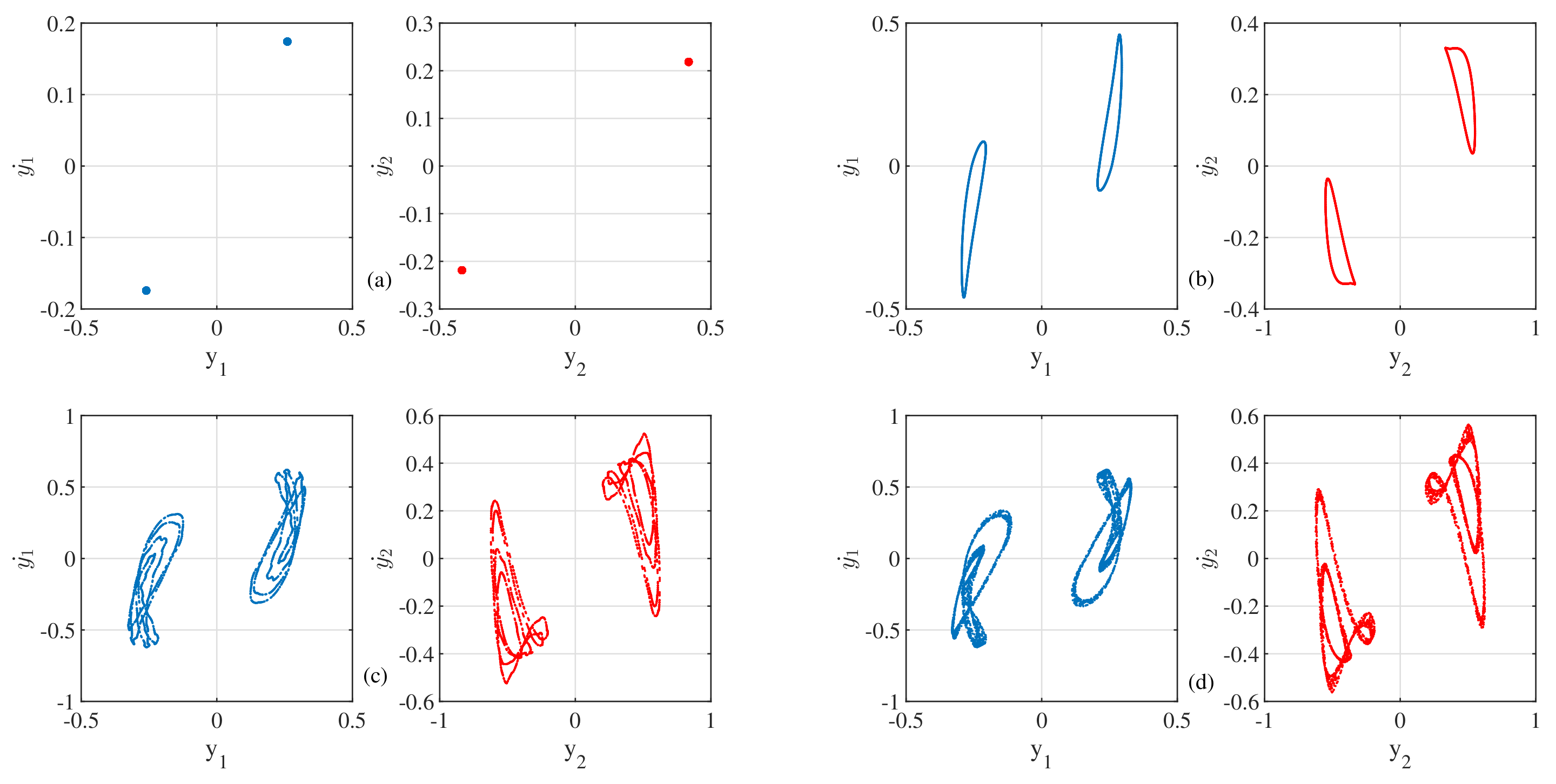
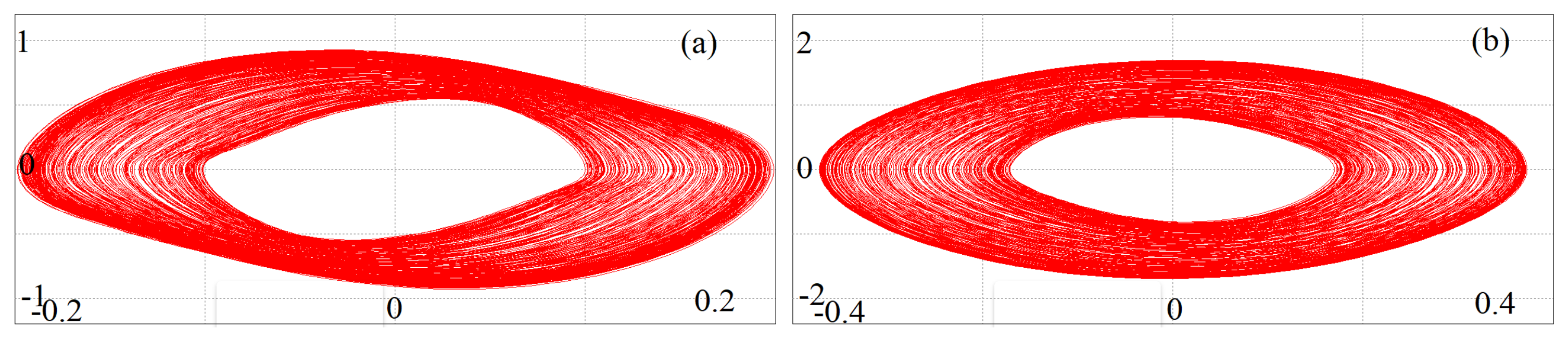
4.3. Time-Series and Phase-Space Plots of the Considered System
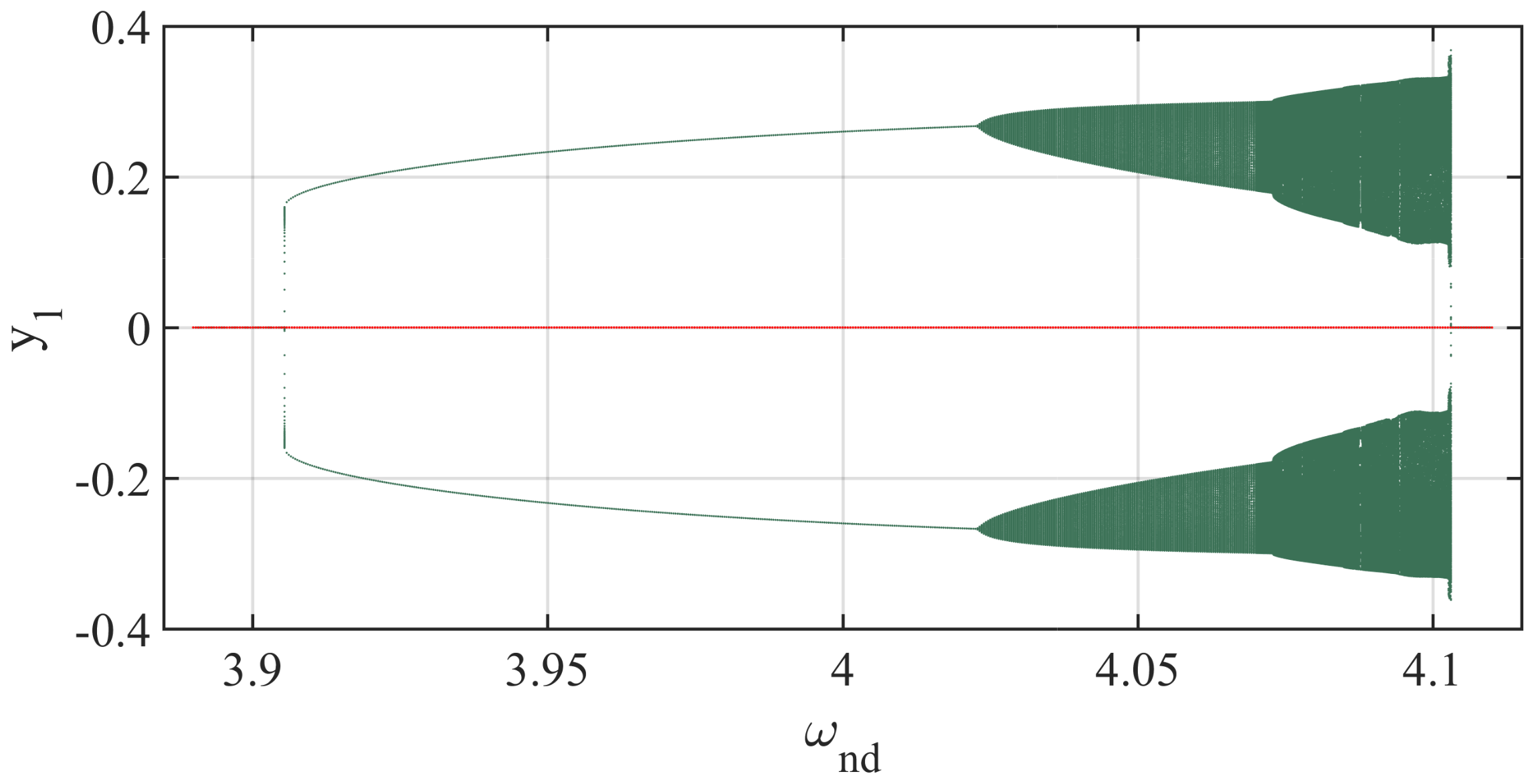
4.4. Bifurcation Diagrams and the Corresponding Maximal Lyapunov Exponent
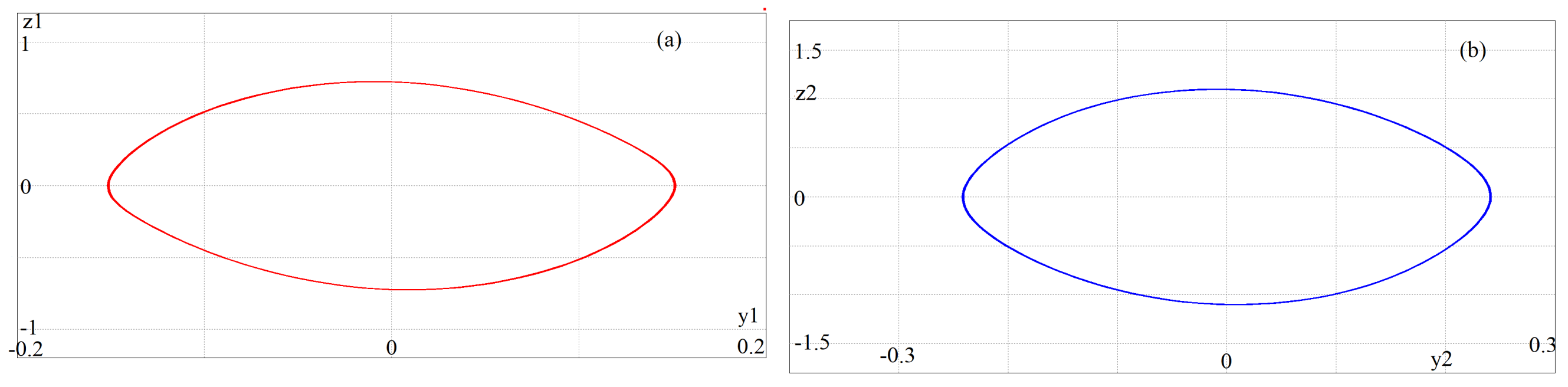
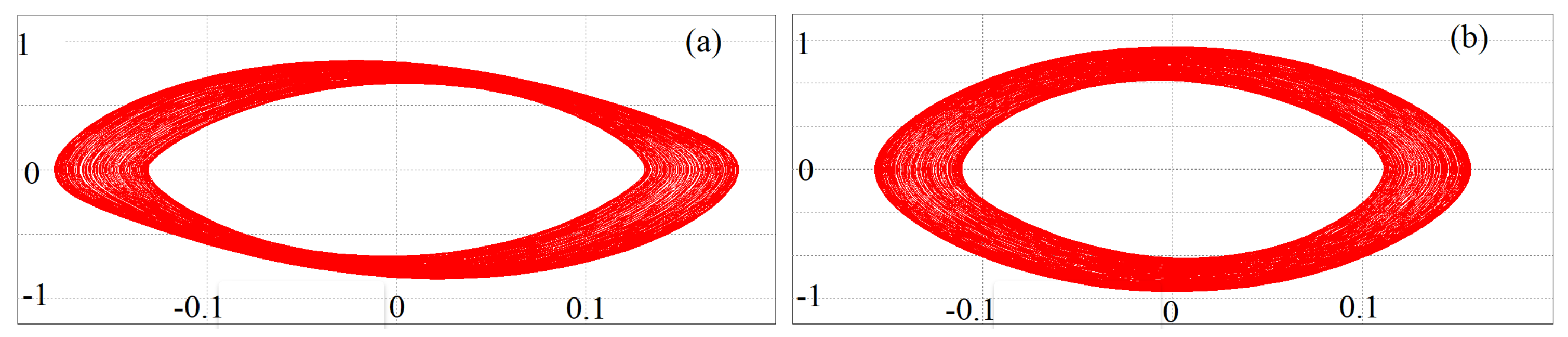
4.5. Co-Existence of Two Attractors
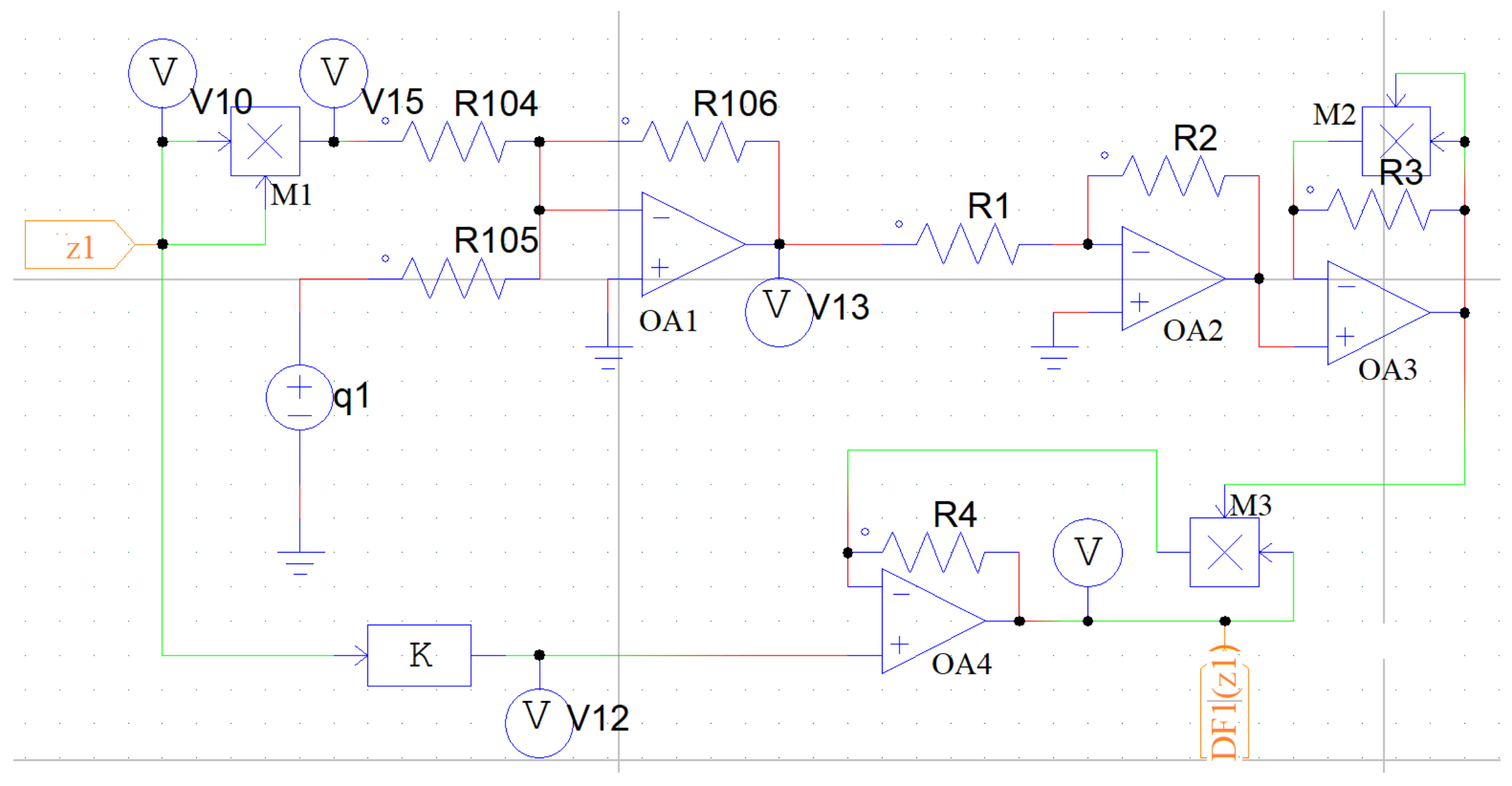
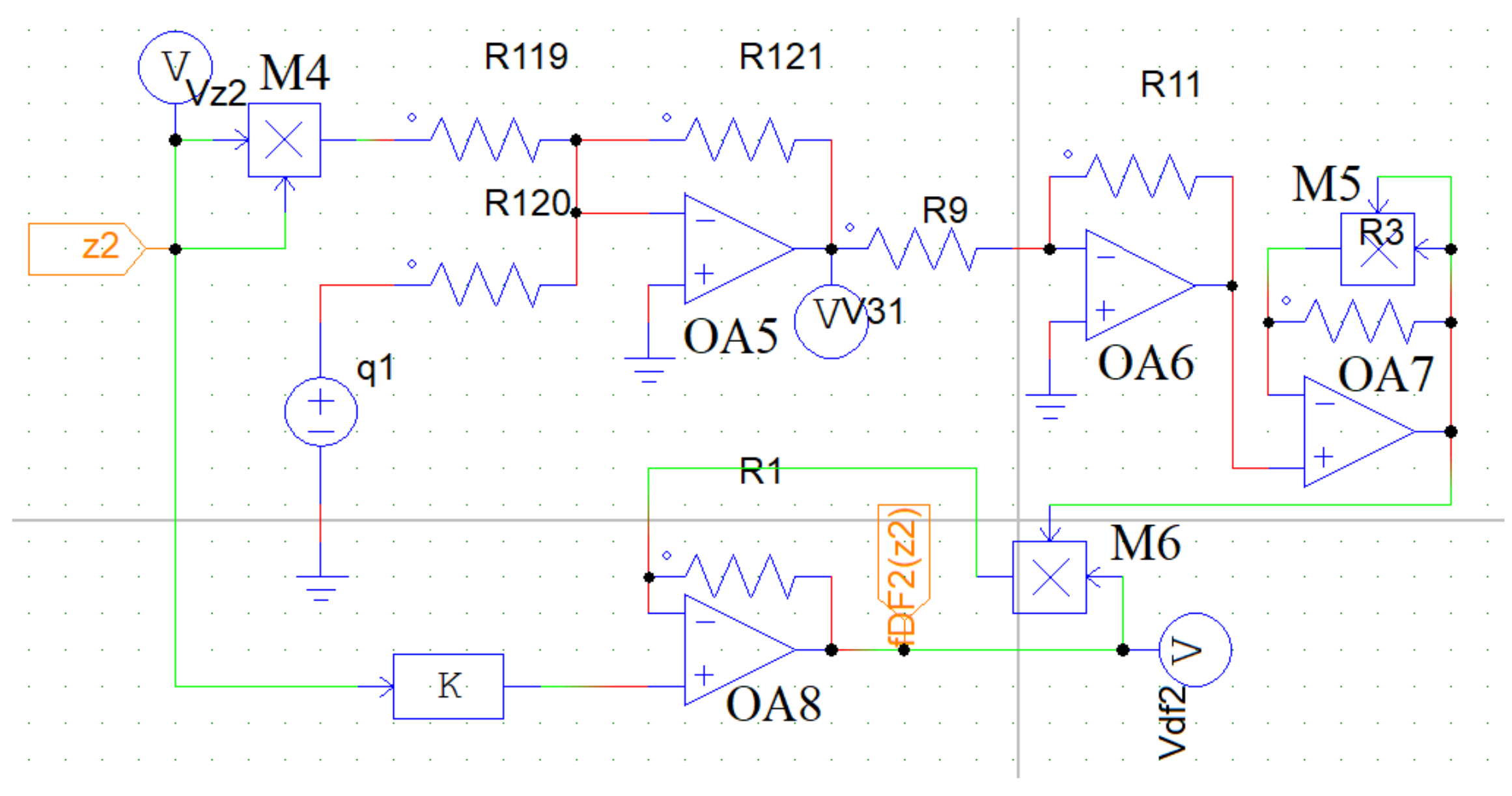
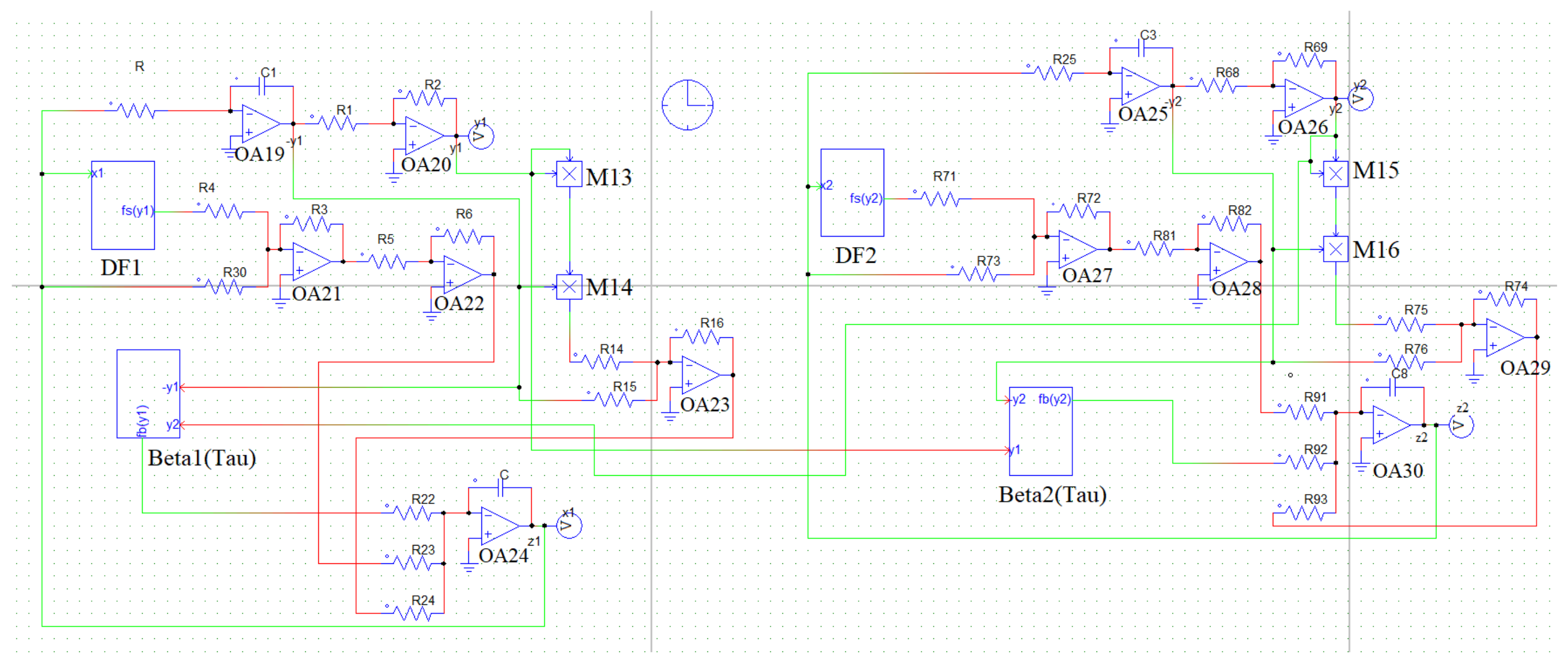
5. Equivalent Circuit of the Coupled Mechanical Oscillators
- 1.
- = + = ; . is the non-dimensional resistance force of the bearings. is the linear damping force, and is the force due to the dry-friction. The values of , , , and are , , , , and respectively.
- 2.
- = ; ., is the non-dimensional force due to the magnetic spring. The values of , , , and are , , , and 1 respectively. To reduce the complexity of the equations, we have chosen the most straightforward expressions of the non-dimensional force due to the magnetic spring, which are in the Equations (7) and (8).
- 3.
- The non-dimensional stiffness couplings of the considered system, = and = . The parameter values are , . The non-dimensional angular frequency, , will have to be varied in order to obtain the bifurcation diagram.
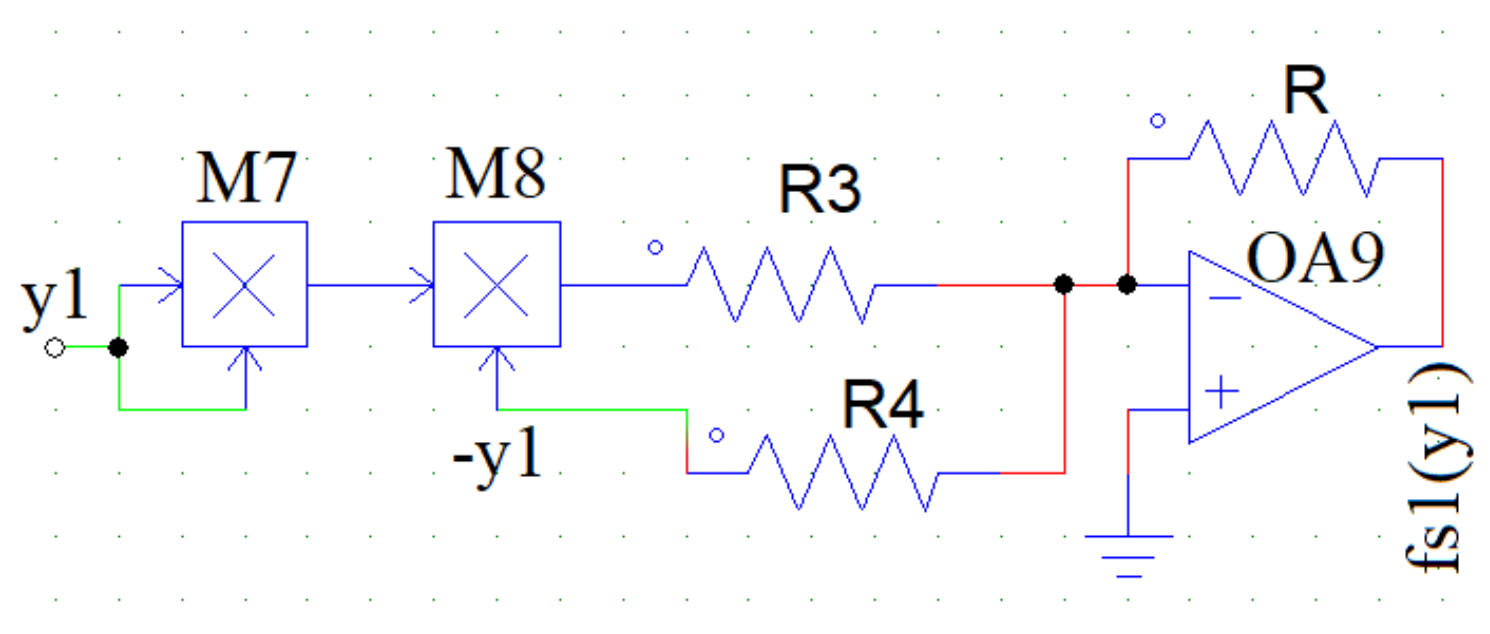
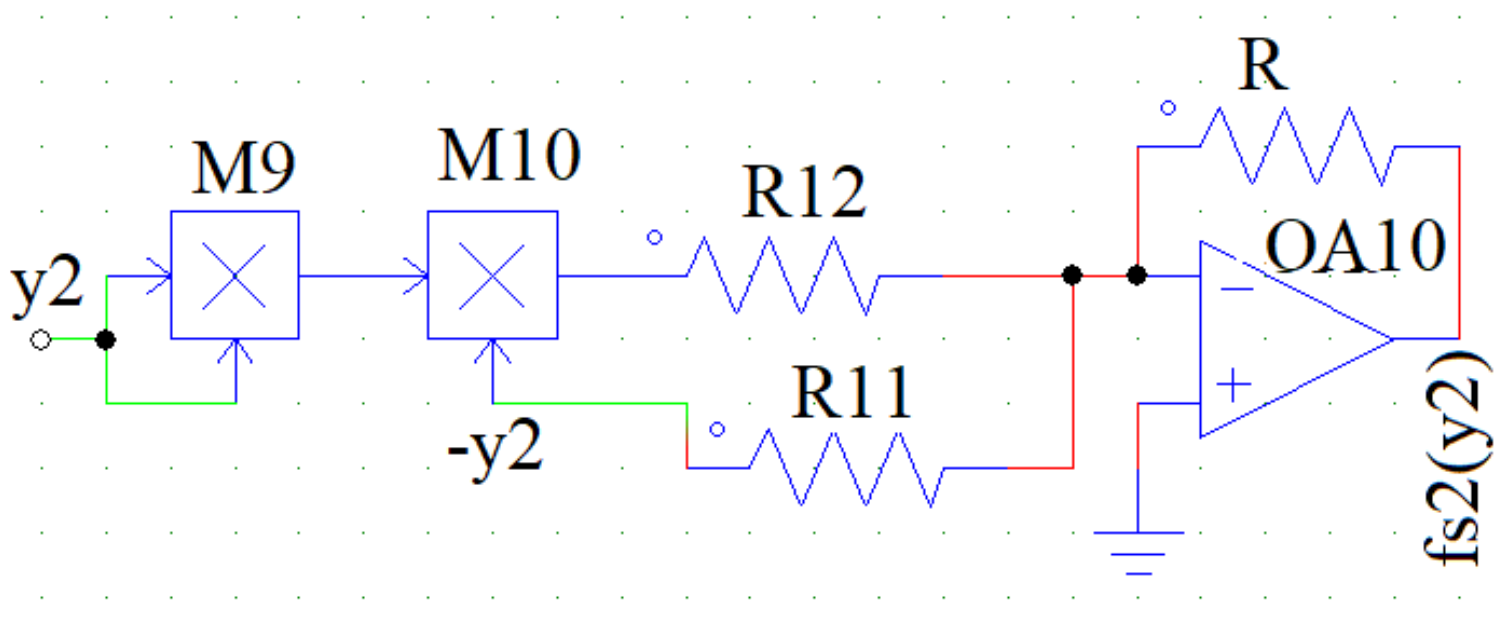
5.1. Equivalent Circuit Diagram of the Dry-Friction Term
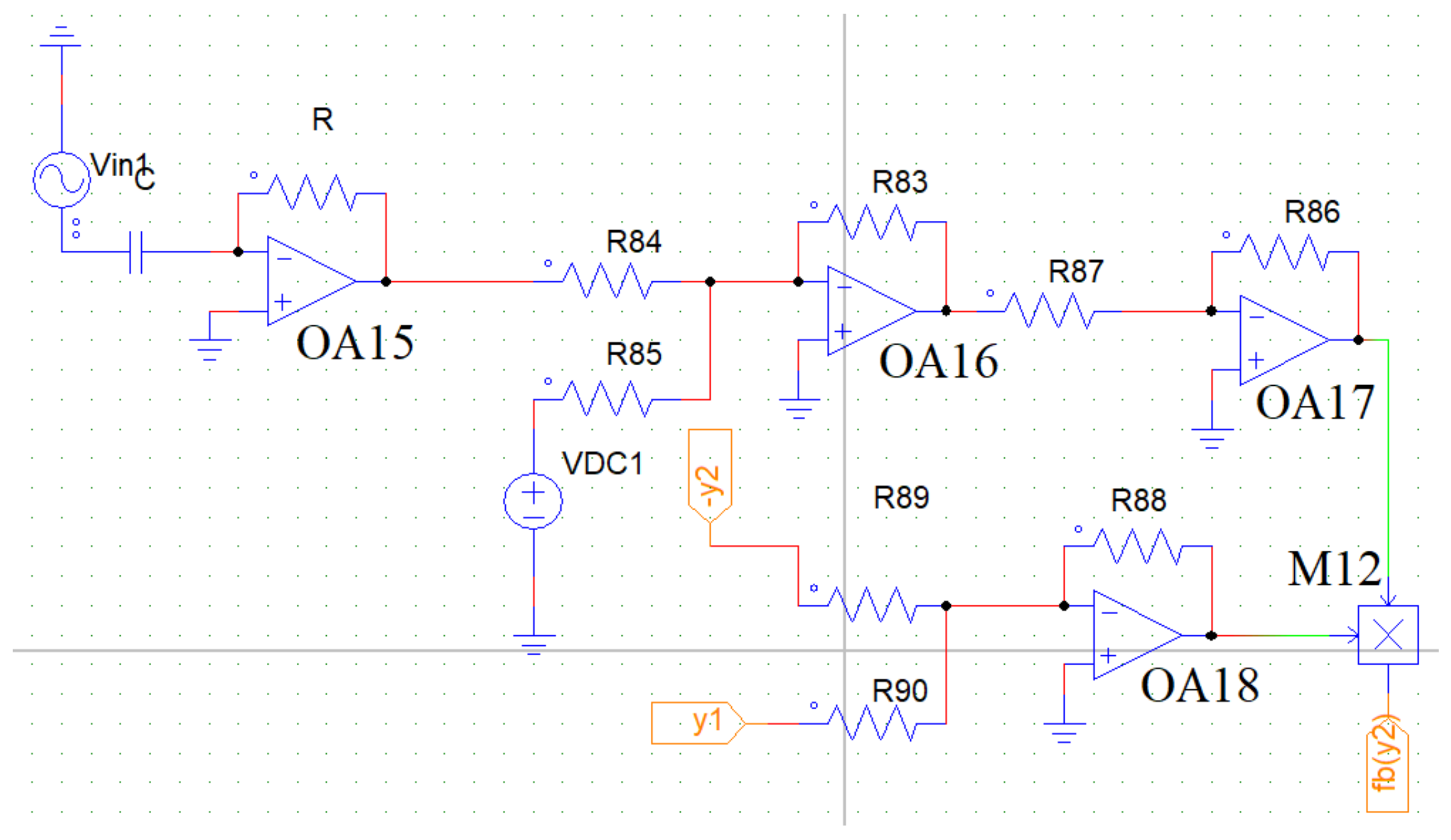
5.2. Equivalent Circuit Diagram of the Magnetic Spring Force Term
5.3. Equivalent Circuit Diagram of
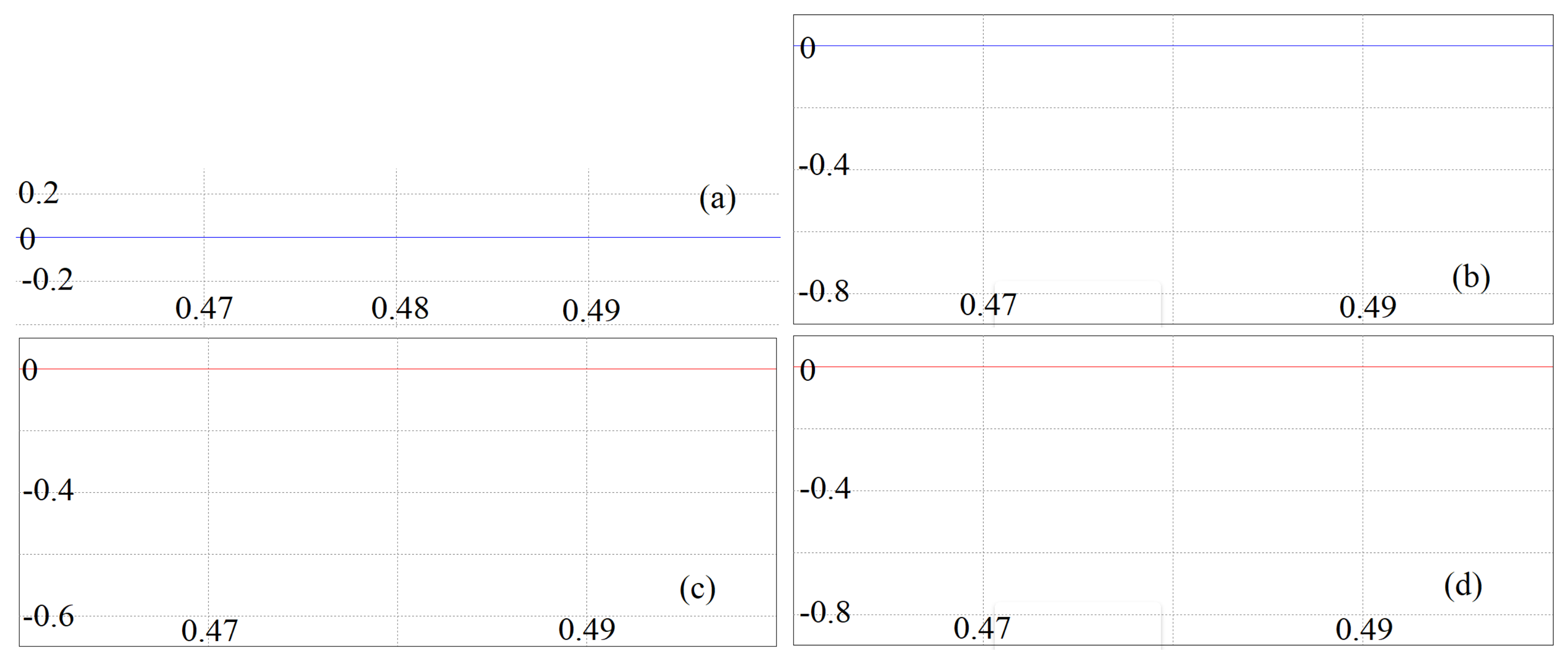
6. Results Obtained from Simulating the Circuit
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Awrejcewicz, J.; Lamarque, C.H. Bifurcation and Chaos in Nonsmooth Mechanical Systems; World Scientific: Singapore, 2003; Volume 45. [Google Scholar]
- Sidorets, V.; Pentegov, I. Deterministic Chaos in Nonlinear Circuits with Electric Arc; International Association Welding: Kyiv, Ukraine, 2013. [Google Scholar]
- Witkowski, K.; Kudra, G.; Skurativskyi, S.; Wasilewski, G.; Awrejcewicz, J. Modeling and dynamics analysis of a forced two-degree-of-freedom mechanical oscillator with magnetic springs. Mech. Syst. Signal Process. 2021, 148, 107138. [Google Scholar] [CrossRef]
- Kudra, G.; Witkowski, K.; Seth, S.; Polczyński, K.; Awrejcewicz, J. Parametric Vibrations of a System of Oscillators Connected with Periodically Variable Stiffness. In Proceedings of the DSTA-2021 Conference Books–Abstracts (16th International Conference: Dynamical Systems Theory and Applications DSTA 2021 ABSTRACTS), Łódź, Poland, 16–19 December 2021; Awrejcewicz, J., Ka´zmierczak, M., Olejnik, P., Mrozowski, J., Eds.; Wydawnictwo Politechniki Łódzkiej: Łódź, Poland. ISBN 978-83-66741-20-1. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Ding, H.; Chen, L.Q. Resonance response interaction without internal resonance in vibratory energy harvesting. Mech. Syst. Signal Process. 2019, 121, 767–776. [Google Scholar] [CrossRef]
- Wojna, M.; Wijata, A.; Wasilewski, G.; Awrejcewicz, J. Numerical and experimental study of a double physical pendulum with magnetic interaction. J. Sound Vib. 2018, 430, 214–230. [Google Scholar] [CrossRef]
- Chiacchiari, S.; Romeo, F.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Vibration energy harvesting from impulsive excitations via a bistable nonlinear attachment. Int. J. Non-Linear Mech. 2017, 94, 84–97. [Google Scholar] [CrossRef]
- Chiacchiari, S.; Romeo, F.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Vibration energy harvesting from impulsive excitations via a bistable nonlinear attachment—Experimental study. Mech. Syst. Signal Process. 2019, 125, 185–201. [Google Scholar] [CrossRef]
- Witkowski, K.; Kudra, G.; Wasilewski, G.; Awrejcewicz, J. Modelling and experimental validation of 1-degree-of-freedom impacting oscillator. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2019, 233, 418–430. [Google Scholar] [CrossRef]
- Sanches, L.; Michon, G.; Berlioz, A.; Alazard, D. Response and instability prediction of helicopter dynamics on the ground. Int. J. Non-Linear Mech. 2014, 65, 213–225. [Google Scholar] [CrossRef]
- Danylenko, V.; Skurativskyi, S. Peculiarities of wave fields in nonlocal media. arXiv 2015, arXiv:1503.01351. [Google Scholar]
- Olejnik, P.; Awrejcewicz, J. Coupled oscillators in identification of nonlinear damping of a real parametric pendulum. Mech. Syst. Signal Process. 2018, 98, 91–107. [Google Scholar] [CrossRef]
- Skurativskyi, S.; Kudra, G.; Witkowski, K.; Awrejcewicz, J. Bifurcation phenomena and statistical regularities in dynamics of forced impacting oscillator. Nonlinear Dyn. 2019, 98, 1795–1806. [Google Scholar] [CrossRef] [Green Version]
- Ing, J.; Pavlovskaia, E.; Wiercigroch, M.; Banerjee, S. Bifurcation analysis of an impact oscillator with a one-sided elastic constraint near grazing. Phys. D Nonlinear Phenom. 2010, 239, 312–321. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Genov, D.; Bardaweel, H. Mono-stable and bi-stable magnetic spring based vibration energy harvesting systems subject to harmonic excitation: Dynamic modeling and experimental verification. Mech. Syst. Signal Process. 2019, 134, 106361. [Google Scholar] [CrossRef]
- Afsharfard, A. Application of nonlinear magnetic vibro-impact vibration suppressor and energy harvester. Mech. Syst. Signal Process. 2018, 98, 371–381. [Google Scholar] [CrossRef]
- Novak, M.; Cernohorsky, J.; Kosek, M. Simple electro-mechanical model of magnetic spring realized from FeNdB permanent magnets. Procedia Eng. 2012, 48, 469–478. [Google Scholar] [CrossRef] [Green Version]
- Seth, S.; Banerjee, S. Electronic circuit equivalent of a mechanical impacting system. Nonlinear Dyn. 2020, 99, 3113–3121. [Google Scholar] [CrossRef]
- Skilling, H. An Electric Analog of Friction For Solution of Mechanical Systems Such as the Torsional-Vibration Damper. Trans. Am. Inst. Electr. Eng. 1931, 50, 1155–1158. [Google Scholar] [CrossRef]
- Berthet, R.; Petrosyan, A.; Roman, B. An analog experiment of the parametric instability. Am. J. Phys. 2002, 70, 744–749. [Google Scholar] [CrossRef] [Green Version]
- Jezierski, E. On electrical analogues of mechanical systems and their using in analysis of robot dynamics. In Robot Motion and Control; Springer: Berlin/Heidelberg, Germany, 2006; pp. 391–404. [Google Scholar]
- Kacar, S.; Wei, Z.; Akgul, A.; Aricioglu, B. A novel 4D chaotic system based on two degrees of freedom nonlinear mechanical system. Zeitschrift für Naturforschung A 2018, 73, 595–607. [Google Scholar] [CrossRef]
- López-Martínez, J.; Martínez, J.C.; García-Vallejo, D.; Alcayde, A.; Montoya, F.G. A new electromechanical analogy approach based on electrostatic coupling for vertical dynamic analysis of planar vehicle models. IEEE Access 2021, 9, 119492–119502. [Google Scholar] [CrossRef]
- Nishimori, Y.; Ooiso, H.; Mochizuki, S.; Fujiwara, N.; Tsuchiya, T.; Hashiguchi, G. A multiple degrees of freedom equivalent circuit for a comb-drive actuator. Jpn. J. Appl. Phys. 2009, 48, 124504. [Google Scholar] [CrossRef]
- Chang, F.; Wang, Z.; Tao, Y. Circuit simulation of two-degree-of-freedom unilateral impact dynamics system with gap. J. Phys. Conf. Ser. 2021, 1827, 012002. [Google Scholar] [CrossRef]
- Xu, Q.; Fan, W.; Luo, Y.; Wang, S.; Jiang, H. Nonlinear effect of forced harmonic oscillator subject to sliding friction and simulation by a simple nonlinear circuit. Am. J. Phys. 2019, 87, 116–124. [Google Scholar] [CrossRef]
- Awrejcewicz, J. Ordinary Differential Equations and Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Xu, Q.; Zhu, D. FPGA-based experimental validations of electrical activities in two adjacent FitzHugh–Nagumo neurons coupled by memristive electromagnetic induction. IETE Tech. Rev. 2021, 38, 563–577. [Google Scholar] [CrossRef]
- Savi, M.A.; Pereira-Pinto, F.H.I.; Viola, F.M.; de Paula, A.S.; Bernardini, D.; Litak, G.; Rega, G. Using 0–1 test to diagnose chaos on shape memory alloy dynamical systems. Chaos Solitons Fractals 2017, 103, 307–324. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seth, S.; Kudra, G.; Witkowski, K.; Awrejcewicz, J. Equivalent Electronic Circuit of a System of Oscillators Connected with Periodically Variable Stiffness. Appl. Sci. 2022, 12, 2024. https://doi.org/10.3390/app12042024
Seth S, Kudra G, Witkowski K, Awrejcewicz J. Equivalent Electronic Circuit of a System of Oscillators Connected with Periodically Variable Stiffness. Applied Sciences. 2022; 12(4):2024. https://doi.org/10.3390/app12042024
Chicago/Turabian StyleSeth, Soumyajit, Grzegorz Kudra, Krzysztof Witkowski, and Jan Awrejcewicz. 2022. "Equivalent Electronic Circuit of a System of Oscillators Connected with Periodically Variable Stiffness" Applied Sciences 12, no. 4: 2024. https://doi.org/10.3390/app12042024
APA StyleSeth, S., Kudra, G., Witkowski, K., & Awrejcewicz, J. (2022). Equivalent Electronic Circuit of a System of Oscillators Connected with Periodically Variable Stiffness. Applied Sciences, 12(4), 2024. https://doi.org/10.3390/app12042024






