TorchEsegeta: Framework for Interpretability and Explainability of Image-Based Deep Learning Models
Abstract
:1. Introduction
Contributions
2. Methods
2.1. Incorporated Libraries
2.2. Implemented Interpretability Techniques
2.2.1. Model Attribution Techniques
- Feature-Based Techniques:Methods under this group bring into play input and/or output feature space to compute local or global model attributions.
- (a)
- Feature Permutation—This is a perturbation-based technique [14,15] in which the value of an input or group of inputs is changed, utilising the random permutation of values in a batch of inputs and calculating its corresponding change in output. Hence, meaningful feature attributions are calculated only when a batch of inputs is provided.
- (b)
- Shapley Value Sampling—The proposed method defines an input baseline to which all possible permutations of the input values are added one at a time, and the corresponding output values and hence each feature attribution is calculated. For permutation O, given a player set N, the set of all possible permutations , and the predecessors of player i , the Shapley value is given byAs all possible permutations are considered, this technique is computationally expensive, and this can be overcome by sampling the permutations and averaging their marginal contributions instead of considering all possible permutations such as the ApproShapley sampling technique [16].
- (c)
- Feature Ablation—This method works by replacing an input, or a group of inputs with another value defined by a range or reference value, and the feature attribution of the input or group of inputs such as a segment are computed. This method works based on perturbation.
- (d)
- Occlusion—Similar to the Feature Ablation method, Occlusion [17] works as a perturbation-based approach wherein the continuous inputs in a rectangular area are replaced by a value defined by a range or a reference value. Using this approach, the change in the corresponding outputs is calculated in order to find the attribution of the feature.
- (e)
- RISE Randomised Input Sampling for Explanation of Black-box Models—It generates an importance map indicating how salient each pixel is for the model’s prediction [18]. RISE works on black-box models, since it does not consider gradients while making the computations. In this approach, the model’s outputs are tested by masking the inputs randomly and calculating the importance of the features.
- (f)
- Extremal Perturbations—They are regions of an image that maximally affect the activation of a certain neuron in a neural network for a given area in an image [9]. Extremal Perturbations lead to the largest change in the prediction of the deep neural network when compared to other perturbations defined byfor the chosen area a. The paper also introduces area loss to enforce the restrictions while choosing the perturbations.
- (g)
- Score-Weighted Class Activation (Score CAM)—It is a gradient-independent interpretability technique based on class activation mapping [19]. Activation maps are first extracted, and each activation then works as a mask on the original image, and its forward-passing score on the target class is obtained. Finally, the result can be generated by the linear combination of score-based weights and activation maps (https://github.com/haofanwang/Score-CAM). Given a convolutional layer l, class c, number of channels k, and activations A:
Gradient-Based Techniques
- (a)
- Saliency—It was initially designed for visualising the image classification done by convolutional networks and the saliency map for a specific image [20]. It is used to check the influence of each pixel of the input image in assigning a final class score to the image I using the linear score model for weight w and bias b.
- (b)
- Guided Backpropagation—In this approach, during the backpropagation, the gradients of the outputs are computed with respect to the inputs [21]. The RELU activation function is applied to the input gradients, and direct backpropagation is performed, ensuring that the backpropagation of non-negative gradients does not occur.
- (c)
- Deconvolution—This approach is similar to the guided backpropagation approach wherein it applies RELU to the output gradients instead of the input gradients and performs direct backpropagation [17]. Similarly, RELU backpropagation is overridden to allow only non-negative gradients to be backpropagated.
- (d)
- Input X Gradient—It extends the saliency approach such that the contribution of each input to the final prediction is checked by multiplying the gradients of outputs and their corresponding inputs in a setting of a system of linear equations AX = B where A is the gradient and B is the calculated final contribution of input X [22].
- (e)
- Integrated Gradients—This technique [23] calculates the path integral of the gradients along the straight line path from the baseline to the input x. It satisfies the axioms of Completeness i.e., the attributions must account for the difference in output for the baseline and input x, Sensitivity—i.e., a non-zero attribution must be provided even to inputs that flatten the prediction function where the input differs from the baseline—and Implementation Invariance of gradients—i.e., two functionally equivalent networks must have identical feature attributions. It requires no instrumentation of the deep neural network for its application. All the gradients along the straight line path from to x are integrated along the ith dimension as:
- (f)
- Grad Times Image—In this technique [22], the gradients are multiplied with the image itself. It is a predecessor of the DeepLift method, as the activation of each neuron for a given input is compared to its reference activation, and contribution scores are assigned according to the difference for each neuron.
- (g)
- DeepLift—It is a method [24] that considers not only the positive but also the negative contribution scores of each neuron based on its activation concerning its reference activation. The difference in the output of the activation function of the neuron t under observation is calculated based on the difference in input with respect to a reference input. Contribution scores for each of the preceding neurons that influence t are assigned , which sums up to the difference in t’s activation:
- (h)
- DeepLiftShap—This method extends the DeepLift method and computes the SHAP values on an equivalent, linear approximation of the model [13]. It assumes the independence of input features. For model f, the effective linearization from SHAP for each component is computed as:
- (i)
- GradientShap—This technique also assumes the independence of the inputs and computes the game-theoretic SHAP values of the gradients on the linear approximation of the model [13]. Gaussian noise is added to randomly selected points, and the gradients of their corresponding outputs are computed.
- (j)
- Guided GradCAM—The Gradient-Weighted Class Activation Mapping approach provides a means to visualise the regions of an image input that are predominant in influencing the predictions made by the model. This is done by visualising the gradient information pertaining to a specific class in any layer of the user’s choice. It can be applied to any CNN-based model architecture. The guided backpropagation and GradCAM approaches are combined by computing the element-wise product of guided backpropagation attributions with upsampled GradCAM attributions [25].
- (k)
- Grad-Cam++—Generalised Gradient-Based Visual Explanations for Deep Convolutional Networks is a method [26] that claims to provide better predictions than the Grad-CAM and other state-of-the-art approaches for object localisation and explaining occurrences of multiple object instances in a single image. This technique uses a weighted combination of the positive partial derivatives of the last convolutional layer’s feature maps concerning a specific class score as weights to generate a visual explanation for the corresponding class label. The importance of an activation map over class score is given byGrad-CAM++ provides human-interpretable visual explanations for a given CNN architecture across multiple tasks, including classification, image caption generation, and 3D action recognition.
- (l)
- Vanilla Backpropagation and Layer Visualisation—It is the standard gradient backpropagation technique through the deep neural network wherein the gradients are visualised at different layers and what is being learnt by the model is observed, given a random input image.
- (m)
- Smooth Grad—In this method [19,27], random Gaussian noise is added to the given input image, and the corresponding gradients are computed to find the average values over n image samplesVanilla and guided backpropagation techniques can be used to calculate the gradients.
2.2.2. Layer Attribution Techniques
- Inverted Representation—The aim of this technique is to generate the given input image after a number of n target layers. An inverse of the given input image representation is computed [28] in order to find an image whose representation best matches the input image while minimising the given loss l such that
- Layer Activation with Guided Backpropagation—This method [21] is quite similar to guided backpropagation, but instead of guiding the signal from the last layer and a specific target, it guides the signal from a specific layer and filter. The guided backpropagation method adds an additional guidance signal from the higher layers to the usual backpropagation.
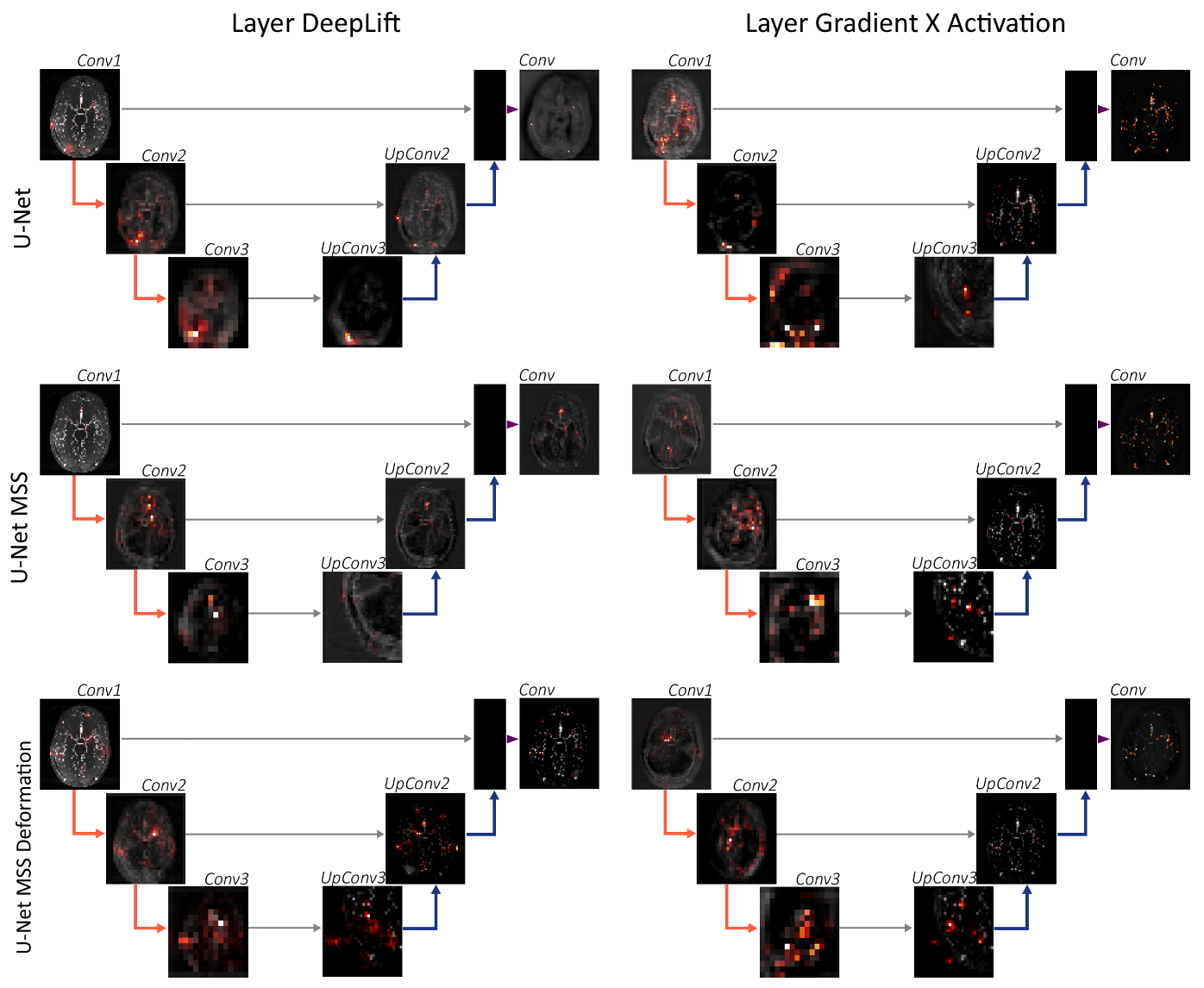
- Layer DeepLift—This is the DeepLift method as mentioned in the model attribution techniques [13] but applied with respect to the particular hidden layer in question.
- Layer DeepLiftShap—This method is similar to the DeepLIFT SHAP technique mentioned in the model attribution techniques [13], which was applied for a particular layer. The original distribution of baselines is taken, the attribution for each input–baseline pair is calculated using the Layer DeepLIFT method, and the resulting attributions are averages per input example. Assuming model linearity, .
- Layer GradCam—The GradCam attribution for a given layer is provided by this method [25]. The target output’s gradients are computed concerning the particularly given layer. The resultant gradients are averaged for each output channel (dimension 2 of output). Then, the average gradient for each channel is multiplied by the layer activations. Then, the results are added over all the channels. For the class feature weights w, global average pooling is performed over the feature maps A such that
- Layer GradientShap—This is analogous with the GradientSHAP [13] method as mentioned in the model attribution techniques but applied for a particular layer. Layer GradientSHAP adds Gaussian noise to each input sample multiple times, wherein a random point along the path between the baseline and input is selected, and the gradient of the output with respect to the identified layer is computed. The final SHAP values approximate the expected value of gradients ∗ (layer activation of inputs − layer activation of baselines).
- Layer Conductance—This method [29] provides the conductance of all neurons of a particular hidden layer. Conductance of a particular hidden unit refers to the flow of Integrated Gradients attribution through this hidden unit. The main idea behind using this method is to decompose the computation of the Integrated Gradients via the chain rule. One property that this method of conductance satisfies is that of completeness. Completeness means that the conductances of a particular layer add up to the prediction difference of F(x) – F() for input x and baseline input . Other properties that are satisfied by this method are those of Linearity and insensitivity.
- Internal Influence—This method calculates the contribution of a layer to the final prediction of the model by integrating the gradients with respect to the particular layer under observation. The internal representation is influenced by an element j as defined by [30] such thatwherein for the slice of the network represented by s as a function of tuple g,h. It is similar to the integrated gradients approach where instead of the input, the gradients are integrated with respect to the layer.
- Contrastive Excitation Backpropagation/Excitation Backpropagation—This approach is used to generate and visualise task-specific attention maps. The Excitation Backprop method as proposed by [31] is to pass along top–down signals downwards in the network hierarchy via a probabilistic Winner-Take-All process wherein the most relevant neurons in the network are identified for a given top–down signal. Both top–down and bottom–up information is integrated to compute the winning probability of each neuron as defined byfor input x and weight matrix w. The contrastive excitation backpropagation is used to make the top–down attention maps more discriminative.
- Layer Activation—It computes the activation of a particular layer for a particular input image [32]. It helps to understand how a given layer reacts to an input image. One can get an excellent idea of at what part or features of the image a particular layer looks.
- Linear Approximator—This is a technique to overcome inconsistencies of post hoc model interpretation; linear approximator combines a piecewise linear component and a nonlinear component [9,33]. The piecewise linear component describes the explicit feature contributions by piecewise linear approximation that increases the expressiveness of the deep neural network. The nonlinear component uses a multi-layer perceptron to capture feature interactions and implicit nonlinearity, which in turn increases the prediction performance. Here, the interpretability is obtained once the model is learned in the form of feature shapes and has high accuracy.
- Layer Gradient X Activation—This method [34] computes the element-wise product of a given layer’s gradient and activation. It is a combination of the gradient and activation methods of layer attribution. The output attributions are returned as a tuple if the layer input/output contains multiple tensors or a single tensor is returned.
2.3. Implemented Explainability Techniques
2.3.1. DeepDream
2.3.2. LIME
2.3.3. SHAP
2.3.4. Lucent
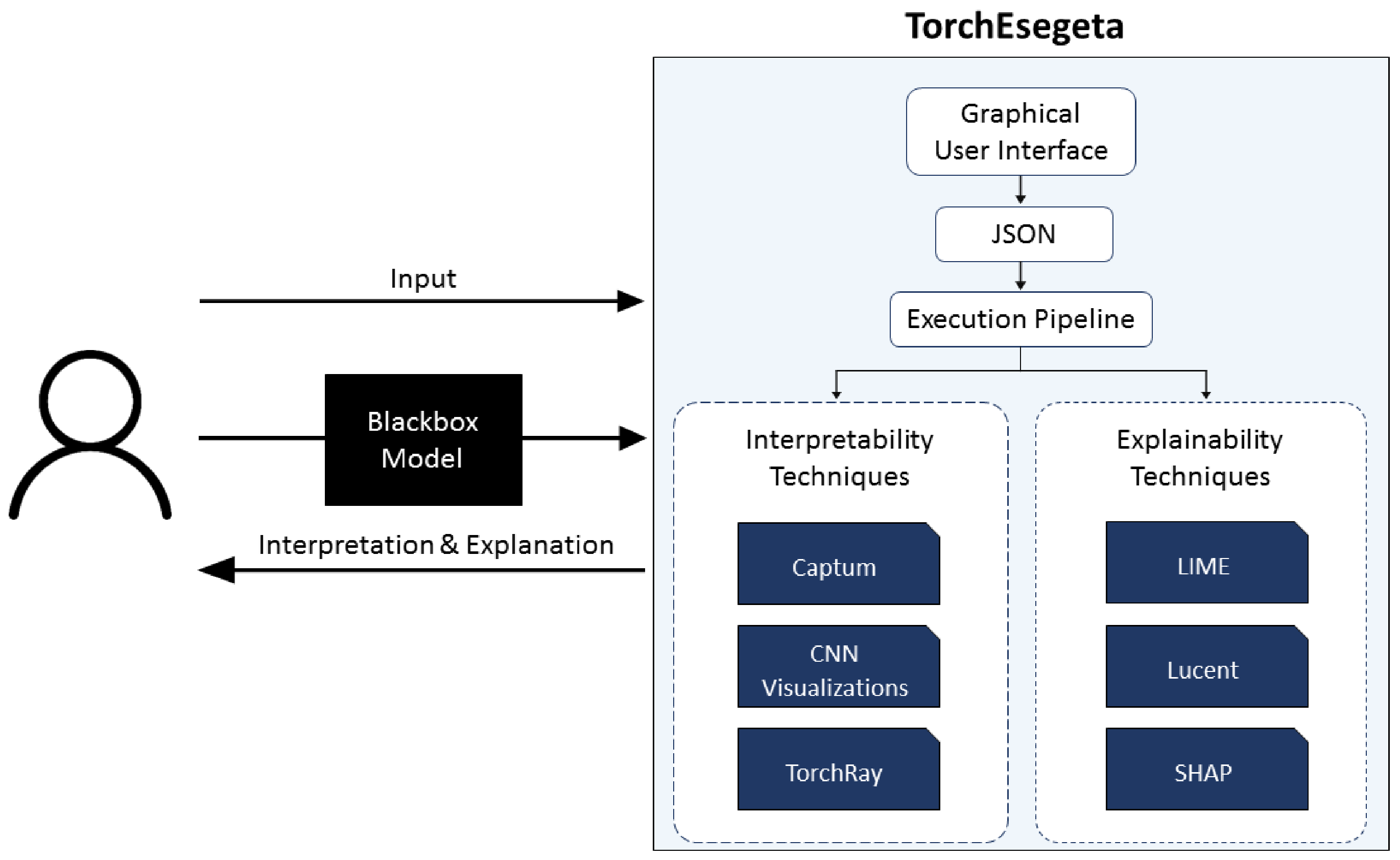
2.4. The Pipeline: TorchEsegeta
2.5. Features of TorchEsegeta
2.5.1. Parallel Execution
2.5.2. Patch-Based Execution
2.5.3. Automatic Mixed Precision
2.5.4. Wrapper for Segmentation Models
- Pixel-wise multi-class classification;
- Threshold-based pixel classification.
Pixel-Wise Multi-Class Classification
Threshold-Based Pixel Classification
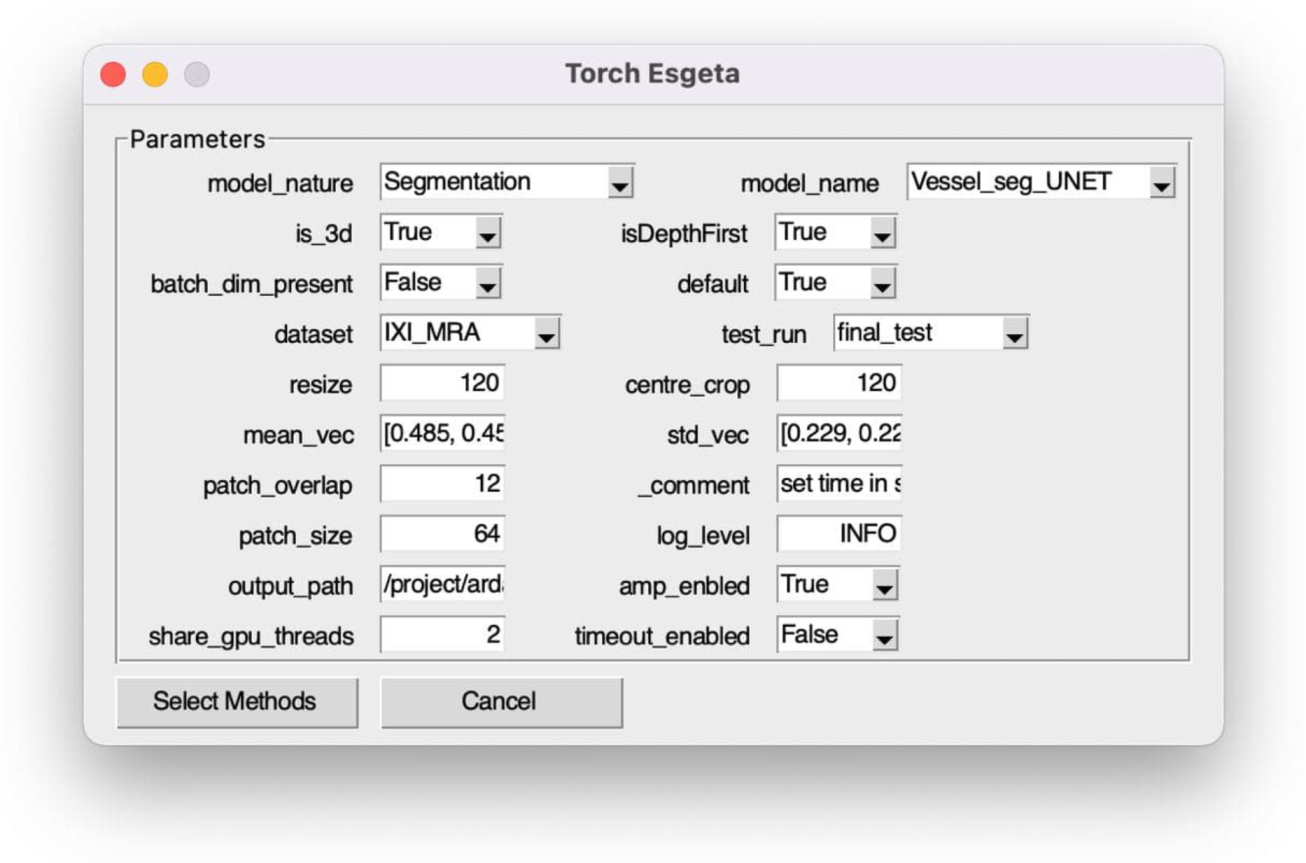
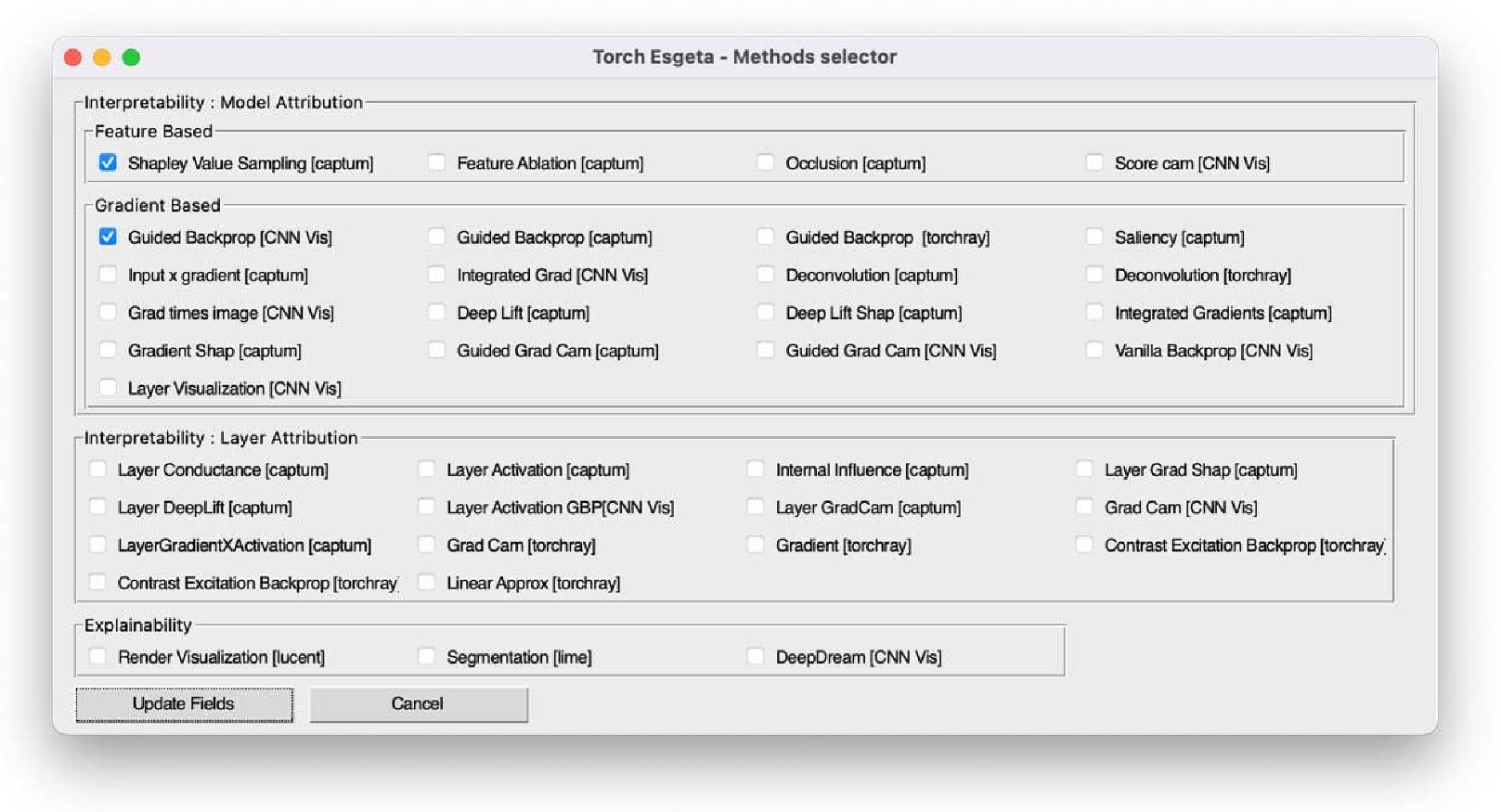
2.5.5. Graphical User Interface
2.6. Evaluation Methods
2.6.1. Qualitative Evaluation
2.6.2. Quantitative Evaluation
3. Results
3.1. Models
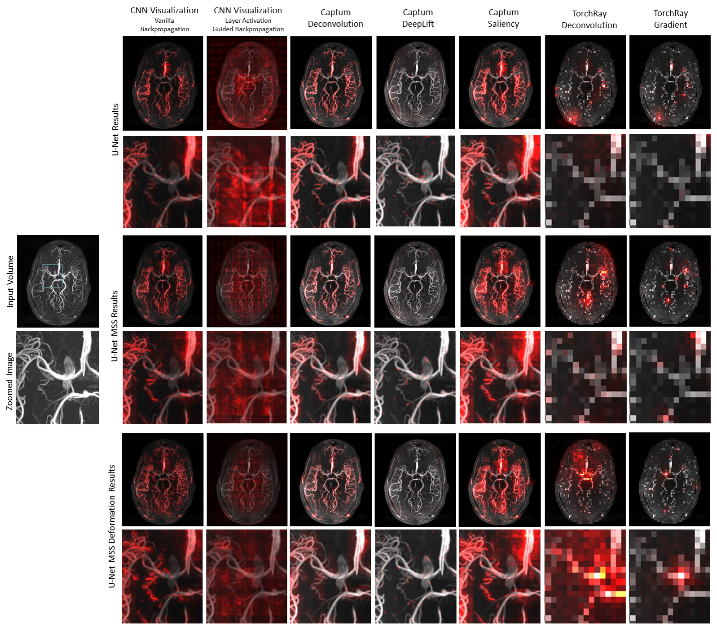
3.2. Use Case Experiment
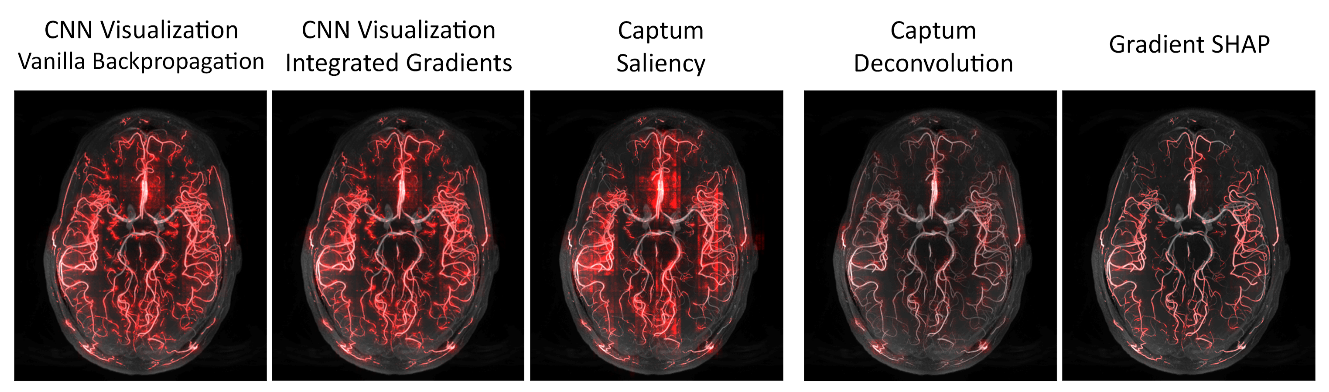
3.3. Notable Observations
3.4. Evaluation
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marcinkevičs, R.; Vogt, J.E. Interpretability and explainability: A machine learning zoo mini-tour. arXiv 2020, arXiv:2012.01805. [Google Scholar]
- Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE Smartworld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (smartworld/SCALCOM/UIC/ATC/CBDcom/IOP/SCI), San Francisco, CA, USA, 4–8 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Emmert-Streib, F.; Yli-Harja, O.; Dehmer, M. Explainable artificial intelligence and machine learning: A reality rooted perspective. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1368. [Google Scholar] [CrossRef]
- Belle, V.; Papantonis, I. Principles and practice of explainable machine learning. arXiv 2020, arXiv:2009.11698. [Google Scholar] [CrossRef] [PubMed]
- Dubost, F.; Bortsova, G.; Adams, H.; Ikram, A.; Niessen, W.J.; Vernooij, M.; De Bruijne, M. Gp-unet: Lesion detection from weak labels with a 3d regression network. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2017; pp. 214–221. [Google Scholar]
- Gu, R.; Wang, G.; Song, T.; Huang, R.; Aertsen, M.; Deprest, J.; Ourselin, S.; Vercauteren, T.; Zhang, S. CA-Net: Comprehensive attention convolutional neural networks for explainable medical image segmentation. IEEE Trans. Med. Imaging 2020, 40, 699–711. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Choo, J.; Liu, S. Visual analytics for explainable deep learning. IEEE Comput. Graph. Appl. 2018, 38, 84–92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fong, R.; Patrick, M.; Vedaldi, A. Understanding deep networks via extremal perturbations and smooth masks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2950–2958. [Google Scholar]
- Chatterjee, S.; Saad, F.; Sarasaen, C.; Ghosh, S.; Khatun, R.; Radeva, P.; Rose, G.; Stober, S.; Speck, O.; Nürnberger, A. Exploration of interpretability techniques for deep covid-19 classification using chest x-ray images. arXiv 2020, arXiv:2006.02570. [Google Scholar]
- Ozbulak, U. PyTorch CNN Visualizations. 2019. Available online: https://github.com/utkuozbulak/pytorch-cnn-visualizations (accessed on 10 July 2021).
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Müller, K.R. Toward interpretable machine learning: Transparent deep neural networks and beyond. arXiv 2020, arXiv:2003.07631. [Google Scholar]
- Lundberg, S.; Lee, S.I. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Castro, J.; Gómez, D.; Tejada, J. Polynomial calculation of the Shapley value based on sampling. Comput. Oper. Res. 2009, 36, 1726–1730. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Petsiuk, V.; Das, A.; Saenko, K. RISE: Randomized Input Sampling for Explanation of Black-Box Models. arXiv 2018, arXiv:1806.07421. [Google Scholar]
- Wang, H.; Wang, Z.; Du, M.; Yang, F.; Zhang, Z.; Ding, S.; Mardziel, P.; Hu, X. Score-CAM: Score-weighted visual explanations for convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 24–25. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Shcherbina, A.; Kundaje, A. Not just a black box: Learning important features through propagating activation differences. arXiv 2016, arXiv:1605.01713. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3145–3153. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-cam++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 839–847. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Mahendran, A.; Vedaldi, A. Understanding Deep Image Representations by Inverting Them. arXiv 2014, arXiv:c1412.0035. [Google Scholar]
- Dhamdhere, K.; Sundararajan, M.; Yan, Q. How important is a neuron? arXiv 2018, arXiv:1805.12233. [Google Scholar]
- Leino, K.; Sen, S.; Datta, A.; Fredrikson, M.; Li, L. Influence-directed explanations for deep convolutional networks. In Proceedings of the 2018 IEEE International Test Conference (ITC), Phoenix, AZ, USA, 29 October–1 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Zhang, J.; Bargal, S.A.; Lin, Z.; Brandt, J.; Shen, X.; Sclaroff, S. Top-down neural attention by excitation backprop. Int. J. Comput. Vis. 2018, 126, 1084–1102. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Brock, A.; Simonyan, K.; Le, Q.V. Evolving normalization-activation layers. arXiv 2020, arXiv:2004.02967. [Google Scholar]
- Guo, M.; Zhang, Q.; Liao, X.; Zeng, D.D. An Interpretable Neural Network Model through Piecewise Linear Approximation. arXiv 2020, arXiv:2001.07119. [Google Scholar]
- Ancona, M.; Ceolini, E.; Öztireli, C.; Gross, M. Towards better understanding of gradient-based attribution methods for deep neural networks. arXiv 2017, arXiv:1711.06104. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Micikevicius, P.; Narang, S.; Alben, J.; Diamos, G.; Elsen, E.; Garcia, D.; Ginsburg, B.; Houston, M.; Kuchaiev, O.; Venkatesh, G.; et al. Mixed precision training. arXiv 2017, arXiv:1710.03740. [Google Scholar]
- Adebayo, J.; Gilmer, J.; Muelly, M.; Goodfellow, I.; Hardt, M.; Kim, B. Sanity checks for saliency maps. arXiv 2018, arXiv:1810.03292. [Google Scholar]
- Yeh, C.K.; Hsieh, C.Y.; Suggala, A.S.; Inouye, D.I.; Ravikumar, P. On the (in) fidelity and sensitivity for explanations. arXiv 2019, arXiv:1901.09392. [Google Scholar]
- Chatterjee, S.; Prabhu, K.; Pattadkal, M.; Bortsova, G.; Sarasaen, C.; Dubost, F.; Mattern, H.; de Bruijne, M.; Speck, O.; Nürnberger, A. DS6, Deformation-aware Semi-supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data. arXiv 2020, arXiv:2006.10802. [Google Scholar]



| U-Net | U-NetMSS | U-NetMSS_Deform | |
|---|---|---|---|
| Guided Backprop | 5.87e−7 | 2.08e−17 | 2.59e−18 |
| Deconvolution | 3.20e−16 | 2.62e−16 | 1.48e−16 |
| Saliency | 1.95e−15 | 1.54e−15 | 1.23e−16 |
| U-Net | U-NetMSS | U-NetMSS_Deform | |
|---|---|---|---|
| Guided Backprop | 1.156 | 0.917 | 0.831 |
| Deconvolution | 1.210 | 1.188 | 1.140 |
| Saliency | 1.171 | 1.197 | 1.153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, S.; Das, A.; Mandal, C.; Mukhopadhyay, B.; Vipinraj, M.; Shukla, A.; Nagaraja Rao, R.; Sarasaen, C.; Speck, O.; Nürnberger, A. TorchEsegeta: Framework for Interpretability and Explainability of Image-Based Deep Learning Models. Appl. Sci. 2022, 12, 1834. https://doi.org/10.3390/app12041834
Chatterjee S, Das A, Mandal C, Mukhopadhyay B, Vipinraj M, Shukla A, Nagaraja Rao R, Sarasaen C, Speck O, Nürnberger A. TorchEsegeta: Framework for Interpretability and Explainability of Image-Based Deep Learning Models. Applied Sciences. 2022; 12(4):1834. https://doi.org/10.3390/app12041834
Chicago/Turabian StyleChatterjee, Soumick, Arnab Das, Chirag Mandal, Budhaditya Mukhopadhyay, Manish Vipinraj, Aniruddh Shukla, Rajatha Nagaraja Rao, Chompunuch Sarasaen, Oliver Speck, and Andreas Nürnberger. 2022. "TorchEsegeta: Framework for Interpretability and Explainability of Image-Based Deep Learning Models" Applied Sciences 12, no. 4: 1834. https://doi.org/10.3390/app12041834
APA StyleChatterjee, S., Das, A., Mandal, C., Mukhopadhyay, B., Vipinraj, M., Shukla, A., Nagaraja Rao, R., Sarasaen, C., Speck, O., & Nürnberger, A. (2022). TorchEsegeta: Framework for Interpretability and Explainability of Image-Based Deep Learning Models. Applied Sciences, 12(4), 1834. https://doi.org/10.3390/app12041834









