Unsteady-State Creep of an Asphalt Concrete
Abstract
:1. Introduction
2. Materials and Methods
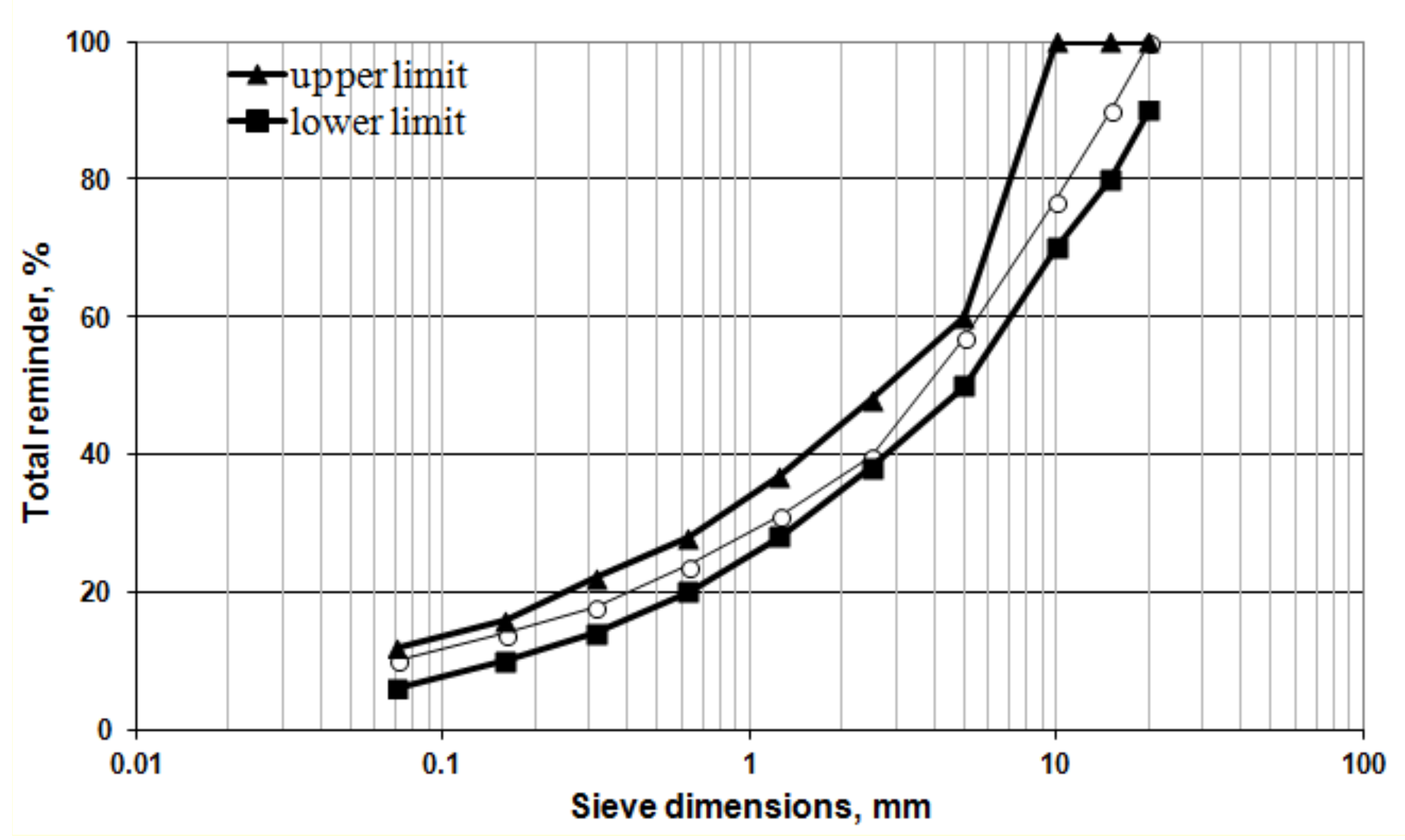
2.1. Asphalt Concrete
2.2. Bitumen
2.3. Creep Test
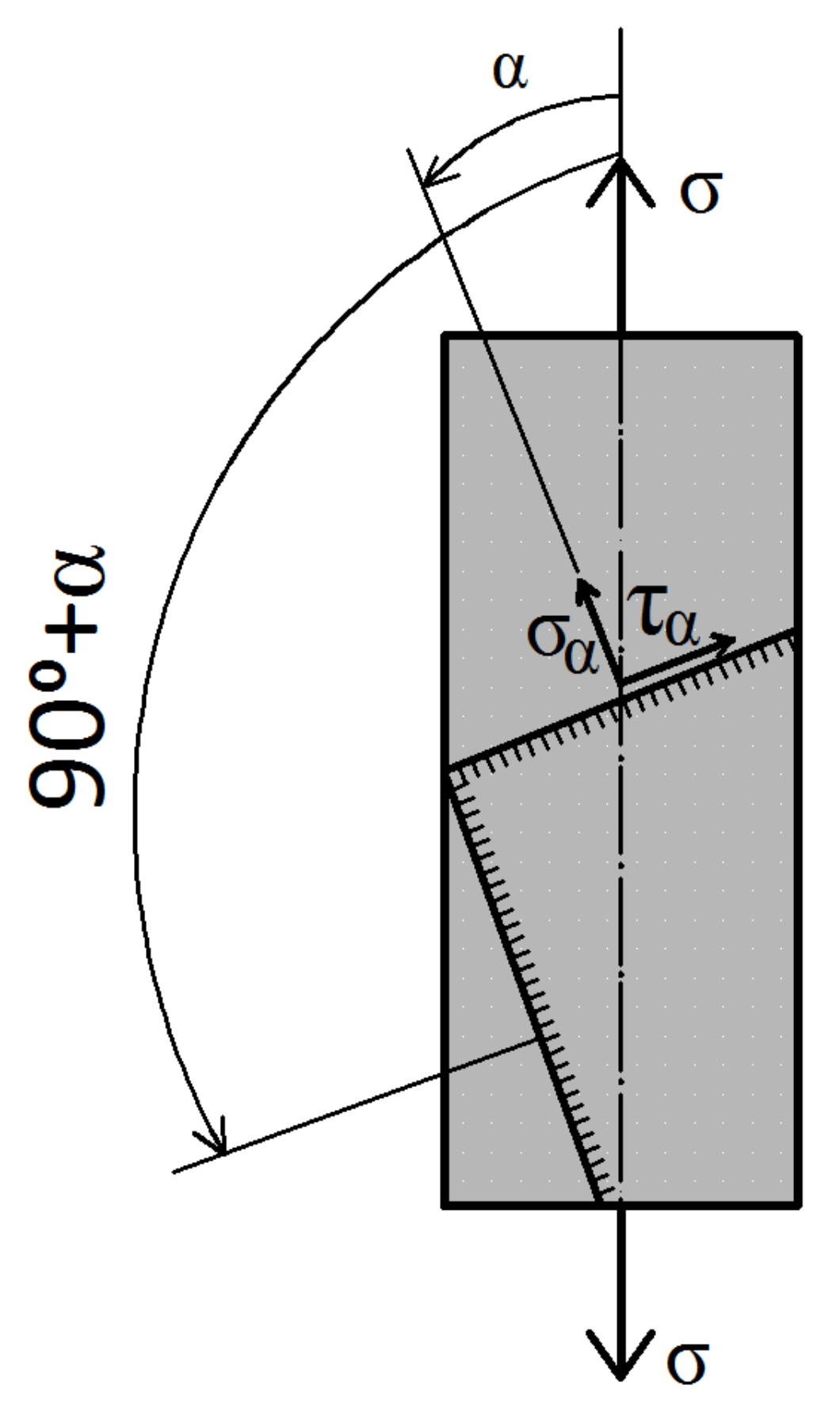
3. Theory
3.1. Integral Equation
3.2. Creep Kernel
3.3. Determination of Parameters ε0, α, δ
4. Results and Discussion
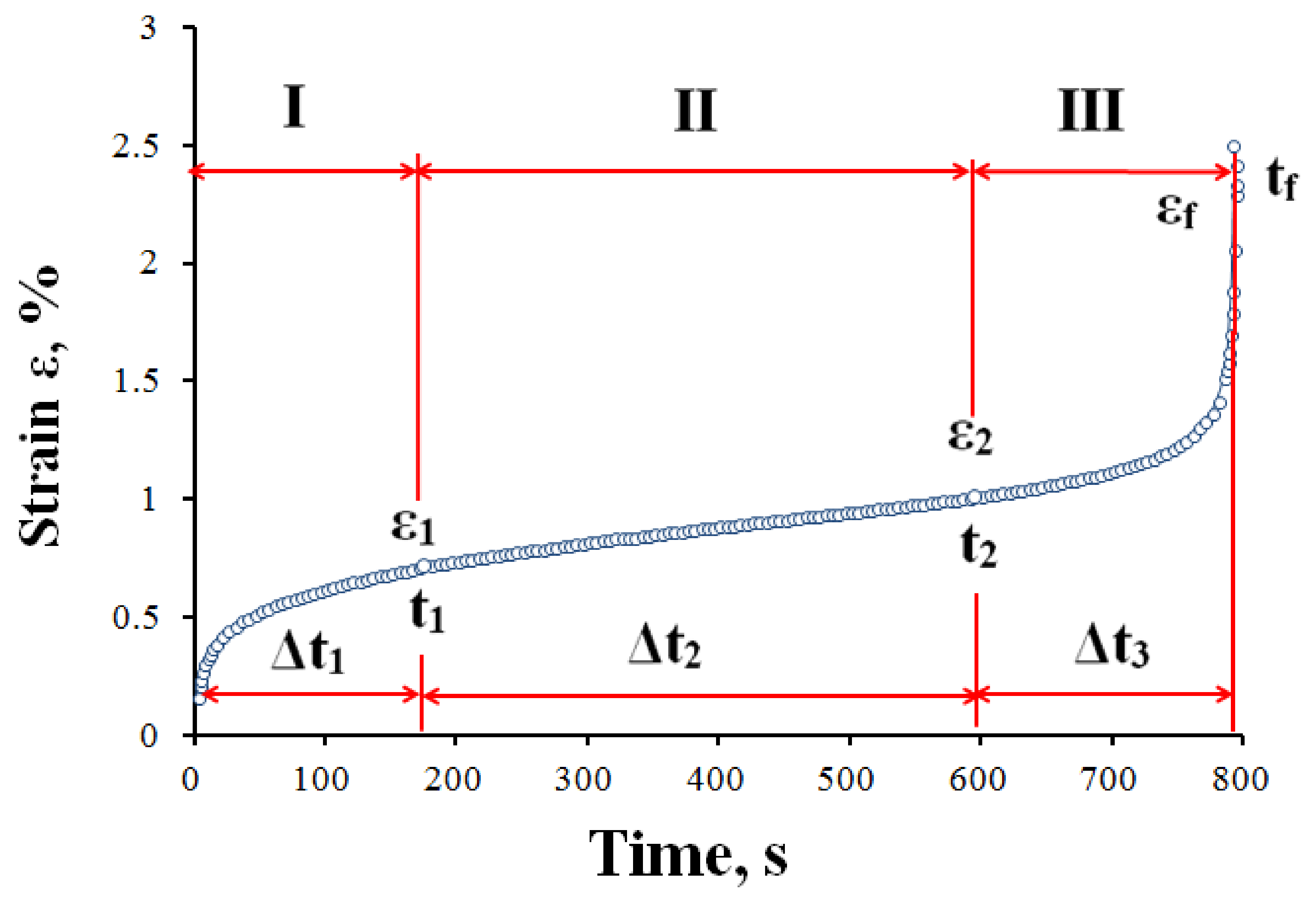
4.1. Creep Curve Characteristics
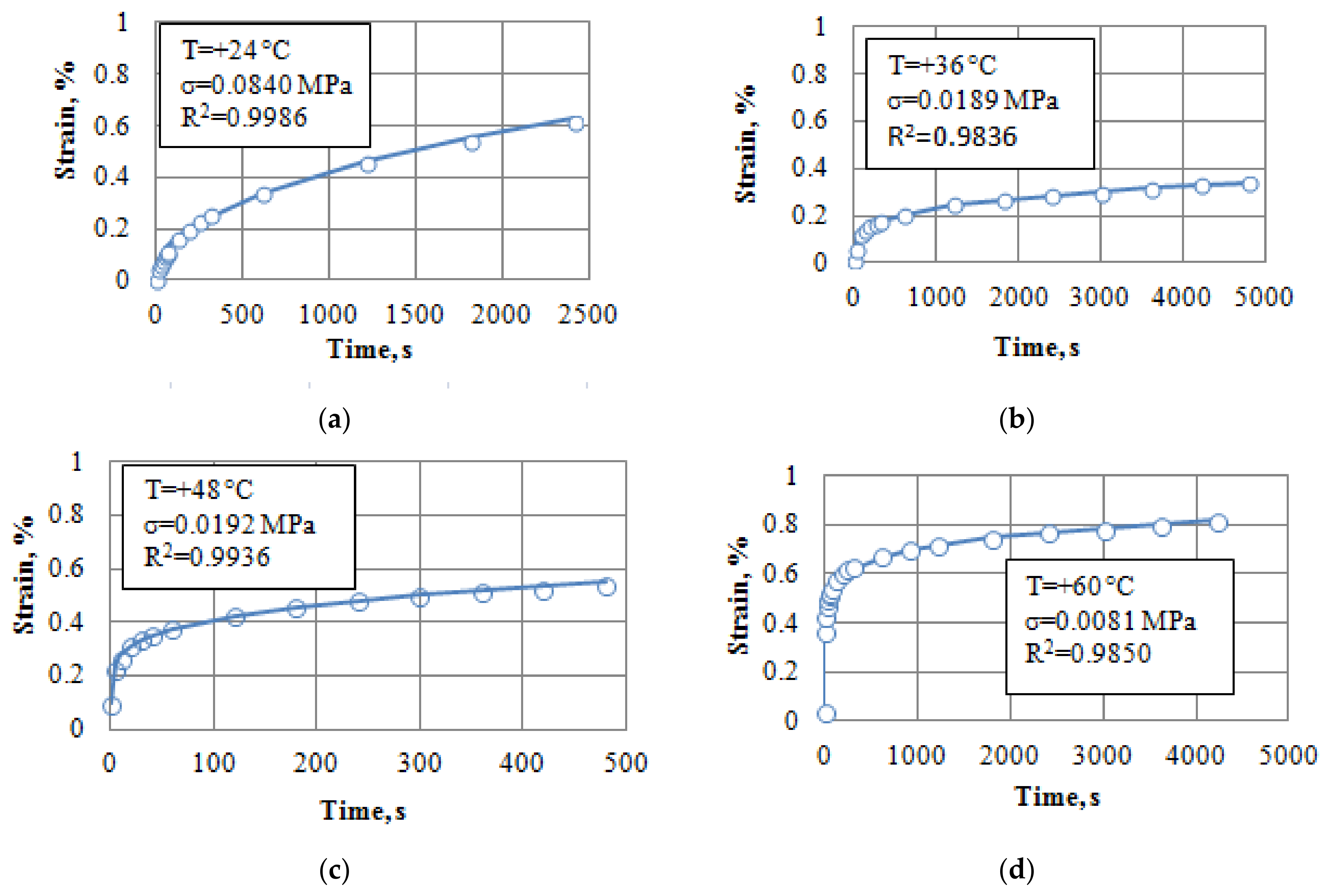
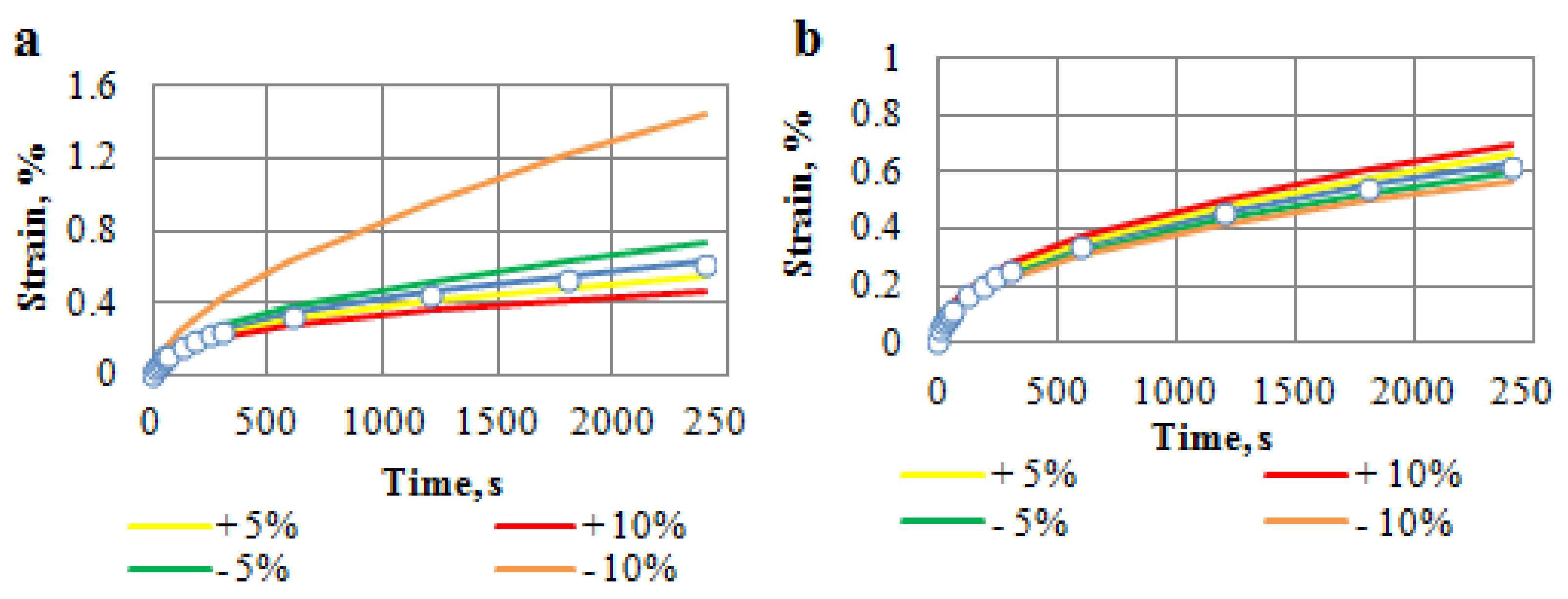
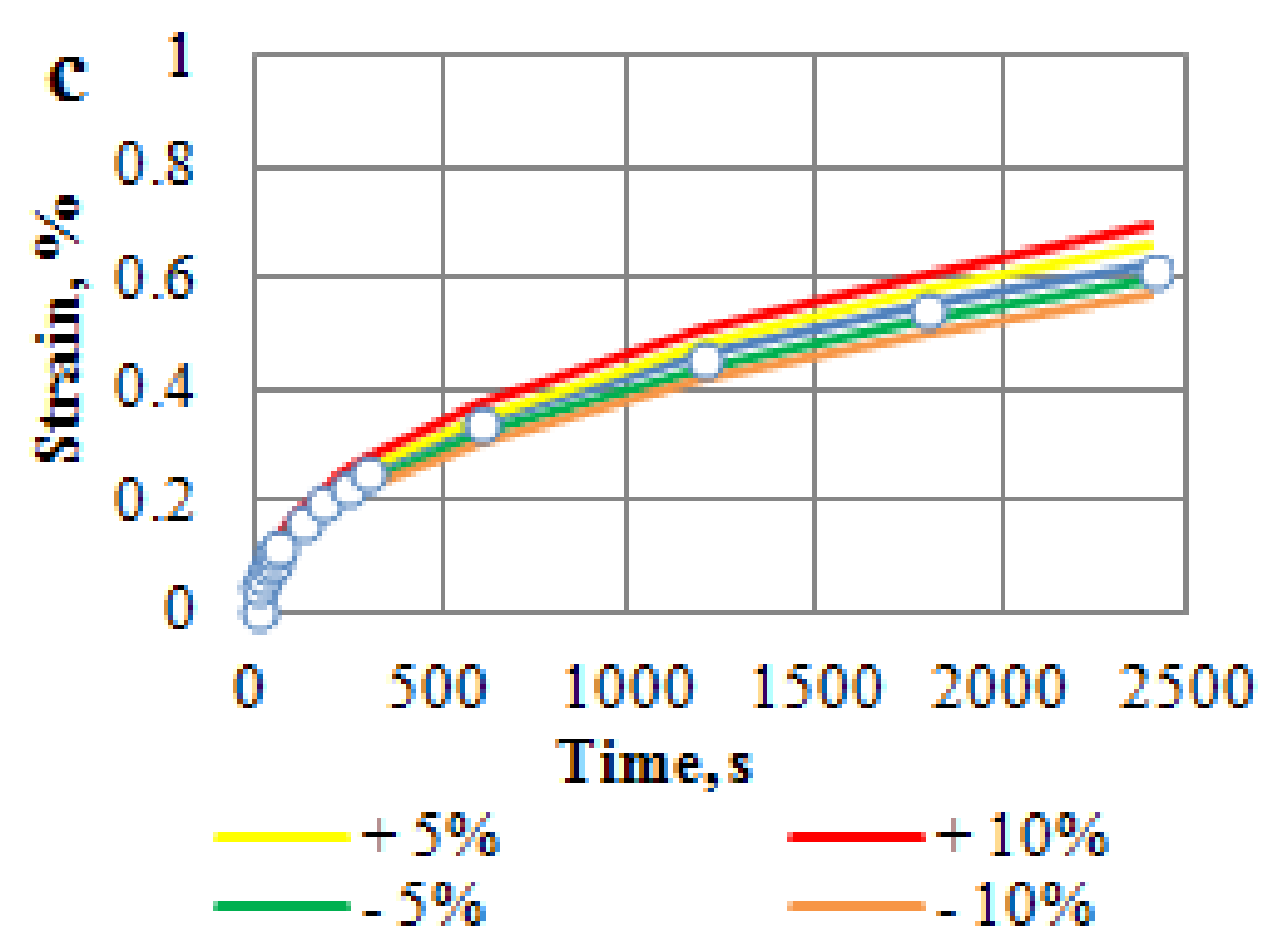
4.2. Unsteady-State Creep Approximation
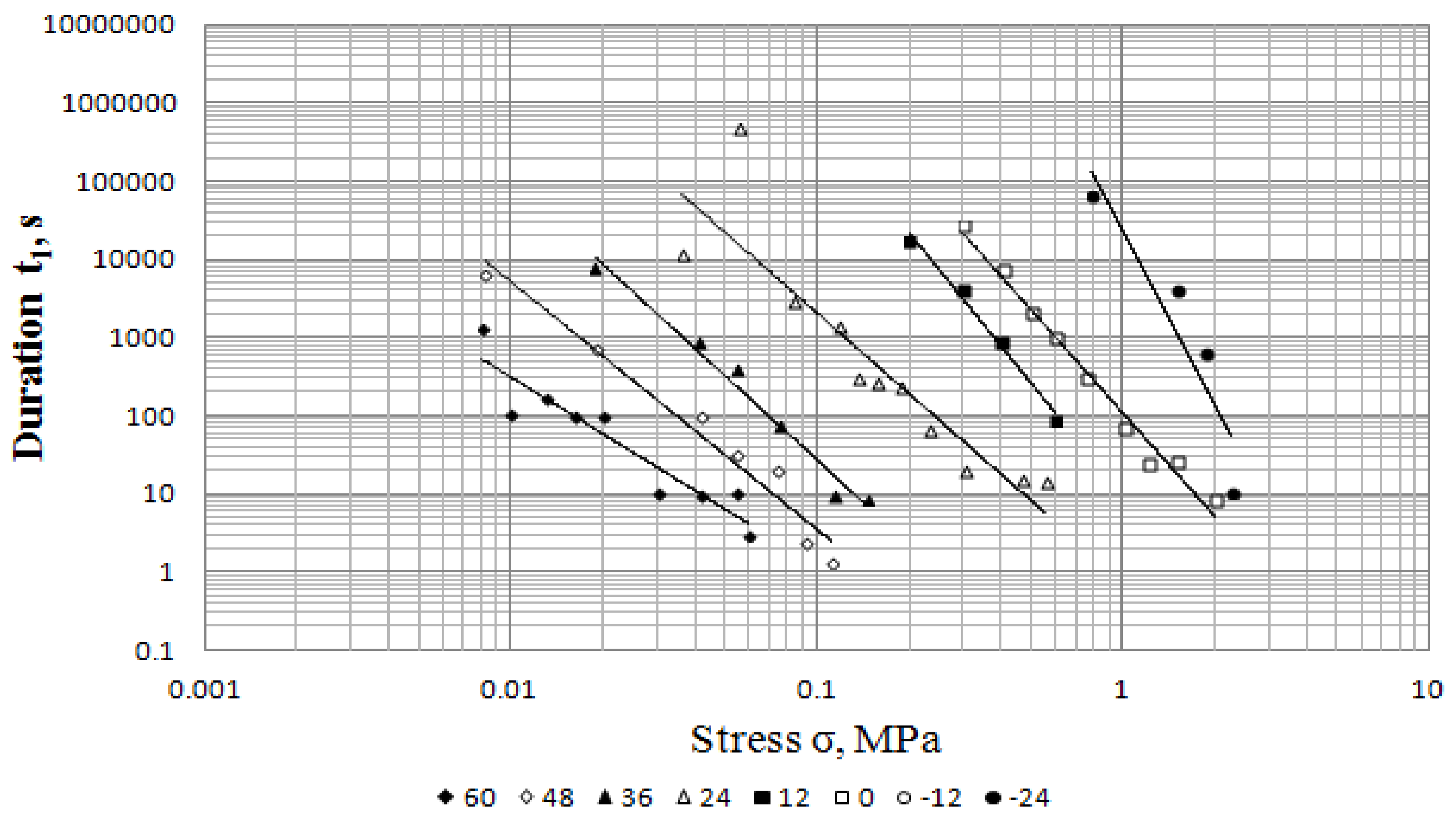
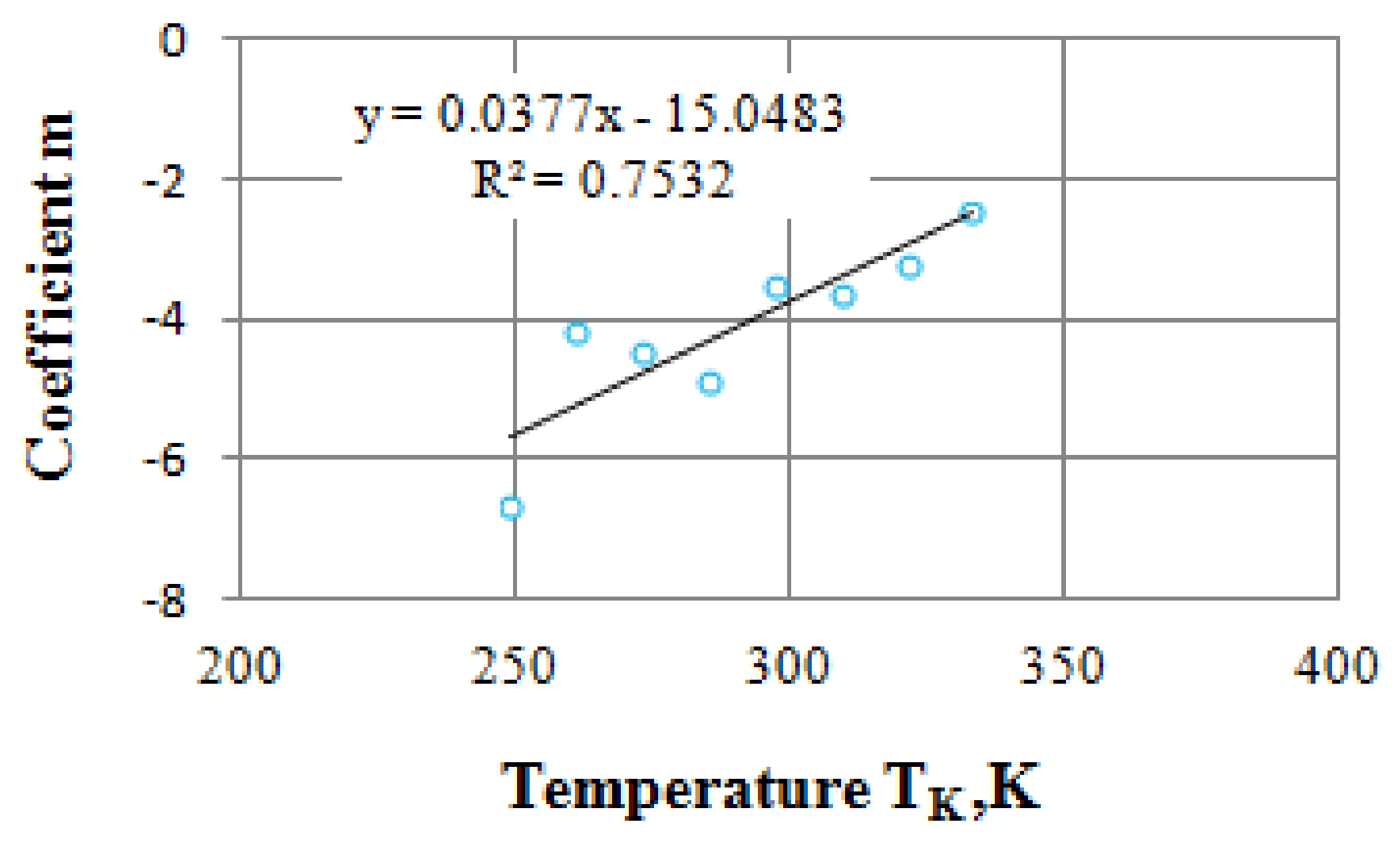
4.3. Unsteady-State Creep Duration
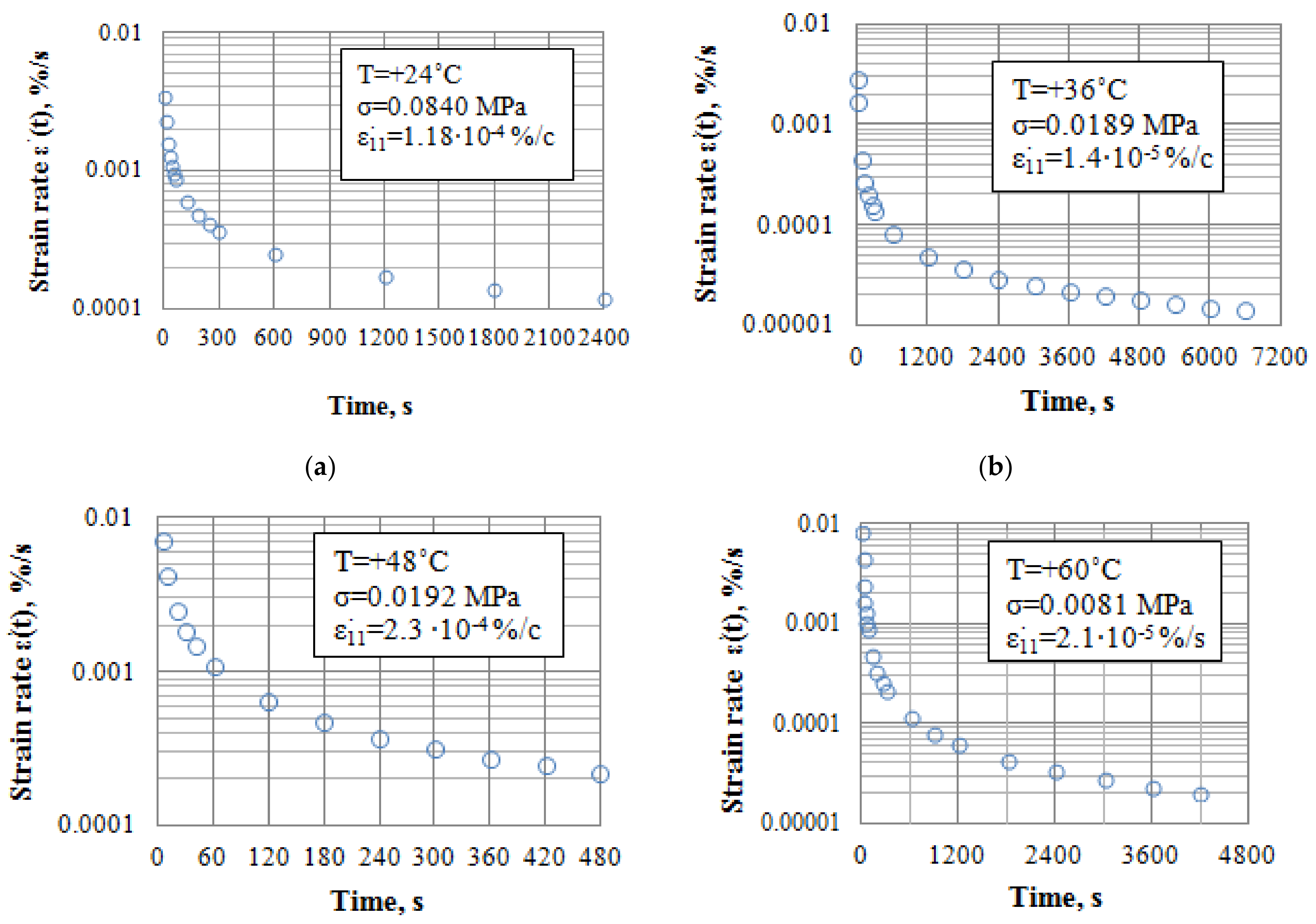
4.4. Unsteady-State Creep Rate
4.5. Steady-State Creep Rate
4.6. Viscosity
5. Conclusions
- It should be well understood that there are characteristic time stages within which an asphalt concrete is deformed in different ways with the effect of a constant load at operating temperatures for road asphalt concrete; the first stage, called “unsteady-state creep”, has the following features: strain increases in time nonlinearly to the time moment t1 (t1 is the unsteady-state creep duration), which also depends on a stress and a temperature; strain rate decreases nonlinearly over time.
- A simple power function can be used to satisfactorily describe the strain, the strain rate and the steady-state creep duration of an asphalt concrete.
- By analogy with the flow of viscous liquid, the creep process of viscoelastic materials, including an asphalt concrete, can be characterized by a fundamental physical indicator-viscosity; using the classical works of Newton and Trouton, the example of an asphalt concrete shows the possibility for obtaining a mechanical (rheological) model of the unsteady-state and steady-state creep of viscoelastic materials.
- The resulting rheological model can be connected to the principles of molecular physics, thermodynamics and quantum physics for a more in-depth explanation of viscosity and plastic deformation of asphalt concrete and other materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MS-4. The Asphalt Handbook, 7th ed.; Asphalt Institute: Lexington, KY, USA, 2007. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design, 2nd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Papagiannakis, A.T.; Masad, E.A. Pavement Design and Materials; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cristensen, R.M. Theory of Viscoelasticity: An Introduction; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Tschoegl, N.N. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Park, S.W.; Kim, Y.R. Fitting Prony-Series viscoelastic models with power-low presmoothing. J. Mater. Civ. Eng. 2001, 13, 26–32. [Google Scholar] [CrossRef]
- Gibson, N.H.; Schwartz, C.W.; Schapery, R.A.; Witczak, M.W. Viscoelastic, viscoplastic and damage modeling of asphalt concrete in unconfined compression. Transp. Res. Rec. 2003, 1860, 3–15. [Google Scholar] [CrossRef]
- Katisha, S.; Flintsch, G.W.; Loulizi, A.; Wang, L. Conversion of testing frequency to loading time applied to the mechanistic-empirical pavement design guide. Transp. Res. Rec. 2008, 2087, 99–108. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Huang, B. Characterization of asphalt concrete linear viscoelastic behavior utilizing Havriliak-Negami complex model. Constr. Build. Mater. 2015, 99, 226–234. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, B.; Burdette, E.G.; Chen, J.; Jia, X.; Ding, Y. Characterizing rheological behavior of asphalt binder over a complete range of pavement service loading frequency and temperature. Constr. Build. Mater. 2016, 123, 661–672. [Google Scholar] [CrossRef]
- Christensen, D.W.; Anderson, D.A. Interpretation of dynamic mechanical test data for paving grade asphalt cements. J. Assoc. Asph. Pav. Technol. 1992, 61, 67–116. [Google Scholar]
- Christensen, D.W. Mathematical Modeling of the Linear Viscoelastic Behavior of Asphalt Cements; Pennsylvania State University: State College, PA, USA, 1992. [Google Scholar]
- Orald, F.; Di Benedetto, H. General “2S2P1D” model and relation between the linear viscoelastic behaviors of bituminous binders and mixes. Road Mater. Pav. Des. 2003, 4, 158–224. [Google Scholar]
- Teltayev, B.; Radovskiy, B. Low temperature cracking problem for asphalt pavements in Kazakhstan. In Proceedings of the eighth RILEM International Conference on Mechanics of Cracking and Debonding in Pavements, Nantes, France, 7–9 June 2016; pp. 139–145. [Google Scholar]
- Teltayev, B.; Radovskiy, B. Predicting thermal cracking of asphalt pavements from bitumen and mix properties. Road Mater. Pav. Des. 2018, 19, 1832–1847. [Google Scholar] [CrossRef]
- Radovskiy, B.; Teltayev, B. Viscoelastic Properties of Asphalts Based on Penetration and Softening Point; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Teltayev, B.B.; Amirbayev, E.D.; Radovskiy, B.S. Viscoelastic characteristics of blown bitumen at low temperatures. Constr. Build. Mater. 2018, 189, 54–61. [Google Scholar] [CrossRef]
- Taherkhani, H. Compressive creep behavior of asphalt mixtures. Eng. Procedia 2011, 10, 583–588. [Google Scholar] [CrossRef] [Green Version]
- Hassan, M.M. Relationship between creep time dependent index and Paris low parameters for bituminous mixtures. J. S. Afr. Inst. Civ. Eng. 2013, 2, 8–11. [Google Scholar]
- Soleimanbeigi, A.; Edil, T.B.; Benson, C.H. Creep response of recycled asphalt shingles. Can. Geotech. J. 2013, 51, 103–114. [Google Scholar] [CrossRef]
- Mahan, H.M. Behavior of permanent deformation in asphalt concrete pavements under temperature variation. Al-Qadisiya J. Eng. Sci. 2013, 1, 62–73. [Google Scholar]
- Zhou, Z.G.; Feng, L.; Yuan, X.X.; Xiong, H. Study of the creep damage properties of asphalt mixture under static load. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013. [Google Scholar]
- Jaczewski, M.; Judycki, J. Effects of deviations from thermo-rheologically simple behavior of asphalt mixtures in creep on developing of master curves of their stiffness modulus. In Proceedings of the 9th International Conference on Environmental Engineering, Vilnius, Lithuania, 22–23 May 2014. [Google Scholar]
- Little, D.N.; Button, J.W.; Youssef, H. Development of Criteria to Evaluate Uniaxial Creep Data and Asphalt Concrete Permanent Deformation Potential; National Academies of Sciences, Engineering, Medicine: Washington, DC, USA, 1993; pp. 49–57. [Google Scholar]
- Taherkhani, H.; Collop, A.C. Characterization of uniaxial creep deformation behavior of asphalt mixtures. In Proceedings of the 7th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Rondheim, Norway, 25–27 June 2005; pp. 1–10. [Google Scholar]
- Taherkhani, H.; Afroozi, S. Investigating the creep properties of asphaltic concrete containing nano-silica. Sadhana 2018, 43, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Taherkhani, H.; Arshadi, M.R. Investigating the creep properties of PET-modified asphalt concrete. Civ. Eng. Infrastruct. J. 2018, 51, 277–292. [Google Scholar]
- Li, Y.; Yombah, M.; Temitope, A.A.; Zou, X.; Yang, F.; Li, W.; Jing, H. Research on creep characteristics and influencing factors of cement asphalt composite binder. Math. Probl. Eng. 2020, 2020, 6614920. [Google Scholar] [CrossRef]
- Saoudi, B.S.; Haddadi, S.H. Predicting creep deformation of asphalts modified with polymer using artificial neural networks. Mag. Civ. Eng. 2021, 101, 10106. [Google Scholar]
- Pszczola, M.; Jaczewski, M.; Szydlowski, C. Assessment of thermal stresses in asphalt mixtures at low temperatures using the tensile creep test and the bending beam creep test. Appl. Sci. 2019, 9, 846. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Li, B.; Zhang, Y.; Yin, B.; Dai, J. A creep model of asphalt mixture based on variable order fractional derivative. Appl. Sci. 2020, 10, 3862. [Google Scholar] [CrossRef]
- NCHRP 1-37A. Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavements Structures. Final Report; AASHTO: Washington, DC, USA, 2004. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Rossi, C.O. Steady-state creep of asphalt concrete. Appl. Sci. 2017, 7, 142. [Google Scholar] [CrossRef] [Green Version]
- Iskakbayev, A.; Teltayev, B.; Rossi, C.O.; Yensebayeva, G. Determination of nonlinear creep parameters for hereditary materials. Appl. Sci. 2018, 8, 760. [Google Scholar] [CrossRef] [Green Version]
- Teltayev, B.; Iskakbayev, A.; Rossi, O.C. Regularities of creep and long-term strength of hot asphalt concrete under tensile. Functional Pavement Design. In Proceedings of the 4th Chinese-European Workshop on Functional Pavement Design, Delft, The Netherlands, 29 June–1 July 2016; pp. 169–178. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.; Andriadi, F.; Estayev, K.; Suppes, E.; Iskakbayeva, A. Experimental research of creep, recovery and fracture processes of asphalt concrete under tension. In Proceedings of the 24th International Congress of Theoretical and Applied Mechanics, Montreal, QC, Canada, 22–26 August 2016. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.I.; Rossi, C.O. Deformation and strength of asphalt concrete under static and step loadings. In Proceedings of the AIIT International Congress on Transport Infrastructure and Systems (TIS 2017), Rome, Italy, 10–12 April 2017; Transport Infrastructure and Systems: Rome, Italy, 2017; pp. 3–8. [Google Scholar]
- ST RK 1225-2019. Road, Airfield Asphalt Concrete Mixtures and Asphalt Concrete; Technical Specifications: Astana, Kazakhstan, 2019. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Yestayev, K.Z.; Abu, B.D. Long-term strength of asphalt concrete and its applications. Constr. Build. Mater. 2020, 244, 1–11. [Google Scholar] [CrossRef]
- ST RK 1373-2003. Bitumens and Bitumen Binders. Oil Road Viscous Bitumens; Technical specifications: Astana, Kazakhstan, 2013. [Google Scholar]
- Superpave Series. Performance graded asphalt binder specification and testing, No. 1 (SP-1), 3rd ed.; Asphalt Institute Inc.: Lexington, KY, USA, 2001. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.I.; Andriadi, F.K. Patent of the Republic of Kazakhstan for invention 33244. In Device for Determining the Mechanical Characteristics of Materials under Tension; Springer: Astana, Kazakhstan, 2018. [Google Scholar]
- Rabotnov, Y.N. Balance of the elastic medium with an aftereffect. Appl. Math. Mech. 1948, 12, 53–62. [Google Scholar]
- Rabotnov, Y.N. Solid Mechanics; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Rabotnov, Y.N. Creep of Structures Elements; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Mechanics of Solids; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Iskakbayev, A.; Teltayev, B.; Alexandrov, S. Determination of the creep parameters of linear viscoelastic materials. J. Appl. Math. 2016, 2016, 6568347. [Google Scholar] [CrossRef] [Green Version]
- Iskakbayev, A.I.; Teltayev, B.B.; Yensebayeva, G.M.; Kutimov, K.S. Computer modeling of creep for hereditary materials by Abel’s Kernel. News NAS RK. Ser. Geol. Tech. Sci. 2018, 431, 66–76. [Google Scholar]
- Zhurinov, M.Z.; Iskakbayev, A.I.; Teltayev, B.B.; Kutimov, K.S. Modeling of hereditary materials relaxation by Abel kernel. News NAS RK. Ser. Geol. Tech. Sciences. 2020, 6, 254–260. [Google Scholar] [CrossRef]
- Nadai, A. Theory of Flow and Fracture of Solids; MacGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Hill, R. Mathematical Theory of Plasticity; Oxford University Press Inc.: New York, NY, USA, 1950. [Google Scholar]
- Newton, I.S. Philosophia Naturalis Principia Mathematica; Juffu Societ atis Regie ac Typis Josephi Streater; Prostat apud Plures Bibliopolas: London, England, 1687. [Google Scholar]
- Newton, I.S. Mathematical Principles of Natural PhilosophyTranslated from Latin and Comments by Krylov, A.N., Academician; Nauka: Moscow, Russia, 1989. [Google Scholar]
- Reiner, M. Ten Lectures on Theoretical Rheology; Rubin Mass: Jerusalem, Israel, 1943. [Google Scholar]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers; Khimiya: Moscow, Russia, 1977. [Google Scholar]
- Malkin, A.Y.; Isayev, A.I. Rheology. Concepts, Methods and Applications, 2nd ed.; ChemTec Publishing: Toronto, ON, Canada, 2012. [Google Scholar]
- Trouton, F.T. On the coefficient of viscous traction and its relation to that of viscosity. Proc. R. Soc. London. Ser. A 1906, 77, 426–440. [Google Scholar]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Frenkel, Y.I. The Kinetic Theory of Liquids; Nauka: Leningrad, Russia, 1975. [Google Scholar]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of Rate Processes; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Fox, T.G.; Gratch, S.; Loshaek, S. Viscosity relationship for polymers in bulk and concentrated solutions. In Rheology. Theory and Applications; Eirich, F.R., Ed.; Academic Press Inc.: New York, NY, USA, 1956; Volume 1, pp. 431–492. [Google Scholar]



| Indicator | Measurement Unit | Requirements of ST RK 1373 | Value |
|---|---|---|---|
| Penetration, 25 °C, 100 g, 5 s | 0.1 mm | 101–130 | 104 |
| Penetration Index PI | - | −1.0, …, +1.0 | −0.34 |
| Tensility at temperature: | cm | - | - |
| 25 °C | ≥90 | 140 | |
| 0 °C | ≥4.0 | 5.7 | |
| Softening point | °C | ≥43 | 46.0 |
| Fraas point | °C | ≤−22 | −25.9 |
| Dynamic viscosity, 60 °C | Pa·s | ≥120 | 175.0 |
| Kinematic viscosity, 135 °C | mm2/s | ≥180 | 398.0 |
| Temperature, °C | Number of Samples | Stress Limits, MPa | |
|---|---|---|---|
| Min | Max | ||
| +60 | 42 | 0.0081 | 0.06 |
| +48 | 35 | 0.0083 | 0.1123 |
| +36 | 30 | 0.0189 | 0.146 |
| +24 | 70 | 0.0363 | 0.557 |
| +12 | 12 | 0.2 | 0.6 |
| 0 | 26 | 0.3 | 2.0 |
| −12 | 14 | 0.5 | 3.0 |
| −24 | 12 | 0.785 | 2.271 |
| Total: | 241 | - | - |
| Notation of a Characteristic | Description of a Characteristic |
|---|---|
| I | unsteady-state creep site |
| II | steady-state creep site |
| III | accelerating creep site |
| Δt1 | unsteady-state creep site duration |
| Δt2 | steady-state creep site duration |
| Δt3 | accelerating creep site duration |
| ε1 | strain in the end of Site I (in the beginning of Site II) of a creep curve |
| ε2 | strain in the end of Site II (in the beginning of Site III) of a creep curve |
| ε3 | failure strain corresponding to failure time |
| Temperature, °C | Stress σ, MPa | Parameters | ||
|---|---|---|---|---|
| ε0, % | α | δ | ||
| +24 | 0.0840 | 0.0066 | 0.54 | 1.23 |
| +36 | 0.0189 | 0.0139 | 0.74 | 0.67 |
| +48 | 0.0192 | 0.0954 | 0.76 | 0.26 |
| +60 | 0.0081 | 0.0297 | 0.89 | 1.17 |
| Temperature, °C | Coefficients | R2 | |
|---|---|---|---|
| B | m | ||
| +60 | 0.0046 | −2.4156 | 0.8819 |
| +48 | 0.0023 | −3.1739 | 0.9627 |
| +36 | 0.0072 | −3.5787 | 0.9754 |
| +24 | 0.7639 | −3.4318 | 0.8277 |
| +12 | 9.2648 | −4.8324 | 0.9877 |
| 0 | 107.6331 | −4.4062 | 0.9820 |
| −12 | 449.6749 | −4.1046 | 0.6895 |
| −24 | 29,865.4511 | −6.6253 | 0.6623 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teltayev, B.; Iskakbayev, A.; Oliviero Rossi, C.; Abu, B. Unsteady-State Creep of an Asphalt Concrete. Appl. Sci. 2022, 12, 1615. https://doi.org/10.3390/app12031615
Teltayev B, Iskakbayev A, Oliviero Rossi C, Abu B. Unsteady-State Creep of an Asphalt Concrete. Applied Sciences. 2022; 12(3):1615. https://doi.org/10.3390/app12031615
Chicago/Turabian StyleTeltayev, Bagdat, Alibai Iskakbayev, Cesare Oliviero Rossi, and Bekdaulet Abu. 2022. "Unsteady-State Creep of an Asphalt Concrete" Applied Sciences 12, no. 3: 1615. https://doi.org/10.3390/app12031615
APA StyleTeltayev, B., Iskakbayev, A., Oliviero Rossi, C., & Abu, B. (2022). Unsteady-State Creep of an Asphalt Concrete. Applied Sciences, 12(3), 1615. https://doi.org/10.3390/app12031615








