Abstract
This paper reports the experimental investigation of the unsteady-state creep process for road hot fine-grained asphalt concrete within the variation for a stress (from 0.0081 to 3 MPa) and a temperature (from +60 to −24 °C) at uniaxial tension. It is found out that unsteady-state creep for the asphalt concrete is approximated with a high accuracy at all the considered temperatures and stresses by the power function (with 3 parameters: ε0, α, δ) obtained from the Rabotnov’s fraction-exponential function; at temperatures from −12 to +12 °C the parameter α has the mean value of 0.5; unsteady-state creep duration for the asphalt concrete depends strongly on the stress and the temperature. It is satisfactorily described by the mathematical expression in the form of multiplication of the exponential and the power functions. Mathematical expressions have been obtained which describe the unsteady-state creep and the steady-state creep rates for the asphalt concrete. It was found that the strain rate is varied sharply in the initial time moments from t ≈ 0 to 500–600 s (theoretically from ∞ at t = 0 to ≈1 − 2 × 10−3%/s at t = 500–600 s); then it decreases monotonously in the following time moments, approximately according to a straight-line dependence. An asphalt concrete creep as a physical process can be similar to the viscous liquid flow: it is proposed to call the sites of the unsteady-state and the steady-state creeps as the sites of the transient and the constant viscosities respectively; a mechanical (rheological) model is represented which describes the sites of the transient and the constant viscosities for the creep curve of the asphalt concrete through Trouton and Newton viscosities respectively. Meanwhile, it has been stated that the viscosity of the asphalt concrete can reach 26,000 and 45,000 MPa at the temperatures of +24 and +36 °C respectively at the end of the unsteady-state creep.
1. Introduction
At present, an asphalt concrete, it seems, is the most widespread road material all over the world. It is mainly used for the construction of the upper strong layers of highway pavement [1,2,3,4]. Asphalt concretes as part of pavements are subjected to the combined impact of mechanical loads from vehicles’ wheels and climatic factors (temperature, moisture) during their whole service life. The impact of the above factors is of a complicated and nonstationary nature: their values and action duration are varied in time stochastically. Therefore, research of mechanical behavior for asphalt concretes under load impact having various values and action duration and at various temperatures is very important for the road science and practice.
There are well-developed research methods in the viscoelasticity theory [5,6,7] for the impact of time on the mechanical behavior of materials: creep test, stress relaxation, deformation at a constant strain rate, deformation at a constant loading rate, step-by-step loading, cyclic loading, etc. The specified stress is applied to the tested sample of a material “instantaneously” (this is in theory, but in practice, it is applied during the period as quickly as possible) at testing for the creep at the initial time moment (t = 0), and it is kept constant to the specific time (to the sample failure, if required); the sample strain varied (increased) in time is measured. At testing for stress relaxation, the tested sample of the material is “instantaneously” deformed to the specific value in the initial time moment, and it is kept constant during the whole specific period; the sample stress varied (decreased) in time is measured.
Road researchers during description of the mechanical behavior for asphalt concretes and bitumens often perform tests for the stress relaxation, and they describe the relaxation function analytically using the so-called Prony-Series [8,9,10,11,12]. There is also the more popular Christensen and Anderson model [13,14] and the so-called 2S2P1D model (two springs, two parabolic elements and one linear dashpot) [15], used at approximation for the complex (dynamic) modulus of bitumens and asphalt concretes. The works [16,17,18,19] show the possibility for the description of viscoelastic functions for bitumens and asphalt concretes with a high accuracy using the model representing the modified power function.
Many road researchers understand that an asphalt concrete creep is an important type of behavior under the influence of applied load, and they have carried out many studies in this direction [20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Asphalt creep testing is included in the current American Guide for Road Pavement Design [34]. Meanwhile, many of the researchers note that a typical creep curve of an asphalt concrete has three characteristic sites [20,21,26,27,28,29]. Almost all of them believe that the first site (an unsteady-state creep site) is satisfactorily approximated by a power function.
It should be noted that researchers mainly try to connect the asphalt concrete creep with its rut resistance [26,27,28]. Therefore, they began to test not only a conventional asphalt concrete but also asphalt concretes with various additives [28,29,31], even a composite asphalt concrete [30].
The above models describe accurately enough viscoelastic functions of bitumens and asphalt concretes for the practical use. However, in the authors’ opinion, their serious drawback is that the researchers pay attention mainly to the accuracy of the approximations during their use; they ignore the peculiarities of the characteristic stages of the deformation as a physical process. For example, the work [30] investigated creep of a composite asphalt concrete with unloading. Without paying the required attention to the differences in the deformation of the asphalt concrete at different stages, unloading was carried out at all three stages of deformation. The results of these tests are not analyzed in this work. The paper [26] adopts the total strain at 1 h as an indicator of an asphalt concrete sensitivity to permanent strains. However, it is necessary to know that depending on level of applied load and temperature after 1 h of loading, the asphalt concrete creep can be at different stages of three, where the asphalt concrete is deformed differently.
In the authors’ opinion, a creep curve constructed according to experimental data characterizes the mechanical behavior of a material to the fullest possible extent providing information regarding evolution as for the deformation as well as for the destructions (due to the failure accumulation). For example, according to the results of the experimental investigations, our previous works [35,36,37,38,39] show that a creep curve of an asphalt concrete has three characteristic sites, and an asphalt concrete is deformed differently within the limits for any of them.
This paper is a logical continuation of the above authors’ works, and it investigates experimentally the mechanical and physical characteristics for the asphalt concrete deformation on the first site (unsteady-state creep site) of creep curve within the wide limits of a stress variation (from 0.0081 to 3 MPa) and a temperature variation (from +60 to −24 °C) at the uniaxial tension. “The main characteristic of creep is the time-varying strain ε(t) which is approximated by a power function derived from the Rabotnov’s fraction-exponential function. In the theory of viscoelasticity, the Rabotnov’s fraction-exponential function is used as a kernel of an integral equation that models the hereditary properties of a material. The fraction-exponential function is well studied and it has great versatility: with its help it is possible to model viscoelastic behavior of many classes of materials with a high accuracy. One of its advantages is that if the parameters of the creep kernel are known, then the parameters of the relaxation kernel become known”.
2. Materials and Methods
2.1. Asphalt Concrete
A hot dense fine-grained asphalt concrete has been accepted to test under the laboratory conditions. This type of asphalt concrete is widely used in the road construction in Kazakhstan and in many countries of the world. The prepared asphalt concrete satisfies the requirements of the standard of Kazakhstan ST RK 1225 [40].
The following fractions of aggregate have been used for the asphalt concrete preparation: 5–10 mm (20%), 10–15 mm (13%), 15–20 mm (10%); sand: 0–5 mm (50%) and activated mineral powder (7%). A granulometric curve for mineral part of the asphalt concrete is shown in Figure 1. Road viscous bitumen of the grade 100–130 has been accepted in the amount of 4.8% by weight of the mineral materials. The asphalt concrete mix has been prepared by continuous joint mixing of the mineral materials (aggregate, sand, mineral powder) and the bitumen at the temperature of 150 °C for 120 s. The compaction of the prepared asphalt concrete has been performed by a Cooper compactor (model CRT-RC25), Cooper, Nottingham, UK) at temperatures 140–150 °C.
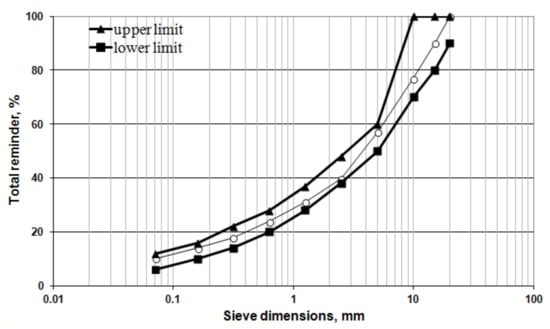
Figure 1.
Granulometric curve of mineral part of the asphalt concrete.
More detailed information regarding composition of the asphalt concrete can be obtained in the works [35,41].
2.2. Bitumen
A road bitumen of the grade 100–130 on penetration has been used to prepare the asphalt concrete. The bitumen has been produced by the Pavlodar petrochemical plant (Kazakhstan) by method of direct oxidation from the oil of Western Siberia (Russian Federation). The bitumen satisfies the requirement of the standard of Kazakhstan ST RK 1373 [42]; its grade under Superpave PG (Performance grade) is 64–40 [43]. Basic standard indicators of the bitumen are shown in Table 1. The content of the bitumen in the asphalt concrete is 4.8% by weight of a dry mineral material. More detailed information regarding the characteristics of the bitumen is in the works [19,35].

Table 1.
Basic standard indicators of the bitumen, ST RK: Standard of the Republic of Kazakhstan.
2.3. Creep Test
The research of the unsteady-state strain of the asphalt concrete has been performed by testing of samples (50 × 50 × 150 mm) for creep at direct tension at the temperatures of +60 °C, +48 °C, +36 °C, +24 °C, +12 °C, 0 °C, −12 °C and −24 °C. Several suitable stress levels have been selected for each temperature. Stress levels were accepted at different temperatures so that, firstly, the unsteady-state creep duration for the samples of the asphalt concrete was approximately in the range of 1 s to 100,000 s and secondly, so that real loads from vehicles (from the lightest to the heaviest) were within these limits. All samples of the asphalt concrete at testing were under the applied load to failure. The applied load and the temperature were kept constant from the beginning to the end of testing for all samples. Two hundred and forty-one samples of the asphalt concrete have been selected to analyze the unsteady-state deformation. More detailed information regarding the tested samples of the asphalt concrete and the applied stresses is in Table 2.

Table 2.
Characteristics of the tested asphalt concrete samples.
The tests of the asphalt concrete samples have been performed at various constant temperatures and stresses in the device specially designed [44] and assembled in Kazakhstan Highway Research Institute. More detailed information regarding preparation of the asphalt concrete samples and their testing is in the papers [35,41].
3. Theory
3.1. Integral Equation
The works [45,46,47,48] show that the isochronous creep curves for many viscoelastic materials have the property of similarity, and the following nonlinear integral equation was proposed for description of their deformation:
where is a strain at a time moment t; is a stress at a time moment t; is a stress applied at a time moment τ; is a creep kernel; t is observation time; τ is time before observation time t.
Expression φ[ε(t)] in the left part of the integral Equation (1) represents the so-called “instantaneous strain curve” which is determined on the basis of the experimental data.
3.2. Creep Kernel
Creep kernel K(t − τ) of the integral Equation (1) is described by the Rabotnov’s fraction-exponential function [45,46,47,48]:
where is the Rabotnov’s fraction-exponential function; λ, α, β are the parameters of the creep kernel (λ > 0, 0 < α < 1, β > 0); (·) is the gamma-function.
Inserting Expression (2) for the creep kernel into the integral Equation (1) and considering that σ = constant creep, we will have:
The improved methods for determination of the parameters λ, α, β have been developed in the works [49,50], and it is shown that the unsteady-state creep for an asphalt concrete can be approximated with a high accuracy using the Rabotnov’s fraction-exponential function.
The works [38,50] show the possibility for description of the unsteady-state creep of an asphalt concrete with a high accuracy by more simple expression than Equation (3).
Accepting n = 0, from Equation (3) we have:
Dividing the right and the left parts of the Equation (4) by instantaneous elasticity modulus E0, we will have the following expression for the description of the unsteady-state creep deformation:
Where is a conditional instantaneous strain.
3.3. Determination of Parameters ε0, α, δ
Equation (5) contains three unknown parameters: ε0, α and δ. The works [36,50,51] propose to consider α as the known parameter, and the parameters ε0 and δ are calculated according to the expressions:
Specifying sequentially the values of the parameter α within the limit of (0, 1) with the selected step, from Expression (6) we determine the values of the parameter ε0. Inserting this obtained value of the parameter ε0 and the relevant value of the parameter α into Expression (7), we determine the value of the parameter δ. The set of values of the parameters α, ε0 and δ, providing the least deviations of the creep strain calculated under Expression (5) from the experimental values, is accepted as the real one.
4. Results and Discussion
4.1. Creep Curve Characteristics
The creep curve of an asphalt concrete has three characteristic sites (Figure 2): Site I unsteady-state creep; Site II steady-state creep; Site III accelerating creep. On Site I the strain increases with the time. On Site II the strain increases with a constant rate . On the third site the strain rate increases with the time, and in the end of the site the tested sample is failed. The description of all characteristics for a creep curve shown in Figure 2 is given in Table 3.
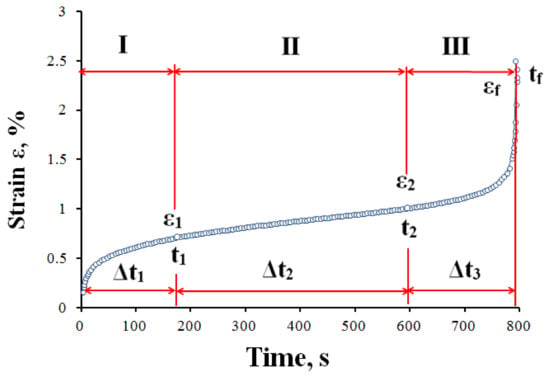
Figure 2.
Asphalt concrete creep curve under the stress of σ = 0.041 MPa at the temperature of T = 48 °C.

Table 3.
Description of the creep curve characteristics.
Then the deformation characteristics of Site I (unsteady-state creep) for a creep curve of the asphalt concrete are investigated at various stresses and temperatures.
4.2. Unsteady-State Creep Approximation
The graphs of Figure 3 represent the unsteady-state creep curve of the asphalt concrete constructed according to the experimental data obtained at various stresses and different temperatures. The experimentally obtained strain values are dotted in these figures, and the lines represent the relevant approximations according to Expression (5). As it is seen, the compliance of the approximating curves and the experimental strains is very good. Such good compliance of the experimental and the calculated strains is obtained practically at all the considered stresses and temperatures.
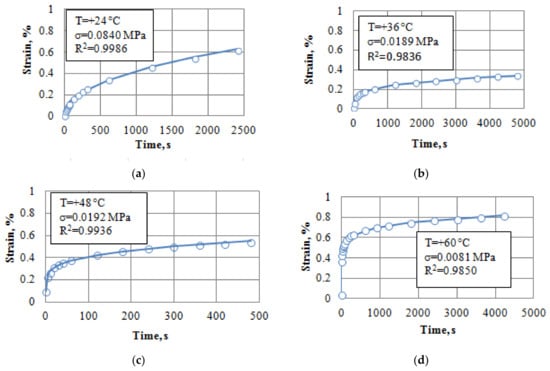
Figure 3.
Unsteady-state creep curves of the asphalt concrete: (a)—T = 24 °C, (b)—T = 36 °C, (c)—T = 48 °C, (d)—T = 60 °C: ◦ experiment, ― approximation.
The values of the parameters ε0, α and δ for the unsteady-state creep curves shown in Figure 3 and found according to the method specified in the Section 3.3 are represented in Table 4.

Table 4.
Values of parameters ε0, α, δ.
Figure 4 shows the dependence of the parameter α on a stress. It is seen that the average values of the parameter α at all the stresses and temperatures are concentrated near the value of 0.5. Meanwhile, the scatter of the average values of the parameter α decreases with the temperature reduction. Meanwhile, the scattering in the values of the parameter α at temperatures from −12 to +12 °C is insignificant, and there are significant scatters at temperatures from +24 to +60 °C. Therefore, it is recommended in the calculations to accept the parameter α value equal to 0.5 at different stresses in the temperature range from −12 to +12 °C and to accept its values determined experimentally for specific stresses in the temperature range from +24 to +60 °C.
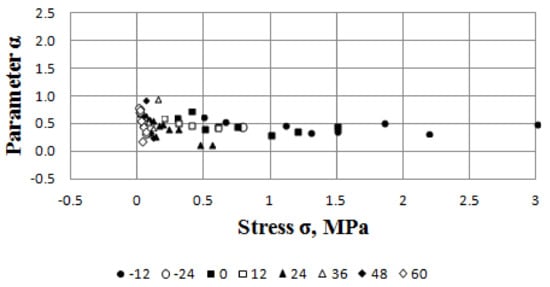
Figure 4.
Dependence of the parameter α on a stress.
Therefore: (1) it can be stated that Expression (5) with the parameters ε0, α and δ determined according to the method specified in Section 3.3 describes the unsteady-state creep of the asphalt concrete with a high accuracy; (2) we have the analytical expression (5) for the unsteady-state creep of the asphalt concrete which can be used for the analysis of its other physical and mechanical characteristics.
Figure 5 represents graphical data showing sensitivity of Expression (5) for the unsteady-state creep of the asphalt concrete to variations of the parameters: α, δ and ε0. The following four values of parameters have been adopted in the sensitivity calculations: reduced by 5 and 10%and increased by 5 and 10%. As can be seen, the strain is more sensitive to variation of the parameter α; especially, a reduction in its value by 10% causes a lot of scattering. The scattering increases with time fast; it can achieve the value of 220% at long duration of the stress.
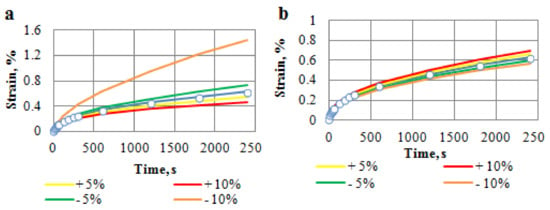
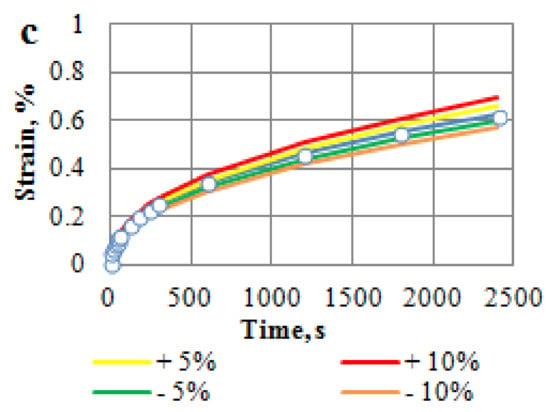
Figure 5.
Sensitivity analysis of Equation (5): (a) change in α; (b) in δ; (c) in ε0.
It turned out that variation of values of the parameters δ and ε0 has little impact on the strain.
4.3. Unsteady-State Creep Duration
An important characteristic of the unsteady-state creep of a material is its duration t1. The whole creep process occurs in time, including the unsteady-state creep one. The unsteady-state creep is continued only to the time t1, after which another characteristic type of the creep of a material (steady-state creep) with different physical mechanisms and parameters starts. Therefore, it is very important to study the dependence of the unsteady-state creep duration on the effecting factors, and it is desirable to have a mathematical expression which describes it for practical use.
The graphs showing the dependence of the unsteady-state creep duration of the asphalt concrete on a stress at all the considered temperatures are represented in Figure 6. As it is seen, the unsteady-state creep duration depends greatly on temperature as well as on stress. As one should expect, it decreases with the stress increase and the temperature increase.
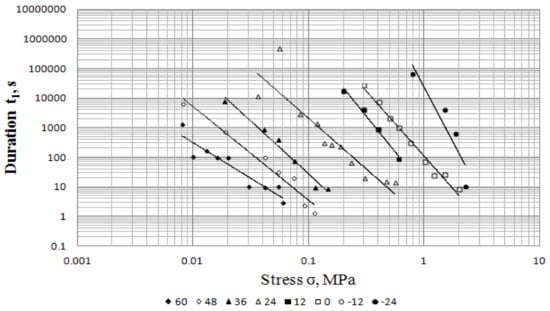
Figure 6.
Graphs for the dependence of the unsteady-state creep duration for the asphalt concrete on stress at various temperatures.
The dependences of the unsteady-state creep duration on stress at all the considered temperatures are satisfactorily described by the power function of the following form:
where t1 is the unsteady-state creep duration, sand σ are stress and MPa, B and m are correlation coefficients.
t1 = B·σm,
The correlation coefficients B and m are of physical nature. The coefficient B is numerically equal to the unsteady-state creep duration of the asphalt concrete at the stress equal to 1 MPa.
Having taken the logarithm of Expression (8), we will have:
logt1 = logB + m·logσ.
It is seen from Expression (9) that the correlation coefficient m characterizes the variation rate of the unsteady-state creep duration with the stress variation, and it shows to which order the duration decreases with the stress increase by one order.
The values of the correlation coefficients B and m of Equation (8) at the considered temperatures calculated by the least square method are represented in Table 5. One can see from the table that there is a reliable correlation relationship between the unsteady-strain creep duration of the asphalt concrete and a stress at all the considered temperatures.

Table 5.
Values of the coefficients B and m.
As it is seen from Equation (8), the unsteady-state creep duration t1 is directly proportional to the coefficient B. The higher the temperature and the less the unsteady-state creep duration, the coefficient B decreases with the temperature increase. Meanwhile, it should be noted that the coefficient B is strongly varied at low temperatures; statistically it has a constant value at high temperatures (from +36 to +60 °C): only from the temperature of +24 °C it increases fast with the temperature decrease. For example, within the range of the temperatures of +24 °C and −24 °C, it increases by more than four orders.
Coefficient m has a negative sign, and its absolute value increases with the temperature decrease. It follows that the effect of a stress on the unsteady-state creep duration becomes stronger with the temperature decrease.
It is found that the dependence of the coefficient B on the inverse thermodynamic temperature in semi-logarithmic coordinates is approximated with a high accuracy (R2 = 0.965) by a straight line (Figure 7). Furthermore, the dependence of the coefficient m on the temperature can be approximately considered as the linear one (Figure 8).
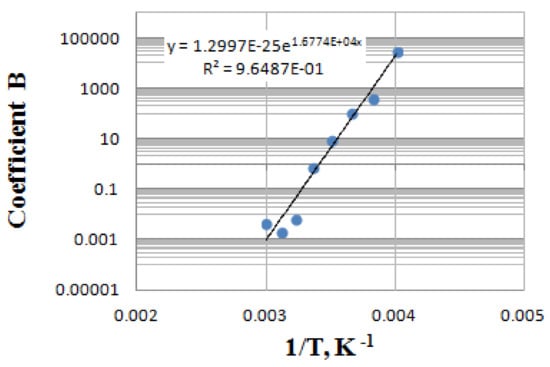
Figure 7.
Dependence of the coefficient B on the inverse thermodynamic temperature.
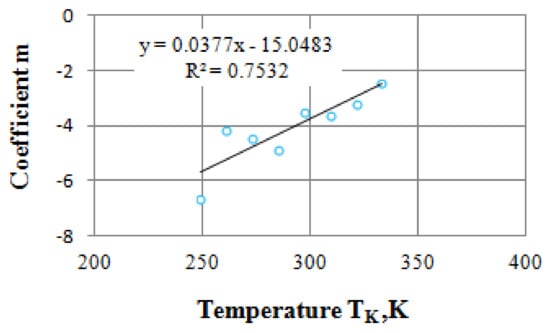
Figure 8.
Dependence of the coefficient m on the thermodynamic temperature.
Thus, the following expressions have been obtained for the temperature dependences of the coefficients B and m:
m = −15.05 + 0.038 · TK,
Inserting Expressions (10) and (11) into Equation (8) we will have the following expression:
Thus, Expression (12) has been obtained for the unsteady-state creep duration for the investigated type of the asphalt concrete. As it is seen, the obtained expression consists of the multiplication of the exponential function and the power function. Both functions have temperature as an argument, which indicates the specifically important value of temperature at any stress value.
4.4. Unsteady-State Creep Rate
The strain rate is an important characteristic for deformation of viscoelastic materials. It is included in the governing equations as a physical characteristic of a material in the fundamental theories of viscous flow and plastic deformation of viscous liquids and solids [52,53]. In our case, the strain rate will show how quickly the strain value of the asphalt concrete is varied in time on the unsteady-state creep site.
Having differentiated Equation (5) for the unsteady-state creep strain, we will have the following expression for the unsteady-state creep rate of the asphalt concrete:
It is seen from Expression (13) that the strain rate (theoretically) is infinite at the initial time moment (t = 0); it decreases with time according to the power dependence, and it has a value equal to the steady-state creep rate on the second site of the creep curve in the end of the unsteady-state creep site (t = t1), i.e.,:
These characteristic peculiarities for variation of the unsteady-state creep rate for the asphalt concrete in time are visually demonstrated in Figure 9, where it can be seen that the strain rate is varied sharply in the initial time moments from t ≈ 0 to 500–600s (theoretically from ∞ at t = 0 to ≈1 − 2 × 10−3%/s at t = 500–600 s); then it decreases monotonously in the following time moments, approximately according to a straight-line dependence.
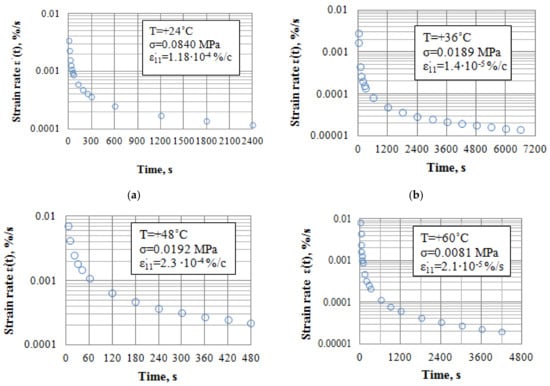
Figure 9.
Graphs for the unsteady-state creep rate variation of the asphalt concrete: (a)—T = 24 °C, (b)—T = 36 °C, (c)—T = 48 °C, (d)—T = 60 °C.
From Expression (13) it is also seen that the multiplication of the parameters ε0·δ is of physical nature: its numerical value is equal to the strain rate at the load duration of 1 s.
Having taken the logarithm of Expression (13), we have:
As it is seen from Expression (14), the parameter α characterizes the rate of variation (decrease) of the strain rate, i.e., it is the strain acceleration. As in Expression (14), the parameter α has a negative sign, and it shows by what order the strain rate decreases at the time increase by one order. It can be called “the logarithmic strain deceleration”.
4.5. Steady-State Creep Rate
It is accepted in the theory of viscoelasticity that all the strains of the materials are plastic ones on the steady-state creep site [45,46,47]. In other words, the material “flows” under the impact of load like a viscous liquid on this site. The works [37,38,39,51] show experimentally that a creep curve of an asphalt concrete is approximated on the unsteady-state creep site with a high accuracy by a straight line, and therefore, it can be characterized by only one parameter—the steady-state creep rate .
Inserting Expression (12) for the unsteady-state creep duration into Expression (13), we will have the following expression for the steady-state creep rate of the asphalt concrete:
The steady-state creep rate is an important indicator for an asphalt concrete, as it characterizes directly the process of the plastic deformation. Furthermore, it can be included into the models for the prediction of a rut on an asphalt concrete pavement of a highway.
The obtained Expression (15), therefore, is of important practical value. Usually, the creep test of the material should be performed to the end of the steady-state creep site to determine experimentally the value of the steady-state creep rate, i.e., a long duration of the experiment is required. The peculiarity of Expression (15) is in the fact that it enables us to determine the numerical value of the steady-state creep rate according to the creep test results of an asphalt concrete only to the end of Site I (unsteady-state creep site). It enables us to reduce considerably consumption of time and material resources, as well as the volumes of the calculation works. For example, the experimental results have shown that the average relative duration of Sites I, II and III (Section 4.1) of the creep curves for the asphalt concrete are equal to 13, 63 and 24% respectively at the temperature of 20 °C [37]. In other words, the methodical approach, according to which Expression (15) has been obtained, enables us to reduce the duration of the experiments almost by five times.
Another important peculiarity of Expression (15) is the fact that all the parameters, included into it, are of clear physical nature: the thermodynamic temperature Tk, the stress σ, the creep parameters ε0, δ, α. From Expression (15) it is seen that the steady-state rate is directly proportional to the strain rate at load duration for 1 s (ε0 · δ), and the effect of the unsteady-state creep duration on it is characterized by the parameter α (the logarithmic strain deceleration).
4.6. Viscosity
As the creep of materials under a load impact represents a process developed in time [5,6,7,46,47,48], then such process can be logically similar to a viscous liquid flow under the impact of its own weight and described through the viscosity as an object of rheology.
I. Newton introduced the notion regarding viscosity in his well-known book “The mathematical principles of natural philosophy” [54,55] to explain the rotation of the planets of the Solar system around its axis. At present it is one of the fundamental indicators in rheology [56,57,58], characterizing the viscous flow (viscous deformation). For example, the Newton’s law describes the behavior of the so-called Newton’s liquid (the ideal viscous liquid) in rheology in the following way:
where is a shearing stress; is a shear strain rate; is a viscosity (shear viscosity).
The numerical values of the strain rate discussed above had a dimension of%/s. For the convenience of further reasoning, we present its dimension as 1/s. To do this, the right part of Expression (13) is multiplied by 10−2.
Studies of viscous liquid tension were initiated by Trouton in the beginning of the last century [59]. By analogy with the Newton’s law, he recorded a relationship between a strain rate and a normal stress. For our case, this relationship is presented in the following form:
where is longitudinal viscosity (Trouton’s viscosity), MPa · s.
Inserting Expression (13) into Expression (17), we have:
At first glance, when considering a material deformation at uniaxial tension, the usual idea prevails that the realized longitudinal strain ε is the result of the action of only normal stresses occurring at the points of the tested material sample. However, it is known [60] that normal stresses occur only on normal planes, and both normal and shear stresses occur on all inclined sites (except when α = 45°) (Figure 10); only shear stresses occur on sites having the angle of 45°. In view of this, it should be understood that the longitudinal viscosity included in Expression (18) takes into account the total contribution of the linear strain and the shear one at points of a sample to the longitudinal strain.
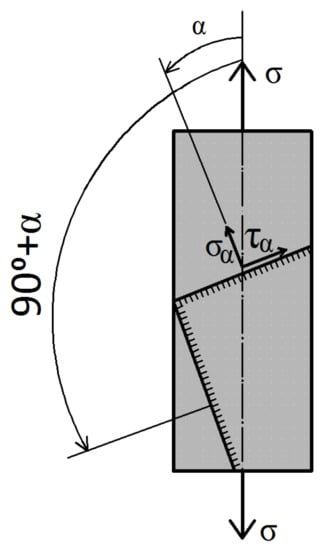
Figure 10.
Stresses on an inclined plane at sample tension.
Now from Expression (18) for the longitudinal viscosity of the asphalt concrete, we will have:
From Expression (19) it is seen that the longitudinal viscosity of the asphalt concrete is directly proportional to the stress and the time at the degree of α, and it is inversely proportional to the strain rate with the load duration of 1 s. In this case, the viscosity of the asphalt concrete is always (at all temperatures and stresses) equal to zero λ (0) = 0 at the initial time moment (t = 0), and over the period it increases in power dependence to the end of the unsteady-state creep site (t = t1). Furthermore, at the end of the unsteady-state creep and within the entire the steady-state creep site the viscosity of the asphalt concrete has a constant value determined by the expression:
When writing Expression (20), it is taken into account that in accordance with Trouton’s law for purely viscous liquids (bodies), the longitudinal viscosity λ is equal to the tripled shear viscosity η (Newton’s viscosity) [57,58].
Figure 11 represents the graphs of the asphalt concrete viscosity variation in the unsteady-state creep site at different stresses and temperatures. It is seen that the asphalt concrete has a very small (theoretically zero) viscosity at the initial moments of loading (t ≈ 0) at any stresses and temperatures; therefore, the strain rate of the asphalt concrete is very large (theoretically infinite) at this time moment; the viscosity increases rapidly over time and the strain rate decreases rapidly in power dependence; however, the viscosity of the asphalt concrete can reach 26,000 and 45,000 MPa at the temperatures of +24 and +36 °C respectively at the end of the unsteady-state creep.
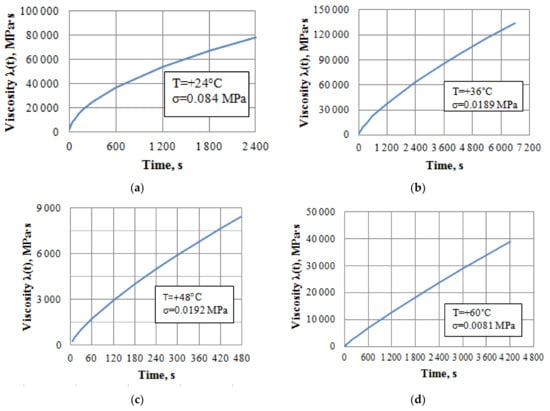
Figure 11.
Graphs for viscosity variation of the asphalt concrete: (a)—T = 24 °C, (b)—T = 36 °C, (c)—T = 48 °C, (d)—T = 60 °C.
The discussion and results presented above allow us to consider the entire process of creep for a viscoelastoplastic material (including an asphalt concrete) as a flow of viscous liquid and characterize it by viscosity. Then we may call Site I of the unsteady-state creep and Site II of the steady-state creep for a creep curve of a material as the variable viscosity (Site I) and the constant viscosity (Site II).
The mechanical (rheological) behavior of the asphalt concrete under study can be described by the following model:
This model is of important practical value, since it characterizes directly the ability of the asphalt concrete to shear deformation, and it can be used in predicting the accumulation of plastic strains (rut depth) in flexible pavements of highways. In the future, it can be associated with expressions for the viscosity of liquids obtained by J.I. Frenkel based on the kinetic theory of liquids [61] and G. Eyring based on the theory of rate processes [62,63], which will explain the phenomena of viscous and plastic deformation of asphalt concretes based on the fundamentals of the molecular physics, the thermodynamics and the quantum physics.
5. Conclusions
The results of the research for the unsteady-state creep of the asphalt concrete at different stresses (from 0.0081 to 3 MPa) and temperatures (from +60 to −24 °C) performed in this work make it possible to draw the following conclusions:
- It should be well understood that there are characteristic time stages within which an asphalt concrete is deformed in different ways with the effect of a constant load at operating temperatures for road asphalt concrete; the first stage, called “unsteady-state creep”, has the following features: strain increases in time nonlinearly to the time moment t1 (t1 is the unsteady-state creep duration), which also depends on a stress and a temperature; strain rate decreases nonlinearly over time.
- A simple power function can be used to satisfactorily describe the strain, the strain rate and the steady-state creep duration of an asphalt concrete.
- By analogy with the flow of viscous liquid, the creep process of viscoelastic materials, including an asphalt concrete, can be characterized by a fundamental physical indicator-viscosity; using the classical works of Newton and Trouton, the example of an asphalt concrete shows the possibility for obtaining a mechanical (rheological) model of the unsteady-state and steady-state creep of viscoelastic materials.
- The resulting rheological model can be connected to the principles of molecular physics, thermodynamics and quantum physics for a more in-depth explanation of viscosity and plastic deformation of asphalt concrete and other materials.
Author Contributions
B.T.: conceptualization, investigation, methodology, formal analysis, writing—original draft. A.I.: conceptualization, investigation, methodology, writing—review and editing. C.O.R.: investigation, methodology, writing—review and editing. B.A.: investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the JSC “Kazakhstan Highway Research Institute”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- MS-4. The Asphalt Handbook, 7th ed.; Asphalt Institute: Lexington, KY, USA, 2007. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design, 2nd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Papagiannakis, A.T.; Masad, E.A. Pavement Design and Materials; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cristensen, R.M. Theory of Viscoelasticity: An Introduction; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Tschoegl, N.N. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Park, S.W.; Kim, Y.R. Fitting Prony-Series viscoelastic models with power-low presmoothing. J. Mater. Civ. Eng. 2001, 13, 26–32. [Google Scholar] [CrossRef]
- Gibson, N.H.; Schwartz, C.W.; Schapery, R.A.; Witczak, M.W. Viscoelastic, viscoplastic and damage modeling of asphalt concrete in unconfined compression. Transp. Res. Rec. 2003, 1860, 3–15. [Google Scholar] [CrossRef]
- Katisha, S.; Flintsch, G.W.; Loulizi, A.; Wang, L. Conversion of testing frequency to loading time applied to the mechanistic-empirical pavement design guide. Transp. Res. Rec. 2008, 2087, 99–108. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Huang, B. Characterization of asphalt concrete linear viscoelastic behavior utilizing Havriliak-Negami complex model. Constr. Build. Mater. 2015, 99, 226–234. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, B.; Burdette, E.G.; Chen, J.; Jia, X.; Ding, Y. Characterizing rheological behavior of asphalt binder over a complete range of pavement service loading frequency and temperature. Constr. Build. Mater. 2016, 123, 661–672. [Google Scholar] [CrossRef]
- Christensen, D.W.; Anderson, D.A. Interpretation of dynamic mechanical test data for paving grade asphalt cements. J. Assoc. Asph. Pav. Technol. 1992, 61, 67–116. [Google Scholar]
- Christensen, D.W. Mathematical Modeling of the Linear Viscoelastic Behavior of Asphalt Cements; Pennsylvania State University: State College, PA, USA, 1992. [Google Scholar]
- Orald, F.; Di Benedetto, H. General “2S2P1D” model and relation between the linear viscoelastic behaviors of bituminous binders and mixes. Road Mater. Pav. Des. 2003, 4, 158–224. [Google Scholar]
- Teltayev, B.; Radovskiy, B. Low temperature cracking problem for asphalt pavements in Kazakhstan. In Proceedings of the eighth RILEM International Conference on Mechanics of Cracking and Debonding in Pavements, Nantes, France, 7–9 June 2016; pp. 139–145. [Google Scholar]
- Teltayev, B.; Radovskiy, B. Predicting thermal cracking of asphalt pavements from bitumen and mix properties. Road Mater. Pav. Des. 2018, 19, 1832–1847. [Google Scholar] [CrossRef]
- Radovskiy, B.; Teltayev, B. Viscoelastic Properties of Asphalts Based on Penetration and Softening Point; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Teltayev, B.B.; Amirbayev, E.D.; Radovskiy, B.S. Viscoelastic characteristics of blown bitumen at low temperatures. Constr. Build. Mater. 2018, 189, 54–61. [Google Scholar] [CrossRef]
- Taherkhani, H. Compressive creep behavior of asphalt mixtures. Eng. Procedia 2011, 10, 583–588. [Google Scholar] [CrossRef] [Green Version]
- Hassan, M.M. Relationship between creep time dependent index and Paris low parameters for bituminous mixtures. J. S. Afr. Inst. Civ. Eng. 2013, 2, 8–11. [Google Scholar]
- Soleimanbeigi, A.; Edil, T.B.; Benson, C.H. Creep response of recycled asphalt shingles. Can. Geotech. J. 2013, 51, 103–114. [Google Scholar] [CrossRef]
- Mahan, H.M. Behavior of permanent deformation in asphalt concrete pavements under temperature variation. Al-Qadisiya J. Eng. Sci. 2013, 1, 62–73. [Google Scholar]
- Zhou, Z.G.; Feng, L.; Yuan, X.X.; Xiong, H. Study of the creep damage properties of asphalt mixture under static load. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013. [Google Scholar]
- Jaczewski, M.; Judycki, J. Effects of deviations from thermo-rheologically simple behavior of asphalt mixtures in creep on developing of master curves of their stiffness modulus. In Proceedings of the 9th International Conference on Environmental Engineering, Vilnius, Lithuania, 22–23 May 2014. [Google Scholar]
- Little, D.N.; Button, J.W.; Youssef, H. Development of Criteria to Evaluate Uniaxial Creep Data and Asphalt Concrete Permanent Deformation Potential; National Academies of Sciences, Engineering, Medicine: Washington, DC, USA, 1993; pp. 49–57. [Google Scholar]
- Taherkhani, H.; Collop, A.C. Characterization of uniaxial creep deformation behavior of asphalt mixtures. In Proceedings of the 7th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Rondheim, Norway, 25–27 June 2005; pp. 1–10. [Google Scholar]
- Taherkhani, H.; Afroozi, S. Investigating the creep properties of asphaltic concrete containing nano-silica. Sadhana 2018, 43, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Taherkhani, H.; Arshadi, M.R. Investigating the creep properties of PET-modified asphalt concrete. Civ. Eng. Infrastruct. J. 2018, 51, 277–292. [Google Scholar]
- Li, Y.; Yombah, M.; Temitope, A.A.; Zou, X.; Yang, F.; Li, W.; Jing, H. Research on creep characteristics and influencing factors of cement asphalt composite binder. Math. Probl. Eng. 2020, 2020, 6614920. [Google Scholar] [CrossRef]
- Saoudi, B.S.; Haddadi, S.H. Predicting creep deformation of asphalts modified with polymer using artificial neural networks. Mag. Civ. Eng. 2021, 101, 10106. [Google Scholar]
- Pszczola, M.; Jaczewski, M.; Szydlowski, C. Assessment of thermal stresses in asphalt mixtures at low temperatures using the tensile creep test and the bending beam creep test. Appl. Sci. 2019, 9, 846. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Li, B.; Zhang, Y.; Yin, B.; Dai, J. A creep model of asphalt mixture based on variable order fractional derivative. Appl. Sci. 2020, 10, 3862. [Google Scholar] [CrossRef]
- NCHRP 1-37A. Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavements Structures. Final Report; AASHTO: Washington, DC, USA, 2004. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Rossi, C.O. Steady-state creep of asphalt concrete. Appl. Sci. 2017, 7, 142. [Google Scholar] [CrossRef] [Green Version]
- Iskakbayev, A.; Teltayev, B.; Rossi, C.O.; Yensebayeva, G. Determination of nonlinear creep parameters for hereditary materials. Appl. Sci. 2018, 8, 760. [Google Scholar] [CrossRef] [Green Version]
- Teltayev, B.; Iskakbayev, A.; Rossi, O.C. Regularities of creep and long-term strength of hot asphalt concrete under tensile. Functional Pavement Design. In Proceedings of the 4th Chinese-European Workshop on Functional Pavement Design, Delft, The Netherlands, 29 June–1 July 2016; pp. 169–178. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.; Andriadi, F.; Estayev, K.; Suppes, E.; Iskakbayeva, A. Experimental research of creep, recovery and fracture processes of asphalt concrete under tension. In Proceedings of the 24th International Congress of Theoretical and Applied Mechanics, Montreal, QC, Canada, 22–26 August 2016. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.I.; Rossi, C.O. Deformation and strength of asphalt concrete under static and step loadings. In Proceedings of the AIIT International Congress on Transport Infrastructure and Systems (TIS 2017), Rome, Italy, 10–12 April 2017; Transport Infrastructure and Systems: Rome, Italy, 2017; pp. 3–8. [Google Scholar]
- ST RK 1225-2019. Road, Airfield Asphalt Concrete Mixtures and Asphalt Concrete; Technical Specifications: Astana, Kazakhstan, 2019. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Yestayev, K.Z.; Abu, B.D. Long-term strength of asphalt concrete and its applications. Constr. Build. Mater. 2020, 244, 1–11. [Google Scholar] [CrossRef]
- ST RK 1373-2003. Bitumens and Bitumen Binders. Oil Road Viscous Bitumens; Technical specifications: Astana, Kazakhstan, 2013. [Google Scholar]
- Superpave Series. Performance graded asphalt binder specification and testing, No. 1 (SP-1), 3rd ed.; Asphalt Institute Inc.: Lexington, KY, USA, 2001. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.I.; Andriadi, F.K. Patent of the Republic of Kazakhstan for invention 33244. In Device for Determining the Mechanical Characteristics of Materials under Tension; Springer: Astana, Kazakhstan, 2018. [Google Scholar]
- Rabotnov, Y.N. Balance of the elastic medium with an aftereffect. Appl. Math. Mech. 1948, 12, 53–62. [Google Scholar]
- Rabotnov, Y.N. Solid Mechanics; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Rabotnov, Y.N. Creep of Structures Elements; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Mechanics of Solids; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Iskakbayev, A.; Teltayev, B.; Alexandrov, S. Determination of the creep parameters of linear viscoelastic materials. J. Appl. Math. 2016, 2016, 6568347. [Google Scholar] [CrossRef] [Green Version]
- Iskakbayev, A.I.; Teltayev, B.B.; Yensebayeva, G.M.; Kutimov, K.S. Computer modeling of creep for hereditary materials by Abel’s Kernel. News NAS RK. Ser. Geol. Tech. Sci. 2018, 431, 66–76. [Google Scholar]
- Zhurinov, M.Z.; Iskakbayev, A.I.; Teltayev, B.B.; Kutimov, K.S. Modeling of hereditary materials relaxation by Abel kernel. News NAS RK. Ser. Geol. Tech. Sciences. 2020, 6, 254–260. [Google Scholar] [CrossRef]
- Nadai, A. Theory of Flow and Fracture of Solids; MacGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Hill, R. Mathematical Theory of Plasticity; Oxford University Press Inc.: New York, NY, USA, 1950. [Google Scholar]
- Newton, I.S. Philosophia Naturalis Principia Mathematica; Juffu Societ atis Regie ac Typis Josephi Streater; Prostat apud Plures Bibliopolas: London, England, 1687. [Google Scholar]
- Newton, I.S. Mathematical Principles of Natural PhilosophyTranslated from Latin and Comments by Krylov, A.N., Academician; Nauka: Moscow, Russia, 1989. [Google Scholar]
- Reiner, M. Ten Lectures on Theoretical Rheology; Rubin Mass: Jerusalem, Israel, 1943. [Google Scholar]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers; Khimiya: Moscow, Russia, 1977. [Google Scholar]
- Malkin, A.Y.; Isayev, A.I. Rheology. Concepts, Methods and Applications, 2nd ed.; ChemTec Publishing: Toronto, ON, Canada, 2012. [Google Scholar]
- Trouton, F.T. On the coefficient of viscous traction and its relation to that of viscosity. Proc. R. Soc. London. Ser. A 1906, 77, 426–440. [Google Scholar]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Frenkel, Y.I. The Kinetic Theory of Liquids; Nauka: Leningrad, Russia, 1975. [Google Scholar]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of Rate Processes; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Fox, T.G.; Gratch, S.; Loshaek, S. Viscosity relationship for polymers in bulk and concentrated solutions. In Rheology. Theory and Applications; Eirich, F.R., Ed.; Academic Press Inc.: New York, NY, USA, 1956; Volume 1, pp. 431–492. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).