1. Introduction
In a wireless communication network, the location of user equipment (UE) must be kept to successfully connect an incoming call to the UE. Mobility management in wireless communication networks consists of two important processes: location registration and paging [
1,
2,
3]. To provide successful mobility management services, the wireless communication network consists of non-overlapped tracking area (TA). Several TAs constitute a TA list (TAL). When a UE moves to another TA whose TAL is different from the stored TAL in the mobility management entity (MME) database, registration process is performed. When an incoming call to a UE occurs, a paging procedure is performed to connect it to the UE. MME sends paging message to all base stations in a TA whose TAL is stored in MME. In general, there exists a trade-off relation to treat the signaling cost between the location registration and paging [
2,
4,
5,
6,
7]. So far, many studies have been conducted to reduce the total signaling cost for registration and paging [
4,
8,
9,
10,
11,
12,
13].
Various results on mobility management schemes to minimize the total signaling cost have been proposed, such as zone-based registration [
14,
15,
16], movement-based registration [
5,
17], distance-based registration [
18,
19,
20,
21], TAL-based registration [
11,
22], and so on. Among them, Grigoreva et al. [
10] have proposed a registration scheme with flexible TAL forming to reduce total signaling cost for automotive users in LTE-advanced communication network using information of UE’s moving direction. In this scheme, based on the known geographical area of the trace, its map, and the UE’s moving statistics, the UE’s moving direction can be predicted. Furthermore, they proposed to form TALs not only as rings of TAs, but also as sectors of different sizes that depend on the most probable movement angle. Through a simulation analysis, the performance of the proposed scheme was compared with the movement-based and distance-based registration schemes. However, their study did not present user’s accurate mobility and corresponding analytical model to evaluate its performance and show its superiority. Note that the improved TAL-based algorithm proposed by Jang and Baek [
11] did not consider the UE’s mobility prediction.
In this study, we present a registration scheme considering mobility prediction and corresponding flexible TAL forming. In this scheme, based on mobility prediction and corresponding TAL forms, a new TAL was constructed such that the registration cost can be minimized. We also newly present a semi-Markov process model for the flexible registration scheme with TAL forming. In addition, a simulation study was performed using RAPTOR [
23] to validate the analytical results. Its performance was compared with those of distance-based [
20,
21] and TAL-based registration schemes [
11,
22] previously proposed in LTE networks.
This paper is composed of as follows:
Section 2 introduces the registration scheme with flexible TAL forming based on the prediction of UE’s moving direction, where two different environments are considered: urban and rural. In
Section 3, the signaling cost of the proposed scheme is analyzed using the semi-Markov process model. In
Section 4, the simulation model is explained. Numerical results on the performance of the proposed scheme are presented in
Section 5. Finally,
Section 6 provides conclusions of this paper.
2. Registration Scheme with Flexible TAL Forming
In this study, we present a registration scheme considering mobility prediction and corresponding flexible tracking area list (TAL) forming, which is similar to that present in [
10] from the viewpoint of basic concept. However, the previous study on mobility prediction and flexible TAL did not present user’s accurate mobility and corresponding analytical model to evaluate its performance. Thus, we constructed user’s accurate mobility and corresponding analytical model from the viewpoint of the mobility prediction and flexible TAL forming.
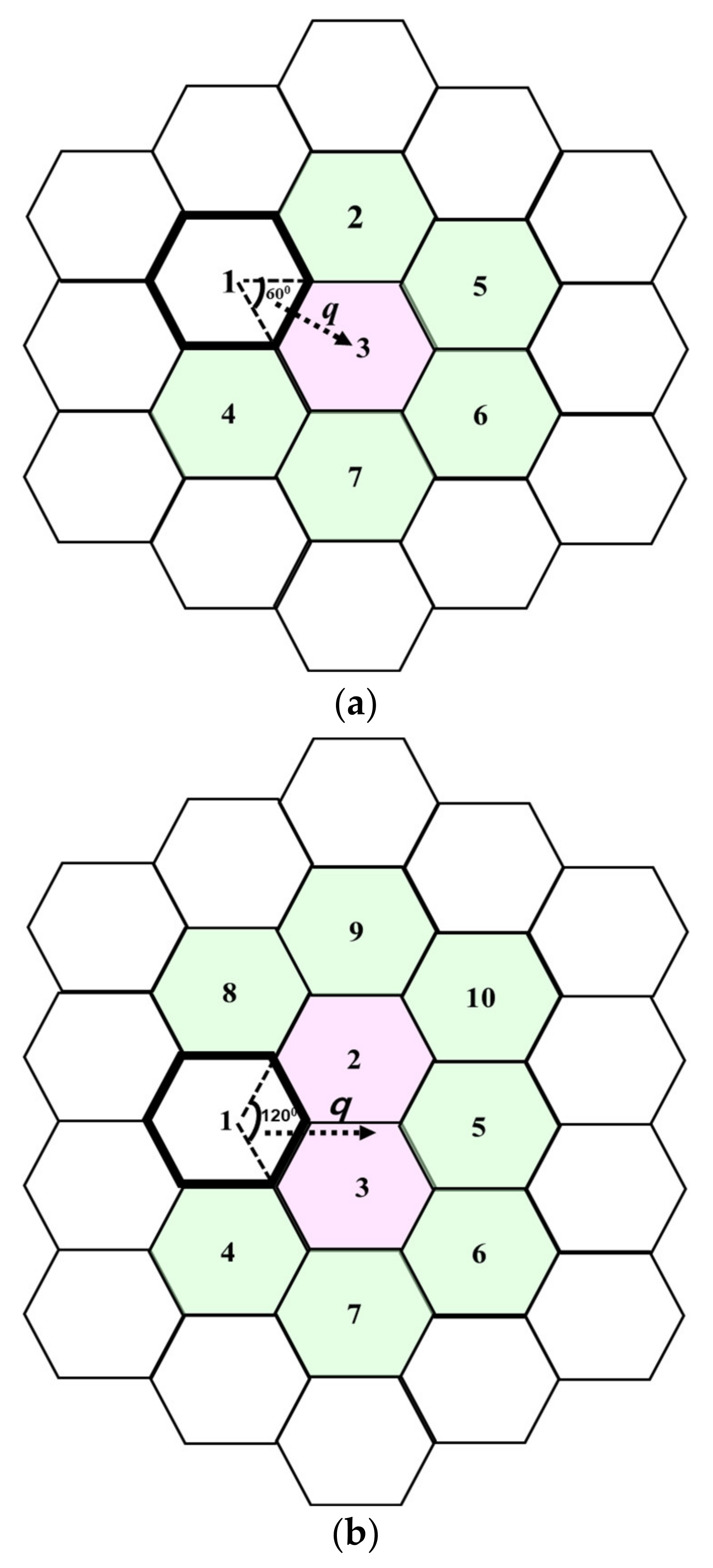
In this scheme, we used mobility trace of certain residing area for each UE. Based on a known geographical area of the trace, its map, and statistics from previously studied results, we deployed two different cell sizes for urban and rural parts of the area as in [
10]. In
Figure 1, a bold frame is the initial cell (cell 1), where the UE has registered its location. In this study, it is assumed that a TA consists of one cell for convenience of analysis. Allocated TAL (or cells) for the UE is marked in colored cells and the predicted direction angle (with moving probability to the direction,
q) is shown in the dotted line.
In the urban area with restricted moving environments under compact road structure of small sector, the UE can move to the center cell with an angle of 60° and a predicted direction of q. On the other hand, an angle of 120° is assumed for rural environments with relatively wide moving roads (big sector).
In both cases, the following mobility model is considered:
- (1)
The UE predicts the movement direction based on the accumulated past data “every time the UE performs location registration (or leaves the current location area)” and configures the location area accordingly, (The UE moves to the center cell(s) of new location area with probability q).
- (2)
When moving between cells in the location area, it moves according to the random walk model (that is, the probability of selecting one of the 6 surrounding cells is the same).
First, let us consider urban environment in
Figure 1.
The UE registering in cell 1 can enter cell 3 with probability q or enter any one of the remaining five cells with probability (1 − q)/5. If it enters one of the three neighboring cells that are not in the current TAL, it will register its location.
The UE entering cell 3 can enter any one of the six neighboring cells with equal probability, 1/6. Similarly, the UE entering cell 2 can enter any one of the six neighboring cells with probability 1/6. Such a mobility model is called a (symmetric) random walk model. Note that movements of the UE registered in cell 1 are not random walks, although all remaining movements are random walks.
If the UE moves to one of the neighboring cells that is not in the current TAL, it will register its location and a new TAL is set up so that entered cell is cell 1 of
Figure 1.
Next, let us consider a rural environment in
Figure 1, which is very similar to an urban environment.
The UE registering in cell 1 can enter cell 2 or cell 3 with probability q or enter any one of the remaining four cells with probability (1 − q)/4. If it enters one of the two neighboring cells that is not in the current TAL, it will register its location.
The UE entering cell 2 can enter any one of the six neighboring cells with probability 1/6. Similarly, the UE entering cell 3 can enter any one of the six neighboring cells with probability 1/6. Note that the movements of the UE that registered in cell 1 are not random walks, although all remaining movements are random walks.
If the UE moves to one of the neighboring cells that is not in current TAL, it will register its location and a new TAL is set up so that entered cell is cell 1 of
Figure 1.
To analyze the performance by adopting a semi-Markov process model, we assume the random walk model when the UE moves to another cell except for movements of the UE that have been registered in the current cell.
Note that in the ring-based TAL scheme [
22], which is previously proposed in LTE network, the TAL is allocated only when the future direction cannot be predicted. A central-policy is then adopted in the scheme. For example, the UE registers its new TAL such that the central cell (cell 3 in urban area or cells 2 and 3 in the rural area) is included in the new TAL.
3. Modeling and Performance Analysis
To analyze the total cost (registration and paging cost) on radio channels, we defined the following notations:
U: The location registration cost for one registration
CU: The location registration cost in an hour
V: The paging cost for one cell
CP: The paging cost in an hour
Tc: The interarrival time between two calls (r.v., Tc ~ Exp[λc], E(Tc) = 1/λc)
Tm: The time spent in a cell (r.v., E(Tm) = 1/λm)
: The Laplace-Stieltjes Transform for Tm (=)
Rm: The remaing time from the call occurrence to the time the UE moves out of the cell (r.v.)
Adopting the additional nature of Poisson processes [
24], we assumed that there are incoming calls with mean 1/
λin and outgoing calls with mean 1/
λout from total calls with mean 1/
λc = 1/(
λin +
λout).
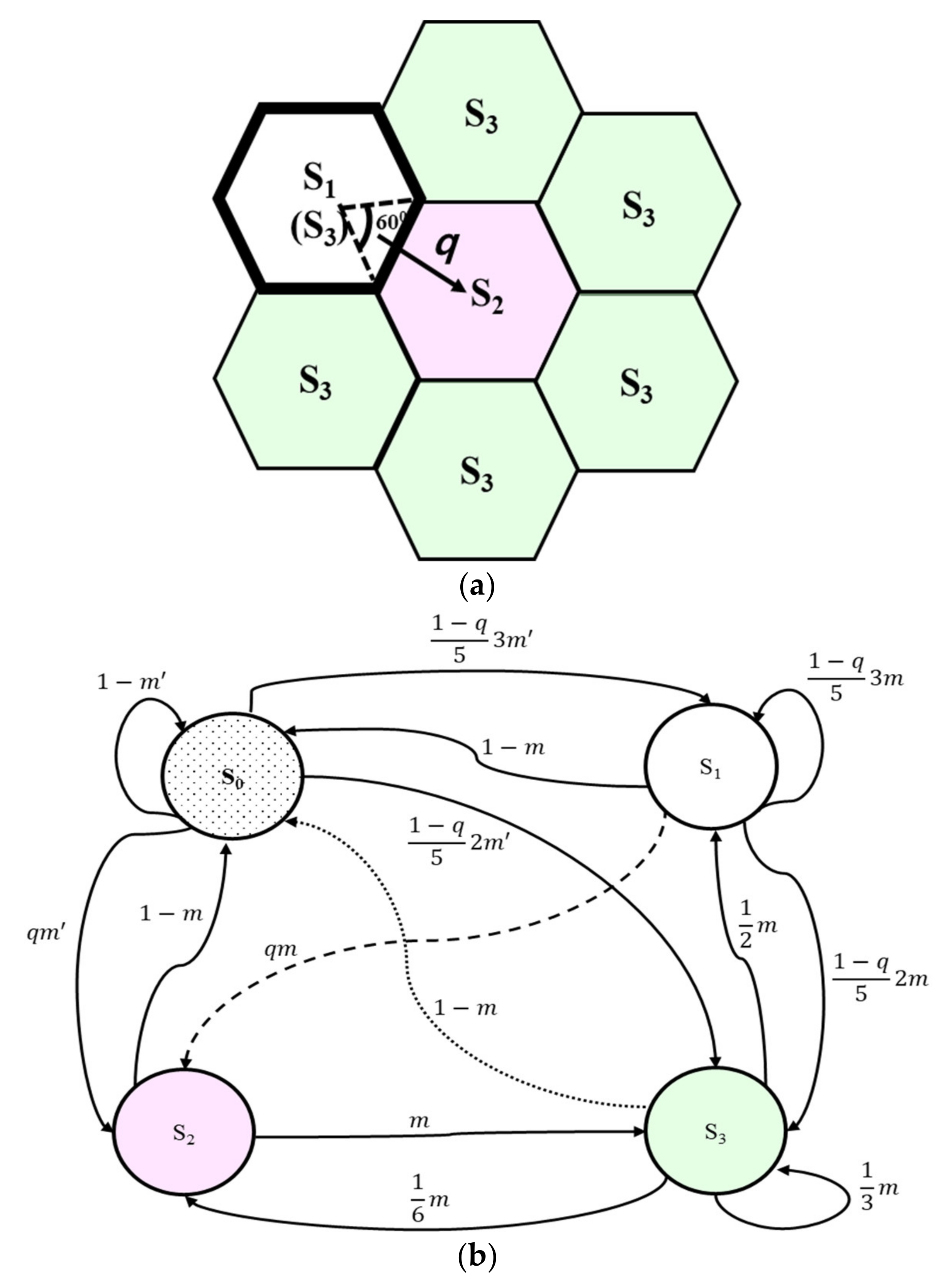
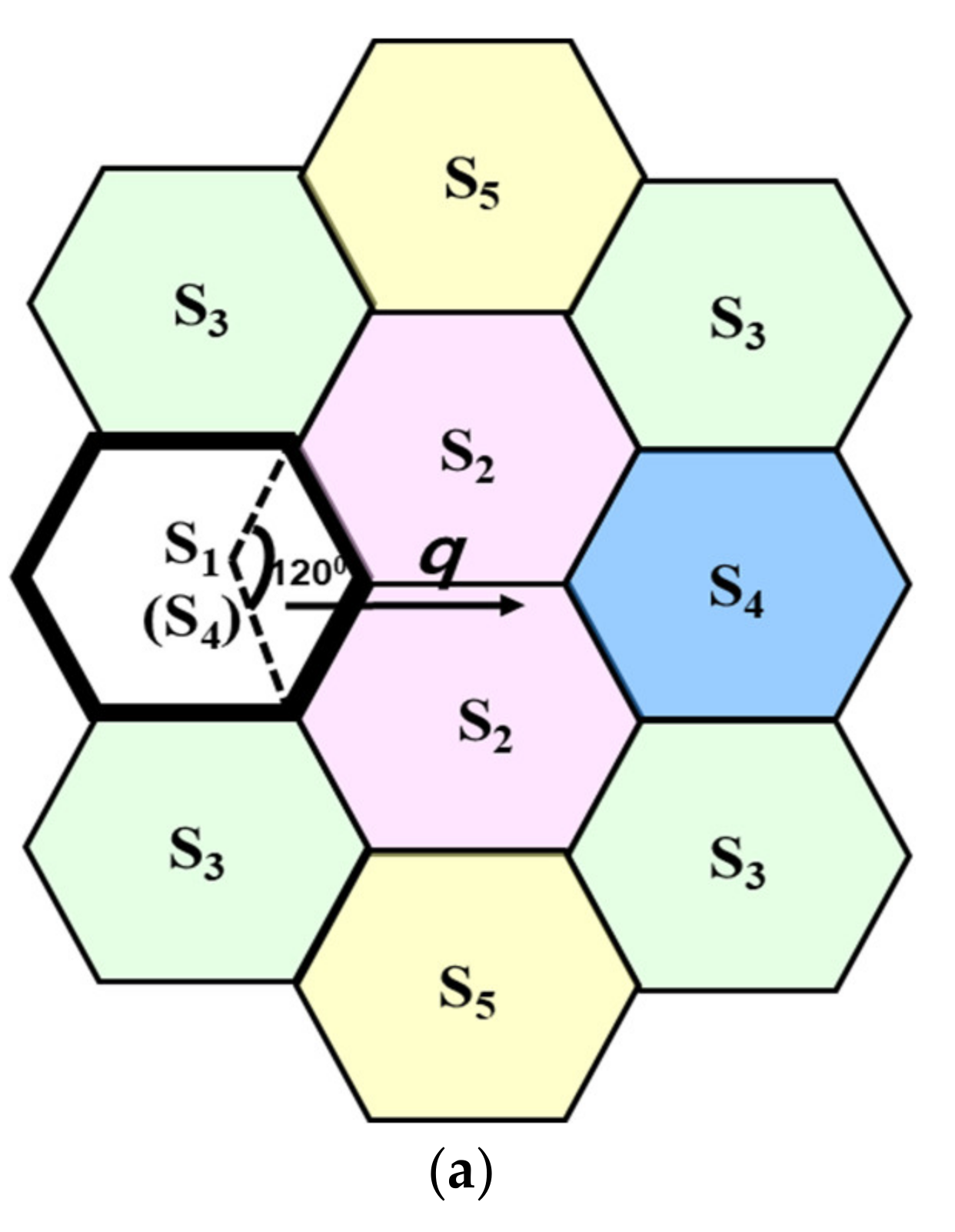
For each case of urban and rural areas, we define the following states to obtain the registration cost as shown in
Figure 2 (urban area) and
Figure 3 (rural area), respectively.
- ○
State S1: The state that UE is in the initial cell, where the user requires registration and forms new TAL. In an urban case, due to random walk assumption, the state S1 changes to S3 after the user moves to the center cell (cell 3). For the rural case, if the user moves to cell 2 or cell 3, the S1 changes to S4. On the other hand, when the user moves into outer cells which are not included in the same TAL, the state S1 does not change and another registration is requested.
- ○
State S2: The state that UE is in central cells (cell 3 in urban area, and cell 2 or 3 in rural area) depicted as S2.
- ○
State S3: The state that UE is in outer cells.
- ○
State S4: The state that UE is in two outer cells (cell 1 or 5) in the rural environment.
- ○
State S5: The state that UE is bottom and top cells (cell 7 or 9) in the rural case.
- ○
State S
0: The state that a call occurs to/from the UE and the cell is changed to central cell. Note that state S
0 is related to implicit registration [
4,
7,
25]. That is, when an incoming or outgoing call to/from the UE occurs, the UE’s location can be updated without additional registration cost.
Based on the states’ definition, Markov-chain models can be obtained for urban and rural areas as shown in
Figure 2 and
Figure 3, respectively.
3.1. Urban Environment
Now, let us consider state transition diagram for urban environment as shown in
Figure 2. There are two kinds of transitions: one is entering a cell and another one is call occurrence.
Let us consider the case of entering a cell before call occurrence. The probability that a UE moves to a neighboring cell before a call occurs,
m, is as follows:
Therefore, the UE registering in cell 1 (state S1) can enter cell 3 (state S2) with a probability of qm or enter any one of the remaining 5 cells with a probability of (1 − q)m/5. If it enters one of 3 neighboring cells that are not in the current TAL, it will register its location (state S1).
If a call occurs to/from the UE before the UE registering in cell 1 (state S
1) enters a neighboring cell (state S
2 or state S
3), the state of the UE becomes state S
0. Such a state transition occurs with a probability of 1 −
m =
P[
Tc ≤
Tm]. Note that, in this case, cell is not changed. However, a new TAL is set up (by implicit registration) and the cell becomes cell 1 in
Figure 1.
One more important probability in
Figure 2 is that, given that a call has already occurred, UE enters a neighboring cell before another call occurs,
m’ =
P[
Tc >
Rm].
To calculate
m’ =
P[
Tc >
Rm], let us consider
Rm. The density function of
Rm,
fr(
t) is from a random observer property [
20,
21]:
The Laplace–Stieltjes transform for the distribution can be written as follows:
From the state transition diagram, we can obtain transition probability matrix
Purban as follows:
3.2. Rural Environment
Now, let us consider state transition diagram for rural environment as shown in
Figure 3.
The UE registering in cell 1 (state S1) can enter cell 2 or cell 3 (state S2) with a probability of qm or enter any one of the remaining four cells with a probability of (1 − q)m/4. If it enters one of the two neighboring cells that are not in the current TAL, it will register its location (state S1).
If a call occurs to/from the UE, before the UE registering in cell 1 (state S
1) enters a neighboring cell (state S
2 or state S
3), the state of the UE becomes state S
0. Such a state transition occurs with a probability of 1 −
m =
P[
Tc ≤
Tm]. Note that in this case, cell is not changed. However, a new TAL is set up (by implicit registration) and the cell becomes cell 1 in
Figure 1.
Similar to an urban environment, we can obtain transition probability matrix
Prural for a rural environment as follows:
3.3. Semi-Markov Process Model
In both cases, the time spent in state S0 is different from the time spent in other states. The time spent in state S0 is the interval from the call occurrence to/from a UE in a cell to the time it moves to a neighboring cell or when a call occurs again. On the other hand, the time spent in other states except for state S0 is the interval from the time the UE enters a cell to the time it moves to a neighboring cell or when a call occurs.
To properly analyze the performance, different time spent in each state should be considered. First, the time spent in state S
0 can be expressed as follows:
Its mean can be obtained as follows:
Next, the time spent in other states except for state S
0 can be expressed as follows:
Its mean
τi (
i = 1, 2, …, 5) can be obtained as follows:
To obtain the steady-state probability,
, considering different time spent in a state, we first calculated the steady-state probability
for the typical Markov chain [
24] with transition probability matrix
P (
Purban or
Prural) using the following balanced equations:
Finally, the steady-state probability of the semi-Markov process can be obtained as follows:
The total signaling cost on radio channels is the sum of the registration cost and the paging cost. The registration cost per UE per unit time,
, can be obtained as follows:
where
B is the set of states for boundary cells in each TAL and
is the probability that a UE in state
j enters a neighboring cell to request location registration.
Assuming a simultaneous paging method, the paging cost per UE per unit time is as follows:
where
is the number of cells in each TAL (
= 7 in urban, and
= 10 in rural). Finally, total cost can be obtained as follows:
4. Simulation
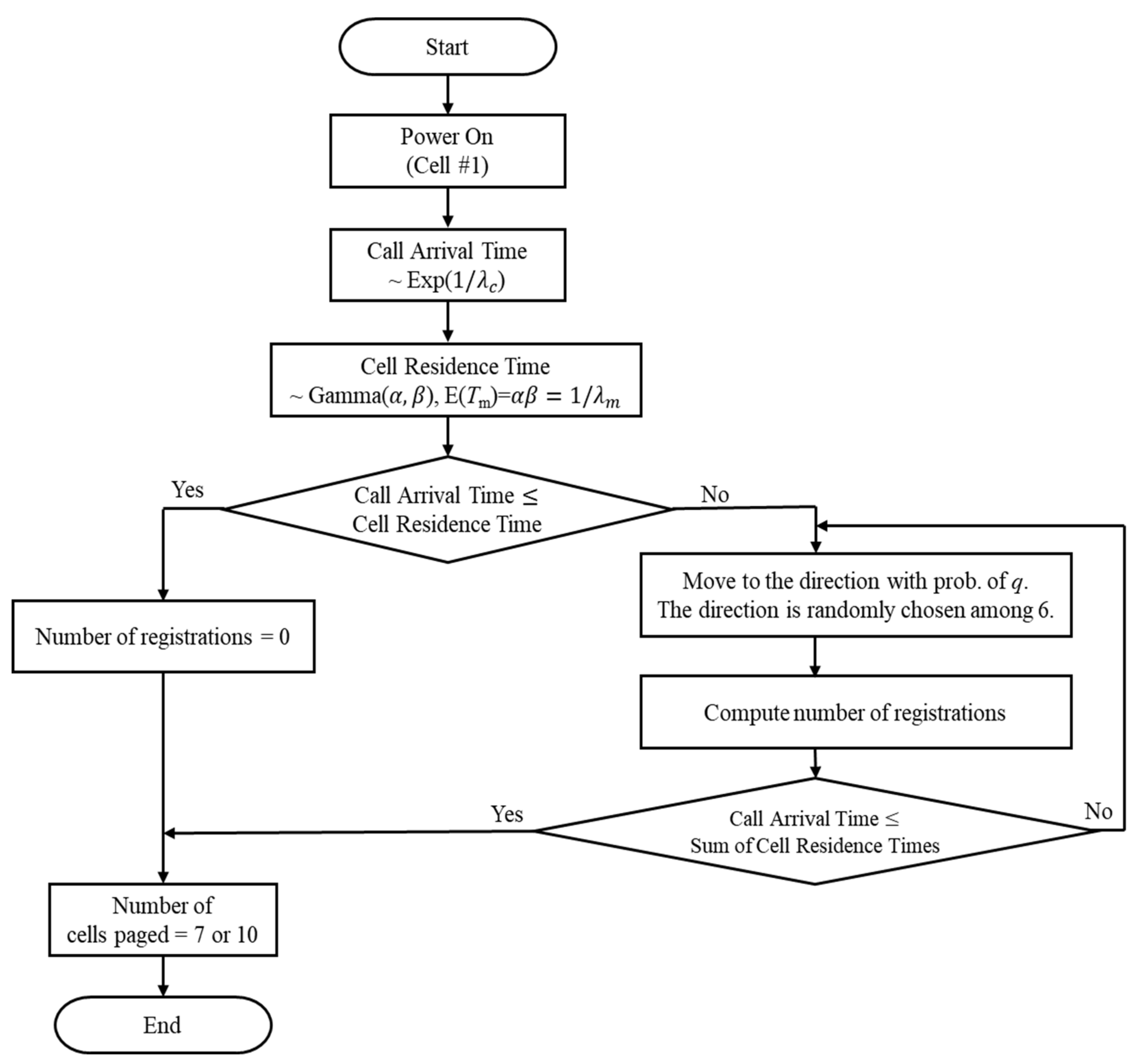
To evaluate the accuracy of the analytical results, we performed computer simulations using RAPTOR [
23]. As shown in
Figure 4, a UE first turns on the power in cell 1 and moves to other cells until it receives another incoming call.
The simulation was carried out with the following procedures.
- (i)
Every UE turns on the power in cell number 1.
- (ii)
The call arrival time (incoming or outgoing) to the UE follows an exponential distribution with a mean of 1/λc (Tc ~ Exp[λc]).
- (iii)
The time spent in a cell follows a gamma distribution with a mean of 1/
λm [
25] (
Tm ~ Gamma(
α,
β), E(
Tm) =
αβ = 1/
λm).
- (iv)
If the call occurrence time is less than the time spent in a cell, the UE does not require registration as the system knows the UE’s location without any additional registration cost.
- (v)
Otherwise, when the call arrival time is greater than or equal to the time in a cell, the UE moves to the direction with a probability of q. Note that the moving direction is randomly chosen among six directions. The number of registrations can be updated whenever the UE crosses the new TA.
- (vi)
If the call arrival time is less than equal to the sum of time spent in a cell, the simulation procedure of the UE stops.
- (vii)
Finally, the paging cost (number of paged cells) is evaluated. Note that the paging cost is 7 in an urban environment and 10 in a rural environment.
In the simulation model, the process for 1000 UEs was repeated. After 10 simulations, final results for 10,000 UEs were evaluated to compute average number of registrations.
5. Numerical Results
To obtain numerical results, the following parameters were assumed:
Incoming and outgoing calls were generated according to the Poison Process with mean 1/λin and 1/λout, respectively. The time spent in a cell followed a gamma distribution with parameters 1 and 1/λm.
Figure 5 shows the number of registrations for each UE with various call-to-mobility ratio (CMR) and
q when
Nc = 7 (urban case). From the numerical results, it was observed that the number of registrations decreased as the moving probability,
q, to the predicted direction increased, and the number of registrations decreased as CMR increased. Above all, it was observed that analytical and simulation results were very close. It could be concluded that the semi-Markov process model gave accurate results since differences between analytical results and simulation results were less than 1.42% on average. Therefore, subsequent numerical results were obtained using the semi-Markov process model. Therefore, subsequent mathematical results were obtained using the semi-Markov process model.
Figure 6 shows total costs for various CMR and
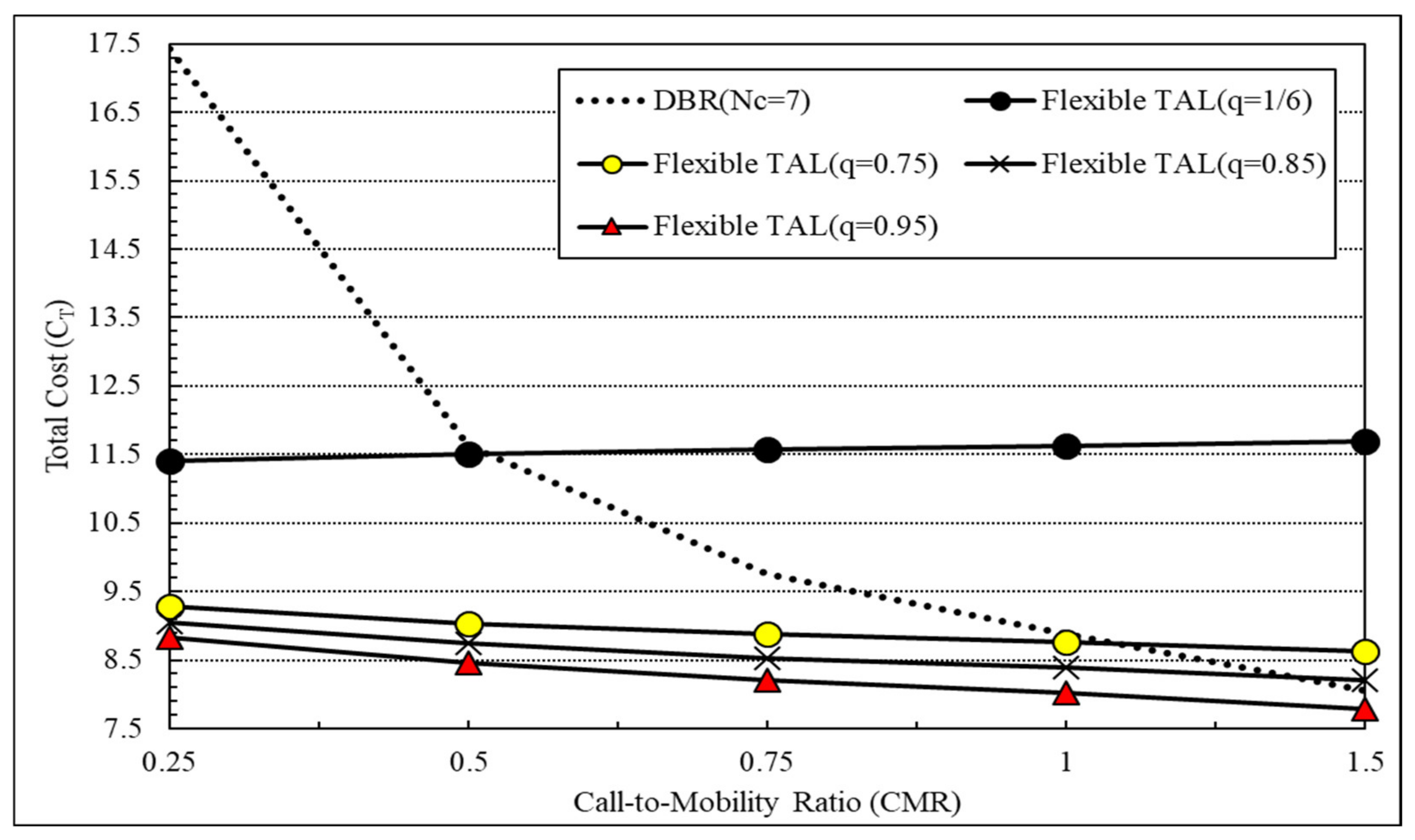
q in urban case. From the figure, it was observed that the total cost decreased as CMR increased because of less cell residence time, and that the total cost decreased as
q increased because of mobility prediction effect. It was also observed that, if CMR < 1 corresponding to current small cell configurations was considered, the registration scheme with our flexible TAL forming outperformed the distance-based registration (DBR) scheme with
Nc = 7 when
q ≥ 0.75, although the registration cost of the proposed scheme with random walk mobility (
q = 1/6) was higher compared to the performance of the DBR.
Figure 7 shows total costs for various CMR and
q in rural case. Similar to urban case, from the figure, it was observed that, even though absolute value of the total cost is large compared to urban case, the total cost decreased as CMR increased, and the total cost decreased as
q increased. It was also observed that, if CMR < 1 corresponding to current small cell configurations was considered, the registration scheme with our flexible TAL forming outperformed the original TAL scheme with
Nc = 10 at
q ≥ 0.85.
From numerical results, we had the following observations:
- (i)
The number of registrations (or registration cost) decreased as the CMR increased because the UE resided longer in a cell with less registrations required.
- (ii)
The number of registrations decreased as the moving probability,
q, to the predicted direction increased. Note that, as
q increased, the number of UEs moving to the center cell (the state S
2 in
Figure 2 and
Figure 3) increased while the registration cost decreased.
- (iii)
If CMR < 1 corresponding to current small cell configurations was considered, the registration scheme with our flexible TAL forming outperformed the typical DBR and the original TAL-based scheme.
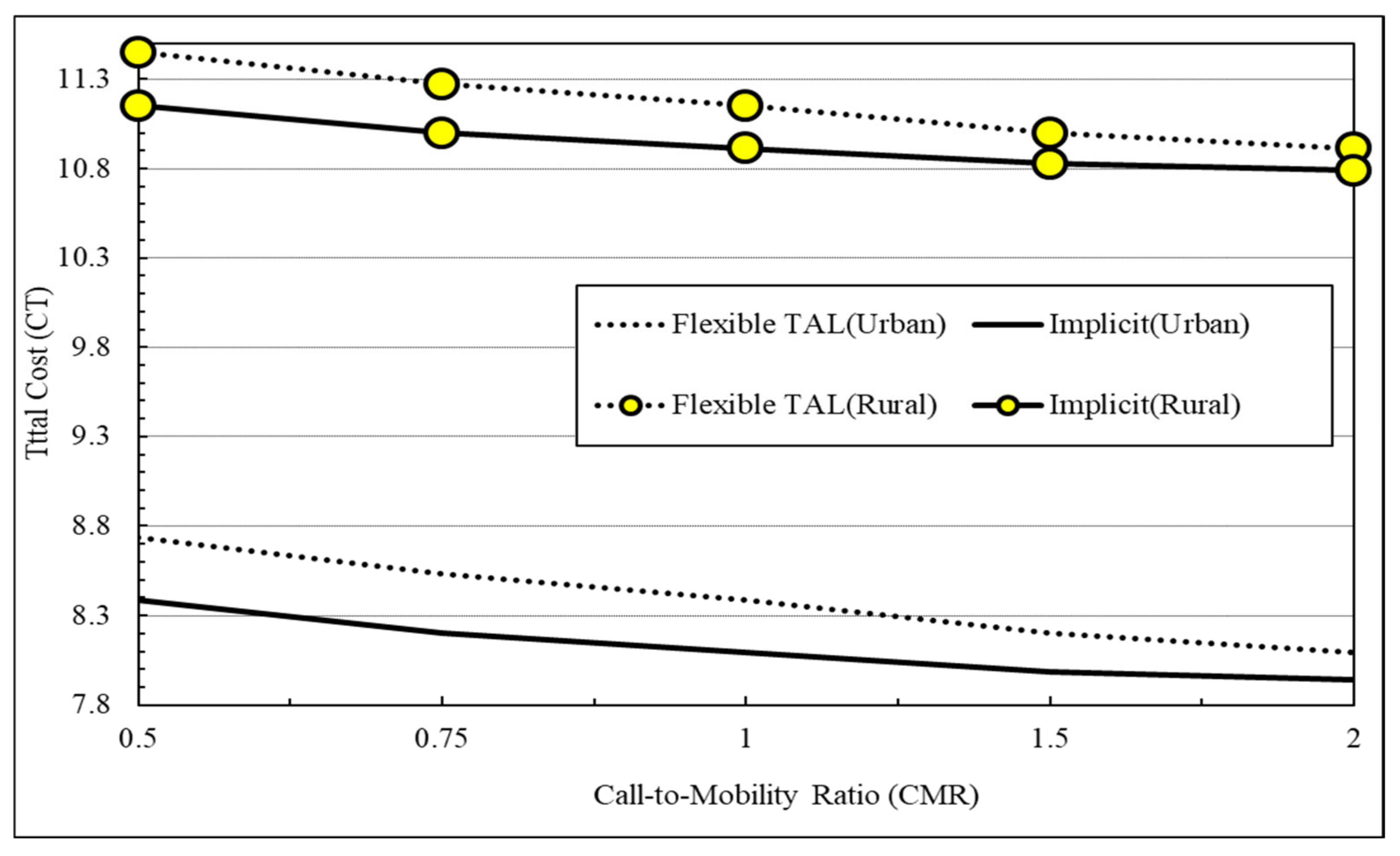
Finally,
Figure 8 shows performance improvement by implicit registration on total signaling cost. In general, when implicit registration is adopted, the registration cost is reduced. For example, when CMR = 1, if implicit registration is not adopted, the total cost would be 8.384 in the urban case. On the other hand, if implicit registration is adopted, the total cost would be 8.095. In the rural area, the total cost will be also reduced to 10.914 compared to 11.151 when implicit registration is not adopted. From results shown in
Figure 8, the total cost can be decreased by 2.16% if implicit registration is adopted.
6. Conclusions
In this study, we presented a registration scheme considering mobility prediction and corresponding flexible tracking area list (TAL) forming. In this scheme, based on prediction of moving direction and corresponding TAL forms, a new TAL was constructed such that the registration cost can be minimized.
This study also presented a semi-Markov process model for the registration scheme with flexible TAL forming assuming two different environments: urban and rural. In this scheme with flexible TAL forming, the moving direction of a user’s equipment (UE) could be predicted (with the probability q) using UE’s moving information in the geographical area.
To validate the semi-Markov process model, computer simulations were performed using flowchart-based RAPTOR. Through simulation studies, it was observed that analytical and simulation results were very close with a relative error of 1.4%. Numerical results for various system environments using the semi-Markov process model showed that the registration cost decreased as the moving probability to the predicted direction, q, increased. Results also showed that when call-to-mobility ratio (CMR) was less than or equal to 1 that corresponds to current small cell configurations, the registration scheme with flexible TAL forming outperformed the distance-based registration scheme when q was high (q ≥ 0.75 in an urban case with a small sector, q ≥ 0.85 in a rural case with a big sector). In addition, results showed that the total cost would be decreased on average 2.2% by adopting the implicit registration.
This study presented analytical results only for a small number of TAs (7 and 10). Further studies on the registration scheme with flexible TAL need to be performed by taking into account a larger number of TAs. In that case, the registration scheme with flexible TAL forming under the selective paging method can also be studied to reduce the paging cost.