Towards a Vectorial Approach to Predict Beef Farm Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Aim and Scope
2.2. The Dataset
2.3. Standard vs. Vectorial Approaches: Genetic Programming
2.4. Standard vs. Vectorial Approaches: Experimental Settings
3. Results
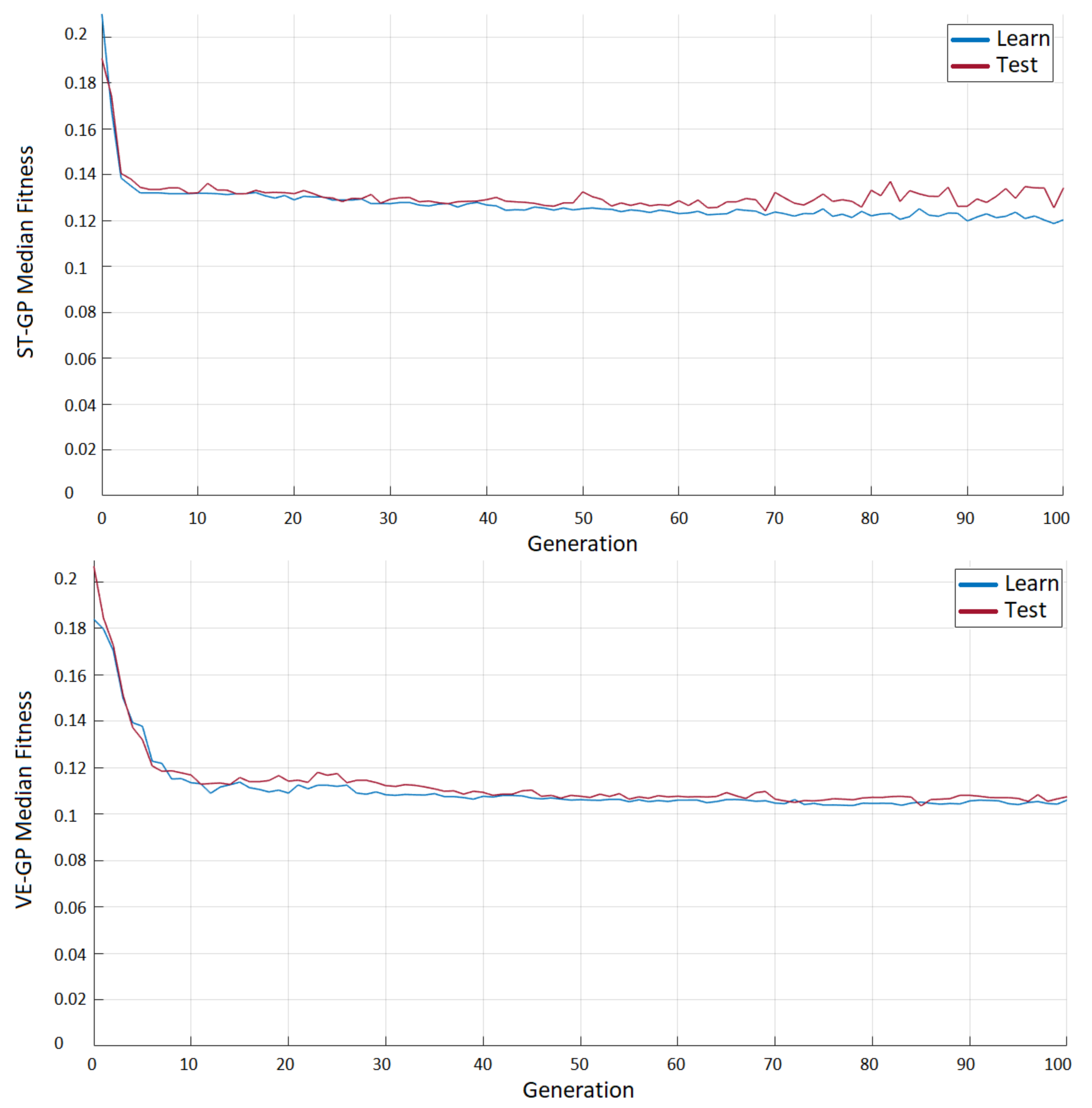
3.1. ST-GP vs. VE-GP
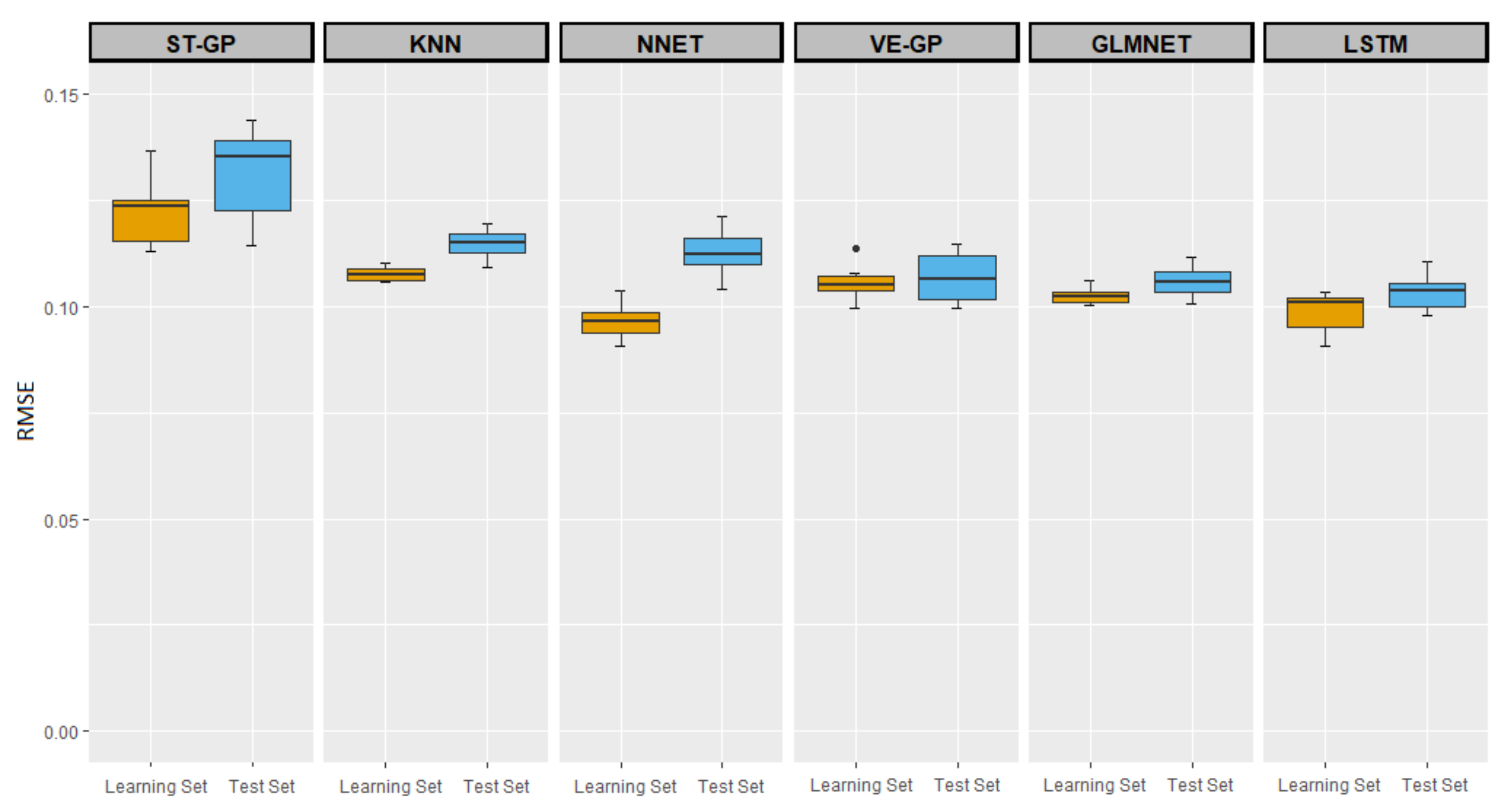
3.2. Comparisons of ST-GP and VE-GP with Other ML Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PLF | Precision Livestock Farming |
| ML | Machine Learning |
| ANABORAPI | National Association of Piemontese Cattle Breeders |
| GP | Genetic Programming |
| ST-GP | Standard Genetic Programming |
| VE-GP | Vectorial Genetic Programming |
| EA | Evolutionary Algorithm |
| KNN | k-Nearest Neighbors |
| NN | Neural Network |
| LM | Linear Model |
| GLMNET | Generalized Linear Model with Elastic Net Regularization |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
References
- Berckmans, D. Precision livestock farming technologies for welfare management in intensive livestock systems. Rev. Sci. Tech. 2014, 33, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Berckmans, D.; Guarino, M. Precision livestock farming for the global livestock sector. Anim. Front. 2017, 7, 4–5. [Google Scholar] [CrossRef] [Green Version]
- Cole, J.B.; Newman, S.; Foertter, F.; Aguilar, I.; Coffey, M. Breeding and Genetics Symposium: Really big data: Processing and analysis of very large datasets. J. Anim. Sci. 2012, 90, 723–733. [Google Scholar] [CrossRef] [PubMed]
- Lokhorst, C.; de Mol, R.M.; Kamphuis, C. Invited review: Big Data in precision dairy farming. Animal 2012, 13, 1519–1528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berckmans, D. General introduction to precision livestock farming. Anim. Front. 2017, 7, 6–11. [Google Scholar] [CrossRef]
- Halachmi, I.; Guarino, M. Editorial: Precision livestock farming: A ’per animal’ approach using advanced monitoring technologies. Anim. Int. J. Anim. Biosci. 2016, 10, 1482–1483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liakos, K.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morota, G.; Ventura, R.V.; Silva, F.F.; Koyama, M.; Fernando, S.C. Big data analytics and precision animal agriculture symposium: Machine learning and data mining advance predictive big data analysis in precision animal agriculture. J. Anim. Sci. 2018, 96, 1540–1550. [Google Scholar] [CrossRef] [PubMed]
- Gahegan, M. Is inductive machine learning just another wild goose (or might it lay the golden egg)? Int. J. Geogr. Inf. Sci. 2003, 17, 69–92. [Google Scholar] [CrossRef]
- Craninx, M.; Fievez, V.; Vlaeminck, B.; Baets, B. Artificial neural network models of the rumen fermentation pattern in dairy cattle. Comput. Electron. Agric. 2008, 60, 226–238. [Google Scholar] [CrossRef]
- Gonzalez-Recio, O.; Rosa, G.J.M.; Gianola, D. Machine learning methods and predictive ability metrics for genome-wide prediction of complex traits. Livest. Sci. 2014, 166, 217–231. [Google Scholar] [CrossRef]
- Yao, C.; Zhu, X.; Weigel, K.A. Semi-supervised learning for genomic prediction of novel traits with small reference populations: An application to residual feed intake in dairy cattle. Genet. Sel. Evol. 2016, 48, 84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Associazione Nazionale Allevatori Bovini Razza Piemontese. Available online: http://www.anaborapi.it (accessed on 8 December 2021).
- Bona, M.; Albera, A.; Bittante, G.; Moretta, A.; Franco, G. L’allevamento della manza e della vacca piemontese. Tec. Allev. 2005, 44, 65–129. [Google Scholar]
- Abbona, F.; Vanneschi, L.; Bona, M.; Giacobini, M. A GP approach for precision farming. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Abbona, F.; Vanneschi, L.; Bona, M.; Giacobini, M. Towards modelling beef cattle management with Genetic Programming. Livest. Sci. 2020, 241, 104205. [Google Scholar] [CrossRef]
- Abraham, A.; Nedjah, N.; Mourelle, L.M. Evolutionary Computation: From Genetic Algorithms to Genetic Programming. In Genetic Systems Programming; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Azzali, I.; Vanneschi, L.; Silva, S.; Bakurov, I.; Giacobini, M. A Vectorial Approach to Genetic Programming. In Proceedings of the EuroGP 2019, Leipzig, Germany, 24–26 April 2019. [Google Scholar]
- Azzali, I.; Vanneschi, L.; Bakurov, I.; Silva, S.; Ivaldi, M.; Giacobini, M. Towards the use of vector based GP to predict physiological time series. Appl. Soft Comput. 2020, 89, 106097. [Google Scholar] [CrossRef] [Green Version]
- Koza, J. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Poli, R.; Langdon, W.; McPhee, N. A Field Guide to Genetic Programming; Lulu Enterprises, UK Ltd.: Egham, UK, 2008. [Google Scholar]
- Spiess, A.; Neumeyer, N. An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alfaro-Cid, E.; Sharman, K.; Esparcia-Alcázar, A. Genetic Programming and Serial Processing for Time Series Classification. Evol. Comput. 2014, 22, 265–285. [Google Scholar] [CrossRef]
- Bartashevich, P.; Bakurov, I.; Mostaghim, S.; Vanneschi, L. A Evolving PSO algorithm design in vector fields using geometric semantic GP. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018. [Google Scholar]
- Holladay, K.; Robbins, K.A. Evolution of Signal Processing Algorithms using Vector Based Genetic Programming. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 503–506. [Google Scholar]
- Silva, S. GPLAB—A Genetic Programming Toolbox for MATLAB. 2007. Available online: http://gplab.sourceforge.net/index.html (accessed on 8 December 2021).
- Kuhn, M. Classification and Regression Training [R Package Caret Version 6.0-86]. 2020. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 8 December 2021).
- Lantz, B. Machine Learning with R, 2nd ed.; Packt Publishing: Birmingham, UK; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
| FARM | YEAR | PRIMIPAROUS | PLURIPAROUS | HEIFERS | INTERPARTO |
|---|---|---|---|---|---|
| Farm 1 | 2014 | 22 | 36 | 7 | 365 |
| Farm 1 | 2015 | 10 | 46 | 13 | 375 |
| Farm 1 | 2016 | 16 | 47 | 12 | 381 |
| Farm 1 | 2017 | 14 | 46 | 11 | 375 |
| Farm 1 | 2018 | 16 | 47 | 12 | 374 |
| Farm 2 | 2014 | 11 | 90 | 9 | 396 |
| Farm 2 | 2015 | 10 | 93 | 9 | 391 |
| Farm 2 | 2016 | 9 | 95 | 7 | 380 |
| Farm 2 | 2017 | 7 | 97 | 10 | 387 |
| Farm 2 | 2018 | 9 | 92 | 11 | 385 |
| Farm 3 | 2014 | 7 | 42 | 3 | 414 |
| Farm 3 | 2015 | 4 | 43 | 4 | 439 |
| Farm 3 | 2016 | 4 | 44 | 10 | 452 |
| Farm 3 | 2017 | 10 | 44 | 11 | 425 |
| Farm 3 | 2018 | 9 | 60 | 4 | 473 |
| Variable Name | Variable Description | |
|---|---|---|
| 1 | Consistency for cows, i.e., number of cows | |
| 2 | Consistency for heifers, i.e., number of heifers | |
| 3 | Calving interval in days, based on currently pregnant cows | |
| 4 | Average parity | |
| 5 | __1 | Age at first calving |
| 6 | N. of cows that delivered with easy calving | |
| 7 | N. of primiparous that delivered with easy calving | |
| 8 | _ | Calving ease (EBV for cows) |
| 9 | _ | Birth ease (EBV for heifers) |
| 10 | Birth ease (EBV for A.I. bulls) | |
| 11 | Calving ease (EBV for A.I. bulls) | |
| 12 | UBA referred to bovines 6 months–2 years old | |
| 13 | UBA referred to bovines 4–6 months old | |
| 14 | N. of dead calves in the first 60 days after birth | |
| 15 | Total number of calves born | |
| 16 | Total number of calves born alive | |
| 17 | Percentage of calves born without defects (e.g., Macroglossia, Arthrogryposis) | |
| 18 | _ | Consanguinity calculated on future calves |
| 19 | Y | N. of weaned calves per cow per year (2) |
| 2017 | 2018 | ||||||
|---|---|---|---|---|---|---|---|
COWS | COW_AGE | CALVING_INT | N_CALVING | ||||
| FARM 1- | 104 | 3020 | 387 | 60 | 0.95 | ||
| FARM 2- | 54 | 3112 | 425 | 54 | 0.9 | ||
| FARM 3- | 63 | 2824 | 515 | 48 | 0.69 | ||
| … | 49 | 3131 | 466 | 49 | 0.67 | ||
| 108 | 2766 | 407 | 50 | 0.85 | |||
| 74 | 3448 | 459 | 62 | 0.84 | |||
| 2014–2017 | 2018 | |||||
|---|---|---|---|---|---|---|
COWS | COW_AGE | CALVING_INT | ||||
| FARM 1- | [98, 101, 107, 104] | [2999, 3001, 2998, 3020] | [391, 391, 380, 387] | 0.95 | ||
| FARM 2- | [61, 49, 53, 54] | [3076, 3002, 3056, 3112] | [408, 376, 402, 425] | 0.9 | ||
| FARM 3- | [53, 55, 64, 63] | [2799, 2813, 2802, 2824] | [367, 376, 406, 515] | 0.69 | ||
| … | [31, 36, 47, 49] | [3102, 3075, 3009, 3131] | [434, 480, 461, 466] | 0.67 | ||
| [102, 99, 105, 108] | [2704, 2795, 2789, 2766] | [404, 371, 395, 407] | 0.85 | |||
| [69, 71, 75, 74] | [3401, 3388, 3406, 3448] | [387, 367, 373, 459] | 0.84 | |||
| Parameter | Description |
|---|---|
| ST-GP | |
| Maximum number of generations | 40 |
| Population size | 250 |
| Selection Method | Lexicographic Parsimony Pressure |
| Elitism | Keepbest |
| Initialization Method | Ramped half and half |
| Tournament Size | 2 |
| Subtree Crossover Rate | 0.7 |
| Subtree Mutation Rate | 0.1 |
| Subtree Shrinkmutation Rate | 0.1 |
| Subtree Swapmutation Rate | 0.1 |
| Maxtreedepth | 17 |
| VE-GP | |
| Maximum number of generations | 40 |
| Population size | 250 |
| Selection Method | Lexicographic Parsimony Pressure |
| Elitism | Keepbest |
| Initialization Method | Ramped half and half |
| Tournament Size | 2 |
| Subtree Crossover Rate | 0.7 |
| Subtree Mutation Rate | 0.3 |
| Mutation of aggregate function parameters | 0.2 |
| Maxtreedepth | 17 |
| ML Technique | Parameters |
|---|---|
| knn | k = 15 |
| nnet | size = 7; decay = 0.2 |
| glmnet | = 0.8, = 0.85 |
| LSTM | hidden units = 200; epochs = 50; batchsize = 1; learning algorithm = adam. |
| Variable | % of Use (ST-GP) | % of Use (VE-GP) |
|---|---|---|
| X1 | 70% | 100% |
| X2 | 10% | 10% |
| X3 | 0% | 10% |
| X4 | 50% | 0% |
| X5 __1 | 0% | 10% |
| X6 | 0% | 10% |
| X7 | 0% | 10% |
| X8 _ | 0% | 0% |
| X9 _ | 0% | 0% |
| X10 | 10% | 0% |
| X11 | 0% | 0% |
| X12 | 0% | 0% |
| X13 | 20% | 0% |
| X14 | 70% | 40% |
| X15 | 0% | 80% |
| X16 | 60% | 0% |
| X17 | 30% | 0% |
| X18 _ | 20% | 30% |
| Prediction Model | Fitness on Test | N. of Variables | % of Variables |
|---|---|---|---|
| ST-GP | |||
| model 1 | 0.1335 | 9 | 50% |
| model 2 | 0.1207 | 6 | 33% |
| model 3 | 0.1143 | 11 | 61% |
| model 4 | 0.1383 | 8 | 44% |
| model 5 | 0.1392 | 7 | 39% |
| model 6 | 0.1439 | 7 | 39% |
| model 7 | 0.1395 | 8 | 44% |
| model 8 | 0.1370 | 6 | 33% |
| model 9 | 0.1285 | 15 | 83% |
| model 10 | 0.1184 | 7 | 39% |
| VE-GP | |||
| model 1 | 0.1117 | 5 | 26% |
| model 2 | 0.1016 | 3 | 16% |
| model 3 | 0.1044 | 9 | 47% |
| model 4 | 0.1085 | 8 | 42% |
| model 5 | 0.1134 | 3 | 16% |
| model 6 | 0.0998 | 8 | 42% |
| model 7 | 0.1018 | 4 | 21% |
| model 8 | 0.1149 | 4 | 21% |
| model 9 | 0.0999 | 8 | 42% |
| model 10 | 0.1121 | 3 | 16% |
| STGP | KNN | NN | VEGP | GLMNET | LSTM | |
|---|---|---|---|---|---|---|
| Learning sets | ||||||
| Median | 0.1238 | 0.1074 | 0.0967 | 0.1052 | 0.1025 | 0.1011 |
| Mean | 0.1220 | 0.1077 | 0.0967 | 0.1054 | 0.1025 | 0.0988 |
| Test sets | ||||||
| Median | 0.1353 | 0.1151 | 0.1122 | 0.1065 | 0.1057 | 0.1037 |
| Mean | 0.1314 | 0.1147 | 0.1128 | 0.1068 | 0.1056 | 0.1034 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbona, F.; Vanneschi, L.; Giacobini, M. Towards a Vectorial Approach to Predict Beef Farm Performance. Appl. Sci. 2022, 12, 1137. https://doi.org/10.3390/app12031137
Abbona F, Vanneschi L, Giacobini M. Towards a Vectorial Approach to Predict Beef Farm Performance. Applied Sciences. 2022; 12(3):1137. https://doi.org/10.3390/app12031137
Chicago/Turabian StyleAbbona, Francesca, Leonardo Vanneschi, and Mario Giacobini. 2022. "Towards a Vectorial Approach to Predict Beef Farm Performance" Applied Sciences 12, no. 3: 1137. https://doi.org/10.3390/app12031137
APA StyleAbbona, F., Vanneschi, L., & Giacobini, M. (2022). Towards a Vectorial Approach to Predict Beef Farm Performance. Applied Sciences, 12(3), 1137. https://doi.org/10.3390/app12031137








