Leader-Following Formation Tracking Control of Nonholonomic Mobile Robots Considering Collision Avoidance: A System Transformation Approach

Abstract

In this paper, the obstacle avoidance problem-based leader–following formation tracking of nonholonomic wheeled mobile robots with unknown parameters of desired trajectory is investigated. First, the under-actuated system is transformed into a fully-actuated system by obtaining an auxiliary control variable using the transverse function. Second, by introducing a potential function for each obstacle, the influence of obstacles is considered in trajectory tracking, and the effect of the potential field on mobile robots is taken into account in the system tracking error. Third, the adaptive laws are designed to estimate the unknown parameters of the desired trajectory. Fourth, the results show that the formation error with respect to the actual position and orientation can be arbitrarily small by selecting appropriate design parameters. Finally, simulation examples are used to demonstrate that the proposed control scheme is effective.

1. Introduction

Due to the widespread practical applications of multi-agent systems (MASs) in various fields such as material transportation, environmental detection and civilian tasks, they have attracted the attention of many scholars in the past few decades, and many achievements have been made in the research of MASs, including but not limited to [1,2,3,4,5,6]. The latest technological progress in the field of communication and computing has promoted the development of multi-agents, which can finish complex tasks that cannot usually be accomplished by a single agent. Various vehicles, such as aerial vehicles [7], unmanned surface vehicles [8], and mobile robots [9,10], are used to enrich multi-agent systems. As one of the most attractive topics in the field of multi-agent systems, formation control has formed several typical control methods in many years of robot control research, including: leader–following method [11,12], virtual structure method [13,14], behavior-based method [15,16].

Among these methods, the one that is mathematically easy-to-understand is the leader–follower method. Furthermore, the method has good scalability since it is easy to extend the problem of maintaining the expected distance and angle between leaders and followers to the multi-robots formation control problem in a similar manner. Therefore, this method is extensively utilized in multi-robots formation control, and it will be used in this paper.

It is worth noting that the great majority of the available algorithms are constructed for simple integrator multi-agent systems. However, this would hinder their practical application, because there are many mechanical systems that are so complex that a simple integrator is insufficient to describe their dynamics. In practice, there are many mechanical systems that can be described as nonholonomic dynamics, such as mobile robots (e.g., [17,18]). Therefore, cooperative control of nonholonomic systems as one of the important applications of consensus control has attracted many scholars’ attention. In [19], the cooperative tracking rendezvous problem of nonholonomic mobile robots (NMRs) subject to uncertain and unmodeled dynamics has been investigated. In [20], the design of a distributed formation controller for multiple nonholonomic mobile robots without global position measurement information is considered. In [21], a protocol for shifting states is reached in order to achieve formation control. In addition, finite time cooperative control of nonholonomic mobile robots is studied in [22].

As it can easily find that vehicles with nonholonomic constraint characteristics can cause the system to underactuate, the characteristic of an under-actuated system is that the independent control input dimension is insufficient, resulting in mismatch with the system degree of freedom, which makes the control difficulty of the under-actuated system significantly higher than that of a fully-actuated system. Therefore, the system is expected to be fully-actuated. However, references [17,18,19,20,21,22] mentioned above have not considered how to transform the under-actuated system into fully-actuated system.

In addition, obstacle avoidance was not taken into account in the above studies on nonholonomic multi-mobile robot systems. In fact, in practical applications, robots will inevitably encounter obstacles, so it is necessary to consider the anti-collision problem of robots. So far, the existing research on obstacle avoidance methods has taken the form of the combination of various methods, and the research methods are diverse [23]. In [24], the collision avoidance of nonholonomic multi-robot formation systems is achieved without employing any potential functions. However, it can only avoid collisions between robots by keeping them in formation and satisfying distance constraints, and it cannot avoid other obstacles outside the system. Therefore, the artificial potential field method proposed in [25] is suitable for the unknown environment with relatively high real-time requirements for obstacle avoidance and will be used in this paper. In [26], formation control of the multi-agent under the constraints of visibility and communication has been studied and a feedback control strategy that can realize obstacle avoidance and internal collision avoidance of robots has been proposed. In [27], an obstacle avoidance control strategy including a leader–following formation model and obstacle avoidance separation distance model has been proposed to ensure that the mobile robots formed a formation while avoiding collision. Among various obstacle avoidance methods, the artificial potential field method realizes robot obstacle avoidance by a repulsion potential field around obstacles. With the advantages of a clear physical principle and low algorithm complexity, it is widely used in the research of robot obstacle avoidance control [28,29,30]. In [31], the repulsion field and the gravitational field function through the artificial potential field method have been introduced to ensure that the robot can form a formation and avoid obstacles while tracking the target. In [32], obstacles between robots were expressed as a new form of potential function by invoking the concept of an electric field. In [33], $H_{\infty }$ analysis was conducted on the undesired effect of an artificial potential field to give the formation good robustness in obstacle avoidance, and the control effect based on Lyapunov stability theory was proved.

Note that some of the aforementioned literature has research on leader–following formation tracking control of nonholonomic mobile robots considering collision avoidance. However, few studies consider converting under-actuated systems into fully-actuated and obstacle avoidance systems at the same time.

Motivated by the above discussion, the following issues are discussed by us. The transverse function will be applied to transform the under-actuated system into a fully-actuated system. Meanwhile, the repulsive potential field function will be introduced for robot obstacle avoidance, and the adaptive laws for each robot are designed for estimating the unknown parameter of the tracked trajectory. The contributions of this paper are formally summarized as follows:

• For the nonholonomic mobile robot model studied in this paper, since the number of output state variables is larger than the number of input controls, it is considered to be an under-actuated system. The transverse function will be applied to transform the under-actuated system into a fully-actuated system.
• In order to describe the effect of obstacles on the robot, the repulsive potential field function is introduced. The effect of potential field on mobile robots is taken into account in the system tracking error to obtain the corrected position error. In addition, to deal with the unknown parameters of the desired trajectory, the adaptive laws are designed.

The paper is organized as follows. Section 2 gives some preliminaries and problem formulation. The design procedure of leader–following formation control for nonholonomic mobile robots considering obstacle avoidance is demonstrated in Section 3. Section 4 shows the simulation result. The conclusion of this paper can be seen in Section 5.

2. Preliminaries and Problem Formulation

Before starting the next part, here some notations are introduced. $\mathbb{R}$ represents real number set. ${\mathbb{R}}^n$ represents n-dimensional Euclidean space. ${\mathbb{R}}^{n\times m}$ represents $n\times m$ real matrix space. The matrix $A^T$ is the transpose of the matrix A. $\left|\right|B\left|\right|$ denotes the norm of the vector B. $\left|b\right|$ denotes the absolute value of b.

2.1. Preliminaries

In this paper, a directed graph $\overline{\mathcal{G}}$ is used to represent the communication state between agents. $\overline{\mathcal{G}}$ consists of a set of nodes $\mathcal{V}=\{{\mathcal{V}}_1,{\mathcal{V}}_2,\cdots ,{\mathcal{V}}_n\}$ and a set of edges between nodes $\mathcal{E}\in \mathcal{V}\times \mathcal{V}$. In the graph, $(i,j)\in \mathcal{E}$ means that agent i can receive the date from agent j. A self-loop connection is not considered here, i.e., $(i,i)\notin \mathcal{E}$. $A=\left[a_{ij}\right]\in {\Re }^{n\times n}$ represents the connectivity matrix, and the elements of A are demonstrated as: (1) $a_{ij}=1$ if $(i,j)\in \mathcal{E}$, (2) $a_{ij}=0$ if $(i,j)\notin \mathcal{E}$. As $(i,i)\notin \mathcal{E}$, which means that $a_{ii}=0$. $△=\mathrm{diag}\left({△}_i\right)\in {\Re }^{n\times n}$ represents the in-degree matrix and ${△}_i={\sum }_{j\in N_i}{a}_{ij}$. $L=△-A$ is the Laplacian matrix of $\overline{\mathcal{G}}$. Use ${\mu }_i$ to indicate whether the data of the leader can be transferred to other nodes. ${\mu }_i=0$ indicates that follower i can not receive the date from the leader, while ${\mu }_i=1$ means yes. Define $U=diag\{{\mu }_1,{\mu }_2,\cdots ,{\mu }_n\}$.

2.2. Problem Formulation

The investigated NMR is a typical two-wheel driven mobile robot as shown in Figure 1. In this paper, we consider a group of N two-wheeled mobile robots. The velocity of each of the two driving wheels ($v_{il}$ and $v_{ir}$) can result in linear velocity $v_i=(v_{ir}+v_{il})/2$ and angular velocity ${\omega }_i=(v_{ir}-v_{il})/\left(2b_i\right)$, with the half distance between two wheels being $b_i$ (for $i=1,\cdots ,N$). The positions of the robot i are denoted by $(s_{xi},s_{yi})$ and the orientation is ${\theta }_i$. Then, the kinematics model of each robot can be described by

$$\begin{array}{cc}\hfill {\dot{\mathbf{x}}}_i=\left[\begin{array}{c}{\dot{s}}_{xi}\\ {\dot{s}}_{yi}\\ {\dot{\theta }}_i\end{array}\right]=& \left[\begin{array}{c}{v}_{i}cos{\theta }_i\\ v_{i}sin{\theta }_i\\ {\omega }_i\end{array}\right]\hfill \end{array}$$

(1)

where ${\mathbf{x}}_i={[s_{xi},s_{yi},{\theta }_i]}^T$ is the state variable, $r_i$ is the radius of the wheel.

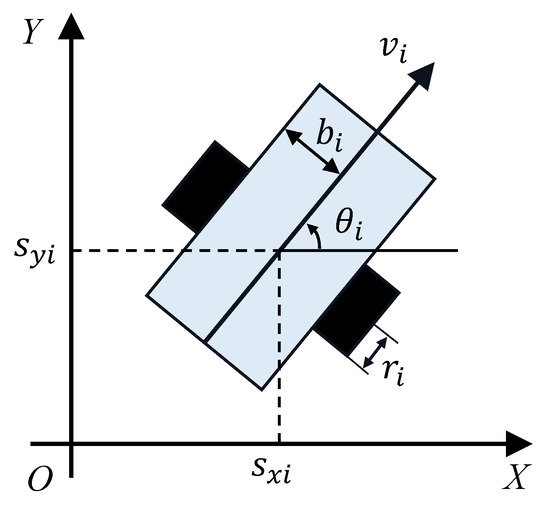
Figure 1. A two-wheeled nonholonomic mobile robot.

By applying the equation $v_i={\omega }_i{r}_i$, the following equation can be further obtained:

$$\begin{array}{c}\hfill {\dot{\mathbf{x}}}_i=\frac{r_i}{2}\left[\begin{array}{c}cos{\theta }_i\\ sin{\theta }_i\\ 1/b_i\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}cos{\theta }_i\\ sin{\theta }_i\\ -1/b_i\end{array}\right]\left[\begin{array}{c}{w}_{ir}\\ w_{il}\end{array}\right]\end{array}$$

(2)

In order to study the formation control of nonholonomic mobile robots, assumptions about the communication between multi-agents and system parameters are given in the following:

Assumption 1. 

The upper and lower bounds of the value range of parameters $r_i$ and $b_i$ are known, i.e., there exist some known positive constants ${\overline{r}}_i$, ${\underline{r}}_i$, ${\overline{b}}_i$ and ${\underline{b}}_i$ such that ${\underline{r}}_i<r_i<{\overline{r}}_i$ and ${\underline{b}}_i<b_i<{\overline{b}}_i$.

Assumption 2. 

Assume that the directed graph $\overline{\mathcal{G}}$ is connected and the leader is the root of the spanning tree.

Lemma 1. 

Based on Assumption 2, the matrix $(L+U)$ is nonsingular where $U=diag\{{\mu }_1,\cdots ,{\mu }_N\}$. Define

$$\begin{array}{cc}\hfill \overline{q}& ={[{\overline{q}}_1,\cdots ,{\overline{q}}_N]}^T=diag{(L+U)}^{-1}{[1,\cdots ,1]}^T\hfill \\ \hfill P& =diag\{P_1,\cdots ,P_N\}=diag\{1/{\overline{q}}_1,\cdots ,1/{\overline{q}}_N\}\hfill \\ \hfill Q& =P(L+U)+{(L+U)}^{T}P,\hfill \end{array}$$

then ${\overline{q}}_i>0$ for $i=1,\cdots ,N$, Q is positive definite.

3. Formation Tracking Control of Nonholonomic Mobile Robots

In this section, we will design the leader–following formation control strategy for nonholonomic mobile robots considering obstacle avoidance.

3.1. Change of Coordinates

By observing the kinematic model of the nonholonomic mobile robot, we can find that the number of inputs (i.e., ${\omega }_{il}$ and ${\omega }_{ir}$) is less than the number of state variables (i.e., $s_{xi}$, $s_{yi}$ and ${\theta }_i$. Therefore, in this part, in order to realize three control variables to control three outputs $s_{xi}$, $s_{yi}$ and ${\theta }_i$, respectively, to be able to track the target, that is, to convert the under-actuated system into a fully-actuated system shown in the blue part in Figure 2. The transverse function will be introduced later.

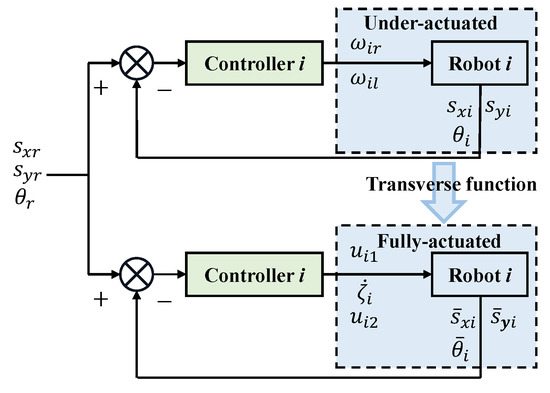
Figure 2. The under-actuated system is transformed into a fully-actuated system.

Some symbols in Figure 2 will be shown later. It can be seen from the picture that if the trajectory of the fully-actuated system can track the desired trajectory, the original under-actuated system will also follow the desired trajectory within a certain error range, since $\left|\right|(s_{xi}-{\overline{s}}_{xi},s_{yi}-{\overline{s}}_{yi})\left|\right|\le \sqrt{2{\varpi }_{i1}^2}$ and $|{\theta }_i-{\overline{\theta }}_i|\le {\varpi }_{i2}$, which will be seen later. Therefore, the original system can be controlled by controlling the converted system. Here, we will describe how to transform the system.

At first, by adding some variables to change the original coordinates of the ith robot. By referring to [34], the variables $h_{li}\left({\zeta }_i\right)$ for $l=1,2,3$ are selected as follows:

$$\begin{array}{cc}\hfill & h_{1i}\left({\zeta }_i\right)={\varpi }_{1i}sin\left({\zeta }_i\right)\frac{sin\left(h_{3i}\right)}{h_{3i}}\hfill \\ \hfill & h_{2i}\left({\zeta }_i\right)={\varpi }_{1i}sin\left({\zeta }_i\right)\frac{1-cos\left(h_{3i}\right)}{h_{3i}}\hfill \\ \hfill & h_{3i}\left({\zeta }_i\right)={\varpi }_{2i}cos\left({\zeta }_i\right)\hfill \end{array}$$

(3)

with ${\varpi }_{1i}$ and ${\varpi }_{2i}$ being positive constants and ${\varpi }_{2i}$ satisfying $0<{\varpi }_{2i}<\frac{pi}{2}$.

From (3), we can know that $h_{li}$ are functions of ${\zeta }_i$, which will be designed later. By simple derivation, the properties of $h_{li}$ can be shown as follows:

$$\begin{array}{c}\hfill |h_{1i}|<{\varpi }_{1i},|h_{2i}|<{\varpi }_{1i},\left|h_{3i}\right|<{\varpi }_{2i}.\end{array}$$

(4)

After introducing the variables $h_{li}$, add the variables to the original system to change the coordinates of the original system. The specific equation is as follows:

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{\overline{s}}_{xi}\\ {\overline{s}}_{yi}\end{array}\right]=\left[\begin{array}{c}{s}_{xi}\\ s_{yi}\end{array}\right]+R\left({\overline{\theta }}_i\right)\left[\begin{array}{c}{h}_{1i}\left({\zeta }_i\right)\\ h_{2i}\left({\zeta }_i\right)\end{array}\right]\hfill \\ \hfill & {\overline{\theta }}_i={\theta }_i-h_{3i}\left({\zeta }_i\right)\hfill \end{array}$$

(5)

where

$$\begin{array}{c}\hfill R\left({\overline{\theta }}_i\right)=\left[\begin{array}{cc}cos\left({\overline{\theta }}_i\right)& -sin\left({\overline{\theta }}_i\right)\\ sin\left({\overline{\theta }}_i\right)& cos\left({\overline{\theta }}_i\right)\end{array}\right]\end{array}$$

The derivatives of ${\overline{s}}_{xi}$, ${\overline{s}}_{yi}$ and ${\overline{\theta }}_i$ are calculated as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{\overline{s}}}_{xi}\\ {\dot{\overline{s}}}_{yi}\end{array}\right]=& Q_i\left[\begin{array}{c}{r}_i{u}_{i1}\\ {\dot{\zeta }}_i\end{array}\right]+\frac{\partial R\left({\overline{\theta }}_i\right)}{\partial {\overline{\theta }}_i}\left[\begin{array}{c}{h}_{1i}\left({\zeta }_i\right)\\ h_{2i}\left({\zeta }_i\right)\end{array}\right]\hfill \\ \hfill & \times \left(r_i{b}_i^{-1}{u}_{i2}-\frac{\partial h_{3i}\left({\zeta }_i\right)}{\partial {\zeta }_i}{\dot{\zeta }}_i\right)\hfill \\ \hfill {\dot{\overline{\theta }}}_i=& r_i{b}_i^{-1}{u}_{i2}-\frac{\partial h_{3i}\left({\zeta }_i\right)}{\partial {\zeta }_i}\dot{{\zeta }_i}\hfill \end{array}$$

(6)

where $u_{i1}=0.5(w_{ir}+w_{il})$ and $u_{i2}=0.5(w_{ir}-w_{il})$.

$$\begin{array}{c}\hfill Q_i=\left[\begin{array}{cc}\left(\begin{array}{c}cos\left({\overline{\theta }}_i\right)\hfill \\ sin\left({\overline{\theta }}_i\right)\hfill \end{array}\right)& R\left({\overline{\theta }}_i\right)\left(\begin{array}{c}\frac{\partial h_{1i}\left({\zeta }_i\right)}{\partial {\zeta }_i}\hfill \\ \frac{\partial h_{2i}\left({\zeta }_i\right)}{\partial {\zeta }_i}\hfill \end{array}\right)\end{array}\right]\end{array}$$

is ensured to be invertible [34]. From Equation (6), we can find that $({\overline{s}}_{xi},{\overline{s}}_{yi},{\overline{\theta }}_i)$ can be dominated, respectively, by adjusting $u_{i1}$, $u_{i2}$ and ${\dot{\zeta }}_i$, and this is different from the original system.

3.2. Establishment of Obstacle Potential Field

Before establishing the obstacle potential field, the function $B_n\left(L_o\right)$ is introduced first:

$$\begin{array}{c}\hfill B_n\left(L_o\right)=\left\{\begin{array}{cc}+\infty & L_o\le r_o\\ e^{\xi \left(\frac{L_o-r_o}{L_o-R_o}\right)}& r_o<L_o<R_o\\ 0& L_o\ge R_o\end{array}\right.\end{array}$$

(7)

where n represents the nth obstacle in the environment, $L_o=\sqrt{{(x-x_{obs})}^2+{(y-y_{obs})}^2}$ indicates the distance between the robot and the obstacle, $(x_{obs},y_{obs})$ represents the obstacle coordinate, and $r_o$ and $R_o$ represent the radius parameters of the inner and outer boundaries of the obstacle potential field, respectively.

By converting $B_n\left(L_o\right)$, the obstacle potential field function $E_n\left(L_o\right)$ corresponding to the $nth$ obstacle can be obtained as follows:

$$\begin{array}{c}\hfill E_n\left(L_o\right)=\frac{B_n\left(L_o\right)}{1-B_n\left(L_o\right)}\end{array}$$

(8)

For $E_n\left(L_o\right)$, changing the value of $\xi$ in $B_n\left(L_o\right)$ can change the speed of the value of potential field function, which can adjust the strength of potential field.

The variation of $B_n\left(L_o\right)$ and $E_n\left(L_o\right)$ with $L_o$ is shown in Figure 3 and Figure 4, respectively. Combining the expressions of $B_n\left(L_o\right)$ and $E_n\left(L_o\right)$, it can be seen that the obstacle potential field can be regarded as a ring with the obstacle as the center and $r_o$ and $R_o$ as the inner and outer radius, as shown in Figure 5. When the robot is outside the range of $R_o$, it is not affected by the potential field. With the decreasing of $L_o$, that is, the robot is approaching the obstacle, the potential field value increases gradually, and the potential field repulsion to the robot increases gradually, when the robot is away from the obstacle $r_o$, the potential repulsion is maximized.

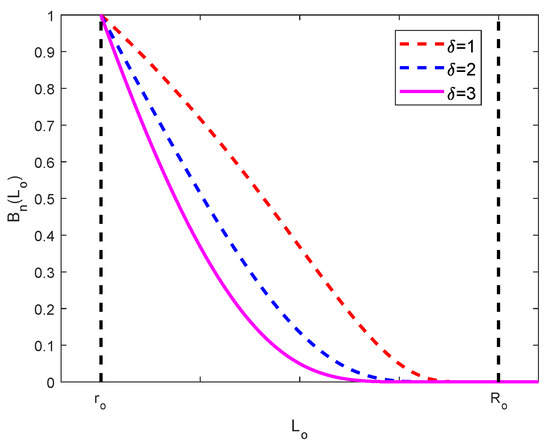
Figure 3. The curve of $B_n\left(L_o\right)$.

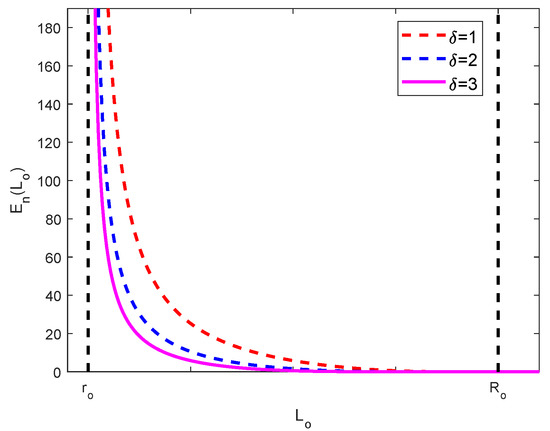
Figure 4. The curve of $E_n\left(L_o\right)$.

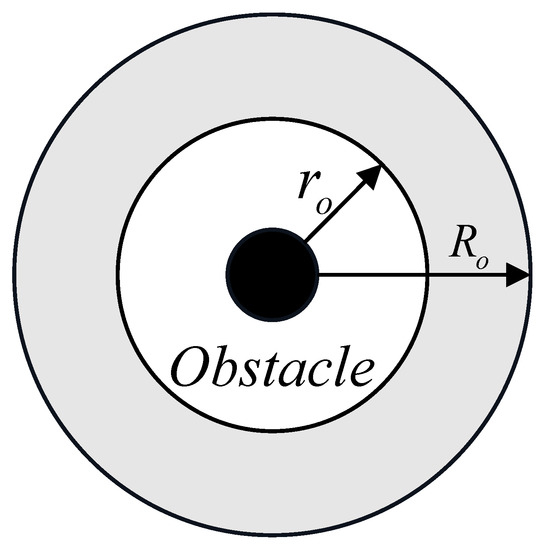
Figure 5. Potential field region.

3.3. Formation Control Objective

Here, we express the desired trajectory of the system in terms of the components in the X and Y directions shown below.

$$\begin{array}{c}\hfill s_{xr}\left(t\right)=a_{rx}{\rho }_{rx}\left(t\right)+d_{rx}{s}_{yr}\left(t\right)=a_{ry}{\rho }_{ry}\left(t\right)+d_{ry}\end{array}$$

(9)

where ${\rho }_{rx}\left(t\right)$ and ${\rho }_{ry}\left(t\right)$ are the basis functions and are assumed to be known by all robots, while the constant parameters $a_{rx}$, $a_{ry}$, $d_{rx}$ and $d_{ry}$ can not be obtained by all robots. Additionally, ${\theta }_r\left(t\right)=arctan\left(\frac{{\dot{s}}_{yr}}{{\dot{s}}_{xr}}\right)$ represents the reference trajectory for each robot orientation, because ${\rho }_{rx}\left(t\right)$ and ${\rho }_{ry}\left(t\right)$ are known to all robots. Then, by calculation, ${\dot{s}}_{xr}$ and ${\dot{s}}_{yr}$ are both constants. Hence, ${\theta }_r\left(t\right)$ is known by all the followers.

The control goal of this paper is to design distributed adaptive formation controllers so that all robots, while considering obstacle avoidance, follow a desired trajectory in the X-Y plane by keeping specified distances from the desired trajectory, i.e.,

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\left[{\overline{s}}_{xi}\left(t\right)-s_{xr}\left(t\right)-\sum _{i=1}^{m_i}{E}_{ix}\right]=-{\varrho }_{ix}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\left[{\overline{s}}_{yi}\left(t\right)-s_{yr}\left(t\right)-\sum _{i=1}^{m_i}{E}_{iy}\right]=-{\varrho }_{iy}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\left[{\overline{\theta }}_i\left(t\right)-{\theta }_r\left(t\right)\right]=0\hfill \end{array}$$

(12)

Remark 1. 

In this paper, when the robot detects an obstacle, the robot avoids the obstacle first, and then forms a given formation after avoiding the obstacle. From the previous analysis, we can know that when the robot does not detect the obstacle, the terms ${\displaystyle \sum _{i=1}^{m_i}}{E}_{ix}$ and ${\displaystyle \sum _{i=1}^{m_i}}{E}_{iy}$ are equal to zero, so the expressions (10) and (11) become the regular formation expressions as in [34]. When there is an obstacle, the formation formed by multiple robots will change, that is, the distance between the robots will change, so the obstacle avoidance term is introduced into Equations (10) and (11).

Remark 2. 

We consider the leader–follower formation strategy, where the desired trajectory is expected to act as the leader to guide the overall movement of the robot crowd, and each robot in the swarm will track its adjacent robot as a reference model. We refer to the reference model as the leader and the robots following it as followers. Notice about that in the leader–follower formation structure, any follower can be assigned as the intermediate leader of another robot, so there will be many pairs of leaders and followers in such a structure. This method does not need global knowledge and computation, and can be extended in the case of multiple agents. Suppose that for each robot $R_i$, $i\in N$, there is a fixed and unique leader $R_{iL}$, $i_L\ne i$, $i_L\in \overline{N}$ in the leader–follower structure. Thus, in the leader–follower formation with N mobile robots, they will be decomposed into $N-1$ pairs of leaders and followers.

From the above, we can already know that the graph $\overline{\mathcal{G}}$ stands for the communication status between N robots, and Assumption 2 is made. In order to realize the formation control goal, it is necessary to make the following assumption.

Assumption 3. 

${\rho }_{rx}$, ${\rho }_{ry}$, ${\dot{\rho }}_{rx}$, ${\dot{\rho }}_{ry}$ and ${\ddot{\rho }}_{rx}$, ${\ddot{\rho }}_{ry}$ are bounded and piece-wise continuous bounded. Additionally, all robots know them.

Remark 3. 

It is worth mentioning that the design trajectory shown in Equation (9) is similar to the designed trajectory that has been shown in many studies, including but not limited to [2,35,36]. Therefore, by looking up similar literature, we can know Assumption 3 is reasonable.

Assumption 4. 

The neighbors of robot i can obtain the required distances ${\varrho }_{ix}$ and ${\varrho }_{iy}$.

3.4. Control Design

Note that (6) constitutes the new system to be controlled. In (6), $u_{i1}$, ${\dot{\zeta }}_i$ and $u_{i2}$ are the control inputs while ${\overline{s}}_{xi}$, ${\overline{s}}_{yi}$ and ${\overline{\theta }}_i$ act as the outputs, which has difference with the traditional under-actuated kinematic model in [37]. The transformed system can be treated as three separate single-input single-output systems by applying transverse function technique.

Define local error variables as

$$z_{ix}=\sum _{j=1}^N{a}_{ij}\left({\overline{s}}_{xi}+{\varrho }_{ix}-\sum _{i=1}^{m_i}{E}_{ix}-{\overline{s}}_{xj}-{\varrho }_{jx}+\sum _{j=1}^{m_j}{E}_{jx}\right)+{\mu }_i\left({\overline{s}}_{xi}+{\varrho }_{ix}-s_{xr}-\sum _{i=1}^{m_i}{E}_{ix}\right)$$

$$z_{iy}=\sum _{j=1}^N{a}_{ij}\left({\overline{s}}_{yi}+{\varrho }_{iy}-\sum _{i=1}^{m_i}{E}_{iy}-{\overline{s}}_{yj}-{\varrho }_{jy}+\sum _{j=1}^{m_j}{E}_{jy}\right)+{\mu }_i\left({\overline{s}}_{yi}+{\varrho }_{iy}-s_{yr}-\sum _{i=1}^{m_i}{E}_{iy}\right)$$

$$e_{ix}={\overline{s}}_{xi}-{\mu }_i{s}_{xr}-(1-{\mu }_i)({\rho }_{rx}{\widehat{a}}_{rx,i}-{\widehat{d}}_{rx,i})+{\varrho }_{ix}-\sum _{i=1}^{m_i}{E}_{ix}$$

$$e_{iy}={\overline{s}}_{yi}-{\mu }_i{s}_{yr}-(1-{\mu }_i)({\rho }_{ry}{\widehat{a}}_{ry,i}-{\widehat{d}}_{ry,i})+{\varrho }_{iy}-\sum _{i=1}^{m_i}{E}_{iy}$$

$${\xi }_{i\theta }={\theta }_i-{\theta }_r$$

where ${\widehat{a}}_{rx,i}$, ${\widehat{a}}_{ry,i}$, ${\widehat{d}}_{rx,i}$ and ${\widehat{d}}_{ry,i}$ are used by the ith robot to estimate unknown trajectory parameters when ${\mu }_i=0$. The control laws $u_{i1}$, $u_{i2}$ and $\dot{\zeta }$ in transverse function technique are selected as

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{u}_{i1}\\ {\dot{\zeta }}_i\end{array}\right]=\left[\begin{array}{cc}1/r& 0\\ 0& 1\end{array}\right]Q_i^{-1}{\Omega }_i\hfill \\ \hfill & u_{i2}=b_i/r_i\left(-k_2{\xi }_{i\theta }+\frac{\partial h_{3i}\left({\zeta }_i\right)}{\partial {\zeta }_i}{\dot{\zeta }}_i+{\dot{\theta }}_r\right)\hfill \end{array}$$

(13)

where

$$\begin{array}{cc}\hfill {\Omega }_i=& -k_1{P}_i\left[\begin{array}{c}{z}_{ix}\\ z_{iy}\end{array}\right]-\left[\begin{array}{c}{\dot{\varrho }}_{ix}\\ {\dot{\varrho }}_{iy}\end{array}\right]+{\mu }_i\left[\begin{array}{c}{\dot{\rho }}_{rx}{a}_{rx}\\ {\dot{\rho }}_{ry}{a}_{ry}\end{array}\right]+(1-{\mu }_i)\times \left[\begin{array}{c}{\dot{\rho }}_{rx}{\widehat{a}}_{rx,i}+{\rho }_{rx}{\dot{\widehat{a}}}_{rx,i}+{\dot{\widehat{d}}}_{rx,i}\\ {\dot{\rho }}_{ry}{\widehat{a}}_{ry,i}+{\rho }_{ry}{\dot{\widehat{a}}}_{ry,i}+{\dot{\widehat{d}}}_{ry,i}\end{array}\right]\hfill \\ \hfill & -{\displaystyle \frac{\partial R\left({\overline{\theta }}_i\right)}{\partial {\overline{\theta }}_i}}\left[\begin{array}{c}{h}_{1i}\left({\zeta }_i\right)\\ h_{2i}\left({\zeta }_i\right)\end{array}\right]\left(-k_2{\xi }_{i\theta }+{\dot{\theta }}_i\right)+\left[\begin{array}{c}{\displaystyle \sum _{i=1}^{m_i}}\nabla E_{ix}\\ {\displaystyle \sum _{i=1}^{m_i}}\nabla E_{iy}\end{array}\right]\hfill \end{array}$$

where $k_1$ and $k_2$ are positive constants to be selected. $P_i$ is defined in Lemma 1. Based on the above design, we obtain the following formula:

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{\dot{e}}_{ix}\\ {\dot{e}}_{iy}\end{array}\right]=-k_1{P}_i\left[\begin{array}{c}{z}_{ix}\\ z_{iy}\end{array}\right]\hfill \\ & {\dot{\xi }}_{i\theta }=-k_2{\xi }_{i\theta }\hfill \end{array}$$

(14)

The structure of the parameter estimators in this step is as follows:

$$\begin{array}{cc}\hfill & {\dot{\widehat{a}}}_{rx,i}=-{\gamma }_{ri}{\rho }_{rx}{z}_{ix}\hfill \\ \hfill & {\dot{\widehat{a}}}_{ry,i}=-{\gamma }_{ri}{\rho }_{ry}{z}_{iy}\hfill \\ \hfill & {\dot{\widehat{d}}}_{rx,i}=-{\gamma }_{ri}{z}_{ix}\hfill \\ \hfill & {\dot{\widehat{d}}}_{ry,i}=-{\gamma }_{ri}{z}_{iy}\hfill \end{array}$$

(15)

In this step, the Lyapunov candidate function is selected as

$$\begin{array}{c}\hfill \begin{array}{c}V=\frac{1}{2}{\displaystyle \sum _{i=1}^N}\left(e_{ix}^2+e_{iy}^2+{\xi }_{i\theta }^2\right)+\frac{k_1}{2}{\displaystyle \sum _{i=1}^N}(1-{\mu }_i)\hfill \\ \times \frac{P_i}{{\gamma }_{ri}}({\tilde{a}}_{rx,i}^2+{\tilde{a}}_{ry,i}^2+{\tilde{d}}_{rx,i}^2+{\tilde{d}}_{ry,i}^2)\hfill \end{array}\end{array}$$

(16)

where ${\tilde{a}}_{rx,i}=a_{rx,i}-{\widehat{a}}_{rx,i}$, ${\tilde{a}}_{ry,i}=a_{ry,i}-{\widehat{a}}_{ry,i}$, ${\tilde{d}}_{rx,i}=d_{rx,i}-{\widehat{d}}_{rx,i}$, ${\tilde{d}}_{ry,i}=d_{ry,i}-{\widehat{d}}_{ry,i}$ are parameter estimation errors.

Then, combining Equation (14), the derivative of V is obtained as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{V}=-k_1{\displaystyle \sum _{i=1}^N}{P}_i\left(e_{ix}{z}_{ix}+e_{iy}{z}_{iy}\right)-k_2{\displaystyle \sum _{i=1}^N}{\xi }_{i\theta }^2+{\displaystyle \sum _{i=1}^N}(1-{\mu }_i)\hfill \\ \times \frac{P_i}{{\gamma }_{ri}}(-{\tilde{a}}_{rx,i}{\dot{\widehat{a}}}_{rx,i}-{\tilde{a}}_{ry,i}{\dot{\widehat{a}}}_{ry,i}-{\tilde{d}}_{rx,i}{\dot{\widehat{d}}}_{rx,i}-{\tilde{d}}_{ry,i}^2{\dot{\widehat{d}}}_{ry,i}^2)\hfill \end{array}\end{array}$$

(17)

We can rewrite the expressions of $e_{ix}$ and $e_{iy}$ as $e_{ix}={\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{ix}-(1-{\mu }_i)({\rho }_{rx}{\widehat{a}}_{rx,i}-{\widehat{d}}_{rx,i}-s_{xr})$ and $e_{iy}={\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{iy}-(1-{\mu }_i)({\rho }_{ry}{\widehat{a}}_{ry,i}-{\widehat{d}}_{ry,i}-s_{yr})$.

Then substitute $e_{ix}$ and $e_{iy}$ into $\dot{V}$ to obtain

$$\begin{array}{cc}\hfill \dot{V}=& -k_1\sum _{i=1}^N{P}_i\left(\left({\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-\sum _{i=1}^{m_i}{E}_{ix}\right)z_{ix}+\left({\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-\sum _{i=1}^{m_i}{E}_{iy}\right)z_{iy}\right)-k_2\sum _{i=1}^N{\xi }_{i\theta }^2\hfill \\ & +\sum _{i=1}^N(1-{\mu }_i)\times \frac{P_i}{{\gamma }_{ri}}\left(-{\tilde{a}}_{rx,i}{\dot{\widehat{a}}}_{rx,i}-{\tilde{d}}_{rx,i}{\dot{\widehat{d}}}_{rx,i}+{\gamma }_{ri}({\rho }_{rx}{\widehat{a}}_{rx,i}-{\widehat{d}}_{rx,i}-s_{xr})z_{ix}\right)\hfill \\ & +\sum _{i=1}^N(1-{\mu }_i)\times \frac{P_i}{{\gamma }_{ri}}\left(-{\tilde{a}}_{ry,i}{\dot{\widehat{a}}}_{ry,i}-{\tilde{d}}_{ry,i}^2{\dot{\widehat{d}}}_{ry,i}^2+{\gamma }_{ri}({\rho }_{ry}{\widehat{a}}_{ry,i}-{\widehat{d}}_{ry,i}-s_{yr})z_{iy}\right)\hfill \end{array}$$

(18)

By selecting the parameter estimators of Equation (15), we can obtain

$$\begin{array}{c}\hfill \dot{V}=-k_1{\displaystyle \sum _{i=1}^N}{P}_i\left(\left({\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{ix}\right)z_{ix}+\left({\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{iy}\right)z_{iy}\right)-k_2{\displaystyle \sum _{i=1}^N}{\xi }_{i\theta }^2\end{array}$$

Let ${\xi }_{ix}={\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-{\displaystyle \sum _{i=1}^{m_i}}{E}_i$, ${\xi }_{iy}={\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-{\displaystyle \sum _{i=1}^{m_i}}{E}_i$. Hence, $z_{ix}$ and $z_{iy}$ can be rewritten as $z_{ix}={\displaystyle \sum _{j=1}^N}{a}_{ij}\left({\xi }_{ix}-{\xi }_{jx}\right)+{\mu }_i{\xi }_{ix}$ and $z_{iy}={\displaystyle \sum _{j=1}^N}{a}_{ij}\left({\xi }_{iy}-{\xi }_{jy}\right)+{\mu }_i{\xi }_{iy}$.

Combining Lemma 1, the derivative of V can be obtained as

$$\begin{array}{c}\hfill \dot{V}=-\frac{k_1}{2}\left({\xi }_x^{T}Q{\xi }_x+{\xi }_y^{T}Q{\xi }_y\right)-k_2{\xi }_{\theta }^T{\xi }_{\theta }\end{array}$$

(19)

where ${\xi }_x=[{\xi }_{1x},\cdots ,{\xi }_{Nx}]$, ${\xi }_y=[{\xi }_{1y},\cdots ,{\xi }_{Ny}]$ and ${\xi }_{\theta }=[{\xi }_{1\theta },\cdots ,{\xi }_{N\theta }]$.

Theorem 1. 

For multiple nonholonomic mobile robots (2) satisfying Assumptions 1–4, apply controller (13) and parameter estimator (15) to it. Then, the formation errors of each robot can be guaranteed to meet the following requirements:

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}{\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-\sum _{i=1}^{m_i}{E}_{ix}\le \sqrt{2}{\varpi }_{i1}\hfill \\ \hfill & \underset{t\to \infty }{lim}{\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-\sum _{i=1}^{m_i}{E}_{iy}\le \sqrt{2}{\varpi }_{i1}\hfill \end{array}$$

(20)

$$\underset{t\to \infty }{lim}{\overline{\theta }}_i-{\theta }_r\le \sqrt{2}{\varpi }_{i2}$$

Proof. 

By applying Barblet’s lemma, we can easily get that ${\xi }_{ix}$, ${\xi }_{iy}$ and ${\xi }_{\theta }$ will converge to zero asymptotically. Hence, we can find that ${lim}_{t\to \infty }{s}_{xi}-s_{xr}-{\displaystyle \sum _{i=1}^{m_i}}{E}_i=-{\varrho }_{ix}$, ${lim}_{t\to \infty }{s}_{yi}-s_{yr}-{\displaystyle \sum _{i=1}^{m_i}}{E}_i=-{\varrho }_{iy}$ and ${lim}_{t\to \infty }{\theta }_i-{\theta }_r=0$.

From (3)–(5), the following equations can be obtained

$$\begin{array}{c}\hfill \left|\right|(s_{xi}-{\overline{s}}_{xi},s_{yi}-{\overline{s}}_{yi})\left|\right|\le \sqrt{2{\varpi }_{i1}^2},|{\theta }_i-{\overline{\theta }}_i|\le {\varpi }_{i2}\end{array}$$

(21)

and then it follows

$$\begin{array}{cc}\hfill & |{\overline{s}}_{xi}-s_{xr}+{\varrho }_{ix}-\sum _{i=1}^{m_i}{E}_{ix}|\le |{\overline{s}}_{xi}-s_{xi}|+D_{ix}\hfill \\ \hfill & |{\overline{s}}_{yi}-s_{yr}+{\varrho }_{iy}-\sum _{i=1}^{m_i}{E}_{iy}|\le |{\overline{s}}_{yi}-s_{yi}|+D_{iy}\hfill \\ \hfill & |{\overline{\theta }}_i-{\theta }_r|\le |{\overline{\theta }}_i-{\theta }_i|+|{\theta }_i-{\theta }_r|\hfill \end{array}$$

(22)

where $D_{ix}=|s_{xi}-s_{xr}+{\varrho }_{ix}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{ix}|$, $D_{iy}=|s_{yi}-s_{yr}+{\varrho }_{iy}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{iy}|$. Due to $s_{xi}-s_{xr}+{\varrho }_{ix}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{ix}$, $s_{yi}-s_{yr}+{\varrho }_{iy}-{\displaystyle \sum _{i=1}^{m_i}}{E}_{iy}$ and ${\theta }_i-{\theta }_r$ will converge to zero asymptotically, we can draw the conclusion that (20) holds. This means that the formation errors of the entire system can be as small as expected by properly adjusting ${\varpi }_{i1}$ and ${\varpi }_{i2}$. □

4. Simulation

In this part, we will use Matlab 2020b software to simulate the following examples to verify whether the control algorithm is effective.

A directed graph (Figure 6) is considered, in which there is a leader and two followers. Laplacian matrix L and matrix U are as follows:

$$\begin{array}{c}\hfill L=\left[\begin{array}{cc}0& 0\\ -1& 1\end{array}\right]U=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\end{array}$$

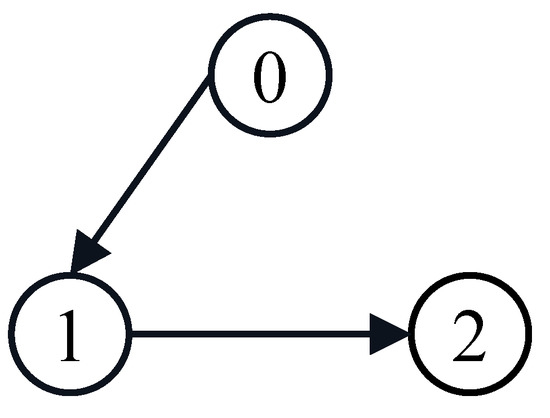
Figure 6. The directed communication graph.

The reference trajectory is given by $s_{xr}\left(t\right)=t$, $s_{yr}\left(t\right)=10sin\left(0.1t\right)$. The demanding distances corresponding to each robot are ${\varrho }_{1x}=2$, ${\varrho }_{2x}=3$, ${\varrho }_{1y}=3$, ${\varrho }_{1y}=-5$. The parameters of the robots under simulation are as follows. $b_i=0.75$, $r_i=0.25$. The control parameters are chosen as: ${\varpi }_{11}=0.1$, ${\varpi }_{12}=0.1$, ${\varpi }_{21}=1$, ${\varpi }_{22}=1$. $k_1=2$, $k_2=2$; ${\gamma }_{r2}=4$. The initial values are chosen as: $x_1\left(0\right)=1$, $y_1\left(0\right)=1$, ${\theta }_1=1$, $x_2\left(0\right)=1$, $y_2\left(0\right)=1.2$, ${\zeta }_1={\zeta }_2=0.1$, ${\theta }_2=1$, ${\widehat{a}}_{2x}\left(0\right)=0.8$, ${\widehat{a}}_{2y}\left(0\right)=1.2$, ${\widehat{d}}_{2x}\left(0\right)=0.5$, ${\widehat{d}}_{2y}\left(0\right)=0.5$.

Figure 7 shows the multi-robots without obstacle avoidance and Figure 8 demonstrates their corresponding tracking errors. Figure 9 shows the multi-robots with obstacle avoidance and Figure 10 depicts their corresponding tracking errors. We can know that in the absence of obstacles, the multi-mobile robot maintains a fixed formation. However, in the case of obstacles, priority is given to obstacle avoidance, and the formation changes. The proposed approach is compared with the collision avoidance method reported in [24]. Figure 11 shows that the method proposed in [24] cannot avoid the obstacles represented by black cross shown in this paper.

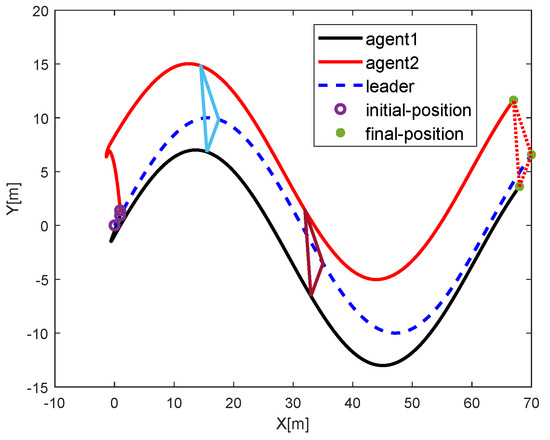
Figure 7. Formation control without considering obstacles.

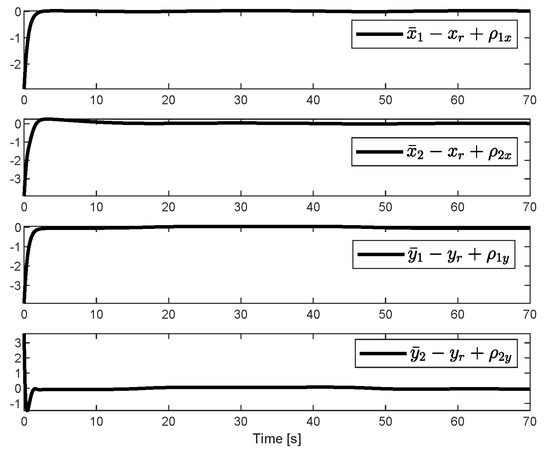
Figure 8. The tracking errors in the X and Y directions corresponding to the two followers without considering obstacle avoidance.

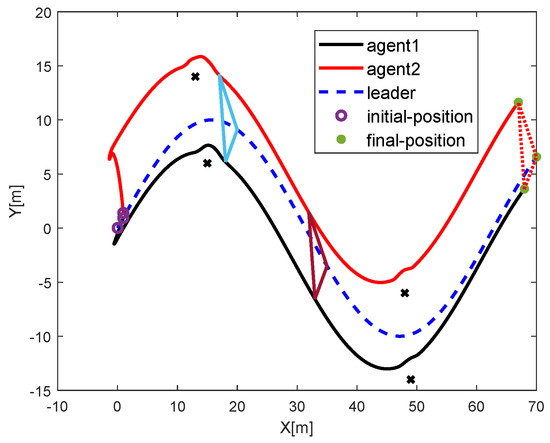
Figure 9. Formation control while considering obstacles (black cross).

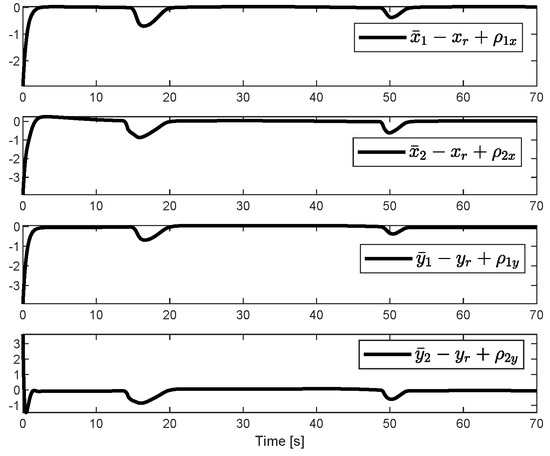
Figure 10. The tracking errors in the X and Y directions corresponding to the two followers while considering obstacle avoidance.

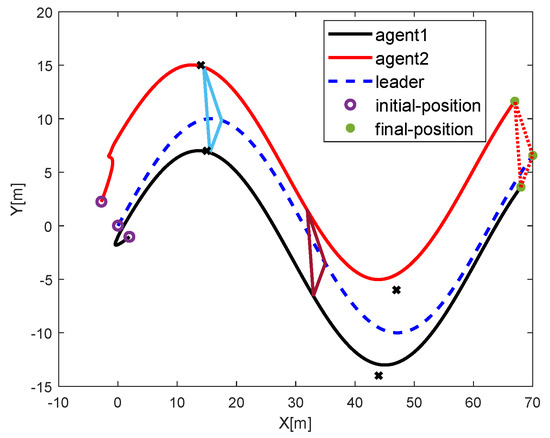
Figure 11. Formation control while considering obstacles (black cross). Trajectory obtained by using the control algorithm in reference [24].

5. Conclusions

The obstacle avoidance problem-based leader–following formation tracking of a nonholonomic wheeled mobile robot with mismatched unknown parameters has been investigated in this paper. Compared with the existing work, we consider the multi-agent obstacle avoidance problem while considering the transformation of the under-actuated problem into the fully-actuated problem. At first, the transformation of coordinates is accomplished by adding the additional design variables $h_{li}$. By using transverse function approach, the under-actuated problem can be transformed by obtaining an auxiliary variable. Then, the influence of the obstacle on the system is introduced into the tracking error, and the controller is designed based on this. In addition, there are unknown parameters in the desired trajectory. Additionally, the adaptive laws are designed to deal with the unknown parameters of the desired trajectory. Finally, the simulation examples show the effectiveness of the designed control scheme.

Considering that the detection angle and distance of the camera carried by the robot are limited, the detection range of the robot is constrained. In addition, there are nonlinear constraints on the physical components themselves, such as the backlash constraints of gear. The existence of these nonlinear constraints makes the control of the system more difficult. Therefore, future research work will be devoted to solving the problem of the limited vision of the robot field, as well as the existence of backlash, saturation and other nonlinear constraints in the system.