Investigations on the Complex Band Diagram of Flexural Wave through the Fluid-Loaded Phononic Plate

Abstract

This paper investigates the complex band diagram of flexural waves in the phononic plate with semi-infinite heavy fluid loading. The system under examination is a square plate lattice with two-dimensional periodicity immersed in a fluid domain with infinite height. The numerical models based on the wave field transformation and the Galerkin method combined with the finite element discretization technique are developed to investigate the real and imaginary parts of the dispersion relation of flexural waves propagating through the phononic plate incorporating the fluid-loading effects. A perfect agreement is found between the location and width of stop bands from the real band diagram and the attenuation diagram, which supports the validity of the numerical models. Moreover, the complex band diagram is verified by the transverse vibration transmittance of the finite phononic plate. The results demonstrate that the external fluid loading is able to adjust the location, bandwidth, and decaying level as well as affect the degree of attenuation anisotropy of the complete and directional band gaps.

1. Introduction

During the past two decades, the phononic crystals [1,2,3,4,5] have attracted the great interests of researchers for their novel physical characteristics. The most striking feature of such periodic structures is the ability of exhibiting band gaps in certain frequency ranges where no acoustic or elastic wave propagation is allowed. This physical phenomenon of the phononic crystal makes it particularly useful in designing applications for vibration suppression and sound attenuation. By employing the Floquet–Bloch theorem, a representative cell with less computation costs is allowed to be modeled to investigate the wave motion of the infinite periodic medium. Several numerical approaches such as the transfer matrix method [6,7], the multi-scattering theory [8,9,10], the plane wave expansion method [11,12], and the finite element method [13,14] have been extensively used to analyze the band gap properties. In phononic crystals, band gaps due to Bragg scattering were required to satisfy the constraint that the wavelength should be on the order of the lattice spacing. Thus, to generate low-frequency Bragg gaps, low-wave speeds or large-sized structures are needed [15]. To overcome this shortcoming, Liu [16] proposed a new type of composite material based on the localized resonant mechanisms. Local resonance gaps have been widely used to improve the vibration and sound reduction performance from low to medium frequency ranges [17,18,19]. In addition, the mechanisms of inertial amplification have attracted increasing attention as the induced band gaps can be created as a result of amplifying the motion of the small mass [20,21,22].

Regardless of the Bragg gaps, the local resonance gaps, or the inertial-amplification-induced gaps, the dispersion curves of phononic crystals and metamaterials are commonly presented in the form of the function of frequencies for real wavenumbers, or conversely, complex wavenumbers as a function of real frequencies. The former condition corresponds to the ω(k) form, where the wavenumbers are given in Bloch conditions and the underlying eigenvalue problem is solved for frequencies to detect wave modes within pass bands. The latter condition, on the other hand, follows the form of k(ω), which can be used to calculate complex wave vectors for a given frequency so that evanescent wave modes inside gaps can be obtained. It can be seen that the location, width, and attenuation characteristics of stop bands can be obtained simultaneously via the k(ω) form. The formulation based on the ω(k) path is easily implemented as the resulting characteristic determinant is usually set-up from a linear equation and, thus, a large number of studies have been conducted to examine the location and width of elastic wave band gaps [13,23,24,25,26,27]. In contrast, the k(ω) path is more computationally complicated as the calculations of complex Bloch wavenumbers are enforced to find solutions from transcendent equations [28], especially for the case concerned with detecting the decaying level of elastic waves from an arbitrary direction. In order to reduce the transcendental complexity of the k(ω) form, a wave field transformation capable of eliminating the dependence of phase constants is employed by researchers. Lewinska et al. [29] measured the effects of viscoelastic behavior on the longitudinal and shear wave band gaps by the formulation in the k(ω) form where the Bloch displacement function with special periodicity was used to reformulate the eigenvalue problem. Combing the Dirichlet-to-Neumann method with cylindrical wave expansions, Li et al. analyzed the effects of viscosity on the anti-plane transverse wave band gaps of a two-dimensional phononic crystal composed of square or triangular lattices of elastic circular solid cylinders in a viscoelastic solid matrix [30]. An efficient reduced formulation of the Bloch Operator Finite Element method was conducted to calculate the complex band structure by Palermo et al. [31] based on the wave field transformation, with accurate predictions of propagative, evanescent, and complex wave solutions with a reduction in computational time of more than one order of magnitude with respect to the full model calculations. The authors also extended this technique to observe the complex band structure of elastic waves in a three-dimensional phononic slab with viscoelastic effects [32]. One can notice that the studies applying the k(ω) approach were mainly focused on the wave band gaps in the purely elastic medium and the present work aims to present a general numerical framework that is able to predict the location, the bandwidth, and the attenuation characteristics of flexural wave band gaps when multi-field coupling effects are taken into consideration. In order to observe not only the real band diagram but also the degree of wave attenuation, the numerical formulations from ω(k) and k(ω) approaches are derived, respectively, and the results can support the correctness of each other.

It is acknowledged that the coupled fluid–structure mechanical systems have been widely applied in various engineering applications such as submarines, anechoic coatings, and offshore platforms, and, thus, it is necessary to tailor the propagation and attenuation of waves in continuous periodic structures with heavy fluid loading. Especially, plate-like periodic structures generally serve as the fundamental components in the underwater applications and, thus, the investigation of the flexural wave band gaps of the PnC plate has significant research value. However, to the best knowledge of the authors, the analysis of the band structure for the fluid–structure coupled system is concentrated on the periodic pipe structures with internal fluid, lacking accurate and efficient models to calculate the complex band structure of flexural waves with external heavy fluid. By proposing a periodic waveguide made of an array of expansionary mufflers, Liu et al. showed that the introduction of a muffler array to form a periodic structure in the piping system can suppress the propagation of acoustic waves with longer wavelengths [33]. The band structure of deploying pipes conveying fluid with periodic varying parameters was investigated by Liang et al. based on the Bragg scattering mechanisms [34], the results of which demonstrated that the fluid–structure interaction, deploying motion, and component geometry have significant effects on the location and width of the Bragg band gaps of the pipe. With a periodically varying cross-section of fluid-conveying pipes, Yu et al. attained the band gap distribution by the spectral element method and showed the effects of the substructure length and fluid–structure interaction on the band gaps [35]. For the numerical simulations on the periodic structures with external fluid, Sorokin [36] gave an analytical algorithm to compute Bloch parameters for the one-dimensional case incorporating fluid loading, and Zhang et al. proposed a tunable fluid–solid metamaterial consisting of several liquid inclusions in a solid matrix where the tunability of the band gaps is achieved by controlling the liquid distribution while the theoretical analysis is only available at the sub-wavelength scale [37]. In order to accurately predict the propagation and attenuation characteristics of flexural waves, the present work is concerned with the complex band structure of the phononic plate with external infinite heavy fluid, which is more widely used, and aims to construct a general numerical model that is available at full wavelength to discover the effects of fluid loading on the real and imaginary parts of dispersion relations. Obviously, the present work is helpful to gain a comprehensive study within multifield phononic crystals and extend the range of applications based on the band gap engineering in underwater vibration and sound reduction.

This paper is organized in four sections. Following the introduction, the theoretical derivations of ω(k) and k(ω) formulations are presented in Section 2. As an example, we pay attention to a phononic plate composed of two phase materials. The propagation and attenuation of flexural waves in this plate with heavy fluid loading are explored in Section 3. Finally, the conclusions are summarized in Section 4.

2. Descriptions and Model Formulations

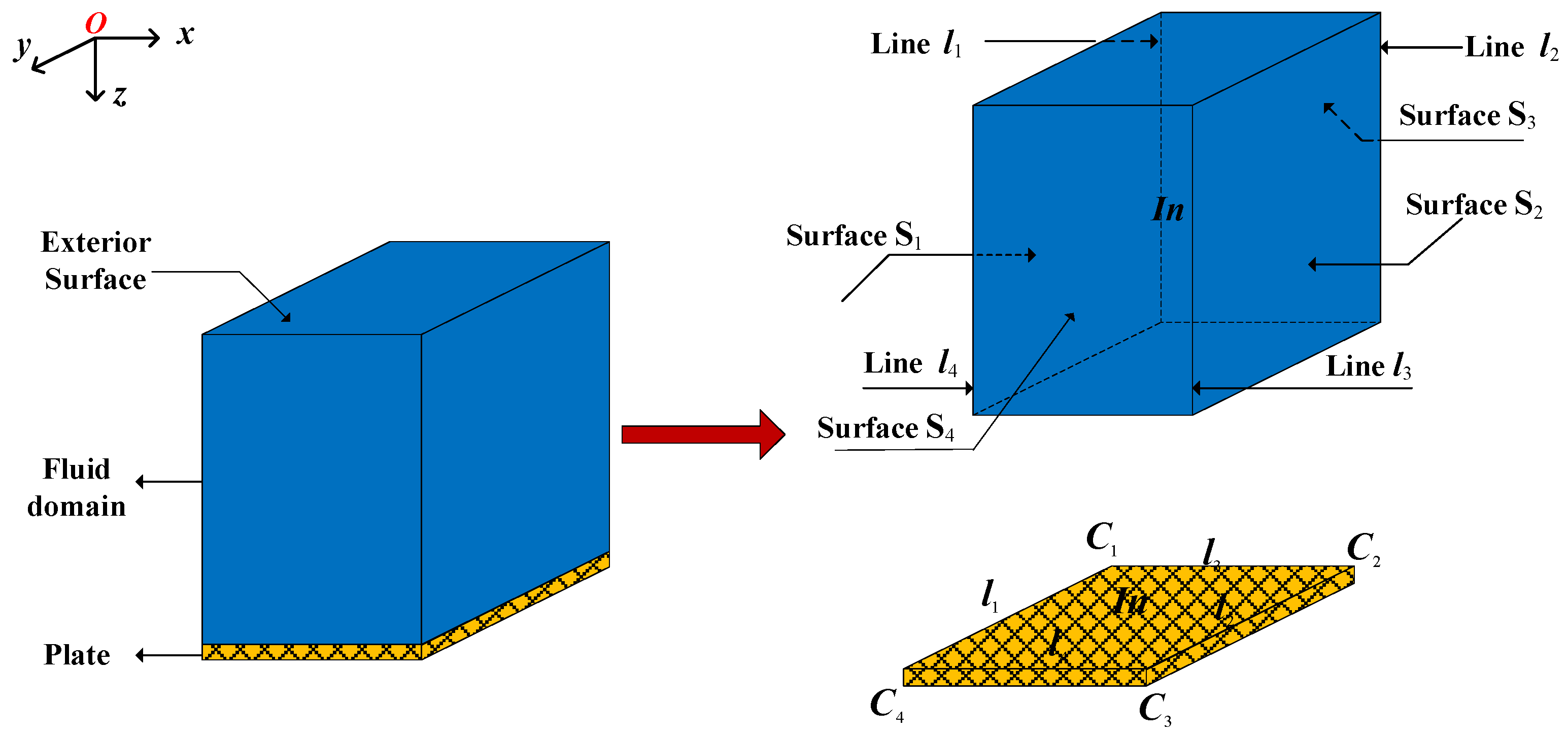
The strongly coupled structural-acoustic wave guide is designed as an infinite phononic plate with heavy external fluid in this study. The representative unit cell that has a two-dimensional periodicity in the xoy plane is sketched in Figure 1. The fluid domain is assumed to have a finite height and a radiation boundary condition is imposed on its exterior surface to approximate the exact wave-absorbing phenomenon.

The finite element method is employed to obtain the dynamic property of the system. The discrete formulations for a structure–fluid interaction problem without incident waves can be derived as [38]:

$$\left[\begin{array}{l}{\mathbf{M}}_s\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\mathbf{0}\\ {\rho }_f{\mathbf{R}}^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{M}}_f\end{array}\right]\left[\begin{array}{l}\ddot{\mathbf{u}}\\ \ddot{\mathbf{p}}\end{array}\right]+\left[\begin{array}{l}{\mathbf{C}}_s\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\mathbf{0}\\ \mathbf{0}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{C}}_f\end{array}\right]\left[\begin{array}{l}\dot{\mathbf{u}}\\ \dot{\mathbf{p}}\end{array}\right]+\left[\begin{array}{l}{\mathbf{K}}_s\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-\mathbf{R}\\ \mathbf{0}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{K}}_f\end{array}\right]\left[\begin{array}{l}\mathbf{u}\\ \mathbf{p}\end{array}\right]=\left[\begin{array}{l}{\mathbf{F}}_m\\ \mathbf{0}\end{array}\right]$$

(1)

where, K_s, M_s, and C_s represent the global stiffness, mass, and damping matrix of the plate; K_f and M_f are the global matrices for the fluid domain; ρ_f is the density of the fluid medium; C_f represents the “damping” matrix arising from the radiation boundary; matrix R denotes the coupling effects between the plate and the fluid; u and p denote the vectors of displacement and pressure, respectively. F_m represents the applied force to the plate.

2.1. The ω(k) Numerical Approach

The frequency band gaps and spatial filtering phenomenon are examined by the ω(k) approach with regard to the unknown frequency as a function of real Bloch wave vectors. According to the Floquet–Bloch theory, periodic boundary conditions for both structure and fluid should be applied on the unit cell model. As shown in Figure 1, the plate and the fluid domain are divided into different parts due to their locations in the global coordinate. The periodic boundary condition for the periodic plate is described as:

$$\left\{\begin{array}{c}{\mathbf{u}}_{l_1}\hfill \\ {\mathbf{u}}_{l_2}\hfill \\ {\mathbf{u}}_{l_3}\hfill \\ {\mathbf{u}}_{l_4}\hfill \\ {\mathbf{u}}_{c_1}\hfill \\ {\mathbf{u}}_{c_2}\hfill \\ {\mathbf{u}}_{c_3}\hfill \\ {\mathbf{u}}_{c_4}\hfill \\ {\mathbf{u}}_{in}\hfill \end{array}\right\}=\left[\begin{array}{cccc}\mathbf{I}\hfill & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{I}\exp \left(i{\mu }_x\right)\hfill & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{I}\exp \left(i{\mu }_y\right)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_x\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_x+i{\mu }_y\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_y\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{0}& \mathbf{I}\end{array}\right]\left[\begin{array}{l}{\mathbf{u}}_{l_1}\\ {\mathbf{u}}_{l_3}\\ {\mathbf{u}}_{c_1}\\ {\mathbf{u}}_{in}\end{array}\right]$$

(2)

where the subscripts of u denote the specified locations of plate nodes; μ_x and μ_y are phase constants and can be expressed as: μ_x = k_xa₁ and μ_y = k_ya₂, where a₁ and a₂ denote the lattice spacing along the x axis and the y axis, respectively.

Similarly, periodic boundary conditions for the fluid interacting with the base plate can be expressed as:

$$\left\{\begin{array}{l}{\mathbf{p}}_{s_1}\\ {\mathbf{p}}_{s_2}\\ {\mathbf{p}}_{s_3}\\ {\mathbf{p}}_{s_4}\\ {\mathbf{p}}_{l_1}\\ {\mathbf{p}}_{l_2}\\ {\mathbf{p}}_{l_3}\\ {\mathbf{p}}_{l_4}\\ {\mathbf{p}}_{in}\end{array}\right\}=\left[\begin{array}{cccc}\mathbf{I}\hfill & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{I}\exp \left(i{\mu }_x\right)\hfill & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{I}\exp \left(i{\mu }_y\right)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_x\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_x+i{\mu }_y\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}\exp \left(i{\mu }_y\right)& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{0}& \mathbf{I}\end{array}\right]\left[\begin{array}{l}{\mathbf{p}}_{s_1}\\ {\mathbf{p}}_{s_3}\\ {\mathbf{p}}_{l_1}\\ {\mathbf{p}}_{in}\end{array}\right]$$

(3)

where the subscripts of p indicate the specified locations (divided in fluid domain) of fluid nodes. In addition, the correlation lying in the adjacent unit cell of the periodic structure requires the applied force to satisfy the following relation:

$$\begin{array}{c}{\mathbf{F}}_{L_1}+\exp \left(-i{\mu }_x\right){\mathbf{F}}_{L_2}=\mathbf{0}\\ {\mathbf{F}}_{L_3}+\exp \left(-i{\mu }_y\right){\mathbf{F}}_{L_4}=\mathbf{0}\\ {\mathbf{F}}_{C_1}+\exp \left(-i{\mu }_x\right){\mathbf{F}}_{C_2}+\exp \left(-i{\mu }_x-i{\mu }_y\right){\mathbf{F}}_{C_3}+\exp \left(-i{\mu }_y\right){\mathbf{F}}_{C_4}=\mathbf{0}\end{array}$$

(4)

The periodic conditions including Equations (2)–(4) are further rewritten in the matrix form for brevity:

$$\begin{array}{c}\mathbf{u}={\mathbf{H}}_u{\mathbf{u}}_s\\ \mathbf{p}={\mathbf{H}}_p{\mathbf{p}}_s\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{F}}_m={[\mathbf{0}\hspace{0.33em}\hspace{0.33em}\mathbf{0}\hspace{0.33em}\hspace{0.33em}\mathbf{0}\hspace{0.33em}\hspace{0.33em}\mathbf{0}]}^{\mathrm{T}}\end{array}$$

(5)

where the subscript s represents the values on master nodes (i.e., ${\mathbf{u}}_s={[{\mathbf{u}}_{l_1}^{\mathrm{T}}\hspace{0.33em}{\mathbf{u}}_{l_3}^{\mathrm{T}}\hspace{0.33em}{\mathbf{u}}_{c_1}^{\mathrm{T}}\hspace{0.33em}{\mathbf{u}}_{in}^{\mathrm{T}}]}^{\mathrm{T}}$, ${\mathbf{p}}_s={[{\mathbf{p}}_{s_1}^{\mathrm{T}}\hspace{0.33em}{\mathbf{p}}_{s_3}^{\mathrm{T}}\hspace{0.33em}{\mathbf{p}}_{l_1}^{\mathrm{T}}\hspace{0.33em}{\mathbf{p}}_{in}^{\mathrm{T}}]}^{\mathrm{T}}$).

By substituting Equation (5) into Equation (1) and assuming time-harmonic motion, the discrete equations for the unit cell model of the periodic-fluid-loaded phononic plate are:

$$\left(-{\omega }^2\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{M}}_s{\mathbf{H}}_u\hfill & \mathbf{0}\\ {\rho }_f{\mathbf{H}}_p^{\mathrm{H}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{H}}_u\hfill & {\mathbf{H}}_p^{\mathrm{H}}{\mathbf{M}}_f{\mathbf{H}}_p\end{array}\right]+j\omega \left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{C}}_s{\mathbf{H}}_u\hfill & \mathbf{0}\\ \mathbf{0}& {\mathbf{H}}_p^{\mathrm{H}}{\mathbf{C}}_f{\mathbf{H}}_p\hfill \end{array}\right]+\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{K}}_s{\mathbf{H}}_u\hfill & -{\mathbf{H}}_u^{\mathrm{H}}\mathbf{R}{\mathbf{H}}_p\\ \mathbf{0}& {\mathbf{H}}_p^{\mathrm{H}}\hspace{0.33em}{\mathbf{K}}_f{\mathbf{H}}_p\end{array}\right]\hspace{0.33em}\right)\left[\begin{array}{l}{\mathbf{u}}_s\\ {\mathbf{p}}_s\end{array}\right]=\left[\begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}\right]$$

(6)

To compare with the results in previous work and validate the proposed method, the rigid wall boundary conditions are also adopted and the formulations to describe the motion of the fluid-loaded phononic plate with the rigid wall boundary are also derived as below. If a rigid wall boundary condition is imposed on the outer surface of the fluid domain, the damping matrix C_f from the radiation boundary is negligible. Hence, Equation (6) can be rewritten as the following when the structural model is assumed to be undamped:

$$\left(-{\omega }^2\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{M}}_s{\mathbf{H}}_u\hfill & 0\\ {\rho }_f{\mathbf{H}}_p^{\mathrm{H}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{H}}_u\hfill & {\mathbf{H}}_p^{\mathrm{H}}{\mathbf{M}}_f{\mathbf{H}}_p\end{array}\right]+\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{K}}_s{\mathbf{H}}_u\hfill & -{\mathbf{H}}_u^{\mathrm{H}}\mathbf{R}{\mathbf{H}}_p\\ \mathbf{0}& {\mathbf{H}}_p^{\mathrm{H}}\hspace{0.33em}{\mathbf{K}}_f{\mathbf{H}}_p\end{array}\right]\hspace{0.33em}\right)\left[\begin{array}{l}{\mathbf{u}}_s\\ {\mathbf{p}}_s\end{array}\right]=\left[\begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}\right]$$

(7)

It can be seen that the dispersion relation is able to be achieved by solving a linear eigenvalue problem. To further reduce the computation costs of the underlying equations, the fluid medium can be assumed as incompressible for which the sound speed is infinitely large. In that case, there is no need to take into account the matrix M_f, and Equation (7) becomes:

$$\left(-{\omega }^2\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{M}}_s{\mathbf{H}}_u\hfill & \mathbf{0}\hspace{0.33em}\hspace{0.33em}\\ {\rho }_f{\mathbf{H}}_p^{\mathrm{H}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{H}}_u& \mathbf{0}\hspace{0.33em}\hspace{0.33em}\end{array}\right]+\left[\begin{array}{cc}{\mathbf{H}}_u^{\mathrm{H}}{\mathbf{K}}_s{\mathbf{H}}_u& -{\mathbf{H}}_u^{\mathrm{H}}\mathbf{R}{\mathbf{H}}_p\\ \mathbf{0}& {\mathbf{H}}_p^{\mathrm{H}}\hspace{0.33em}{\mathbf{K}}_f{\mathbf{H}}_p\end{array}\right]\hspace{0.33em}\right)\left[\begin{array}{l}{\mathbf{u}}_s\\ {\mathbf{p}}_s\end{array}\right]=\left[\begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}\right]$$

(8)

Then, the pressure vector can be easily solved:

$${\mathbf{p}}_s={\omega }^2{\rho }_f{({\mathbf{H}}_p^{\mathrm{H}}{\mathbf{K}}_f{\mathbf{H}}_p)}^{-1}({\mathbf{H}}_p^{\mathrm{H}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{H}}_u){\mathbf{u}}_s$$

(9)

Substituting this relation to the structural dynamic equation, the numerical formulations for obtaining the band structure of periodic plates in the presence of fluid loading can be achieved:

$$({\mathbf{H}}_u^{\mathrm{H}}{\mathbf{K}}_s{\mathbf{H}}_u){\mathbf{u}}_s+(-{\omega }^2({\mathbf{H}}_u^{\mathrm{H}}{\mathbf{M}}_s{\mathbf{H}}_u+{\rho }_f{\mathbf{H}}_u^{\mathrm{H}}\mathbf{R}{\mathbf{H}}_p{({\mathbf{H}}_p^{\mathrm{H}}{\mathbf{K}}_f{\mathbf{H}}_p)}^{-1}({\mathbf{H}}_p^{\mathrm{H}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{H}}_u))){\mathbf{u}}_s=\mathbf{0}$$

(10)

This approach allows one to calculate the spatial dispersion for an arbitrary phononic plate with heavy fluid loading. The lower and upper edge frequencies of the band gap can be captured by specifying the Bloch wave vector at the boundary lines of the first irreducible Brillouin zone, i.e., IBZ.

2.2. The k(ω) Numerical Approach

In the k(ω) approach, complex wave vectors are required to be obtained for a given real frequency. The real and imaginary components of wavenumbers can be used to predict the propagation and attenuation of flexural waves, respectively. Therefore, either the stop band or the degree of wave decaying can be examined or assessed by this approach. However, when using the general FEM formulations, it is impossible to evaluate the propagation and attenuation constants from a polynomial eigenvalue problem in the arbitrary direction of k as the nature depends on whether the ratio between k_y and k_x is rational [28]. If k_y/k_x is rational, the polynomial eigenvalue equation can be formed; otherwise, the transcendental eigenvalue equation is preferred. For instance, when focusing on the ΓX direction and k_x is assumed as the unknown variable in Equation (7), the eigenvalue problem needs to be rewritten in the form:

$$\begin{array}{l}[{\lambda }_x^{-r-1}{\mathbf{A}}_1+{\lambda }_x^{-r}{\mathbf{A}}_2+{\lambda }_x^{-1}{\mathbf{A}}_3+{\mathbf{A}}_4+{\lambda }_x^{-r+1}{\mathbf{A}}_5\\ +{\lambda }_x^{r-1}{\mathbf{A}}_6+{\lambda }_x{\mathbf{A}}_7+{\lambda }_x^r{\mathbf{A}}_8+{\lambda }_x^{r+1}{\mathbf{A}}_9]\mathbf{Q}=\mathbf{0}\end{array}$$

(11)

where ${\lambda }_x=e^{i{k}_{x}a}=e^{i{\mu }_x}$ and parameter r denotes the ratio of k_y/k_x. From Equation (11), we can see that the eigenvalue equation remains in polynomial form only if r is rational. In order to reduce the computation difficulties, a wave field transformation capable of eliminating the phase-constant-dependent matrixes is applied [39]. The framework for dealing with the fluid–structure interaction problem is reformulated and presented as follows.

The transverse displacement and the pressure under the wave field transformation operator are:

$$\begin{array}{l}p=p_k\left(x,y,z,t\right)e^{\left(\lambda \cos \theta x+\lambda sin\theta y\right)}\\ w=w_k\left(x,y,t\right)e^{\left(\lambda \cos \theta x+\lambda \sin \theta y\right)}\end{array}$$

(12)

where λ = jk and λ = |λ|. In this case, the fluid domain is divided into three sections: the surfaces S_I, S_II and the inner domain V_in. S_I and S_II denote the fluid–structure interface and the exterior surface, respectively.

The wave motion equation in the inviscid and nonflowing fluid medium is:

$$\ddot{p}/c^2={\mathbf{L}}^T\left(\mathbf{L}p\right),\hspace{0.33em}\hspace{0.33em}p\in V_{in}$$

(13)

where the differential operator L is expressed as: $\mathbf{L}={\left[\partial /\partial x\hspace{0.33em}\hspace{0.33em}\partial /\partial y\hspace{0.33em}\hspace{0.33em}\partial /\partial z\right]}^{\mathrm{T}}$. The continuity between normal velocity and stress at the fluid–structure interface is ensured by:

$$\partial p/\partial n_{\mathrm{I}}=-{\rho }_f\ddot{w},\hspace{0.33em}p\in S_{\mathrm{I}}$$

(14)

where n_I denotes the normal direction of the interface S_I, and in this study, it implies the positive z direction.

The wave-absorbing boundary imposed on the exterior surface is assumed as:

$$\partial p/\partial n_{\mathrm{I}\mathrm{I}}=-\dot{p}/c,\hspace{0.33em}p\in S_{\mathrm{I}\mathrm{I}}$$

(15)

where n_II denotes the normal direction of the exterior surface S_II of the fluid domain.

Substituting the expressions of the displacement and the pressure of Equation (12) to Equation (13), Equation (14) and Equation (15) yield a new formulation to describe the time-harmonic motion of acoustic waves in the fluid medium:

$$\begin{array}{l}\frac{-{\omega }^2}{c^2}{p}_k-{\mathbf{L}}^{\mathrm{T}}\left(\mathbf{L}{p}_k\right)-\lambda \left({\mathbf{h}}^{\mathrm{T}}\mathbf{L}{p}_k+{\mathbf{L}}^{\mathrm{T}}\mathbf{h}{p}_k\right)-{\lambda }^2{\mathbf{h}}^{\mathrm{T}}\mathbf{h}{p}_k=0\hspace{0.33em};\hspace{0.33em}{p}_k\in V_{in}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{n}}_{\mathrm{I}}^{\mathrm{T}}\mathbf{L}{p}_k+\lambda {\mathbf{n}}_{\mathrm{I}}^{\mathrm{T}}\mathbf{h}{p}_k-{\rho }_f^2{\omega }^2{w}_k=0\hspace{0.33em};\hspace{0.33em}{p}_k\in S_{\mathrm{I}}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{n}}_{\mathrm{I}\mathrm{I}}^{\mathbf{T}}\mathbf{L}{p}_k+\lambda {\mathbf{n}}_{\mathrm{I}\mathrm{I}}^{\mathrm{T}}\mathbf{h}{p}_k-j\omega \frac{1}{c}{p}_k=0\hspace{0.33em};\hspace{0.33em}{p}_k\in S_{\mathrm{I}\mathrm{I}}\end{array}$$

(16)

where the vector h is: h = [cos(θ) sin(θ) 0]^T. The angle θ denotes the propagation direction of the flexural wave. Then, we consider the effects of fluid loading on the periodic plate. The transverse motion of the plate in the presence of external fluid can be characterized by:

$${\rho }_{s}t\ddot{w}+{\mathrm{\Theta }}^{\mathrm{T}}\mathbf{D}\left(\mathrm{\Theta }w\right)=p$$

(17)

where $\mathrm{\Theta }={\left[{\partial }^2/\partial x^2\hspace{0.33em}\hspace{0.33em}{\partial }^2/\partial y^2\hspace{0.33em}\hspace{0.33em}2{\partial }^2/\partial x\partial y\right]}^{\mathrm{T}},$ and D is the flexural modulus matrix. In addition, substituting the displacement and pressure with the expressions in Equation (12) to the governing equation of the host phononic plate, the governing equation is rewritten as:

$$-{\omega }^2{\rho }_{s}t{w}_k+\left\{\begin{array}{l}{\mathbf{\Theta }}^{\mathrm{T}}\mathbf{D}\mathbf{\Theta }{w}_k+\lambda \left(2{\mathbf{\Theta }}^{\mathrm{T}}\mathbf{D}\mathbf{\Gamma }+{\mathbf{\Gamma }}^{\mathrm{T}}\mathbf{D}\mathbf{\Theta }\right)w_k+{\lambda }^2\left({\mathbf{\Theta }}^{\mathrm{T}}\mathbf{D}\mathbf{H}+{\mathbf{\Gamma }}^{\mathbf{T}}\mathbf{D}\mathbf{\Theta }\right)w_k\\ +{\lambda }^3\left(2{\mathbf{\Gamma }}^{\mathrm{T}}\mathbf{D}\mathbf{H}+2{\mathbf{H}}^{\mathrm{T}}\mathbf{D}\mathbf{\Gamma }\right)w_k+{\lambda }^4{\mathbf{H}}^{\mathrm{T}}\mathbf{D}\mathbf{H}{w}_k\end{array}\right\}-p_k=0$$

(18)

where the operator Γ is: $\mathrm{\Gamma }=\left[\begin{array}{cc}\cos \left(\theta \right)& 0\\ 0& \sin \left(\theta \right)\\ \sin \left(\theta \right)& \cos \left(\theta \right)\end{array}\right]\left[\begin{array}{l}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\end{array}\right]$. Applying the standard Galerkin approach on Equations (16) and (18), the discrete forms of the coupled system are eventually derived:

$$\left\{\begin{array}{l}\left[\begin{array}{l}-{\omega }^2{\mathbf{M}}_s+{\mathbf{K}}_{s0}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-{\mathbf{R}}^{\mathrm{T}}\\ -{\omega }^2{\rho }_f\mathbf{R}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-{\omega }^2{\mathbf{M}}_f-j\omega {\mathbf{C}}_f+{\mathbf{K}}_{f0}\end{array}\right]+\lambda \left[\begin{array}{cc}{\mathbf{K}}_{s1}\hfill & \mathbf{0}\\ \mathbf{0}\hfill & {\mathbf{K}}_{f1}\end{array}\right]+\\ {\lambda }^2\left[\begin{array}{cc}{\mathbf{K}}_{s2}\hfill & \mathbf{0}\\ \mathbf{0}\hfill & {\mathbf{K}}_{f2}\end{array}\right]+{\lambda }^3\left[\begin{array}{ll}{\mathbf{K}}_{s3}\hfill & \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}\end{array}\right]+{\lambda }^4\left[\begin{array}{ll}{\mathbf{K}}_{s4}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\end{array}\right\}\left[\begin{array}{l}{\mathbf{W}}_k\\ \hspace{0.33em}{\mathbf{P}}_k\end{array}\right]=\left[\begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}\right]$$

(19)

The assembled matrixes for the periodic plate are formulated as:

$$\begin{array}{l}{\mathbf{K}}_{s0}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}{\mathbf{B}}_{\mathrm{\Theta }}\mathbf{D}{\mathbf{B}}_{\mathrm{\Theta }}dxdy}\\ {\mathbf{K}}_{s1}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}2\left({\mathbf{B}}_{\mathrm{\Theta }}^{\mathrm{T}}\mathbf{D}{\mathbf{B}}_{\mathrm{\Gamma }}-{\mathbf{B}}_{\mathrm{\Gamma }}^{\mathrm{T}}\mathbf{D}{\mathbf{B}}_{\mathrm{\Theta }}\right)}dxdy\\ {\mathbf{K}}_{s2}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}\left({\mathbf{B}}_{\mathrm{\Theta }}^{\mathrm{T}}\mathbf{D}\mathbf{H}{\mathbf{N}}_s+{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{H}}^{\mathrm{T}}\mathbf{D}{\mathbf{B}}_{\mathrm{\Theta }}-4{\mathbf{B}}_{\mathrm{\Gamma }}\mathbf{D}{\mathbf{B}}_{\mathrm{\Gamma }}\right)}dxdy\\ {\mathbf{K}}_{s3}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}2\left(-{\mathbf{B}}_{\mathrm{\Gamma }}^{\mathrm{T}}\mathbf{D}\mathbf{H}{\mathbf{N}}_s+{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{H}}^{\mathrm{T}}\mathbf{D}{\mathbf{B}}_{\mathrm{\Gamma }}\right)dxdy}\\ {\mathbf{K}}_{s4}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{H}}^{\mathrm{T}}}\mathbf{H}{\mathbf{N}}_{s}dxdy\\ {\mathbf{M}}_s={\rho }_{s}t{\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}{\mathbf{N}}_s^{\mathrm{T}}}{\mathbf{N}}_{s}dxdy\end{array}$$

(20)

where N_s is the matrix of shape functions for w_k, B_Θ = ΘN_s, and B_Γ = ΓN_s. ρ_s represents the density of the plate. The discrete matrixes to describe wave motion in a fluid are given as:

$$\begin{array}{l}{\mathbf{K}}_{f0}={\displaystyle \underset{{\mathrm{\Omega }}_f}{\mathrm{\iiint }}{\mathbf{B}}_{\mathrm{L}}^{\mathrm{T}}{\mathbf{B}}_{\mathrm{L}}}dxdydz\\ {\mathbf{K}}_{f1}={\displaystyle \underset{{\mathrm{\Omega }}_f}{\mathrm{\iiint }}\left({\mathbf{B}}_{\mathrm{L}}^{\mathrm{T}}\mathbf{h}{\mathbf{N}}_p-{\mathbf{N}}_p^{\mathrm{T}}{\mathbf{h}}^{\mathrm{T}}{\mathbf{B}}_{\mathrm{L}}\right)}dxdydz\\ {\mathbf{K}}_{f2}=-{\displaystyle \underset{{\mathrm{\Omega }}_f}{\mathrm{\iiint }}{\mathbf{N}}_p^{\mathrm{T}}}{\mathbf{h}}^{\mathrm{T}}\mathbf{h}{\mathbf{N}}_{p}dxdydz\\ {\mathbf{M}}_f=\frac{1}{c_f^2}{\displaystyle \underset{{\mathrm{\Omega }}_f}{\mathrm{\iiint }}{\mathbf{N}}_p^{\mathrm{T}}{\mathbf{N}}_{p}dxdydz}\\ {\mathbf{C}}_f=\frac{1}{c_f}{\displaystyle \underset{S_{\mathrm{I}\mathrm{I}}}{\mathrm{\iint }}{\mathbf{N}}_p^{\mathrm{T}}{\mathbf{N}}_{p}dxdy}\end{array}$$

(21)

where N_p is the matrix with shape functions for p_k and B_L = LN_p. In addition, the coupling matrix R is formulated as: $\mathbf{R}={\displaystyle \underset{S_{\mathrm{I}}}{\mathrm{\iint }}{\mathbf{N}}_p^{\mathrm{T}}}{\mathbf{N}}_{s}dxdy.$

As the unknown nodal value is transformed from w(p) to w_k(p_k) after using the wave field transformation, the periodic boundary conditions also need to be modified. The mechanical field of the displacement and pressure should satisfy the following relation at the unit cell boundaries [39]:

$$\begin{array}{l}\left\{\begin{array}{l}{\mathbf{W}}_{k,l_2}={\mathbf{W}}_{k,l_1},{\mathbf{W}}_{k,l_4}={\mathbf{W}}_{k,l_3}\hspace{0.33em}\\ {\mathbf{W}}_{k,c_4}={\mathbf{W}}_{k,c_3}={\mathbf{W}}_{k,c_2}={\mathbf{W}}_{k,c_1}\end{array}\right.\\ \left\{\begin{array}{l}{\mathbf{P}}_{k,S_2}={\mathbf{P}}_{k,S_1},\hspace{0.33em}{\mathbf{P}}_{k,S_4}={\mathbf{P}}_{k,S_3}\\ {\mathbf{P}}_{k,l_4}={\mathbf{P}}_{k,l_3}={\mathbf{P}}_{k,l_2}={\mathbf{P}}_{k,l_1}\end{array}\right.\end{array}$$

(22)

Thus, H_u and H_p are reduced to matrixes without any phase constants, i.e., Bloch wave vectors. The applied force induced by the adjacent cell should also satisfy the new relation:

$$\begin{array}{c}{\mathbf{F}}_{L_1}+{\mathbf{F}}_{L_2}=\mathbf{0}\\ {\mathbf{F}}_{L_3}+{\mathbf{F}}_{L_4}=\mathbf{0}\\ {\mathbf{F}}_{C_1}+{\mathbf{F}}_{C_2}+{\mathbf{F}}_{C_3}+{\mathbf{F}}_{C_4}=\mathbf{0}\end{array}$$

(23)

After substituting the modified periodic boundary conditions into Equation (19), a new polynomial eigenvalue problem with respect to λ can be formed:

$$\left({\mathbf{D}}_0+\lambda {\mathbf{D}}_1+{\lambda }^2{\mathbf{D}}_2+{\lambda }^3{\mathbf{D}}_3+{\lambda }^4{\mathbf{D}}_4\right){\mathbf{U}}_k=\mathbf{0}$$

(24)

where U_k represents the general displacement vector that consists of node values of w_k and p_k. From Equation (24), we can see that the wave vector is independent of the assembled matrixes of the system. Furthermore, to reduce the quartic eigenvalue problem to a linear one, a simple space transformation is employed and Equation (24) is rewritten as:

$$\left[\begin{array}{cccc}-{\mathbf{D}}_3\hfill & -{\mathbf{D}}_2& -{\mathbf{D}}_1& -{\mathbf{D}}_0\\ \mathbf{I}\hfill & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}\hfill & \mathbf{0}& \mathbf{I}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}{\lambda }^3{\mathbf{U}}_k\\ {\lambda }^2{\mathbf{U}}_k\\ \lambda {\mathbf{U}}_k\\ {\mathbf{U}}_k\end{array}\right]=\lambda \left[\begin{array}{cccc}{\mathbf{D}}_4\hfill & \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}\\ \mathbf{0}\hfill & \hspace{0.33em}\hspace{0.33em}\mathbf{I}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}\\ \mathbf{0}\hfill & \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{I}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}\\ \mathbf{0}\hfill & \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{0}& \hspace{0.33em}\hspace{0.33em}\mathbf{I}\end{array}\right]\left[\begin{array}{c}{\lambda }^3{\mathbf{U}}_k\\ {\lambda }^2{\mathbf{U}}_k\\ \lambda {\mathbf{U}}_k\\ {\mathbf{U}}_k\end{array}\right]$$

(25)

The variable λ is acquired by solving Equation (25), by which one is able to examine the propagation and attenuation of flexural waves in space when the effects of external heavy fluid are taken into consideration. In addition, the directionality of wave decaying can be obtained through varying the direction of propagation θ.

3. Numerical Examples and Discussions

In this section, the dynamic characteristics of flexural waves in a fluid-loaded plate with two-dimensional periodicity are investigated by the proposed ω(k) and k(ω) formulations, from which the location, width, attenuation level, and directionality of the stop bands can be observed directly. Before we perform the analysis of a general two-dimensional case, the numerical model in the form of ω(k) is validated by comparing to a one-dimensional case derived from Ref. [36]. As the rigid wall condition is applied in [36], the matrix C_f is eliminated from the dynamic equations of the fluid–structure system and Equation (7) is adopted to calculate the real band diagram. The physical model is infinitely extended in the x direction and made up of the set of alternating elements of two different materials.

Table 1. Locations of band gaps of the periodic plate from [36].

	Proposed Method		Reference [36]
	System with Fluid	System without Fluid	System with Fluid	System without Fluid
First band gap	0.95 < Ω < 2.81	3.09 < Ω < 9.08	0.81 < Ω < 3.01	2.85 < Ω < 9.05
Second band gap	9.78 < Ω < 15.2	22.4 < Ω < 35.07	9.78 < Ω < 15.17	22.4 < Ω < 35.82

presents the boundary of the first and second stop bands obtained by the proposed method and Ref. [36], which is in terms of the normalized frequency Ω. The formulation of Ω can be derived from Ref. [36] and is omitted here. A perfect agreement is clearly seen, which validates the numerical formulations given in the present work. Additionally, it is noted that the fluid loading is expected to narrow the band gap width in this one-dimensional periodic lattice.

3.1. The Band Diagram Based on ω(k) Formulations

Then, the numerical simulation for acquiring the real band diagram of a two-dimensional phononic plate with a square lattice is performed based on the ω(k) formulations. The unit cell with the corresponding IBZ is shown in Figure 2. The material properties of the components are specified by elastic moduli E₁ and E₂, densities ρ₁ and ρ₂, and Poisson’s ratios ν₁ and ν₂, and the ratio r_e between the elastic modulus is assumed as 0.001 while the other material parameters remain the same. The material with larger elastic modulus is assumed as steel, the exterior fluid is assumed as water, and its sonic wave speed and density are 1500 m/s and 1025 kg/m³, respectively. The unit cell length and the thickness of the phononic plate are denoted by l and t, which are designed as 0.02 m and 0.0002 m, respectively. The height of the fluid domain H is set as 0.02 m. It is noted that the above parameters are kept unchanged unless otherwise stated.

It is obvious that the unit cell possesses the highest-level symmetry and, thus, the complete band gap can be easily obtained by scanning the k-space along the edges of the IBZ depicted by the grey region in Figure 2b. It is well known that the coordinates of points Γ, X, and M are (0,0), (π/l,0), and (π/l, π/l), respectively. 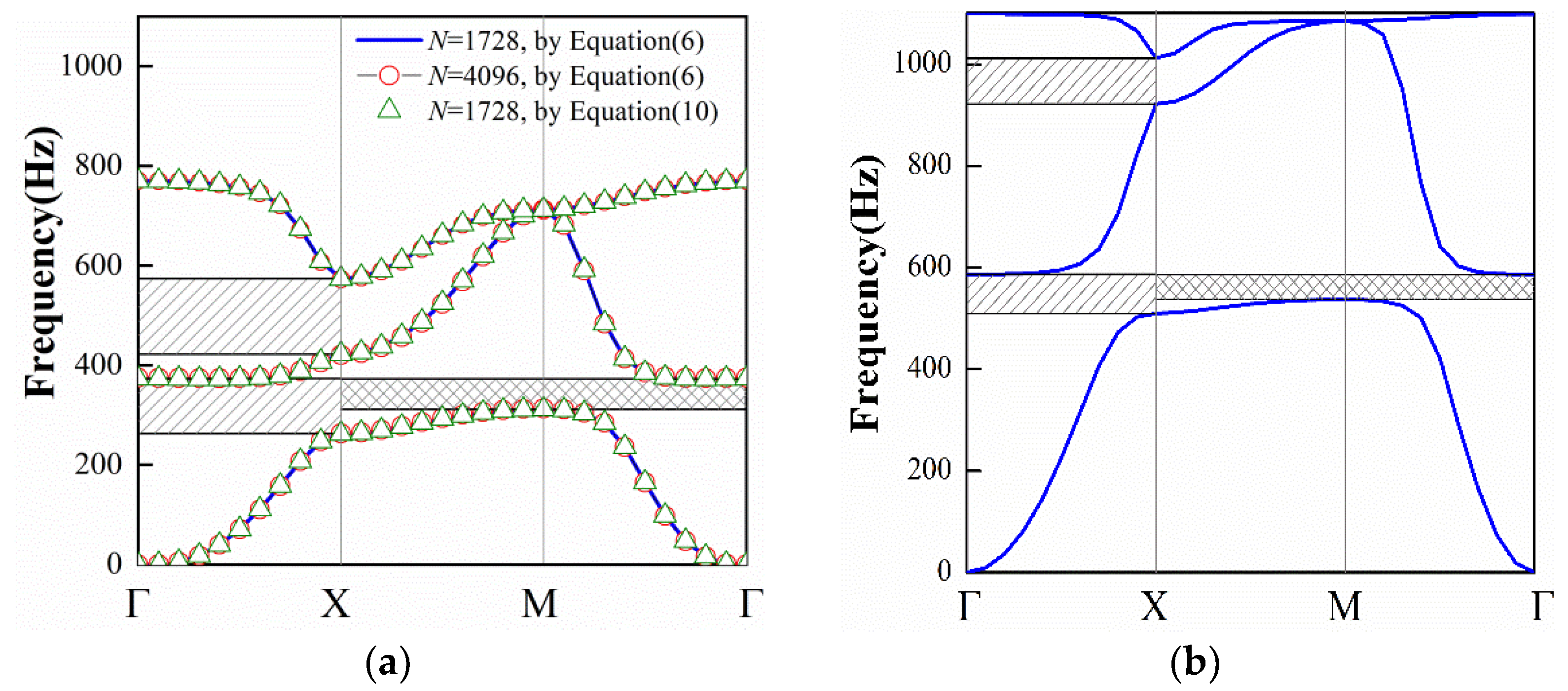Equation (6) is adopted and solved using a state-space transformation method [40]. To verify the incompressible fluid assumption, the discrete formulation with less computation costs from Equation (10) is also applied to obtain the band diagram.

The dispersion curves with high frequencies are ignored; henceforth, only the first to third band regions are given. The fluid–structure coupled system is meshed into 12, 12, 12 and 16, 16, 16 finite element divisions, respectively, in the x, y, and z directions, respectively. The dispersion relations obtained by Equations (6) and (10) with different mesh schemes are illustrated in Figure 3a. It can be found that the results are merely overlapped, which validates the incompressible fluid assumption used in band gap calculations. Figure 3b provides the band diagram for the pure phononic plate without fluid loading. Obviously, there are two ΓX directional and one complete band gaps in both spatial dispersion plots. The first directional band gap is induced by the local resonance and the second one is generated by the phenomenon of Bragg scattering. In addition, the complete band gap induced by the localized resonant mechanisms is found between the first and second dispersion curves.

One can also see that the band structure is strongly shifted to low frequencies and the absolute bandwidths of the stop bands are enlarged by the fluid loading. However, in Ref. [36], the fluid loading is able to narrow the band gap width. This dramatic difference indicates that the relative change in the bandwidth induced by heavy fluid loading cannot be simply quantified. It is dependent on the material distribution and physical characteristics of the unit cell.

3.2. Vibration Transmittance of Finite Structures

Vibration transmittance of finite structures has drawn particular interest as plate structures are usually applied with finite extension in practice. A finite plate made of 1 × 10 unit cells is considered to evaluate the attenuation magnitude of flexural waves. We adopt the finite element method to calculate the transverse vibration transmittance of such a finite structure. As illustrated in Figure 4, the excitation is designed as a line harmonic force excitation as it is more likely to produce waves propagating along the ΓX direction. The notations of ‘Point A’ and ‘Point B’ denote the locations where the transverse vibration responses are interested. The transmittance T is given by the following equation [41]:

$$T=20\log \left(\left|\frac{w_A}{w_B}\right|\right)$$

(26)

where w represents the transverse displacement of the finite plate.

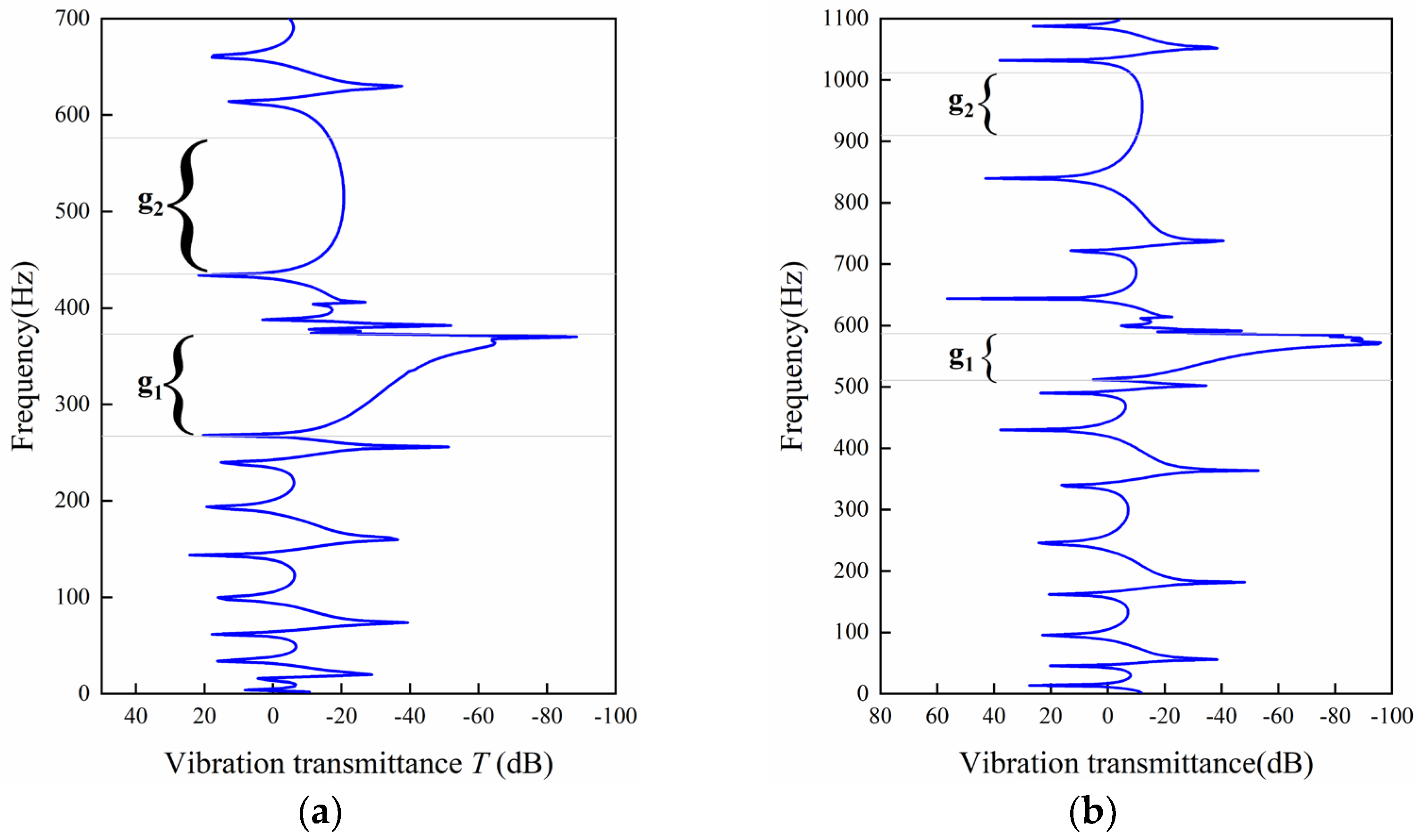
The external fluid is assumed infinite and interacted with the finite plate. The Rayleigh integral on the plate surface is coupled with the derived finite element formulation to model fluid–structure interaction of the baffled plate subject to heavy fluid loading [42]. Then, the displacement of the finite plate with heavy fluid loading can be obtained. Figure 5a shows the values of T as a function of frequency. Due to the existence of the directional stop bands, two frequency ranges with significant transmittance loss are observed. They are depicted by grey rectangles in the plot. The fist gap g₁ appears as a sharp notch and the second one g₂ appears as a smooth valley, whose bandwidth is in accordance with those of the local resonance and the Bragg directional band gaps observed from Figure 3a. One can also find that the maximum absolute value of the transmittance dip inside the gap g₁ is much larger than that in the gap g₂, and this can be explained by the attenuation constant that is presented subsequently. Figure 5b shows the vibration transmittance of the same finite plate without fluid loading. The transmittance gaps are seen at higher frequencies. The two plots show different values of the maximum transmission drop inside the gaps, and this is further explored in the following subsections.

3.3. Wave Attenuation Based on k(ω) Formulations

The attenuation characteristics of flexural waves of the heavy fluid-loaded periodic plate is evaluated by the k(ω) approach in this subsection. The simulation is performed using the finite element method combined with the wave field transformation. To validate the derived formulas, the imaginary parts of wavenumbers from the ΓX direction are also calculated by the general finite element method for comparison. The sound absorbing condition is replaced by a rigid wall condition when the general finite element method is applied. The imaginary component of the wavenumber represents the spatial attenuation and, thus, the wave decaying rate μ_θ can be evaluated by:

$${\mu }_{\theta }=real\left(\max \left(\lambda l\cos \theta ,\hspace{0.33em}\lambda l\sin \theta \right)\right)$$

(27)

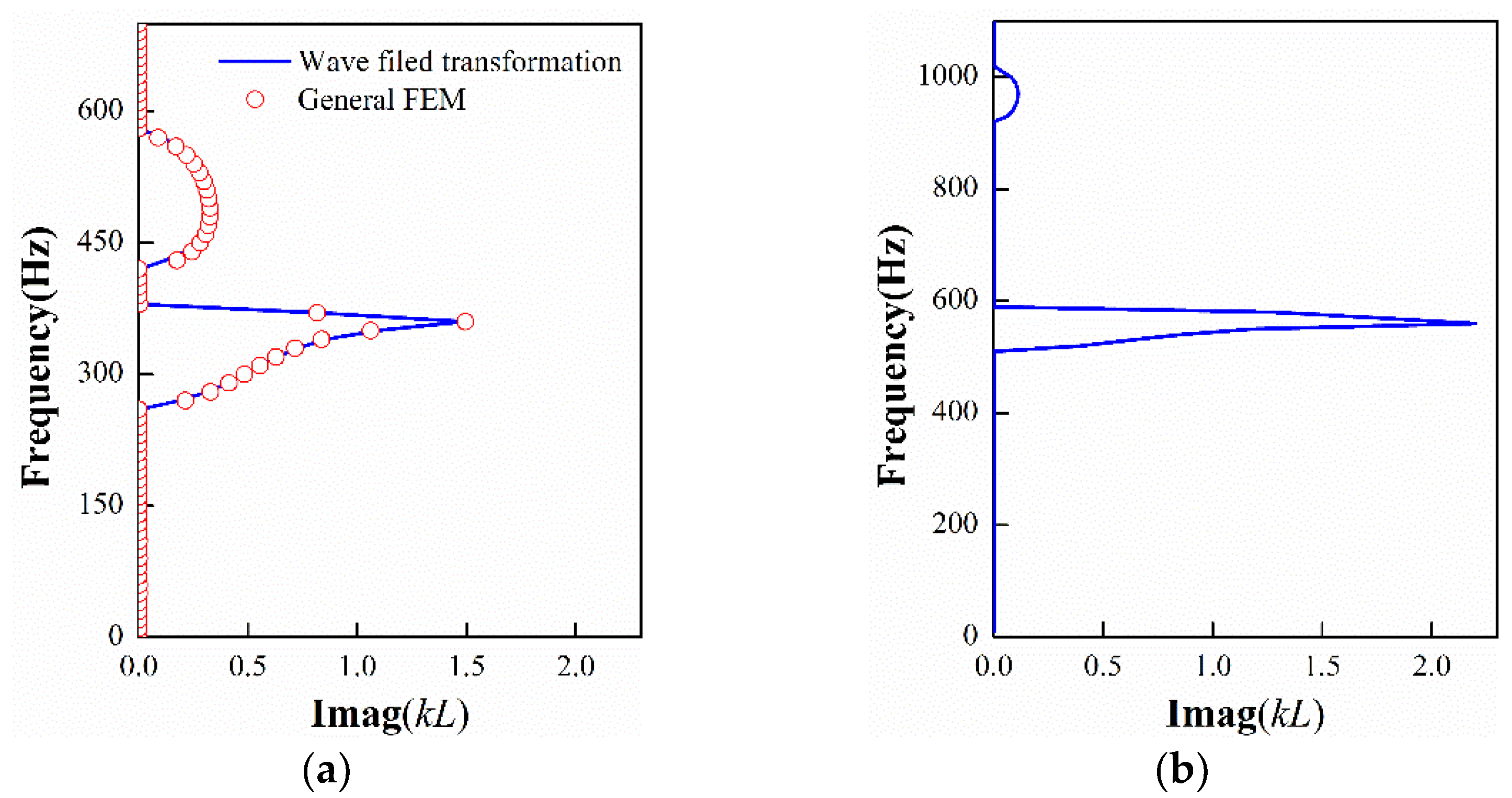
Focusing on the wave attenuation from the ΓX direction, the propagating angle θ is specified as zero. Figure 6 presents the spatial attenuation of flexural waves obtained by the wave field transformation and general FEM, from which the directional band gap is easily distinguished from the frequency range with non-zero attenuation constants. In Figure 6a, the dispersion curve of the attenuation constant based on the proposed method is in good agreement with the result by the finite element method, which not only validates the proposed approach but also indicates that the boundary condition imposed on surface S_II has little influence on the band structure. The first band gap is shown as a local resonance gap and the second one is shown as a Bragg gap, whose locations are consistent with that displayed in Section 3.1.

It can be seen that the maximum attenuation constant of the local resonance gap is higher than that of the Bragg gap. This is why the transmission loss in g₁ is larger than that in g₂. The corresponding results of the bare periodic plate are given in Figure 6b. From Figure 6, one can notice that the value of the attenuation peak is decreased within the local resonance gap while increased in the Bragg gap due to the effects of heavy fluid loading. Such a phenomenon is able to explain the transmission drops of finite plates in Section 3.2, where the maximum absolute value in g₁ of Figure 5a is smaller than that in Figure 5b. Likewise, the depth profiles of gaps in the transmittance function plots also demonstrate the viewpoint that the fluid loading is capable of weakening the maximum attenuation performance of the resonance gap and enhancing that of the Bragg gap.

To further observe the effects of r_e on the attenuation performance, the parameter r_e is designed ranging from 0.001 to 0.002. Considering the fluid–structure interaction effects, Figure 7a shows the influence of r_e on the wave decaying inside the directional band gaps of the unit cell with fluid loading. From Figure 7a, one can see that the locations of band gaps are shifting to high frequencies as the elastic modulus ratio is further increased. In addition, a special phenomenon is observed in this attenuation variations diagram. When the ratio r_e is tuned to 0.00135, the two directional band gaps are nearly coupled together and form a super-wide gap with which only a very narrow pass band between them exists. Furthermore, as the ratio r_e is smaller than this specific value, the first directional band gap is generated by the local resonance mechanisms and the second one is induced by the Bragg scattering. However, if the ratio r_e exceeds this specific value, the first gap behaves like a Bragg gap and the second gap becomes a local resonance gap. A similar phenomenon can also be found in the plate without fluid loading. As seen in Figure 7b, when the ratio r_e exceeds 0.0028, the nature of directional band gaps is exchanged. Thus, if the elastic modulus ratio is tuned within a range from 0.00135 to 0.0028, the mechanisms for generating the directional band gaps of the fluid-loaded plate would not be consistent with the case of the bare phononic plate. As a consequence, the dispersion curves are significantly changed. This is because the upper boundary representing the local resonance mode of the fluid-loaded unit cell becomes larger than the Bragg frequency, while, in the case of the unit cell without heavy fluid, the upper edge is still lower than the corresponding Bragg frequency.

3.4. Directionality of Flexural Wave Decaying

The above discussions are mainly focused on the attenuation constant in the horizontal direction. In order to observe the directionality of wave attenuation of the coupled plate, the spatial attenuation constants from all directions are calculated at the frequencies of the attenuation peaks, that is, 360 Hz and 490 Hz. As the considered lattice possesses the highest-level symmetry characteristics, the complete attenuation profile can be obtained by calculating the attenuation constants only within the range of θ from 0 to π/4. The evaluations of attenuation constants with respect to the propagating direction θ at 360 Hz and 490 Hz are shown in Figure 8a,b, respectively. It is worth noting that the complete band gap is generated by the local resonance around 360 Hz and, thus, a comparable attenuation degree of flexural waves can be observed from all directions in Figure 8a. Notably, the magnitude varies slightly with respect to changing θ. In contrast, the Bragg band gap is an angular gap, which shows a great dependence on θ as observed from Figure 8b. The maximum attenuation in the Bragg gap is not found in horizontal or vertical directions—it is attained around the directional angle θ of π/12.

The results for the plate without fluid loading at 560 Hz and 970 Hz, i.e., the attenuation peaks, are given in Figure 8c,d. The shape of the wave attenuation profile of the local resonance gap is similar but with larger amplitudes, while the Bragg gap deviates a lot. By comparing Figure 8b–d, one can also notice that the angular dependence of wave attenuation in the fluid-loaded plate is not as strong as that in the plate without fluid loading; in other words, the external fluid has the ability to reduce the attenuation anisotropy of the Bragg stop band in the phononic plate. To quantify the degree of anisotropy in the wave attenuation profile, a new quantity s defined as the standard deviation in the angle-dependent attenuation constant μ_θ for a given frequency ω is introduced. This quantity can be obtained by:

$$s=\frac{1}{\overline{\mu }\left(\omega \right)}\sqrt{\frac{1}{n_{\theta }-1}{\displaystyle \sum _{i=1}^{n_{\theta }}{\left({\mu }_i\left(\omega ,{\theta }_i\right)-\overline{\mu }\left(\omega \right)\right)}^2}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\overline{\mu }\left(\omega \right)={\displaystyle \sum _{i=1}^{n_{\theta }}\mu \left(\theta ,\omega \right)}$$

(28)

where θ_i indicates the direction of wave propagation and μ_i is the attenuation constant at θ_i; i is the sampling index and n_θ is the total number of sampling points in the range of 0 to π/4. For the fluid-loaded phononic plate, the value of s inside the Bragg gap (at 490 Hz) is 1.109, and for the bare phononic plate, the corresponding value (at 970 Hz) is 2.33. A lower value indicates that the fluid loading tends to smooth the results of the attenuation directionality and make the phononic plate behave less anisotropically.

4. Conclusions

As it is necessary to control wave propagation and attenuation in a strongly coupled structural acoustic wave guide, the complex band diagram of flexural waves in the fluid-loaded phononic plates is investigated in the present work. The numerical models based on the ω(k) approach and the k(ω) approach are developed, respectively, to study the propagating and evanescent flexural waves. It is noted that the ω(k) formulation is in accordance with the general finite element form but the k(ω) approach capable of determining the attenuation constants of flexural waves from all directions provides a new avenue to deal with the fluid–structure interaction problem in periodic wave guides. The numerical model in the k(ω) form is established by applying the wave field expansion to the out-of-plane displacement and the acoustic pressure, while using the Galerkin method with the finite element discretization technique to acquire the discrete formulations.

The comparison results of the real band structure of the square phononic plate with and without external heavy fluid show that the locations of the band gaps are modulated into lower frequencies and the bandwidths are expanded to larger frequency ranges due to the external heavy fluid. This trend can be found from both complete and directional band gaps generated by the mechanisms of the local resonance and the Bragg scattering. Further, from the results of the attenuation diagrams, one can notice that the fluid loading is able to reduce the maximum attenuation constant inside the local resonance gap but enhance the decaying level of the Bragg gap. The location and width of the stop bands are also consistent with those observed from the real band structure. Moreover, these influences caused by the heavy fluid loading are demonstrated by the calculation results of the vibration transmittance of finite phononic plate composed of numerous unit cells. It is seen that the transmission loss regions match well with the stop bands. The directionality of wave attenuation in the fluid-loaded plate is also investigated. Regarding the complete stop band induced by the local resonance, the propagation of flexural waves from all directions can be prohibited and, thus, the attenuation level varies slightly with respect to the wave direction. In contrast, the Bragg gap is an angular gap and shows a strong attenuation anisotropy. The results indicate that the heavy fluid loading is able to reduce the level of the anisotropy degree of the Bragg gap. Additionally, a special phenomenon of forming a super-wide directional band gap occurs by varying the elastic modulus ratio, in which case the local resonance frequency is expected to coincide with the Bragg frequency and only a narrow pass band exists inside the stop band. However, due to the heavy fluid loading, the specific values of the elastic modulus ratio corresponding to such a phenomenon are different. As a result, the mechanisms to induce the first and second directional band gaps are switched for the considered cases if the ratio is tuned to range from 0.00135 to 0.0028; in other words, the first stop band is a Bragg scattering gap and the second one is a local resonance gap for the fluid-loaded phononic plate, while that for the bare phononic plate is just the opposite.

The presented study provides a new numerical framework for characterizing wave propagation and attenuation in the phononic plate with heavy fluid loading. Potentially, it could be extended to more complex structures such as composite plates, shells, and membranes. In the case of heavy fluid loading, the anisotropic dissipation of metamaterial plates with viscoelastic damping will be investigated in further works.