Performance Analysis of Hardware Implementations of Reverse Conversion from the Residue Number System

Abstract

The Residue Number System (RNS) is a non-positional number system that allows parallel computations without transfers between digits. However, some operations in RNS require knowledge of the positional characteristic of a number. Among these operations is the conversion from RNS to the positional number system. The methods of reverse conversion for general form moduli based on the Chinese remainder theorem and the mixed-radix conversion are considered, as well as the optimized methods for special form moduli. In this paper, a method is proposed that develops the authors’ ideas based on the modified mixed-radix conversion and reference points. The modified method based on the mixed-radix conversion in this case makes it possible to replace the operation of finding the residue of division by a large modulo with the sequential calculation of the residue. The method of reference points allows to reduce the size of the stored information compared to the use of ROM to store all the residues of RNS. The application of this approach makes it possible to find a balance between the speed of the calculation and the hardware used, by varying the number of moduli of one method and the other.

1. Introduction

Position-based calculations with binary and decimal numbers require transfers between digits, which have a negative impact on performance or device overhead for calculations with large numbers. In non-position-based number systems, such as the Residue Number System (RNS), transfers between digits are avoided. Interest in RNS as a basis for computing system development emerged as early as the 1950s [1,2]. In particular, in the USSR, long-range detection radar stations operating on the basis of modular arithmetic and built under the leadership of I.Ya. Akushsky and D.I. Yuditsky were deployed in the 1960s. Currently, various aspects of the residue number system are applied in patents of companies from the USA (Olsen IP Reserve, LLC; The Athena Group, Inc.; Cisco Technology, Inc.), China (Tianjin University; No 30 Inst China Electronic Technology Group Corp.; Univ Xidian), and the UK (Samsung Electronics Co., Ltd.).

The architecture of computing systems operating in RNS generally consists of forward conversion of positional numbers into RNS [3], computation of the main problem using modular addition [4], multiplication [5], number comparison and sign determination [6] operations, reconversion from RNS to positional number system [7,8,9,10,11,12,13,14]. Furthermore, if addition, subtraction, multiplication in RNS have a parallel structure with numbers of small dimensions, then the operations of sign determination, comparison, conversion from RNS to the positional number system require the calculation of the positional characteristic of the number, which is computationally complex.

The work is structured as follows. In Section 2, reverse conversion methods for general form moduli, such as Chinese Remainder Theorem (CRT), Mixed-Radix Conversion (MRC), CRT with fractional numbers, New CRT I, and New CRT II are discussed. In Section 3, we consider the application of RNS moduli of the special kind $2^n\pm 1$, $2^n$. Section 4 considers the MRC-based method proposed by the authors. In Section 5, the authors’ proposed method based on reference points is considered. However, the result of the work is the method considered in Section 6, which combines the use of modified MRC and the method of reference points. The results of the physical synthesis of the reverse conversion methods are presented in Section 7. Section 8 analyzes the results of the physical synthesis and draws conclusions about the applicability of the proposed approaches.

2. Reverse Conversion for General View Moduli

Most methods of reverse conversion are based on the use of CRT and MRC.

Reconstruction of a number X from its modular form $\left(x_1,x_2,\dots ,x_n\right)$ using the classical form of the Chinese Residue Theorem (CRTc) [7] is possible by the formula:

$$X={\left|\sum _{i=1}^n{\left|P_i^{-1}\right|}_{p_i}·P_i·x_i\right|}_P,$$

(1)

where $p_1,p_2,\dots ,p_n$ are RNS moduli, $P={\prod }_{i=1}^n{p}_i$ is RNS dynamic range, $P_i=\frac{P}{p_i}$, ${\left|P_i^{-1}\right|}_{p_i}$ is multiplicative inversion of $P_i$ modulo $p_i$.

To illustrate the considered methods, let us consider examples of RNS with 8-bit range, in particular $\left\{7,8,9\right\}$ with range $P=7·8·9=504$.

For the given RNS the auxiliary coefficients are:

$$\begin{array}{ccc}\hfill P_1=\frac{504}{7}=72,& P_2=63,& P_3=56,\hfill \\ \hfill {\left|P_1^{-1}\right|}_{p_1}=4,& {\left|P_2^{-1}\right|}_{p_2}=7,& {\left|P_3^{-1}\right|}_{p_3}=5.\hfill \end{array}$$

Consider the reconstruction of the number $X=\left(3,2,1\right)=10$. Then, using the Formula (1), we obtain:

$$X={\left|4·72·3+7·63·2+5·56·1\right|}_{504}={\left|2026\right|}_{504}=10.$$

In the case of the hardware implementation, the product calculations are performed in parallel, and the summation can be performed by tree doubling, which speeds up the calculations, but it is necessary to find the remainder of the division by a large number P.

Although in some cases it helps to simplify the scheme by using the Formula (1) to find the remainder for each summand ${\left|{\left|P_i^{-1}\right|}_{p_i}·P_i·x_i\right|}_P$, the hardware implementation of the classical CRT leads to large areas and delays.

Another approach to reverse conversion is using the mixed-radix conversion [7], according to which the number $\left(x_1,x_2,\dots ,x_n\right)$ can be transformed into a positional number system based on the formula:

$$X=d_1+d_2·p_1+d_3·p_1·p_2+\dots +d_n·p_1·\dots ·p_{n-1},$$

(2)

In this case, the MRC numbers $d_i$ can be calculated with the formulas:

$$\begin{array}{cc}\hfill & d_1=x_1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & d_2=\left(x_2-d_1\right)·{\left|p_1^{-1}\right|}_{p_2}mod{p}_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & d_3=\left(\left(x_3-d_1\right)·{\left|p_1^{-1}\right|}_{p_3}-d_2\right)·{\left|p_2^{-1}\right|}_{p_3}mod{p}_3\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \dots \hfill \end{array}$$

$$\begin{array}{cc}\hfill & d_n=\left(\dots \left(\left(x_n-d_1\right)·{\left|p_1^{-1}\right|}_{p_n}-d_2\right)·{\left|p_2^{-1}\right|}_{p_n}-\dots -d_{n-1}\right)·{\left|p_{n-1}^{-1}\right|}_{p_n}mod{p}_n.\hfill \end{array}$$

Consider the reconstruction process for the number $X=\left(3,2,1\right)=10$, then

$$\begin{array}{cc}\hfill & d_1=3,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & d_2=\left(2-3\right)·{\left|7^{-1}\right|}_{8}mod8=\left(-1·7\right)mod8=1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & d_3=\left(\left(1-3\right)·{\left|7^{-1}\right|}_9-1\right)·{\left|8^{-1}\right|}_{9}mod9=\left(-2·4-1\right)·8mod9=0.\hfill \end{array}$$

Then, by the Formula (2), we obtain:

$$X=3+1·7+0·7·8=10.$$

The main advantage of MRC is that calculations can be performed with small numbers without having to determine the remainder by a large modulo. However, the sequential architecture MRC leads to an increase in delay when the number of moduli increases.

To solve the problem of finding the remainder of the division by the dynamic range in the classical Chinese remainder theorem, its modification with fractional numbers in which the left and right parts of the expression (1) are divided by the dynamic range P [15]:

$$\overline{X}=\frac{X}{P}={\left|\sum _{i=1}^n\frac{{\left|P_i^{-1}\right|}_{p_i}}{p_i}·x_i\right|}_1={\left|\sum _{i=1}^n{k}_i·x_i\right|}_1,$$

(3)

where the symbol ${\left|\circ \right|}_1$ denotes the fractional part of the number, and

$$k_i=\frac{{\left|P_i^{-1}\right|}_{p_i}}{p_i},i=1,2,\dots ,n.$$

(4)

In this case, the sum value in (3) is a positional characteristic that lies in the range $\left[0,1\right)$ and enables number comparison and sign detection. The number X we are looking for is obtained by multiplying $\overline{X}$ by the dynamic range P, i.e.,

$$X=\overline{X}·P.$$

For the RNS with moduli $\left\{7,8,9\right\}$, the coefficients calculated by the Formula (4) will be:

$$k_1=\frac{{\left|P_1^{-1}\right|}_{p_1}}{p_1}=\frac{4}{7},k_2=\frac{7}{8},k_3=\frac{5}{9}.$$

The number $X=\left(3,2,1\right)=10$ is reconstructed with the Formula (3):

$$\overline{X}={\left|\frac{4·3}{7}+\frac{7·2}{8}+\frac{5·1}{9}\right|}_1={\left|\frac{1013}{252}\right|}_1=\frac{5}{252},$$

then $X=\frac{5}{252}·504=10$.

However, the coefficients $k_i$ can rarely be represented as a finite fraction, so the question of the accuracy of rounding the coefficients is acute.

In the article [7], there is an approximate modification of the method based on the CRT scaling by $2^N$, where $N=⌈{log}_{2}P\mu ⌉-1$, $\mu ={\sum }_{i=1}^n\left(p_i-1\right)$. Then the Formulas (3) and (4) can be written as:

$$X^{\prime }={\left|\sum _{i=1}^n{k}_i^{\prime }·x_i\right|}_{2^N},$$

(5)

where the coefficients $k_i^{\prime }$ are rounded upwards

$$k_i^{\prime }=⌈\frac{{\left|P_i^{-1}\right|}_{p_i}}{p_i}·2^N⌉,i=1,2,\dots ,n.$$

Then, the recovered number can be obtained by the formula with rounding down:

$$X=⌊\frac{X^{\prime }·P}{2^N}⌋.$$

(6)

For RNS $\left\{7,8,9\right\}$ the required accuracy is $N=13$, so the calculation is performed modulo $2^N=8192$. Then the coefficients are $k_i^{\prime }$:

$$k_1^{\prime }=⌈\frac{{\left|P_1^{-1}\right|}_{p_1}}{p_1}·2^N⌉=⌈\frac{4}{7}·2^{13}⌉=4682,k_2^{\prime }=7168,k_3^{\prime }=4552.$$

From the Formula (5) for the number $X=\left(3,2,1\right)=10$ we obtain:

$$X^{\prime }={\left|4682·3+7168·2+4552·1\right|}_{2^{13}}={\left|32934\right|}_{2^{13}}=166.$$

Then X will be equal to:

$$X=⌊\frac{166·504}{8192}⌋=10.$$

Another method based on the CRT is a method called New CRT [8], which is given by the formula:

$$X={\left|x_1+k_1\left(x_2-x_1\right)p_1+k_2(x_3-x_2)p_1{p}_2+\dots +k_{n-1}\left(x_n-x_{n-1}\right)p_1\dots p_{n-1}\right|}_P,$$

(7)

where

$$k_i={\left|\frac{1}{{\prod }_{j=1}^i{p}_j}\right|}_{{\prod }_{j=i+1}^n{p}_j},1\ge i\ge r-1.$$

(8)

For the above considered RNS $\left\{7,8,9\right\}$ the coefficients $k_i$ of the new CRT will be:

$$k_1={\left|\frac{1}{p_1}\right|}_{p_2{p}_3}=31,k_2={\left|\frac{1}{p_1{p}_2}\right|}_{p_3}=5.$$

Then, using the Formula (7) for the number $X=\left(3,2,1\right)=10$ we obtain:

$$X={\left|3+31·\left(2-3\right)·7+5·(1-2)·7·8\right|}_{504}={\left|-494\right|}_{504}=10.$$

The article [16] proposes two modifications of the New CRT, which are denoted as New CRT I and New CRT II.

Let us consider each of these methods separately. In New CRT I, the Formula (8) similarly calculates constants $k_i$, which are used to find coefficients $a_i$, $i=0,\dots ,n-1$:

$$\begin{array}{cc}\hfill & a_0={\left|1-k_1{p}_1\right|}_{p_1{p}_2\dots p_{n-1}{p}_n}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_1={\left|k_1-k_2{p}_2\right|}_{p_2\dots p_{n-1}{p}_n}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \dots \hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_{n-2}={\left|k_{n-2}-k_{n-1}{p}_{n-1}\right|}_{p_{n-1}{p}_n}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_{n-1}={\left|k_{n-1}\right|}_{p_n}\hfill \end{array}$$

Then, for these coefficients we build a matrix of characteristics:

$$A=\left(\begin{array}{ccccc}{a}_{0,0}& 0& \dots & 0& 0\\ a_{0,1}& a_{1,1}& \dots & 0& 0\\ \dots & \dots & \dots & \dots & \dots \\ a_{0,n-2}& a_{1,n-2}& \dots & a_{n-2,n-2}& 0\\ a_{0,n-1}& a_{1,n-1}& \dots & a_{n-2,n-1}& a_{n-1,n-1}\end{array}\right)$$

which coefficients are obtained from the representation of $a_i$ in the mixed-radix conversion:

$$\begin{array}{cc}\hfill & a_0=a_{0,0}+a_{0,1}{p}_1+\dots +a_{0,n-1}{p}_1{p}_2\dots p_{n-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_1=a_{1,1}+a_{1,2}{p}_2+\dots +a_{1,n-1}{p}_2\dots p_{n-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \dots \hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_{n-2}=a_{n-2,n-2}+a_{n-2,n-1}{p}_{n-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_{n-1}=a_{n-1,n-1}\hfill \end{array}$$

Then, from the matrix A and the value $X=\left(x_1,x_2,\dots ,x_n\right)$ a vector $B=A\times X$ can be obtained, i.e.:

$$B=\left(\begin{array}{c}{B}_0\\ B_1\\ \dots \\ B_{n-2}\\ B_{n-1}\end{array}\right)=\left(\begin{array}{ccccc}{a}_{0,0}& 0& \dots & 0& 0\\ a_{0,1}& a_{1,1}& \dots & 0& 0\\ \dots & \dots & \dots & \dots & \dots \\ a_{0,n-2}& a_{1,n-2}& \dots & a_{n-2,n-2}& 0\\ a_{0,n-1}& a_{1,n-1}& \dots & a_{n-2,n-1}& a_{n-1,n-1}\end{array}\right)\times \left(\begin{array}{c}{x}_1\\ x_2\\ \dots \\ x_{n-1}\\ x_n\end{array}\right)$$

Then, the number X can be reconstructed by the formula:

$$X={\left|B_0+B_1{p}_1+B_2{p}_1{p}_2+\dots +B_{n-1}{p}_1{p}_2\dots p_{n-1}\right|}_{p_1{p}_2\dots p_n}$$

Consider a similar example for which the coefficients of $a_i$ are:

$$\begin{array}{cc}\hfill & a_0={\left|1-31·7\right|}_{504}=288=1+1p_1+5p_1{p}_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_1={\left|31-5·8\right|}_{72}=63=7+7p_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_2={\left|5\right|}_9=5.\hfill \end{array}$$

For the number $X=\left(3,2,1\right)=10$ we obtain the vector B:

$$B=\left(\begin{array}{ccc}1& 0& 0\\ 1& 7& 0\\ 5& 7& 5\end{array}\right)\times \left(\begin{array}{c}3\\ 2\\ 1\end{array}\right)=\left(\begin{array}{c}3\\ 17\\ 34\end{array}\right).$$

From which we obtain:

$$X={\left|3+17·7+34·7·8\right|}_{504}=10.$$

For the case of ordered RNS with moduli satisfying the expression $p_i>p_1+{\dots }_{+}{p}_{i-1}$ or more strictly $p_i>2p_{i-1}$, the reverse conversion can be obtained without taking into account the remainder modulo P.

In this case, the function $Y<2P$ is given by

$$Y=B_0+B_1{p}_1+B_2{p}_1{p}_2+\dots +{\left|B_{n-1}\right|}_{p_n}{p}_1{p}_2\dots p_{n-1}$$

and the required value of X is

$$X=\left\{\begin{array}{cc}Y\hfill & \mathrm{if}Y<P,\hfill \\ Y-P\hfill & \mathrm{if}Y\ge P.\hfill \end{array}\right.$$

(9)

The restriction of moduli in this case leads to an unbalanced RNS. So, for the 8-bit range, we can take a set of moduli $\left\{3,7,13\right\}$, where the dimensionality of each module is one binary digit larger. In this case:

$$\begin{array}{cc}\hfill & k_1=61,k_2=5\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_0=91,a_1=26,a_2=5.\hfill \end{array}$$

Then for the number $X=(1,3,10)=10$ we obtain:

$$B=\left(\begin{array}{ccc}1& 0& 0\\ 2& 5& 0\\ 4& 3& 5\end{array}\right)\times \left(\begin{array}{c}1\\ 3\\ 10\end{array}\right)=\left(\begin{array}{c}1\\ 17\\ 63\end{array}\right)$$

The desired value of X can be obtained from (9) and the vector $B=\left(B_0,B_1,{\left|B_2\right|}_{p_3}\right)$: $Y=1+17·3+11·3·7=283$, since $Y\ge P=273$, then $X=Y-P=10$.

This method requires matrix multiplication with small-digit numbers, finding the remainder modulo RNS, and multiplication with accumulation for n summands.

Another method proposed in [16] is called New CRT II.

For a two-moduli CRT with $\left\{p_1,p_2\right\}$ moduli, the Algorithm 1 denoted by findno $\left(x_1,\right.$$x_2,$$p_1,$$p_2,\left.X\right)$.

Algorithm 1 Algorithm findno number recovery for a two-moduli RNS

Require: $\left(x_1,x_2\right),\left\{p_1,p_2\right\}$

Ensure: $X<p_1·p_2$

1: $k_0={\left|p_2^{-1}\right|}_{p_1}$ 2: return$X=x_2+{\left|k_0\left(x_1-x_2\right)\right|}_{p_1}·p_2$

For ordered RNS with moduli $p_1<p_2<\dots <p_n$ a recursive Algorithm 2 translate $((x_1,x_2,\dots ,x_n),X)$ is used.

Consider an example of applying the Algorithm 2 to RNS $\left\{7,8,9\right\}$ and the number $X=\left(3,2,1\right)=10$.

Since $n=3$, according to step 5 of the Algorithm 2 we obtain two new calls of this algorithm translate $\left(\left(x_1\right),N_1\right)$ and translate $\left(\left(x_2,x_3\right),N_2\right)$.

Calling translate $\left(\left(x_1\right),N_1\right)$ leads to step 11 of the Algorithm 2, for which we obtain $N_1=x_{1}mod{p}_1$, $P_1=p_1$, i.e., $N_1=3,P_1=7$.

Calling translate $\left(\left(x_2,x_3\right),N_2\right)$ leads to step 9 of the Algorithm 2, for which from the Algorithm 1 findno we obtain $N_2=x_3+{\left|{\left|p_3^{-1}\right|}_{p_2}·\left(x_2-x_3\right)\right|}_{p_2}·p_3$, $P_2=p_2·p_3$. That is, $N_2=1+{\left|1·\left(2-1\right)\right|}_8·9=10,P_2=8·9=72$.

Algorithm 2 Algorithm translate of number reconstruction in RNS

Require: $\left(x_1,x_2,\dots ,x_n\right),\left\{p_1,p_2,\dots ,p_n\right\}$

1: if $n=2t>2$ (n—even, greater than 2) then 2:     translate $\left(\left(x_1,\dots ,x_t\right),N_1\right)$, $P_1={\prod }_{i=1}^t{p}_i$ 3:     translate $\left(\left(x_{t+1},\dots ,x_n\right),N_2\right)$, $P_2={\prod }_{i=t+1}^n{p}_i$ 4:     findno $\left(N_1,N_2,P_1,P_2,X\right)$ 5: else if $n=2t+1>2$ (n—odd, greater than 2) then 6:     translate $\left(\left(x_1,\dots ,x_t\right),N_1\right)$, $P_1={\prod }_{i=1}^t{p}_i$ 7:     translate $\left(\left(x_{t+1},\dots ,x_n\right),N_2\right)$, $P_2={\prod }_{i=t+1}^n{p}_i$ 8:     findno $\left(N_1,N_2,P_1,P_2,X\right)$ 9: else if $n=2$ then 10:     findno $\left(x_1,x_2,p_1,p_2,X\right)$ 11: else if $n=1$ then 12:     $X=x_{1}mod{p}_1$ 13: end if

Then, according to step 8 of the Algorithm 2, the call findno $\left(N_1,\right.$$N_2,$$P_1,$$P_2,$$\left.X\right)$, that is, the calculation

$$X=N_2+{\left|{\left|P_2^{-1}\right|}_{P_1}·\left(N_1-N_2\right)\right|}_{P_1}·P_2=10+{\left|{\left|{72}^{-1}\right|}_7·\left(3-10\right)\right|}_7·72=10.$$

Thus, the New CRT II method is based on the recursive use of MRC with two moduli. In this case, there are difficulties in calculating the multiplicative inversion in the last steps of the algorithm, but in the hardware implementation these values can be written to memory.

In [11] the set of odd moduli $\left\{p_1,p_2,\dots ,p_{n-1}\right\}$ whose range $P_h={\prod }_{i=1}^{n-1}{p}_i$ and from the Formula (1) we can obtain

$$X_h={\left|\sum _{i=1}^{n-1}{P}_i{\left|\frac{x_i}{P_i}\right|}_{p_i}\right|}_{P_h}.$$

Adding the remainder $x_n$ modulo $p_n=2^k$ leads to the expression:

$$X={\left|2^k{\left|\frac{X_h}{2^k}\right|}_{P_h}+P_h{\left|\frac{x_n}{P_h}\right|}_{2^k}\right|}_{2^k{P}_h}={\left|2^k\sum _{i=1}^{n-1}{P}_i{\left|\frac{x_i}{2^k{P}_i}\right|}_{p_i}+P_h{\left|\frac{x_n}{P_h}\right|}_{2^k}\right|}_{2^k{P}_h}$$

(10)

For $d\ge ⌈{log}_2\left(n-1\right)⌉$, denote $x_n^{\prime }={\left|\frac{x_n}{P_h}\right|}_{2^k}$, which splits into blocks $x_q$ and $x_p$ by $k-d$ and d bits, respectively, that is, $x_n^{\prime }=2^{k-d}{x}_p+x_q$.

Next, the variables introduced are:

$$x_i^{\prime }={\left|\frac{x_i}{2^{k-d}{P}_i}\right|}_{p_i}\mathrm{and}{x}_p^{\prime }={\left|x_p-\sum _{i=1}^{n-1}\frac{x_i^{\prime }}{p_i}\right|}_{2^d}$$

and $x_n^{″}=2^{k-d}{x}_p^{\prime }+x_q=\left(x_p^{\prime }\left|\right|x_q\right)$, ($\left|\right|$—concatenation of binary values).

Then the Formula (10) can be rewritten as:

$$X={\left|2^{k-d}\sum _{i=1}^{n-1}{P}_i{x}_i^{\prime }+P_h{x}_n^{″}\right|}_{2^k{P}_h},$$

(11)

In this case, as in (9), the value of $X<2·2^k{P}_h$, i.e., does not exceed the double range and can be computed without computing the remainder by a large modulo.

Consider a similar example, with moduli $\left\{7,9,8\right\}$, then $n=3,k={log}_{2}8=3.$$P_h=p_1·p_2=63,P_1=\frac{P_h}{p_1}=p_2=9,P_2=p_1=7.$$d=⌈{log}_2\left(3-1\right)⌉=1.$

For the number $X=\left(3,1,2\right)=10$, calculate $x_i^{\prime }$ and $x_q,x_p$, $x_p^{\prime },x_n^{″}$.

$$\begin{array}{cc}\hfill & x_1^{\prime }={\left|\frac{x_1}{2^{3-1}{P}_1}\right|}_{p_1}={\left|3·{\left|{\left(2^2·9\right)}^{-1}\right|}_7\right|}_7=3,x_2^{\prime }=1,x_p=1,x_q=2.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & x_p^{\prime }={\left|x_p-\sum _{i=1}^{n-1}\frac{x_i^{\prime }}{p_i}\right|}_{2^d}=1,x_n^{″}=2^{k-d}{x}_p^{\prime }+x_q=6.\hfill \end{array}$$

Then, from (11) we obtain $X={\left|514\right|}_{504}=10$.

This method allows you to find the reconstructed number without calculating the remainder large modulo, because $X<2·2^k{P}_h$.

3. Use of Special Type Moduli

To improve the performance of RNS, many researchers are considering moduli of a special kind $\left\{2^n-1,2^n,2^n+1\right\}$ [8], $\left\{2^{2n},2^{2n-1}-1,2^{2n}-1,2^{2n+1}-1\right\}$ [9], $\left\{2^k-3,\right.2^k-2,\left.2^k-1\right\}$ and $\left\{2^k+1,2^k+2,2^k+3\right\}$ [10], $\left\{2^{2n-5}-1,\right.$$2^{2n-3}-1,$$2^{2n-2}+1,$$2^{2n-1}-1,$$2^{2n-1}+1,$$2^{2n},$$\left.2^{2n}+1\right\}$ [12], $\left\{2^{2n},2^n+1,2^n-1,2^n+3,2^n-3\right\}$ [13].

The most interesting among the reverse conversion methods is the optimization for the moduli set $\left\{2^n-1,2^n,2^n+1\right\}$, which was proposed in the article [8].

The most efficient implementations are based on the modulo $2^n-1$ for which a number of properties are satisfied:

• The sign change (additive inversion) is achieved by bitwise negation, i.e., ${\left|-z\right|}_{2^n-1}={\left|\overline{z}\right|}_{2^n-1}={\left|\left({\overline{z}}_{n-1}\dots {\overline{z}}_0\right)\right|}_{2^n-1}$, e.g., ${\left|-5\right|}_7={\left|-{101}_2\right|}_7={\left|{\overline{101}}_2\right|}_7={\left|\left({010}_2\right)\right|}_7=2.$
• The multiplication by $2^d$ can be performed by a cyclic shift to the left by d digits, i.e., ${\left|2^{d}z\right|}_{2^n-1}={\left|z_{n-d-1}\dots z_0{z}_{n-1}\dots z_{n-d}\right|}_{2^n-1}$, e.g., ${\left|2·5\right|}_7={\left|2·{101}_2\right|}_7={\left|{011}_2\right|}_7=3.$
• Multiplication by multiplicative inversion ${\left|2^{-d}\right|}_{2^n-1}$ can be performed by a cyclic shift to the right by d positions or to the left by $n-d$ positions, since ${\left|2^{-d}z\right|}_{2^n-1}={\left|2^{n-d}z\right|}_{2^n-1}$, i.e., ${\left|2^{-d}z\right|}_{2^n-1}={\left|z_{d-1}\dots z_0{z}_{n-1}\dots z_d\right|}_{2^n-1}$, e.g., ${\left|2^{-1}·5\right|}_7={\left|2^{-1}·{101}_2\right|}_7={\left|{110}_2\right|}_7=3.$
• For any non-negative integer i, ${\left|2^{i·n}\right|}_{2^n-1}=1$, then the $\left(sn\right)-$bit number can be represented as

  $${\left|\sum _{i=0}^{s-1}{2}^{ni}\left(y_{n\left(i+1\right)-1}\dots y_{ni}\right)\right|}_{2^n-1}={\left|\sum _{i=0}^{s-1}\left(y_{n\left(i+1\right)-1}\dots y_{ni}\right)\right|}_{2^n-1}$$

The article [8] is based on the idea that an expression for the reverse conversion based on the CRT (1) can be represented in a form, where the constant and the variables can be separated:

$$X={\left|\left(\sum _{i=1}^n{b}_i·x_i\right)+C_k\right|}_P$$

First, one takes from the set $\left\{2^n,2^n-1,2^n+1\right\}$ two moduli $\left\{p_2,p_3\right\}=\left\{2^n-1,2^n+1\right\}$ for which the number $X_{23}=\left\{x_2,x_3\right\}$ is found from CRT:

$$\begin{array}{cc}\hfill X_{23}=& {\left|p_3·x_2·{\left|p_3^{-1}\right|}_{p_2}+p_2·x_3·{\left|p_2^{-1}\right|}_{p_3}\right|}_{p_2{p}_3}=\hfill \\ \hfill & ={\left|\left(2^n+1\right)·2^{n-1}·x_2+\left(2^n-1\right)·2^{n-1}·x_3\right|}_{2^{2n}-1}=\hfill \\ \hfill & ={\left|2^{n-1}·\left(\left(2^n+1\right)·x_2+\left(2^n-1\right)x_3\right)\right|}_{2^{2n}-1}\hfill \end{array}$$

Based on the MRC for the set of moduli $\left\{p_1,p_2{p}_3\right\}$, the number $X=\left\{x_1,X_{23}\right\}$ is found:

$$X=x_1+p_1{\left|(X_{23}-x_1)\frac{1}{p_1}\right|}_{p_2{p}_3}=x_1+2^n{X}_h,$$

(12)

where

$$\begin{array}{cc}\hfill X_h=& {\left|\left(X_{23}-x_1\right)2^{-1}\right|}_{2^{2n}-1}=\hfill \\ \hfill & ={\left|\left(2^{n-1}\left(\left(2^n+1\right)x_2+\left(2^n-1\right)x_3\right)-x_1\right)2^{-1}\right|}_{2^{2n}-1}=\hfill \\ \hfill & ={\left|-x_1{2}^{-n}+x_2\left(2^n+1\right)2^{-1}+x_3\left(2^n-1\right)2^{-1}\right|}_{2^{2n}-1}\hfill \end{array}$$

(13)

The optimization of the expression (13) is possible by bitwise operations. The first term can be represented as follows:

$${\left|-x_1·2^{-n}\right|}_{2^{2n}-1}={\left|2^{-1}\left(\left({\overline{x}}_{1,n-2}\dots {\overline{x}}_{1,0}\right)\left|\right|\underset{n}{\underbrace{\left(0\dots 0\right)}}\left|\right|{\overline{x}}_{1,n-1}\right)+\left(2^{-n}-1\right)\right|}_{2^{2n}-1}.$$

The second term appears as:

$${\left|x_2\left(2^n+1\right)2^{-1}\right|}_{2^{2n}-1}={\left|2^{-1}\left(x_2\left|\right|x_2\right)\right|}_{2^{2n}-1}.$$

The third term can be represented as:

$$\begin{array}{cc}\hfill & {\left|x_3\left(2^n-1\right)2^{-1}\right|}_{2^{2n}-1}=\hfill \\ \hfill & ={\left|2^{-1}\left(\begin{array}{c}\left(\left(x_{3,n-1}\vee x_{3,n}\right)\dots \left(x_{3,0}\vee x_{3,n}\right)\left|\right|{\overline{x}}_{3,n-1}\dots {\overline{x}}_{3,0}+2^n\right)+\\ +\left(1-2^{n+1}\right)\end{array}\right)\right|}_{2^{2n}-1}\hfill \end{array}$$

(14)

or

$${\left|x_3\left(2^n-1\right)2^{-1}\right|}_{2^{2n}-1}={\left|2^{-1}\left(\begin{array}{c}\left(x_{3,n-1}\dots x_{3,0}\left|\right|{\overline{x}}_{3,n-1}\dots {\overline{x}}_{3,1}\left|\right|\left(\overline{x_{3,0}\vee x_{3,n}}\right)\right)+\\ +\left(\underset{n-1}{\underbrace{0\dots 0}}\left|\right|{\overline{x}}_{3,n}\left|\right|\underset{n-1}{\underbrace{0\dots 0}}\left|\right|x_{3,n}\left|\right|0\right)+\\ +\left(1-2^{n+1}\right)\end{array}\right)\right|}_{2^{2n}-1}$$

(15)

Depending on the chosen representation of the third term (14) or (15), the article [8] forms two variants of the reverse conversion constructed using the formula:

$$X_h={\left|w_1+w_2+w_3+C_k\right|}_{2^{2n}-1}$$

(16)

In the first case, based on the Formula (14) we have:

$$\begin{array}{cc}\hfill & w_1=\left({\overline{x}}_{1,n-1}\dots {\overline{x}}_{1,0}\left|\right|\underset{n}{\underbrace{\left(0\dots 0\right)}}\right)\hfill \\ \hfill & w_2=\left(x_{2,0}\left|\right|x_{2,n-1}\dots x_{2,0}\left|\right|x_{2,n-1}\dots x_{2,1}\right)\hfill \\ \hfill & w_3=\left({\overline{x}}_{3,0}\left|\right|\left(x_{3,n-1}\vee x_{3,n}\right)\dots \left(x_{3,0}\vee x_{3,n}\right)\left|\right|{\overline{x}}_{3,n-1}\dots {\overline{x}}_{3,1}\right)\hfill \\ \hfill & C_k={\left|\left(2^{-n}-1\right)+2^{-1}\left(1-2^{n+1}\right)+2^{n-1}\right|}_{2^{2n}-1}=2^{2n-1}+2^{n-1}-1=\left(1\underset{n}{\underbrace{0\dots 0}}\underset{n-1}{\underbrace{1\dots 1}}\right)\hfill \end{array}$$

In the article [8], there is a typo that $C_k$ has $n+2$ zeros. However, it is obvious that $2^{2n-1}$ contains one and $2n-1$ zeros, and the number ($2^{n-1}-1$) contains $n-1$ one. Then adding the numbers will result in the lowest number $n-1$ being a one, and the remaining $2n-1-\left(n-1\right)=n$ zeros will remain zeros. For example, for $n=2$: $2^3+2-1=9={1001}_2$.

For the second case, the formula (15) gives:

$$\begin{array}{cc}\hfill & w_1=\left({\overline{x}}_{1,n-1}\dots {\overline{x}}_{1,0}\left|\right|{\overline{x}}_{3,n}\left|\right|\underset{n-2}{\underbrace{\left(0\dots 0\right)}}\left|\right|x_{3,n}\right)\hfill \\ \hfill & w_2=\left(x_{2,0}\left|\right|x_{2,n-1}\dots x_{2,0}\left|\right|x_{2,n-1}\dots x_{2,1}\right)\hfill \\ \hfill & w_3=\left(\overline{\left(x_{3,0}\vee x_{3,n}\right)}\left|\right|x_{3,n-1}\dots x_{3,0}\left|\right|{\overline{x}}_{3,n-1}\dots {\overline{x}}_{3,1}\right)\hfill \\ \hfill & C_k={\left|\left(2^{-n}-1\right)+2^{-1}\left(1-2^{n+1}\right)\right|}_{2^{2n}-1}=2^{2n-1}-1=\left(0\underset{2n-1}{\underbrace{1\dots 1}}\right)\hfill \end{array}$$

The addition of $C_k$ in the calculation of $X_h$ by the Formula (16) is equivalent to the addition of $2^n{C}_k$ to $X_{23}$. Moreover, the latter can also be obtained by simultaneous addition of $c_2={\left|2^n{C}_k\right|}_{2^n-1}={\left|C_k\right|}_{2^n-1}$ to $x_2$ modulo $2^n-1$ and $c_3={\left|2^n{C}_k\right|}_{2^n+1}={\left|-C_k\right|}_{2^n+1}$ to $x_3$ modulo $2^n+1$ (leaving the remainder $x_1$ of even modulo unchanged, since ${\left|2^n{C}_k\right|}_{2^n}=0$).

In the first case we obtain:

$$\begin{array}{c}\hfill c_2={\left|2^n\left(2^{2n-1}+2^{n-1}-1\right)\right|}_{2^n-1}=0,\end{array}$$

$$\begin{array}{c}\hfill c_3={\left|2^n\left(2^{2n-1}+2^{n-1}-1\right)\right|}_{2^n+1}=1.\end{array}$$

In the second case:

$$\begin{array}{c}\hfill c_2={\left|2^n\left(2^{2n-1}-1\right)\right|}_{2^n-1}=2^{n-1}-1=0\underset{n-1}{\underbrace{1\dots 1}},\end{array}$$

$$\begin{array}{c}\hfill c_3={\left|2^n\left(2^{2n-1}-1\right)\right|}_{2^n+1}=2^{n-1}+1=01\underset{n-2}{\underbrace{0\dots 0}}1.\end{array}$$

Then the Formula (16) will be reduced to:

$$X_h={\left|w_1+w_2+w_3\right|}_{2^{2n}-1}$$

with further use of the Formula (12).

Consider a similar example with RNS $\left\{8,7,9\right\}$, $n=3$, for the number $X=10=\left(2,3,1\right)$.

In the first case, the coefficients $c_2=0$ and $c_3=1$ do not depend on the value of n. Then the offset value of $X^{\prime }=\left(2,3,{\left|1+1\right|}_9\right)$. From this follows

$$\begin{array}{cc}\hfill x_1^{\prime }=2={010}_2,& w_1=101\left|\right|{000}_2=40,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_2^{\prime }=3={011}_2,& w_2=1\left|\right|011\left|\right|{01}_2=45,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_3^{\prime }=2={0010}_2,& w_3=1\left|\right|010\left|\right|{10}_2=42.\hfill \end{array}$$

Then $X_h={\left|40+45+42\right|}_{63}=1,$ and $X=2+2^3·1=10$.

For the second case for $n=3$  $c_2=2^2-1=3$ and $c_3=2^3+1=5$. Then the offset value of $X^{\prime }=\left(2,{\left|3+3\right|}_7,{\left|1+5\right|}_9\right)$. From here

$$\begin{array}{cc}\hfill x_1^{\prime }=2={010}_2,& w_1=101\left|\right|1\left|\right|0\left|\right|0_2=44,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_2^{\prime }=6={110}_2,& w_2=0\left|\right|110\left|\right|{11}_2=27,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_3^{\prime }=6={0110}_2,& w_3=1\left|\right|110\left|\right|{00}_2=56.\hfill \end{array}$$

Then $X_h={\left|44+27+56\right|}_{63}=1,$ and $X=2+2^3·1=10.$

In the first case, only addition with $c_3$ is required, but n of OR logical operators are required when calculating $w_3$, in the second case there is one OR operator, but addition is performed on both $c_2$ and $c_3$.

4. Modified Method Based on MRC

The patent [17] presents a new Algorithm 3 for translation of RNS to the positional number system and base extension based on the mixed-radix conversion, which we will hereafter call “the modified mixed-radix conversion method”. This algorithm works with moduli of the generalized form.

Algorithm 3 Reconstructing numbers and expanding bases

Require: $\left(x_1,\dots ,x_n\right),$$p_{n+1}$

Ensure: $X$, ${\left|X\right|}_{p_{n+1}}$

1: $P_i=\frac{P}{p_i};$${\left|P_i^{-1}\right|}_{p_i};$$B_i=P_i·{\left|P_i^{-1}\right|}_{p_i}$ 2: ${\widehat{w}}_1=1;$${\widehat{w}}_j={\prod }_{i=1}^{j-1}{p}_i,$$j=\overline{2,n}$ 3: $B_i\stackrel{\mathrm{MRC}}{\to }\left[{\widehat{b}}_{i,j}\right],$$i,j=\overline{1,n},$$B_i={\sum }_{j=1}^n{\widehat{b}}_{i,j}·{\widehat{w}}_j$ 4: $U_i={\sum }_{j=1}^i{x}_j·{\widehat{b}}_{j,i}$, $i=\overline{1,n}$ 5: ${\sigma }_0=0$, ${\widehat{x}}_i={\left|{\sigma }_{i-1}+U_i\right|}_{p_i},$${\sigma }_i=⌊\frac{{\sigma }_{i-1}+U_i}{p_i}⌋$ 6: $X={\sum }_{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i,$ 7: ${\left|X\right|}_{p_{n+1}}={\left|{\sum }_{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i\right|}_{p_{n+1}}$ 8: return $X,$${\left|X\right|}_{p_{n+1}}$

In some cases it is necessary to add one or more additional moduli to detect range overflows or to detect and correct errors. If the modulo $p_{n+1}$ is added, then the new range allows the display of any number $X<P·p_{n+1}$.

Consider the Algorithm 3 in detail. Set of a residue number system with moduli $\left\{p_1,p_2,\dots ,p_n\right\}$ for which the orthogonal bases of RNS $B_i=P_i·{\left|P_i^{-1}\right|}_{p_i}$, $i=\overline{1,n}$. Compute the bases of the MRC ${\widehat{w}}_j={\prod }_{i=1}^{j-1}{p}_i$, $j=\overline{2,n}$, with $w_1=1$. The orthogonal RNS bases are represented in MRC as a vector of values ${\widehat{b}}_{i,j}$, for which $B_i={\sum }_{j=1}^n{\widehat{b}}_{i,j}·{\widehat{w}}_j$. The values of ${\widehat{b}}_{i,j}$ form a triangular matrix.

Given $X=\left(x_1,x_2,\dots ,x_n\right)$, we need to recover the number X in the positional number system and find the remainder of the division of X by an additional modulo $p_{n+1}$, which we denote by ${\left|X\right|}_{p_{n+1}}$.

To do this, $\left(x_1,x_2,\dots ,x_n\right)$ is multiplied by the triangular matrix ${\widehat{b}}_{i,j}$, so $U_i={\sum }_{j=1}^i{x}_j·{\widehat{b}}_{j,i}$, $i=\overline{1,n}$.

Then ${\widehat{x}}_i={\left|{\sigma }_{i-1}+U_i\right|}_{p_i}$ and ${\sigma }_i=⌊\frac{{\sigma }_{i-1}+U_i}{p_i}⌋$ are calculated, assuming that ${\sigma }_0=0$.

We can substitute that ${\widehat{x}}_i$ and ${\sigma }_i$ are related as the remainder of the division of the sum $\left({\sigma }_{i-1}+U_i\right)$ by the modulo $p_i$ and the rank of the sum, i.e., the carry by how many times the sum value exceeds the modulo.

Then find the value of the expression $X={\sum }_{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i$ to convert a number from RNS to a positional number system, and to expand the bases, find ${\left|X\right|}_{p_{n+1}}={\left||{\sum }_{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i\right|}_{p_{n+1}}$.

Let us consider an example to illustrate how the algorithm works. Given a residue number system with three moduli $\left\{7,8,9\right\}$. Then let $P={\prod }_{i=1}^3{p}_i=504$.

Let us calculate $P_i=\frac{P}{p_i},$${\left|P_i^{-1}\right|}_{p_i}$ and $B_i=P_i·{\left|P_i^{-1}\right|}_{p_i}$:

$$\begin{array}{ccc}\hfill P_1=8·9=72,& {\left|P_1^{-1}\right|}_{p_1}={\left|{72}^{-1}\right|}_7=4,& B_1=288,\hfill \\ \hfill P_2=7·9=63,& {\left|P_2^{-1}\right|}_{p_2}={\left|{63}^{-1}\right|}_8=7,& B_2=441,\hfill \\ \hfill P_3=7·8=56,& {\left|P_3^{-1}\right|}_{p_3}={\left|{56}^{-1}\right|}_9=5,& B_3=280.\hfill \end{array}$$

Let us calculate ${\widehat{w}}_j={\prod }_{i=1}^{j-1}{p}_i$:

$${\widehat{w}}_1=1,{\widehat{w}}_2=7,{\widehat{w}}_3=7·8=56.$$

Let us calculate the representation of $B_i$ in MRC:

$B_1\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_1=\left[{\widehat{b}}_{1,1},{\widehat{b}}_{1,2},{\widehat{b}}_{1,3}\right]=\left[1,1,5\right]$, checking $1+1·7+5·56=288$,

$B_2\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_2=\left[{\widehat{b}}_{2,1},{\widehat{b}}_{2,2},{\widehat{b}}_{2,3}\right]=\left[0,7,7\right]$, checking $0+7·7+7·56=441$,

$B_3\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_3=\left[{\widehat{b}}_{3,1},{\widehat{b}}_{3,2},{\widehat{b}}_{3,3}\right]=\left[0,0,5\right]$, checking $0+0·7+5·56=280$.

Given $X=10=\left(3,2,1\right)$, we can compute $U_i={\sum }_{j=1}^i{x}_j·{\widehat{b}}_{j,i}$:

$$\begin{array}{cc}\hfill & U_1=x_1·{\widehat{b}}_{1,1}=3·1=3,\hfill \\ \hfill & U_2=x_1·{\widehat{b}}_{1,2}+x_2·{\widehat{b}}_{2,2}=3·1+2·7=17,\hfill \\ \hfill & U_3=x_1·{\widehat{b}}_{1,3}+x_2·{\widehat{b}}_{2,3}+x_3·{\widehat{b}}_{3,3}=3·5+2·7+1·5=34.\hfill \end{array}$$

Let us calculate ${\widehat{x}}_i={\left|{\sigma }_{i-1}+U_i\right|}_{p_i}$ and ${\sigma }_i=⌊\frac{{\sigma }_{i-1}+U_i}{p_i}⌋$:

$$\begin{array}{cccc}\hfill & {\widehat{x}}_1={\left|U_1\right|}_{p_1}={\left|3\right|}_7=3,\hfill & \hfill & {\sigma }_1=⌊\frac{U_1}{p_1}⌋=⌊\frac{3}{7}⌋=0,\hfill \\ \hfill & {\widehat{x}}_2={\left|{\sigma }_1+U_2\right|}_{p_2}={\left|0+17\right|}_8=1,\hfill & \hfill & {\sigma }_2=⌊\frac{{\sigma }_1+U_2}{p_2}⌋=⌊\frac{17}{8}⌋=2,\hfill \\ \hfill & {\widehat{x}}_3={\left|{\sigma }_2+U_3\right|}_{p_3}={\left|2+34\right|}_9=0.\hfill \end{array}$$

From this we obtain:

$$X=\sum _{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i=3·1+1·7+0·56=10.$$

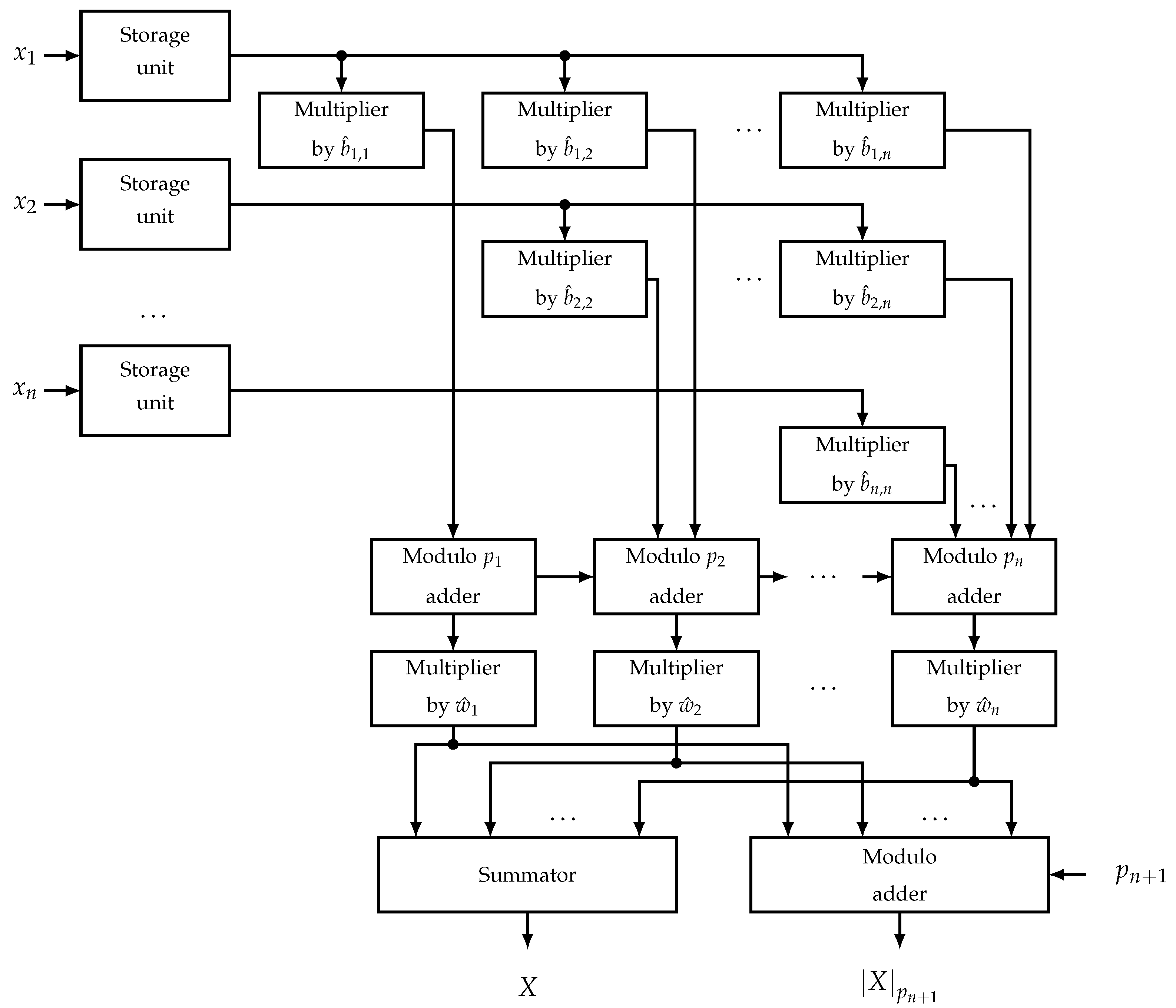
Consider the block diagram for converting numbers from RNS and base expansion based on the Algorithm 3 shown in Figure 1.

Figure 1. Computational unit for translating numbers from RNS and expanding bases.

The number $\left(x_1,x_2,\dots ,x_n\right)$ represented in RNS is fed to the n inputs of the residues, where n is the number of moduli of the residue number system.

The residues from the corresponding residue inputs are written to n residue storage units. From the outputs of the residue storage units, the residues moduli $\left\{p_1,p_2,\dots ,p_n\right\}$ are fed to multipliers which form a triangular matrix and calculated values of the products of the residue with the base coefficients in the MRC $x_j·{\widehat{b}}_{j,i}$, where $B_i=P_i·{\left|P_i^{-1}\right|}_{p_i}={\sum }_{j=1}^n{\widehat{b}}_{i,j}·{\widehat{w}}_j$, are orthogonal bases of RNS, ${\widehat{w}}_j={\prod }_{i=1}^{j-1}{p}_i,j=\overline{1,n}$ are bases of MRC, with ${\widehat{w}}_0=1$.

The output of the first residue storage unit modulo $p_1$ is connected to the inputs of n multipliers by ${\widehat{b}}_{1,1}$, …, ${\widehat{b}}_{1,n}$, which compute the values $x_1·{\widehat{b}}_{1,i}$, $i=\overline{1,n}$.

The output of the second residue storage unit modulo $p_2$ is connected to the inputs of the $(n-1)$-th multiplier by ${\widehat{b}}_{2,2}$, …, ${\widehat{b}}_{2,n}$, which compute the values $x_2·{\widehat{b}}_{2,i}$, $i=\overline{2,n}$, and so on, the output of the n-th residue storage unit modulo $p_n$ are connected to the input of the multiplier by ${\widehat{b}}_{n,n}$, which calculates the value $x_n·{\widehat{b}}_{n,n}$.

The outputs of the multipliers are connected to the inputs of n modular adders modulo $p_i$, $i=\overline{1,n}$, and the output of the multiplier by ${\widehat{b}}_{1,1}$ is connected to the input of the first modular adder modulo $p_1$ and performs calculations ${\widehat{x}}_1={\left|U_1\right|}_{p_1}={\left|x_1·{\widehat{b}}_{1,1}\right|}_{p_1}$, ${\sigma }_1=⌊\frac{x_1·{\widehat{b}}_{1,1}}{p_1}⌋$, the value ${\widehat{x}}_1$ goes to the output of the first modular adder modulo $p_1$, the value ${\sigma }_1$ goes to the carry output of the first modular added modulo $p_1$.

The outputs of the multipliers by ${\widehat{b}}_{1,2}$ and by ${\widehat{b}}_{2,2}$ are connected to the inputs of the second modular adder modulo $p_2$, whose carry input is connected to the carry output of the first modular adder modulo $p_1$, and calculates ${\widehat{x}}_2={\left|{\sigma }_1+U_2\right|}_{p_2}={\left|{\sigma }_1+x_1·{\widehat{b}}_{1,2}+x_2·{\widehat{b}}_{2,2}\right|}_{p_2}$, ${\sigma }_2=⌊\frac{{\sigma }_1+x_1·{\widehat{b}}_{1,2}+x_2·{\widehat{b}}_{2,2}}{p_2}⌋$, the value of ${\widehat{x}}_2$ goes to the output of the second modular adder modulo $p_2$, the value of ${\sigma }_2$ goes to the carry output of the second modular adder modulo $p_2$.

Therefore, the outputs of the multipliers by ${\widehat{b}}_{i,n}$, $i=\overline{1,n}$, are connected to the inputs of the $n-th$ modular adder modulo $p_n$, whose carry input is connected to the carry output of the $(n-1)$-th modular adder modulo $p_{n-1}$, and calculates ${\widehat{x}}_n={\left|{\sigma }_{n-1}+U_n\right|}_{p_n}={\left|{\sigma }_{n-1}+{\sum }_{i=1}^n{x}_i{\widehat{b}}_{i,n}\right|}_{p_n}$, ${\sigma }_n=⌊\frac{{\sigma }_{n-1}+{\sum }_{i=1}^n{x}_i{\widehat{b}}_{i,n}}{p_n}⌋$, the value ${\widehat{x}}_n$ arrives at the output n of the modular adder modulo $p_n$, the value of ${\sigma }_n$ arrives at the carry output of the $n$-th modular adder modulo $p_n$, which is not connected to other elements.

The values of ${\widehat{x}}_i$ from the outputs of i-th modular adders modulo $p_i$ are fed to the inputs of i-th multipliers by the bases of MRC ${\widehat{w}}_i$, $i=\overline{1,n}$, where multiplication of ${\widehat{x}}_i$ by ${\widehat{w}}_i={\prod }_{j=1}^{i-1}{p}_j$ takes place.

The output of the i-th multiplier by the bases of the MRC ${\widehat{w}}_i$ is connected to the i-th inputs of the adder and the modular adder, $i=\overline{1,n}$, the input of the extended base of the modular adder receives the modulo value $p_{n+1}$, the output of the reduced number of the adder receives the reduced number X in the positional number system, and the output of the remainder on the extended basis of the modular adder receives the number on the extended basis, i.e., ${\left|X\right|}_{p_{n+1}}$.

This method has a similar matrix structure to New CRT, but uses a sequential calculation without the remainder over a large modulo, as in MRC.

5. Method Based on Reference Points

In [18], a method of reference points based on the use of LUT tables is proposed for translation from a residue number system.

For a given set of moduli $\left\{p_1,p_2,\dots ,p_n\right\}$ is chosen by the reference point modulo $p_n$, which to reduce the number of values in memory it is more efficient to choose the largest modulo RNS.

Then the contents of the LUT will consist of $P_h={\prod }_{i=1}^{n-1}{p}_i$ reference points, which correspond to numbers $X=\left(x_1,x_2,\dots ,x_{n-1},0\right)$, which are completely divided by the modulo $p_n$.

In order to obtain an arbitrary number $Y=\left(y_1,y_2,\dots ,y_n\right)$ that is completely divided by $p_n$, you must subtract $y_n$ from the number Y, that is, calculate $x_i={\left|y_i-y_n\right|}_{p_i},i=1,\dots ,n$.

For example, for a RNS $\left\{7,8,9\right\}$ and an initial number $Y=10=\left(3,2,1\right)$, the reference point is $X\left(\left|3-1\right|{|}_7,{\left|2-1\right|}_8,{\left|1-1\right|}_9\right)=\left(2,1,0\right)$.

Thus, by analogy with New CRT II and the MRC for two moduli, the reference point will be $X={\left|X_h·{\left|p_n^{-1}\right|}_{P_h}\right|}_{P_h}·p_n$, where $X_h$ is the positional number obtained from $\left(x_1,x_2,\dots ,x_{n-1}\right)$ for the set of moduli $\left\{p_1,p_2,\dots ,p_{n-1}\right\}$.

For example, for the number $Y=228=\left(4,4,3\right)$, the reference point would be the value $X\left({\left|4-3\right|}_7,{\left|4-3\right|}_8,{\left|3-3\right|}_9\right)=\left(1,1,0\right)$. Since $\left(1,1\right)$ for the set of moduli $\left\{7,8\right\}$ is 1, and ${\left|9^{-1}\right|}_{7·8}=25$, the reference point is $X={\left|1·25\right|}_{56}·9=225$, which corresponds to the subtraction from $Y=228$ of residue $y_n=3$.

It can be seen that the value of the reference point depends on the number $\left(x_1,x_2,\dots ,x_{n-1}\right)$ with moduli $\left\{p_1,p_2,\dots ,p_{n-1}\right\}$ and range $P_h={\prod }_{i=1}^{n-1}{p}_i$. Then the computation can be replaced by a memory access, which by the value $X_h=\left(x_1,x_2,\dots ,x_{n-1}\right)$ will give the value ${\left|X_h·{\left|p_n^{-1}\right|}_{P_h}\right|}_{P_h}·p_n$.

In this case, the reverse converter based on the reference points can have a hierarchical structure, for example, as shown in Figure 2. In this case, based on the differences of the residues ${\left|x_1-x_3\right|}_{p_1}$ and ${\left|x_2-x_3\right|}_{p_2}$ by moduli $p_1$ and $p_2$, respectively, using LUT with the values of the reference points, which are ${\left|X_{12}·{\left|p_3^{-1}\right|}_{p_1{p}_2}\right|}_{p_1{p}_2}·p_3$, where $X_{12}$ is—the restored value over the moduli $p_1,p_2$, and adding with the remainder $x_3$ modulo $p_3$ find the restored number $X_{123}$ modulo $p_1,p_2,p_3$.

Figure 2. Reverse converter based on reference point.

Then similarly are the differences of the residues by moduli $p_4$ and $p_5$ and the reconstructed number $X_{123}$, and since the value of $X_{123}$ can greatly exceed the values of modules $p_4$ and $p_5$, forward conversion blocks are used, which can be implemented both arithmetically and using memory. Similarly, the values in the LUT of reference points are found, where the pre-calculated values ${\left|X_{45}·{\left|{\left(P_{123}\right)}^{-1}\right|}_{P_{45}}\right|}_{P_{45}}·P_{123}$ for $P_{123}=p_1·p_2·p_3$ and $P_{45}=p_4·p_5$.

Thus, by varying the number of LUT inputs from 1 to $n-1$ and the number of reverse conversion layers, a solution with better time or area can be obtained.

6. Modification of the Reference Points Method Based on the MRC

As the number of moduli and their dimensionality increase, the method of reference points requires a significant amount of memory.

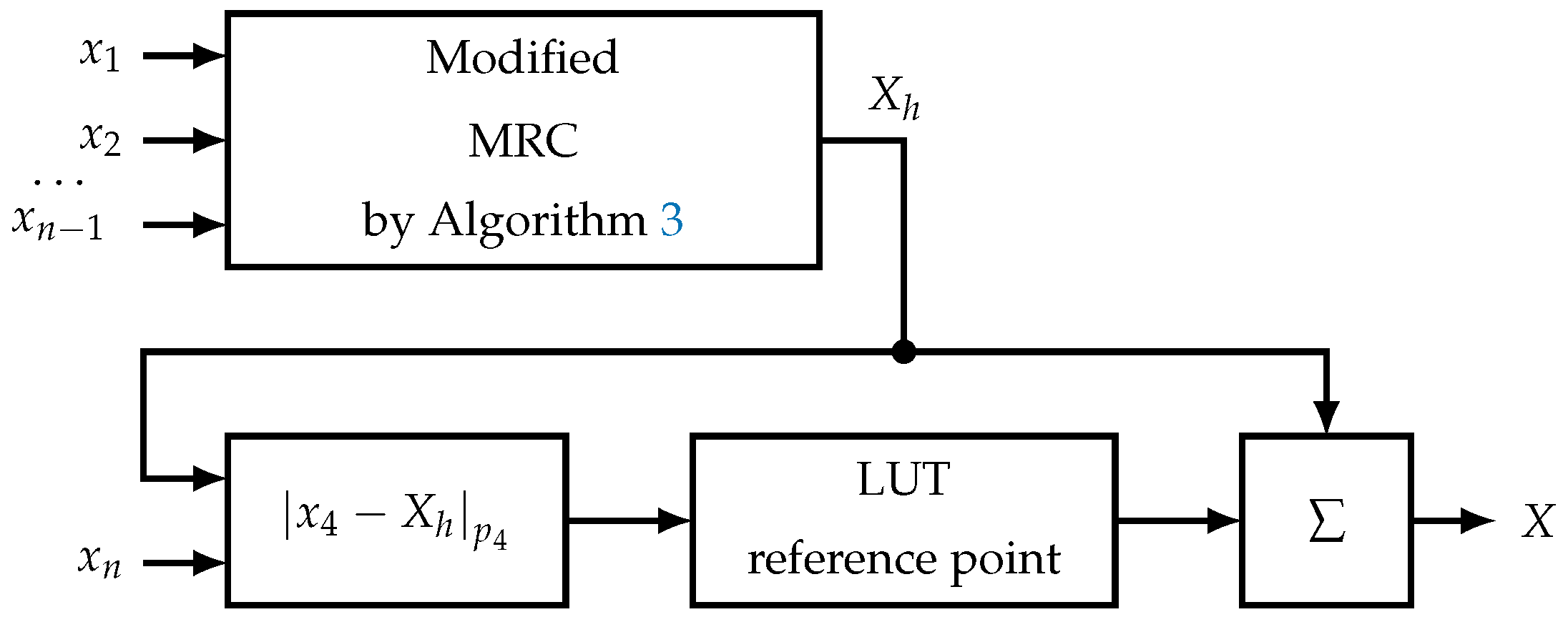
First, we introduce a method based on the proposed methods of reference points and modified MRC. Let us take RNS $\left\{p_1,\dots ,p_{n-1},p_n\right\}$, where $p_n=2^k$, i.e., degree 2. Then using the Algorithm 3 we find $X_h$ by the moduli $\left\{p_1,\dots ,p_{n-1}\right\}$, and using the method of reference point we compute ${\left|x_n-X_h\right|}_{p_n}$. Since $p_n=2^k$, this expression can be reduced to taking k lower bits of the sum $x_n+{\overline{X}}_h+1$, where ${\overline{X}}_h$ is the bitwise inversion.

Then, based on this value, a precomputed value equal to ${\left|{\left|x_n+{\overline{X}}_h+1\right|}_{2^k}·{\left|P_h^{-1}\right|}_{2^k}\right|}_{2^k}·P_h$ is selected from the LUT table of size $2^k$, where $P_h={\prod }_{i=1}^{n-1}{p}_i$. The final value is obtained by adding ${\left|x_n+{\overline{X}}_h+1\right|}_{2^k}$. In this case, the reverse converter can have a structure, for example, as shown in Figure 3.

Figure 3. Reverse converter based on reference point and modified MRC.

Consider an example for RNS $\left\{3,5,7,8\right\}$ and the number $X=115=\left(1,0,3,3\right)$. To calculate the Algorithm 3, find the parameters of the RNS $\left\{3,5,7\right\}$:

$$\begin{array}{cc}& P_h=3·5·7=105,\\ \hfill P_1=5·7=35,& {\left|P_1^{-1}\right|}_{p_1}={\left|{35}^{-1}\right|}_3=2,& B_1=70,\hfill \\ \hfill P_2=3·7=21,& {\left|P_2^{-1}\right|}_{p_2}={\left|{21}^{-1}\right|}_5=1,& B_2=21,\hfill \\ \hfill P_3=3·5=15,& {\left|P_3^{-1}\right|}_{p_3}={\left|{15}^{-1}\right|}_7=1,& B_3=15.\hfill \end{array}$$

Let us calculate ${\widehat{w}}_j={\prod }_{i=1}^{j-1}{p}_i$:

$${\widehat{w}}_1=1,{\widehat{w}}_2=3,{\widehat{w}}_3=3·5=15.$$

Let us calculate the representation of $B_i$ in the MRC:

$$\begin{array}{cc}\hfill & B_1\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_1=\left[{\widehat{b}}_{1,1},{\widehat{b}}_{1,2},{\widehat{b}}_{1,3}\right]=\left[1,3,4\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & B_2\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_2=\left[{\widehat{b}}_{2,1},{\widehat{b}}_{2,2},{\widehat{b}}_{2,3}\right]=\left[0,2,1\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & B_3\stackrel{\mathrm{MRC}}{\to }{\widehat{B}}_3=\left[{\widehat{b}}_{3,1},{\widehat{b}}_{3,2},{\widehat{b}}_{3,3}\right]=\left[0,0,1\right].\hfill \end{array}$$

To calculate $X_h=\left(1,0,3\right)$ we then compute $U_i={\sum }_{j=1}^i{x}_j·{\widehat{b}}_{j,i}$:

$$\begin{array}{cc}\hfill & U_1=x_1·{\widehat{b}}_{1,1}=1·1=1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & U_2=x_1·{\widehat{b}}_{1,2}+x_2·{\widehat{b}}_{2,2}=1·3+0·2=3,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & U_3=x_1·{\widehat{b}}_{1,3}+x_2·{\widehat{b}}_{2,3}+x_3·{\widehat{b}}_{3,3}=1·4+0·1+3·1=7.\hfill \end{array}$$

Let us calculate ${\widehat{x}}_i={\left|{\sigma }_{i-1}+U_i\right|}_{p_i}$ and ${\sigma }_i=⌊\frac{{\sigma }_{i-1}+U_i}{p_i}⌋$:

$$\begin{array}{cccc}\hfill & {\widehat{x}}_1={\left|U_1\right|}_{p_1}={\left|1\right|}_3=1,\hfill & \hfill & {\sigma }_1=⌊\frac{U_1}{p_1}⌋=⌊\frac{1}{3}⌋=0,\hfill \end{array}$$

$$\begin{array}{cccc}\hfill & {\widehat{x}}_2={\left|{\sigma }_1+U_2\right|}_{p_2}={\left|0+3\right|}_5=3,\hfill & \hfill & {\sigma }_2=⌊\frac{{\sigma }_1+U_2}{p_2}⌋=⌊\frac{3}{5}⌋=0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\widehat{x}}_3={\left|{\sigma }_2+U_3\right|}_{p_3}={\left|0+7\right|}_7=0.\hfill \end{array}$$

From this we obtain:

$$X_h=\sum _{i=1}^n{\widehat{x}}_i·{\widehat{w}}_i=1·1+3·3+0·15=10.$$

According to the method of reference vectors we find the difference

$$X_4={\left|x_4-X_h\right|}_{p_4}={\left|3-10\right|}_8=1.$$

In the case of a hardware implementation, to obtain $X_4$, one must add $x_4$ to one and $k=3$ to the lowest bits of the inverted value of $X_h$, i.e.,

$$X_4={\left|11+\overline{1010}+1\right|}_8={\left|11+101+1\right|}_8={\left|1001\right|}_8=1.$$

LUT of reference point stores values ${\left|X_4·{\left|P_h^{-1}\right|}_{2^k}\right|}_{2^k}·P_h$, values for this case are shown in Table 1.

Table 1. LUT values for the example at hand.

${\mathit{X}}_4$	Reference Point Value	${\mathit{X}}_4$	Reference Point Value
0	0	4	420
1	105	5	525
2	210	6	630
3	315	7	735

Since $X_4=1$, based on the Table 1 we obtain a value of 105 and then the initial value $X=105+X_h=115$.

Changing the ratio of the number of moduli over which the reconstruction in the modified MRC and the method of reference points, as well as the number of steps in the method of reference points allows you to flexibly adjust the system according to the constraints on the used area and computation time.

7. Physical Synthesis of Reverse Conversion Methods

Physical synthesis of methods for translating from a residue number system to a positional number system was performed on an ASIC in the RTL and physical synthesis Cadence Genus Synthesis Solution environment using the NangateOpenCellLibrary and computation time optimization. The parameters measured were the signal propagation time across the circuit (picoseconds, ps) and the area used (square micrometer, µm²).

The Chinese residue theorem-based method (Formula (1)), the approximated CRT-based method (Formulas (5) and (6)), the mixed-radix conversion-based method (Formula (2)), a method based on special moduli $\left\{2^n-1,2^n,2^n+1\right\}$ [8], the reference points method proposed by the authors and discussed in Section 5, the modified MRC-based method (Algorithm 3), and the introduced method based on reference points and modified MRC (Section 6).

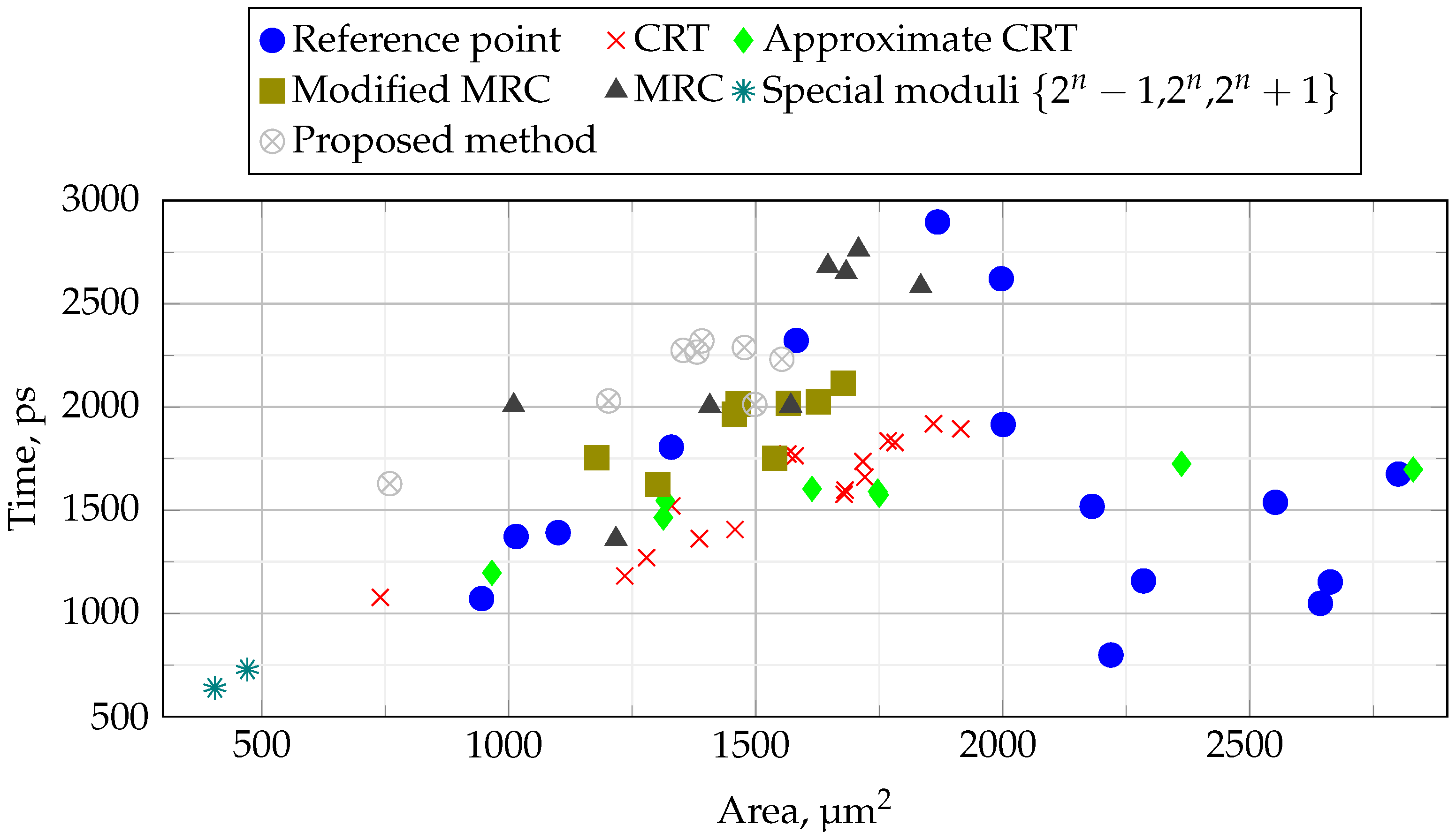
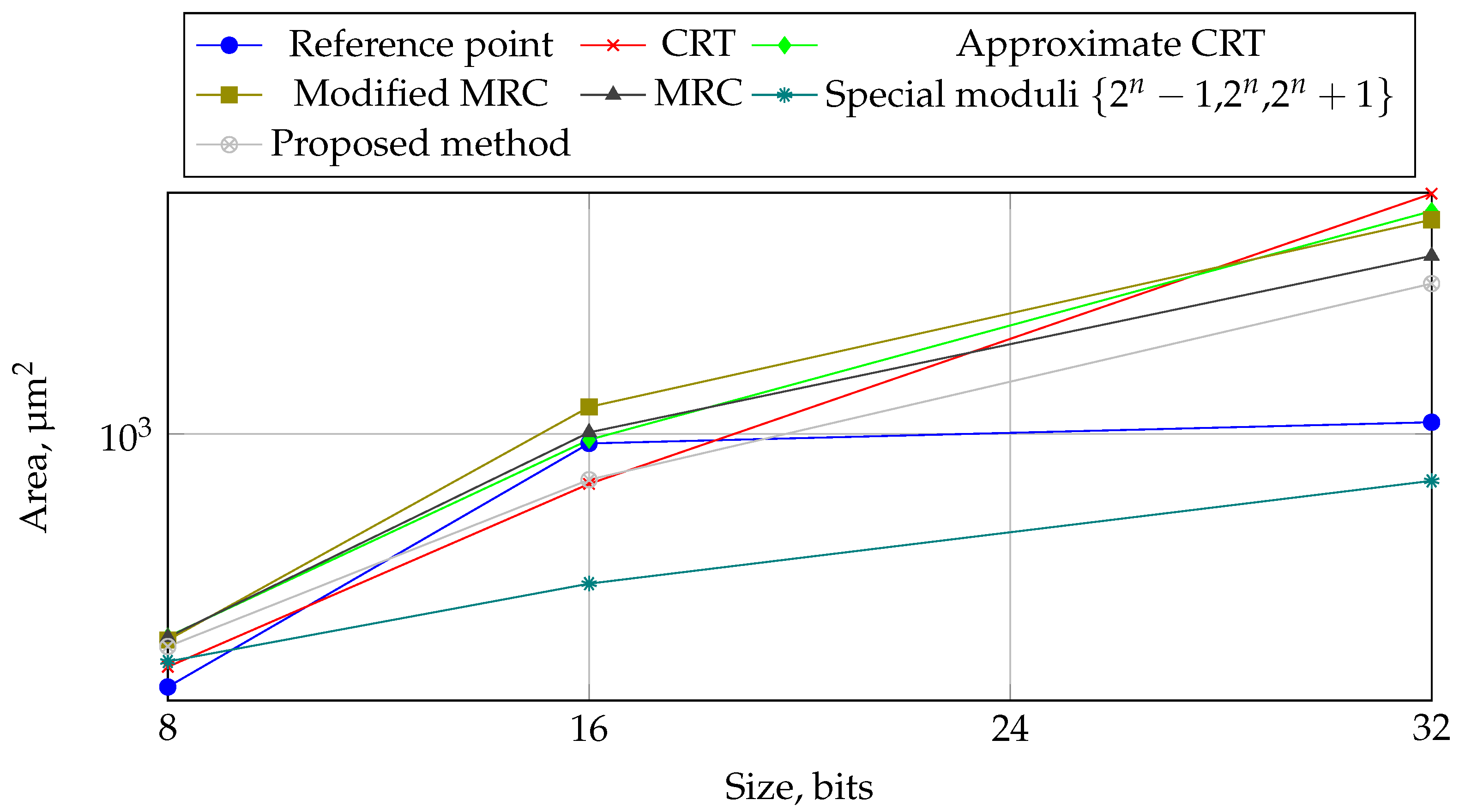
Simulation results for the reference points method, CRT, approximate CRT, modified MRC, MRC, special moduli $\left\{2^n-1,2^n,2^n+1\right\}$ and the proposed method are shown in Figure 4, Figure 5, Figure 6 for 8, 16 and 32 bits, respectively.

Figure 4. Reverse conversion for 8 bits.

Figure 5. Reverse conversion for 16 bits.

Figure 6. Reverse conversion for 32 bits.

In addition, Table 2, Table 3, Table 4 are given to compare the proposed modification with the previously developed methods. In these tables, the reference points based method is denoted as I, the modified mixed-radix conversion based method—II, the proposed modification—III. The configuration of the layers for the reference points method is given in the second column.

Table 2. Time and area comparison for 8 bits.

RNS Moduli	Layer	Area, µm2			Time, ps
		I	II	III	I	II	III
{3, 5, 7, 8}	3-5-7/8	553	442	408	654	987	987
	3-7/5-8	425			729
{3, 5, 32}	3-5/32	236	483	279	521	787	787
	32/3-5	266			494
{3, 7, 16}	3-7/16	217	350	315	523	691	1016
{5, 7, 8}	5-7/8	293	288	277	277	845	1051
{5, 9, 16}	5-9/16	409	444	414	611	984	1277
	16/5-9	371			508
{7, 9, 16}	7-9/16	406	426	342	568	979	970
{7, 15, 16}	7-15/16	604	579	543	713	1197	1486
	15-16/7	392			903

Table 3. Time and area comparison for 16 bits.

RNS Moduli	Layer	Area, µm2			Time, ps
		I	II	III	I	II	III
{3, 5, 7, 17, 64}	3-5-7/64/17	1582	1538	1498	2322	1752	2012
{5, 7, 9, 17, 32}	5-7-9/17/32	2181	1677	1477	1518	2115	2288
	5-32/7-17/9	1868			2896
{7, 15, 17, 64}	7-17/15/64	1329	1627	1553	1805	2025	2231
{7, 15, 31, 32}	7-31/15-32	2552	1566	1381	1538	2018	2266
{15, 17, 31, 32}	31/32 /15-17	2001	1464	1353	1915	2014	2274
{31, 33, 128}	31/33/128	945	1302	759	1071	1625	1628
	128/31-33	2219			798
{31, 63, 64}	31/63/64	1015	1457	1391	1372	1964	2320
	31-63/64	2643			1048

Table 4. Time and area comparison for 32 bits.

RNS Moduli	Layer	Area, µm2			Time, ps
		I	II	III	I	II	III
{3, 7, 17, 31, 65, 127, 128}	3-17-31/7-127/65/128	12,153	5658	5982	5077	4731	4837
	3-128/7-127/17-65/31	10,730			5461
{7, 17, 31, 65, 127, 256}	7-65/17-256/31-127	30,741	5421	6168	3321	4212	4545
{9, 17, 31, 65, 127, 128 }	127/17-65/128/9-31	9601	5339	5314	4190	4190	4675
	128/127/65/9-17-31	25,870			4383
{31, 33, 65, 127, 512}	31-33/65/127/512	6996	5391	5397	3746	4270	4392
	31-127/65-33/512	19,691			3356
{31, 65, 127, 129, 256}	31-65/127/129/256	10,903	5297	6333	4763	4510	4727
{127, 129, 257, 1024}	127/129/1024/257	3509	5226	3906	3707	3589	3917
	127-129/1024/257	11,075			3407
{127, 255, 257, 1024}	127/255/257/1024	4318	6025	4535	3589	4075	4284
{127, 255, 511, 512}	127/255/511/512	4837	5945	5726	3108	4221	4377
{1023, 1025, 8192}	1023/1025/8192	1074	3652	2482	1366	2821	2984
	8192/1023/1025	2659			3081
{1023, 2047, 4096}	4096/2047/1023	1535	5031	3966	2179	3323	3638

The analysis of the Figure 4 shows that the reference point based method has the smallest area in the 8-bit domain and is only slightly inferior to the special type moduli in terms of time. The MRC and approximate CRT-based methods have complex computational algorithms and perform poorly in terms of both area and time.

In the 16-bit domain (Figure 5), the method using special moduli has a clear advantage, and the method based on reference points has a low execution time, but at the same time significant hardware costs. The proposed method allows to reduce the used area, but slightly increases the computation time.

In the 32-bit domain (Figure 6), the reference points method shows both some of the best and some of the worst results in terms of time and area, and thus a strong dependence on the set of moduli and the configuration of layer over which the residues are grouped for the LUT. The MRC-based method performs worse than the CRT and the approximate CRT in most cases, but has less area as the dimensionality increases.

Figure 7 and Figure 8 show the best time and area, respectively, for the methods considered.

Figure 7. Comparison of the time required for the methods of translation from RNS to positional number system.

Figure 8. Comparison of the area used for methods of translation from RNS to positional number system.

8. Conclusions

In this paper, an overview of the methods of conversion from the residue number system to the positional number system is given. Reverse conversion methods for general form moduli, such as the Chinese residue theorem, mixed-radix conversion, the Chinese residue theorem with fractional numbers, new CRT I, and new CRT II, were considered. The application of RNS moduli of the special form 2ⁿ ± 1, 2ⁿ was also considered. Based on the modified mixed-radix conversion presented by Algorithm 3 and the method of reference points (Section 5), a method of reverse conversion of a number from a residue number system to a positional number system is proposed (Section 6). The results of physical synthesis have shown that the use of moduli of a special type makes it possible to significantly reduce the computational time and the claimed area, however, the task of working with moduli of a general type often arises.

The reference points method proposed by the authors in [18] makes it possible to obtain computationally efficient implementations, but the used area can differ up to 30 times within one dimension (for the sets {7, 17, 31, 65, 127, 256} and {1023, 1025, 8192}), which leads to the need to check a large number of sets of a given dimension in the search for the optimal set.

The method proposed in this work reduces the required area (up to five times for the set {7, 17, 31, 65, 127, and 256}) for RNS with a large number of moduli compared to the reference point method and reduces the area for RNS with three and four moduli compared to the modified MRC. It is possible to combine the reference point method with different configurations of layers and methods based on CRT and MRC to obtain efficient implementations in terms of computational speed and required area.