Combining Biomechanical Features and Machine Learning Approaches to Identify Fencers’ Levels for Training Support
Abstract
1. Introduction
2. Background and Related Works
2.1. Background
2.1.1. En Garde Position
2.1.2. Distance Traveled
2.1.3. Speed
2.1.4. Lunge
2.2. Related Works
- The devices used to collect data;
- The knowledge obtained from device-gathered data (3D kinematic and vertical ground reaction forces may be predicted);
- The processing of data from devices (classification methods can separate data into relevant packages that would have previously required sports scientists to spend much time on them);
- How processed data can improve our comprehension of athletic performance and injury risk prediction.
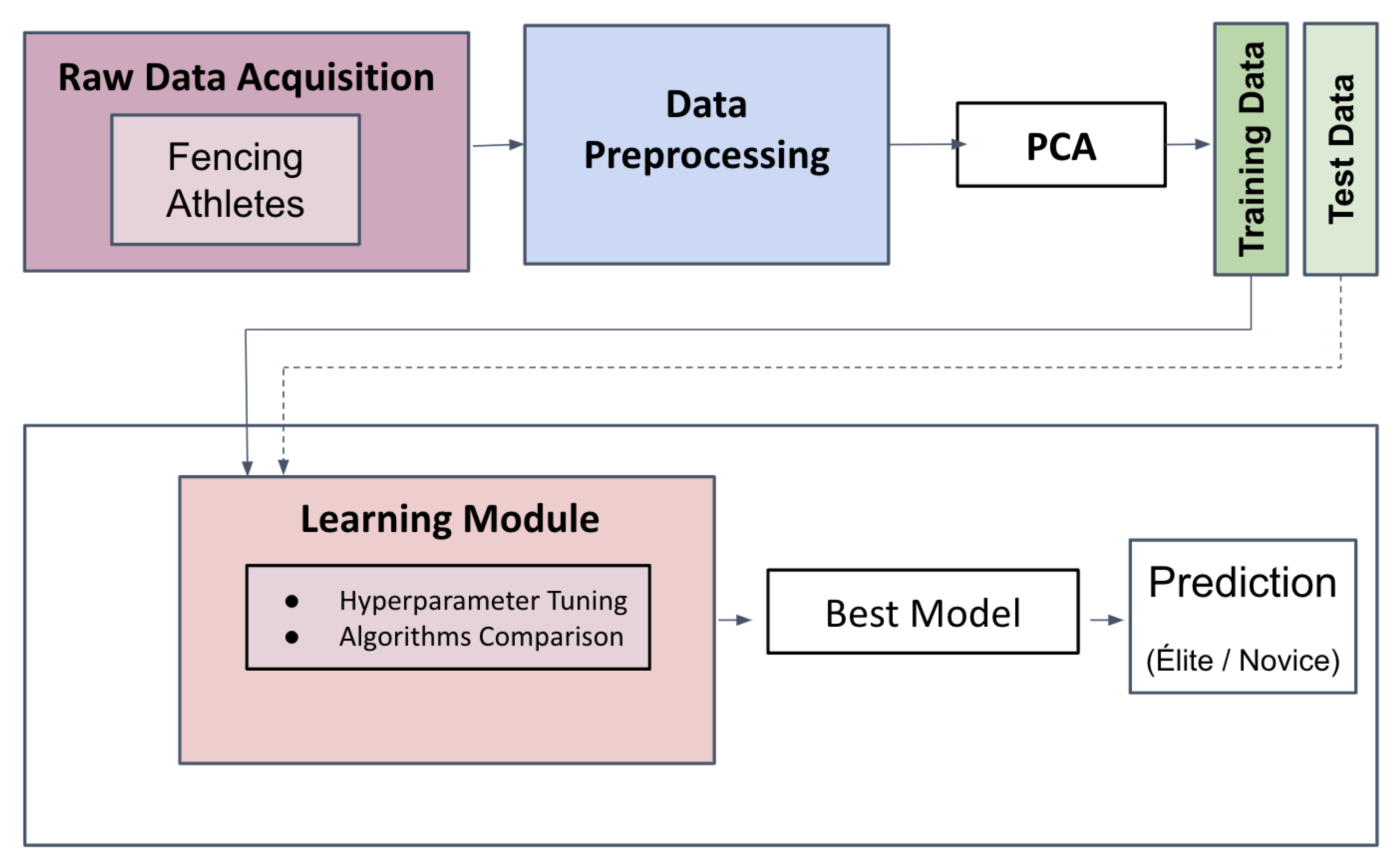
3. Materials and Methods
3.1. Experiment Environments
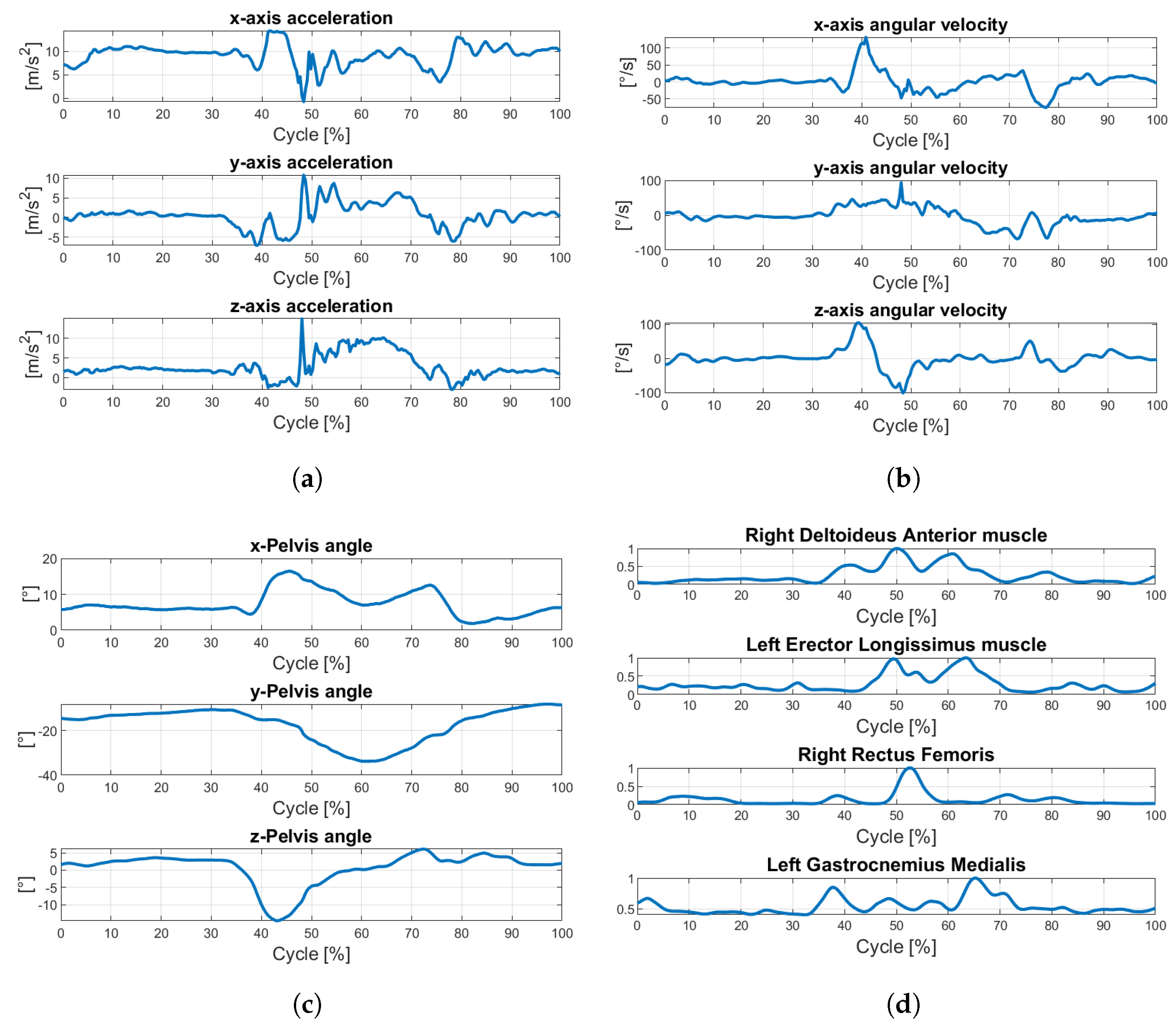
3.2. Data Collection
3.3. Instruments
3.4. Experimental Protocol
- Explosive lunge: the subject had to execute a lunge that was not demonstrative but pushed in order to hit the target as fast as possible;
- Step forward lunge: the subject was placed further away from the lunge, as the exercise consists of carrying out an offensive action in which the fencer must take a step forward to get to lunge distance in order to execute it and then stop the target;
- Step back lunge: the subject takes a step backward to get within lunge distance and then scores a hit.
3.5. Data Pre-Processing
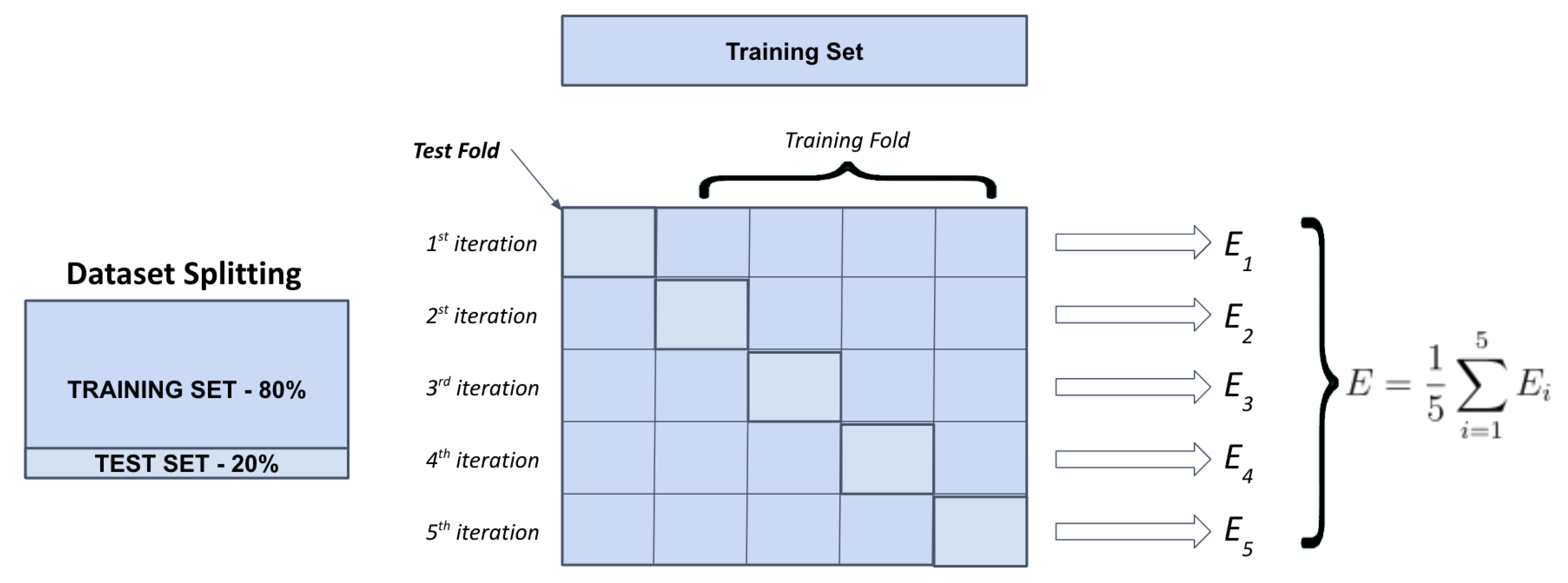
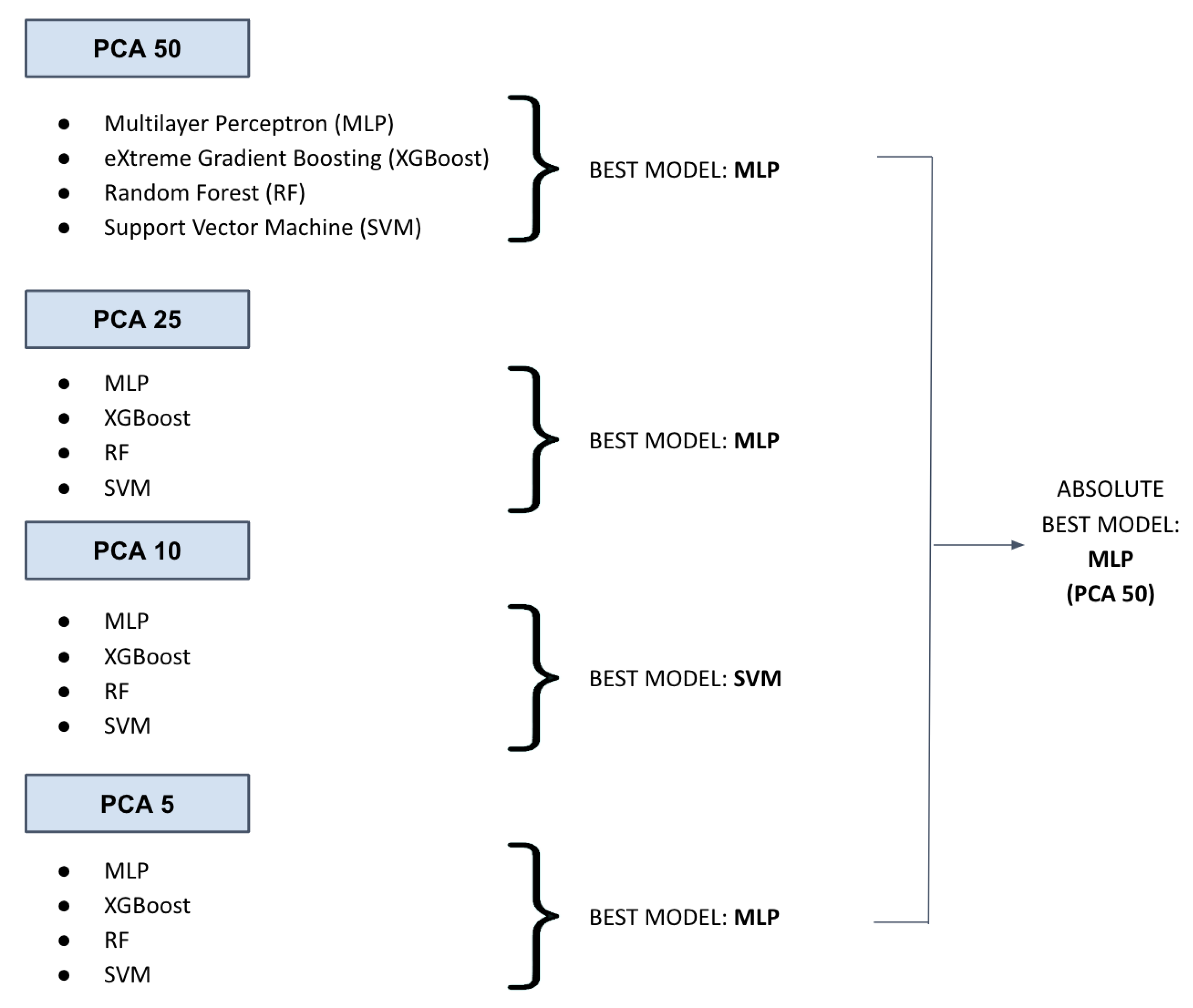
3.6. Data Splitting and Dimensionality Reduction
- , for an overall of 650 total features;
- , for an overall of 325 total features;
- , for an overall of 130 total features;
- , for an overall of 65 total features.
3.7. Machine Learning Algorithms
- eXtreme Gradient Boosting (XGBoost) classifier [40]. The most crucial factor behind the success of XGBoost is its scalability in all scenarios due to several essential systems and algorithmic optimizations. It is an ensemble of K classification and regression trees (CART) , where is the given training set of descriptors associated with a prediction of the class label, . A CART assigns a real score to every leaf (outcome or target), so a combination of all prediction scores is used to get the final score, as indicated in . represents an independent tree structure with leaf scores, and F represents the space of all CARTs. This objective is defined as follows: . In the first term, we have a differentiable loss function, l, which measures the difference between and before prediction. The second regularization term, , penalizes the complexity of the model to avoid overfitting, and it is provided by . A leaf score is determined by the number of leafs T and the number of leafs w. The constants and control how much regularization occurs. Using regularization, shrinkage, and descriptor subsampling are additional methods of preventing overfitting.
- Multilayer Perceptron (MLP) [41]. It is a supervised learning algorithm that uses a feed-forward neural network technique. It consists of a layer of input, a hidden layer of threshold logic units (TLUs), and a layer of output. The hidden layers are all connected, and each TLU computes a weighted sum of its inputs before applying an activation function to provide a result that will be used as input for the next layer. Generally, activation functions are not linear and can take on 1-differential forms. Back-propagation algorithms are based on making predictions and measuring performance (error) for every training instance. Thus, each layer is reversed to assess the contribution of each connection to the error; then, edge weights are modified to improve performance.
- Random forest (RF) classifier [42]. It is one of the best classifiers in terms of predictability and efficiency for high-dimensional datasets. It is a supervised learning algorithm based on constructing a collection of decision trees. For prediction, the RF model produces a variety of decision trees in the training phase, intending to reduce the variance of the final result by determining the class predicted most commonly by each tree within the forest. RF training algorithm consists of incorporating bootstrap aggregation to trees under training. denotes the pair of training set X and target vector Y, where , and . By replacing a random sample from X with a repeated (B times) extraction, the trees are fitted to this sample and repeated. In particular, for , the procedure is as follows: (1) Random sampling with replacement of n observations from the training set X to obtain subsets. To reduce the correlation between trees originating from bagging, the cardinality of the subset is usually of order for a classification problem with p features. Step (2) involves training the tree on . (3) Out-of-sample prediction on unseen dataset is the response outcome resulting from most of the results generated from every single tree. The number of trees in the forest is the free parameter of the model, usually set to at least .
- Support Vector Machine (SVM) classifier [43]. The SVM is a supervised learning algorithm based on the concept of optimal hyper-planes that separate observations belonging to two different classes. Assuming that n points belong to two linearly separable sets in p-dimensional space, the goal of the linear classification problem is to find a (p-1)-dimensional hyperplane that can classify two classes with the most extensive margins, e.g., the most significant distance from the nearest points in each set to the boundary. In cases where the original data cannot be linearly separable, one possibility is to map the original data onto a higher-dimensional feature space to achieve more effective separation. Hence, support vector classifiers are generalized linear classifiers based on an “augmented” feature space with significantly high dimensionality. Suppose the transformed feature vectors are given by the function . In that case, the optimization problem can easily be transformed into a quadratic programming problem using Lagrange multipliers in which the transformed vectors are scalar products. Thanks to this trick, it is not important to know the transformation, but only the type of the kernel function . The selection of a kernel function and the regularization parameter C determine the configuration of an SVM classifier. The following functions were chosen for the hyper-parameter tuning phase: (1) degree polynomials: ; (2) radial basis function (RBF): , where values of parameters d, , , and span specific ranges.
4. Results
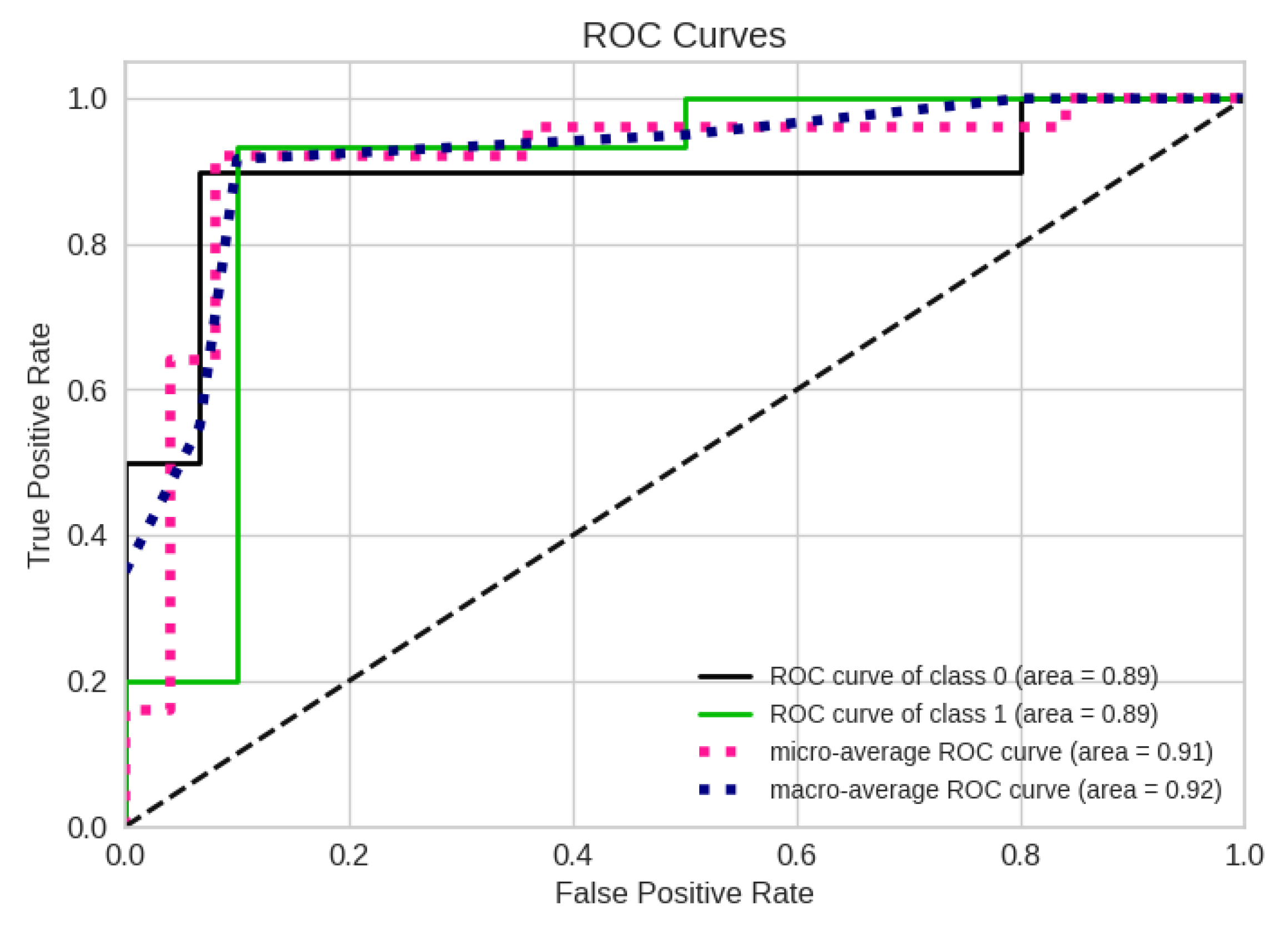
4.1. Evaluation Metrics
4.2. Best Model Performance Analysis
4.3. Best Model Hyperparameter Tuning
- hidden_layer_sizes’: [(sp_randint.rvs(100, 600, 1), sp_randint.rvs(100, 600, 1),),(sp_randint.rvs(100, 600, 1),)]
- activation: tanh, relu, logistic;
- solver: sgd, adam, lbfgs;
- alpha: 0.0001, 0.001, 0.01, 0.1, 0.9;
- learning_rate: "constant", "adaptive".
- hidden_layer_sizes: (586);
- activation: relu;
- solver: lbfgs;
- alpha: 0.1;
- learning_rate: constant.
4.4. Experimental Setup
- Raw data acquisition of the signal;
- Creating the dataset through preprocessing;
- Applying PCA to the preprocessed data (k is determined based on the best model);
- The ML algorithm performs the prediction using the data described in the previous step.
4.5. Performance Evaluation of the Absolute Best Model
5. Concluding Remarks and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, T.L.W.; Wong, D.W.C.; Wang, Y.; Ren, S.; Yan, F.; Zhang, M. Biomechanics of fencing sport: A scoping review. PLoS ONE 2017, 12, e0171578. [Google Scholar] [CrossRef]
- Sorel, A.; Plantard, P.; Bideau, N.; Pontonnier, C. Studying fencing lunge accuracy and response time in uncertain conditions with an innovative simulator. PLoS ONE 2019, 14, e0218959. [Google Scholar] [CrossRef]
- Bottoms, L.; Greenhalgh, A.; Sinclair, J. Kinematic determinants of weapon velocity during the fencing lunge in experienced épée fencers. Acta Bioeng. Biomech. 2013, 15, 4. [Google Scholar]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends supporting the in-field use of wearable inertial sensors for sport performance evaluation: A systematic review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Bortone, I.; Moretti, L.; Bizzoca, D.; Caringella, N.; Delmedico, M.; Piazzolla, A.; Moretti, B. The importance of biomechanical assessment after Return to Play in athletes with ACL-Reconstruction. Gait Posture 2021, 88, 240–246. [Google Scholar] [CrossRef]
- Ardito, C.; Di Noia, T.; Di Sciascio, E.; Lofú, D.; Mallardi, G.; Pomo, C.; Vitulano, F. Towards a trustworthy patient home-care thanks to an edge-node infrastructure. In Proceedings of the International Conference on Human-Centred Software Engineering, Eindhoven, The Netherlands, 24–26 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 181–189. [Google Scholar]
- Pazienza, A.; Anglani, R.; Mallardi, G.; Fasciano, C.; Noviello, P.; Tatulli, C.; Vitulano, F. Adaptive Critical Care Intervention in the Internet of Medical Things. In Proceedings of the 2020 IEEE International Conference on Evolving and Adaptive Intelligent Systems (EAIS), Bari, Italy, 27–29 May 2020; pp. 1–8. [Google Scholar]
- Ardito, C.; Di Noia, T.; Fasciano, C.; Lofú, D.; Macchiarulo, N.; Mallardi, G.; Pazienza, A.; Vitulano, F. Management at the Edge of Situation Awareness during Patient Telemonitoring. In Proceedings of the 19th International Conference of the Italian Association for Artificial Intelligence (AIxIA 2020), Virtually, 25–27 November 2020; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12414, pp. 372–387. [Google Scholar]
- Ardito, C.; Di Noia, T.; Fasciano, C.; Lofú, D.; Macchiarulo, N.; Mallardi, G.; Pazienza, A.; Vitulano, F. Towards a Situation Awareness for eHealth in Ageing Society. In Proceedings of the Italian Workshop on Artificial Intelligence for an Ageing Society (AIxAS 2020), Virtually, 25–27 November 2020; pp. 40–55. [Google Scholar]
- Ardito, C.; Di Noia, T.; Di Sciascio, E.; Lofú, D.; Pazienza, A.; Vitulano, F. User Feedback to Improve the Performance of a Cyberattack Detection Artificial Intelligence System in the e-Health Domain. In Proceedings of the Human–Computer Interaction—INTERACT 2021, Bari, Italy, 30 August–3 September 2021; pp. 295–299. [Google Scholar]
- Ardito, C.; Di Noia, T.; Di Sciascio, E.; Lofù, D.; Pazienza, A.; Vitulano, F. An Artificial Intelligence Cyberattack Detection System to Improve Threat Reaction in e-Health. In Proceedings of the ITASEC, Virtually, 7–9 April 2021. [Google Scholar]
- Ardito, C.; Bellifemine, F.; Di Noia, T.; Lofú, D.; Mallardi, G. A proposal of case-based approach to clinical pathway modeling support. In Proceedings of the 2020 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Bari, Italy, 27–29 May 2020; pp. 1–6. [Google Scholar]
- Sorino, P.; Caruso, M.G.; Misciagna, G.; Bonfiglio, C.; Campanella, A.; Mirizzi, A.; Franco, I.; Bianco, A.; Buongiorno, C.; Liuzzi, R.; et al. Selecting the best machine learning algorithm to support the diagnosis of Non-Alcoholic Fatty Liver Disease: A meta learner study. PLoS ONE 2020, 15, e0240867. [Google Scholar] [CrossRef]
- Lella, E.; Pazienza, A.; Lofú, D.; Anglani, R.; Vitulano, F. An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification. Electronics 2021, 10, 249. [Google Scholar] [CrossRef]
- Tatoli, R.; Lampignano, L.; Bortone, I.; Donghia, R.; Castellana, F.; Zupo, R.; Tirelli, S.; De Nucci, S.; Sila, A.; Natuzzi, A.; et al. Dietary Patterns Associated with Diabetes in an Older Population from Southern Italy Using an Unsupervised Learning Approach. Sensors 2022, 22, 2193. [Google Scholar] [CrossRef]
- Pazienza, A.; Anglani, R.; Fasciano, C.; Tatulli, C.; Vitulano, F. Evolving and Explainable Clinical Risk Assessment at the Edge. Evol. Syst. 2022, 1–20. [Google Scholar] [CrossRef]
- Lofú, D.; Pazienza, A.; Ardito, C.; Di Noia, T.; Di Sciascio, E.; Vitulano, F. A Situation Awareness Computational Intelligent Model for Metabolic Syndrome Management. In Proceedings of the 2022 IEEE Conference on Cognitive and Computational Aspects of Situation Management (CogSIMA), Salerno, Italy, 6–10 June 2022; pp. 118–124. [Google Scholar] [CrossRef]
- Pazienza, A.; Monte, D. Introducing the Monitoring Equipment Mask Environment. Sensors 2022, 22, 6365. [Google Scholar] [CrossRef]
- Sorino, P.; Campanella, A.; Bonfiglio, C.; Mirizzi, A.; Franco, I.; Bianco, A.; Caruso, M.G.; Misciagna, G.; Aballay, L.R.; Buongiorno, C.; et al. Development and validation of a neural network for NAFLD diagnosis. Sci. Rep. 2021, 11, 20240. [Google Scholar] [CrossRef] [PubMed]
- Ardito, C.; Di Noia, T.; Fasciano, C.; Lofù, D.; Macchiarulo, N.; Mallardi, G.; Pazienza, A.; Vitulano, F. An Edge Ambient Assisted Living Process for Clinical Pathway. In Ambient Assisted Living; Bettelli, A., Monteriù, A., Gamberini, L., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 363–374. [Google Scholar]
- Mawgoud, A.; Abu-Talleb, A.; El Karadawy, A.; Eltabey, M. The Appliance of Artificial Neural Networks in Fencing Sport Via Kinect Sensor; ResearchGate: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Timpka, T.; Ekstrand, J.; Svanström, L. From sports injury prevention to safety promotion in sports. Sport. Med. 2006, 36, 733–745. [Google Scholar] [CrossRef] [PubMed]
- Bai, D.; Liu, T.; Han, X.; Yi, H. Application research on optimization algorithm of sEMG gesture recognition based on light CNN+ LSTM model. Cyborg Bionic Syst. 2021, 2021. [Google Scholar] [CrossRef]
- Alhasan, H.S.; Wheeler, P.C.; Fong, D.T. Application of interactive video games as rehabilitation tools to improve postural control and risk of falls in prefrail older adults. Cyborg Bionic Syst. 2021, 2021. [Google Scholar] [CrossRef]
- Guan, Y.; Guo, L.; Wu, N.; Zhang, L.; Warburton, D.E. Biomechanical insights into the determinants of speed in the fencing lunge. Eur. J. Sport Sci. 2018, 18, 201–208. [Google Scholar] [CrossRef]
- Turner, A.; James, N.; Dimitriou, L.; Greenhalgh, A.; Moody, J.; Fulcher, D.; Mias, E.; Kilduff, L. Determinants of Olympic fencing performance and implications for strength and conditioning training. J. Strength Cond. Res. 2014, 28, 3001–3011. [Google Scholar] [CrossRef]
- Suchanowski, A.; Boryszewski, Z.; Pakosz, P. Electromyography signal analysis of the fencing lunge by Magda Mroczkiewicz, the leading world female competitor in foil. Balt. J. Health Phys. Act. 2011, 3, 4. [Google Scholar] [CrossRef]
- Gholipour, M.; Tabrizi, A.; Farahmand, F. Kinematics analysis of lunge fencing using stereophotogrametry. World J. Sport Sci. 2008, 1, 32–37. [Google Scholar]
- Borysiuk, Z. Type of perception vs. lunge in fencing technique structure. Rev. Artes Marciales Asiát. 2016, 11, 36–37. [Google Scholar] [CrossRef][Green Version]
- Gutierrez-Davila, M.; Rojas, F.J.; Antonio, R.; Navarro, E. Response timing in the lunge and target change in elite versus medium-level fencers. Eur. J. Sport Sci. 2013, 13, 364–371. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Dávila, M.; Rojas, F.J.; Caletti, M.; Antonio, R.; Navarro, E. Effect of target change during the simple attack in fencing. J. Sport. Sci. 2013, 31, 1100–1107. [Google Scholar] [CrossRef]
- Borysiuk, Z.; Markowska, N.; Niedzielski, M. Analysis of the fencing lunge based on the response to a visual stimulus and a tactile stimulus. J. Combat Sport. Martial Arts 2014, 5, 117–122. [Google Scholar] [CrossRef]
- Borysiuk, Z.; Piechota, K.; Minkiewicz, T. Analysis of performance of the fencing lunge with regard to the difficulty level of a technical-tactical task. J. Combat. Sport. Martial Arts 2013, 4, 135–139. [Google Scholar] [CrossRef][Green Version]
- Richter, C.; O’Reilly, M.; Delahunt, E. Machine learning in sports science: Challenges and opportunities. Sport. Biomech. 2021, 1–7. [Google Scholar] [CrossRef]
- Malawski, F. Depth versus inertial sensors in real-time sports analysis: A case study on fencing. IEEE Sens. J. 2020, 21, 5133–5142. [Google Scholar] [CrossRef]
- O’Reilly, M.A.; Whelan, D.F.; Ward, T.E.; Delahunt, E.; Caulfield, B. Classification of lunge biomechanics with multiple and individual inertial measurement units. Sport. Biomech. 2017, 16, 342–360. [Google Scholar] [CrossRef]
- Malawski, F.; Kwolek, B. Classification of basic footwork in fencing using accelerometer. In Proceedings of the 2016 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 21–23 September 2016; pp. 51–55. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fodor, I.K. A Survey of Dimension Reduction Techniques; Technical Report; Lawrence Livermore National Lab.: Livermore, CA, USA, 2002. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hinton, G.E. Connectionist learning procedures. In Machine Learning, Volume III; Elsevier: Amsterdam, The Netherlands, 1990; pp. 555–610. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. Encycl. Database Syst. 2009, 5, 532–538. [Google Scholar]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Zago, M.; Kleiner, A.F.R.; Federolf, P.A. Machine learning approaches to human movement analysis. Front. Bioeng. Biotechnol. 2021, 1573. [Google Scholar] [CrossRef]
- Hammes, F.; Hagg, A.; Asteroth, A.; Link, D. Artificial intelligence in elite sports—A narrative review of success stories and challenges. Front. Sport. Act. Living 2022, 4, 861466. [Google Scholar] [CrossRef]


| Variables | Novice | élite | Effect Size (ES) |
|---|---|---|---|
| Age (years) | 10.50 ± 3.14 | 0.72 (0.48, 0.97) | |
| BMI (kg/m) | 0.39 (0.09, 0.73) | ||
| W (kg) | 0.68 (0.48, 0.9) | ||
| H (m) | 0.75 (0.63, 0.9) | ||
| HGUARD (m) | 0.76 (0.63, 0.91) | ||
| LLL (cm) | 0.74 (0.61, 0.9) | ||
| CLL (cm) | 0.53 (0.26, 0.83) | ||
| CUL (cm) | 0.44 (0.12, 0.77) | ||
| Leq (cm) | 0.86 (0.77, 0.95) |
| Model | k | Accuracy | Average | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| MLP | 5 | 0.88 | macro | 0.87 | 0.88 | 0.88 |
| weighted | 0.88 | 0.88 | 0.88 | |||
| SVM | 10 | 0.84 | macro | 0.83 | 0.83 | 0.83 |
| weighted | 0.84 | 0.84 | 0.84 | |||
| MLP | 25 | 0.84 | macro | 0.83 | 0.83 | 0.83 |
| weighted | 0.84 | 0.84 | 0.84 | |||
| MLP | 50 | 0.92 | macro | 0.92 | 0.92 | 0.92 |
| weighted | 0.92 | 0.92 | 0.92 |
| Category | Precision | Recall | F1-Score |
|---|---|---|---|
| Novice (0) | |||
| élite (1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aresta, S.; Bortone, I.; Bottiglione, F.; Di Noia, T.; Di Sciascio, E.; Lofù, D.; Musci, M.; Narducci, F.; Pazienza, A.; Sardone, R.; et al. Combining Biomechanical Features and Machine Learning Approaches to Identify Fencers’ Levels for Training Support. Appl. Sci. 2022, 12, 12350. https://doi.org/10.3390/app122312350
Aresta S, Bortone I, Bottiglione F, Di Noia T, Di Sciascio E, Lofù D, Musci M, Narducci F, Pazienza A, Sardone R, et al. Combining Biomechanical Features and Machine Learning Approaches to Identify Fencers’ Levels for Training Support. Applied Sciences. 2022; 12(23):12350. https://doi.org/10.3390/app122312350
Chicago/Turabian StyleAresta, Simona, Ilaria Bortone, Francesco Bottiglione, Tommaso Di Noia, Eugenio Di Sciascio, Domenico Lofù, Mariapia Musci, Fedelucio Narducci, Andrea Pazienza, Rodolfo Sardone, and et al. 2022. "Combining Biomechanical Features and Machine Learning Approaches to Identify Fencers’ Levels for Training Support" Applied Sciences 12, no. 23: 12350. https://doi.org/10.3390/app122312350
APA StyleAresta, S., Bortone, I., Bottiglione, F., Di Noia, T., Di Sciascio, E., Lofù, D., Musci, M., Narducci, F., Pazienza, A., Sardone, R., & Sorino, P. (2022). Combining Biomechanical Features and Machine Learning Approaches to Identify Fencers’ Levels for Training Support. Applied Sciences, 12(23), 12350. https://doi.org/10.3390/app122312350







