New Construction Solutions of Gear Using in Space Vehicle Control Systems

Abstract

Outer space presents construction challenges that are completely different from the terrestrial environment. They should be characterized by high resilience and indefinite durability because there is no possibility of repair during exploitation. There are drives in spacecraft control systems that are necessary to move solar panels, robotic arms, and manipulators, and also to position antennas. In these devices, they have applications where harmonic drives are characterized by high kinematic accuracy but relatively low mechanical strength. The analysis presented in this study is aimed at modifying the shape of the harmonic drive to increase its durability and reliability. In this study, the most vulnerable damage element of the harmonic drive is the flexspline. The calculation was carried out using the finite element method (FEM) in the computer program ABAQUS. A standardized shape was tested as a basic model, and several other design solutions were proposed. For each of them, the mechanical strength was determined, which allowed the selection of the most preferred shape for the flexspline of the harmonic drive. The specific environmental requirements of the expectations for sand for gear used in spacecraft control systems were included in the analysis. The selected construction solutions of the flexspline allow for longer work and transfer of greater loads by the harmonic driver than the solutions currently used. The choice of harmonic driver design shape allows for failure-free and maintenance-free work in space vehicle control systems.

1. Introduction

In the set and control layouts of space vehicles and air plants, high precision of action is important. Each small setting error conjugated with flight speed may cause significant deviations from the designated trajectory. Moreover, the appropriate communication antenna and solar panels need to be highly accurate and often need corrections of their settings [1,2,3,4]. Operating in outer space cannot allow for unforced breakdowns in the operation of research and measurement instruments because there exist communication problems with their corrections.

As a drive of the control system of a space vehicle, but also in a drive of vehicles, they can work perfectly well with harmonic drives. Their key advantage is high kinematic accuracy and, therefore, under earthly conditions, are used in robots and manipulators, measuring devices, or regulation and control systems, e.g., numerically controlled machine tools [5,6,7]. Standardized construction-toothed wave gears also have applications in devices during subsequent Mars missions, for example, in landing gear opening mechanisms and manipulator arms [8], Mars rover drive [9], or in antenna control and stabilization systems [10]. It is clear that the possibility of using toothed wave gears is not limited to Mars missions, and it is necessary to look for future and more urgent applications [11,12,13]. Research and development work on changes in wave gear design is still in progress [14]; an important focus is improving their kinematic accuracy [15] to extend the possibilities of their use in space devices. Many research centers carry out projects to improve the durability of wave gears by selecting appropriate lubrication [16,17] or using new materials [18].

In view of the high transport costs and negligible service options, outer-space-bound devices must be characterized by high durability and reliability, which is often the main construction problem. Mechanical drives used under earth conditions are not exposed to extremely low temperatures or still contamination by very fine dust. It can also be periodically cleaned, lubricated, and preserved, which cannot be done in outer space. The Sojourner rover from the Mars Pathfinder mission ran for two and a half months, which, from today’s perspective, is a short period of operation. Therefore, controlled drives in currently designed space vehicles should have greater durability to allow their application in future, more challenging space missions.

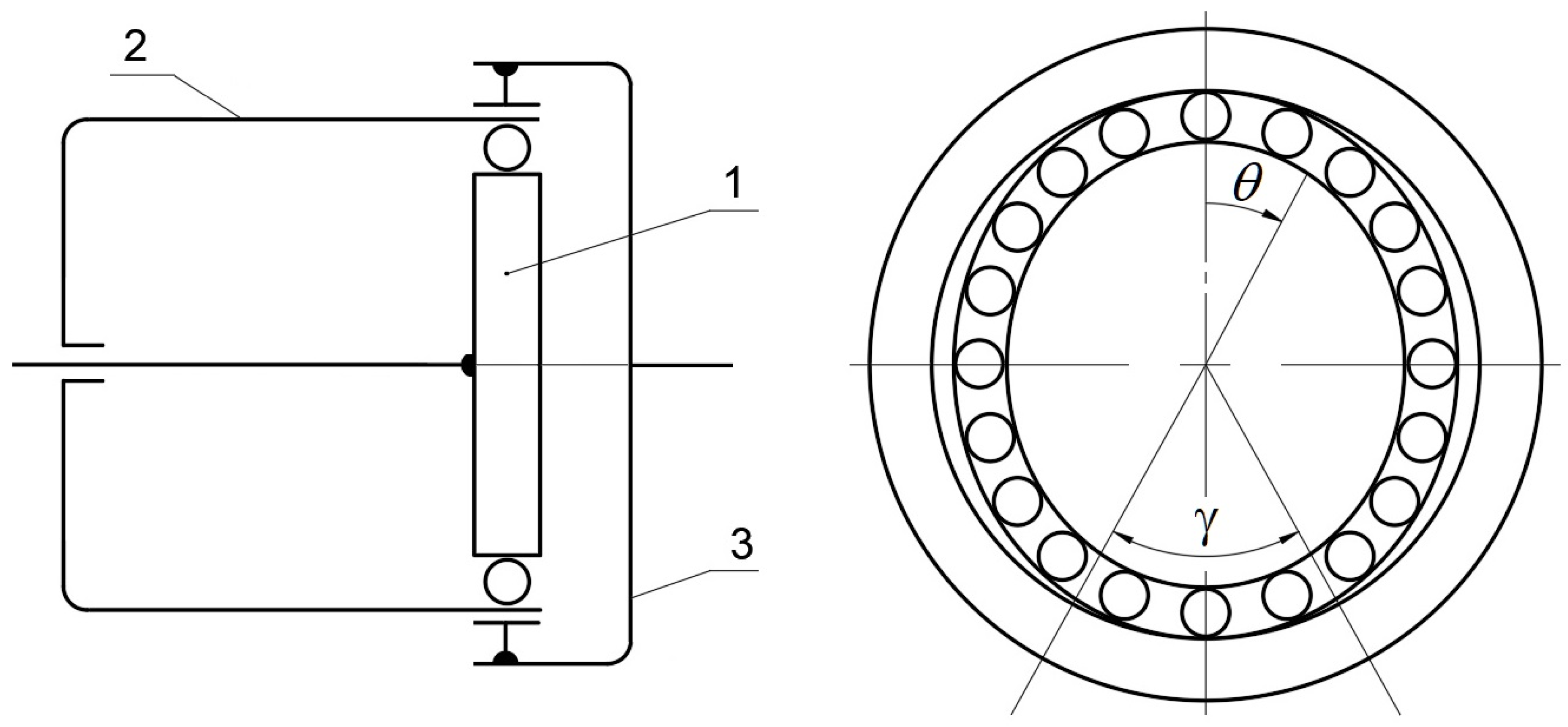
One of the drives used in space vehicle control systems are harmonic drives. They are a unique type of gear transmission, not only in view of characteristic constructions but also regarding the special schemes of transferring loads. The unique character of harmonic drives is based on the relative movement of the mating gears as a result of the elastic deformation of one of them. The main components of the harmonic drive are shown in Figure 1, and include the flexspline (1), circular spline (2), and wave generator (3). The generator deforms the toothed wheel rim of the flexspline into an ellipse, and then it engages with the circular spline in the mating areas (4); limited by angle γ in the large axes (Y) of the harmonic drive, the teeth of both gears are in contact, while in the small axes (X), the teeth of these gears pass each other [19,20,21]. Typically, the driving element of the gearbox is a wave generator, and the driven element can be both a flexspline and a circular spline. During the transmission operation, the rotating generator causes the deformation waves to move along the circumference of the flexspline, transferring the motion to the mating circular spline. For most harmonic drives, the load is simultaneously carried by 20–50% of the total number of teeth of the flexspline [22,23]. Its exceptional way of working the wave gear allows one to achieve a very large gear ratio, usually to a single degree, from 40:1 to 100:1 and, in some cases, even 300:1 [24,25]. Hence, one of the most important advantages of toothed wave gears is their high kinematic accuracy. A disadvantage of wave gears is their manufacturing difficulties, especially concerning the flexspline, which requires special equipment during processing. Moreover, the very small modules used in these types of gears can be a problem when performing them using traditional methods. The basic problem of harmonic drives is their durability, which is based on the fact that endurance is the most loaded element, hence the flexspline. Computational and experimental work has been performed for years to increase the durability of harmonic drives by changing the design of flexsplines or using new materials.

The vast majority of research so far has referred to typical harmonic drives with the flexspline with bottom and collar [26,27,28,29]. The geometric parameters of the constructions encountered most often are presented in Figure 2. These gears are long parts with a toothed rim on one side and a bottom or flange on the other side. The harmonic drive has a standard shape of the thin-walled sleeve, and a slightly thicker bottom or collar is used to fix it to the shaft or body (Figure 2a). The classical bodies can have external (Figure 2b) or internal (Figure 2c) flanges. Their overall dimensions, especially the overall length (L), are significant relative to the width of the toothed wheel rim.

Introducing new drives with such complicated construction and principles of operation must be preceded by a cautious analysis of the initial stages of design.

The standard shapes of the flexspline of the harmonic drives shown in Figure 2 are solutions based on the cylindrical sleeve. The chamfers or rounding introduced are small, resulting from technological limitations that occur when making wheels using traditional processing methods. In a classical flexspline, the flat bottom stiffens the structure, causing high stress levels in the sleeve, which directly results in its destruction. Therefore, there is still the need for new construction and material solutions [20,30] which will allow lowering the maximum stress values in this element by changing the shape of its body. However, only contemporary production possibilities, including numerically controlled machines (CNC) or incremental methods, can handle many restrictions in this range and allow one to make a flexspline with an unprecedented shape. The aim of the presented analysis is to fix the shape of the flexspline to improve it in terms of its durability and reliability. During the design of flexsplines intended for application in precise control and regulation of space vehicles, it is necessary to pay attention to maintaining their high kinematic accuracy and reliability that allow for working in space.

Hence, an attempt was made to establish the best shape of the flexspline which would improve the durability of the harmonic drive considering the lack of possibility of servicing it over a long period of time.

To accomplish this research task, over a dozen construction variants were designed and researched, from which a few of the characteristics are presented in the next part of this study.

2. Materials and Methods

The shape of the flexible was modified bearing in mind that it has a considerable length (L); therefore, attempts were made to reduce it. During the search for the most favourable solutions, the values of the radius (R₂) at the bottom and the flange were also changed. In the Siemens NX computer program, many models of flexsplines with different body shapes were developed. All tested structures had the same parameters for the rim of the toothed wheel. In the analysis presented, only a few of the most characteristic design solutions were taken into account, allowing coherent and constructive conclusions to be drawn.

A strength analysis of the harmonic drives was done in the Abaqus program using the finite element method (FEM). In numerical calculations using FEM, the spatial model of a harmonic drive with a cam generator was used to guarantee the most thorough inspection of the form of deformation of the flexspline. The geometrical parameters of the gear were previously designated by the created calculation sheet. The analysis showed that the harmonic drive is a double wave with the number of flexspline teeth equal to 198, while the circular spine has two or more teeth. The modulus is equal to 0.76 mm, so the pitch diameter has the value d₁ = 150.4 mm. The harmonic drive moves the power N = 1.1 [kW], and its gear ratio is equal to u = 100.

The form of neutral layer deformation of the flexspline has a significant impact on the accuracy of the gear and correctness of tooth engagement in the meshing area. Wave gear elements also transmit a torsional moment, which directly influences stresses in the flexspline. By the wave generator, the flexspline not only deforms radially with respect to its center of rotation, but also turns [20,21]. In view of the above, numerical strength calculations include the fact that the flexspline works under complex load conditions and its elastic deformation is large.

During the FEM analysis of the impact of the sleeve shape on the flexspline strength, particular attention was paid to mapping real work conditions and gear loads. Used in calculations, the Abaqus program is an advanced calculation tool, so it is possible to exact the definition of material strength properties, contact conditions, cooperation parts of harmonic drive, and the impact of external factors. Because a very large amount of output data was gathered as a result of the calculations, it was necessary to filter and analyze in the postprocessor of the Abaqus program to show conclusions from the research in a clear and precise way.

To determine the impact and shape of the flexspline on its strength, spatial models of harmonic drives were used. However, in view of the large number of finite elements necessary for discretization, it is advisable to introduce some limitations. Due to the symmetry of deformation and load, only partial models of the transmission elements were used. The circular spline, flexspline, and cam wave generator were cut and left only for half of the models, which were limited by a minor generator axis (Figure 3). Furthermore, it was designed for most rounds, holes, or chamfers, which would affect increasing the number of finite elements necessary for the description of geometry. These actions allow for a significant speeding up of the calculation time, which is important with a large number of solutions, but do not have an impact on the accuracy of the results obtained.

Ultimately, all calculation models were subjected to a discretization process mainly by means of hexahedral square elements (hexagonal 20 node quadratic brick—C3D20R), which in the models were from 250,000 (variant 2) to more than 2,700,000 depending on the analyzed case. A constant size of finite elements has been imposed on the body of the flexspline for all calculation variants, and hence a different number of them results when discretized for different shapes of the flexspline. For all calculation variants on the toothed wheel, the rim forced a higher density of finite element mesh. However, on the rim of the toothed wheel, for all calculation variants, both the size and arrangement of mesh elements were the same. Between cooperating models, a contact of type surface-to-surface and friction conditions fine sliding was defined. It was assumed that all elements are made of steel for which the Young’s modulus is equal to E = 2.1 × 10⁵ MPa, and the Poisson ratio ν = 0.3. Calculations included an elastic range of materials according to Hooke’s law and inclusion of the non-linear effect of large displacements.

Figure 3 shows a simplified model of wave gear with a cam wave generator, which was used for the FEM calculation in the Abaqus program. In this model, the division edge of models lying on the major axis of the generator is visible, and it was created for easier processing of results and flexspline deformation control marked as 1.

The figure also presents the enlarged fragment of the tooth wheel rim to show a way of preparing models to include a contact of models. The sides of the flexspline were defined as the master surface and the mating surfaces of the rigid wheel teeth were defined as the slave. Contact surfaces between the flexspline and the generator were also defined. In calculations, the load of harmonic drive of torque about value T = 200 Nm was simulated on the stiff wheel. It was achieved by using reference points (RP), which were placed in the axis of the stiff wheel, and then their position was blocked. Then, this point was associated with the outer surface of the stiff wheel by using rigid links and assigned a torque load.

The model after the discretization process is shown in Figure 4. To maintain the real nature of the work, some parts of the model were deprived of some degree of freedom. The nodes lying in a longitudinal section plane (marked in Figure 3 by symbol 1) were allowed to move only in the XZ plane. However, the nodes at the bottom of the flexspline (marked in Figure 2 the by symbol 2) were fixed. The Y in the prepared calculation model correspond to the Y of the major wave generator axis, while the other Y corresponds to the X of the minor axis. The applied limitations and simplifications of the geometry do not reflect the precise load conditions because the torque is not symmetric with respect to the plane of model division. Half of the harmonic drive on one side of the plane containing the minor axis and normal to the major axis was assumed for the calculations. However, based on previous research [31,32,33], it was assumed that the distribution and values of stress in the body of the flexspline depend mainly on its deformation. In addition, the same boundary conditions were adopted in all models, and the obtained results should only allow us to reject erroneous constructions and for future more detailed research to select the most favourable shape of the flexspline. Displacements (3) of the generator model with respect to the main value equal to the deformation w₀ = 0.84 [mm] were limited only to the direction of the Y-axis. The contact surfaces were defined between the flexspline and the flexspline wave generator, so the model was precisely deformed to the proper form for the cam generator.

The defined assumptions were repeated in all calculation causes including different variants of the flexspline. Dimensions and boundary conditions for the other two parts of the harmonic drive were constants in all subsequent calculation cases for the prepared models. This way, several results were obtained which served as the basis for the analysis of the impact of the shape of the flexspline body on its strength.

3. Results

The results for stresses obtained for many analyzed construction solutions differed considerably from each other. Many of the researched shapes of the flexspline turned out to be completely useless because of their little durability. Therefore, they were considered inappropriate for application in space vehicles and they were not included as part of the analysis. Therefore, only the most characteristic cases were presented, for which key information was obtained. Using this as a basis, a new shape for the flexspline body was designed.

Table 1. Shapes of flexsplines used in the next part of the calculation.

No.	Sleeve Shape Diagram	Parameters to Be Changed
Variant I		L = 150 mm R2 = 5 mm dw = 150 mm
Variant II		L = 75 mm R2 = 5 mm dw = 150 mm
Variant III		L = 150 mm R2 = 35 mm dw = 150 mm
Variant IV		L = 75 mm R2 = 35 mm dw = 150 mm
Variant V		L = 150 mm R2 = 5 mm dw = 150 mm dz = 200 mm
Variant VI		L = 150 mm R2 = 5 mm dw = 150 mm dz = 200 mm
Variant VII		L = 150 mm a = 35 mm b = 105 mm dw = 150 mm
Variant VIII		L = 75 mm a = 15 mm b = 30 mm dw = 150 mm dz = 200 mm
Variant IX		L = 75 mm a = 35 mm b = 30 mm dw = 150 mm
Variant X		L = 115 mm a = 35 mm b = 70 mm dw = 150 mm

shows figures of model shapes of the flexspline considered in the next steps of calculation. It also includes the values of the most important geometric parameters, which were changed in the next variant of the flexspline.

The results of the numerical calculations obtained using FEM in the program for the model in the flexspline in basis variant (variant I) are presented in Figure 5. The distribution of stresses in the flexspline is an effect of its deformation by the wave generator. The basic variant of the flexspline has dimensions similar to the standard construction offered by leading manufacturers of harmonic drives [30,34]. The flexspline in variant I has a total length equal to L = 150 [mm], which is comparable to the pitch diameter.

The length L was the main parameter modified in the next calculation variants for the flexspline. An important geometric parameter assumed based on variant I was the fillet radius at the bottom equal to R₂ = 5 [mm]. The highest stress values occurred directly near the wave generator, in its major and minor axes. The stress level is not high and confirms the correctness of such a structure. However, it is clear that increased stress values occurred in areas of the toothed wheel rim, but are low in other parts of the wheel. Therefore, the cylindrical sleeve of the flexspline was shortened by about half, and this solution was marked as variant II. The length of the shortened flexspline was equal to L = 75 [mm] and was significantly affected by the reduction in the size of the total harmonic drive. After the calculations, the results obtained indicate a large increase in the maximum stress values in the body. Especially dangerous accumulation of stresses occurred on the main axis of the flexspline (Figure 6). This design solution is not appropriate, as it would result in very quick damage to the compliant wheel in this area. Except for the toothed wheel rim, increased stress also occurred with the radius of transition from the cylindrical part to the bottom of the flexspline.

To reduce the shape impact of the change in the bottom area of the flexspline with stresses in its body, the next calculation variants were proposed with the following names: variant III and variant IV. These solutions are based on previously analyzed constructions of the flexspline (variants I and II). Only the radius value between the cylindrical body and the flat bottom was changed. When modeling the flexspline in variant III and variant IV, the maximum possible value of this radius was assumed to be R₂ = 35 [mm]. The results on the distribution of the stresses in the flexspline model with a large radius between the bottom and the body are shown in Figure 7 and Figure 8.

In the case of the long model (variant III), this change did not bring significant benefits. The short solution (variant IV) was considered to be more correct owing to the values of the stresses at the radius R₂. The maximum stress values in the rim area have increased slightly compared with variant III, due to the greater stiffness of this solution. The previous results of the calculations showed that excessive shortening of the body is not favourable for the durability of the gear wheel and such a solution should be rejected. Changing the radius at the bottom of the flexspline has resulted in a lower stress in this area, so further changes should take place in this area.

The literature contains theoretical descriptions of other flexspline design solutions with a shape significantly different from the classical one [20,35]. Some of them, instead of being cup-shaped, have a flange located outside the body of the compliant wheel. Therefore, for this model, a strength analysis was carried out considering the possibility of its application in spacecraft. One of the expected solutions is the construction of dimensions reduced to relatively standardized; therefore, for the next computational models (variant V and variant IV), the less assumed about the length of the flexspline was reduced by half, which is L = 75 [mm], for the two constructions with an assumed value of the fillet radius of R₂ = 5 [mm]. Figure 9 shows the shortened length results obtained for the flexspline model in variant V. The highest stress values were on the radius between the cylindrical body and the flexspline flange. In the next VI variant shown in Figure 10, the flexspline corpus changed from cylindrical to conical. However, this modification of the shape did not have any beneficial effects. Due to the modification of the structure and the use of a small fillet radius, the highest stress values were obtained in this solution.

After these trials, the length of the model is too small because the total length, which is half of the pitch diameter, does not guarantee the required strength.

Based on the results obtained for the previously presented computation variants, it was concluded that the desired state of stress occurs in situations where the body has the shape of a thin-walled cylindrical sleeve in places near the toothed wheel rim. On the other hand, the transition to the collar or bottom is achieved on an arc with the largest possible radius. A combination of these requirements provided the answer that the shape that can best meet expectations would be a quarter of an ellipse, limited by its major and minor axes. The large axis of the ellipse will be parallel to the axis of the flexspline and would decide its total length.

The radially directed minor axis has a length limited by the inside diameter (d_w) of the flexspline with a bottom and the diameter of the thickening of the bottom (d₂), which are used to fix the flexspline to the case. For the wheel with the outer flange, the minor axis would have length limits based on the outer diameter (d_z) of the flexspline.

This new shape of the body was used to model the harmonic drive at the bottom (variant VII) and the outer flange (variant VIII). In these models, we assumed the total length of the flexspline as in the basic solution (variant I), so L = 150 [mm]. The results of the numerical calculations using FEM for the proposed constructions are presented in Figure 11 and Figure 12, as appropriate for variants VII and VIII. For both constructions, we obtained satisfying low-stress values on the flexspline model. However, also in this case, the flexspline with an outer flange has a more unfavourable stress distribution, so it is not recommended in constructions with high demands for durability and reliability.

According to the initial assumption, an attempt was made to shorten the flexspline. Therefore, the construction in variant IX was modeled, where the length L was reduced by half. However, the stress distributions obtained for this model (shown in Figure 13) did not allow for this solution to be correct. The area of dangerously high stress values near the rim of the toothed wheel and the major axis of the generator makes a risk of damaging the flexspline during exploitation. Ultimately, a solution was decided in which the length of the flexspline was equal to L = 115 [mm]. Such a shortening allowed us to reduce the dimensions of the harmonic drive by about a quarter of its initial length. This final solution was marked as variant X, and, like the previous ones, it was subjected to FEM numerical analysis in the Abaqus program. The results of the calculations, in the form of the stress distribution on the surface of the flexspline, are shown in Figure 14. The maximum stress values observed near the toothed rim are equal to 340.78 [MPA], which do not exceed the limit values for the assumed wheel material (30HGSA).

In other areas of the flexspline, for example, at the bottom, the stress values are also on a safe level and are below 100 [MPa]. It can be assumed that the construction of the flexspline proposed in variant X is the right solution and can be the basis for future research. Stress values indicate that the structural safety factor of the analyzed flexspline is high and allows it to be used in devices requiring long-term and failure-free operation.

Figure 15 shows a new shape of the flexspline, which was proposed based on the conclusions of the FEM analysis for many different construction variants. The recommended values of the geometric parameters for which a flexspline with a more compact structure and a strength comparable to that in classic constructions can be obtained are given in

Table 2. Main geometric parameters for the new shape of flexspline (variant X), where: z₁ = 198, m₁ = 0.76, $2{\mathrm{h}}_{\mathrm{a}}^{*}$—tooth head height factor, ${\mathrm{c}}^{*}$—tip clearance factor.

Parametr	Range
${\mathrm{d}}_1$	${\mathrm{z}}_1·{\mathrm{m}}_1$
${\mathrm{d}}_{\mathrm{f}1}$	${\mathrm{m}}_1·({\mathrm{z}}_1-2{\mathrm{h}}_{\mathrm{a}}^{*}-2{\mathrm{c}}^{*})$
${\mathrm{d}}_{\mathrm{w}}$	${\mathrm{d}}_{\mathrm{f}1}-2·{\mathrm{h}}_1$
${\mathrm{d}}_2$	$\le 0.6{\mathrm{d}}_1$
${\mathrm{h}}_1$	$\left(0.005÷0.015\right)·{\mathrm{d}}_1$
${\mathrm{h}}_2$	$\left(0.5÷0.85\right)·{\mathrm{h}}_1$
${\mathrm{h}}_3$	$\left(2÷3\right)·{\mathrm{h}}_1$
${\mathsf{\beta }}_{\mathrm{b}}$	$\left(45°÷60°\right)$
${\mathrm{R}}_1$	$\left(10÷20\right)·\mathrm{m}$
${\mathrm{R}}_2$	$\left(2÷3\right)·{\mathrm{h}}_2$
${\mathrm{b}}_{\mathrm{w}}$	$\left(0.1÷0.3\right)·{\mathrm{d}}_1$
${\mathrm{a}}_{\mathrm{w}}$	$\left(0.15÷0.25\right)·{\mathrm{b}}_{\mathrm{w}}$
L	$\left(0.7÷1.2\right)·{\mathrm{d}}_1$
${\mathrm{L}}_{\mathrm{c}}$	$\mathrm{L}+{\mathrm{h}}_3$
a	$\mathrm{L}-({\mathrm{b}}_{\mathrm{w}}+ {\mathrm{a}}_{\mathrm{w}}+{\mathrm{R}}_1$)
b	$0.5·\left({\mathrm{d}}_{\mathrm{w}}-{\mathrm{d}}_2\right)$
${\mathrm{O}}_{\mathrm{a}}$	${\mathrm{b}}_{\mathrm{w}}+{\mathrm{a}}_{\mathrm{w}}+{\mathrm{R}}_1$
${\mathrm{O}}_{\mathrm{b}}$	$0.5·\left({\mathrm{d}}_{\mathrm{w}}-\mathrm{b}\right)$

. The proposed elliptical shape of the flexspline body has the advantages of solutions requiring a long body and reduces the probability of breakage to the radius near the bottom.

To perform a quantitative analysis, the stresses σ_z in the longitudinal sections were determined through the major axis of the generator for the ten construction variants of the flexspline. The compared diagrams will help to assess the impact of individual design solutions on the stress level in the analyzed models. Figure 16 shows the diagrams for selected variants of the flexspline with a standard length L = 150 [mm], while Figure 17 shows solutions for a few characteristic models with reduced lengths. Both diagrams show the results for variant X, which was positively evaluated and recommended for future exploration. Most of the models of the flexspline made in long variants have a similar nature of stress diagrams in the plane passing through the major axis of the wave generator. For the proposed variant X, the maximum stress values near the tooth wheel were slightly higher than those of other solutions analyzed. However, they did not differ significantly from them; it is necessary to keep in mind that this is a solution with a reduced length. The base model (variant I) had the lowest stress values in the rim of the area of the tooth wheel rim. Therefore, if the external dimensions are not decisive for the wave gear, this proven solution should definitely be used.

Figure 17 is a set of the results of stresses on the major axis of models deformed by the cam generator for selected short variants of flexsplines. Maximum stress levels for these constructions are significantly higher than the results obtained for standard length models (Figure 16). This is the result of a design with significantly fewer flexsplines, directly increasing the flexural stiffness of the body.

The most unfavorable stress distribution occurred in variant V because areas of very high stress also occurred in the transition from the sleeve body to its outer flange. In the variant X given for the stress comparison, the values in both the rim and bottom of the flexspline were much lower than in the other constructions.

All stress diagrams shown in Figure 16 and Figure 17 have the highest stress values at the transition radius from the toothed wheel rim to the flexspline body. It is caused by the unsymmetrical pressure of the wave generator on the internal diameter of the flexspline, resulting from the rigidity of the wheel body on one bottom. On the opposite side of the toothed rim, the stresses are lower because they result only from deformations of the flexspline.

The generator edge effect only occurs in compliant flexsplines with a bottom or flange, and its impact decreases with increasing length.

4. Discussion

The analysis of the flexspline body shape allowed one to assess the possibility of reducing the dimensions of harmonic drives without limiting their strength.

Multiple studies of different construction variants allowed us to draw conclusions that are useful for future research. Our search for the new corpus shape of the flexspline was aimed at reducing its length. However, as shown in the results on stress distribution in FEM calculations, too short a flexspline body causes a transgression of its strength and could lead to its eventual damage. Additionally, in harmonic drives with short flexsplines, problems with the accuracy of the wheels in the mesh area may occur. Flexsplines with an outer flange have lower strength for the same length as cup-type models. The sleeve body of the flexsplines must be able to deform during operation, but the flange stiffens the structure, causing a significant increase in the stress value.

During the determination of the geometric parameters of the toothed wheel rim, it is necessary to avoid solutions in which there exists the possibility of stress concentrations occurring, for example, small rounding radii or sharp changes in body thickness.

Note that the stresses are not distributed symmetrically on the rim of the toothed wheel. They are much higher on the bottom side than on the free end of the flexspline. This nature has already been pointed out in previous studies [36,37], and solutions have been proposed, for example, in the form of intermediate rings to improve the cooperation between the flexspline and the wave generator [19,38]. The starting point for the analysis was a flexspline with a bottom modeled with commercial solutions (variant I). This model obtained a uniform stress distribution, and its level was not too high. Therefore, large dimensions of the gears are not a problem, and this solution can be used successfully.

However, there are often limitations concerning the size and weight of toothed wave gears, as these devices are launched into space. Therefore, as a result of the analysis, a new type of flexspline (variant X) was proposed.

This solution allows for shortening the flexspline by about 25% from the starting solution. In the modified construction, correct stress distribution was achieved without threat of destruction in strategic places for the strength of the flexspline. The maximum stress values after deformation of the flexspline occurred in the area of the toothed rim, but they are at a safe level, lower than the allowable stress.

The proposed design solution in terms of the shape of the flexspline body extends the scope of their application, while maintaining all the unique advantages of the wave gear, such as kinematic accuracy or the possibility of transferring heavy loads. The new shape of the flexspline is characterized by high mechanical strength and durability, and the reduced dimensions mean that it can be used successfully in the drive of space vehicles.