Laser Generated Broadband Rayleigh Waveform Evolution for Metal Additive Manufacturing Process Monitoring
Abstract
Featured Application
Abstract
1. Introduction
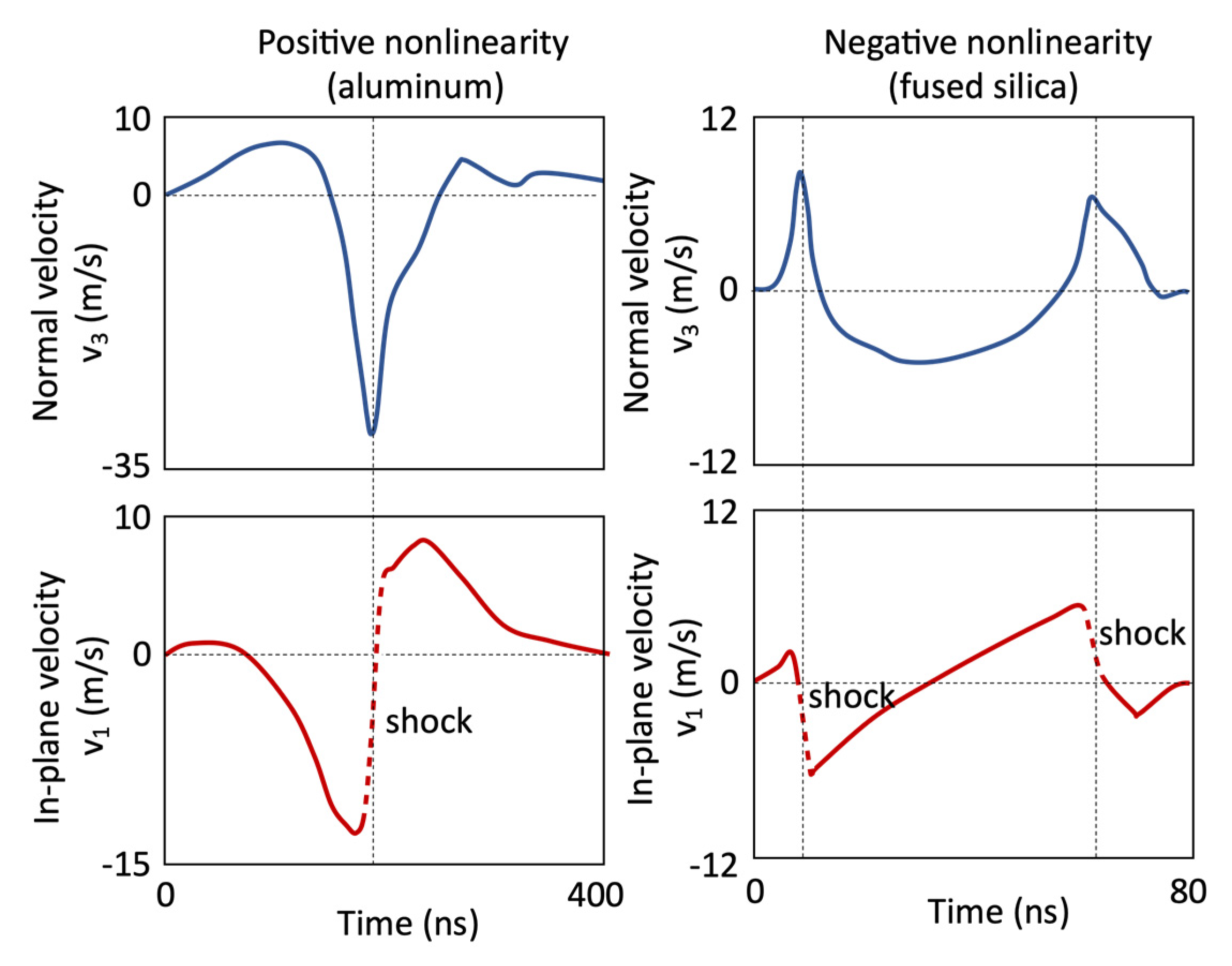
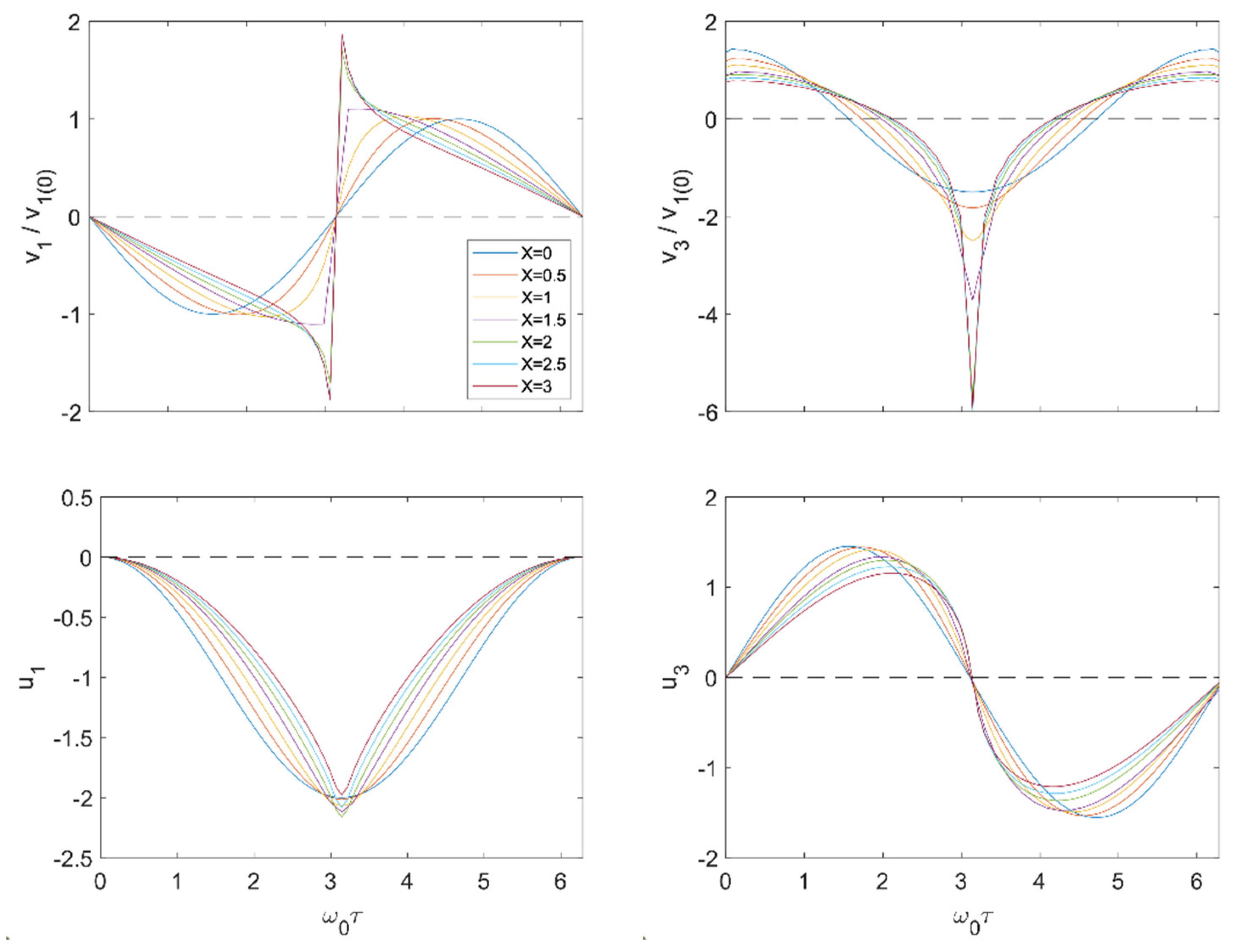
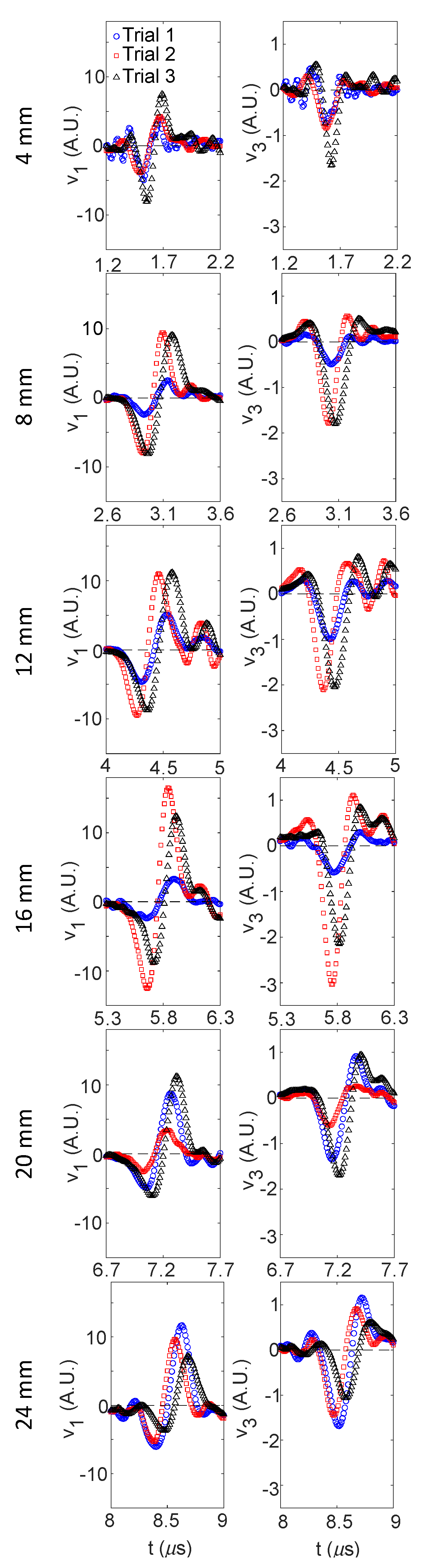
1.1. Laser Generated Finite Amlitude Rayleigh Waves
- (1)
- for materials having a ‘positive nonlinearity’ the shock front in the v1 waveform corresponds with a negative spike-like pulse in the v3 waveform that narrows with increasing amplitude with propagation,
- (2)
- for materials having a ‘negative nonlinearity’ shock fronts in the v1 waveform form at the leading and trailing edges, which correspond to two positive peaks in the v3 waveform that are separating as the valley between them expands with propagation.
1.2. Additive Manufacturing Process Monitoring
- the act of monitoring should not impede the manufacturing process;
- detection of both flaws and micro/mesostructure variations that affect mechanical properties are important;
- the surface of the deposited material is rough.
2. Materials and Methods
3. Results
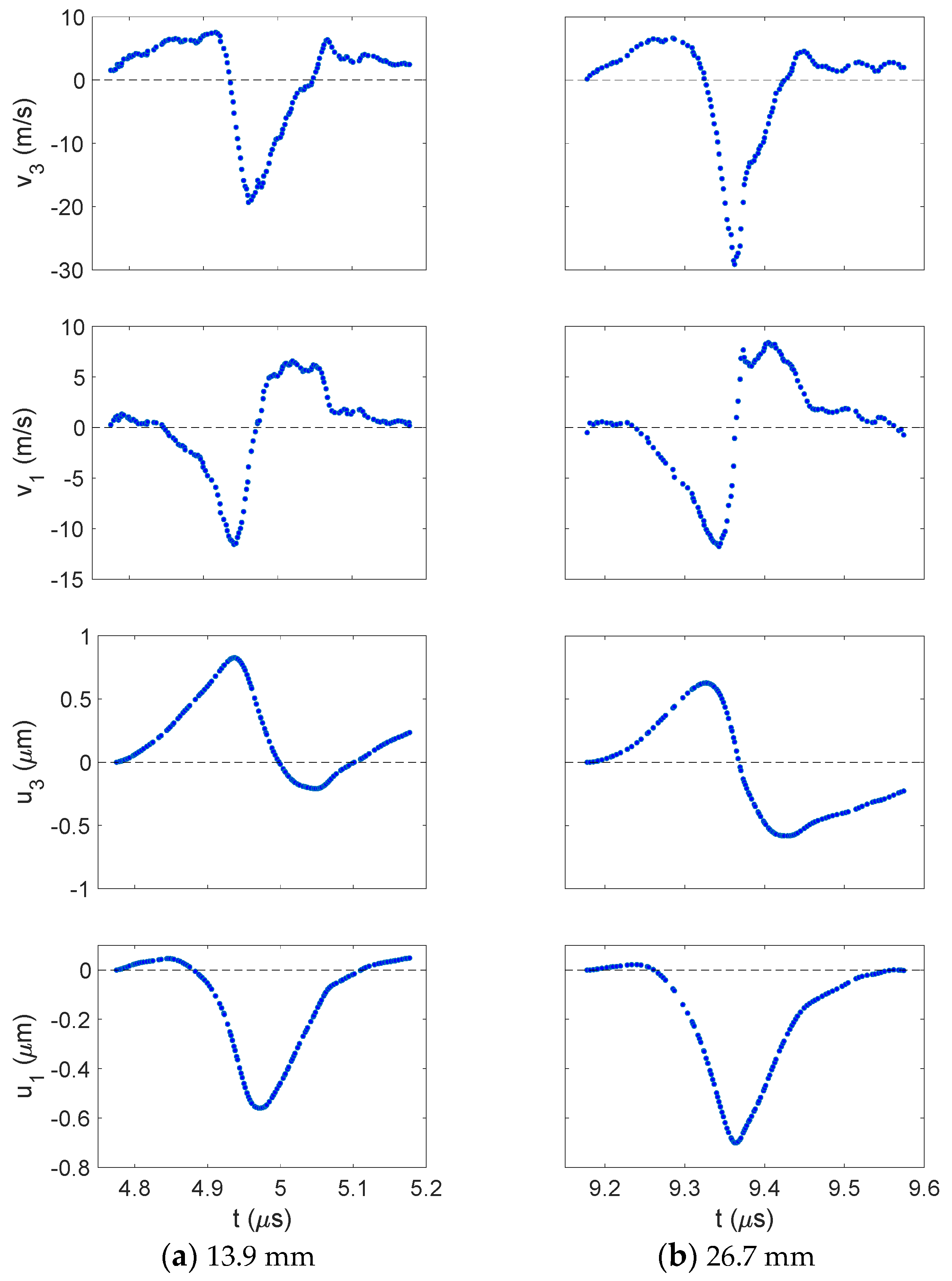
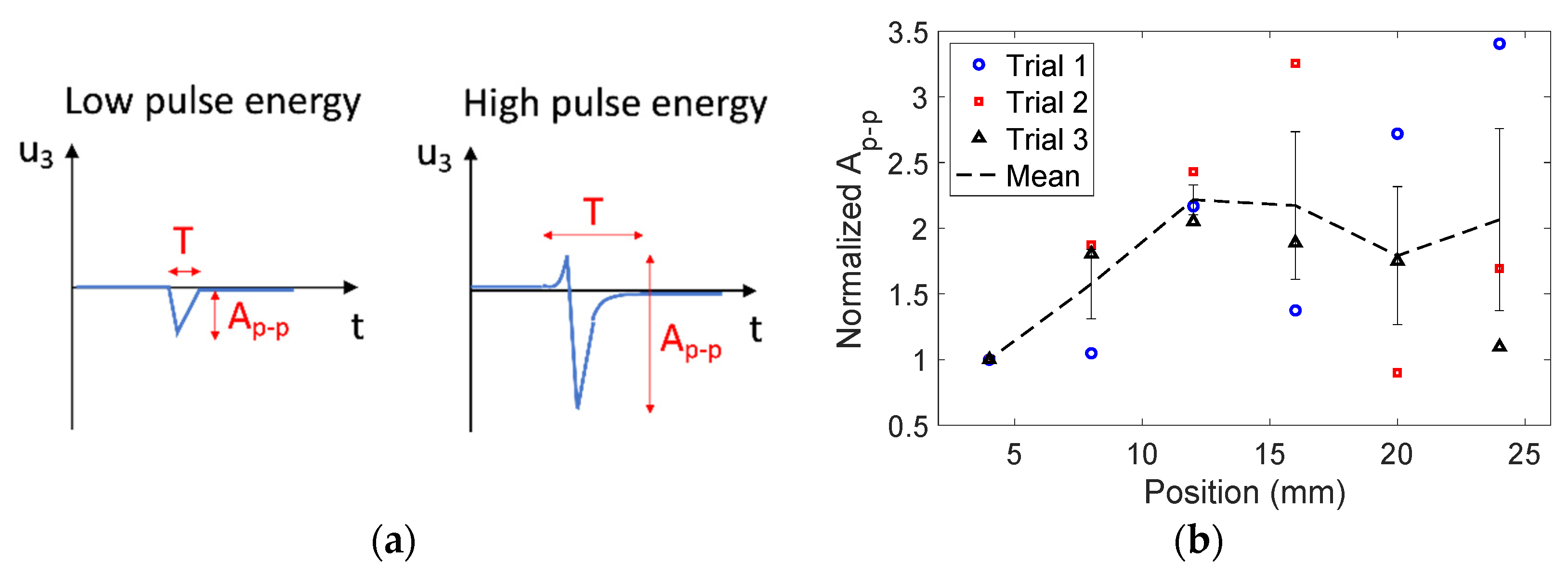
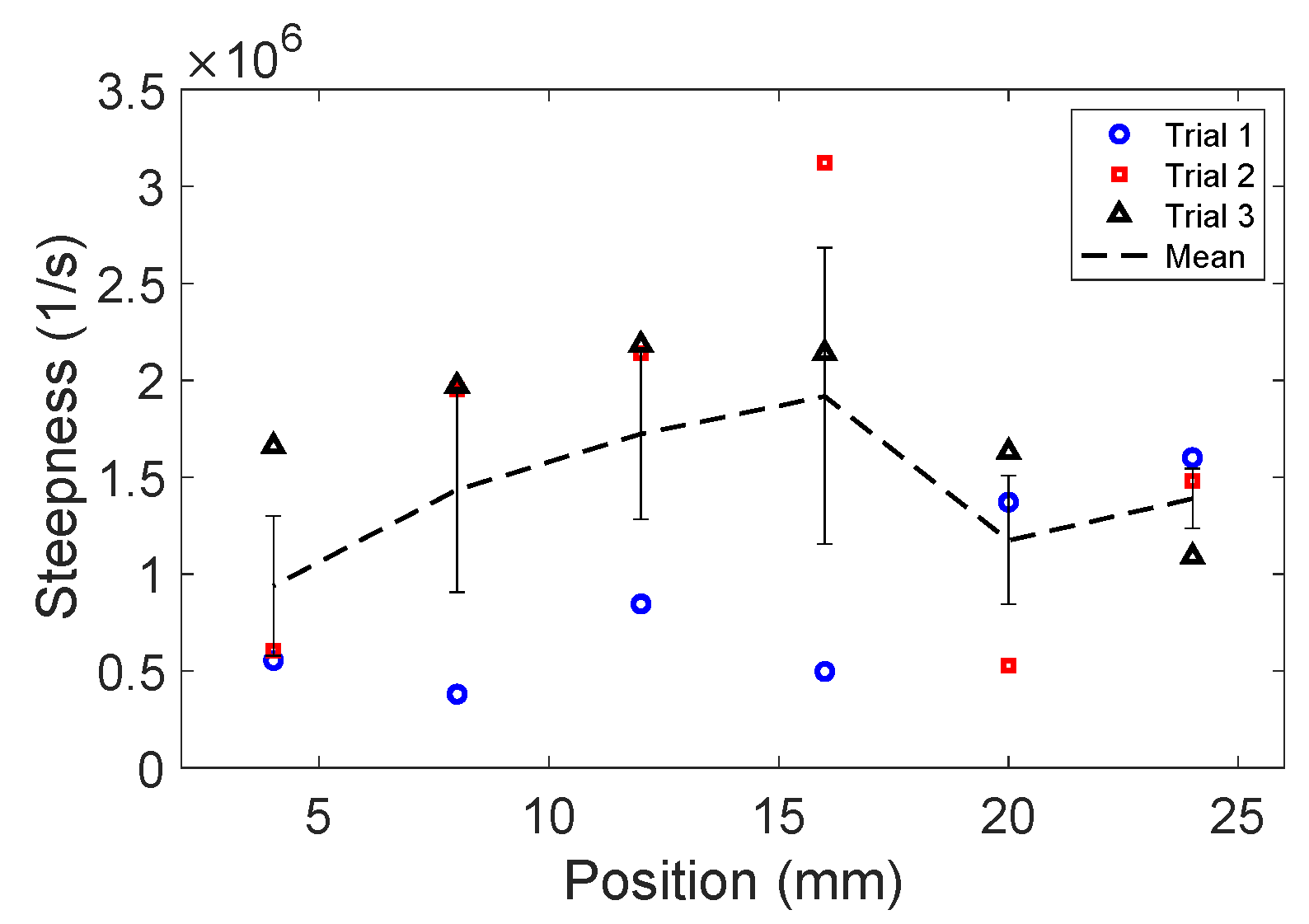
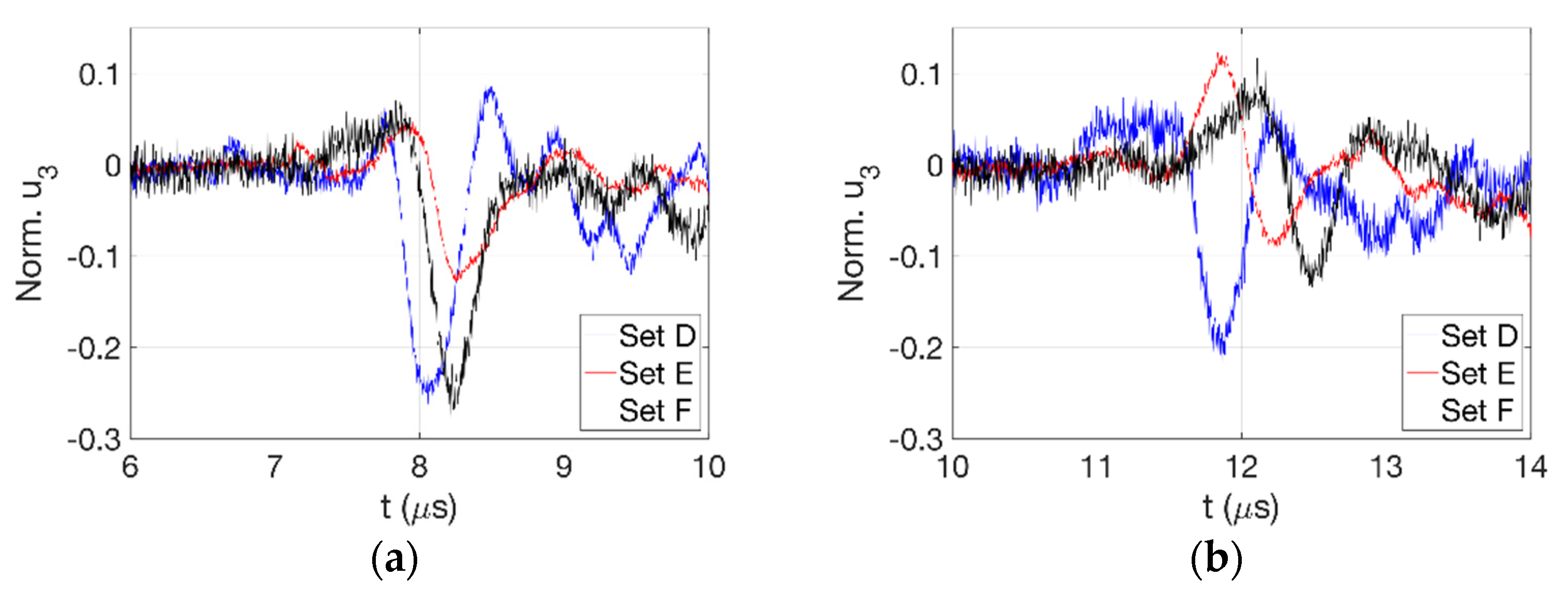
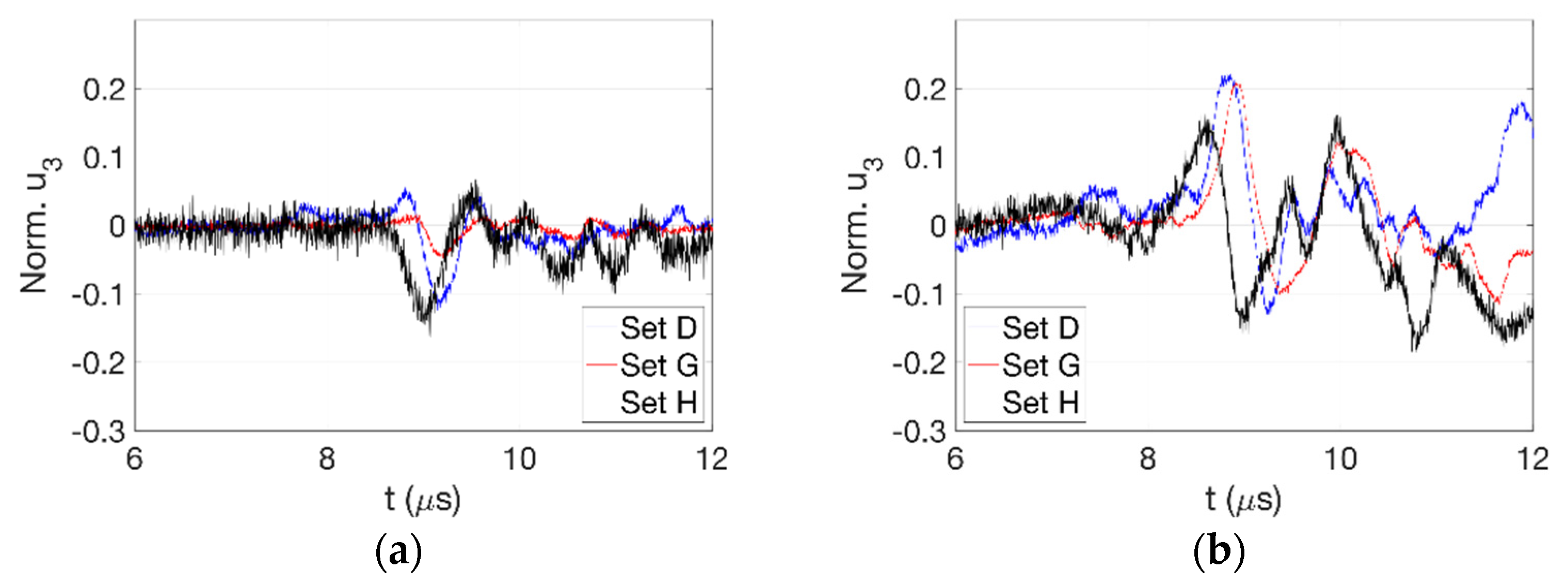
3.1. Detected Waveform Evolution
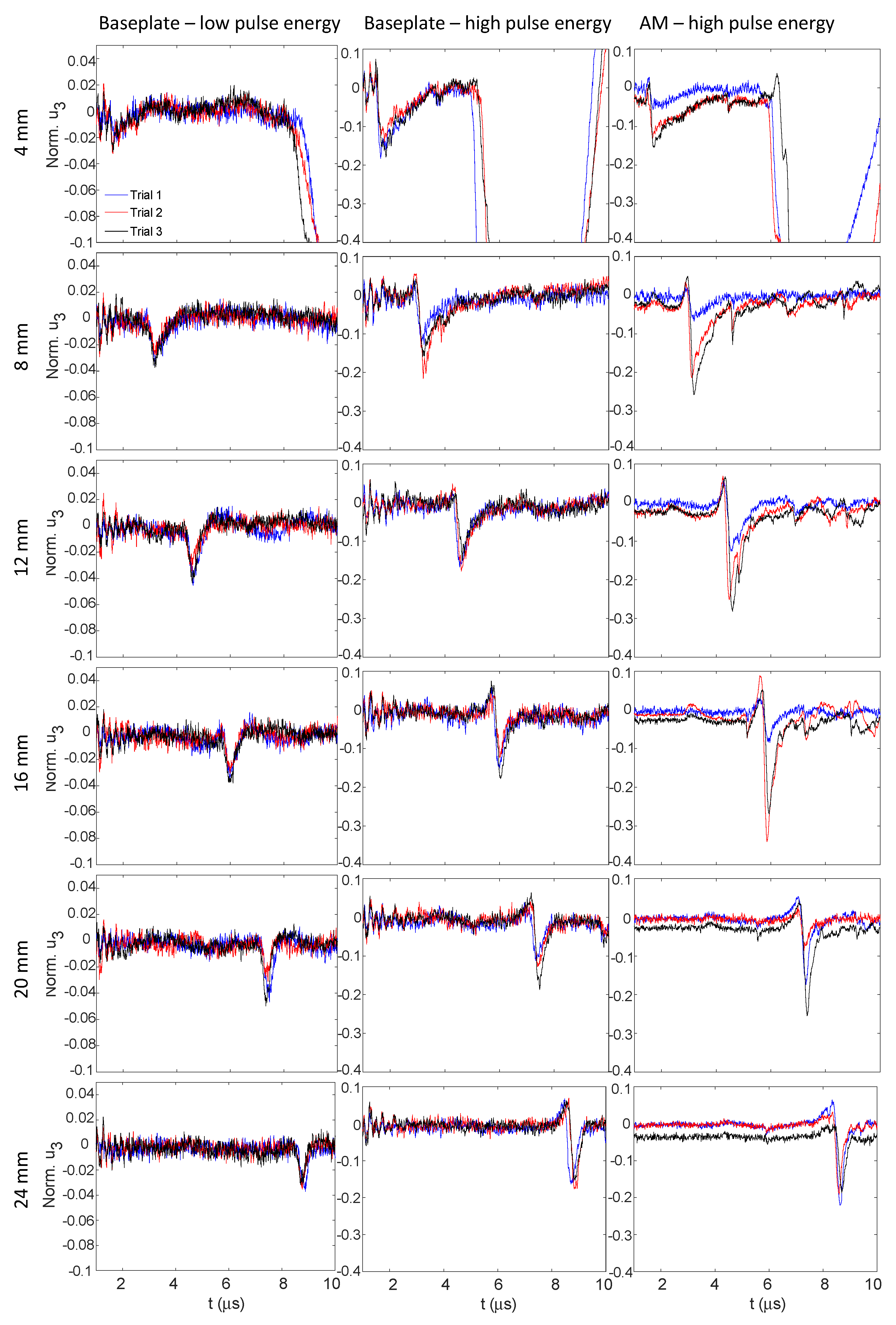
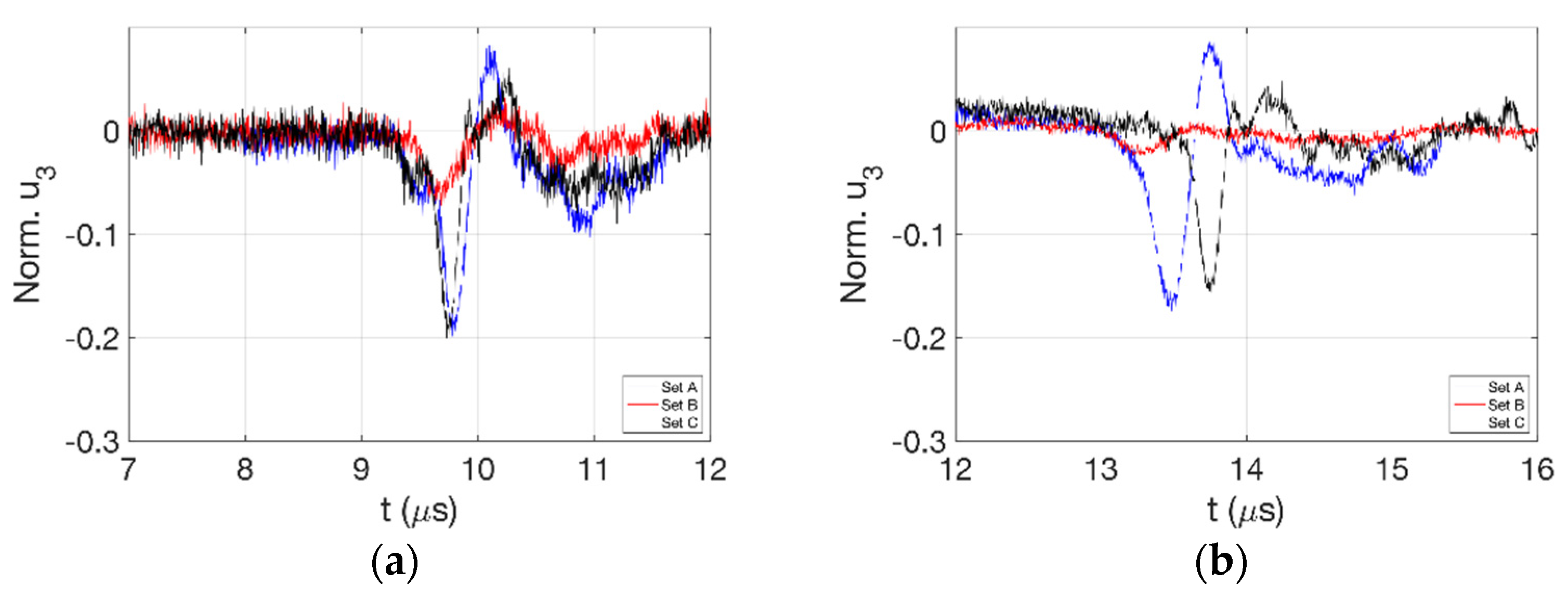
3.2. Effect of Off-Normal Processing Parameters
3.2.1. Ti-6Al-4V
3.2.2. IN-718
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cantrell, J.H. Fundamentals and Applications of Nonlinear Ultrasonic Nondestructive Evaluation. In Ultrasonic Nondestructive Evaluation: Engineering and Biological Material Characterization; Kundu, T., Ed.; CRC Press: Boca Raton, FL, USA, 2004; pp. 363–433. [Google Scholar]
- Jhang, K.-Y. Nonlinear Ultrasonic Techniques for Nondestructive Assessment of Micro Damage in Material: A Review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.-Y.; Jacobs, L.J.; Qu, J. Review of Second Harmonic Generation Measurement Techniques for Material State Determination in Metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Korneev, V.A.; Demčenko, A. Possible Second-Order Nonlinear Interactions of Plane Waves in an Elastic Solid. J. Acoust. Soc. Am. 2014, 135, 591–598. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Nagy, P.B.; Hassan, W. Analytical and Numerical Modeling of Non-Collinear Shear Wave Mixing at an Imperfect Interface. Ultrasonics 2016, 65, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Hasanian, M.; Lissenden, C.J. Second Order Ultrasonic Guided Wave Mutual Interactions in Plate: Arbitrary Angles, Internal Resonance, and Finite Interaction Region. J. Appl. Phys. 2018, 124, 164904. [Google Scholar] [CrossRef]
- Norris, A. Finite Amplitude Waves in Solids. In Nonlinear Acoustics; Academic Press: Cambridge, MA, USA, 1998; pp. 263–277. [Google Scholar]
- Guyer, R.A.; Johnson, P.A. Nonlinear Mesoscopic Elasticity: The Complex Behaviour of Granular Media Including Rocks and Soil; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Lomonosov, A.; Hess, P. Laser Excitation and Propagation of Nonlinear Surface Acoustic Wave Pulses. In Proceedings of the Nonlinear Acoustics in Perspective; Wei, R.J., Ed.; Nanjing University Press: Nanjing, China, 1996. [Google Scholar]
- Kolomenskii, A.A.; Lomonosov, A.M.; Kuschnereit, R.; Hess, P.; Gusev, V.E. Laser Generation and Detection of Strongly Nonlinear Elastic Surface Pulses. Phys. Rev. Lett. 1997, 79, 1325–1328. [Google Scholar] [CrossRef]
- Lomonosov, A.; Mikhalevich, V.G.; Hess, P.; Knight, E.Y.; Hamilton, M.F.; Zabolotskaya, E.A. Laser-Generated Nonlinear Rayleigh Waves with Shocks. J. Acoust. Soc. Am. 1999, 105, 2093–2096. [Google Scholar] [CrossRef]
- Kolomenskii, A.A.; Lioubimov, V.A.; Jerebtsov, S.N.; Schuessler, H.A. Nonlinear Surface Acoustic Wave Pulses in Solids: Laser Excitation, Propagation, Interactions (Invited). Rev. Sci. Instrum. 2003, 74, 448–452. [Google Scholar] [CrossRef]
- Kolomenskii, A.A.; Schuessler, H.A.; Mikhalevich, V.G.; Maznev, A.A. Interaction of Laser-Generated Surface Acoustic Pulses with Fine Particles: Surface Cleaning and Adhesion Studies. J. Appl. Phys. 1998, 84, 2404–2410. [Google Scholar] [CrossRef]
- Kolomenskii, A.A.; Schuessler, H.A. Characterization of Isotropic Solids with Nonlinear Surface Acoustic Wave Pulses. Phys. Rev. B 2001, 63, 085413. [Google Scholar] [CrossRef]
- Schuessler, H.A.; Jerebtsov, S.N.; Kolomenskii, A.A. Determination of Linear and Nonlinear Elastic Parameters from Laser Experiments with Surface Acoustic Wave Pulses. Spectrochim. Acta Part B At. Spectrosc. 2003, 58, 1171–1175. [Google Scholar] [CrossRef]
- Jerebtsov, S.N.; Kolomenskii, A.A.; Schuessler, H.A. Characterization of a Polycrystalline Material with Laser-Excited Nonlinear Surface Acoustic Wave Pulses. Int. J. Thermophys. 2004, 25, 485–490. [Google Scholar] [CrossRef]
- Lomonosov, A.M.; Hess, P. Impulsive Fracture of Silicon by Elastic Surface Pulses with Shocks. Phys. Rev. Lett. 2002, 89, 095501. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, G.; Lomonosov, A.M.; Hess, P.; Gumbsch, P. Impulsive Fracture of Fused Quartz and Silicon Crystals by Nonlinear Surface Acoustic Waves. J. Appl. Phys. 2003, 94, 2907–2914. [Google Scholar] [CrossRef]
- Kozhushko, V.V.; Hess, P. Anisotropy of the Strength of Si Studied by a Laser-Based Contact-Free Method. Phys. Rev. B 2007, 76, 144105. [Google Scholar] [CrossRef]
- Kozhushko, V.V.; Lomonosov, A.M.; Hess, P. Intrinsic Strength of Silicon Crystals in Pure- and Combined-Mode Fracture without Precrack. Phys. Rev. Lett. 2007, 98, 195505. [Google Scholar] [CrossRef] [PubMed]
- Gusev, V.E.; Lauriks, W.; Thoen, J. Theory for the Time Evolution of Nonlinear Rayleigh Waves in an Isotropic Solid. Phys. Rev. B 1997, 55, 9344–9347. [Google Scholar] [CrossRef]
- Gusev, V.E.; Lauriks, W.; Thoen, J. New Evolution Equations for the Nonlinear Surface Acoustic Waves on an Elastic Solid of General Anisotropy. J. Acoust. Soc. Am. 1998, 103, 3203–3215. [Google Scholar] [CrossRef]
- Zabolotskaya, E.A. Nonlinear Propagation of Plane and Circular Rayleigh Waves in Isotropic Solids. J. Acoust. Soc. Am. 1992, 91, 2569–2575. [Google Scholar] [CrossRef]
- Shull, D.J.; Hamilton, M.F.; Il’insky, Y.A.; Zabolotskaya, E.A. Harmonic Generation in Plane and Cylindrical Nonlinear Rayleigh Waves. J. Acoust. Soc. Am. 1993, 94, 418–427. [Google Scholar] [CrossRef]
- Shull, D.J.; Kim, E.E.; Hamilton, M.F.; Zabolotskaya, E.A. Diffraction Effects in Nonlinear Rayleigh Wave Beams. J. Acoust. Soc. Am. 1995, 97, 2126–2137. [Google Scholar] [CrossRef]
- Hamilton, M.F.; Il’insky, Y.A.; Zabolotskaya, E.A. Local and Nonlocal Nonlinearity in Rayleigh Waves. J. Acoust. Soc. Am. 1995, 97, 882–890. [Google Scholar] [CrossRef]
- Hamilton, M.F.; Il’insky, Y.A.; Zabolotskaya, E.A. Evolution Equations for Nonlinear Rayleigh Waves. J. Acoust. Soc. Am. 1995, 97, 891–897. [Google Scholar] [CrossRef]
- Knight, E.Y.; Hamilton, M.F.; II’inskii, Y.A.; Zabolotskaya, E.A. General Theory for the Spectral Evolution of Nonlinear Rayleigh Waves. J. Acoust. Soc. Am. 1997, 102, 1402–1417. [Google Scholar] [CrossRef]
- Rudenko, O.V.; Solui͡an, S.I. Theoretical Foundations of Nonlinear Acoustics; Studies in Soviet science; Consultants Bureau: New York, NY, USA, 1977; ISBN 978-0-306-10933-1. [Google Scholar]
- Gartsev, S.; Köhler, B. Direct Measurements of Rayleigh Wave Acoustoelastic Constants for Shot-Peened Superalloys. NDT E Int. 2020, 113, 102279. [Google Scholar] [CrossRef]
- Song, B.; Dong, S.; Liao, H.; Coddet, C. Process Parameter Selection for Selective Laser Melting of Ti6Al4V Based on Temperature Distribution Simulation and Experimental Sintering. Int. J. Adv. Manuf. Technol. 2012, 61, 967–974. [Google Scholar] [CrossRef]
- Saboori, A.; Gallo, D.; Biamino, S.; Fino, P.; Lombardi, M. An Overview of Additive Manufacturing of Titanium Components by Directed Energy Deposition: Microstructure and Mechanical Properties. Appl. Sci. 2017, 7, 883. [Google Scholar] [CrossRef]
- Reutzel, E.W.; Nassar, A.R. A Survey of Sensing and Control Systems for Machine and Process Monitoring of Directed-Energy, Metal-Based Additive Manufacturing. Rapid Prototyp. J. 2015, 21, 159–167. [Google Scholar] [CrossRef]
- Boddu, M.R.; Landers, R.G.; Liou, F.W. Control of Laser Cladding for Rapid Prototyping—A Review. In Proceedings of the 2001 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2001. [Google Scholar]
- Bi, G.; Gasser, A.; Wissenbach, K.; Drenker, A.; Poprawe, R. Identification and Qualification of Temperature Signal for Monitoring and Control in Laser Cladding. Opt. Lasers Eng. 2006, 44, 1348–1359. [Google Scholar] [CrossRef]
- Svetlizky, D.; Das, M.; Zheng, B.; Vyatskikh, A.L.; Bose, S.; Bandyopadhyay, A.; Schoenung, J.M.; Lavernia, E.J.; Eliaz, N. Directed Energy Deposition (DED) Additive Manufacturing: Physical Characteristics, Defects, Challenges and Applications. Mater. Today 2021, 49, 271–295. [Google Scholar] [CrossRef]
- Ahn, D.-G. Directed Energy Deposition (DED) Process: State of the Art. Int. J. Precis. Eng. Manuf.-Green Tech. 2021, 8, 703–742. [Google Scholar] [CrossRef]
- Zhu, L.; Xue, P.; Lan, Q.; Meng, G.; Ren, Y.; Yang, Z.; Xu, P.; Liu, Z. Recent Research and Development Status of Laser Cladding: A Review. Opt. Laser Technol. 2021, 138, 106915. [Google Scholar] [CrossRef]
- Liu, W.-W.; Tang, Z.-J.; Liu, X.-Y.; Wang, H.-J.; Zhang, H.-C. A Review on In-Situ Monitoring and Adaptive Control Technology for Laser Cladding Remanufacturing. Procedia CIRP 2017, 61, 235–240. [Google Scholar] [CrossRef]
- Tapia, G.; Elwany, A. A Review on Process Monitoring and Control in Metal-Based Additive Manufacturing. J. Manuf. Sci. Eng. 2014, 136, 060801. [Google Scholar] [CrossRef]
- Steen, W.M.; Mazumder, J. Laser Automation and In-Process Sensing. In Laser Material Processing; Springer: London, UK, 2010; pp. 485–518. [Google Scholar]
- Nassar, A.R.; Reutzel, E.W.; Brown, S.W.; Morgan, J.P.; Morgan, J.P.; Natale, D.J.; Tutwiler, R.L.; Feck, D.P.; Banks, J.C. Sensing for Directed Energy Deposition and Powder Bed Fusion Additive Manufacturing at Penn State University; Gu, B., Helvajian, H., Piqué, A., Eds.; SPIE: Bellingham, WA, USA, 2016; p. 97380R. [Google Scholar]
- Song, L.; Mazumder, J. Real Time Cr Measurement Using Optical Emission Spectroscopy During Direct Metal Deposition Process. IEEE Sens. J. 2012, 12, 958–964. [Google Scholar] [CrossRef]
- Stutzman, C.B.; Nassar, A.R.; Reutzel, E.W. Multi-Sensor Investigations of Optical Emissions and Their Relations to Directed Energy Deposition Processes and Quality. Addit. Manuf. 2018, 21, 333–339. [Google Scholar] [CrossRef]
- Honarvar, F.; Varvani-Farahani, A. A Review of Ultrasonic Testing Applications in Additive Manufacturing: Defect Evaluation, Material Characterization, and Process Control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-H.; Hong, J.-Y.; Ha, T.; Choi, S.; Jhang, K.-Y. Deep Learning-Based Ultrasonic Testing to Evaluate the Porosity of Additively Manufactured Parts with Rough Surfaces. Metals 2021, 11, 290. [Google Scholar] [CrossRef]
- Sotelo, L.D.; Karunakaran, R.; Pratt, C.S.; Sealy, M.P.; Turner, J.A. Ultrasound in Situ Characterization of Hybrid Additively Manufactured Ti6Al4V. J. Acoust. Soc. Am. 2021, 150, 4452–4463. [Google Scholar] [CrossRef]
- Smoqi, Z.; Sotelo, L.D.; Gaikwad, A.; Turner, J.A.; Rao, P. Ultrasonic Nondestructive Evaluation of Additively Manufactured Wear Coatings. NDT E Int. 2023, 133, 102754. [Google Scholar] [CrossRef]
- Hespeler, S.; Dehghan-Niri, E.; Juhasz, M.; Luo, K.; Halliday, H.S. Deep Learning for In-Situ Layer Quality Monitoring during Laser-Based Directed Energy Deposition (LB-DED) Additive Manufacturing Process. Appl. Sci. 2022, 12, 8974. [Google Scholar] [CrossRef]
- Sreeraj, P.R.; Mishra, S.K.; Singh, P.K. A Review on Non-Destructive Evaluation and Characterization of Additively Manufactured Components. Prog. Addit. Manuf. 2022, 7, 225–248. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stravroulakis, P.; Leach, R.K.; Clare, A.T. Review of In-Situ Process Monitoring and in-Situ Metrology for Metal Additive Manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Smith, R.J.; Hirsch, M.; Patel, R.; Li, W.; Clare, A.T.; Sharples, S.D. Spatially Resolved Acoustic Spectroscopy for Selective Laser Melting. J. Mater. Process. Technol. 2016, 236, 93–102. [Google Scholar] [CrossRef]
- Millon, C.; Vanhoye, A.; Obaton, A.-F.; Penot, J.-D. Development of Laser Ultrasonics Inspection for Online Monitoring of Additive Manufacturing. Weld. World 2018, 62, 653–661. [Google Scholar] [CrossRef]
- Davis, G.; Nagarajah, R.; Palanisamy, S.; Rashid, R.A.R.; Rajagopal, P.; Balasubramaniam, K. Laser Ultrasonic Inspection of Additive Manufactured Components. Int. J. Adv. Manuf. Technol. 2019, 102, 2571–2579. [Google Scholar] [CrossRef]
- Pieris, D.; Stratoudaki, T.; Javadi, Y.; Lukacs, P.; Catchpole-Smith, S.; Wilcox, P.D.; Clare, A.; Clark, M. Laser Induced Phased Arrays (LIPA) to Detect Nested Features in Additively Manufactured Components. Mater. Des. 2019, 187, 108412. [Google Scholar] [CrossRef]
- Park, S.-H.; Liu, P.; Yi, K.; Choi, G.; Jhang, K.-Y.; Sohn, H. Mechanical Properties Estimation of Additively Manufactured Metal Components Using Femtosecond Laser Ultrasonics and Laser Polishing. Int. J. Mach. Tools Manuf. 2021, 166, 103745. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, D.; Li, H.; Song, C.; Zhou, X.; Shen, S.; Zhang, G.; Yang, Y.; Wang, H. Detection of Internal Holes in Additive Manufactured Ti-6Al-4V Part Using Laser Ultrasonic Testing. Appl. Sci. 2020, 10, 365. [Google Scholar] [CrossRef]
- Zou, Y.; Chai, Y.; Wang, D.; Li, Y. Measurement of Elastic Modulus of Laser Cladding Coatings by Laser Ultrasonic Method. Opt. Laser Technol. 2022, 146, 107567. [Google Scholar] [CrossRef]
- Bakre, C.; Lissenden, C.J. Surface Roughness Effects on Self-Interacting and Mutually Interacting Rayleigh Waves. Sensors 2021, 21, 5495. [Google Scholar] [CrossRef] [PubMed]
- Bakre, C.; Nassar, A.R.; Reutzel, E.W.; Lissenden, C.J. Ultrasonic Rayleigh Wave Interrogation of Directed Energy Deposition Ti–6Al–4V Having a Rough Surface. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2022, 5, 031008. [Google Scholar] [CrossRef]
- Bakre, C.; Meyer, T.; Jamieson, C.; Nassar, A.R.; Reutzel, E.W.; Lissenden, C.J. In-Situ Laser Ultrasound-Based Rayleigh Wave Process Monitoring of DED-AM Metals. Res. Nondestruct. Eval. 2022, 1–25. [Google Scholar] [CrossRef]
- Krishnaswamy, S. Theory and Applications of Laser-Ultrasonic Techniques. In Ultrasonic Nondestructive Evaluation; CRC Press: Boca Raton, FL, USA, 2004; pp. 436–489. [Google Scholar]
- Dong, Z.; Liu, Y.; Wen, W.; Ge, J.; Liang, J. Effect of Hatch Spacing on Melt Pool and As-Built Quality During Selective Laser Melting of Stainless Steel: Modeling and Experimental Approaches. Materials 2018, 12, 50. [Google Scholar] [CrossRef] [PubMed]



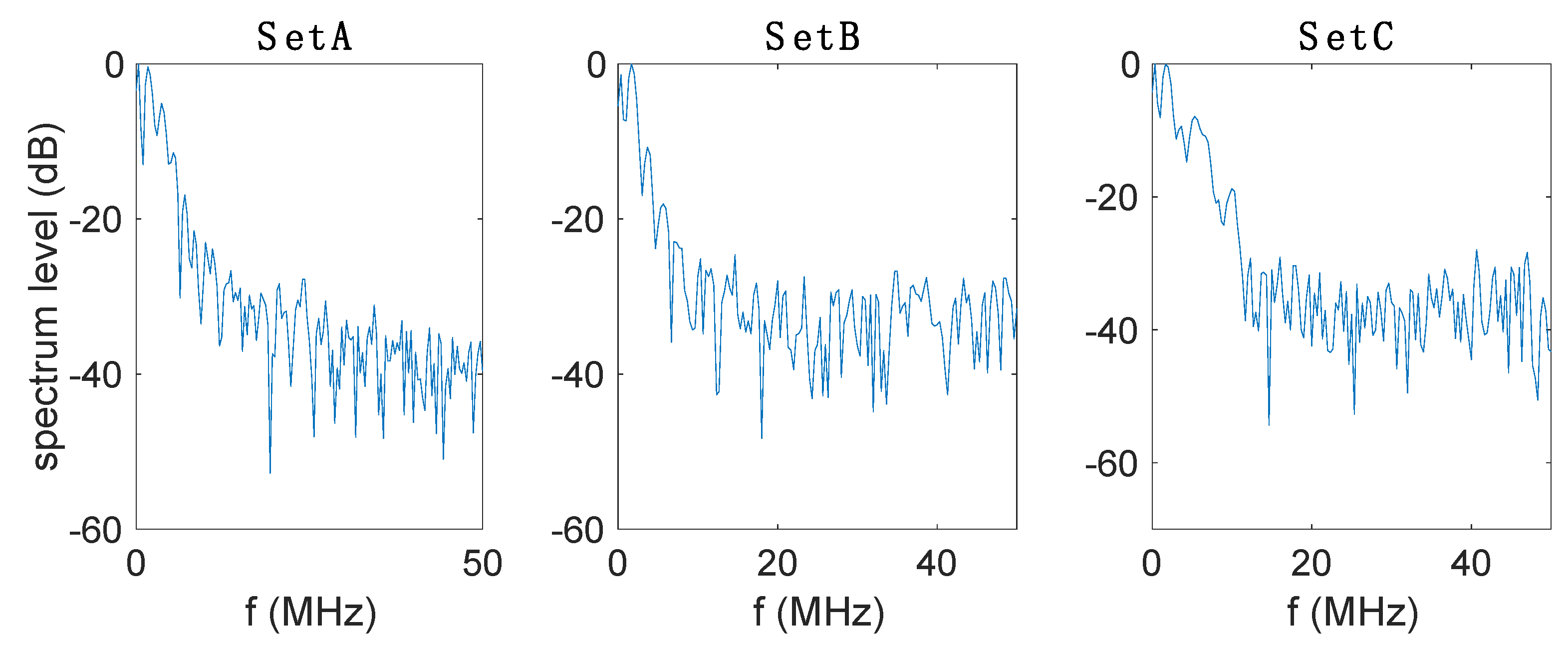
| Set | Material | Laser Power (W) | Scan Speed (mm/s) | Hatch Spacing (mm) |
|---|---|---|---|---|
| A 1 | Ti-6Al-4V | 450 | 10.6 | 0.8 |
| B | Ti-6Al-4V | 380 | 10.6 | 0.8 |
| C | Ti-6Al-4V | 450 | 10.6 | 0.9 |
| D 1 | IN-718 | 400 | 10.6 | 0.6 |
| E | IN-718 | 400 | 9.3 | 0.6 |
| F | IN-718 | 400 | 11.8 | 0.6 |
| G | IN-718 | 400 | 10.6 | 0.75 |
| H | IN-718 | 400 | 10.6 | 0.85 |
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| Ti-6Al-4V | Ti-6Al-4V | IN-718 | IN-718 |
| baseplate | baseplate | baseplate | baseplate |
| 4 layers Set A | 4 layers Set A | 4 layers Set D | 4 layers Set D |
| LU test | LU test | LU test | LU test |
| 4 layers Set B | 4 layers Set C | 4 layers Set E | 4 layers Set G |
| LU test | LU test | LU test | LU test |
| 4 layers Set F | 4 layers Set H | ||
| LU test | LU test |
| Material | Sa (µm) | Sq (µm) | Sz (μm) |
|---|---|---|---|
| Ti-6Al-4V baseplate | 1.14 | 1.42 | 10.25 |
| Ti-6Al-4V Set A | 33.04 | 41.39 | 371.4 |
| Ti-6Al-4V Set B | 33.09 | 42.26 | 385.7 |
| Ti-6Al-4V Set C | 30.63 | 38.84 | 397.0 |
| IN-718 baseplate | 3.72 | 4.64 | 33.94 |
| IN-718 Set D | 19.59 | 25.23 | 264.7 |
| IN-718 Set E | 18.27 | 22.65 | 318.5 |
| IN-718 Set F | 17.52 | 21.76 | 352.1 |
| IN-718 Set G | 13.89 | 18.16 | 237.8 |
| IN-718 Set H | 25.60 | 31.82 | 293.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakre, C.; Afzalimir, S.H.; Jamieson, C.; Nassar, A.; Reutzel, E.W.; Lissenden, C.J. Laser Generated Broadband Rayleigh Waveform Evolution for Metal Additive Manufacturing Process Monitoring. Appl. Sci. 2022, 12, 12208. https://doi.org/10.3390/app122312208
Bakre C, Afzalimir SH, Jamieson C, Nassar A, Reutzel EW, Lissenden CJ. Laser Generated Broadband Rayleigh Waveform Evolution for Metal Additive Manufacturing Process Monitoring. Applied Sciences. 2022; 12(23):12208. https://doi.org/10.3390/app122312208
Chicago/Turabian StyleBakre, Chaitanya, Seyed Hamidreza Afzalimir, Cory Jamieson, Abdalla Nassar, Edward W. Reutzel, and Cliff J. Lissenden. 2022. "Laser Generated Broadband Rayleigh Waveform Evolution for Metal Additive Manufacturing Process Monitoring" Applied Sciences 12, no. 23: 12208. https://doi.org/10.3390/app122312208
APA StyleBakre, C., Afzalimir, S. H., Jamieson, C., Nassar, A., Reutzel, E. W., & Lissenden, C. J. (2022). Laser Generated Broadband Rayleigh Waveform Evolution for Metal Additive Manufacturing Process Monitoring. Applied Sciences, 12(23), 12208. https://doi.org/10.3390/app122312208







