Investigation of the Fatigue Life of Bottom-Up Cracking in Asphalt Concrete Pavements
Abstract
1. Introduction
2. Experimental Study of the Dynamic Modulus and OT of Asphalt Pavements
2.1. Test Materials
2.2. Dynamic Modulus Test
- (1)
- According to the mix proportion (of the asphalt mixture obtained by the Superpave test method), the temperature of the mixer was raised to 155 °C in advance and kept warm. The aggregate was placed in the oven at 165 °C and a constant temperature for 4–6 h of drying, and the asphalt was placed in the oven at 135 °C at a constant temperature for 2–3 h for the flow stage. Then, the aggregate was poured into the blender and stirred for 60 s, as shown in Figure 1a. Then the asphalt was added quickly and continually stirred for 60 s. At last, the mineral powder was added and continually stirred for 60 s. After mixing, the asphalt mixture was placed in the oven at 135 ± 5 °C for 2 h for aging. This process was used to simulate the short-term aging phenomenon in the transportation process;
- (2)
- After the short-term aging, the required quality of the hot asphalt mixture was weighed according to the sampling method in the specification (four-point method), and then they were evenly poured into the rotary compaction test mold, which was kept warm at 165 °C in the oven in advance. A Superpave gyratory compactor (SGC) rotary compactor was used for molding, as shown in Figure 1b. After cooling for 15 min, the specimen was demolded and left at an indoor temperature for at least 8 h;
- (3)
- A Φ 100 × 170 mm cylinder was drilled from a cylinder specimen with dimensions of Φ 150 × 170 mm by a core-taking machine, as shown in Figure 1c. In the process of coring, it is essential to ensure that the drill bit of the coring machine was perpendicular to the ground. According to different types of mixture, the rotation speed, descent speed, and water spraying amount of the drill bit were reasonably adjusted to ensure that the specimen was parallel, with no grooves, a smooth surface, and being perpendicular to the two end faces;
- (4)
- A double-sided saw was used to form a test specimen with a height of 150 ± 2.0 mm, as shown in Figure 1d;
- (5)
- After the above process was completed, the physical parameters (the diameter, height, density, and voidage) of the specimen were measured, and then the specimen was placed in a ventilated place at room temperature for at least two days to dry the specimen.
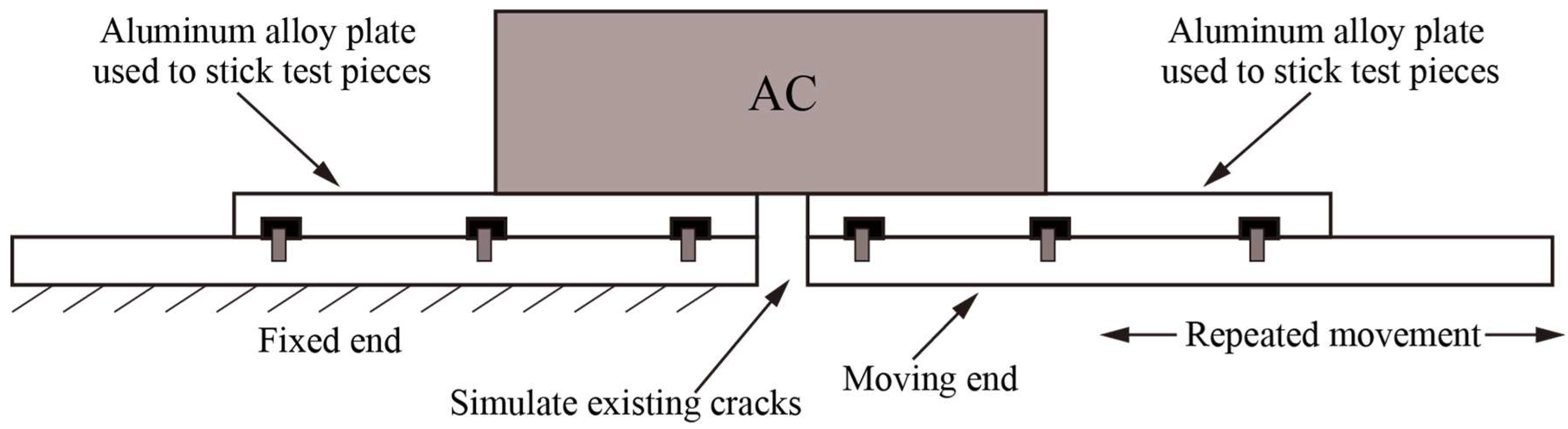
2.3. Overlay Test
- (1)
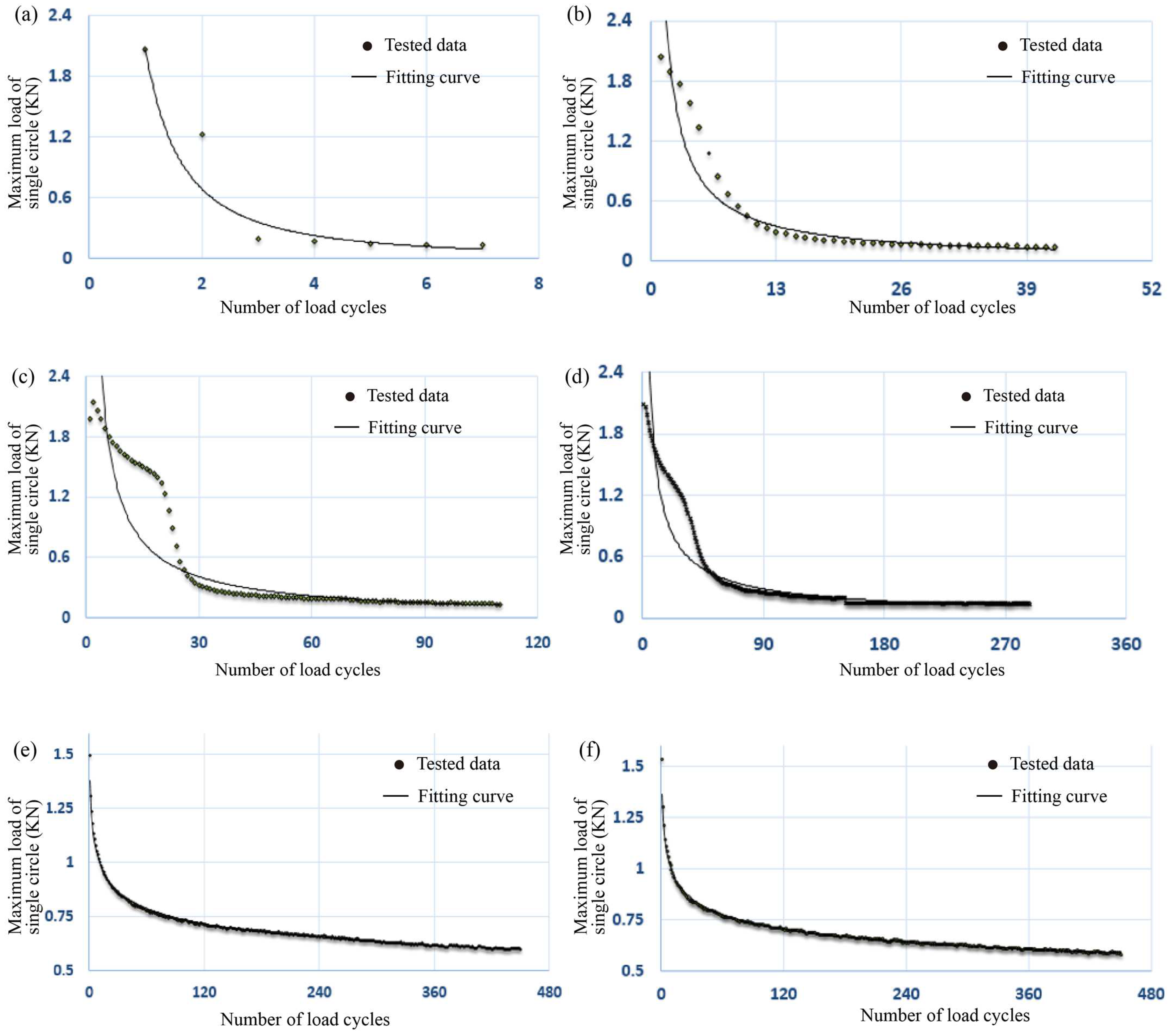
- When the temperature dropped from 25 °C to −10 °C, the load cycles of the AC-20 and AC-13 asphalt mixtures decreased sharply. With a decrease in temperature, the crack resistance of both the AC-20 and AC-13 asphalt mixture gradually deteriorated, which was consistent with the fact that the asphalt pavement was prone to cracking in a low-temperature environment;
- (2)
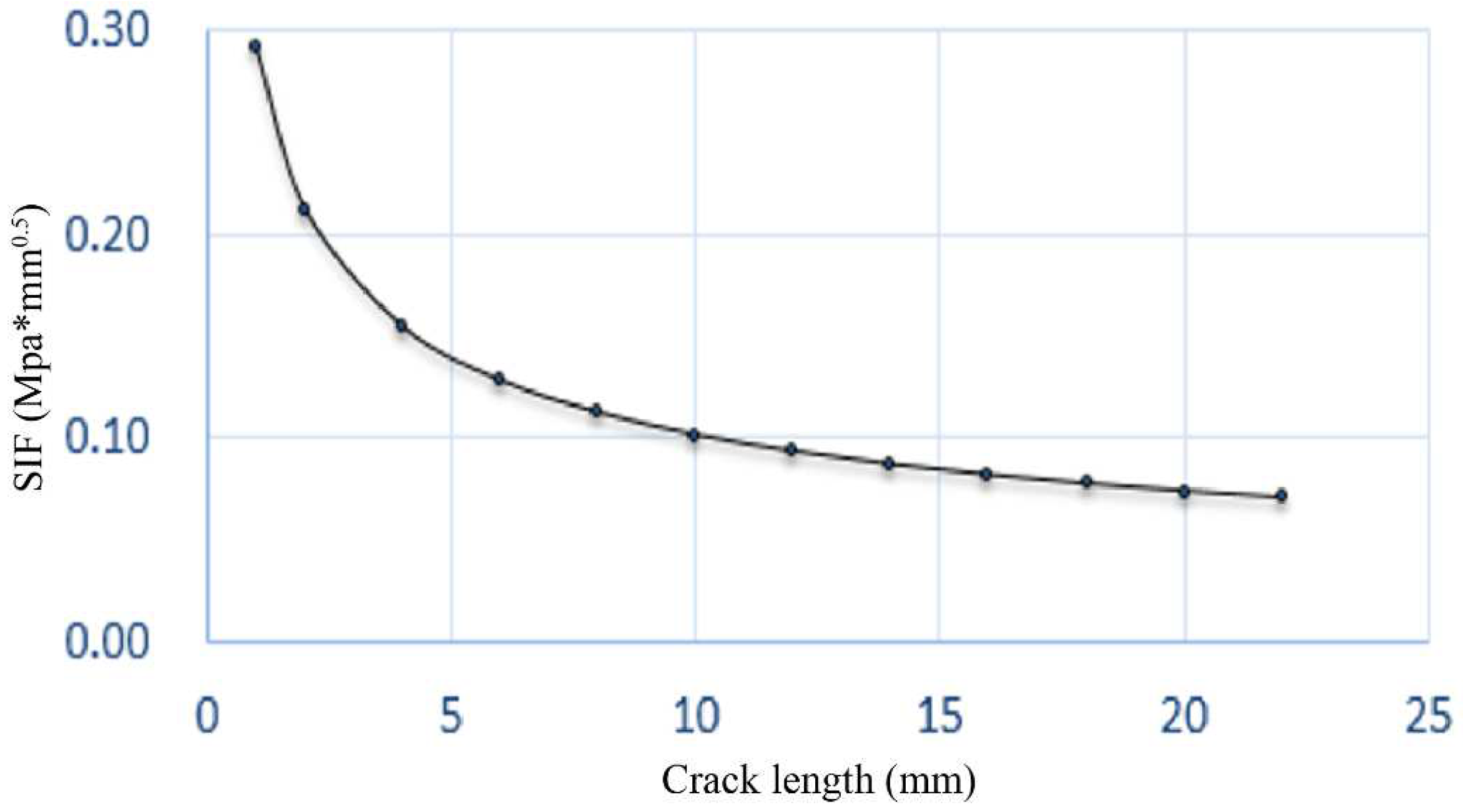
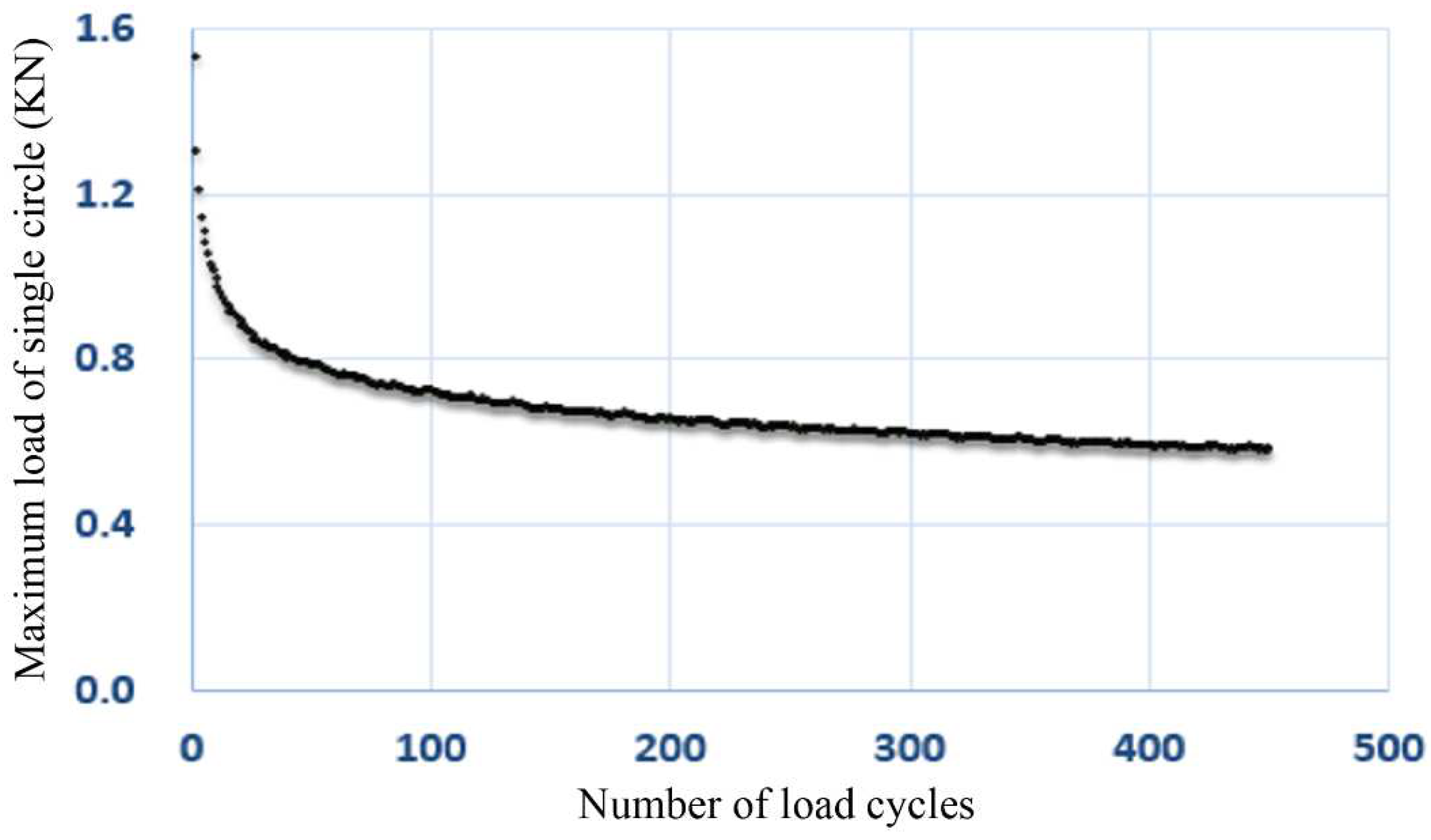
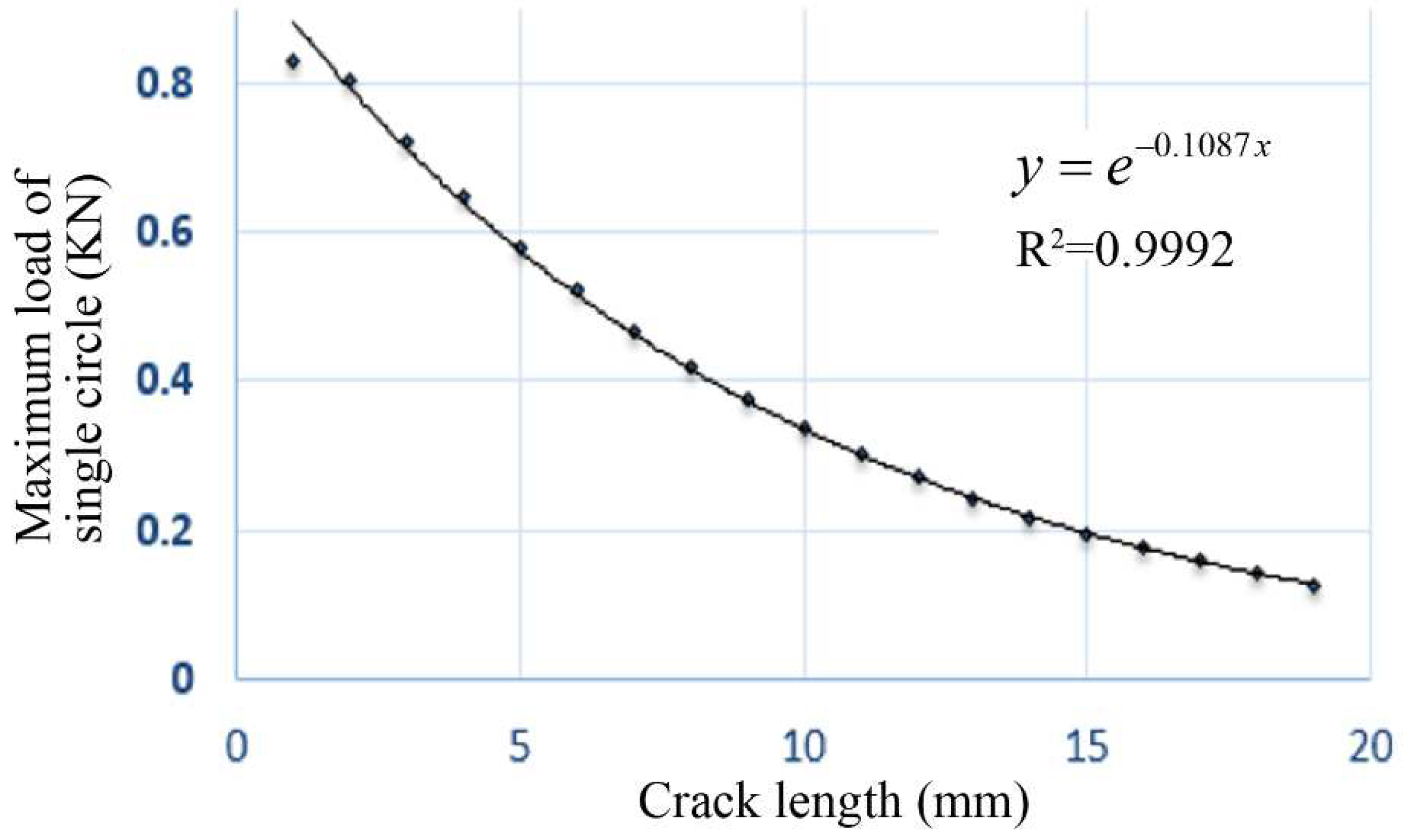
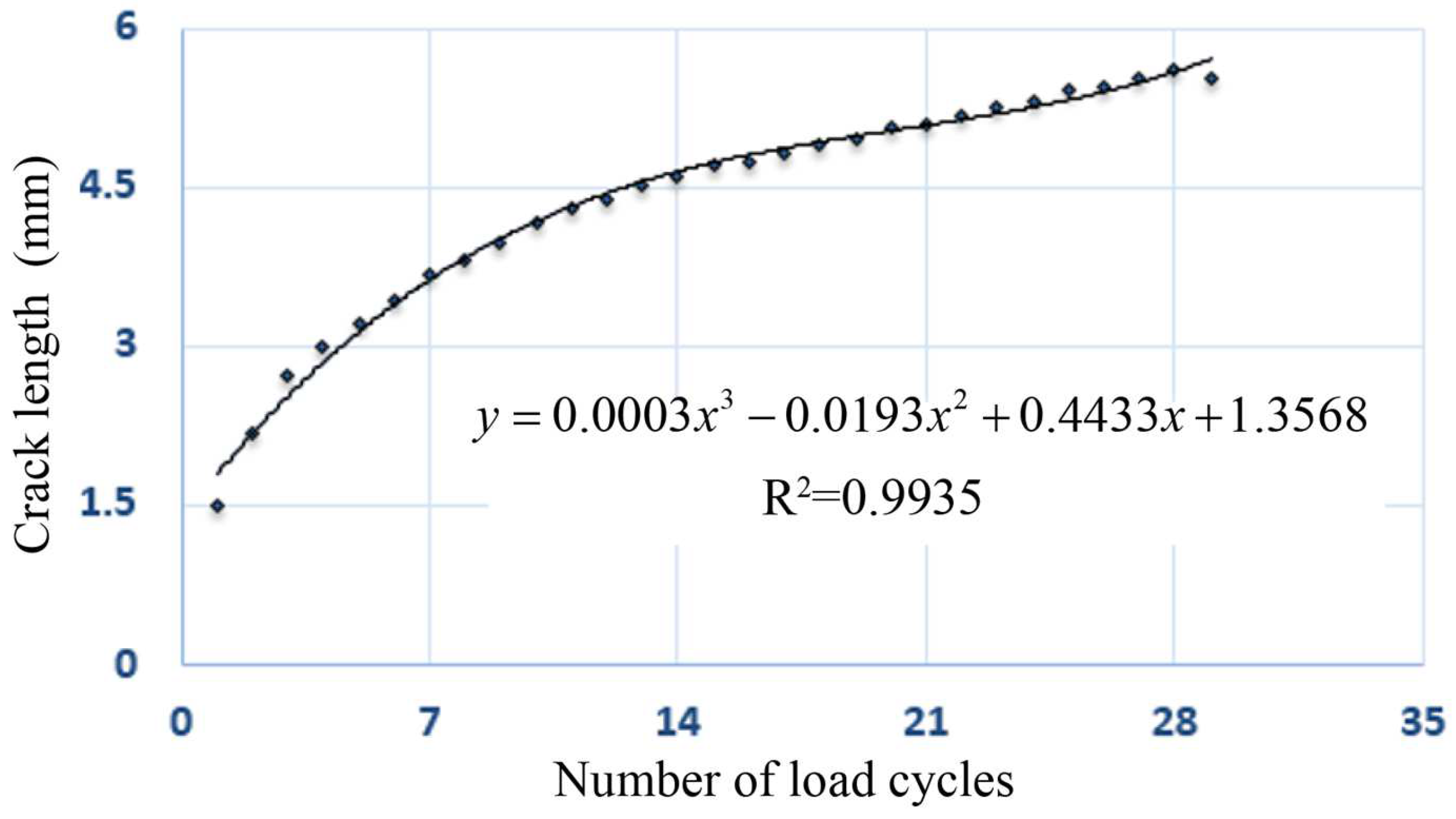
- In the early stages of the OT, the test load decreased rapidly with the increase in the number of load cycles. When the number of cycles continued to increase, the decline rate of the maximum load in a single circle gradually slowed down, and the curve gradually tended to level; that is, the attenuation rate of the load slowed down. The reason was that the stress transferred to the crack tip decreased with the increase in crack length at the same maximum tensile displacement before the instability failure of the structure, so the crack propagation became more and more difficult.
3. Evaluating the Tensile Stress and Fracture Parameters A and n
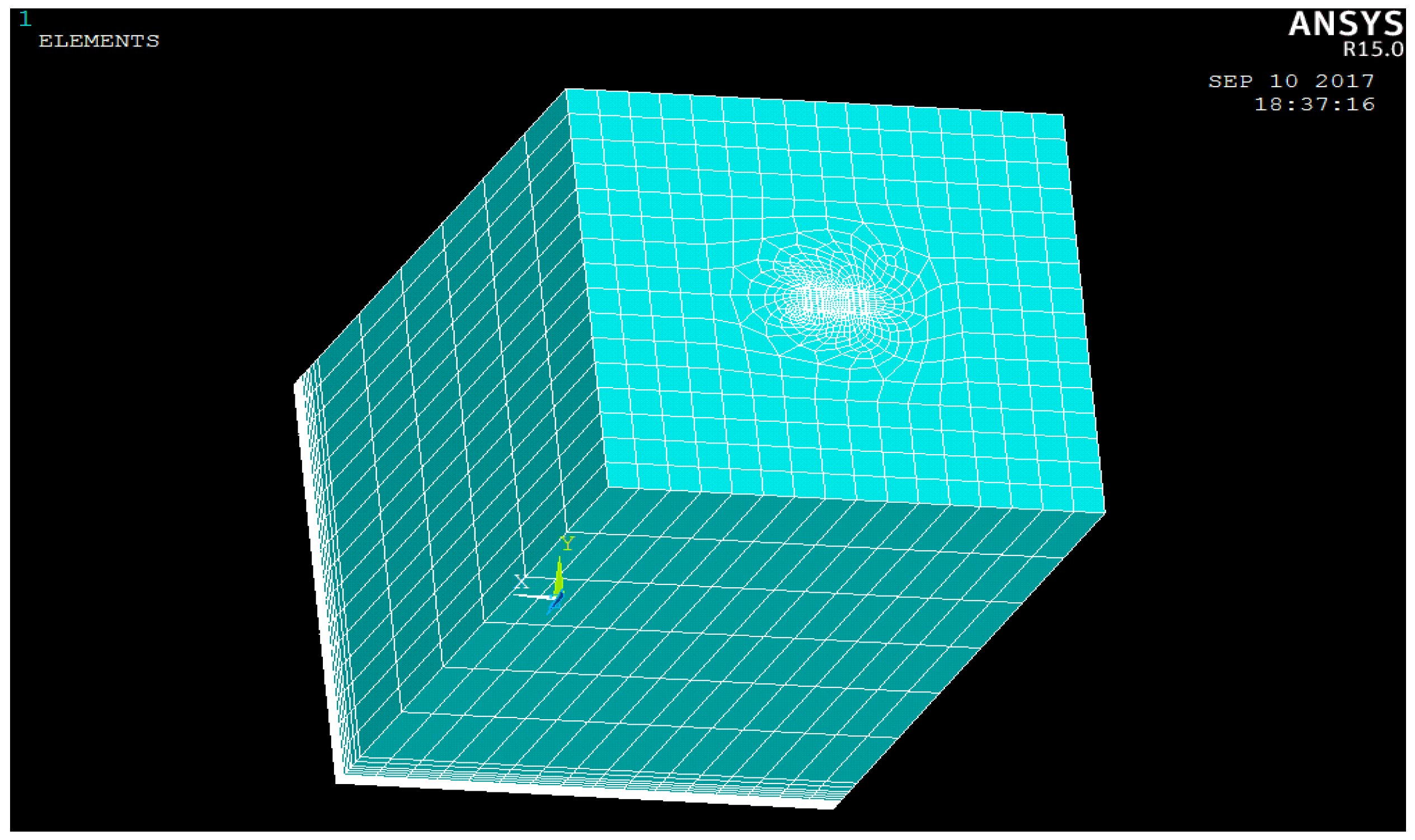
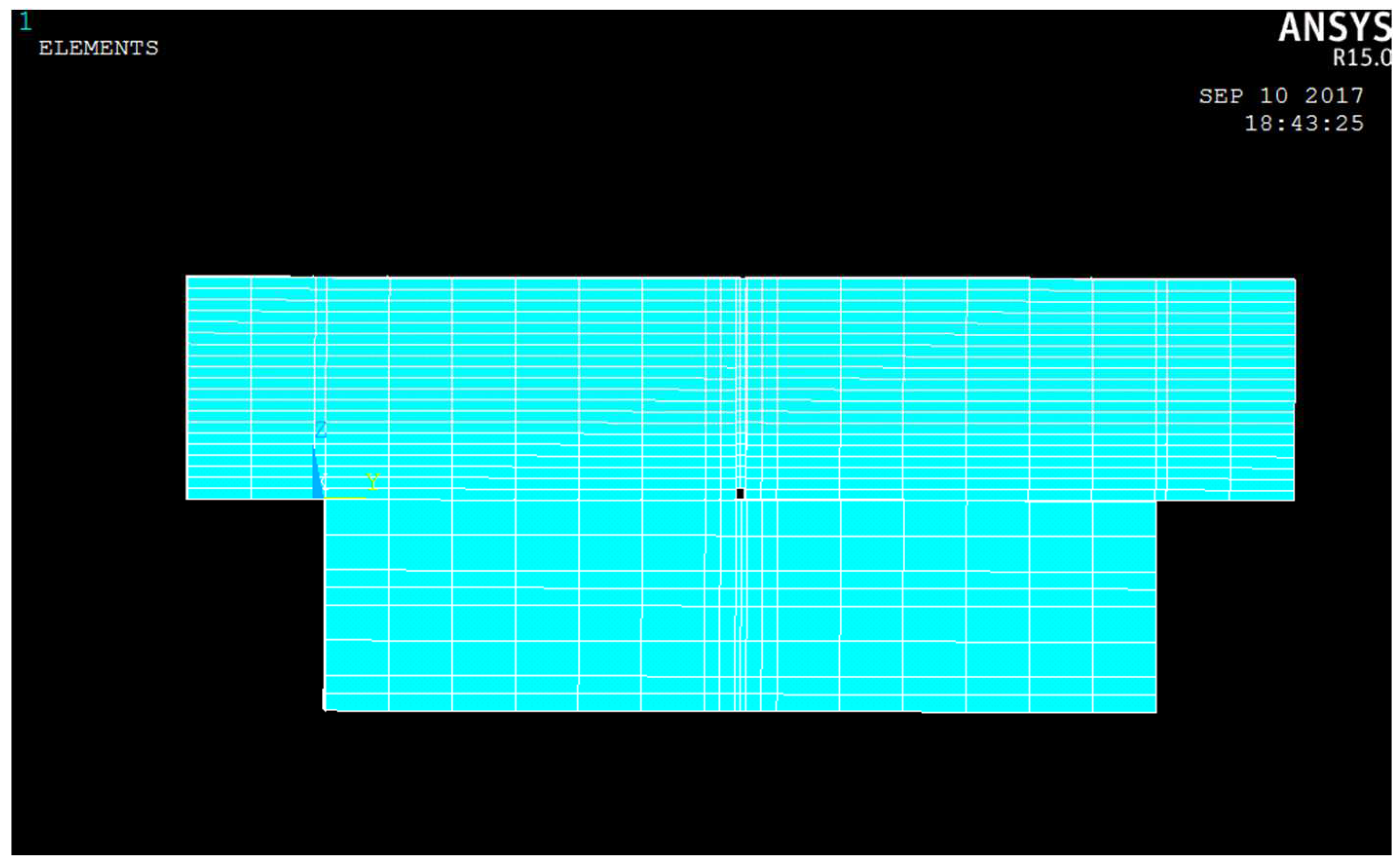
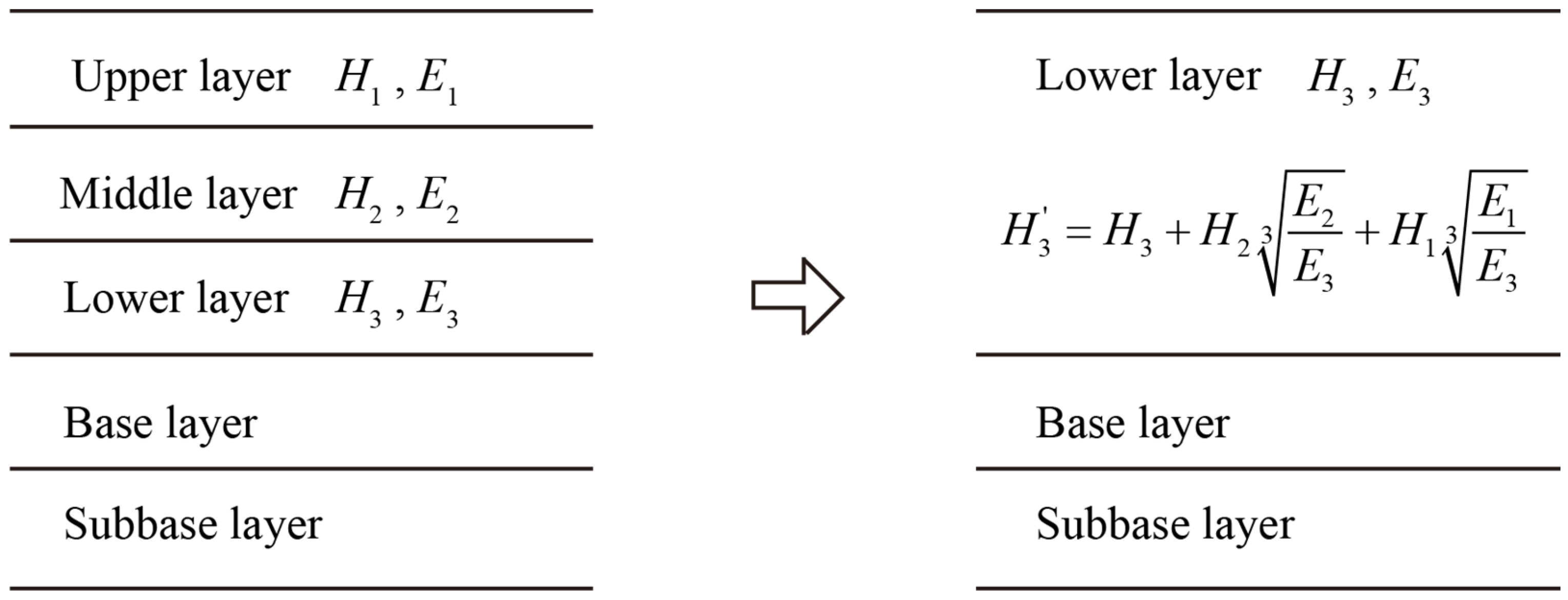
3.1. Tensile Stress by Numerical Simulation
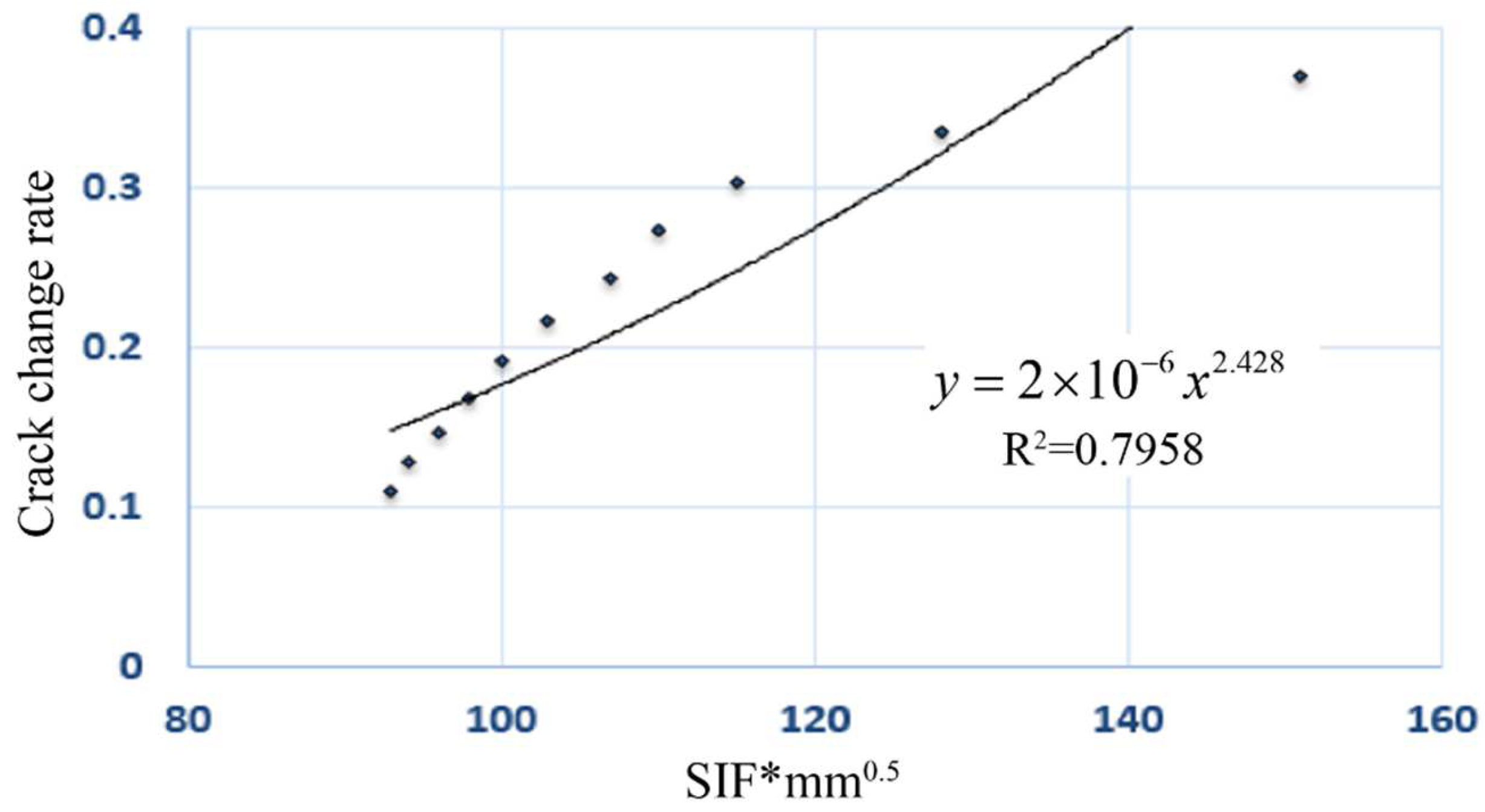
3.2. Calculation of Fracture Parameters A and n
4. Prediction of Fatigue Crack Life of Asphalt Pavements
4.1. Fatigue Cracking Life
4.2. Crack Propagation Life
4.3. Fatigue Crack Life
5. Conclusions
- (1)
- The proportion of fatigue propagation life to the fatigue life of cracks at different temperatures varied significantly. Therefore, it is essential to consider the fatigue propagation life of cracks at different temperatures for accurately calculating the entire fatigue life of asphalt pavement structures. That is, the fatigue life calculation model of a pavement structure can be expressed as ;
- (2)
- For the fatigue life of a pavement structure, the crack propagation life decreased sharply with the decrease in temperature. When the temperature dropped from 25 °C to 0 °C, the crack propagation life of the three types of surface layer structures decreased by more than 300 times. When the temperature dropped from 0 °C to −10 °C, the crack propagation life of the three types of surface layer structures decreased by more than 600 times;
- (3)
- The increase in asphalt surface thickness can effectively improve the fatigue crack life of a pavement structure. Therefore, it is an ideal choice to increase the thickness of an asphalt surface appropriately for improving the service life of pavements. Certainly, high AC thicknesses might make the pavement vulnerable to top-down cracking, and considering the cost, understanding a reasonable thickness is worth further study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.S.; Zhang, Y. Study on the fatigue cracking of expressway asphalt pavement. J. Inn. Mong. Agric. Univ. 2007, 28, 169–172. [Google Scholar]
- Ge, R.G.; Yue, Y.; Mao, Z.M.; Cao, S.Y. Calculate the stress intensity factor by the finite element software ANSYS. J. Hunan City Univ. Nat. Sci. 2009, 18, 10–12. [Google Scholar]
- Uzan, J.; Sides, A.; Perl, M. Viscoelastoplastic model for predicting performance of asphaltic mixtures. Transp. Res. Rec. 1985, 1043, 78–89. [Google Scholar]
- Ceylan, H.; Gopalakrishnan, K.; Lytton, R.L. Neural networks modeling of stress growth in asphalt overlays due to load and thermal effects during reflection cracking. J. Mater. Civ. Eng. 2011, 23, 221–229. [Google Scholar] [CrossRef]
- Hu, X.D.; Walubita, L.F. Modelling tensile strain response in asphalt pavements: Bottom-up and/or top-down fatigue crack initiation. Road Mater. Pavement Des. 2009, 10, 125–154. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, S.; Scullion, T. Development and verification of the overlay tester based fatigue cracking prediction approach (with discussion). In Asphalt Paving Technology: Association of Asphalt Paving Technologists-Proceedings of the Technical Sessions; The Texas A&M University System: College Station, TX, USA, 2007; Volume 76, pp. 627–662. [Google Scholar]
- Walubita, L.F.; Faruk, A.; Koohi, Y.; Luo, R.; Scullion, T.; Lytton, R. The Overlay Tester (OT): Comparison with Other Crack Test Methods and Recommendations for Surrogate Crack Test; Rep. No. FHWA/TX-13/0-6607-2; A&M Transportation Institute: College Station, TX, USA, 2013. [Google Scholar]
- Hiltunen, D.R.; Roque, R. A mechanics-based prediction model for thermal cracking of asphaltic concrete pavements (with discussion). J. Assoc. Asph. Paving Technol. 1994, 63, 81–117. [Google Scholar]
- Paris, P.C.; Erdogan, F.A. A critical analyses of crack propagation laws. J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Majidzadeh, K.; Kaufmann, E.M.; Ramsamooj, D.V. Application of fracture mechanics in the analysis of pavement fatigue. Assoc. Asph. Paving Technol. Proc. 1971, 40, 227–246. [Google Scholar]
- Majidzadeh, K.; Kauffmann, E.M.; Saraf, C.L. Analysis of Fatigue of Paving Mixtures from the Fracture Mechanics Viewpoint; ASTM Special Technical Publications; ASTM International: West Conshehoken, PA, USA, 1971; Volume 508, pp. 67–83. [Google Scholar]
- Moghadas, N.F.; Toolabi, S.F.E. Study of critical cracking condition in Asphalt overlay. In Proceedings of the 10th International Conference on Asphalt Pavements, Québec, Canada; 2006; Volume 1, pp. 67–75. [Google Scholar]
- Lytton, R.L. Use of geotextiles for reinforcement and strain relief in asphalt concrete. Geotext. Geomembr. 1989, 8, 217–237. [Google Scholar] [CrossRef]
- Abo-Qudais, S.; Shatnawi, I. Prediction of bituminous mixture fatigue life based on accumulated strain. Constr. Build. Mater. 2007, 21, 1370–1376. [Google Scholar] [CrossRef]
- Doh, Y.S.; Baek, S.H.; Kim, K.W. Estimation of relative performance of reinforced overlaid asphalt concretes against reflection cracking due to bending more fracture. Constr. Build. Mater. 2009, 23, 1803–1807. [Google Scholar] [CrossRef]
- Wei, H.; Li, J.; Wang, F.; Zheng, J.; Tao, Y.; Zhang, Y. Numerical investigation on fracture evolution of asphalt mixture compared with acoustic emission. Int. J. Pavement Eng. 2022, 23, 3481–3491. [Google Scholar] [CrossRef]
- Zhou, L.; Ling, J.M.; Lin, X.P. Prediction model for fatigue crack of asphalt pavement with environmental factors considered. China J. Highw. Transp. 2013, 26, 47–52. [Google Scholar]
- Zheng, M.; Li, P.; Yang, J.; Li, H.; Qiu, Y.; Zhang, Z. Fatigue life prediction of high modulus asphalt concrete based on the local stress-strain method. Appl. Sci. 2017, 7, 305. [Google Scholar] [CrossRef]
- Praticò, F.G.; Fedele, R.; Naumov, V.; Sauer, T. Detection and monitoring of bottom-up cracks in road pavement using a machine-learning approach. Algorithms 2020, 13, 81. [Google Scholar] [CrossRef]
- Alshandah, M.; Huang, Y.; Lu, P.; Tolliver, D. Bottom-up crack detection in concrete pavements using in-pavement strain sensors. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10598, pp. 616–625. [Google Scholar]
- JTG F40-2004; Technical Specification for Construction of Highway Asphalt Pavement. People’s Communications Publishing House: Beijing, China, 2004.
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. People’s Communications Publishing House: Beijing, China, 2017.
- Luo, R.; Huang, X.M. Calculation on the stress intensity factor for the bottom crack of asphalt layer in asphalt pavement considering partial constraint by weight function. Chin. J. Geotech. Eng. 2001, 23, 610–613. [Google Scholar]
- Wang, Z.Y. Selecting and Optimizing of Test Method Performance Based on Low Temperature Performance of Asphalt Crack Propagation Test Method Performance; Wuhan Institute of Technology: Wuhan, China, 2014. [Google Scholar]
- Pugno, N.; Ciavarella, M.; Cornetti, P.; Carpinteri, A. A generalized Paris’ law for fatigue crack growth. J. Mech. Phys. Solids 2006, 54, 1333–1349. [Google Scholar] [CrossRef]


| Test Items | Measured Data AH-70 | Technical Requirements AH-70 | Test Method |
|---|---|---|---|
| Penetration (25 °C, 100 g, 5 s, 0.1 mm) | 79.4 | 60–80 | T0604 |
| Softening point (°C) | 46.76 | ≥46 | T0606 |
| Ductility (10 °C) (cm) | 147.5 | ≥20 | T0605 |
| Ductility (15 °C) (cm) | >200 | ≥100 | |
| 60 °C Dynamic viscosity (Pa.s) | 297 | ≥180 | T0620 |
| Asphalt flash point (°C) | 284 | ≥46 | T0611 |
| Residual needle penetration ratio (25 °C) | 82.1 | ≥61 | T0604 |
| Residual ductility (10 °C) (cm) | 8.5 | ≥6 | T0605 |
| Residual ductility (15 °C) (cm) | 33 | ≥15 | T0605 |
| Mass Percentage (%) through the Square Hole Screen (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Specifications | 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| AC-13 | 100 | 100 | 99.7 | 95.1 | 76.8 | 38.4 | 29.1 | 23.0 | 17.3 | 12.2 | 10.4 | 7.9 |
| AC-20 | 100 | 99.1 | 91.1 | 73.3 | 54.9 | 30.3 | 23.6 | 18.7 | 14.2 | 10.0 | 8.6 | 6.6 |
| AC-25 | 99.1 | 79.0 | 73.0 | 65.7 | 52.7 | 36.7 | 32.0 | 23.7 | 15.0 | 10.2 | 8.2 | 6.8 |
| Gradation | AC-13 | AC-20 | AC-25 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 25 | 0 | −10 | 25 | 0 | −10 | 25 | 0 | −10 |
| Dynamic Modulus (MPa) | 832 | 14,690 | 25,149 | 1497 | 13,009 | 21,916 | 1850 | 15,813 | 15,813 |
| Gradation | AC-13 | AC-20 | ||||
|---|---|---|---|---|---|---|
| Temperature | 25 °C | 0 °C | −10 °C | 25 °C | 0 °C | −10 °C |
| OT results | 1000 | 97 | 10 | 1000 | 72 | 42 |
| Pavement Structure | Pitch Depth (mm) | Tensile Stress at the Bottom of Layers (Mpa) | ||
|---|---|---|---|---|
| 25 °C | 0 °C | −10 °C | ||
| A | 0–40 | 0.63 | 0.67 | 0.69 |
| 40–90 | 0.38 | 0.38 | 0.41 | |
| 90–150 | 0.20 | 0.23 | 0.31 | |
| B | 0–40 | 0.43 | 0.53 | 0.56 |
| 40–100 | 0.21 | 0.24 | 0.27 | |
| 100–180 | 0.11 | 0.16 | 0.19 | |
| C | 0–60 | 0.56 | 0.57 | 0.58 |
| 60–140 | 0.28 | 0.29 | 0.31 | |
| 140–240 | 0.12 | 0.14 | 0.16 | |
| Pavement Structure | Pitch Depth (mm) | Tensile Stress at the Bottom of Layers (Mpa) | ||
|---|---|---|---|---|
| 25 °C | 0 °C | −10 °C | ||
| A | 0–40 | 0.29 | 0.31 | 0.33 |
| 40–90 | 0.22 | 0.26 | 0.28 | |
| 90–150 | 0.14 | 0.18 | 0.19 | |
| B | 0–40 | 0.29 | 0.30 | 0.30 |
| 40–100 | 0.21 | 0.23 | 0.24 | |
| 100–180 | 0.11 | 0.13 | 0.15 | |
| C | 0–60 | 0.27 | 0.27 | 0.30 |
| 60–140 | 0.16 | 0.18 | 0.21 | |
| 140–240 | 0.08 | 0.10 | 0.14 | |
| Temperature | AC-13 | AC-20 | ||
|---|---|---|---|---|
| A | n | A | n | |
| 25 °C | 1 × 10−6 | 2.572 | 2 × 10−6 | 2.428 |
| 0 °C | 2 × 10−6 | 2.128 | 1 × 10−5 | 1.906 |
| −10 °C | 6 × 10−6 | 2.515 | 5 × 10−5 | 2.620 |
| Pavement Structure | Pitch Depth (mm) | Cracking Life (time) | ||
|---|---|---|---|---|
| 25 °C | 0 °C | −10 °C | ||
| A | 0–40 | 2240 | 1697 | 1487 |
| 40–90 | 21,784 | 21,783 | 15,475 | |
| 90–150 | 391,312 | 208,632 | 54,454 | |
| B | 0–40 | 12,490 | 4874 | 3804 |
| 40–100 | 314,175 | 172,269 | 101,396 | |
| 100–180 | 5,766,217 | 1,068,115 | 492,909 | |
| C | 0–60 | 3805 | 3513 | 3249 |
| 60–140 | 86,089 | 73,513 | 54,454 | |
| 140–240 | 3,898,005 | 1,947,968 | 1,068,115 | |
| Pavement Structure | Pitch Depth (mm) | Cracking Life (time) | ||
|---|---|---|---|---|
| 25 °C | 0 °C | −10 °C | ||
| A | 0–40 | 73,513 | 54,454 | 41,100 |
| 40–90 | 254,833 | 120,164 | 86,088 | |
| 90–150 | 1,947,968 | 628,683 | 492,909 | |
| B | 0–40 | 73,513 | 63,112 | 63,112 |
| 40–100 | 314,174 | 208,632 | 172,269 | |
| 100–180 | 5,766,216 | 2,719,023 | 1,428,062 | |
| C | 0–60 | 101,396 | 101,396 | 63,112 |
| 60–140 | 1,068,115 | 628,683 | 314,174 | |
| 140–240 | 24,168,688 | 8,854,377 | 1,947,968 | |
| Pavement Structure | Co (mm) | Ci (mm) | 25 °C | 0 °C | −10 °C | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E (MPa) | MOD (mm) | E (MPa) | MOD (mm) | E (MPa) | MOD (mm) | ||||||
| A | 5 | 40 | 832 | 0.625 | 14,628,099 | 14,690 | 0.625 | 47,998 | 25,149 | 0.625 | 78 |
| 5 | 50 | 1497 | 0.625 | 13,009 | 0.625 | 21,916 | 0.625 | ||||
| 5 | 60 | 1850 | 0.625 | 15,813 | 0.625 | 25,843 | 0.625 | ||||
| B | 5 | 40 | 832 | 0.625 | 18,600,394 | 14,690 | 0.625 | 58,390 | 25,149 | 0.625 | 97 |
| 5 | 60 | 1497 | 0.625 | 13,009 | 0.625 | 21,916 | 0.625 | ||||
| 5 | 80 | 1850 | 0.625 | 15,813 | 0.625 | 25,843 | 0.625 | ||||
| C | 5 | 60 | 832 | 0.625 | 26,937,407 | 14,690 | 0.625 | 80,363 | 25,149 | 0.625 | 134 |
| 5 | 80 | 1497 | 0.625 | 13,009 | 0.625 | 21,916 | 0.625 | ||||
| 5 | 100 | 1850 | 0.625 | 15,813 | 0.625 | 25,843 | 0.625 | ||||
| Pavement Structure | Temperature (°C) | |||
|---|---|---|---|---|
| A | 25 | 391,312 | 14,628,099 | 1.5 × 108 |
| 0 | 208,632 | 47,998 | 2.6 × 106 | |
| −10 | 54,454 | 78 | 5.5 × 105 | |
| B | 25 | 5,766,217 | 1,860,0394 | 2.4 × 108 |
| 0 | 1,068,115 | 58,390 | 1.1 × 106 | |
| −10 | 492,909 | 97 | 4.9 × 106 | |
| C | 25 | 3,898,008 | 26,937,407 | 3 × 108 |
| 0 | 1,947,968 | 80,363 | 2 × 107 | |
| −10 | 1,068,115 | 134 | 1 × 107 |
| Pavement Structure | Temperature (°C) | |||
|---|---|---|---|---|
| A | 25 | 1,947,968 | 14,628,099 | 1.7 × 108 |
| 0 | 628,683 | 47,998 | 6.8 × 106 | |
| −10 | 492,909 | 78 | 4.9 × 106 | |
| B | 25 | 5,766,216 | 18,600,394 | 2.4 × 108 |
| 0 | 2,719,023 | 58,390 | 2.8 × 107 | |
| −10 | 1,428,062 | 97 | 1.4 × 107 | |
| C | 25 | 24,168,688 | 26,937,407 | 5.1 × 108 |
| 0 | 8,854,377 | 80,363 | 8.9 × 107 | |
| −10 | 1,947,968 | 134 | 1.9 × 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, G.; Zheng, Y.; Yu, J.; Liu, J.; Hu, X. Investigation of the Fatigue Life of Bottom-Up Cracking in Asphalt Concrete Pavements. Appl. Sci. 2022, 12, 12119. https://doi.org/10.3390/app122312119
Cheng G, Zheng Y, Yu J, Liu J, Hu X. Investigation of the Fatigue Life of Bottom-Up Cracking in Asphalt Concrete Pavements. Applied Sciences. 2022; 12(23):12119. https://doi.org/10.3390/app122312119
Chicago/Turabian StyleCheng, Gang, Yong Zheng, Jie Yu, Jun Liu, and Xinhe Hu. 2022. "Investigation of the Fatigue Life of Bottom-Up Cracking in Asphalt Concrete Pavements" Applied Sciences 12, no. 23: 12119. https://doi.org/10.3390/app122312119
APA StyleCheng, G., Zheng, Y., Yu, J., Liu, J., & Hu, X. (2022). Investigation of the Fatigue Life of Bottom-Up Cracking in Asphalt Concrete Pavements. Applied Sciences, 12(23), 12119. https://doi.org/10.3390/app122312119









