1. Introduction
The digital twin (DT) is the indistinguishable digital replica of an object, a physical system, or a procedure for the simulation, prediction, and optimization of its performance. DT fits, without a doubt, into modern technological and scientific developments. One of the main characteristics of digital twin technology is its connectivity. Distributed, online, low-cost sensors are being developed to support the internet of things (IoT); big data are generated and transmitted through modern wireless networks (e.g., 5G); and artificial intelligence (AI) and deep learning (DL) promise to accomplish complicated data-processing tasks. On the other side, multi-physics computational mechanics modeling reproduces physical reality with confidence. The resulting integrated system is a cyber-physical entity. All these elements pave the way to the so-called Industry 4.0 revolution, following stream power, electricity, and microchips.
‘Industry 4.0’ is the term currently used to describe the trend of digitalization and data exchange in production lines. The emphasis is placed on the ‘digital factory’, where the production is constantly supervised so that an updated and reliable model is available at all times that allows for the study of possible scenarios, including predictions of the remaining life for the predictive maintenance of equipment. Data collection and exchange between physical and digital systems is facilitated through the ‘Internet of Things’ and the availability of quick networks such as 5G.
Multi-physics simulation and data analytics support digital twins. The creation of digital twins and their continuous updating based on the usage of big data of measurements during the life of a system constitutes a natural continuation of scientific disciplines such as modeling, parametric technical modeling, model and parameter identification, and process or structural health monitoring. It is feasible due to the continuous development of computational techniques, large-scale optimization through classical or nature-inspired methods, cheap sensors, and wireless data transfer (IoT and 5G). Looking at the techniques used, one may recognize that digital twins are a balanced mixture of multi-physics models, statistics, and artificial intelligence for the reconstruction of the natural reality through field measurements on possibly simplified or reduced-order digital models. The existence of data and a mechanism for model update and parameter identification are considered to differentiate a DT from a classical engineering model [
1].
The evaluation of the DT concept can be traced in several sources, among them the references [
2,
3,
4,
5,
6], which will be discussed later in this paper. Parametric computational models and classical parameter identification problems were developed earlier, as described in references [
7,
8,
9,
10,
11,
12,
13,
14,
15].
The application of digital twin methodology on civil infrastructures is a current research topic. Wind turbines or floating structures are exposed to unpredictable and extreme loads. Therefore, their fatigue response and life prediction are challenging tasks that can be resolved by digital twin technology. When used as a part of a hybrid energy storage system, even more classical structures, such as hydropower facilities, are loaded unpredictably and require more detailed study.
Applications on infrastructures are described in recent publications such as [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25], with an emphasis on extremely loaded structures such as lightweight steel structures and wind turbines that are prone to fatigue [
26,
27].
The purpose of this paper is to facilitate an introduction to these new fields for people with a classical computational mechanics background, through the review of recent digital twin applications on infrastructure. The ways of connecting the introduced concepts of digital twins with conventional parametric modeling, reverse engineering, and parameter identification will be discussed. The paper focuses on the links between DT and classical computational mechanics and does not aim to be a thorough review of the vast DT literature and its applications in other areas.
2. Digital Twins as the Extension of the Parametric Simulation, Parameter Identification, and Structural Health Monitoring
A digital twin can be defined as a representation of a physical model in a digital form that can be adapted to provide reliable predictions of the response of the physical model in a changing environment. A physical model can be a building, electromechanical equipment, infrastructures, etc. The data collected concerning a structure’s design and operation are significant for creating a DT. According to the Gemini Principles, the digital twin is the digital representation of an element, process, or system in its physical environment [
2].
The digital twin (DT) has been advertised as a standard model that incorporates high-accuracy simulations of a structure, operational parameters (structural and SHM), and maintenance data as well as historical operational data to capture the current state of the physical twin, to conduct lifecycle management, and to estimate the safety, reliability, and maintenance of the structure. It can be considered an extension of classical 3D CAD models into models of higher dimensions, for example, a 5D model if time and measurements were added.
DT was first introduced in the aerospace industry and currently appears in several industries. A digital twin can be created, regardless of size, from individual elements (components, pipelines, etc.) to complex processes and environments (plants, production lines, wind farms, hydroelectric parks, etc.). The complexity depends on the information capability of the infrastructure.
DT is part of modern technological and scientific developments. Low-cost sensors are being developed to support IoT, big data are being generated and transferred via modern wireless networks (5G), artificial intelligence and deep learning promise to perform complex data processing tasks even on-site (edge computing), and multi-physics computational techniques can reproduce the behavior of the physical model with high accuracy. This integrated system with physical and digital properties is called Industry 4.0.
The creation of a digital twin requires several elements, such as:
Sensors that record and collect data for the operational behaviors of the components and processes (vibrations, temperature, pressure, etc.), along with their operating environments (air temperature, humidity, etc.).
Communication networks providing secure, wireless, and reliable data transfer from devices to the digital world.
Local preprocessing, in the case of the limited capacity of communication networks.
A digital platform that works as a modern database. It can collect and store enormous data from a plant, and by combining these data, information can be generated for data-driven decision-making techniques using, among others, advanced artificial intelligence/machine-learning algorithms.
The most common applications of a digital twin are carried out for the following two reasons:
Maintenance prediction: By gaining a holistic view of the operation and the performance of the physical model, the user can detect the deviation in its operations. The maintenance and the replacement of spare parts can be pre-scheduled to minimize time and reduce failures. For manufacturers, predictive maintenance using digital twins can provide new service-based revenue while helping to improve product reliability. Examples are discussed in [
17,
23,
27,
28].
Process design and optimization: A digital footprint that collects sensor data from a production line, as well as data from enterprise resource planning (ERP) systems, can thoroughly analyze key performance indicators (KPIs), such as production rates and data quantities that are practically “useless.” This helps diagnose the cause of any inefficiencies and performance losses, thereby optimizing performance and reducing wasteful information. Going a step further, historical data on equipment (operation time and wear), processes, and the environment (e.g., temperatures and pressures) of the production line can enable the prediction of a shutdown to improve production scheduling. A review of DT in this direction, although relevant to construction industry, lies out of the focus of this paper.
For structures and infrastructures, the prediction of fatigue and other degradation effects is highly connected with the need for DTs. A prediction can be based exclusively on statistic evaluation or data analytics of the big data collected through sensors during the life of the structure or, preferably, by using parallel solid mechanical models, such as the concepts of fracture or damage mechanics. Details and references are given in
Section 4.
3. Description of Methods and Tools
A digital twin can be based on a two-dimensional (2D) or three-dimensional (3D) geometric entity for mechanical equipment or a building, up to a more sophisticated multi-physics model that will represent an entire structure interacting with the environment and its users throughout its lifecycle. It could even be a network of digital twins that would supervise the operation of a whole system.
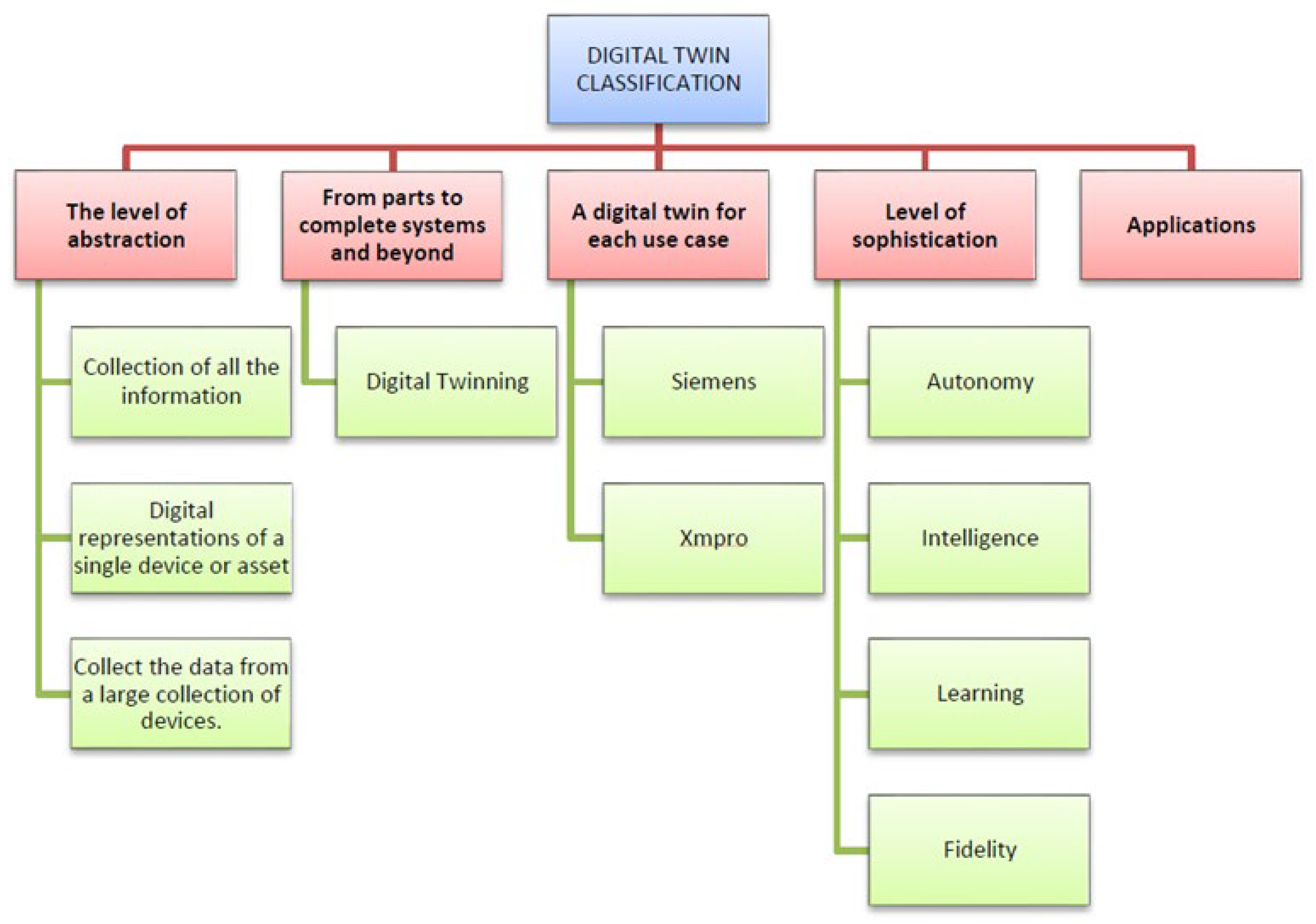
According to analyses, there are 5 ways to categorize a digital twin, as shown in
Figure 1.
The first category concerns the collection of all the system information that is required to create the digital twin, such as engineering drawings, the operation instruction of the plant, etc. The second category contains the collection of historical data from a device to create a digital path. This includes various sensor data from the device as well as recording periods of maintenance or the occurrence of a fault. The third category collects the data from all possible devices, which provides the possibility of collecting information that would help in a statistical analysis of the data, such as the average failure time, the standard deviation, which part fails more easily, etc.
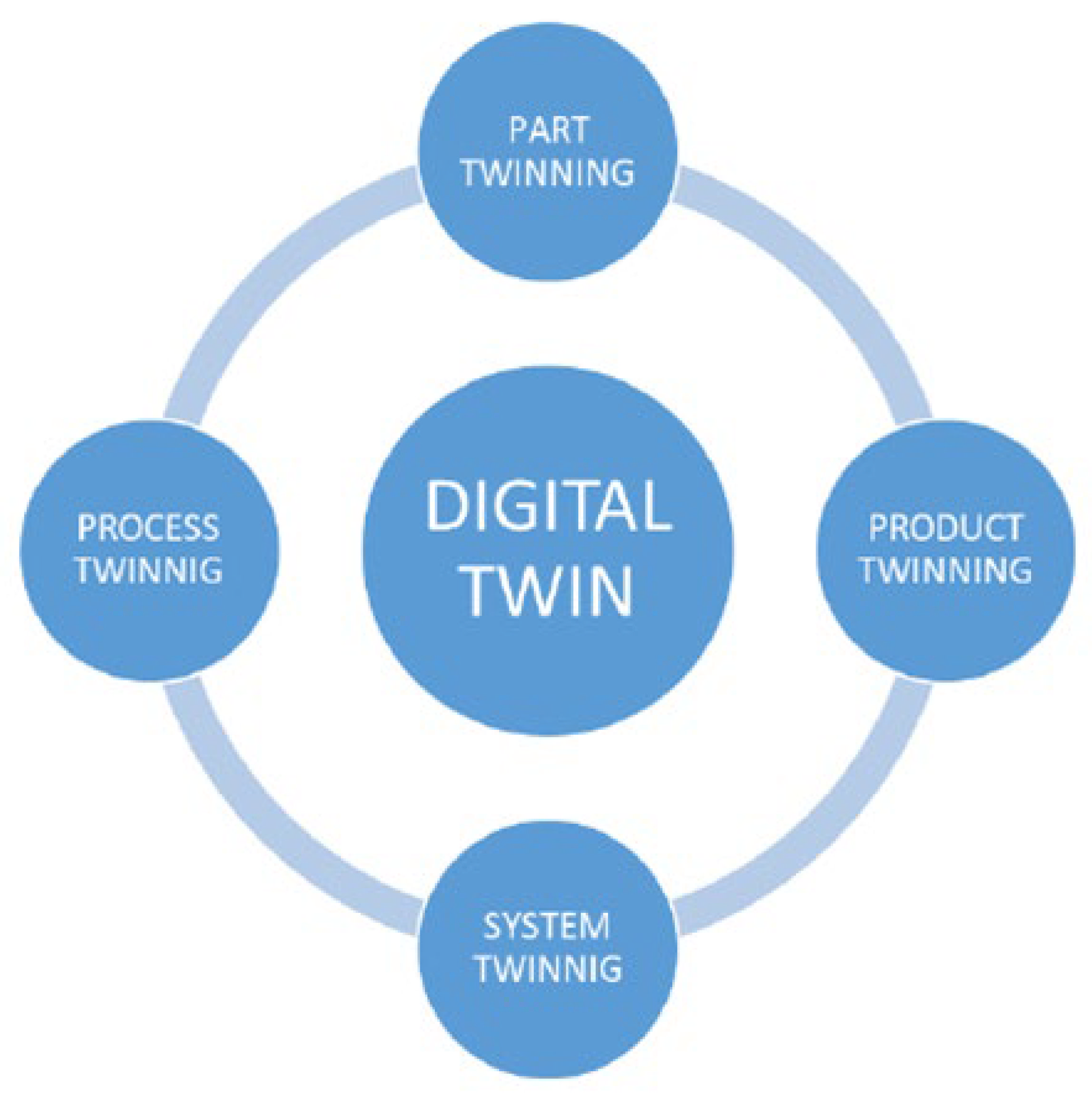
In the second category, the hierarchy of digital twins is concerned as shown in
Figure 2. Firstly, the digital twin of a part is created for better capture of the physical, mechanical, and electrical properties of a component depending on the operational conditions, e.g., a structure under a thermal loading or an electronic circuit. Next, there is the digital twin of the whole product, which consists of many pieces created in the previous stage and studying how they interact with each other. The system twin is the highest and most complex level of analysis, in which an integrated system of products that interact with each other is modeled and can be studied and maintained in parallel by monitoring the operating process through platforms to optimize efficiency and effectiveness. The last category, not necessarily involved with the above or necessary in every application, concerns the digital twin of a process and not a physical one [
3].
In the third category, we have the digital twin depending on the use that is required and how each implementation group’s categorization is formed. For example, Siemens considers that, for applications in digital twin, there are 3 categories. The product category focuses on individual products. The production category is about the representation of a production process and is used to design processes that are robust and flexible, and finally, the digital twin performance category brings together the operational data of a production process to optimize performance [
4].
Another case is that of XMPRO, where the digital twin reflects the current state of a device. In this case, it is simply a dashboard, similar to the one used for supervisory control and data acquisition (SCADA), and the digital twin is used to simulate possible scenarios, utilize the data in it, and adjust the system accordingly [
5].
The application and the idea behind the digital twin are common but differ in implementation, as shown in various application examples. The case of a machine and its operation in a system differs from a production process or an economic digital twin.
The last categorization of a digital twin concerns its complexity. This complexity is expressed in terms of autonomy, intelligence, learning, and fidelity. A scale of 1 to 5 is used, where 5 refers to a digital twin that replaces a human being for certain mundane tasks. This classification system is not easy to use as the digital twin is likely to be competent in one category and not in others. However, these classifications will be improved in the future, and this is due to the use of artificial intelligence that has the ability to be integrated on top of the digital twin [
6].
3.1. Digital Twin Definition and Relations to BIM, BLM, and PLM
A digital twin is a digital representation of a physical asset. It is used to help engineers understand what is happening to a physical building or piece of infrastructure. In contrast to the classical way of designing, the data and information accumulated through the design, construction, and usage of a structure constitute its digital twin. The Gemini Principles define a digital twin as “a realistic digital representation of assets, processes or systems in the built or natural environment” [
2].
Digital twins are adaptive and therefore provide reliable predictions within a changing environment. They are in accordance with the current trend toward digitalization and have a remarkable effect on business and markets. A schematic representation of the elements that are used for a DT application on infrastructures is shown in
Figure 3.
Historically, DT is the evolution of building information modelling (BIM), building lifecycle management (BLM), and product lifecycle management (PLM). Depending on the maturity of DT, it may be restricted to a simple capture of reality, such as a photogrammetry measurement of an existing building, to a fully autonomous system, such as the control mechanism of a drone. The main tools required to create and operate a digital twin are the following:
Computer-aided design (CAD) provides the tools to create a structured geometric model of an entity, which is usually available for a new or well-documented structure. For an existing structure with possible modifications, usage of terrestrial or even aerial laser or photogrammetric scanners can be used [
7]. The automatic creation of a CAD model is not yet an easy task.
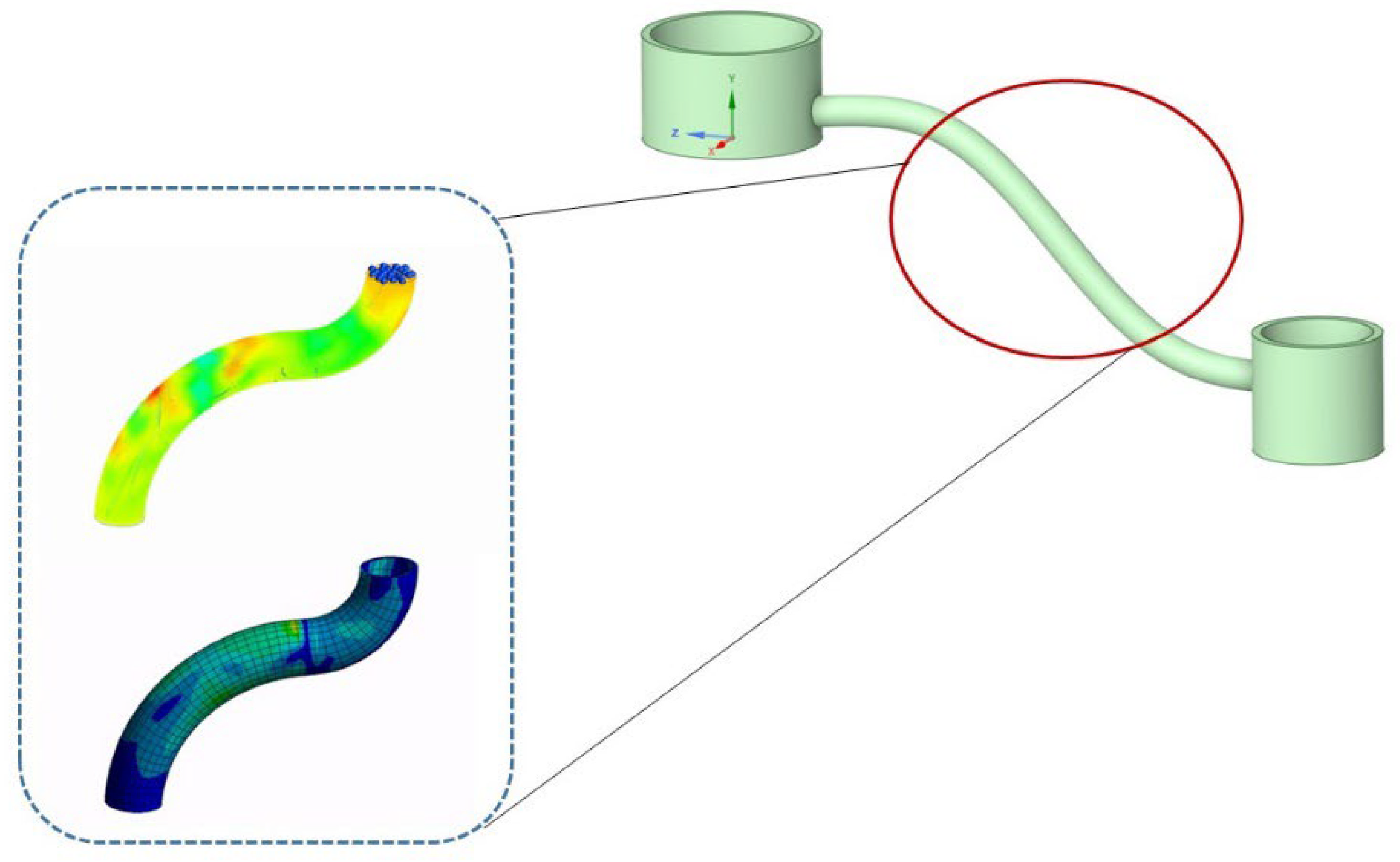
Computational mechanics offers tools for parametric simulation. In this way, it is possible to generate a large amount of data from ideal experiments that can be used for solving optimal design and inverse problems and for evaluating scenarios. The accuracy of the model may be different in regions of particular interest, e.g., a 3D non-linear model in the region where stress concentrates, failures, and other phenomena are expected, and whole regions may be linked to the sub-structure technique and describe the mechanical behavior macroscopically (see
Figure 4). The existence of model(s) that support DT facilitates the cognitive properties of the digital system. The result is characterized by some authors as a cognitive digital twin (CDT) [
29].
A dense large-scale model, which guarantees adequate accuracy and reliability of results, may under certain conditions decrease drastically while maintaining reliability in results. The concept of static and dynamic condensation is well-known in the linear analysis of structures and has been extended to nonlinear systems. A schematic representation of a reduced-order model applied on a reinforced frame is shown in
Figure 4, where areas of interest near joints can be modeled by using nonlinear detailed finite element models, while areas of less importance or less vulnerable to damages are modeled by simpler beam elements.
Optimization is a necessary tool for achieving the best possible results in a problem to be solved by optimizing the parameters of the problem. In addition to the classical optimization methods, there are those inspired by nature that are very efficient (genetic algorithms, particle swarm algorithms, etc.) as well as so-called loose soft computing tools (neural networks and neuro-fuzzy inference).
The processing of data generated from experiments or numerical models by means of neural networks has a long history in structural mechanics [
28]. For example, moment-rotation diagrams of semi-rigid bolted steel structure joints can be simplified and post-processed by using artificial neural networks, which in turn create the desired DT of the joint. See
Figure 5 and [
30].
Finally, it underscores the rapid development of free available tools, such as the Python programming language and its accompanying packages, for solving engineering, artificial intelligence, and combinatorial optimization problems with the capabilities of parametric simulation, parameter identification, use of neural networks, and deep learning.
3.2. Computational Mechanics Tools
Within the classical finite element analysis of large-scale models, the need for reduced order models (ROM) has been studied. The classical tools are focused on linear static and dynamic problems, known as static condensation or Gyan reduction [
8]. Modern approaches deal with nonlinear problems. Provided that an accurate model exists, for example, a finite element model of a high order, the reduction can be based on engineering arguments and techniques, such as hierarchical modeling, macro-modeling, and domain decomposition, or on mathematical tools, such as singular value decomposition (SVD) [
9]. Conversely, data-driven methods produce a reduced order model based on the input/output data that may be collected from an experiment or measurements on a real structure. Data-driven methods using data analytics or artificial intelligence are very popular within the DT community. In both cases, the goal of model reduction is to provide a reliable substitute for the full-scale model, by making the difference between the full-order model and reduced-order model small under some appropriate norm.
Within the context of DT, the existence of ROM allows for quick, possibly real-time implementation. The additional step of extracting local information at areas of interest from the predictions of the reduced model is also of interest. Provided that a warning has been sent by the DT model, one wants to examine a component in more detail, for example by calculating stresses and stresses, to use results from a fracture and fatigue analysis and proceed with the estimation of appeared damages. A schematic representation of the concept is shown in
Figure 6.
3.3. Optimization and Data-Based Tools
Classical parameter identification is based on optimization or soft computing tools [
10,
11,
12]. In fact, the parametrized model provides predictions of the response for every choice of the parameters. Provided that the parametrization is able to model the expected damages, the parametrized results are compared with the measurements, and the values of the parameters are updated. Responses of more than one loading can be used together, fused, in order to enhance effectiveness. Moreover, the parameter identification problem is generally ill-posed, in the sense that a multiplicity of solutions and inefficient scaling arises [
13]. Therefore, quite complicated regularization techniques are needed in order to facilitate the usage of numerical optimization. For this reason, the usage of machine learning and data-based techniques that address the identification question on a reduced-order model or surrogate model is beneficial [
14,
32]. Another promising approach is the usage of filtering, such as Kalman-type filters, for the solution of parameter identification problems [
10,
15].
Processing big data and extracting knowledge or simple predictions is a challenging task. Cooperation with experts and the usage of appropriate tools is a must. Google realized savings of 40% on its own data centers using DeepMind. In mechanics, solid models can assist the user in evaluating and understanding the data. For example, the blind evaluation of data using neural networks (see, e.g., [
33,
34]) can be assisted with the knowledge of the mechanical or mathematical model that governs the underlying relation, such as the physics-informed neural networks (PINNs) developed for the solution of partial differential equations arising in mechanics [
35,
36]. Similarly, a blind attempt to extract knowledge within a digital twin system is facilitated by the usage of computational mechanics models that create data for several possible scenarios, leading to model-assisted, cognitive digital twins [
29].
4. Overview of Recent Applications
The first recent digital twin application appeared in the field of mechanical engineering by General Electric and concerned the entire lifecycle of aircraft and engines. The engineering sector in construction will present great challenges and needs in the future. This company has paid a lot of attention to the field of digital twins with its applications in remote process monitoring, which yields savings [
28], in the transmission of electricity and their units, and in many others that will be analyzed as applications in the work.
Another ambitious project is Britain’s National Digital Twin in collaboration with the University of Cambridge [
2]. The project aims to digitize national infrastructure to enable operations to be carried out that will save time and money and minimize problems in order to provide better services for all. This process is the evolution of building information modelling (BIM), building lifecycle management (BLM), and product lifecycle management (PLM) systems.
Amongst the multitude of approaches to SHM, the digital twin model is gaining increasing attention. This model is a digital reconstruction (the digital twin) of a real-life asset (the physical twin) that, in contrast to other digital models, is frequently and automatically updated using data sampled by a sensor network deployed on the latter [
16].
Ye et al. [
17] presented an exploratory study toward creating a digital twin of bridges for structural health monitoring purposes. The research involved an interdisciplinary collaboration between the Cambridge Centre for Smart Infrastructure and Construction (CSIC) and the Alan Turing Institute (ATI), using two monitored railway bridges in Staffordshire UK as a case study. A synthesis of physics-based and data-driven analytical approaches has been explored and investigated for extracting greater value of information from the bridge SHM data.
Shim et al. [
18] designed a new bridge maintenance system using a digital twin model concept. According to different maintenance tasks, the inventory and information requirements were investigated. The recorded responses from the sensors were used to update the digital twin model. Based on the design of the maintenance system, a pilot application at an existing cable-stayed bridge in Korea was conducted.
Jiang et al. [
19] proposed a DT-driven framework for the fatigue lifecycle management of steel bridges. The primary contribution presented in this work is the integration of the three main components of fatigue prediction, maintenance, and inspection/monitoring, which clarify the flow and dependency among data and form a dynamic closed-loop data stream between the virtual and physical spaces. The advantage of this DT-driven framework is that it returns more accurate management strategy results than existing frameworks do, indicating a further reduction in failure risks and lifecycle costs.
Benzo et al. [
20] presented a novel methodology for creating an operational digital twin for large-scale structures based on drone inspection images. The digital twin was primarily used as a virtualized representation of the structure, which was updated according to the physical changes during the lifecycle of the structure. The methodology was demonstrated on a wind turbine transition piece. A three-dimensional geometry reconstruction of a transition piece as manufactured was created using a large number (>500) of RGB images collected from a drone and/or several LiDAR scans. Comparing the reconstruction to the original design identified and quantified geometric deviations and production tolerances. An artificial intelligence algorithm was used to detect and classify paint defects/damages from images. The detected and classified paint defects/damages were subsequently digitalized and mapped to the three-dimensional geometric reconstruction of the structure. These developed functionalities allowed the digital twin of the structure to be updated with manufacturing-induced geometric deviations and paint defects/damages using inspection images at regular time intervals.
Rojas-Mercedes et al. [
21] presented the development of seismic fragility curves for a precast reinforced concrete bridge in the Dominican Republic, instrumented with a structural health monitoring (SHM) system. In this research, the digital twin is used as a response prediction tool that minimizes modeling uncertainty, significantly improving the predicting capability of the model and the accuracy of the fragility curves. The digital twin was used to perform a nonlinear incremental dynamic analysis (IDA) with selected ground motions that were consistent with the seismic fault and site characteristics.
Rageh et al. [
6] presented and examined the efficacy of a framework for automated model calibration using a measured operational and ambient structural response for the development of a precise digital twin of a physical structure. The guidelines provided in this research aim to assist in choosing the right model class for accurate response prediction. The study used an in-service, double-track, riveted steel plate girder railway bridge as a testbed for the proposed framework.
In the research of Fahim et al. [
27], a 5G Next Generation Radio Access Network (5G-NG-RAN) assisted the cloud-based digital twins’ framework to virtually monitor wind turbines and form a predictive model for forecasting wind speed and predicting the generated power of wind turbines.
Further recent applications on infrastructures, mainly bridges, can be found in [
22,
23,
24,
25,
37,
38].
A schematic representation of a DT that can help predict fatigue in a hydropower plant is shown in
Figure 6. The whole hydraulic network that connects two reservoirs at different levels and is used for storage of energy can be modelled by using classical one-dimensional reduced models. If pressure deviations at a given point are considered to be high, a detailed finite element model can be used to assist damage and fatigue prediction.
5. Technology Required for the Implementation of Digital Twins
The technology proposed is the creation of a simplified model for the whole infrastructure, which contains detailed data and 3D modeling for its critical elements. Subsequently, its parameters are continuously updated using optimization techniques or neural networks. The updated model will be used to support the fuller utilization of the plant, the reduction of inactive time (shutdown), and the reduction of overall operating costs through the support of preventive maintenance. The system is close to the proposals and applications described by Akselos, e.g., for power generation projects [
31] and industrial installations in general [
39]. The digital twins offered by Akselos perform impressive structural simulations in near real-time for the offshore industry but seem less suitable as digital twins for factory production lines. Another solution for structures, which includes hardware for sensing and software for digital twinning, is offered by ASDEA Engineering [
40].
The tools for creating digital twins vary on the market; however, each company tries to orient its platform toward its applications. For example, General Electric, Ansys, Siemens, Altair, and Dassault each offer their platform oriented toward either product and manufacturing simulations, process simulations, or both. Microsoft also has a digital twin, but for the time being it seems to focus mainly on data collection for further analysis. The same applies to PTC’s offering. Thus, everyone in the field projects their interpretation of the concept.
In summary, one could say that a classical computational mechanics specialist interested in using or developing DT applications should refresh his/her knowledge in the areas of:
Parametric modeling using computer-aided design and finite elements.
Parameter identification and inverse problems.
Artificial intelligence for the creation of metamodels.
Furthermore, the link of DT with virtual and augmented reality (VR/AR) deserves more attention. The concepts of VR/AR are older than that of VT. While VR/AR augments the virtual world with reality, DT is based entirely on the digital world. The usage of VR/AR concepts for producing user-friendly interfaces of DTs, which inherit the real behavior of the physical object and bidirectional interaction with the users, that could facilitate training and experimentation with if-then scenarios is a concept that seems to be worthy of investigation [
41,
42]. For the time being, a bidirectional link seems to be very demanding, but this could change in the near future. These steps could lead to the enhancement of enterprise or industrial metaverse with objects recreated and fed with live data in order to behave exactly as they would in the real world. For infrastructures, this could have important civil or defence applications.
6. Conclusions
The field of DT is a topic of rapid development in the last few years. The number of publications is exploding. Nevertheless, at least for applications on structures and infrastructures, this development is based on and supported by solid knowledge of computational mechanics, parameter identification, and machine learning, as well as software and hardware developments. This paper attempts to bridge the gap between more classical communities and the need arising from current DT discussion.
Numerous digital twin applications in infrastructure and industry are presented in this paper. The use of the technology of DT is interpreted in the forms of optimization, data integrity, maintenance, etc. Research and development needs within the areas of computational mechanics, applied optimization, and artificial intelligence can be evaluated in view of current needs of DT. Conversely, engineers with a classical background will hopefully find their orientation in the vast amount of DT material, which in several cases does not provide a clear picture of the goals and techniques used.
DT for structures, possibly with interfaces based on AR/VR, will enhance the experimentation and predictive analysis of existing critical infrastructure, with the potential of reducing downtime and incurred costs and increase the security level and confidence of operators.