Abstract
The tunable properties of nematic liquid crystals (NLC) are here exploited in a peculiar leaky waveguide with artificial magnetic conductors as the lateral walls, a bottom metal ground plane, and a homogenized metasurface on top to obtain dynamic beamsteering at a fixed terahertz frequency. The waveguide consists of an NLC cell sandwiched between two dielectric layers. The proposed antenna system works on its transverse-magnetic leaky mode and is capable of radiating a beam that scans either by frequency or by changing the bias voltage applied across the NLC cell. The design parameters are optimized through a rigorous modal analysis of the structure, and the radiation performance is validated through full-wave simulations. The results are promising for the realization of next-generation tunable terahertz leaky-wave antennas.
1. Introduction
The distinctive frequency-scanning feature of leaky-wave antennas (LWAs) [] recently experienced somewhat of a ‘renaissance’ in the terahertz (THz) range, where it has been proposed as a key feature in a number of promising THz applications spanning from sensing to multiplexing [,,,,,,]. On the other hand, the frequency-scanning feature is undesired in most microwave communication systems, where instead the beam is required to be fixed over a relatively narrow bandwidth (see, e.g., [] and the references therein). This aspect stimulated the design of reconfigurable antennas, i.e., antennas exhibiting a beamscanning feature at a fixed frequency [,,].
As a result, various fixed-frequency LWAs have been proposed in the microwave range based on different technologies, such as active impedances [,,], piezoelectric actuators [], ferroelectric materials [,], or other tunable materials, such as nematic liquid crystals (NLC) [,,,,,]. This ‘abundance’ has no counterpart in the THz domain, where it is already challenging to obtain high-gain antennas, even without featuring any reconfigurable property [,,,]. As a matter of fact, experimental realizations of tunable THz LWAs are yet to appear, although several graphene-based designs have been proposed (see, e.g., [,,]) on a theoretical basis.
Unfortunately, most of graphene-based antenna designs in such frequency ranges rely on rather optimistic assumptions on the graphene properties, as suggested in [], and recently confirmed by experimental measurements via THz time-domain spectroscopy (TDS) in both transmission [] and reflection mode []. Therefore, research on graphene-based THz LWAs is still at an early theoretical stage, and more mature technologies have to be found.
Interestingly, THz-TDS measurements [] have shown that the nematic liquid crystal mixtures w-1825 and w-1852 exhibit attractive electromagnetic properties in the THz range—namely, high birefringence and moderate losses. The former is crucial to considerably affect the phase constant of leaky modes in NLC-filled waveguides and, in turn, steer the beam of an antenna over an appreciable angular range. The latter is key to obtain a sufficiently low leakage rate , and thereby achieve satisfactory antenna performance in terms of directivity and efficiency.
As a result, a number of tunable passive THz devices based on NLC, such as filters, polarizers, cavities, etc., have recently appeared (see [] and the references therein) and, more recently, even NLC-based LWAs [,,]. The concept of tunable LWAs based on NLC at a fixed THz frequency was theoretically proposed in [], where it was applied to a Fabry–Perot cavity-like structure to radiate a pencil beam at broadside and/or a directive conical beam achieving about a of angular reconfigurability in elevation with efficiencies as high as at around 500 GHz.
The results in [] were confirmed by full-wave simulations, whereas experimental results showing similar performance were obtained at lower frequencies—namely, at the W-band, with a 1-D image-line LWA []. More recently, preliminary results [] demonstrated the possibility to achieve beam-steering at approximately 1 THz with a peculiar leaky waveguide filled with NLC and made of perfect electric and magnetic conductors (PEC and PMC, respectively), and a homogenized metasurface that acts as a partially reflecting sheet (PRS).
In this work, we elaborate on the preliminary analysis of [], providing the necessary details to properly design both the artificial magnetic conductor (AMC) and the PRS, which were previously supposed to be an ideal PMC and an ideal isotropic metasurface, respectively. Moreover, we derive a useful analytic formula to evaluate the scan rate at a fixed frequency that is then exploited to determine the optimal working points for the proposed design. An original analysis on the antenna performance clearly reveals that the angular tunability is improved by radiating close to broadside or endfire, whereas the gain monotonically increases when radiating close to endfire. However, LWAs do not usually radiate efficiently at endfire unless properly designed (see, e.g., Ref. [,]); a sub-optimal operating condition is thus selected to deal with such constraints.
The paper is organized as follows: Section 2 covers the necessary background on LWAs to understand the working principle of the original leaky waveguide proposed here. Section 3 provides design rules to optimize the antenna structure, as well as to correctly synthesize both the AMC and the PRS. Finally, in Section 4, full-wave results are reported and commented. Our conclusions are presented in Section 5.
2. Theoretical Analysis
2.1. Closed Waveguide
We start from the analysis of the PEC/PMC air-filled waveguide (see Figure 1, left, with the relevant coordinate systems), which differs from the one analyzed in [] for having the PEC and PMC walls along the short and long sides, respectively, (in our geometry equivalent to the horizontal and vertical sides, respectively). A simple eigenvalue analysis of this structure reveals that the fundamental mode is a transverse electric and magnetic (TEM) mode (the limit case of a transverse electric (TE) mode, as opposed to the TEM mode of the parallel-plate PEC waveguides, which is the limit case of the transverse magnetic (TM) mode), whereas the first higher-order mode is the (the first and second subscript refer to modal indexes along the z- and y-axes, respectively).

Figure 1.
From left to right, an air-filled PEC/PMC waveguide, which evolves first in an open leaky waveguide where the PEC top plate is replaced by a PRS, is then entirely filled with an NLC to allow for dynamic beamsteering and, finally, is only partially filled with an NLC material to compensate for losses.
In the PEC/PMC air-filled waveguide, due to the closed and lossless nature of the problem, the propagation wavenumber of the mode can only be either purely real or purely imaginary [], depending on whether the mode is above or below the cutoff. Hereafter, we will focus exclusively on this mode as the radiating properties of the proposed LWA will be determined by its perturbed (partially open) version.
The eigenvalue analysis also reveals that the mode has only , , and components, with and , being the transverse wavenumber. We note here that this modal configuration has consequences on the required feeding scheme of the waveguide. As shown in [], the sinusoidal profile of the field of the mode couples efficiently with the Gaussian profile of the impinging transversely polarized THz beam commonly used as a free-space excitation source. Conversely, the mode has a non-negligible field component that can be efficiently excited with a longitudinally polarized THz beam. Therefore, sources such as those proposed in [,] are considered here for efficient excitation of the desired mode.
2.2. Open Leaky Waveguide
We now replace the top PEC plate with a PRS (see Figure 1, the second from the left), which enforces a surface impedance boundary condition of the type , where the superscripts refer to the field immediately above (below) the PRS, is the unit vector along the z-axis, and is the surface impedance of an isotropic lossless metasurface, which is thus described by a single scalar reactance value . We also assume the PRS to be highly reflective (i.e., , with as the vacuum impedance) so as to slightly perturb the modal configuration of the mode.
However, the partially open nature of the problem will now allow the propagation wavenumber to be generally complex [,]. This perturbed version of the will be referred to as the TM leaky mode when : it will represent the dominant contribution to radiation when and [,], where and are the phase and attenuation constants of the leaky mode, and is the vacuum wavenumber. Since the modal field of the TM leaky mode is constant with respect to the y-axis, we will study its propagation properties with the aid of a transverse equivalent network (TEN) [], as will be discussed in more detail in Section 3.
As is well-known [], one-dimensional (1-D) PRS-based LWAs, such as those considered here, radiate half of a conical beam. The beam angle (measured from the vertical z-axis) and dB beamwidth are determined by the normalized phase and attenuation constants through the following approximate relations:
The directivity D is instead given by []:
2.3. Tunable Leaky Waveguide Filled with NLC
From the radiating viewpoint, the structure considered thus far is a conventional 1-D PRS-based LWA. Therefore, the beam will scan with frequency f through the approximate formula []:
where c is the speed of light in vacuum, the real part of the relative permittivity of the dielectric material filling the waveguide, and h the height of the waveguide in the vertical direction—here, the z-axis.
However, our goal is to have beamscanning at a fixed frequency around 1 THz. For this purpose, we now fill the waveguide with an NLC material (mixture w-1825, see [] and the references therein) as shown in Figure 1, third schematic from the left. As is known [], the dielectric properties of NLC change when an external low-driving voltage is applied across the cell (see, e.g., Ref. [,] for details). A rigorous electromagnetic analysis would require modeling the NLC with a full permittivity tensor [].
Under this condition, the problem can no longer be decomposed into TE and TM modes, and dyadic Green’s functions [] or coupled transmission-line equations [] are required. Nevertheless, as discussed in [], when the ratio of anisotropy defined as (with as the ordinary (extraordinary) relative permittivity value of the NLC and as its dielectric anisotropy) is less than (as in the case of the mixture w-1825 []), the TE–TM coupling can safely be neglected. Hereafter, TE and TM modes are referred with respect to the -plane; thus, the TE and TM modes are described by and , respectively.
This assumption allows for greatly simplifying the problem. In particular, we model the NLC as a lossy uniaxial crystal with a diagonal relative permittivity tensor with components given by and when no bias (off state) is applied and and at the high-voltage limit (on state) when the NLC optical axis is aligned with the z-axis [].
The NLC orientation at the off-state is determined by properly placing alignment layers, e.g., polyamide films rubbed along the x-axis—a standard practice in LC technology. The thickness of such layers is in the order of tens of nm; hence, their effect at the THz frequency of operation can be neglected. The relative permittivity values of the considered NLC material are and (see, e.g., Ref. [,]).
We consider the case where the NLC voltage bias is applied along the z-axis, leading to a rotation of the NLC optical axis in the -plane. Hence, the orientation of the NLC optical axis can be described by a tilt angle , measured from the x-axis, and the NLC relative permittivity tensor is given by
Although the dynamics of the NLC as a function of the driving voltage are nonlinear (see, e.g., Ref. []), this aspect is secondary in the current context: our goal is to determine the tunable range of the antenna (ultimately bound by the ‘off’ and ‘on’ states) and to optimize its radiation performance. Similarly, the tilt angle, which is generally spatially variant as , can be approximated by its 2-D spatial average (where , , and are the spatial domain of the LC cell along the -plane and its dimensions along the x- and z-axes, respectively) that describes intermediate biasing states—namely, . The components of the NLC permittivity tensor are still provided by Equation (6), where .
Since we are assuming the optical axis of the NLC to switch in the -plane, only the TM leaky modes are affected by the application of a voltage (as can be inferred from the characteristic TE–TM admittances of the NLC layer: see, e.g., Ref. []), thus, motivating the choice of having PMC lateral walls. The variation of the phase constant of the TM leaky mode through voltage biasing will affect the beam angle through Equation (1), thus, producing the desired beamsteering property at a fixed frequency. The scan rate of the TM leaky mode with respect to variation of the relative permittivity can be found from Equation (5) and reads:
which reveals that the angular sensitivity is higher when the antenna radiates at angles close to either broadside or endfire. However, 1-D LWAs do not usually radiate efficiently at such angles, and a trade-off has to be accepted [].
2.4. Tunable Leaky Waveguide Partially Filled with NLC
The structure described in the previous Section 2.3 would not only be unrealistic (the liquid crystal cannot touch the partially open PRS) but also would exhibit poor radiation performance due to the non-negligible loss tangent of the NLC. This feature contributes to considerably raising the total attenuation constant, thus, increasing the beamwidth (see Equation (2)) and reducing the directivity (see Equation (3)) and, consequently, the total efficiency (see, e.g., Equation (4)).
In order to mitigate the losses, one strategy is to reduce the volume of the NLC cell inside the waveguide and to simultaneously increase the volume of a spacer material with significantly lower losses. This is the approach that we exploit in this work and that is shown on the right side of Figure 1, where the NLC cell is sandwiched between two low-loss layers of the cyclo-olefin polymer Zeonor, whose relative permittivity at THz frequencies equals . The side effect of this strategy is the corresponding reduction of the tunability of the device: the lower the volume of the NLC, the lower the tuning range. In Section 3, we will explain how to properly design the structure to optimally deal with this kind of trade-off.
3. Optimization and Design
3.1. Optimization of the Ideal Structure
According to the assumptions made in Section 2, we develop here a TEN model (see Figure 2) for the structure described in Section 2.4. This TEN can be studied through the transverse resonance technique [], which provides the relevant dispersion equation
where the ‘bar’ denotes normalization to (with as the vacuum impedance), whereas , , and , represent the normalized wave admittances of air, spacer, and NLC media, respectively. is the normalized surface admittance of the PRS, and is the normalized input admittance of the three-section transmission-line terminated with a short circuit representing the ground plane. The expression of is a function of both and and is not reported here for the sake of brevity.
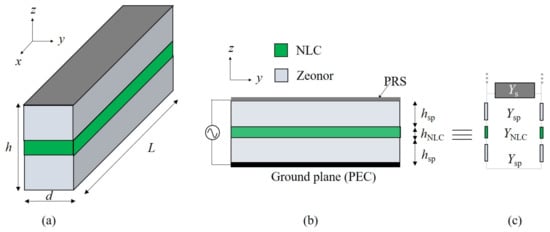
Figure 2.
(a) A schematic 3-D view of a 1-D unidirectional LWA based on PRS and NLC, (b) its cross section along the -plane, and (c) the related transverse equivalent network. The biasing scheme is shown only in (b).
For TM polarization, the characteristic normalized admittances of isotropic nonmagnetic media, such as the spacer and air, are, , with as the relative permittivity of the medium, whereas, for anisotropic uniaxial media, such as the NLC, we have (see, e.g., Ref. []). According to the previous description of the NLC tensor, it becomes clear that the roots of this equation change as the tilt angle of the NLC optical axis changes.
Root-finding methods, such as the Padé algorithm [] can be employed to obtain the wavenumber dispersion of the higher order TM leaky mode. It is worthwhile recalling that the domain of the function at the left-hand sides of Equation (8) is a two-sheeted Riemann surface. The proper and improper sheets are connected through Sommerfeld branch cuts ; leaky modes are found on the improper sheet [].
In our analysis, we are interested in evaluating the wavenumber dispersion of the TM leaky mode as a function of both the frequency and tilt angle and for different choices of the sheet impedance value and the NLC filling factor defined as . We stress that the analytical techniques that are typically adopted to maximize the gain in 1-D unidirectional LWAs [,] cannot be applied here because of the anisotropy of the NLC layer and its non-negligible losses.
In addition, the results from [,] refer to typical frequency-scanning 1-D unidirectional LWAs. Here, the tunable feature enabled by the NLC cell requires the antenna designer to find the parameters that may enhance the maximum angular range at a fixed frequency—not only the gain.
The search for optimal values of FF and , thus, requires a parametric numerical investigation, whose final results are here reported (a qualitative analysis is instead discussed in []). Specifically, we found that the choice of and represents an optimal trade-off among the directivity, radiation efficiency, and tunability.
The numerical results of this optimized structure are reported in the frequency range of – THz for different NLC states in Figure 3a (the colors shade from blue to red as the NLC state switches from ‘off’ to ‘on’), for a cavity height of , which corresponds approximately to a resonant cavity at 1 THz when the NLC is in its off state (note that and that the NLC in its off state and the Zeonor are almost index-matched).
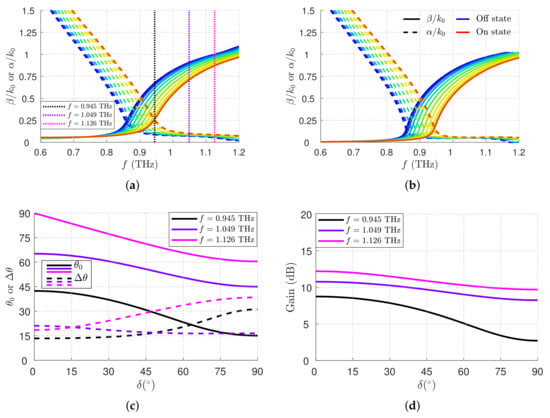
Figure 3.
(a,b) Dispersion curves (solid lines) and (dashed lines) vs. f for NLC states continuously varying from the ‘off’ (blue) to ‘on’ state (red). The results in (a,b) are for the lossy and lossless cases, respectively. Dotted vertical colored lines highlight the frequency at which the antenna performance shown in (c,d) are evaluated. (c) The beam angle (in solid lines) and half-power beamwidth (in dashed lines), and (d) gain G as the optical axis tilts from the horizontal z-axis to the vertical x-axis () for the frequencies shown in (a).
This effect is also appreciable from the dispersion curves depicted in Figure 3a,b, where it is seen that the normalized phase (in solid lines) and attenuation constant (in dashed lines) dispersion curves cross each other (resonant condition for having broadside beams [,]) in the range of 0.85–0.95 THz. In Figure 3b, the same results of Figure 3a are obtained for the lossless version of the optimized structure in order to obtain and , which are essential to compute the radiation efficiency (see Equation (4)) and, in turn, the gain.
In Figure 3a, we also report the fixed frequencies that we selected to evaluate the scan performance through NLC biasing with black, violet, and magenta dotted vertical lines. The rationale behind the choice of these frequencies is as follows.
The lowest frequency (the dotted vertical black line in Figure 3a,b) corresponds to the frequency for which, at the ‘on’ state (see the red-colored dispersion curves), the TM leaky mode is at the leaky cutoff (viz., ) and, thus, radiates efficiently close to broadside (we recall that, for , the gain of 1-D unidirectional LWAs abruptly decreases). The highest frequency (the dotted vertical magenta line in Figure 3a,b) corresponds to the frequency for which, at the ‘off’ state (see the blue-colored dispersion curves), the TM leaky mode radiates at endfire (viz., ). The intermediate frequency (the dotted vertical violet line in Figure 3a,b) is simply a middle-of-the-way choice that represents, in our opinion, a sub-optimal condition at which it is convenient to have the antenna work.
In particular, in Figure 3c, the beamwidth and the beam angle are reported as a function of the NLC tilt angle. The results for the beam angle are in agreement with the formula for the scan rate (viz., Equation (7)), which predicts a greater tunable range for angles either close to the broadside or endfire. However, the results for the beamwidth show that, as the scan rate increases, the beamwidth dynamic range also increases, which is not a desirable property for beamscanning applications.
Figure 3d completes the picture, showing the gain as a function of the average NLC tilt angle, and revealing that there is only a slight improvement in working close to the endfire (magenta curve) with respect to the intermediate condition (violet curve), which instead ensures a quasi-consistent beamwidth through scanning. For these reasons, in the following, we only report results for the fixed frequency of THz (the violet curves in Figure 3c,d), as this choice represents an optimal trade-off.
3.2. Design of the AMC Walls
Thus far, we have assumed ideal PMC lateral walls, which, in practice, have to be realized with AMC-like materials, such as high-impedance surfaces (HIS) [,]). Simple and accurate design rules for HIS can be found in []. Here, we consider a patch unit-cell on top of a grounded slab of Zeonor of thickness whose design parameters are the period and gap .
The parameters have been optimized to obtain a zero-phase reflection coefficient at the desired frequency of THz, for a TE mode propagating impinging at grazing incidence over the -plane (i.e., almost parallel to the propagation x-axis). It is worth noting here that the propagating TM leaky mode will have no component; thus, it will be TE with respect to the y-axis, which corresponds to the normal axis for the AMC wall.
The full-wave results confirm that the designed unit-cell behaves as an AMC over a narrow frequency bandwidth centered around the working frequency (see Figure 4a); since we are interested in a LWA operating at a fixed frequency, this aspect should not be an issue. The lateral walls will, thus, be modeled as ideal PMC walls.
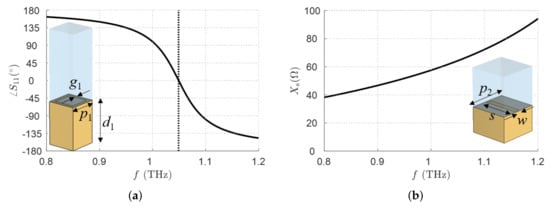
Figure 4.
(a) Phase of the reflection coefficient vs. f (solid black line) of the patch unit cell for realizing the PMC. The vertical dotted line highlights that the phase of the reflection coefficient is zero at the desired frequency of 1.049 THz. (b) Sheet reactance vs. f (solid black line) of the transverse slot for realizing the PRS. The parameters are in the text.
3.3. Design of the PRS
The sheet impedance of the PRS used in the optimized structure described in Section 3.1 is . Homogenized metasurfaces similar to those used for the synthesis of the AMC walls can also be used to realize such a PRS.
However, as opposed to the synthesis of the AMC, where the thickness of the substrate is instrumental to realize the zero-phase condition at the desired frequency, it is here of little importance, since we only require a metasurface that behaves as a PRS. This is fully characterized by a single scalar purely imaginary value of . Moreover, the need to use the PRS as an electrode for the application of the signal driving the liquid crystal demands that the PRS is connected as it acts as one of the electrodes. Additionally, this requires a high filling factor as the LC materials under the gaps suffer from lower reorientation as driven only by the fringe field.
Hence, patch and strip-grating unit cells do not represent optimal choices for our PRS as there are either nonconnected topologies or intrinsically low filling-factor geometries. Conversely, fishnet-like unit cells, such as those studied in [,], possess both the above-mentioned features of having a connected topology and a relatively high filling factor. However, since we deal with a 1-D LWA with PMC walls, the unit cell will be periodic only along the propagation x-axis. This is a relevant difference with respect to the fishnet-like unit cell studied in [,], which is instead 2-D periodic. In particular, we note that the original 2-D periodic fishnet-like unit cell is a superposition of a longitudinal slot and a transverse slot; in our case study, the TM leaky mode will only couple with the transverse slot, and the PMC symmetry along the -planes will cancel the contribution of the longitudinal slot.
Indeed, the longitudinal slot behaves as an x-oriented magnetic dipole, which is parallel to the PMC walls, and thus it does not radiate (the dual case of an electric dipole parallel to a PEC wall []). Therefore, the PRS will be realized considering only a transverse slot unit cell in a 2-D periodic environment, with the contribution of the longitudinal slot being negligible for the reasons above.
The sheet impedance is then extracted by means of conventional Floquet–Bloch full-wave simulations of such a unit cell for different choices of design parameters. After a parametric analysis, we obtained the desired sheet impedance value (see Figure 4b) for the following design parameters: the period , the slot length , and the slot width . In the simulation of the unit-cell, a substrate of Zeonor of thickness is considered so that the extracted considers the inhomogeneous character of the materials at the interface.
The frequency-dispersive character of is then used in the implementation of the surface impedance boundary condition in the CST [] full-wave simulation of the entire structure. Although approximate, this approach allows for a great reduction of computational burden while maintaining excellent accuracy as demonstrated in previous studies [,].
3.4. Liquid-Crystal Switching
Here, we provide some brief considerations regarding the LC biasing scheme and characteristics. As shown in Figure 2, the LC bias voltage is applied along the z-axis, i.e., between the PRS and the bottom PEC ground plane. At the lateral walls, the metallic patch array of the PMC will behave as a uniform conducting surface at the LC bias frequency, which is typically between 1 and 10 kHz. Hence, the PMC walls have to be electrically disconnected from the PRS/ground electrodes in order to avoid short-circuiting by introducing a small lateral gap, e.g., by slightly reducing the width d.
The electric breakdown strength for Zeonor is V/m []; hence, a micron-sized gap provides sufficient protection of the material without notably perturbing the THz modal properties. Regarding potential fringe-field effects from the slotted PRS, the aspect ratio of the slot width over the waveguide height is less than , which is too low to induce detrimental effects [] considering that the NLC layer is located in the middle of the waveguide.
Regarding the operation bias voltage, it can be estimated by first considering the threshold voltage in a standard planar splay NLC cell, which is given by , where is the NLC splay elastic constant, is the free-space permittivity, and is the low-frequency NLC dielectric anisotropy. In particular, at 1 kHz, for the NLC mixture 1825, these parameters are pN and []; hence, V. Given the NLC filling factor FF and the difference of the low frequency relative permittivities of the NLC and Zeonor, the threshold voltage for the LC switching in the proposed antenna is estimated as 10 V.
Finally, the operation speed of the device is determined by the NLC response time as given by : can be controlled by increasing the voltage, and generally , unless operating close to the threshold voltage, which, however, provides limited tunability. Hence, the response time is ruled mainly by the switch-off relaxation process, [], where = 311 mPa·s is the NLC rotational viscosity []. The resulting value is approximately one second, and this can be further reduced by employing optimized low-viscosity and/or dual-frequency NLC mixtures.
4. Results
According to the analysis in the previous Section 3.1, a 3-D model of the optimized 1-D unidirectional NLC-based LWA of length mm (which is about at 1 THz) was designed in CST Microwave Studio and simulated with the time-domain solver.
The results of Section 3.2 and Section 3.3 were exploited to reduce the complexity of the problem; thus, the PRS was implemented with a surface impedance boundary condition, whereas the AMC walls were implemented as PMC boundary conditions. The lateral distance between the two PMC is . The antenna was excited with a waveguide port operating in its first-order TM mode, and another waveguide port was placed at the end of the antenna to simulate the presence of an absorber. The NLC mixture w-1825 is defined as a uniaxial crystal with diagonal components as in Equation (6). Full-wave simulations of the structure were performed at the fixed frequency of THz for a tilt angle that switched from to at steps of .
Full-wave results are shown for both the radiation efficiency and peak gain in Figure 5a,b, respectively, where they are reported as black circles and compared with the analytical results (solid black lines), showing satisfactory agreement. Analytical results were obtained using Equations (3) and (4) for the efficiency and directivity, respectively, with the numerical values of and obtained from the dispersion analysis as described in Section 3.1.
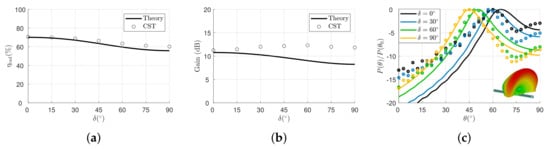
Figure 5.
(a) Radiation efficiency , and (b) gain (in dB) vs. NLC tilt angle for THz. The CST results are shown as black circles, and the numerical results are shown as solid black lines. (c) Normalized radiation patterns at THz for four different LC states—namely, and in black, light blue, green, and yellow, respectively. The CST results are shown as colored circles, and the analytical results are shown as solid colored lines. The inset of (c) shows the normalized 3-D radiation pattern for the last NLC state for which the beam peak points at approximately (as expected from Figure 3c). The intensity of the normalized 3-D radiation pattern goes from −20 dB (green) to 0 dB (red).
In order to have a more complete picture of the radiation performance of the proposed structure, we also report the normalized radiation patterns on the elevation plane for four different bias states (corresponding to and ) obtained with CST and compared with the expected analytical leaky-wave patterns. The latter were computed using the numerical values of and into the following formula []:
where with , , and are normalized variables. The comparison is shown in Figure 5c), where a good agreement between full-wave (colored dots) and analytical (colored solid lines) results is observed for the last three bias states; the analytical results for the first state appear to underestimate the effective beam angle, which is most likely due to edge effects, since the beam peak is not far from the endfire. A 3-D view of the radiation pattern obtained from a full-wave simulation of the last bias state is shown as an inset in Figure 5c.
Full-wave 3-D radiation patterns for all bias states were obtained but are not reported for the sake of brevity. Indeed, as can be inferred from Figure 5, the radiation patterns are similar to one another apart from the different beam angles. The gain peak and the beamwidth, which are the most relevant antenna figures of merit, are slightly affected by the variation of the tilt angle as predicted by the analysis of Figure 3c,d (see the violet curve). The only significant difference among all the patterns is the increase of the sidelobe level at endfire (due to surface-wave radiation []) when the beam angle increases.
5. Conclusions
We discussed the design criteria and the radiation performance of a PRS-based 1-D unidirectional LWA that exploits the tunable properties of NLC to scan the beam at a fixed frequency in the low THz range. The proposed LWA consisted of a rectangular waveguide whose top wall was a PRS, whereas the side walls were replaced by perfect magnetic conductors to result in the LWA operating in its TM leaky mode. A suitable choice of design parameters allowed for beam steering over an angular range of around while maintaining an almost constant beamwidth of .
These results were obtained through an approximate but efficient leaky-wave analysis of the structure and then validated through full-wave simulations. In future works, we will investigate the performance of a more accurate design while considering the realization of the biasing network and its effects on the dynamics of the liquid crystal.
Author Contributions
Conceptualization, W.F., P.B. and A.G.; methodology, W.F., P.B., D.C.Z. and A.G.; software, F.I. and W.F.; data processing, F.I., W.F. and D.C.Z.; writing—original draft preparation, W.F. and D.C.Z.; writing—review and editing, W.F., D.C.Z., F.I., P.B., R.B. and A.G; supervision, W.F., R.B. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project ECS00000024 “Ecosistemi dell’Innovazione”—Rome Technopole of the Italian Ministry of University and Research, public call n. 3277, PNRR—Mission 4, Component 2, Investment 1.5, financed by the European Union, Next GenerationEU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jackson, D.R.; Caloz, C.; Itoh, T. Leaky-wave antennas. Proc. IEEE 2012, 100, 2194–2206. [Google Scholar] [CrossRef]
- Mittleman, D.M. Perspective: Terahertz science and technology. J. Appl. Phys. 2017, 122, 230901. [Google Scholar] [CrossRef]
- Ghasempour, Y.; Shrestha, R.; Charous, A.; Knightly, E.; Mittleman, D.M. Single-shot link discovery for terahertz wireless networks. Nat. Commun. 2020, 11, 2017. [Google Scholar] [CrossRef]
- Guerboukha, H.; Shrestha, R.; Neronha, J.; Ryan, O.; Hornbuckle, M.; Fang, Z.; Mittleman, D. Efficient leaky-wave antennas at terahertz frequencies generating highly directional beams. Appl. Phys. Lett. 2020, 117, 261103. [Google Scholar] [CrossRef]
- Amarasinghe, Y.; Mendis, R.; Mittleman, D.M. Real-time object tracking using a leaky THz waveguide. Opt. Express 2020, 28, 17997–18005. [Google Scholar] [CrossRef]
- Torabi, Y.; Dadashzadeh, G.; Hadeie, M.; Oraizi, H.; Lalbakhsh, A. A wide-angle scanning sub-terahertz leaky-wave antenna based on a multilayer dielectric image waveguide. Electronics 2021, 10, 2172. [Google Scholar] [CrossRef]
- Sato, K.; Monnai, Y. Two-dimensional terahertz beam steering based on trajectory deflection of leaky-Mode. IEEE Trans. THz Sci. Technol. 2021, 11, 676–683. [Google Scholar] [CrossRef]
- Matsumoto, H.; Watanabe, I.; Kasamatsu, A.; Monnai, Y. Integrated terahertz radar based on leaky-wave coherence tomography. Nat. Electron. 2020, 3, 122–129. [Google Scholar] [CrossRef]
- Karmokar, D.K.; Esselle, K.P.; Hay, S.G. Fixed-frequency beam steering of microstrip leaky-wave antennas using binary switches. IEEE Trans. Antennas Propag. 2016, 64, 2146–2154. [Google Scholar] [CrossRef]
- Oliveri, G.; Werner, D.H.; Massa, A. Reconfigurable electromagnetics through metamaterials—A review. Proc. IEEE 2015, 103, 1034–1056. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Tofani, S.; Burghignoli, P.; Baccarelli, P.; Galli, A. Terahertz Leaky-Wave Antennas Based on Metasurfaces and Tunable Materials. In Metamaterials and Metasurfaces; Canet-Ferrer, J., Ed.; IntechOpen: London, UK, 2018; pp. 93–116. [Google Scholar]
- Zeng, C.; Lu, H.; Mao, D.; Du, Y.; Hua, H.; Zhao, W.; Zhao, J. Graphene-empowered dynamic metasurfaces and metadevices. Opto-Electron. Adv. 2022, 5, 200098-1. [Google Scholar] [CrossRef]
- Clemente, A.; Dussopt, L.; Sauleau, R.; Potier, P.; Pouliguen, P. Wideband 400-element electronically reconfigurable transmitarray in X band. IEEE Trans. Antennas Propag. 2013, 61, 5017–5027. [Google Scholar] [CrossRef]
- Lim, S.; Caloz, C.; Itoh, T. Metamaterial-based electronically controlled transmission-line structure as a novel leaky-wave antenna with tunable radiation angle and beamwidth. IEEE Trans. Microw. Theory Tech. 2005, 53, 161–173. [Google Scholar] [CrossRef]
- Ji, L.Y.; Guo, Y.J.; Qin, P.Y.; Gong, S.X.; Mittra, R. A reconfigurable partially reflective surface (PRS) antenna for beam steering. IEEE Trans. Antennas Propag. 2015, 63, 2387–2395. [Google Scholar] [CrossRef]
- Mavridou, M.; Feresidis, A.P. Dynamically reconfigurable high impedance and frequency selective metasurfaces using piezoelectric actuators. IEEE Trans. Antennas Propag. 2016, 64, 5190–5197. [Google Scholar] [CrossRef]
- Lovat, G.; Burghignoli, P.; Celozzi, S. A tunable ferroelectric antenna for fixed-frequency scanning applications. IEEE Antennas Wireless Propag. Lett. 2006, 5, 353–356. [Google Scholar] [CrossRef]
- Varadan, V.K.; Varadan, V.V.; Jose, K.A.; Kelly, J.F. Electronically steerable leaky wave antenna using a tunable ferroelectric material. Smart Mater. Struct. 1994, 3, 470. [Google Scholar] [CrossRef]
- Ma, S.; Wang, P.Y.; Meng, F.Y.; Fu, J.H.; Wu, Q. Electronically controlled beam steering leaky wave antenna in nematic liquid crystal technology. Int. J. RF Microw. CAD Eng. 2020, 30, e22188. [Google Scholar] [CrossRef]
- Hu, W.; Cahill, R.; Encinar, J.A.; Dickie, R.; Gamble, H.; Fusco, V.; Grant, N. Design and measurement of reconfigurable millimeter wave reflectarray cells with nematic liquid crystal. IEEE Trans. Antennas Propag. 2008, 56, 3112–3117. [Google Scholar] [CrossRef]
- Torabi, E.; Erricolo, D.; Chen, P.Y.; Fuscaldo, W.; Beccherelli, R. Reconfigurable beam-steerable leaky-wave antenna loaded with metamaterial apertures using liquid crystal-based delay lines. Opt. Express 2022, 30, 28966–28983. [Google Scholar] [CrossRef]
- Roig, M.; Maasch, M.; Damm, C.; Jakoby, R. Liquid crystal-based tunable CRLH-transmission line for leaky wave antenna applications at Ka-Band. Int. J. Microw. Wireless Technol. 2014, 6, 325–330. [Google Scholar] [CrossRef]
- Che, B.J.; Jin, T.; Erni, D.; Meng, F.Y.; Lyu, Y.L.; Wu, Q. Electrically controllable composite right/left-handed leaky-wave antenna using liquid crystals in PCB technology. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1331–1342. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Ferraro, A.; Beccherelli, R. Liquid-Crystal High-Frequency Microwave Technology: Materials and Characterization. Adv. Mater. Technol. 2019, 4, 1800447. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Tofani, S.; Zografopoulos, D.C.; Baccarelli, P.; Burghignoli, P.; Beccherelli, R.; Galli, A. Systematic design of THz leaky-wave antennas based on homogenized metasurfaces. IEEE Trans. Antennas Propag. 2018, 66, 1169–1178. [Google Scholar] [CrossRef]
- Aqlan, B.; Himdi, M.; Vettikalladi, H.; Le-Coq, L. A 300-GHz low-cost high-gain fully metallic Fabry–Perot cavity antenna for 6G terahertz wireless communications. Sci. Rep. 2021, 11, 7703. [Google Scholar] [CrossRef]
- Llombart, N.; Chattopadhyay, G.; Skalare, A.; Mehdi, I. Novel terahertz antenna based on a silicon lens fed by a leaky wave enhanced waveguide. IEEE Trans. Antennas Propag. 2011, 59, 2160–2168. [Google Scholar] [CrossRef]
- Llombart, N.; Lee, C.; Alonso-del Pino, M.; Chattopadhyay, G.; Jung-Kubiak, C.; Jofre, L.; Mehdi, I. Silicon micromachined lens antenna for THz integrated heterodyne arrays. IEEE Trans. THz Sci. Technol. 2013, 3, 515–523. [Google Scholar] [CrossRef]
- Esquius-Morote, M.; Gómez-Díaz, J.S.; Perruisseau-Carrier, J. Sinusoidally modulated graphene leaky-wave antenna for electronic beamscanning at THz. IEEE Trans. THz Sci. Technol. 2014, 4, 116–122. [Google Scholar] [CrossRef]
- Wang, X.C.; Zhao, W.S.; Hu, J.; Yin, W.Y. Reconfigurable terahertz leaky-wave antenna using graphene-based high-impedance surface. IEEE Trans. Nanotechnol. 2015, 14, 62–69. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Burghignoli, P.; Baccarelli, P.; Galli, A. Graphene Fabry–Perot cavity leaky-wave antennas: Plasmonic versus nonplasmonic solutions. IEEE Trans. Antennas Propag. 2017, 65, 1651–1660. [Google Scholar] [CrossRef]
- Zouaghi, W.; Voß, D.; Gorath, M.; Nicoloso, N.; Roskos, H.G. How good would the conductivity of graphene have to be to make single-layer-graphene metamaterials for terahertz frequencies feasible? Carbon 2015, 94, 301–308. [Google Scholar] [CrossRef]
- D’Arco, A.; Mussi, V.; Petrov, S.; Tofani, S.; Petrarca, M.; Beccherelli, R.; Dimitrov, D.; Marinova, V.; Lupi, S.; Zografopoulos, D.C. Fabrication and spectroscopic characterization of graphene transparent electrodes on flexible cyclo-olefin substrates for terahertz electro-optic applications. Nanotechnology 2020, 31, 364006. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Simone, S.D.; Dimitrov, D.; Marinova, V.; Mussi, V.; Beccherelli, R.; Zografopoulos, D.C. Terahertz characterization of graphene conductivity via time-domain reflection spectroscopy on metal-backed dielectric substrates. J. Phys. D Appl. Phys. 2022, 55, 365101. [Google Scholar] [CrossRef]
- Reuter, M.; Vieweg, N.; Fischer, B.M.; Mikulicz, M.; Koch, M.; Garbat, K.; Dabrowski, R. Highly birefringent, low-loss liquid crystals for terahertz applications. APL Mater. 2013, 1, 012107. [Google Scholar] [CrossRef]
- Vasic, B.; Isic, G.; Beccherelli, R.; Zografopoulos, D.C. Tunable beam steering at terahertz frequencies using reconfigurable metasurfaces coupled with liquid crystals. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–9. [Google Scholar] [CrossRef]
- Tofani, S.; Fuscaldo, W. Fabry-Perot cavity leaky wave antennas with tunable features for terahertz applications. Condens. Matter 2020, 5, 11. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Tofani, S.; Zografopoulos, D.C.; Baccarelli, P.; Burghignoli, P.; Beccherelli, R.; Galli, A. Tunable Fabry-Perot cavity THz antenna based on leaky-wave propagation in nematic liquid crystals. IEEE Antennas Wireless Propag. Lett. 2017, 16, 2046–2049. [Google Scholar] [CrossRef]
- Tesmer, H.; Razzouk, R.; Polat, E.; Wang, D.; Jakoby, R. Reconfigurable liquid crystal Dielectric image line leaky wave antenna at W-band. IEEE J. Microw. 2022, 2, 480–489. [Google Scholar] [CrossRef]
- Imperato, F.; Burghignoli, P.; Zografopoulos, D.C.; Beccherelli, R.; Galli, A.; Fuscaldo, W. Design of a tunable THz 1-D leaky-wave antenna based on nematic liquid crystals. In Proceedings of the 22th Mediterranean Microwave Symposium (MMS 2022), Pizzo Calabro, Italy, 11–12 May 2015; pp. 1–4. [Google Scholar]
- O’Connor, E.M.; Jackson, D.R.; Long, S.A. Extension of the Hansen-Woodyard condition for endfire leaky-wave antennas. IEEE Antennas Wireless Propag. Lett. 2010, 9, 1201–1204. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Jackson, D.R.; Galli, A. Beamwidth properties of endfire 1-D leaky-wave antennas. IEEE Trans. Antennas Propag. 2017, 65, 6120–6125. [Google Scholar] [CrossRef]
- Beltayib, A.; Sebak, A.R. Analytical design procedure for forward wave couplers in RGW technology based on hybrid PEC/PMC waveguide model. IEEE Access 2019, 7, 119319–119331. [Google Scholar] [CrossRef]
- Marcuvitz, N. On field representations in terms of leaky modes or eigenmodes. IRE Trans. Antennas Propag. 1956, 4, 192–194. [Google Scholar] [CrossRef]
- Mendis, R.; Mittleman, D.M. Comparison of the lowest-order transverse-electric (TE1) and transverse-magnetic (TEM) modes of the parallel-plate waveguide for terahertz pulse applications. Opt. Express 2009, 17, 14839–14850. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Rodak, A.; Graham, D.M.; Jamison, S.P. Generation of longitudinally polarized terahertz pulses with field amplitudes exceeding 2 kV/cm. Appl. Phys. Lett. 2014, 105, 191112. [Google Scholar] [CrossRef]
- Minami, Y.; Kurihara, T.; Yamaguchi, K.; Nakajima, M.; Suemoto, T. Longitudinal terahertz wave generation from an air plasma filament induced by a femtosecond laser. Appl. Phys. Lett. 2013, 102, 151106. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Burghignoli, P.; Galli, A. Genealogy of leaky, surface, and plasmonic modes in partially open waveguides. Phys. Rev. Appl. 2022, 17, 034038. [Google Scholar] [CrossRef]
- Tamir, T.; Oliner, A.A. Guided complex waves. Part 1: Fields at an interface. Proc. IEE 1963, 110, 310–324. [Google Scholar] [CrossRef]
- Tamir, T.; Oliner, A.A. Guided complex waves. Part 2: Relation to radiation patterns. Proc. IEE 1963, 110, 325–334. [Google Scholar] [CrossRef]
- Sorrentino, R. Transverse resonance technique. In Numerical Techniques for Microwave and Millimeter-Wave Passive Structures; Itoh, T., Ed.; John Wiley & Sons: New York, NY, USA, 1989; Chapter 11. [Google Scholar]
- Fuscaldo, W.; Galli, A.; Jackson, D.R. Optimization of the radiating features of 1-D unidirectional leaky-wave antennas. IEEE Trans. Antennas Propag. 2022, 70, 111–125. [Google Scholar] [CrossRef]
- Fuscaldo, W. Rigorous evaluation of losses in uniform leaky-wave antennas. IEEE Trans. Antennas Propag. 2020, 68, 643–655. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Jackson, D.R.; Galli, A. A general and accurate formula for the beamwidth of 1-D leaky-wave antennas. IEEE Trans. Antennas Propag. 2017, 65, 1670–1679. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Galli, A.; Jackson, D.R. Optimization of 1-D unidirectional leaky-wave antennas based on partially reflecting sheets. IEEE Trans. Antennas Propag. 2021, 70, 7853–7868. [Google Scholar] [CrossRef]
- Schühler, M.; Wansch, R.; Hein, M.A. On strongly truncated leaky-wave antennas based on periodically loaded transmission lines. IEEE Trans. Antennas Propag. 2010, 58, 3505–3514. [Google Scholar] [CrossRef]
- Khoo, I.C. Liquid Crystals: Physical Properties and Nonlinear Optical Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 64. [Google Scholar]
- Zografopoulos, D.C.; Beccherelli, R. Tunable terahertz fishnet metamaterials based on thin nematic liquid crystal layers for fast switching. Sci. Rep. 2015, 5, 13137. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Prokopidis, K.P.; Dąbrowski, R.; Beccherelli, R. Time-domain modeling of dispersive and lossy liquid-crystals for terahertz applications. Opt. Mater. Exp. 2014, 4, 449–457. [Google Scholar] [CrossRef]
- Pavone, S.C.; Martini, E.; Caminita, F.; Albani, M.; Maci, S. Surface wave dispersion for a tunable grounded liquid crystal substrate without and with metasurface on top. IEEE Trans. Antennas Propag. 2017, 65, 3540–3548. [Google Scholar] [CrossRef]
- Collin, R.E.; Zucker, F.J. Antenna Theory; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Galdi, V.; Pinto, I.M. A simple algorithm for accurate location of leaky-wave poles for grounded inhomogeneous dielectric slabs. Microw. Opt. Technol. Lett. 2000, 24, 135–140. [Google Scholar] [CrossRef]
- Lovat, G.; Burghignoli, P.; Jackson, D.R. Fundamental properties and optimization of broadside radiation from uniform leaky-wave antennas. IEEE Trans. Antennas Propag. 2006, 54, 1442–1452. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Burghignoli, P.; Galli, A. The transition between reactive and radiative regimes for leaky modes in planar waveguides based on homogenized partially reflecting surfaces. IEEE Trans. Microw. Theory Tech. 2020, 68, 5259–5269. [Google Scholar] [CrossRef]
- Luukkonen, O.; Simovski, C.; Granet, G.; Goussetis, G.; Lioubtchenko, D.; Raisanen, A.V.; Tretyakov, S.A. Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Trans. Antennas Propag. 2008, 56, 1624–1632. [Google Scholar] [CrossRef]
- Sievenpiper, D.; Zhang, L.; Broas, R.F.; Alexopolous, N.G.; Yablonovitch, E. High-impedance electromagnetic surfaces with a forbidden frequency band. IEEE Trans. Microw. Theory Tech. 1999, 47, 2059–2074. [Google Scholar] [CrossRef]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; IEEE Press: New York, NY, USA, 2015. [Google Scholar]
- CST Studio Suite. Electromagnetic Field Simulation Software, Dassault Systèmes. Available online: https://www.3ds.com/products-services/simulia/products/cst-studio-suite/ (accessed on 1 June 2022).
- Zeon Corporation. Cyclo-Olefin Polymer: Specialty Plastics. Available online: https://www.zeon.co.jp/en/business/enterprise/resin/cop/ (accessed on 1 June 2022).
- Algorri, J.F.; Morawiak, P.; Bennis, N.; Zografopoulos, D.C.; Urruchi, V.; Rodríguez-Cobo, L.; Jaroszewicz, L.R.; Sánchez-Pena, J.M.; López-Higuera, J.M. Positive-negative tunable liquid crystal lenses based on a microstructured transmission line. Sci. Rep. 2020, 10, 10153. [Google Scholar] [CrossRef]
- Dąbrowski, R.; Kula, P.; Herman, J. High birefringence liquid crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
- Liu, J.; Jackson, D.R.; Long, Y. Substrate integrated waveguide (SIW) leaky-wave antenna with transverse slots. IEEE Trans. Antennas Propag. 2012, 60, 20–29. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).