Analytical Study of a Circular Thin Plate Contacting with an Elastic Sphere
Abstract
1. Introduction
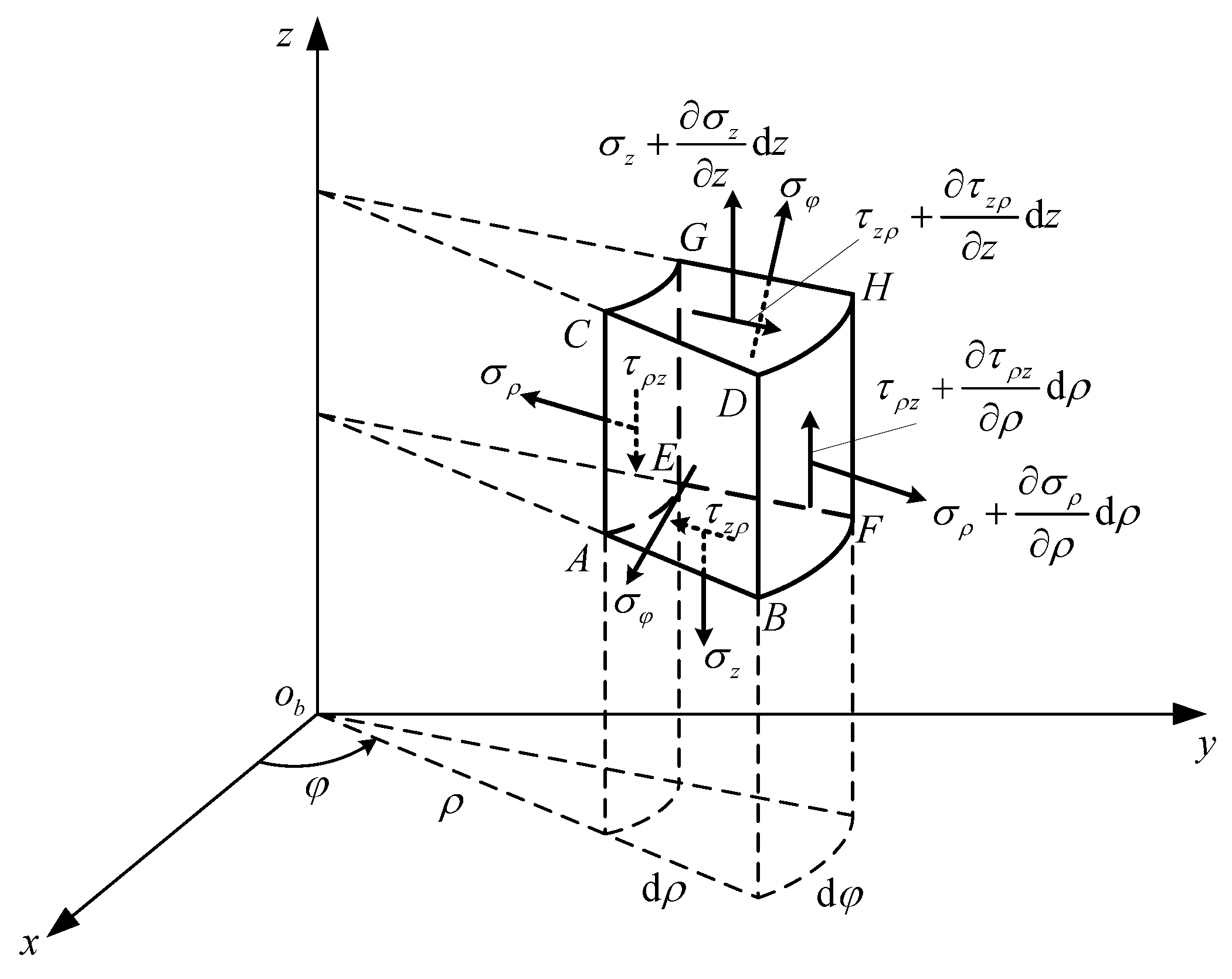
2. Formulation and Governing Equations
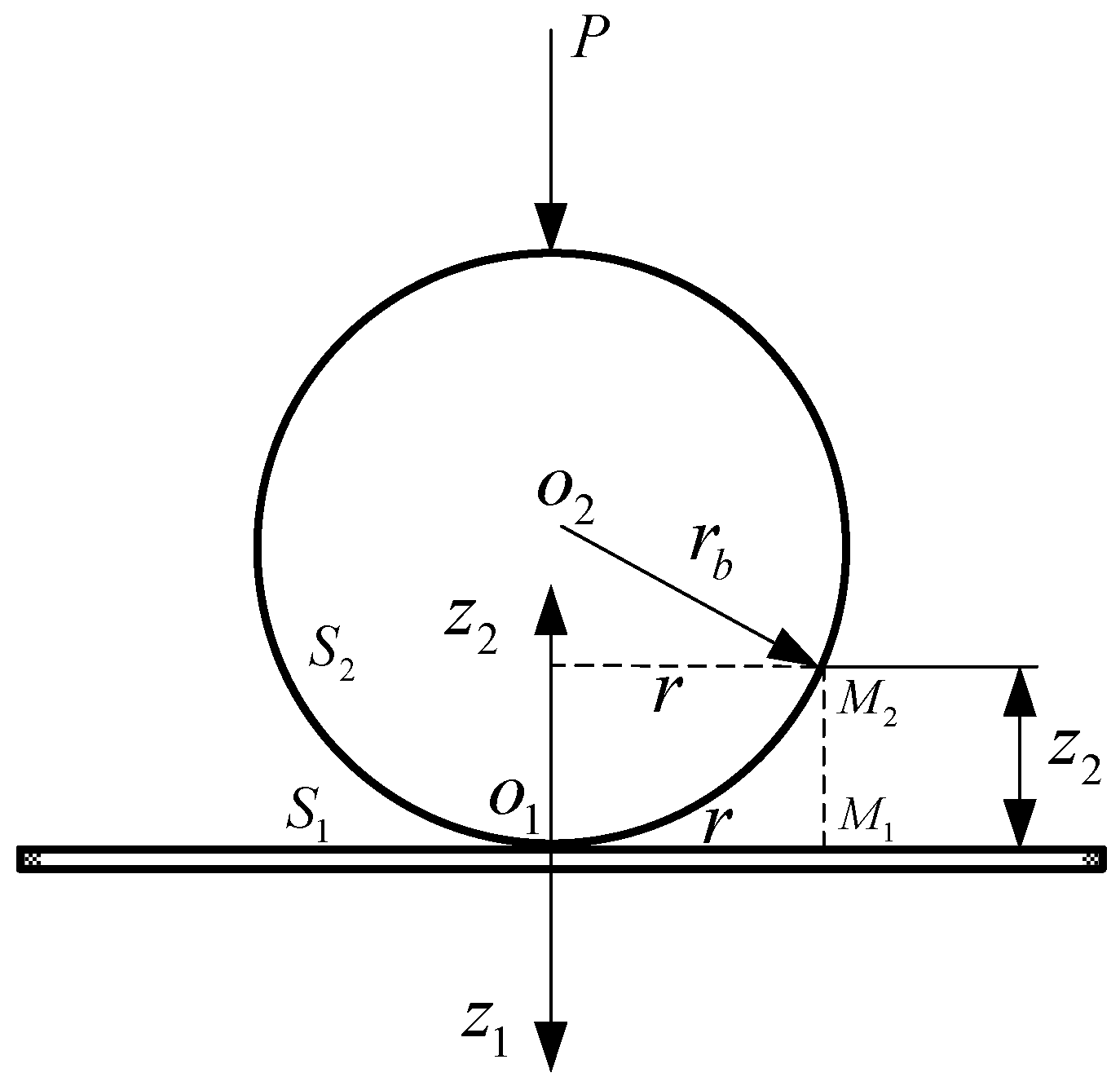
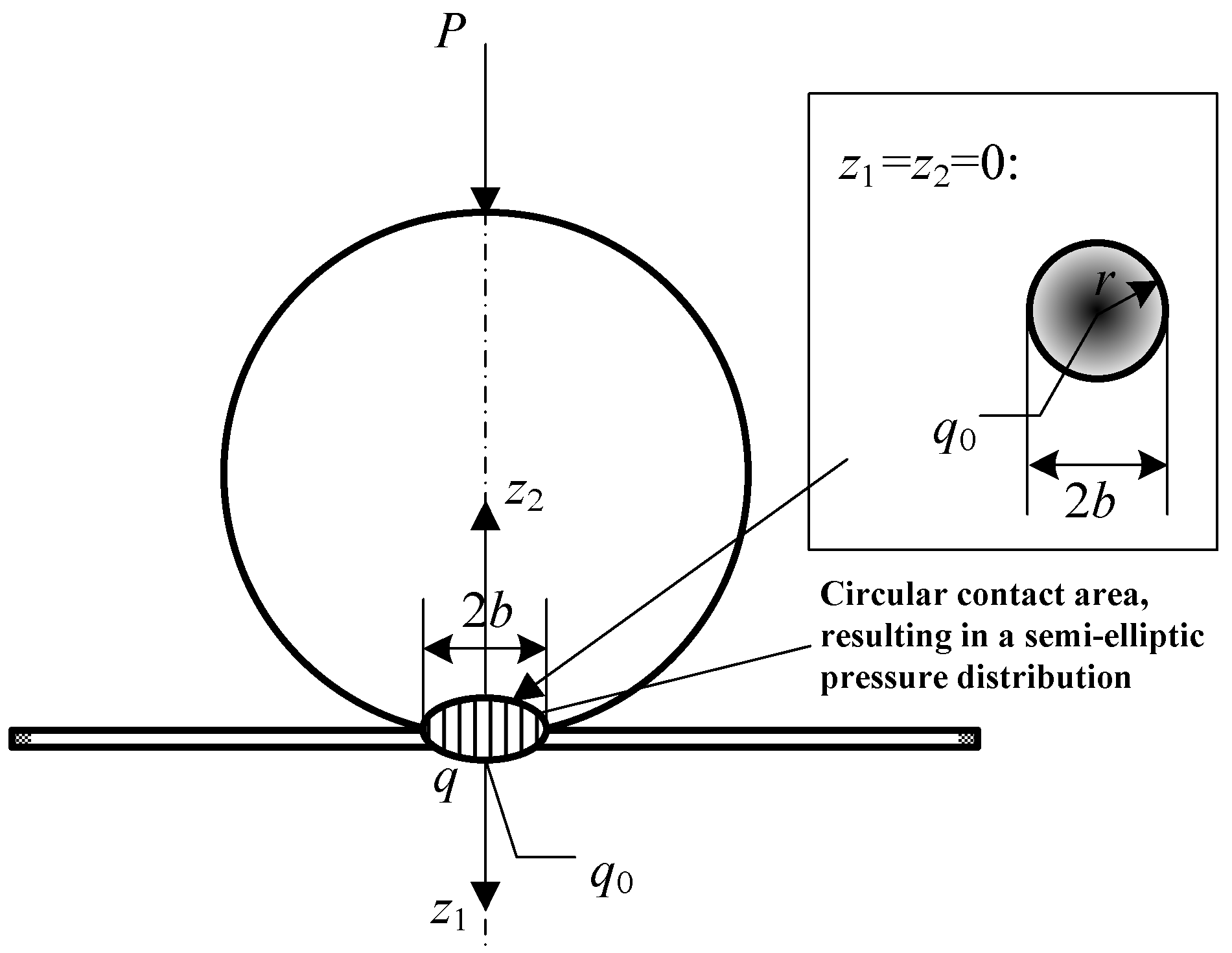
2.1. Contact Analysis
2.2. Contact Deformation of the Sphere
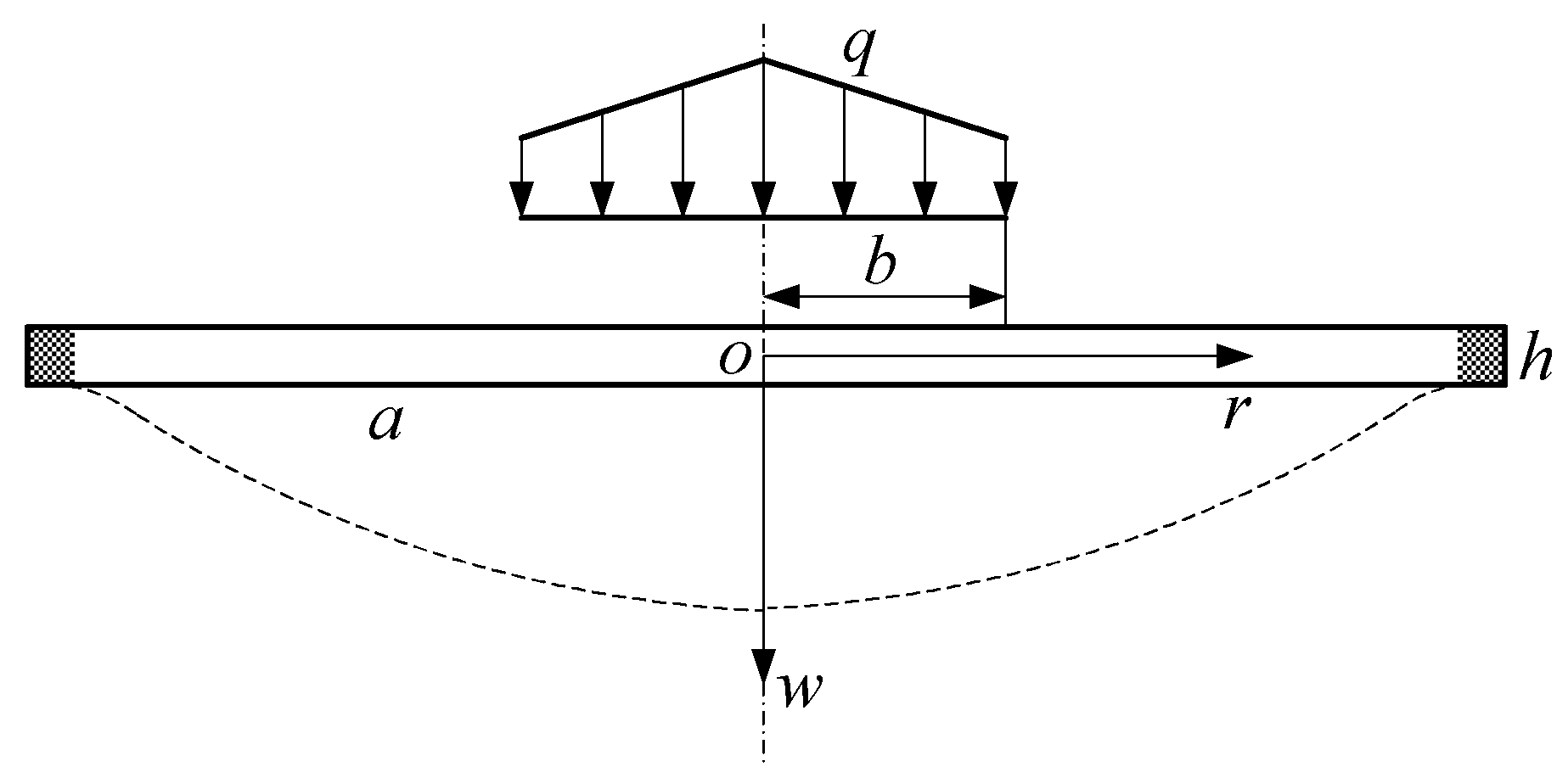
2.3. Contact Deformation of the Circular Thin Plate
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Zhupanska, O.I. Contact problem for elastic spheres: Applicability of the Hertz theory to non-small contact areas. Int. J. Eng. Sci. 2011, 49, 576–588. [Google Scholar] [CrossRef]
- Dubowsky, S.; Freudenstein, F. Dynamic analysis of mechanical systems with clearances, Part 1: Formulation of dynamic model. J. Eng. Ind. 1971, 93, 305–309. [Google Scholar] [CrossRef]
- Deck, J.F.; Dubowsky, S. On the limitations of predictions of the dynamic response of machines with clearance connections. ASME J. Mech. Des. 1994, 116, 833–841. [Google Scholar] [CrossRef]
- Guess, T.M.; Maletsky, L.P. Computational modelling of a total knee prosthetic loaded in a dynamic knee simulator. Medial Eng. Phys. 2005, 27, 357–367. [Google Scholar] [CrossRef]
- Gonzalez-Perez, I.; Iserte, J.L.; Fuentes, A. Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact. Mech. Mach. Theory 2011, 46, 765–783. [Google Scholar] [CrossRef]
- Sanders, A.P.; Brannon, R.M. Assessment of the applicability of the Hertzian contact theory to edge-loaded prosthetic hip bearings. J. Biomech. 2012, 44, 2802–2808. [Google Scholar] [CrossRef]
- Jiang, W.G.; Wang, Z.W.; Li, J.W. Verification of the applicability of classical contact theories for nanoscale contact problems using multiscale simulation. Comput. Mater. Sci. 2012, 60, 186–193. [Google Scholar] [CrossRef]
- Xia, M.H.; Bi, X.H.; Chang, J.C. The Calculation equation for four-edged rectangular plates with work reciprocal theorem of bending thin plates with large deflections. J. Tangshan Coll. 2004, 17, 77–80. [Google Scholar]
- Bakker, M.C.M.; Rosmanit, M.; Hofmeyer, H. Approximate large-deflection analysis of simply supported rectangular plates under transverse loading using plate post-buckling solutions. Thin Walled Struct. 2008, 46, 1224–1235. [Google Scholar] [CrossRef]
- Wierzbizki, T.; Nurick, G.N. Large deformation of thin plates under localized impulsive loading. Int. J. Impact Eng. 1996, 18, 899–918. [Google Scholar] [CrossRef]
- Lee, Y.W.; Woertz, J.C.; Wierzbizki, T. Fracture prediction of thin plates under hemi-spherical punch with calibration and experimental verification. Int. J. Impact Eng. 2004, 46, 751–781. [Google Scholar] [CrossRef]
- Gohari, S.; Sharifi, S.; Burvill, C.; Mouloodi, S.; Izadifar, M.; Thissen, P. Localized failure analysis of internally pressurized laminated ellipsoidal woven GFRP composite domes: Analytical, numerical, and experimental studies. Arch. Civ. Mech. Eng. 2019, 19, 1235–1250. [Google Scholar] [CrossRef]
- Gohari, S.; Mozafari, F.; Moslemi, N.; Mouloodi, S.; Alebrahim, R.; Ahmed, M.; Abdi, B.; Sudin, I.; Burvill, C. Static and dynamic deformation response of smart laminated composite plates induced by inclined piezoelectric actuators. J. Compos. Mater. 2022, 56, 1–25. [Google Scholar] [CrossRef]
- Das, R.; Mishra, S.C.; Ajith, M.; Uppaluri, R. An inverse analysis of a transient 2-D conduction–radiation problem using the lattice Boltzmann method and the finite volume method coupled with the genetic algorithm. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 2060–2077. [Google Scholar] [CrossRef]
- Singla, R.K.; Das, R. Application of Adomian decomposition method and inverse solution for a fin with variable thermal conductivity and heat generation. Int. J. Heat Mass Transf. 2013, 66, 496–506. [Google Scholar] [CrossRef]
- Keer, L.M.; Miller, G.R. Contact between an elastically supported circular plate and a rigid indenter. Int. J. Eng. Sci. 1983, 21, 681–690. [Google Scholar] [CrossRef]
- Thredgold, J.M.; Lucas, S.K.; Howlett, P.G. On the contact of a rigid sphere and a thin plate. Math. Comput. Model. 2006, 43, 119–131. [Google Scholar] [CrossRef]
- Li, M.; Ru, C.Q.; Gao, C.F. Axisymmetric indentation of an elastic thin plate by a rigid sphere revisited. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 2018, 98, 1436–1446. [Google Scholar] [CrossRef]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics; Academic Press: Oxford, UK, 2004. [Google Scholar]
- Lurie, A.I.; Belyaev, A. Theory of Elasticity; Springer: Berlin, Germany, 2005. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Zheng, X.J.; Zhou, Y.H. On the problem of transition from von Karman plate equations to theory of membrane. J. Lanzhou Univ. 1991, 27, 18–25. (In Chinese) [Google Scholar]
- Zheng, X.J. Large Deflection Theory and Application of Circular Thin Plates; Jilin Science and Technology Press: Changchun, China, 1990. (In Chinese) [Google Scholar]
- Zheng, X.J.; Zhou, Y.H. Exact solution to large deflection of circular plates under compound loads. Sci. China 1987, 30, 391–404. [Google Scholar]
- Zheng, X.J.; Zhou, Y.H. On analytical-computerized method to solve nonlinear bending problem of circular plate under a concentrated load. Appl. Math. Mech. 1987, 8, 759–766. [Google Scholar]
- ANSYS Release 10.0 Documentation, Element Reference; ANSYS Inc.: Canonsburg, PA, USA, 2005.


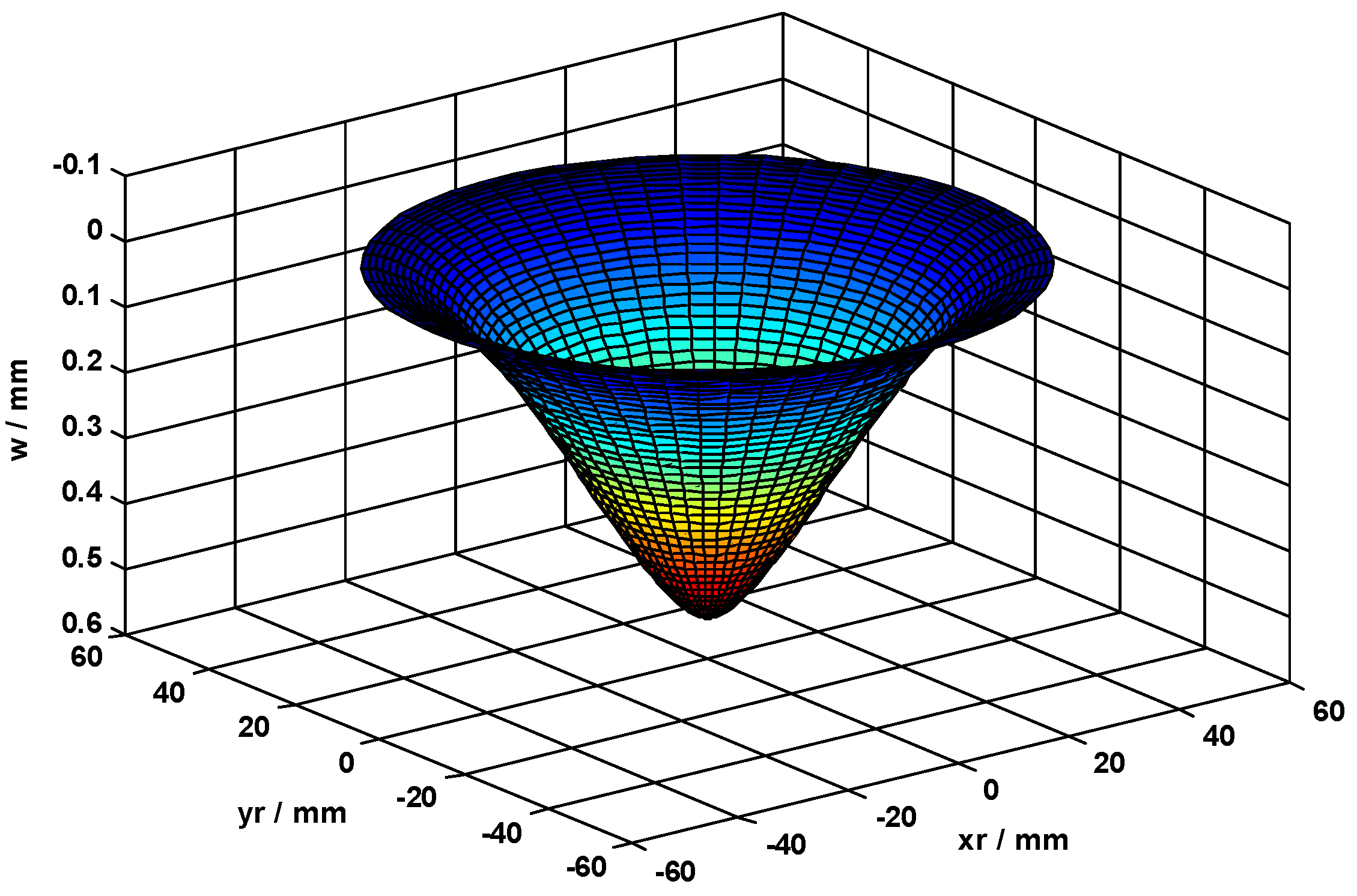
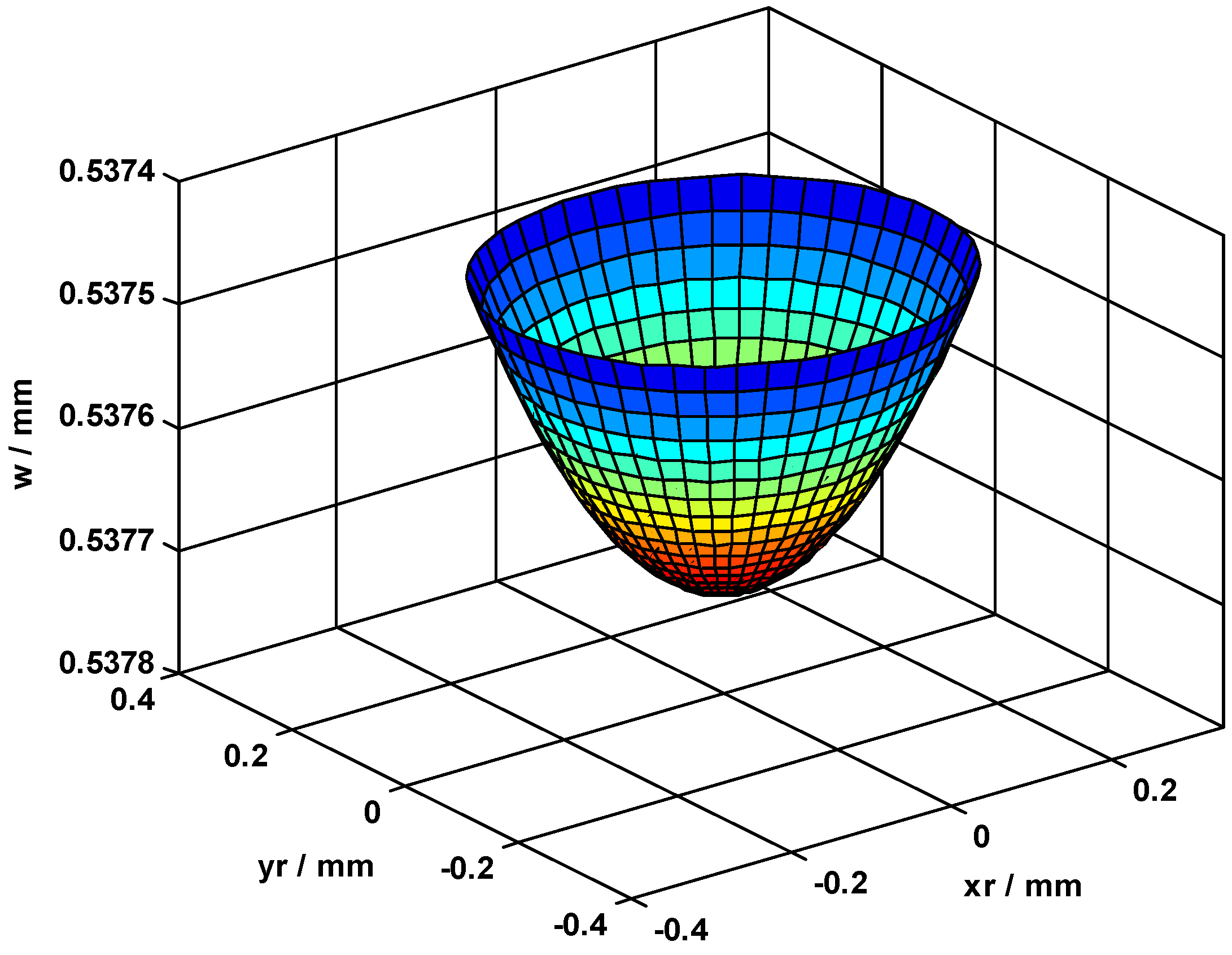


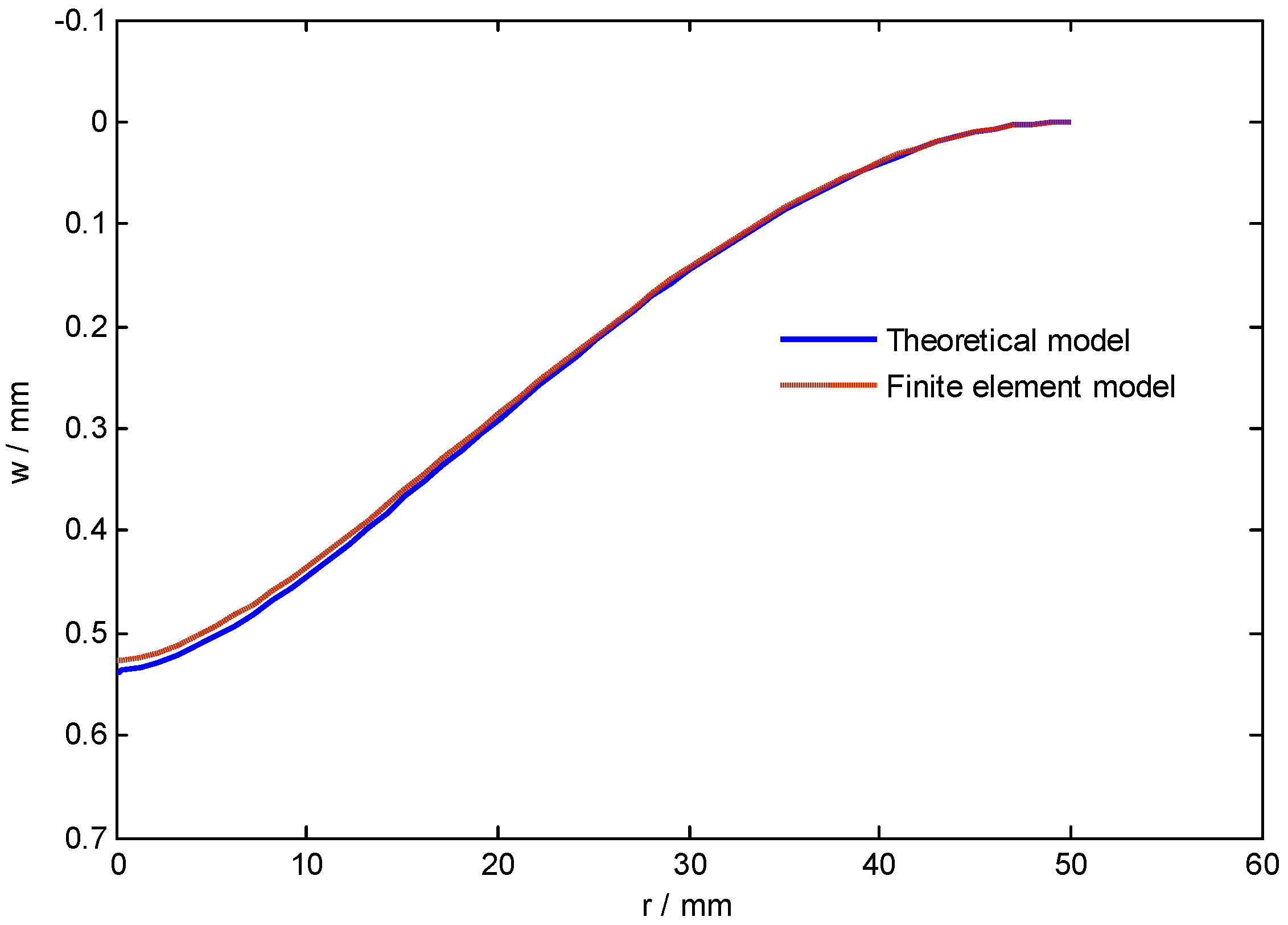
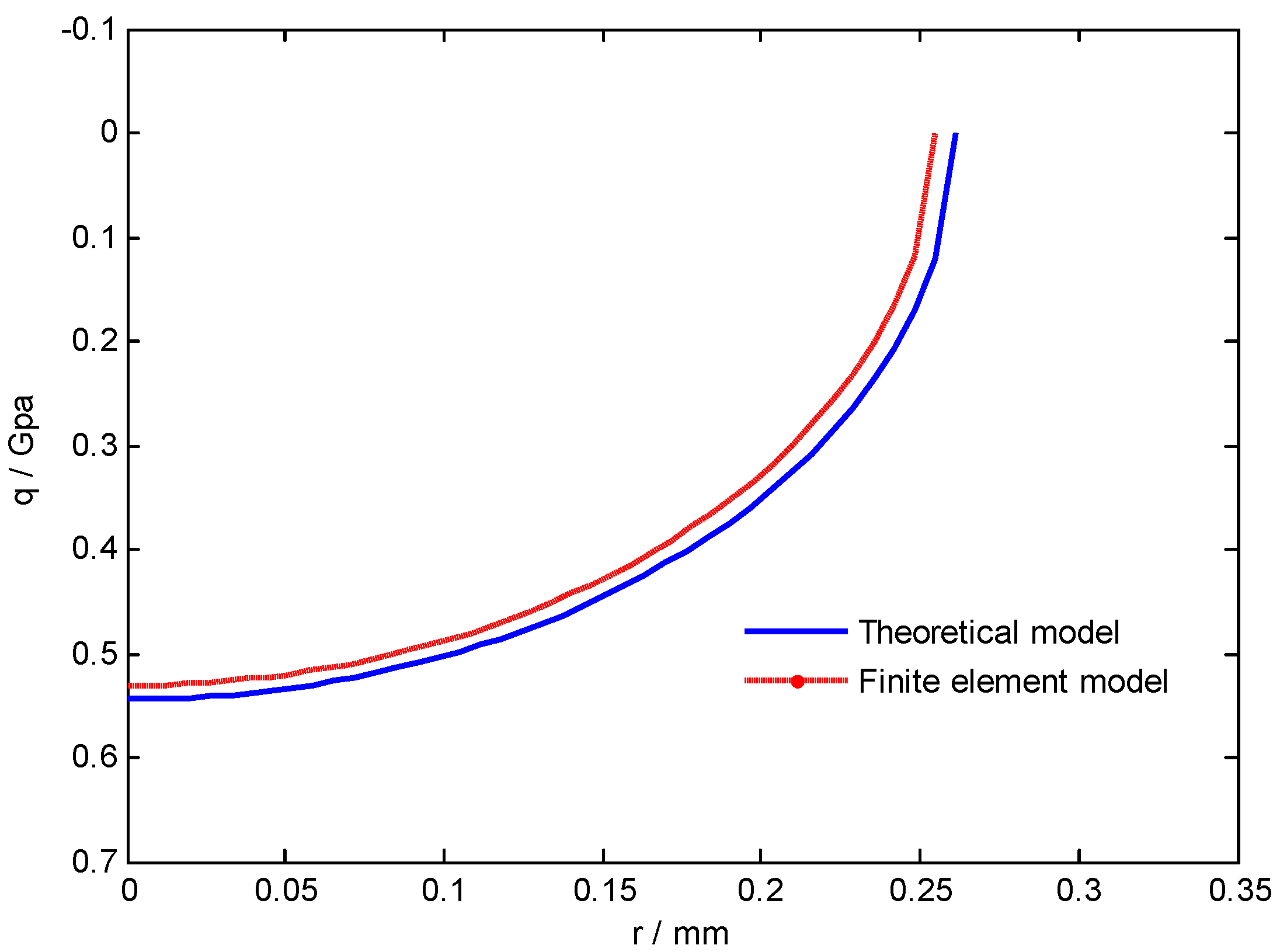
| Sphere | Circular Thin Plate | |
|---|---|---|
| Parameter values | ||
| This Paper | Hertz | |
|---|---|---|
| Action of force | 78 N | 78 N |
| Relative penetration | 0.5406 mm | 0.004873 mm |
| Radius of contact area | 0.2616 mm | 0.3122 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Yang, Y.; Huang, Y.; Xiong, D.; Chen, X. Analytical Study of a Circular Thin Plate Contacting with an Elastic Sphere. Appl. Sci. 2022, 12, 11745. https://doi.org/10.3390/app122211745
Han W, Yang Y, Huang Y, Xiong D, Chen X. Analytical Study of a Circular Thin Plate Contacting with an Elastic Sphere. Applied Sciences. 2022; 12(22):11745. https://doi.org/10.3390/app122211745
Chicago/Turabian StyleHan, Wei, Yanjie Yang, Yiyong Huang, Dan Xiong, and Xiaoqian Chen. 2022. "Analytical Study of a Circular Thin Plate Contacting with an Elastic Sphere" Applied Sciences 12, no. 22: 11745. https://doi.org/10.3390/app122211745
APA StyleHan, W., Yang, Y., Huang, Y., Xiong, D., & Chen, X. (2022). Analytical Study of a Circular Thin Plate Contacting with an Elastic Sphere. Applied Sciences, 12(22), 11745. https://doi.org/10.3390/app122211745






