A Novel Strategy for Computing Routing Paths for Software-Defined Networks Based on MOCell Optimization
Abstract
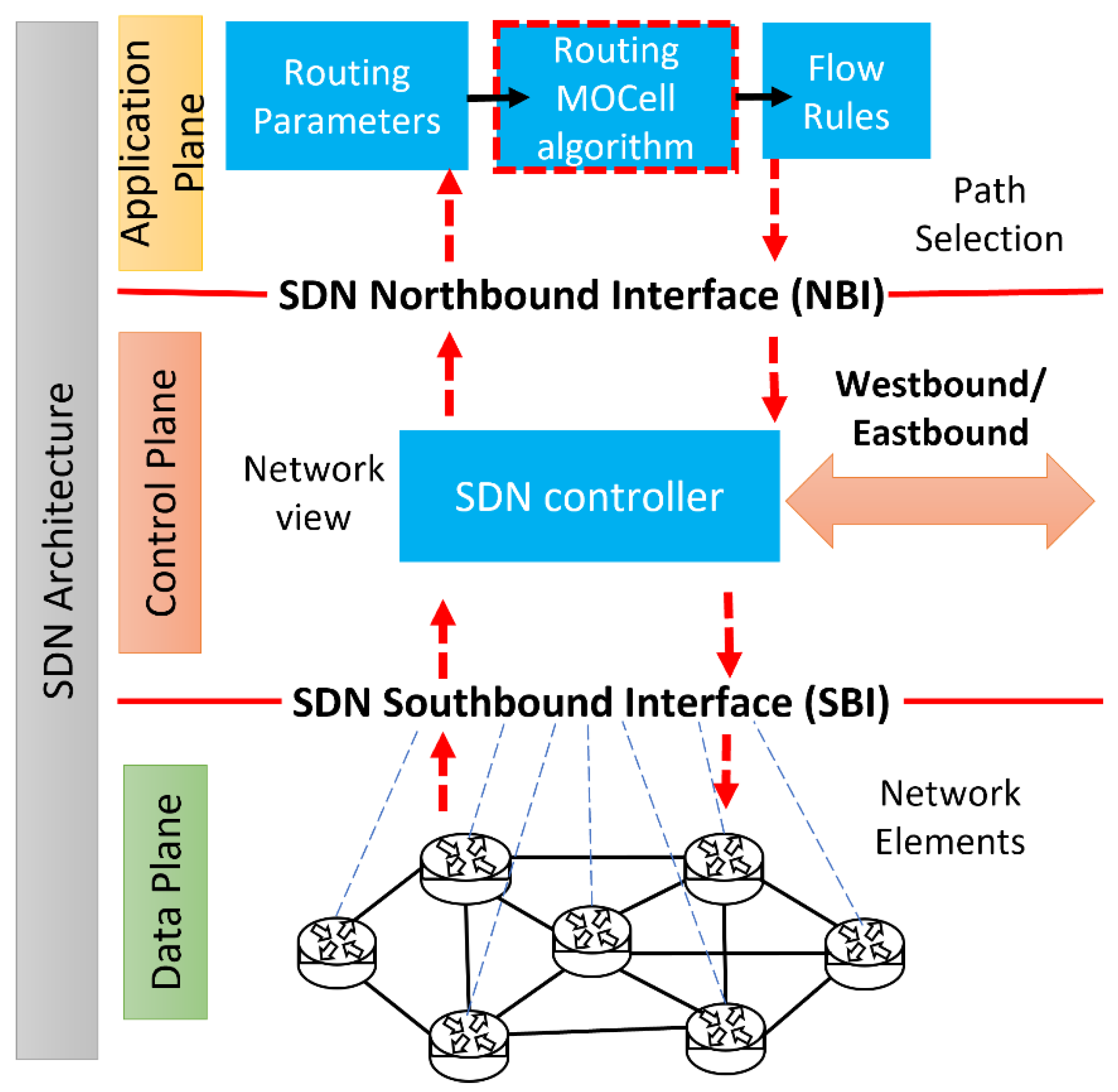
1. Introduction
- Southbound interface: Provides a communication environment between the controller and communication devices. Installs the appropriate flow rules in the device forwarding table. OpenFlow [9] is the open-source community’s most widely implemented Southbound interface standard.
- Northbound interface: Provides communication between the SDN controller and network applications running on the application plane. This communication is critical, as each network application’s requirements can be very different. Applications can communicate with the SDN using various APIs, such as ad hoc and REST APIs, to request network resources or services according to their needs.
- An SDN strategy for routing data flows based on QoS that considers an inter-domain approach and compares its performance with traditional routing algorithms in the context of SDN.
- Using MOCell, the routing strategy considers some of the most critical network parameters: available bandwidth, delay, and packet loss.
2. Related Work
3. Materials and Methods
3.1. Problem Formalization
3.2. QoS Routing
- The minimum hops path computes the shortest path with the minimum number of links between the source and destination node.
- Minimum cost of available bandwidth path:
- Minimum delay path:
- Minimum packet loss path:
3.3. Dijkstra’s Algorithm
| Algorithm 1. Dijkstra’s shortest path algorithm (centralized approach) |
| 1: S = {i} //permanent list; start with source node i |
| 2: S’ = N\{i} // tentative list (of the rest of the nodes) |
| 3: such that //identify a neighboring node k not in the list S with the minimum cost path from i. |
| 4: S = S U {K} //Add k to the permanent list S |
| 5: S’ = S’\{K} //Drop k from the tentative list S’ |
| 6: if S’ = ø //if S’ is empty stop |
| 7: end |
| 8: For j ∩ S’ do //consider the list of neighboring , of the intermediary k. |
| 9: = min () //check for improvement in the minimum cost path |
| 10: return to step 3, |
3.4. Multi-Constrained Optimal Path (MCOP)
- The weighted sum method [35] is the sum of the values corresponding to the different objectives, each multiplied by a weighted coefficient. This method provides a weight for the various network parameters that can be used as a cost for path computation. We use it as a fitness function for our proposed routing method.
- 2.
- The method based on Pareto dominance determines all non-dominated solutions that satisfy the conditions defined for the problem (feasible region). Any point is a feasible solution. The feasible region is defined as follows [36]: Given 3 vectors , , and , we say that dominates and dominates (denoted by ), if and only if is less than and .
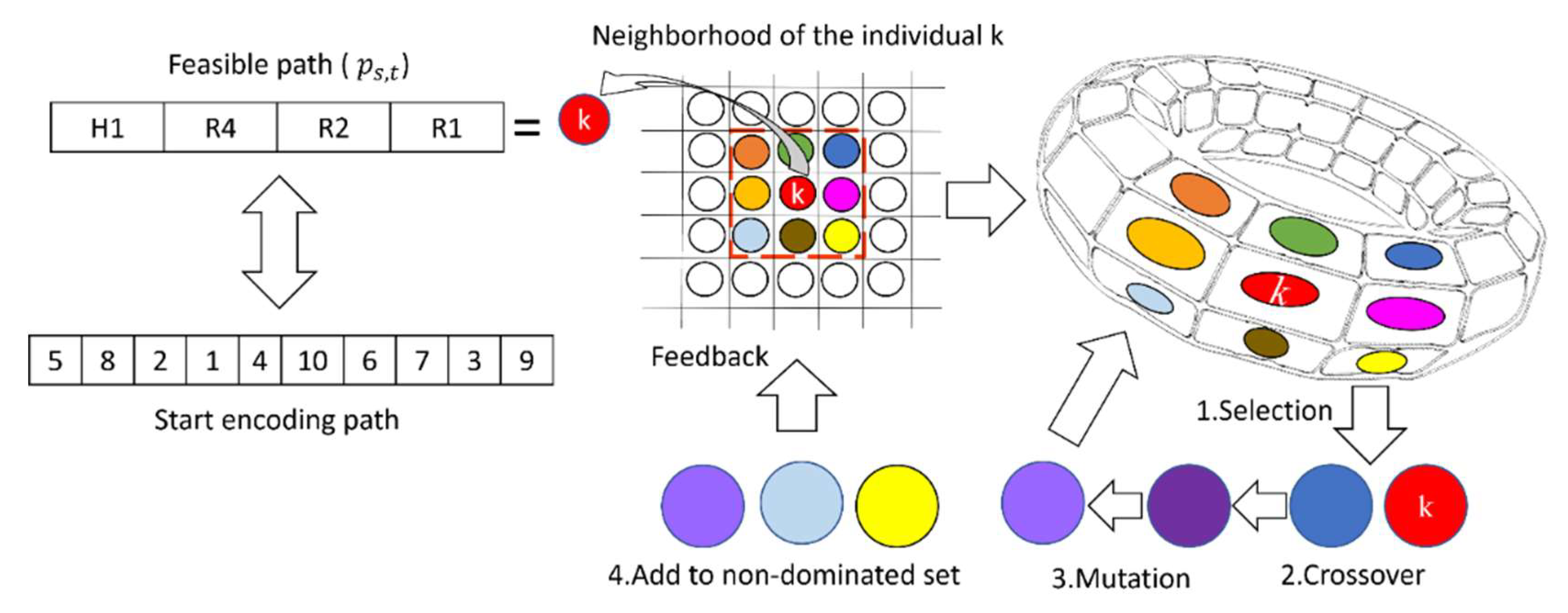
3.5. MOCell-Based QoS Optimal Path
| Algorithm 2. Pseudocode of metaheuristic based on MOCell |
| 1: data = parameters //initial parameter MOCell |
| 2: pop = solution // Create an initial population |
| 3: grip = (pop) //distribute the population in a toroidal grip. |
| 4: = [] //create pareto front = empty |
| 5: While (terminal Condition = = false) do |
| 6: For do |
| 7: neighborhood = (individual) //everyone individual builds a neighborhood |
| 8: parents = (neighborhood) //selection parents |
| 9: offspring = recombination (data, parents) //crossover |
| 10: offspring = mutation (data, offspring) |
| 11: pop = replacement ([parents], offspring) |
| 12: = insert (Offspring) |
| 13: End |
| 14: pop = feedback (ParetoFront) |
| 15: End |
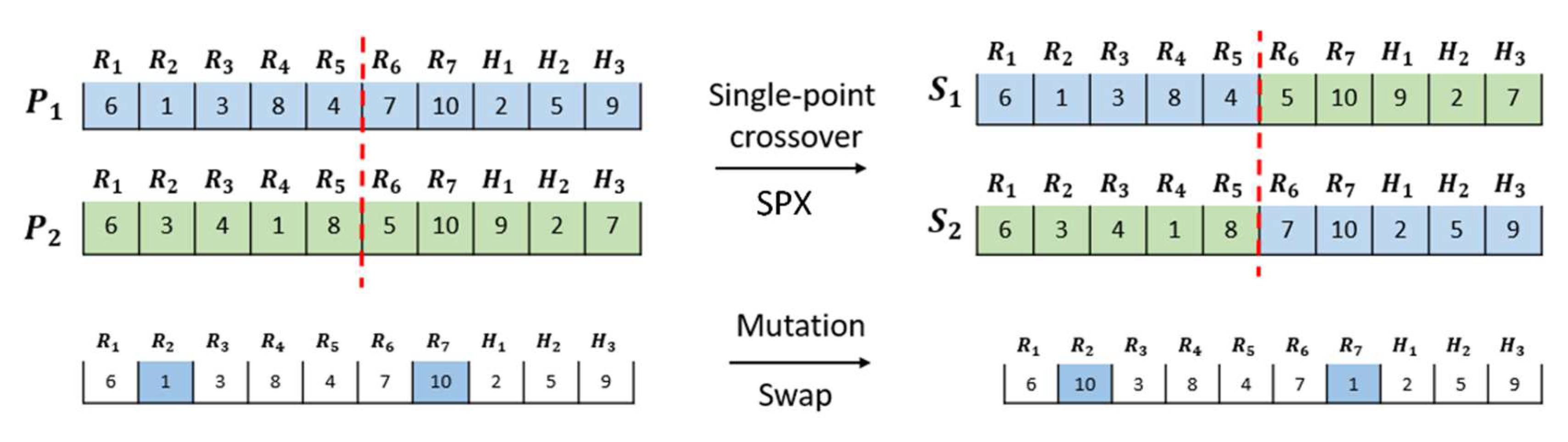
- Generated a chain with 10 elements corresponding to network nodes.
- Filled the string with random numbers from 1 to 10.
- Created a chromosome: 5 8 2 1 4 10 6 7 3 9.
3.6. MOEA/D QoS Optimal Path
| Algorithm 3. Pseudocode of metaheuristics based on MOEA/D |
| 1: data = parameters // Initial parameter MOEA/D |
| 2: pop = solution // Create an initial population |
| 3: (t = 0) // Initialize Weight vectors |
| 4: T = //Calculate neighborhoods by the weight vectors |
| 5: = [] //create pareto front = empty |
| 6: While (terminal Condition==false) do |
| 7: For neighborhood do//everyone Weight vector builds a neighborhood |
| 8: For do |
| 9: parents = (neighborhood) //selection parents by neighborhood |
| 10: offspring = recombination (data, parents) //crossover |
| 11: offspring = mutation (data, offspring) |
| 12: pop = replacement (parents, offspring) |
| 13: = Insert (Offspring) |
| 14: End |
| 15: End |
| 16: pop = feedback (Pareto Front) |
| 17: End |
3.7. Simulation Model
3.8. Experiment Setup
- Linux Debian 9;
- Mininet 2.3;
- OpenDayLight (ODL) SDN Controller;
- MATLAB 2021 for MOCell-based code;
- Python 3 for REST API communication scripts;
- Iperf for data stream transfers performance.
4. Evaluation
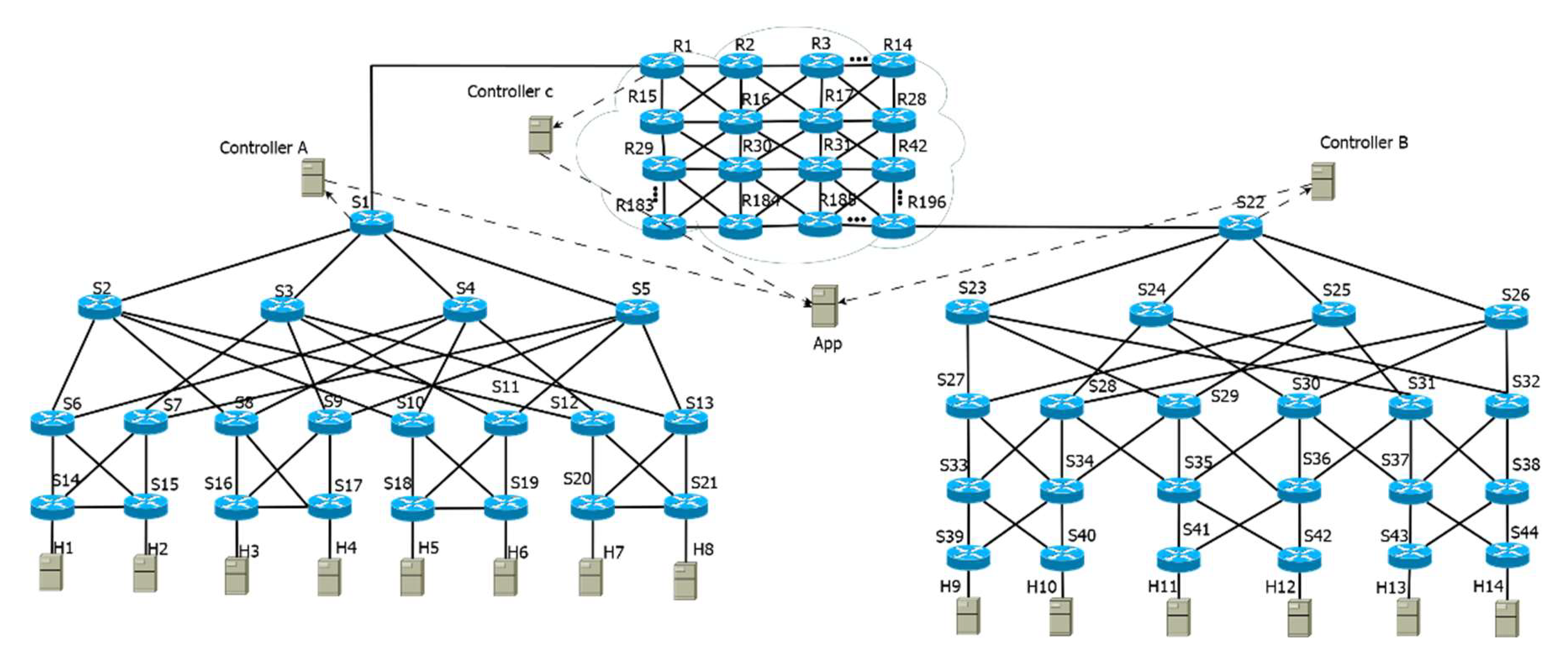
- Design and execute the network topology with three domains (A, B, and C) and an external controller per domain.
- Execute network performance tests between the end nodes with IPERF according to the optimization parameter.
- Transfer the traffic during the specified period.
- Repeat the experiment using data stream forwarding according to the optimization parameter.
- Obtain results.
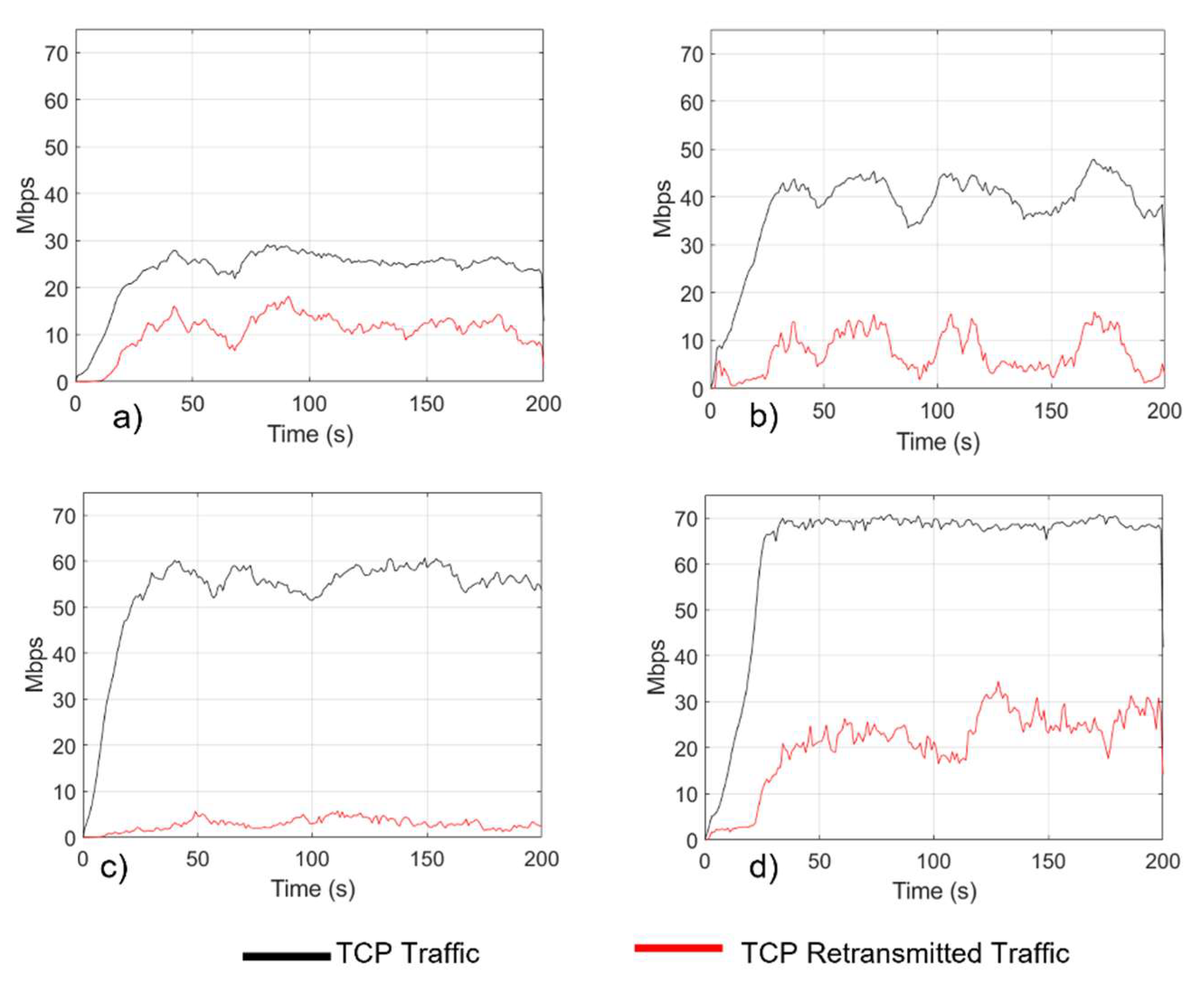
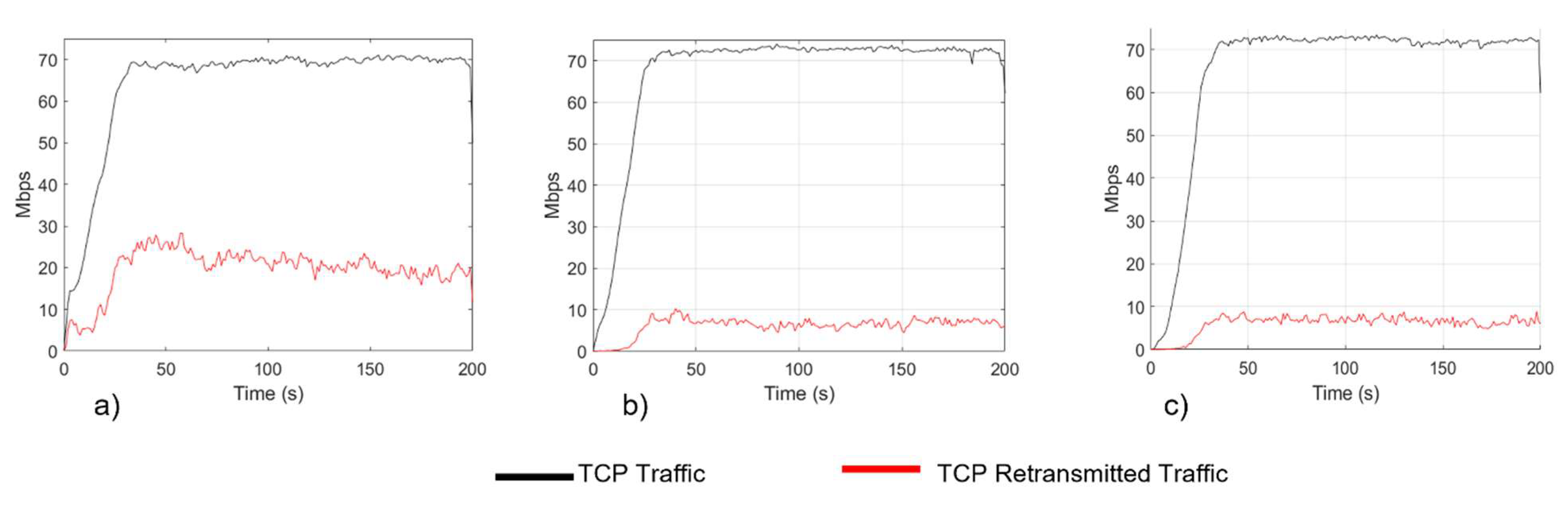
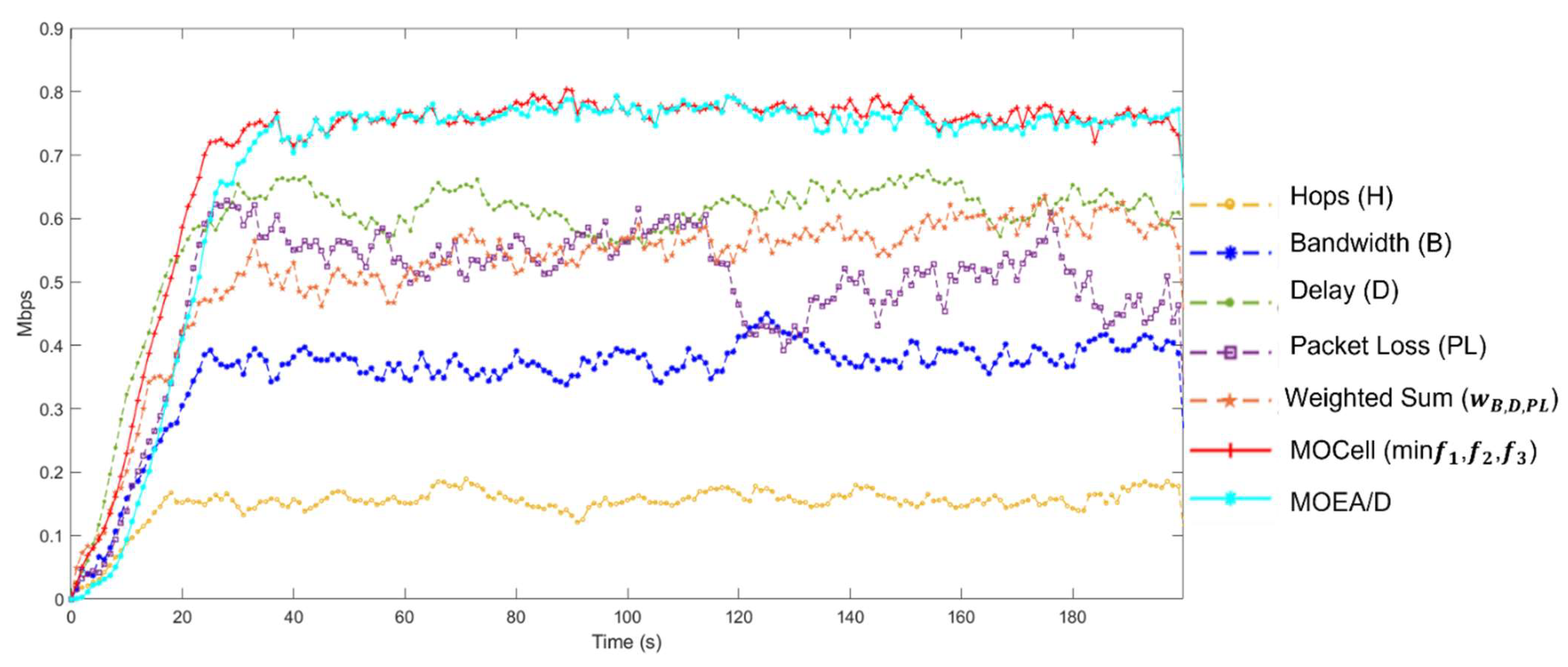
Network Performance
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Link (S) | Metrics | Link (S) | Metrics | Link (S) | Metrics | Link (S) | Metrics |
|---|---|---|---|---|---|---|---|
| 1,2 | 10,0,97 | 3,13 | 16,0.003,82 | 6,15 | 3,0,81 | 11,18 | 22,0,80 |
| 1,3 | 5,0,94 | 4,6 | 13,0,88 | 7,14 | 3,0,79 | 11,19 | 23,0,76 |
| 1,4 | 8,0,99 | 4,8 | 7,0,97 | 7,15 | 2,0,85 | 12,13 | 7,0,80 |
| 1,5 | 3,0,93 | 4,10 | 16,0,90 | 8,l9 | 9,0,78 | 12,20 | 21,0.003,100 |
| 2,6 | 18,0.002,93 | 4,12 | 18,0.001,96 | 8,16 | 18,0.002,96 | 12,21 | 12,0,77 |
| 2,8 | 12,0,90 | 5,7 | 17,0,84 | 8,17 | 12,0,87 | 13,20 | 6,0,80 |
| 2,10 | 24,0.001,98 | 5,9 | 9,0,92 | 9,16 | 7,0,76 | 13,21 | 21,0.001,79 |
| 2,12 | 8,0,91 | 5,11 | 21,0.002,94 | 9,17 | 14,0,83 | 14,15 | 8,0,83 |
| 3,7 | 11,0,86 | 5,13 | 15,0,97 | 10,11 | 11,0,80 | 16,17 | 7,0,80 |
| 3,9 | 21,0.004,97 | 6,7 | 8,0,82 | 10,18 | 13,0,83 | 18,19 | 6,0,80 |
| 3,11 | 9,0,95 | 6,14 | 23,0,86 | 10,19 | 9,0,82 | 20,21 | 9,0,79 |
| H1-H8 | 0,0,100 |
| Link (S) | Metrics | Link (S) | Metrics | Link (S) | Metrics | Link (S) | Metrics |
|---|---|---|---|---|---|---|---|
| 22,23 | 2,0,94 | 25,29 | 8,0,93 | 29,35 | 18,0,82 | 33,40 | 7,0,92 |
| 22,24 | 4,0,96 | 25,31 | 13,0.001,91 | 29,36 | 12,0,87 | 34,39 | 5,0,83 |
| 22,25 | 2,0,98 | 26,28 | 9,0,92 | 30,35 | 5,0,94 | 34,40 | 12,0,95 |
| 22,26 | 16,0,99 | 26,30 | 12,0.001,89 | 30,36 | 1,0.001,86 | 35,41 | 5,0.002,84 |
| 23,27 | 8,0.001,91 | 26,32 | 18,0,94 | 30,37 | 3,0,97 | 35,42 | 4,0,96 |
| 23,29 | 15,0,93 | 27,33 | 7,0.002,93 | 31,36 | 4,0.001,93 | 36,41 | 2,0,87 |
| 23,31 | 12,0.001,95 | 27,34 | 12,0,87 | 31,37 | 6,0,96 | 36,42 | 7,0,93 |
| 24,28 | 2,0,92 | 28,33 | 11,0,88 | 31,38 | 2,0,99 | 37,43 | 6,0,92 |
| 24,l0 | 7,0.001,94 | 28,34 | 6,0,93 | 32,37 | 20,0,94 | 37,44 | 3,0,94 |
| 24,32 | 12,0,97 | 28,35 | 2,0,97 | 32,38 | 5,0.001,86 | 38,43 | 5,0,94 |
| 25,27 | 12,0,98 | 29,34 | 15,0.002,97 | 33,39 | 3,0.002,82 | 38,44 | 3,0.001,95 |
| H9-H14 | 0,0,100 |
| Link (R) | Metrics | Link (R) | Metrics | Link (R) | Metrics | Link (R) | Metrics |
|---|---|---|---|---|---|---|---|
| 1,2 | 2,0,89 | 47,48 | 2,0,89 | 46,60 | 2,0,97 | 92,106 | 3,0.001,93 |
| 1,15 | 2,0.001,86 | 47,60 | 1,0,85 | 46,61 | 3,0,86 | 137,152 | 3,0,86 |
| 1,16 | 1,0,91 | 47,61 | 3,0,93 | 92,107 | 1,0,98 | 38,139 | 3,0,100 |
| 2,3 | 3,0,97 | 47,62 | 1,0,85 | 93,94 | 3,0,93 | 138,151 | 3,0,86 |
| 2,15 | 1,0,97 | 48,49 | 2,0.001,94 | 93,106 | 1,0,100 | 138,152 | 4,0.001,85 |
| 2,16 | 2,0.001,94 | 48,61 | 2,0,99 | 93,107 | 2,0.001,92 | 138,153 | 2,0,86 |
| 2,17 | 4,0.001,91 | 48,62 | 3,0,97 | 93,108 | 2,0,96 | 139,140 | 4,0.001,90 |
| 3,4 | 1,0.001,98 | 48,63 | 1,0,97 | 94,95 | 1,0.001,97 | 139,152 | 3,0,91 |
| 3,16 | 4,0,87 | 49,50 | 2,0,89 | 94,107 | 2,0,96 | 139,153 | 1,0,97 |
| 3,17 | 4,0,95 | 49,62 | 1,0,93 | 94,108 | 2,0.001,94 | 139,154 | 1,0,97 |
| 3,18 | 3,0,86 | 49,63 | 1,0.001,96 | 94,109 | 4,0,90 | 140,153 | 1,0,97 |
| 4,5 | 1,0.001,85 | 49,64 | 2,0,86 | 95,96 | 3,0,87 | 140,154 | 3,0,85 |
| 4,17 | 1,0,91 | 50,51 | 1,0,97 | 95,108 | 2,0,96 | 141,142 | 2,0.001,87 |
| 4,18 | 1,0,84 | 50,63 | 1,0,94 | 95,109 | 2,0,98 | 141,166 | 3,0,91 |
| 4,19 | 4,0.001,87 | 50,64 | 2,0.001,95 | 95,110 | 1,0,95 | 141,156 | 3,0.001,71 |
| 5,6 | 4,0.001,82 | 50,65 | 1,0,95 | 96,97 | 1,0.001,93 | 142,143 | 2,0.001,86 |
| 5,18 | 2,0,82 | 51,52 | 1,0,98 | 96,109 | 4,0,85 | 142,155 | 3,0,98 |
| 5,19 | 4,0,90 | 51,64 | 3,0,100 | 96,110 | 4,0.001,93 | 142,156 | 2,0,91 |
| 5,20 | 3,0.001,94 | 51,65 | 3,0.001,91 | 96,111 | 2,0,88 | 142,157 | 2,0,91 |
| 6,7 | 2,0,99 | 51,66 | 1,0,86 | 97,98 | 4,0,95 | 143,144 | 2,0,89 |
| 6,19 | 4,0,95 | 52,53 | 4,0.001,85 | 97,110 | 3,0,87 | 143,156 | 3,0,95 |
| 6,20 | 2,0,94 | 52,65 | 3,0,96 | 97,111 | 2,0,88 | 143,157 | 4,0.001,96 |
| 6,21 | 2,0,83 | 52,66 | 1,0.001,90 | 97,112 | 3,0,100 | 143,158 | 4,0,90 |
| 7,8 | 3,0,96 | 52,67 | 4,0,85 | 98,111 | 1,0,98 | 144,145 | 4,0,94 |
| 7.20 | 1,0,86 | 53,54 | 4,0,96 | 98,112 | 1,0,91 | 144,157 | 3,0,89 |
| 7,21 | 4,0,95 | 53,66 | 2,0,96 | 99,100 | 2,0.001,83 | 144,158 | 4,0,85 |
| 7,22 | 2,0,88 | 53,67 | 2,0.001,96 | 99,113 | 1,0,99 | 144,159 | 3,0,93 |
| 8,9 | 2,0.001,89 | 53,68 | 1,0,89 | 99,114 | 3,0,76 | 145,146 | 4,0.001,96 |
| 8,21 | 2,0,96 | 54,55 | 4,0.001,85 | 100,101 | 3,0,96 | 145,158 | 1,0,96 |
| 8,22 | 1,0,84 | 54,67 | 1,0,93 | 100,113 | 2,0,87 | 145,159 | 3,0,98 |
| 8,23 | 3,0,84 | 54,68 | 4,0,95 | 100,114 | 3,0,100 | 145,160 | 4,0,89 |
| 9,10 | 1,0,83 | 54,69 | 3,0,85 | 100,115 | 3,0,85 | 146,147 | 1,0.001,96 |
| 9,22 | 3,0,87 | 55,56 | 3,0.001,100 | 101,102 | 2,0.001,86 | 146,159 | 1,0,95 |
| 9,23 | 4,0,95 | 55,68 | 2,0,92 | 101,114 | 1,0,99 | 146,160 | 1,0,100 |
| 9,24 | 4,0.001,85 | 55,69 | 4,0.001,86 | 101,115 | 2,0,94 | 146,161 | 3,0,92 |
| 10,11 | 3,0.001,88 | 55,70 | 1,0,91 | 101,116 | 1,0,92 | 147,148 | 3,0.001,96 |
| 10,23 | 1,0,93 | 56,69 | 3,0.001,87 | 102,103 | 1,0.001,90 | 147,160 | 3,0,85 |
| 10,24 | 4,0,80 | 56,70 | 3,0,85 | 102,115 | 1,0,89 | 147,161 | 1,0,100 |
| 10,25 | 1,0.001,80 | 57,58 | 3,0,88 | 102,116 | 3,0,92 | 147,162 | 3,0,100 |
| 11,12 | 4,0.001,88 | 57,71 | 2,0,78 | 102,117 | 3,0,100 | 148,149 | 3,0,94 |
| 11,24 | 3,0,88 | 57,72 | 1,0,80 | 103,104 | 3,0,91 | 148,161 | 3,0,97 |
| 11,25 | 2,0,86 | 58,59 | 3,0,94 | 103,116 | 3,0.001,97 | 148,162 | 2,0,92 |
| 11,26 | 1,0.001,90 | 58,71 | 2,0,87 | 103,117 | 3,0,90 | 148,163 | 3,0,91 |
| 12,13 | 2,0,89 | 58,72 | 3,0,88 | 103,118 | 2,0,96 | 149,150 | 1,0.001,96 |
| 12,25 | 3,0,81 | 58,73 | 4,0,97 | 104,105 | 3,0.001,87 | 149,162 | 2,0,87 |
| 12,26 | 2,0,96 | 59,60 | 1,0.001,87 | 104,117 | 1,0,92 | 149,163 | 1,0.001,90 |
| 12,27 | 3,0.001,95 | 59,72 | 3,0,96 | 104,118 | 4,0,90 | 149,164 | 1,0,97 |
| 13,14 | 4,0.001,91 | 59,73 | 1,0.001,95 | 104,119 | 2,0,91 | 150,151 | 1,0.001,100 |
| 13,26 | 1,0,81 | 59,74 | 1,0,90 | 105,106 | 4,0,89 | 150,163 | 2,0,95 |
| 13,27 | 1,0,82 | 60,61 | 2,0,86 | 105,118 | 2,0,97 | 150,164 | 1,0,87 |
| 13,28 | 1,0,98 | 60,73 | 4,0,93 | 105,119 | 3,0,100 | 150,165 | 2,0,89 |
| 14,27 | 3,0,86 | 60,74 | 3,0.001,93 | 105,120 | 2,0,91 | 151,152 | 1,0.001,91 |
| 14,28 | 2,0.001,88 | 60,75 | 1,0,85 | 106,107 | 1,0.001,94 | 151,164 | 1,0,91 |
| 15,16 | 2,0.001,86 | 61,62 | 4,0,96 | 106,119 | 2,0,98 | 151,165 | 4,0.001,99 |
| 15,29 | 3,0,89 | 61,74 | 1,0,92 | 106,120 | 1,0,94 | 151,166 | 4,0,95 |
| 15,30 | 2,0.001,72 | 61,75 | 2,0,88 | 106,121 | 3,0,92 | 152,153 | 1,0.001,92 |
| 16,17 | 4,0.001,93 | 61,76 | 3,0,91 | 107,108 | 4,0,95 | 152,165 | 4,0,95 |
| 16,29 | 2,0,86 | 62,63 | 1,0.001,97 | 107,120 | 2,0,90 | 152,166 | 3,0,93 |
| 16,30 | 4,0,92 | 62,75 | 1,0,91 | 107,121 | 4,0,100 | 152,167 | 4,0,100 |
| 16,31 | 3,0,93 | 62,76 | 2,0,92 | 107,122 | 3,0,94 | 153,154 | 1,0.001,92 |
| 17,18 | 3,0.001,91 | 62,77 | 1,0,89 | 108,109 | 4,0,99 | 153,166 | 2,0,93 |
| 17,30 | 4,0,91 | 63,64 | 3,0,98 | 108,121 | 1,0,95 | 153,167 | 3,0.001,94 |
| 17,31 | 4,0,92 | 63,76 | 4,0,97 | 108,122 | 2,0.001,85 | 153,168 | 2,0,93 |
| 17,32 | 2,0,94 | 63,77 | 3,0,100 | 108,123 | 2,0,90 | 154,167 | 4,0,98 |
| 18,19 | 2,0,95 | 63,78 | 4,0,97 | 109,110 | 1,0.001,100 | 154,168 | 4,0,100 |
| 18,31 | 4,0,86 | 64,65 | 2,0.001,86 | 109,122 | 1,0,100 | 155,156 | 2,0,72 |
| 18,32 | 3,0.001,90 | 64,77 | 3,0,99 | 109,123 | 3,0,90 | 155,169 | 1,0,98 |
| 18,33 | 4,0,90 | 64,78 | 4,0,87 | 109,124 | 4,0,85 | 155,170 | 1,0,70 |
| 19,20 | 1,0,98 | 64,79 | 3,0,91 | 110,111 | 2,0.001,98 | 156,157 | 2,0.001,86 |
| 19,32 | 3,0,96 | 65,66 | 3,0.001,93 | 110,123 | 2,0,96 | 156,169 | 3,0,98 |
| 19,33 | 4,0.001,89 | 65,78 | 4,0,90 | 110,124 | 4,0,95 | 156,170 | 2,0,95 |
| 19,34 | 2,0,100 | 65,79 | 3,0.001,97 | 110,125 | 3,0,91 | 156,171 | 3,0,100 |
| 20,21 | 2,0.001,86 | 65,80 | 4,0,92 | 111,112 | 1,0,91 | 157,158 | 4,0,94 |
| 20,33 | 2,0,97 | 66,67 | 3,0.001,87 | 111,124 | 4,0,94 | 157,170 | 2,0,88 |
| 20,34 | 4,0.001,98 | 66,79 | 1,0,99 | 111,125 | 3,0,89 | 157,171 | 3,0.001,94 |
| 20,35 | 4,0,93 | 66,80 | 4,0,88 | 111,126 | 2,0,89 | 157,172 | 4,0,91 |
| 21,22 | 4,0.001,97 | 66,81 | 1,0,100 | 112,125 | 4,0.001,88 | 158,159 | 4,0.001,99 |
| 21,34 | 4,0,93 | 67,68 | 2,0.001,92 | 112,126 | 3,0,88 | 158,171 | 2,0,95 |
| 21,35 | 3,0.001,95 | 67,80 | 2,0,86 | 113,114 | 1,0.001,81 | 158,172 | 2,0,86 |
| 21,36 | 3,0,97 | 67,81 | 3,0,89 | 113,127 | 1,0,81 | 158,173 | 2,0,94 |
| 22,23 | 1,0,90 | 67,82 | 4,0,93 | 113,128 | 3,0.001,87 | 159,160 | 4,0,88 |
| 22,35 | 4,0,92 | 68,69 | 4,0.001,91 | 114,115 | 3,0,95 | 159,172 | 2,0,99 |
| 22,36 | 3,0.001,100 | 68,81 | 4,0,87 | 114,127 | 4,0,86 | 159,173 | 1,0,94 |
| 22,37 | 4,0,100,87 | 68,82 | 3,0.001,100 | 114,128 | 3,0.001,98 | 159,174 | 2,0,91 |
| 23,24 | 4,0,86 | 68,83 | 4,0,99 | 114,129 | 1,0,98 | 160,161 | 2,0.001,98 |
| 23,36 | 3,0,99 | 69,70 | 2,0.001,88 | 115,116 | 3,0.001,92 | 160,173 | 2,0,93 |
| 23,37 | 3,0,89 | 69,82 | 2,0,100 | 115,128 | 4,0,92 | 160,174 | 4,0,95 |
| 23,38 | 2,0,100 | 69,83 | 2,0.001,92 | 115,129 | 2,0.001,85 | 160,175 | 4,0,92 |
| 24,25 | 3,0,100 | 69,84 | 2,0,94 | 115,130 | 1,0,95 | 161,162 | 3,0,95 |
| 24,37 | 1,0,95 | 70,85 | 1,0.001,94 | 116,117 | 4,0,92 | 161,174 | 1,0,96 |
| 24,38 | 3,0.001,98 | 70,84 | 2,0,96 | 116,129 | 2,0,94 | 161,175 | 4,0,88 |
| 24,39 | 2,0,86 | 71,72 | 2,0,70 | 116,130 | 3,0,91 | 161,176 | 3,0,86 |
| 25,26 | 3,0,98 | 71,85 | 2,0,74 | 116,131 | 1,0,95 | 162,163 | 4,0.001,99 |
| 25,38 | 2,0,95 | 71,86 | 3,0.001,95 | 117,118 | 1,0,89 | 162,175 | 3,0,94 |
| 25,39 | 4,0.001,96 | 72,73 | 3,0,98 | 117,130 | 1,0,92 | 162,176 | 3,0.001,85 |
| 25,40 | 4,0,91 | 72,85 | 1,0,96 | 117,131 | 3,0,90 | 162,177 | 1,0,94 |
| 26,27 | 4,0.001,100 | 72,86 | 2,0,93 | 117,132 | 3,0,90 | 163,164 | 3,0,98 |
| 26,37 | 3,0,90 | 72,87 | 3,0,94 | 118,119 | 4,0,87 | 163,176 | 4,0,88 |
| 26,40 | 4,0,90 | 73,74 | 2,0.001,94 | 118,131 | 2,0,94 | 163,177 | 2,0.001,97 |
| 26,4 | 4,0,91 | 73,86 | 1,0,98 | 118,132 | 3,0,96 | 163,178 | 3,0,92 |
| 27,28 | 3,0.001,97 | 73,87 | 2,0,86 | 118,133 | 1,0,94 | 164,165 | 3,0.001,97 |
| 27,20 | 3,0,96 | 73,88 | 3,0,92 | 119,120 | 2,0.001,90 | 164,177 | 1,0,91 |
| 27,41 | 4,0.001,99 | 74,75 | 1,0,100 | 119,132 | 2,0,86 | 164,178 | 1,0.001,99 |
| 27,42 | 2,0,91 | 74,87 | 3,0,86 | 119,133 | 4,0.001,87 | 164,179 | 1,0,95 |
| 28,41 | 4,0.001,97 | 74,88 | 4,0.001,88 | 119,134 | 1,0,88 | 165,166 | 1,0,90 |
| 28,42 | 1,0,96 | 74,89 | 4,0,97 | 120,121 | 4,0.001,91 | 165,178 | 1,0,91 |
| 29,30 | 3,0,96 | 75,76 | 3,0,94 | 120,133 | 3,0,93 | 165,179 | 4,0,97 |
| 29,43 | 1,0,84 | 75,88 | 4,0,95 | 120,134 | 4,0,91 | 165,180 | 3,0,87 |
| 29,44 | 2,0.001,81 | 75,89 | 2,0,91 | 120,135 | 1,0.001,89 | 166,167 | 1,0,89 |
| 30,31 | 3,0,90 | 75,90 | 3,0,90 | 121,122 | 3,0,89 | 166,179 | 1,0,85 |
| 30,43 | 2,0,88 | 76,77 | 1,0.001,91 | 121,134 | 1,0,87 | 166,180 | 2,0,87 |
| 30,44 | 4,0.001,99 | 76,89 | 3,0,98 | 121,135 | 4,0,88 | 166,181 | 3,0,91 |
| 30,45 | 1,0,85 | 76,90 | 4,0.001,92 | 121,136 | 4,0,100 | 167,168 | 3,0,88 |
| 31,32 | 2,0,91 | 76,91 | 4,0,94 | 122,123 | 3,0,86 | 167,180 | 4,0,95 |
| 31,44 | 2,0,95 | 77,78 | 4,0,97 | 122,135 | 2,0,88 | 167,181 | 4,0.001,85 |
| 31,45 | 1,0,95 | 77,90 | 2,0,92 | 122,136 | 3,0,91 | 167,182 | 4,0,94 |
| 31,46 | 1,0,89 | 77,91 | 1,0.001,85 | 122,137 | 1,0.001,91 | 168,181 | 3,0.001,88 |
| 32,33 | 4,0,85 | 77,92 | 4,0,99 | 123,124 | 2,0,98 | 168,182 | 3,0,93 |
| 32,45 | 1,0,88 | 78,79 | 3,0.001,96 | 123,136 | 4,0,92 | 169,170 | 1,0.001,87 |
| 32,46 | 1,0,94 | 78,91 | 2,0,89 | 123,137 | 3,0.001,99 | 169,183 | 2,0,99 |
| 32,47 | 2,0,97 | 78,92 | 1,0.001,98 | 132,138 | 3,0,88 | 169,184 | 2,0,70 |
| 33,34 | 3,0.001,89 | 78,93 | 1,0,99 | 124,125 | 2,0.001,98 | 170,171 | 1,0.001,94 |
| 33,46 | 1,0,93 | 79,80 | 3,0,97 | 124,137 | 3,0,100 | 170,183 | 4,0,96 |
| 33,47 | 1,0.001,98 | 79,92 | 1,0,89 | 124,138 | 4,0.001,85 | 170,184 | 3,0,100 |
| 33,48 | 3,0,89 | 79,93 | 3,0,88 | 124,139 | 1,0,100 | 170,185 | 1,0,86 |
| 34,35 | 2,0.001,89 | 79,94 | 2,0,85 | 125,126 | 1,0,97 | 171,172 | 4,0,97 |
| 34,47 | 4,0,90 | 80,81 | 4,0,94 | 125,138 | 2,0,100 | 171,184 | 1,0,93 |
| 34,48 | 4,0,86 | 80,93 | 4,0,100 | 125,139 | 4,0.001,94 | 171,185 | 1,0.001,99 |
| 34,49 | 1,0,97 | 80,94 | 1,0.001,85 | 125,140 | 4,89,89 | 171,186 | 1,0,96 |
| 35,36 | 4,0,86 | 80,95 | 4,0,98 | 126,139 | 1,94,84 | 172,173 | 1,0.001,94 |
| 35,48 | 1,0,89 | 81,82 | 4,0,85 | 126,140 | 1,95,85 | 172,185 | 3,0.001,91 |
| 35,49 | 3,0.001,95 | 81,94 | 2,0,93 | 127,128 | 3,0.001,91 | 172,186 | 1,0,97 |
| 35,50 | 1,0,85 | 81,95 | 4,0.001,100 | 127,141 | 1,0,76 | 172,187 | 1,0.001,100 |
| 36,37 | 3,0,88 | 81,96 | 2,0,93 | 127,142 | 2,0,85 | 173,174 | 2,0,92 |
| 36,49 | 1,0,99 | 82,83 | 2,0,99 | 128,129 | 3,0.001,91 | 173,186 | 3,0.001,99 |
| 36,50 | 4,0,96 | 82,95 | 2,0,93 | 128,141 | 4,0,96 | 173,187 | 2,0,89 |
| 36,51 | 4,0,88 | 82,96 | 2,0.001,97 | 128,142 | 2,0.001,96 | 173,188 | 1,0,98 |
| 37,38 | 2,0.001,100 | 82,97 | 1,0,86 | 128,143 | 3,0,98 | 174,175 | 2,0.001,99 |
| 37,50 | 4,0,90 | 83,84 | 4,0,99 | 129,130 | 3,0.001,89 | 174,187 | 2,0.001,99 |
| 37,51 | 1,0,90 | 83,96 | 1,0,85 | 129,142 | 4,0,99 | 174,188 | 4,0,90 |
| 37,52 | 2,0,92 | 83,97 | 3,0,91 | 129,143 | 3,0.001,98 | 174,189 | 4,0,97 |
| 38,39 | 2,0.001,89 | 83,98 | 3,0,97 | 129,144 | 4,0,85 | 175,176 | 4,0.001,97 |
| 28,51 | 2,0,97 | 84,97 | 1,0.001,88 | 130,131, | 2,0.001,86 | 175,188 | 4,0,95 |
| 38,52 | 4,0,90 | 84,98 | 4,0,85 | 130,143 | 3,0,91 | 175,189 | 4,0,92 |
| 38,53 | 1,0,97 | 85,86 | 1,0,90 | 130,144 | 3,0.001,91 | 175,190 | 2,0.001,95 |
| 39,40 | 3,0,95 | 85,99 | 1,0,95 | 130,145 | 1,0,90 | 176,177 | 1,0.001,85 |
| 39,52 | 1,0,94 | 85,100 | 2,0.001,91 | 131,132 | 4,0.001,95 | 176,189 | 1,0.001,87 |
| 39,53 | 4,0.001,90 | 86,87 | 2,0,92 | 131,144 | 1,0,88 | 176,190 | 1,0,86 |
| 39,54 | 1,0,87 | 86,99 | 2,0,93 | 131,145 | 4,0.001,94 | 176,191 | 2,0,85 |
| 40,41 | 3,0.001,100 | 86,100 | 3,0.001,98 | 131,146 | 2,0,100 | 177,178 | 4,0,90 |
| 40,53 | 2,0,98 | 86,101 | 4,0,98 | 132,133 | 3,0.001,99 | 177,190 | 1,0.001,100 |
| 40,54 | 1,0,89 | 87,88 | 2,0.001,94 | 132,145 | 2,0,86 | 177,191 | 3,0,93 |
| 40,55 | 4,0,87 | 87,100 | 1,0,93 | 132,146 | 2,0,96 | 177,192 | 1,0.001,94 |
| 41,42 | 4,0,91 | 87,101 | 4,0.001,93 | 132,147 | 1,0,84 | 178,179 | 3,0.001,94 |
| 41,54 | 4,0,92 | 87,102 | 1,0,87 | 133,134 | 3,0,98 | 178,191 | 1,0.001,85 |
| 41,55 | 4,0.001,89 | 88,89 | 1,0,97 | 133,146 | 4,0,88 | 178,192 | 4,0,100 |
| 41,56 | 1,0,98 | 88,101 | 4,0,92 | 133147 | 1,0,91 | 178,193 | 2,0,97 |
| 42,55 | 1,0,96 | 88,102 | 1,0.001,100 | 133,148 | 2,0,85 | 178,180 | 2,0,91 |
| 42,56 | 1,0,98 | 88,103 | 4,0,88 | 134,135 | 3,0,89 | 179,192 | 2,0.001,86 |
| 43,44 | 3,0,87 | 89,90 | 4,0,96 | 134,147 | 3,0,93 | 179,193 | 1,0,98 |
| 43,57 | 1,0,86 | 89,102 | 1,0,86 | 134,148 | 1,0.001,95 | 179,194 | 1,0.001,86 |
| 43,58 | 1,0,74 | 89,103 | 2,0,91 | 134,149 | 3,0,88 | 180,181 | 1,0.001,97 |
| 44,45 | 3,0.001,91 | 89,104 | 2,0,99 | 135,136 | 2,0,86 | 180,193 | 1,0.001,98 |
| 44,57 | 2,0,86 | 90,91 | 2,0,89 | 135,148 | 1,0,91 | 180,194 | 3,0,87 |
| 44,58 | 4,0,93 | 90,103 | 4,0,99 | 135,149 | 2,0,87 | 180,195 | 1,0.001,96 |
| 44,59 | 3,0,93 | 90,104 | 2,0,94 | 135,150 | 2,0,98 | 181,182 | 2,0,86 |
| 45,46 | 4,0.001,100 | 90,105 | 3,0,90 | 136,137 | 4,0.001,91 | 181,194 | 2,0.001,94 |
| 45,58 | 1,0,88 | 91,92 | 1,0,96 | 136,149 | 1,0,88 | 181,195 | 3,0,85 |
| 45,59 | 2,0,82 | 91,104 | 2,0,95 | 136,150 | 3,0.001,98 | 181,196 | 1,0,99 |
| 45,60 | 2,0,98 | 91,105 | 2,0,95 | 136,151 | 3,0,99 | 182,195 | 1,0.001,96 |
| 46,47 | 4,0,87 | 91,106 | 2,0,94 | 137,138 | 4,0,82 | 182,196 | 1,0,85 |
| 46,59 | 4,0,100 | 92,93 | 1,0.001,89 | 92,105 | 4,0,91 | 195,196 | 1,0,92 |
References
- Xu, Y.; Gui, G.; Gacanin, H.; Adachi, F. A Survey on Resource Allocation for 5G Heterogeneous Networks: Current Research, Future Trends, and Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 668–695. [Google Scholar] [CrossRef]
- García-Tadeo, D.A.; Peram, D.R.; Kumar, K.S.; Vives, L.; Sharma, T.; Manoharan, G. Comparing the impact of Internet of Things and cloud computing on organisational behavior: A survey. Mater. Today Proc. 2022, 51, 2281–2285. [Google Scholar] [CrossRef]
- Laghari, A.A.; Wu, K.; Laghari, R.A.; Ali, M.; Khan, A.A. A Review and State of Art of Internet of Things (IoT). Arch. Comput. Methods Eng. 2022, 29, 1–19. [Google Scholar] [CrossRef]
- Hajjaji, Y.; Boulila, W.; Farah, I.R.; Romdhani, I.; Hussain, A. Big data and IoT-based applications in smart environments: A systematic review. Comput. Sci. Rev. 2021, 39, 100318. [Google Scholar] [CrossRef]
- Pavithra, H.; Srinivasan, G.N.; Swarnalatha, K.S. A Survey on Role of SDN in Implementing QoS in Routing in the Network. Lect. Notes Electr. Eng. 2022, 789, 361–366. [Google Scholar] [CrossRef]
- Manguri, K.H.; Omer, S.M. SDN for IoT Environment: A Survey and Research Challenges. ITM Web Conf. 2022, 42, 01005. [Google Scholar] [CrossRef]
- Amin, R.; Rojas, E.; Aqdus, A.; Ramzan, S.; Casillas-Perez, D.; Arco, J.M. A Survey on Machine Learning Techniques for Routing Optimization in SDN. IEEE Access 2021, 9, 104582–104611. [Google Scholar] [CrossRef]
- Alsaeedi, M.; Mohamad, M.M.; Al-Roubaiey, A.A. Toward Adaptive and Scalable OpenFlow-SDN Flow Control: A Survey. IEEE Access 2019, 7, 107346–107379. [Google Scholar] [CrossRef]
- Rudra, B.; Thanmayee, S. Architecture and Deployment Models-SDN Protocols, APIs, and Layers, Applications and Implementations. In Software Defined Internet of Everything; Springer: Cham, Switzerland, 2022; pp. 63–77. [Google Scholar] [CrossRef]
- Akin, E.; Korkmaz, T. Comparison of Routing Algorithms with Static and Dynamic Link Cost in Software Defined Networking (SDN). IEEE Access 2019, 7, 148629–148644. [Google Scholar] [CrossRef]
- Yang, S.; Tan, C.; Madsen, D.Ø.; Xiang, H.; Li, Y.; Khan, I.; Choi, B.J. Comparative Analysis of Routing Schemes Based on Machine Learning. Mob. Inf. Syst. 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Khadir, K.; Guermouche, N.; Guittoum, A.; Monteil, T. A Genetic Algorithm-Based Approach for Fluctuating QoS Aware Selection of IoT Services. IEEE Access 2022, 10, 17946–17965. [Google Scholar] [CrossRef]
- Cui, L.S.; Srivastava, G. QoS Routing Algorithm for OBS Networks Based on a Multi-Objective Genetic Algorithm. IEEE Access 2022, 10, 12047–12056. [Google Scholar] [CrossRef]
- Unger, T. Genetic Algorithms: A Survey of some Mathematical Models-Part I. Ir. Math. Soc. Bull. 2021, 0041, 57–71. [Google Scholar] [CrossRef]
- Zhang, D.; Shou, Y.; Xu, J. A mapreduce-based approach for shortest path problem in road networks. J. Ambient. Intell. Humaniz. Computing 2018, 41, 1–9. [Google Scholar] [CrossRef]
- Pradhan, D.; Wang, S.; Ali, S.; Yue, T.; Liaaen, M. CBGA-ES+: A Cluster-Based Genetic Algorithm with Non-Dominated Elitist Selection for Supporting Multi-Objective Test Optimization. IEEE Trans. Softw. Eng. 2021, 47, 86–107. [Google Scholar] [CrossRef]
- Egilmez, H.E.; Dane, S.T.; Bagci, K.T.; Tekalp, A.M. OpenQoS: An OpenFlow Controller Design for Multimedia Delivery with End-to-End Quality of Service over Software-Defined Networks. In Proceedings of the 2012 Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012; pp. 1–8. [Google Scholar]
- Tajiki, M.M.; Akbari, B.; Shojafar, M.; Ghasemi, S.H.; Barazandeh, M.L.; Mokari, N.; Chiaraviglio, L.; Zink, M. CECT: Computationally efficient congestion-avoidance and traffic engineering in software-defined cloud data centers. Clust. Comput. 2018, 21, 1881–1897. [Google Scholar] [CrossRef]
- Son, J.; Buyya, R. Priority-Aware VM Allocation and Network Bandwidth Provisioning in Software-Defined Networking (SDN)-Enabled Clouds. IEEE Trans. Sustain. Comput. 2019, 4, 17–28. [Google Scholar] [CrossRef]
- Shah, S.A.R.; Noh, S.Y. A dynamic programmable network for large-scale scientific data transfer using AmoebaNet. Appl. Sci. 2019, 9, 4541. [Google Scholar] [CrossRef]
- Bastam, M.; Sabaei, M.; Yousefpour, R. A scalable traffic engineering technique in an SDN-based data center network. Trans. Emerg. Telecommun. Technol. 2018, 29, e3268. [Google Scholar] [CrossRef]
- Ejaz, S.; Iqbal, Z.; Shah, P.A.; Bukhari, B.H.; Ali, A.; Aadil, F. Traffic Load Balancing Using Software Defined Networking (SDN) Controller as Virtualized Network Function. IEEE Access 2019, 7, 46646–46658. [Google Scholar] [CrossRef]
- Joshi, K.D.; Kataoka, K. PRIME-Q: Privacy Aware End-To-End QoS Framework in Multi-Domain SDN. In Proceedings of the 2019 IEEE Conference on Network Softwarization (NetSoft), Paris, France, 24–28 June 2019; pp. 169–177. [Google Scholar] [CrossRef]
- Lozano-Rizk, J.E.; Nieto-Hipolito, J.I.; Rivera-Rodriguez, R.; Cosio-Leon, M.A.; Vazquez-Briseño, M.; Chimal-Eguia, J.C. QOSCOMM: A data flow allocation strategy among sdn-based data centers for iot big data analytics. Appl. Sci. 2020, 10, 7586. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Jin, Y.; Liu, H. Research on QoS routing method based on NSGAII in SDN. J. Phys. Conf. Ser. 2020, 1656, 012027. [Google Scholar] [CrossRef]
- Elbasheer, M.O.; Aldegheishem, A.; Alrajeh, N.; Lloret, J. Video Streaming Adaptive QoS Routing with Resource Reservation (VQoSRR) Model for SDN Networks. Electronics 2022, 11, 1252. [Google Scholar] [CrossRef]
- Lee, G.; Lee, C.; Roh, B. QoS Support Path Selection for Inter-Domain Flows Using Effective Delay and Directed Acyclic Graph in Multi-Domain SDN. Electronics 2022, 11, 2245. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xiao, J.; Zhou, J. MCEAACO-QSRP: A Novel QoS-Secure Routing Protocol for Industrial Internet of Things. IEEE Internet Things J. 2022, 9, 18760–18777. [Google Scholar] [CrossRef]
- Guck, J.W.; van Bemten, A.; Reisslein, M.; Kellerer, W. Unicast QoS Routing Algorithms for SDN: A Comprehensive Survey and Performance Evaluation. IEEE Commun. Surv. Tutor. 2018, 20, 388–415. [Google Scholar] [CrossRef]
- Amalarethinam, D.I.G.; Mercy, P. An analysis on quality of service (Qos) based routing in internet of things (IOT). Int. J. Adv. Sci. Technol. 2020, 29, 139–163. [Google Scholar]
- Naing, M.T.; Khaing, T.T.; Maw, A.H. Evaluation of TCP and UDP Traffic over Software-Defined Networking. In Proceedings of the 2019 International Conference on Advanced Information Technologies (ICAIT), Yangon, Myanmar, 6–7 November 2019. [Google Scholar] [CrossRef]
- Ray, P.P. A survey on cognitive packet networks: Taxonomy, state-of-the-art, recurrent neural networks, and QoS metrics. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 5663–5683. [Google Scholar] [CrossRef]
- Medhi, D.; Ramasamy, K. Network Flow Models. In Network Routing, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 114–157. [Google Scholar] [CrossRef]
- Peña, D.; Tchernykh, A.; Nesmachnow, S.; Massobrio, R.; Feoktistov, A.; Bychkov, I.; Radchenko, G.; Drozdov, A.Y.; Garichev, S.N. Operating cost and quality of service optimization for multi-vehicle-type timetabling for urban bus systems. J. Parallel Distrib. Comput. 2019, 133, 272–285. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L. An efficient solution strategy for bilevel multiobjective optimization problems using multiobjective evolutionary algorithm. Soft Comput. 2021, 25, 8241–8261. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Q.; Hao, K.; Jin, Y. A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems with Irregular Pareto Fronts. IEEE/CAA J. Autom. Sin. 2021, 8, 303–318. [Google Scholar] [CrossRef]
- Nebro, A.J.; Durillo, J.J.; Luna, F.; Dorronsoro, B.; Alba, E. MOCell: A cellular genetic algorithm for multiobjective optimization. Int. J. Intell. Syst. 2009, 24, 726–746. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Tian, Y.; Si, L.; Zhang, X.; Cheng, R.; He, C.; Tan, K.C.; Jin, Y. Evolutionary Large-Scale Multi-Objective Optimization: A Survey. ACM Comput. Surv. 2022, 54, 1–34. [Google Scholar] [CrossRef]
- AEiben, E.; Smith, J.E. Natural Computing Series Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Harrison, K.R.; Garanovich, I.L.; Weir, T.; Boswell, S.G.; Elsayed, S.M.; Sarker, R.A. Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling: An Introduction. In Adaptation, Learning, and Optimization; Springer: Cham, Switzerland, 2022; Volume 26. [Google Scholar] [CrossRef]
- Lavinas, Y.; Aranha, C.; Ochoa, G. Search Trajectories Networks of Multiobjective Evolutionary Algorithms. In International Conference on the Applications of Evolutionary Computation, Madrid, Spain, 20–22 April 2022; Springer: Cham, Switzerland, 2022; pp. 223–238. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Kumar, V.; Jangir, S.; Patanvariya, D.G. Traffic Load Balancing in SDN Using Round-Robin and Dijkstra Based Methodology. In Proceedings of the 2022 International Conference for Advancement in Technology (ICONAT), Goa, India, 21–22 January 2022. [Google Scholar] [CrossRef]
- Tanner, N.H. Wireshark. In Cybersecurity Blue Team Toolkit; John Wiley & Sons: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Ergene, Ö.; Özdemir, A.Ş. Understanding the definite integral with the help of Riemann sums. Particip. Educ. Res. 2021, 9, 445–465. [Google Scholar] [CrossRef]


| Reference | Network Parameters | Path Selection | Domain |
|---|---|---|---|
| [17] | Bandwidth, Delay, Jitter | Min delay and bandwidth as constraints | Single |
| [18] | Bandwidth | Min bandwidth | Single |
| [19] | Bandwidth | Max bandwidth | Inter-domain |
| [20] | Bandwidth | Max bandwidth | Single |
| [21] | Bandwidth | Max bandwidth | Single |
| [22] | Bandwidth, Delay, Jitter | Max bandwidth and delay as constraints | Single |
| [23] | Bandwidth, Delay | (1) Max bandwidth, (2) min delay, and (3) max bandwidth and delay as constraints | Inter-domain |
| [24] | Bandwidth, Delay, Jitter, Packet Loss | Application requirements as constraint | Inter-domain |
| [25] | Bandwidth, Delay, Jitter, Packet Loss | Application requirements as constraint | Single |
| [26] | Bandwidth | Bandwidth as constraint | Single |
| [27] | Bandwidth | Bandwidth as constraint | Inter-domain |
| [28] | Delay, Security, Power Consumption | Application requirements as constraint | Single |
| [13] | Bandwidth, Delay, Packet Loss | Min delay and application requirements as constraints | Single |
| MOCell Routing | Bandwidth, Delay, Packet Loss | Min (bandwidth, delay, and packet loss) | Inter-domain |
| Variable | Description |
|---|---|
| G (V,E) | Represents communication network topology. |
| Sets all nodes in the network. | |
| Sets all links between nodes. | |
| Number of nodes. | |
| Number of edges in the network. | |
| The available bandwidth on a link. | |
| The delay on a link. | |
| The packet loss on a link. | |
| Source node. | |
| Destination node. | |
| Path from a source node to a destination node. | |
| Computes the number of links for a path. | |
| Computes the minimum available bandwidth link on a path. | |
| Computes the total path delay. | |
| Computes the percentage of packets lost concerning the number of packages sent. |
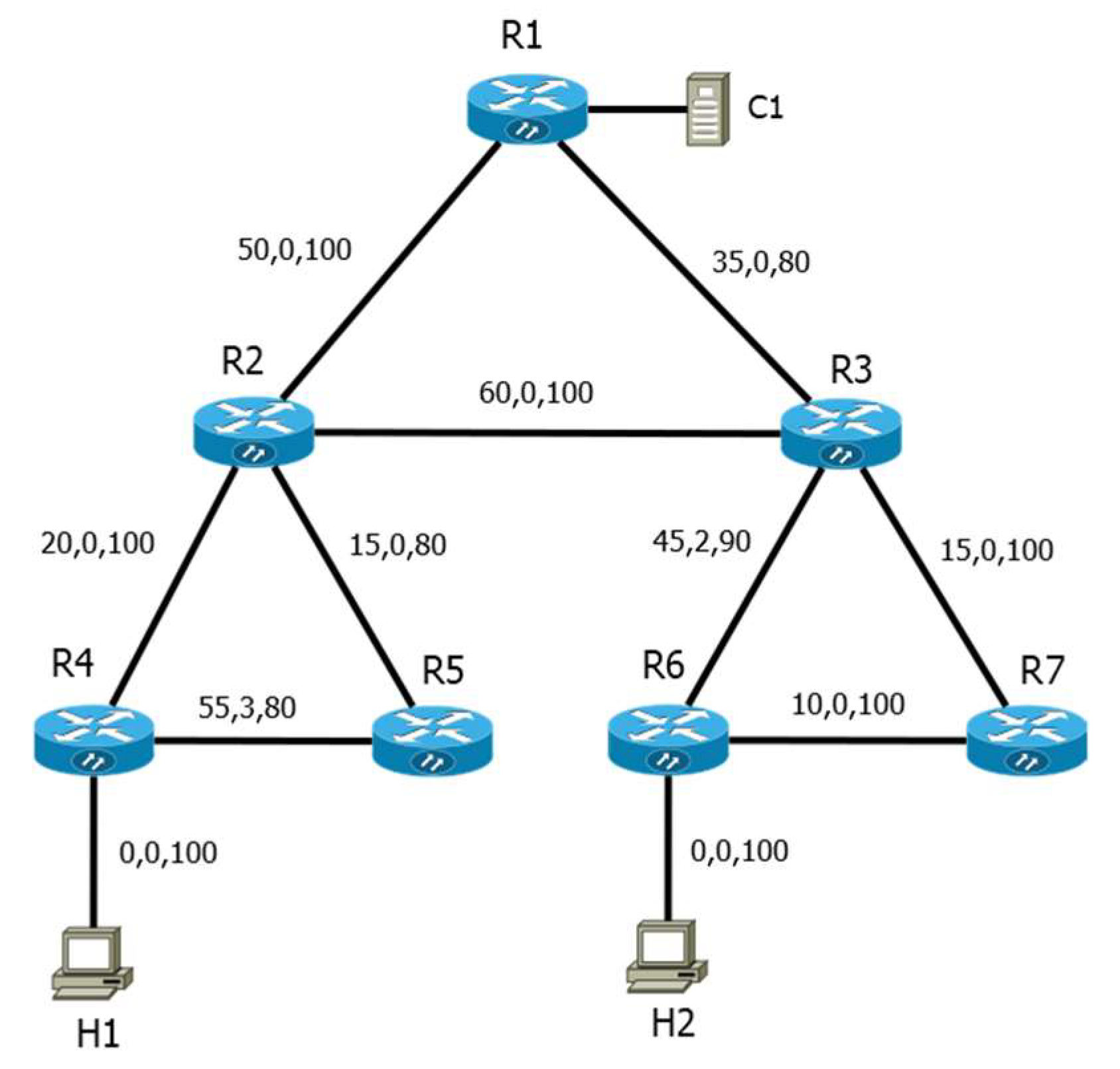
| Chromosome | 5 | 8 | 2 | 1 | 4 | 10 | 6 | 7 | 3 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Nodes | R1 | R2 | R3 | R4 | R5 | R6 | R7 | H1 | H2 | H3 |
| R1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| R2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| R4 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| R5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R6 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| R7 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| H1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| H2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| H3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Metric | Path | H (Hops) | B (Mbps) | D (ms) | PL (0–1) | Data Rate (Mbps) |
|---|---|---|---|---|---|---|
| H1-S14-S6-S2-S1-R1-R16-R31-R46-R61-R76-R91-R106-R121-R136-R151-R166-R181-R196-S22-S26-S32-S38-S44-H14 | 24 | 78 | 130 | 23.8 | ||
| H1-S14-S6-S2-S1-R1-R16-R31-R45-R46-R59-R72-R73-R86-R101-R114-R129-R142-R155-R169-R156-R171-R172-R187-R174-R161-R147-R162-R163-R164-R178-R193-R180-R181-R196-S22-S24-S32-S37-R31-R38-S44-H14 | 42 | 86 | 166 | 38 | ||
| H1-S14-S7-S3-S1-R1-R16-R31-R46-R33-R47-R62-R77-R91-R106-R120-R135-R150-R164-R179-R180-R195-R196-S22-S24-S30-S37-S44-H14 | 28 | 79 | 58 | 53.5 | ||
| H1-S14-S7-S5-S1-R1-R2-R3-R17-R30-R43-R58-57-R72-R85-R99-R114-R129-R144-R145-R160-R174-R189-R190-R191-R192-R193-R194-R195-R196-S22-S26-S32-S37-S44-H14 | 35 | 74 | 138 | 0 | 63.1 | |
| H1-S14-S7-S5-S1-R1-R2-R17-R32-R47-R48-R62-R77-R90-R104-R103-R116-R131-R146-R147-R162-R177-R192-R193-R194-R195-R196-S22-S24-S28-S35-S30-S37-S44-H14 | 34 | 79 | 85 | 64.4 | ||
| MOCell | H1-S14-S7-S5-S1-R1-R15-R29-R43-R57-R72-R86-R85-R100-R115-R130-R117-R118-R133-R148-R149-R164-R179-R194-R195-R196-S22-S24-S28-S35-S30-S37-S44-H14 | 33 | 79 | 75 | 66.9 | |
| MOEA/D | H1-S14-S7-S5-S1-R1-R2-R3-R18-R33-R48-R63-R98-R92-R107-R121-R134-R149-R164-R178-R193-R194-R195-R196-S22-S24-S28-S35-S30-S37-S44-H14 | 31 | 79 | 80 | 66.37 |
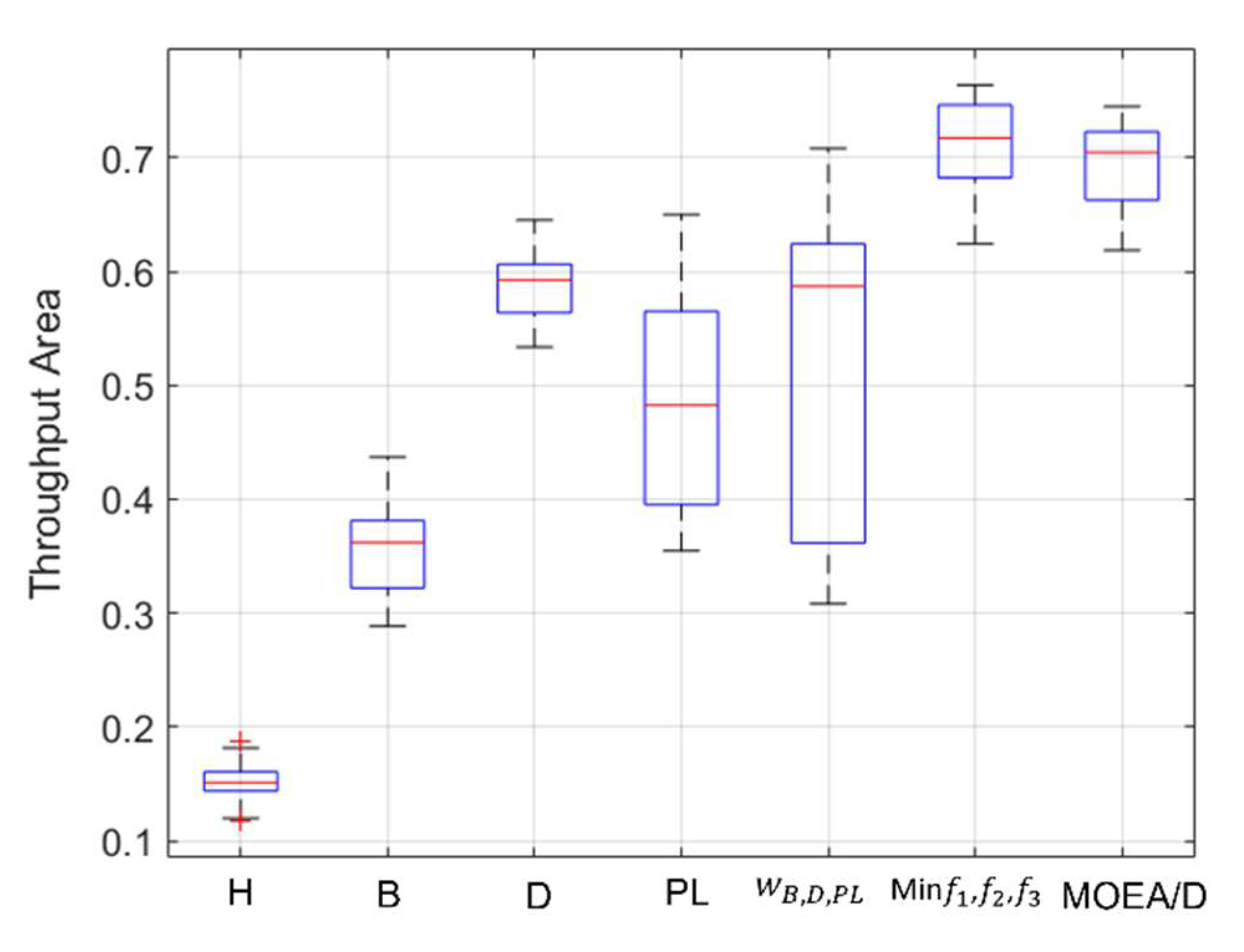
| Algorithm | Median Area |
|---|---|
| (Hops) | 0.1511 |
| (Bandwidth) | 0.3622 |
| (Delay) | 0.5924 |
| (Packet Loss) | 0.4825 |
| (Weighted sum) | 0.5872 |
| (MOCell) | 0.7174 |
| MOEA/D | 0.7046 |
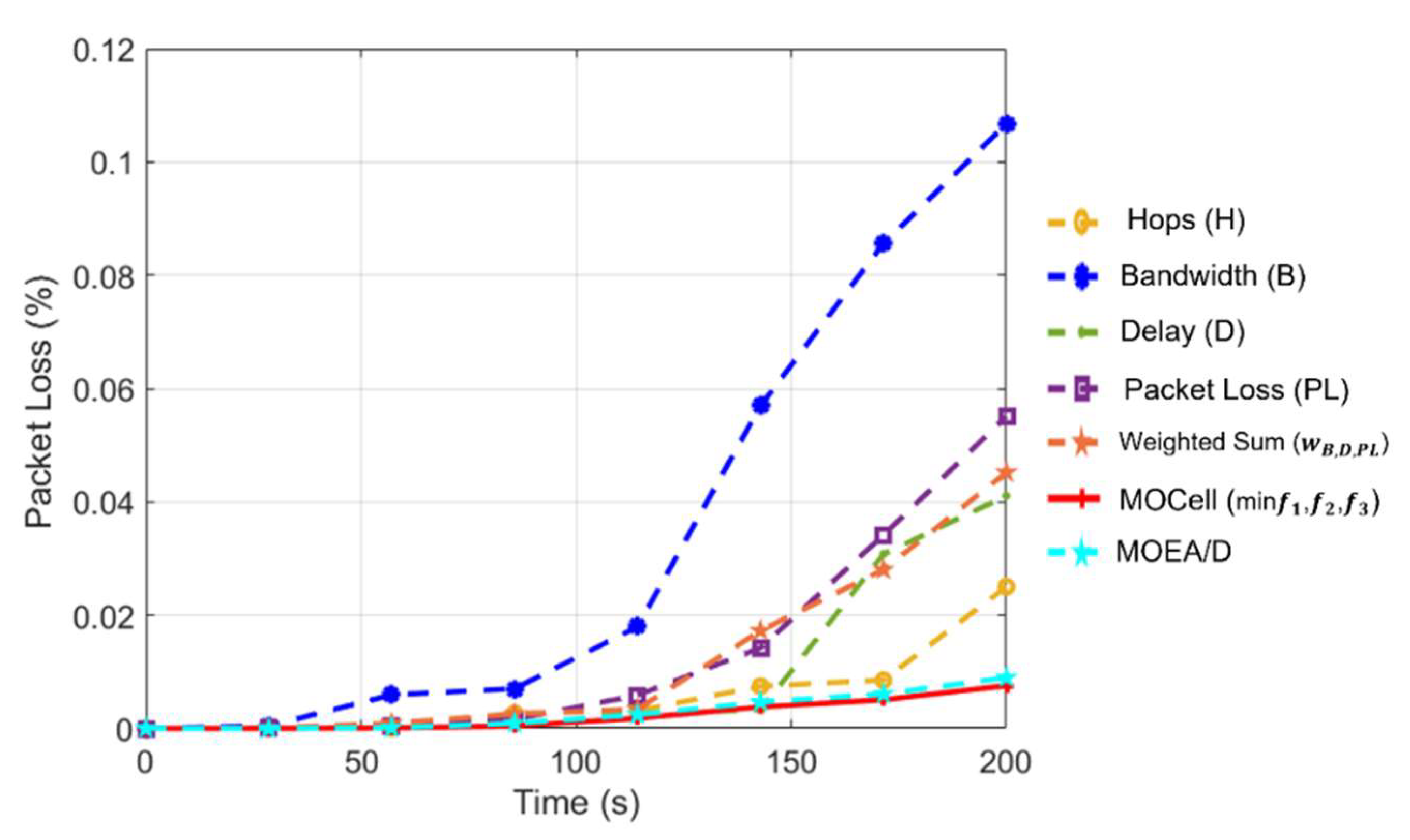
| Algorithm | Data Rate (Mbps) | Jitter (ms) | Packet Loss (%) | Throughput |
|---|---|---|---|---|
| 43.83 | 1.081 | 0.025 | 0.9749 | |
| 40.56 | 1.958 | 0.1067 | 0.8932 | |
| 43.10 | 0.952 | 0.0410 | 0.9589 | |
| 42.58 | 1.71 | 0.0550 | 0.9449 | |
| 43.6 | 1.325 | 0.4519 | 0.9548 | |
| 44.56 | 0.986 | 0.0090 | 0.9909 | |
| MOEA/D | 44.48 | 0.994 | 0.0097 | 0.9902 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Trejo, J.E.; Rivera-Rodriguez, R.; Tchernykh, A.; Lozano-Rizk, J.E.; Villarreal-Reyes, S.; Galaviz-Mosqueda, A.; Gonzalez Compean, J.L. A Novel Strategy for Computing Routing Paths for Software-Defined Networks Based on MOCell Optimization. Appl. Sci. 2022, 12, 11590. https://doi.org/10.3390/app122211590
Gonzalez-Trejo JE, Rivera-Rodriguez R, Tchernykh A, Lozano-Rizk JE, Villarreal-Reyes S, Galaviz-Mosqueda A, Gonzalez Compean JL. A Novel Strategy for Computing Routing Paths for Software-Defined Networks Based on MOCell Optimization. Applied Sciences. 2022; 12(22):11590. https://doi.org/10.3390/app122211590
Chicago/Turabian StyleGonzalez-Trejo, Jose E., Raul Rivera-Rodriguez, Andrei Tchernykh, Jose E. Lozano-Rizk, Salvador Villarreal-Reyes, Alejandro Galaviz-Mosqueda, and Jose L. Gonzalez Compean. 2022. "A Novel Strategy for Computing Routing Paths for Software-Defined Networks Based on MOCell Optimization" Applied Sciences 12, no. 22: 11590. https://doi.org/10.3390/app122211590
APA StyleGonzalez-Trejo, J. E., Rivera-Rodriguez, R., Tchernykh, A., Lozano-Rizk, J. E., Villarreal-Reyes, S., Galaviz-Mosqueda, A., & Gonzalez Compean, J. L. (2022). A Novel Strategy for Computing Routing Paths for Software-Defined Networks Based on MOCell Optimization. Applied Sciences, 12(22), 11590. https://doi.org/10.3390/app122211590












