Rank-Based Ant System with Originality Reinforcement and Pheromone Smoothing

Abstract

Ant Colony Optimization (ACO) encompasses a family of metaheuristics inspired by the foraging behaviour of ants. Since the introduction of the first ACO algorithm, called Ant System (AS), several ACO variants have been proposed in the literature. Owing to their superior performance over other alternatives, the most popular ACO algorithms are Rank-based Ant System (AS${}_{Rank}$), Max-Min Ant System (MMAS) and Ant Colony System (ACS). While AS${}_{Rank}$ shows a fast convergence to high-quality solutions, its performance is improved by other more widely used ACO variants such as MMAS and ACS, which are currently considered the state-of-the-art ACO algorithms for static combinatorial optimization problems. With the purpose of diversifying the search process and avoiding early convergence to a local optimal, the proposed approach extends AS${}_{Rank}$ with an originality reinforcement strategy of the top-ranked solutions and a pheromone smoothing mechanism that is triggered before the algorithm reaches stagnation. The approach is tested on several symmetric and asymmetric Traveling Salesman Problem and Sequential Ordering Problem instances from TSPLIB benchmark. Our experimental results show that the proposed method achieves fast convergence to high-quality solutions and outperforms the current state-of-the-art ACO algorithms $A{S}_{Rank}$, MMAS and ACS, for most instances of the benchmark.

1. Introduction

1.1. Motivation

During the last few decades, many artificial intelligence-based optimization methods have been introduced, mostly aimed at solving problems that were either intractable or very complex to deal with using traditional mathematical optimization techniques. Most of such methods are typically labelled as metaheuristics, a global concept encompassing many different high-level procedures to assist partial search algorithms to find a good solution to a challenging optimization problem, often in NP-hard problems or scenarios where only incomplete information about the problem is commonly available. Some of the first metaheuristics were proposed to enhance local search algorithms (e.g., tabu search, scatter search, simulated annealing, guided local search, stochastic local search, VNS, GRASP, and many others). Shortly afterwards, sophisticated nature-inspired population-based metaheuristics for global search were also introduced. Popular families of such methods include evolutionary algorithms (e.g., genetic algorithms, genetic programming, evolutionary programming; see [1,2]) and swarm intelligence methods (e.g., particle swarm optimization, differential evolution, ant colony optimization, artificial bee colony, bat algorithm, firefly algorithm, cuckoo search algorithm, and many others; see [3,4]), to mention just a few. The interested reader is referred to the handbooks of metaheuristics in [5,6,7] and references within for a general overview of the field and its applications to hard optimization problems.

One of the most popular metaheuristics is Ant Colony Optimization (ACO). Rather than a single method, ACO consists of a family of metaheuristics inspired by the foraging activity of natural ants, capable of finding the shortest path between a food source and their nest through a pheromone deposit mechanism. ACO metaheuristics guide their search through the solution space of combinatorial optimization problems using a problem-specific heuristic and the information saved in the pheromone table, which is learned by means of the reinforcement of the pheromone values corresponding to the best decisions in previous iterations of the algorithm.

The first ant colony-based algorithm, called Ant System (AS) [8,9], was originally applied to solve the Traveling Salesman Problem (TSP): finding the shortest closed loop that traverses once a group of cities. Since the introduction of AS, several ACO algorithms have been proposed. Among them, three algorithms stand out owing to their superior performance and, as a result, for being the most often used ACO algorithms: the Rank-based Ant System (AS${}_{Rank}$) [10], Max-Min Ant System (MMAS) [11] and Ant Colony System (ACS) [12]. All ACO algorithms guide their search through the solution space by means of a probabilistic decision method that combines the information given by the heuristic and the pheromones. However, ACO algorithms may differ in the rules defined to update the pheromone trails or the different transition rules that combine the heuristic and pheromone information. Additionally, more recent metaheuristics combine ACO with other techniques, for instance, Best-Worst Ant System (BWAS) [13], integrates several components from Evolutionary Computation. Nevertheless, the ACO algorithms (MMAS and ACS) are by far more popular than hybrid methods and are used in a variety of combinatorial optimization problems [14,15,16].

The reinforcement of previous best decisions by means of pheromone deposit mechanism enables ACO algorithms to focus the search on promising regions of the search space, making it possible to find high-quality solutions for high-complexity problems in a reasonable computational time. However, the pheromone reinforcement is also responsible for stagnation, an undesirable situation where the algorithm becomes stuck in local minima, preventing the possibility of finding a better solution.

A distinctive feature of AS extensions (such as AS${}_{Rank}$, MMAS and ACS) is that they direct the ant’s search in a more aggressive way than AS, exploiting more strongly the best solutions found during the ants’ search [14,17]. This stronger exploitation of the search experience may promote early stagnation situations. Thus, some AS extensions, in particular, MMAS and ACS, introduce additional features to avoid search stagnation (e.g., pheromone limits in MMAS) [18]. However, Rank-based AS generally obtains slightly worse performance than ACS and MMAS [14].

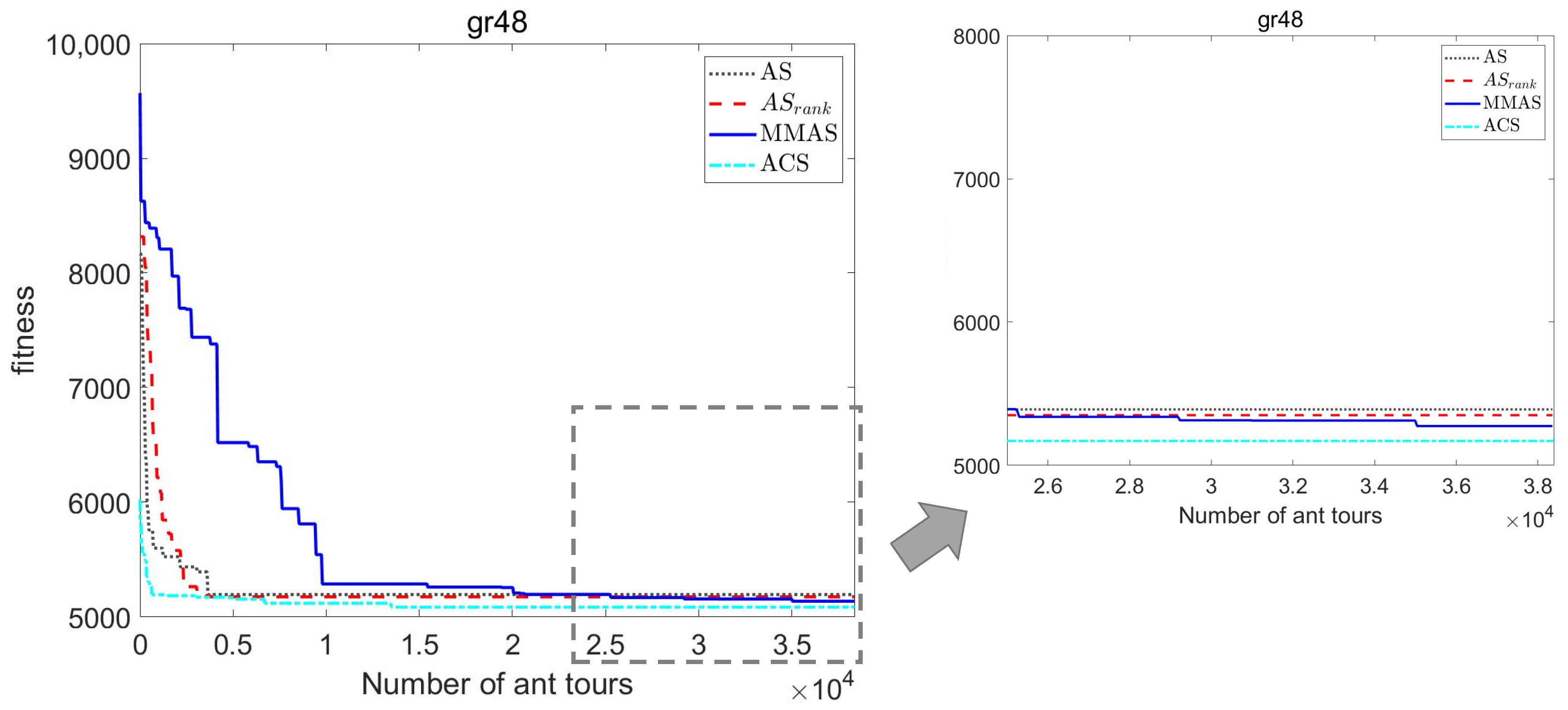
Figure 1 shows the fitness evolution of the tour length of the best-ant tour found by ACO algorithms versus the number of ant tours constructed for a particular instance of TSP called gr48. Although the behaviour of ACO algorithms also depends on the parameter settings, comparative studies usually draw similar conclusions as the ones that can be extracted from Figure 1. The ACO extensions (AS${}_{Rank}$, MMAS and ACS) have the advantage of showing better performance than the original ACO algorithm, Ant System. The best-performing variants usually are MMAS and ACS, closely followed by AS${}_{Rank}$. Regarding the performance of ACS, its local pheromone update rule (which applies the evaporation mechanism only to the traversed arcs) has the advantage of preventing ACS from reaching a stagnation situation, and the disadvantage that it precludes the parallel implementation of the construction loop of the ant tours. An advantage of ACS is that it returns the best solution quality for very short computation times, as happens in the instance shown in Figure 1. Differently, as it can be observed in Figure 1, MMAS has the disadvantage of initially producing rather poor solutions, but the advantage of producing solutions whose quality is often the best among the ACO extensions [14]. Lastly, AS${}_{Rank}$ has the advantage of showing better results than MMAS in the initial iterations, but it usually ends in stagnation situations, obtaining slightly worse performance than ACS and MMAS. This early stagnation behaviour suggests that AS${}_{Rank}$ could profit from strategies that diversify the search [11,14]. Consequently, the good results of AS${}_{Rank}$ during the first iterations and its trend to quickly fall in stagnation situations have motivated the present work.

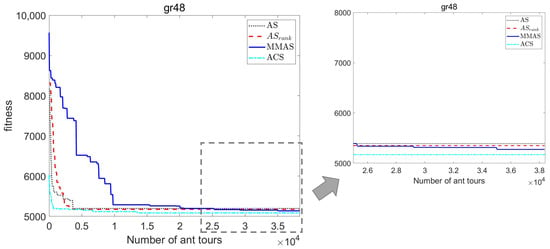
Figure 1. Evolutionary curves of ACO algorithms (AS, AS${}_{Rank}$, MMAS and ACS) for TSP instance gr48.

1.2. Aims and Structure of This Paper

In this work, we aim at improving the performance of AS${}_{Rank}$ algorithm for combinatorial optimization problems. Based on the observations described in the previous paragraphs, this paper proposes an extended version of AS${}_{Rank}$, which includes two diversification strategies:

• an originality reinforcement strategy that rewards the originality (dissimilarity from already searched space) of the solutions with good fitness; and
• a pheromone smoothing mechanism that is triggered before the algorithm reaches stagnation, increasing exploration and making possible it to find better solutions.

This new ACO algorithm, called AS${}_{ORank}^{ps}$, will be compared with the state-of-the-art ACO algorithms using several instances of the popular TSPLIB95 benchmark. Since our main interest is at improving the state-of-the-art ACO algorithms, in this paper we will focus our comparative work on the best ACO algorithms exclusively. Consequently, we will restrict our analysis to ACO algorithms without any addition of external methods, such as local search procedures or hybridization with other metaheuristics. These procedures, although very promising and potentially successful, would obscure the understanding of the behavior of our algorithm with technicalities totally unrelated to the core and principles of the ACO algorithms. The discussion about how to enhance our new ACO algorithm with local search strategies and/or hybridization with other metaheuristics is out of the scope of this paper and will be part of our future work in the field (see our discussion in Section 5 for further details).

The remainder of the paper is organized as follows. Section 2 introduces the ACO metaheuristics, describing the most important ACO algorithms and presenting an overview of the current research lines in ACO state-of-the-art. Section 3 describes the proposed Rank-based Ant System with originality reinforcement and pheromone smoothing. Section 4 analyses the performance of the proposed ACO algorithm over several TSP and Sequential Ordering Problem (SOP) instances, and compares it with the best-performer ACO algorithms in the literature. Finally, Section 5 summarizes the main conclusions of the work and some futures lines of research.

2. Ant Colony Optimization

This section introduces the ant colony optimization metaheuristics. First, it describes the general structure of ACO algorithms, including the first ACO algorithm proposed in 1992 by Dorigo, and its extensions Rank-based Ant System, Max-Min Ant System and Ant Colony System. Later, it gives a brief overview of the more recent research trends in ACO metaheuristics. A more detailed review of ACO state of the art can be found in [16,17].

2.1. Ant Colony Optimization Algorithms

ACO metaheuristics formulate the combinatorial optimization problems as finding the best ant tour (best solution) in a graph $G=(C,L)$ defined by a set of nodes C and arcs L. For instance, in the TSP problem, each node represents a city and each edge has assigned the distance between each pair of cities. Hence, the problem is formulated as finding the closed tour of minimal length that visit once all the nodes in the graph.

ACO metaheuristics are population-based algorithms that at each iteration construct m ant tours (solutions) combining the information learned in previous iterations with a problem-specific heuristic. In order to save the information of previous good ant tours, ACO algorithms use a table that assigns a pheromone value ${\tau }_{i,j}$ to each edge in the graph. These pheromone values are typically initialized with a constant value for all edges, and later reinforced as the ants with better fitness traverse them. The ant tours are constructed component by component according to the probabilities determined by the transition rule, given by Equation (1). This transition rule states the probability $p_{i,j}^k$ that the k-th ant moves from node i to node j, assigning higher probabilities to the edges with higher pheromone ${\tau }_{i,j}$ and heuristic values ${\eta }_{i,j}$ according to:

$$p_{i,j}^k=\frac{{\tau }_{i,j}^{\alpha }{\eta }_{i,j}^{\beta }}{{\sum }_{l\in N_i^k}{\tau }_{i,j}^{\alpha }{\eta }_{i,j}^{\beta }},j\in N_i^k$$

(1)

where $\alpha$ and $\beta$ are the parameters that control the pheromone and heuristic influence, respectively, and $N_i^k$ is the feasible neighbourhood of ant k. For instance, in the case of TSP where the cities (nodes) can only be visited once, $N_i^k$ corresponds to the set of unvisited cities.

The basic operation mode of an ACO algorithm, summarized in Algorithm 1, is as follows: at every algorithm iteration, the m artificial ants start their tours from initial nodes (randomly chosen in TSP) and construct their tours by combining the information of the heuristic $\eta$ and the pheromones $\tau$. In this way, at every iteration, m candidate solutions (ant tours) are constructed, each one having a corresponding fitness value such as the length of the tour in TSP. Optionally, after the tours of the m ants are completed, a local search procedure may be considered (for example k-exchange neighbourhood for TSP). Next, a positive feedback strategy that rewards the best ant tours is implemented by means of the update of the pheromone table. Finally, when the considered stop criterion is met, the algorithm returns the best-found tour.

Once every ant has finished its tour (which corresponds to a candidate solution to the optimization problem), the pheromone update (evaporation and deposit processes) takes place. In AS, the pheromone update process is given by the following rule:

$${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+\sum _{k=1}^m▵{\tau }_{i,j}^k,\forall arc(i,j)\in L$$

(2)

where the parameter $\rho$ (with $0<\rho <1$) is the pheromone evaporation parameter, which controls the rate at which the pheromone is evaporated. The evaporation mechanism affects all the edges in the graph and helps to avoid the unlimited accumulation of the pheromone trails. The second term of Equation (2) corresponds to the pheromone deposit of the m artificial ants. In AS, all the ants deposit a pheromone quantity $▵{\tau }_{i,j}^k$ proportional to their quality in all the arcs belonging to their tour:

$$▵{\tau }_{i,j}^k=\left\{\begin{array}{cc}1/f\left(s_k\right),\hfill & \mathit{if}\mathit{arc}(\mathit{i},\mathit{j})\in {\mathit{s}}_{\mathit{k}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(3)

where $f\left(s_k\right)$ is the fitness of the k-th ant tour $s_k$, which in TSP corresponds to the length of the tour. In general, arcs that are used by many ants and which are contained in shorter tours will receive higher pheromone deposits and therefore, will more likely be chosen in the next iterations of ACO.

Algorithm 1 ACO metaheuristic

Require: ACO parameters     $\tau \leftarrow$ initialise pheromone trails     while termination condition not met do         for $k=1$ to m do                              ▹ for every ant             for every step until the k-th ant has completed the tour do                    select node j to visit next according to transition rule               ▹ Equation (1)             end for         end for         Apply local search (optional)         Update pheromone trails $\tau$ end while

Since the introduction of AS in [8], several ACO algorithms have been proposed, with Rank-based Ant System (AS${}_{Rank}$) [10], Max-Min Ant System (MMAS) [11] and Ant Colony System (ACS) [12] standing out. These ACO algorithms differ from AS in the pheromone update process in Equation (3), with the exception of ACS, which also considers a modified transition rule given by Equation (6) from the one given by Equation (1).

The pheromone reinforcement enables ACO algorithms to focus the search on promising regions of the search space allowing them to find high-quality solutions in reasonable computational time. However, the pheromone reinforcement is also responsible for stagnation, an undesirable situation where no better tour is likely to be found anymore. The stagnation situation happens when at each choice point, the pheromone trail is significantly higher for one choice than for all the others. In such a situation, the ants construct the same tours over and over again and the exploration of the search space stops, limiting the possibility of finding a tour with better fitness. One particularity of AS extensions is that they direct the ant’s search in a more aggressive way and that their search is focused on a specific region of the search space [14]. This higher exploitation may, however, induce early stagnation situations. Thus, AS extensions need to be endowed with features intended to counteract stagnation (e.g., the pheromone limits in MMAS and local update rule in ACS). The pheromone update process of the AS extensions, Rank-based AS, MMAS and ACS, are detailed below.

Rank-based Ant System (AS${}_{\mathit{Rank}}$) is an extension of AS proposed by Bullnheimer et al. [10], which incorporates the idea of ranking to the pheromone update process. Rank-based AS follows a similar procedure to Algorithm 1, but its pheromone update incorporates the idea of ranking of solutions and elitist strategy. While in AS, all ants deposit pheromones according to Equation (2), in Rank-based AS, only w ants deposit pheromones: the best tour found so far, $s_{gb}$, deposits a pheromone quantity proportional to the algorithm parameter w and the $(w-1)$ best ants of the iteration deposit a pheromone quantity proportional to their ranking r, as expressed by Equation (4):

$${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+\sum _{r=1}^{w-1}(w-r)△{\tau }_{i,j}^r+w△{\tau }_{i,j}^{gb}$$

(4)

where w is a parameter of the algorithm chosen by the user that determines the number of ants that deposit pheromones, and r corresponds to the ranking of the classification of the ants according to their fitness (where better fitness is associated with lower ranking). In Equation (4), $(1-\rho ){\tau }_{i,j}$ accounts for the pheromone evaporation, which is applied to all pheromone trails. Additionally, the pheromone trails corresponding to the tours of the ($w-1$) best ants of the iteration are reinforced as by a quantity equal to $(w-r)△{\tau }_{i,j}^r$, where $△{\tau }_{i,j}^r=1/f\left(s_r\right)$. Finally, the pheromone trails corresponding to the global-best found solution $s_{gb}$ are reinforced with a quantity equal to $w△{\tau }_{i,j}^{gb}$, where $△{\tau }_{i,j}^{gb}=1/f\left(s_{gb}\right)$.

Max-Min Ant System (MMAS), proposed by Stüzle and Hoos [11], is one of the best performing variants of AS [14,15,16]. In MMAS only one ant is used to update the pheromone trails at each iteration. Consequently, the modified pheromone update rule is given by

$${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+▵{\tau }_{i,j}^{best}$$

(5)

where only the arcs traversed by the best ant are reinforced with a pheromone quantity inversely proportional to the fitness of the best ant tour $▵{\tau }_{i,j}^{best}=1/f\left(s_{best}\right)$. Depending on the MMAS implementation, it can be considered the iteration-best ($s_{ib}$) ant or the global-best ant ($s_{gb}$).

Furthermore, MMAS imposes lower and upper limits ${\tau }_{min}$ and ${\tau }_{max}$ on all the pheromone values in order to avoid stagnation. Hence, at each iteration after the pheromone update process given by Equation (5) takes place, it is ensured that the pheromone values respects the limits, i.e., ${\tau }_{min}<{\tau }_{i,j}<{\tau }_{max}$, $\forall {\tau }_{i,j}$. Recommended values for the pheromone trail limits indicated by [11,14] are ${\tau }_{max}=1/\left(\rho f\left(s_{gb}\right)\right)$ and ${\tau }_{min}={\tau }_{max}(1-\sqrt[n]{0.05})/(0.5n-1)$, where n is the number of cities (nodes) in the graph. These pheromone limits $[{\tau }_{min},{\tau }_{max}]$ avoid the situation of strict stagnation (all tours of an iteration being the same). Instead, this may lead to a situation (convergence of MMAS) where the pheromone values of the arcs corresponding to the best-found tour have associated a pheromone value equal to ${\tau }_{max}$, and the remaining arcs to ${\tau }_{min}$. In this convergence situation, all the ants do not follow the same tours (stagnation), but still, the exploration of the search space and the possibility of finding better solutions during the following iterations is quite limited. As a further means of increasing the exploration, some MMAS implementations consider occasional reinitializations of the pheromone trails when the algorithm approaches stagnation or when no improved tour has been generated for a large number of iterations [11].

Ant Colony System (ACS), proposed by Dorigo and Gambardella [12], is considered, along with MMAS, the best performing variant of AS [14,15,16]. ACS implements several modifications with respect to AS. First, it exploits the experience accumulated by the ants more strongly than AS does through the use of a more aggressive action choice rule given by Equation (6):

$$j=\left\{\begin{array}{cc}argma{x}_{l\in N_i^k}{\tau }_{il}{\left[{\nu }_{il}\right]}^{\beta }\hfill & q\le q_0\hfill \\ J\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

where q is a random variable uniformly distributed in [0, 1], $q_0$ is an algorithm parameter ($0<q_0<1$), and J is a random variable selected according to the probability distribution given by Equation (1) (with $\alpha =1$). In this way, the ants select with a probability $q_0$ the next node j based on the best decision according to the pheromone trails and heuristic information (the node j with maximum associated probability $p_{i,j}^k$ given by Equation (1)), while with probability $(1-q_0)$, the ants choose the next node according to the probability distribution $p_{i,j}^k$ given by Equation (1).

Regarding the pheromone update process, at the end of each algorithm iteration, ACS only applies the pheromone evaporation and reinforcement to those arcs belonging to best-so-far ant, according to Equation (7):

$${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+▵{\tau }_{i,j}^{gb}\forall arc(i,j)\in s_{gb}$$

(7)

where $\rho$ is the pheromone evaporation parameter and $▵{\tau }_{i,j}^{gb}=1/f\left(s_{gb}\right)$.

In addition to the global pheromone trail update rule given by Equation (7), that is applied after the m ant tours are constructed, ACS also considers a local pheromone update rule that is applied immediately after an ant has crossed an $arc(i,j)$ during the tour construction, according to Equation (8):

$${\tau }_{i,j}=(1-\xi ){\tau }_{i,j}+\xi {\tau }_0$$

(8)

where $\xi$ ($0<\xi <1$) and ${\tau }_0$ are two algorithm parameters. The value ${\tau }_0$ is set to be the same as the initial value of the pheromone trails.

2.2. Recent Trends in ACO Algorithms

Among ACO scientific literature, three main research lines can be distinguished. On the one hand, the majority of the state-of-the-art works are clearly focused on the application of ACO metaheuristics to different and computationally challenging applications and domains, such as UAV search missions [19], maximizing influence in social networks [20] or in wireless sensor networks [21]. For more ACO applications, the reader is kindly referred to [17].

On the other hand, there is a challenging research line (in which this work is also included) that aims to improve ACO metaheuristics through the inclusion of modifications or mechanisms that aim to diversify the search to promising regions of the search space while keeping a good balance between diversification/intensification. Within this research line, we can find several hybrid algorithm proposals that combine ACO with other techniques. For instance, the Hybrid Ant Colony Optimization Algorithm (HACO, [22]) introduces an operator similar to the mutation operator of the genetic algorithms. Or the Best-Worst Ant System (BWAS) [13], integrates components inspired by evolutionary computation such as the inclusion of mutations of the pheromone table. The papers in [23,24] consider the hybridization of ACO with genetic algorithms to solve the supplier selection and multiple sequence alignment problems, respectively. Additionally, the authors of [25] consider an annealing ACO with a mutation operator to solve the TSP. Furthermore, BWAS is hybridized with Particle Swarm Optimization (PSO) ideas in [26] and tested over for TSP benchmark. Another example of hybridization of ACO and PSO is given in [27], related to PID parameter optimization on autonomous underwater vehicle control systems. Other approaches include the hybridization of ACO algorithms with differential evolution in [28,29] to solve TSP and cancer data classification problems. Additionally, the ACO metaheuristic proposed in [30] presents a different approach to diversify the solution space based on combining pairs of searching ants. Lastly, another interesting research line is the study of parameter adaptation techniques, that is, the variation of ACO parameter settings while solving an instance of an optimization problem [31].

Finally, a third current line of research concerns the application of the ACO algorithms to dynamic discrete problems [32]. Some particular features of the ACO algorithms, such as the pheromone-based memory, have proven to be remarkably successful for static combinatorial optimization problems, but such features do not seem to be so favorable for dynamic problems, where some parts of the problem can change at runtime without previous knowledge [33]. In such cases, if the ACO algorithm has achieved convergence to a confined region of the search space which becomes irrelevant after the change in the problem, the algorithm can find it difficult to efficiently escape from that region and adapt its memory structure to the new problem change. As a way to overcome such a limitation, a method called P-ACO has been proposed to optimize the reuse of pheromone information after the problem changes [34]. Other alternative methods are based on the use of immigrant schemes for dynamic problems [35,36]. A very recent paper considers the role of parameter setting and the use of enhanced hybridization with local search procedures [37]. The results in [37] show that the hybridization of MMAS (one of the best ACO performers for static problems) with local search can consistently outperform P-ACO for dynamic combinatorial optimization problems.

3. Extension of Rank-Based Ant System

This section presents the proposed extension of the Rank-based Ant System. Firstly, the two contributions of the proposed algorithms are presented; (i) an originality utility function and (ii) a pheromone smoothing mechanism that is triggered before the algorithm reaches stagnation. Next, the proposed variant of the Rank-based AS algorithm is detailed, highlighting the modifications with respect to the original Rank-based AS already described in Section 2.

3.1. Originality Utility Function

With the objective of promoting exploration of the search space, this section presents a utility function that measures the originality or dissimilarity of one solution with respect to a group of solutions.

A way of measuring the distance $dist(s,s^{\prime })$ between two tours s and $s^{\prime }$ is to count the number of arcs contained in one tour, but not in the other [14]. The average distance between all possible pairs of tours can be used to measure the amount of exploration of the algorithm, as a decrease in the average distance indicates that preferred paths are appearing [14]. Alternatively, this distance definition (i.e., number of non-common arcs) could be used instead for our purpose of measuring the originality of one ant tour with respect to a group of tours, by considering the average distance of all the possible pairs formed by the ant tour s and the rest of the ant tours. However, a disadvantage of this measure is that it is computationally expensive [14].

The proposed originality function, given by Equation (9), is based on the idea that the tours of those ants that traverse arcs that have been visited by a smaller number of ants are more original. The originality function $f_o$ of an ant tour $s_k$ is given by the inverse of the number of ants that have traversed each arc of $s_k$, that is:

$$f_o\left(s_k\right)=\frac{1}{{\displaystyle \sum _{arc(i,j)\in s_k}{\nu }_{i,j}}}$$

(9)

where ${\nu }_{i,j}$ represents the number of ants that have traversed the edge going from node i to node j.

As an illustrative example, below are calculated the originality values given by Equation (9) for each of the following five tours of a TSP problem with $n=10$ cities. The five closed tours are:

$$\begin{array}{c}\hfill s_1=\{1,2,3,4,5,6,7,8,9,10,1\}\\ \hfill s_2=\{1,2,3,4,5,6,7,8,9,10,1\}\\ \hfill s_3=\{6,7,8,9,10,1,2,3,5,4,6\}\\ \hfill s_4=\{1,8,10,9,2,3,4,5,6,7,1\}\\ \hfill s_5=\{2,9,3,6,5,8,7,10,4,1,2\}\end{array}$$

To compute the originality values for each tour, we use the matrix $\nu$ corresponding to the five tours:

$$\nu =\left[\begin{array}{cccccccccc}0& 4& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 4& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 3& 1& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 3& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 3& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0& 4& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 3& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0& 3& 1\\ 0& 1& 1& 0& 0& 0& 0& 0& 0& 3\\ 3& 0& 0& 1& 0& 0& 0& 0& 1& 0\end{array}\right]$$

where each element ${\nu }_{i,j}$ indicates the number of ants that have traversed $arc(i,j)$. For instance, ${\nu }_{1,2}=4$ indicates that four ants (in this example, those associated with the tours $s_1$, $s_2$, $s_3$ and $s_5$) have gone from node 1 to node 2.

According to the originality function given by Equation (9), the following values are obtained: $f_o\left(s_5\right)=0.076>f_o\left(s_4\right)=0.045>f_o\left(s_3\right)=0.037>f_o\left(s_1\right)=f_o\left(s_2\right)=0.030$. These results are in accordance with what could be expected, since $s_1$ and $s_2$ are identical, $s_3$ and $s_4$ have several arcs in common with $s_1$ and $s_2$, while tour $s_5$ is the most different (original) tour from the rest.

3.2. Pheromone Smoothing Mechanism

This section presents a pheromone smoothing strategy to escape from the stagnation situation. For a better understanding of the stagnation situation, visual representations of the pheromone trails obtained with AS${}_{Rank}$ when solving a TSP instance with 14 cities after 0, 5, 10 and 200 iterations are shown in Figure 2. Note that the pheromone matrix is a square matrix of dimension $n\times n$, where n is the number of nodes (cities) and in this TSP example, $n=14$. Each element of the pheromone matrix ${\tau }_{i,j}$ contains the pheromone quantity associated with the edge that goes from node i to node j. For the representations, the pheromone levels are translated into gray scale, where black and white represent the highest and the lowest pheromone trail values, respectively. At the beginning of the algorithm, all the pheromone values are initialized with the same pheromone value ${\tau }_0$, with the exception of the values of the diagonal representing no movement (i.e., $i=j$), which are not allowed in TSP (and thus are represented in white in Figure 2).

Figure 2. A visual representation of the pheromone matrix: (left-right, top-bottom) the pheromone values obtained with AS${}_{Rank}$ applied to the TSPLIB instance burma14 with 14 cities, after 0, 5, 10 and 100 iterations, respectively.

After each AS${}_{Rank}$ iteration, all the pheromone trails are evaporated and some pheromone trails are reinforced (the ones included in the $w-1$ best tours of the iteration and the best-found tour). The effect of this pheromone update can be observed in the pheromone representations of Figure 2. Additionally, the symmetry along the main diagonal of the pheromone matrix is due to the fact that the example is a symmetric TSP instance. As the difference among the pheromone values increases, ants are more likely to choose those arcs that were chosen by the best ants from previous iterations. This pheromone reinforcement enables AS${}_{Rank}$ to explore promising regions of the search space obtaining high-quality solutions in a reasonable time. Yet, this usually leads AS${}_{Rank}$ into early stagnation situations, in which all ants follow the same path. Stagnation can be clearly observed in the pheromone trails after 100 iterations shown in Figure 2 (right-bottom). In this case, the pheromone encodes a unique path (only fourteen of all the possible elements of half of the pheromone matrix have a non-negligible pheromone quantity). For this simple TSP instance with only fourteen cities, the encoded path in the pheromone table happens to be the optimal one. However, this is not usually the case and often AS${}_{Rank}$ is trapped into a local minimum.

The proposed pheromone smoothing mechanism, given by Equation (10), rescales the pheromone trails to the range $[\gamma {\tau }_0,{\tau }_0]$, $0<\gamma <1$. Note that if $\gamma$ equals 1, all the pheromones will be reinitialized to the constant value ${\tau }_0$, and previously learned information would be lost.

$$\tau =\gamma {\tau }_0+\frac{\tau -min\left(\tau \right)}{max\left(\tau \right)-min\left(\tau \right)}(1-\gamma ){\tau }_0$$

(10)

Figure 3 shows an example of the resulting pheromone trails of $A{S}_{rank}$ before and after applying the pheromone smoothing strategy. The image on the left of Figure 3 shows the pheromone trails when the algorithm is near a stagnation situation. The noticeable difference among the pheromone values can be observed, leading to the construction of very similar ant tours and thus a limited exploration of the search space. The image on the right of Figure 3 shows the pheromone trails after applying the pheromone smoothing strategy, where the pheromones are rescaled $[0.1{\tau }_0,{\tau }_0]$ with ${\tau }_0=m/f\left(s_{sb}\right)$ [14]. It can be observed that after applying the pheromone smoothing mechanism, the learned information is still preserved, but the differences among the pheromone trails ${\tau }_{i,j}$ have decreased. In this way, the diversity of the ant tours produced by the algorithm after the pheromone smoothing mechanism is increased, allowing the algorithm to escape from stagnation without losing previously learned information.

Figure 3. Pheromone trails before (on the left) and after (on the right) of pheromone smoothing.

In order to incorporate the smoothing strategy into an ACO algorithm, it is also necessary to define when the pheromone smoothing is triggered. For this purpose, it is necessary to select a measure of how close the algorithm is to stagnation and based on this measure, define a criterion that triggers the pheromone smoothing strategy. Several measures can be used to describe the amount of exploration an ACO algorithm performs in order to detect stagnation situations, such as the standard deviation of the length of the tours, the average number of arcs that are not common in every pair of ant tours, and the average $\lambda$-branching factor [14]. Despite these last two criteria being good indicators of the size of the search space effectively being explored, they require a high computational cost. For instance, the average $\lambda$-branching factor is used in [11] for triggering occasional pheromone initialization of MMAS, but due to its high computational cost, it is only calculated every 100 algorithm iterations. On the contrary, the standard deviation between the fitness of ant’s tours is a more efficient way to measure the diversity among the solutions generated at an iteration. The standard deviation, ${\sigma }_L$, of the ant tours of an iteration decreases when the search starts exploiting a concrete region of the search space. Additionally, in the case where ${\sigma }_L$ reaches a null value, we can assume that all ants are taking the same paths (as it is very unlikely that different tours have the same length) and thus, ${\sigma }_L=0$ is an indicator that the algorithm has fallen in a stagnation situation. Due to its lower computational requirement, ${\sigma }_L$ is the criterion selected for the proposed ACO algorithm.

Lastly, it is worth clarifying the difference between the discussed dissimilarity functions, which measure the dissimilarity of a group of ants tours, with respect to the originality function presented in Section 3.1, which measures the dissimilarity between a unique solution with respect to several of tours. Additionally, while the former are generally used with the intention of detecting the approach to stagnation situation, the latter is proposed with the intention of promoting solutions that diversify the search.

3.3. Algorithm

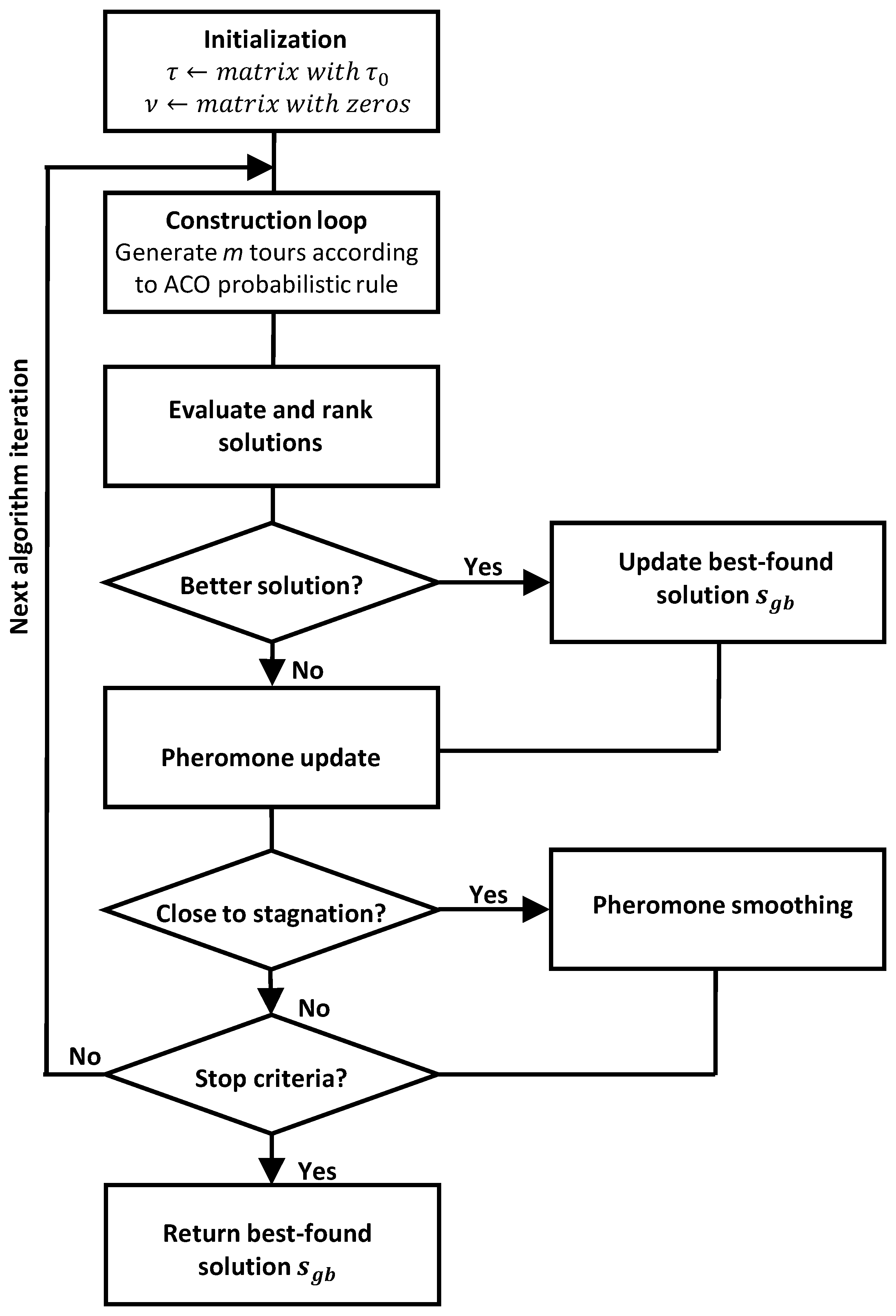
Once the originality utility function and the pheromone smoothing strategy have been introduced, below is described the proposed extension of Rank-based Ant System, which incorporates both strategies. Algorithm 2 shows the pseudocode of the algorithm and Figure 4 its general overflow. The algorithm requires similar parameters to AS${}_{Rank}$: pheromone evaporation rate $\rho$, the number of ants per iteration m, the number of ants that deposit pheromones w, and the pheromone and heuristic influence parameters $\alpha$ and $\beta$.

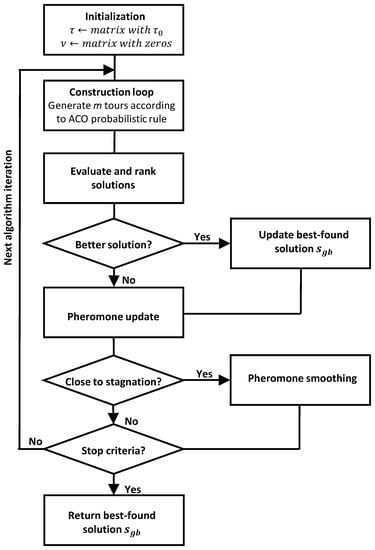
Figure 4. Algorithm flowchart of the proposed AS${}_{ORank}^{ps}$ method.

The steps of the algorithm are the following. First, the algorithm starts with the initialization of the pheromone table to a constant value ${\tau }_0$, and of the matrix $\nu$ to zero (as ${\nu }_{i,j}$ accounts for the number of ants that have traversed each edge $arc(i,j)$ in the graph G). Within the main iteration loop, the tours of m ants are constructed component by component according to the ACO probabilistic transition rule given by Equation (1). Additionally, in line 7, the counter of ants ${\nu }_{i,j}$ that have traversed $arc(i,j)$ is updated. Once the m tours ($s_{1:m}$) have been constructed, they are ranked and selected according to their fitness and originality following the steps sketched in Figure 5 and explained as follows. First, all the tours are evaluated and the ($w-1$) best are selected (line 11). Then, the ($w-1$) best tours of the iteration are evaluated and ranked according to the originality utility function given by Equation (9), obtaining in this way a rank of the dissimilarity of the $(w-1)$ best tours with respect all the explored tours (line 13). Moreover, in the case that the best solution of the iteration is better than the global best solution, $s_{gb}$ is updated (line 12). In line 14, the pheromone update process takes place according to Equation (11); all pheromone values are evaporated, and the ($w-1$) best tours of the current iteration and the global best tour are reinforced.

$${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+\sum _{r_o=1}^{w-1}(w-r_o)△{\tau }_{i,j}^r+w△{\tau }_{i,j}^{gb}$$

(11)

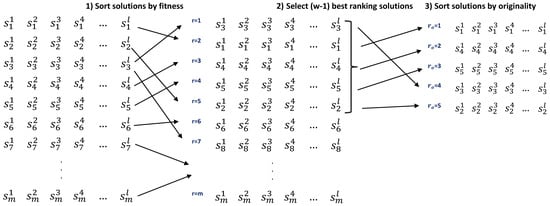
Figure 5. Steps of the process of selection and ranking of solutions for the pheromone reinforcement (where $s_k^i$ represents a solution component of the tour of length l of the k-th ant).

The best-so-far tour gives the strongest feedback, as its contribution is multiplied by the weight equal to w, the $(w-1)$ best ants of the iteration deposit a pheromone quantity multiplied by a weight ($w-r_o$), which is higher for the more original solutions (lower $r_o$). The update of the pheromones is similar to the original AS${}_{Rank}$, with the exception that the ranking considered for the reinforcement is a ranking of originality, instead of fitness. In this way, the proposed algorithm rewards the originality of the tours with good fitness values.

Algorithm 2 AS${}_{Rank}$ with originality reinforcement and pheromone smoothing

Require:  ACO parameters 1: $\tau \leftarrow$ initialise pheromone trails 2: $\nu \leftarrow$ initialise matrix $\nu$ 3: while termination condition not met do 4:     for $k=1$ to m do                                 ▹ for every ant 5:         for every step until the k-th ant has completed the tour do 6:                select next node j according to the transition rule                 ▹ Equation (1) 7:                ${\nu }_{i,j}={\nu }_{i,j}+1$ 8:                (if symmetric) ${\nu }_{j,i}={\nu }_{i,j}$ 9:         end for 10:     end for 11:     $s_{1:(w-1)}\leftarrow EvaluateAndSelectBest\left(s_{1:m}\right)$               ▹ select $(w-1)$ best ant tours 12:     $s_{gb}\leftarrow SelectBest(s_1,s_{gb})$                          ▹ update global-best solution 13:     $r_o\leftarrow EvaluateOriginality(s_{1:(w-1)},\nu )$              ▹ evaluate originality, Equation (9) 14:     ${\tau }_{i,j}=(1-\rho ){\tau }_{i,j}+{\sum }_{r=1}^{w-1}(w-r_o)△{\tau }_{i,j}^r+w△{\tau }_{i,j}^{gb}$                ▹ Update pheromones 15:     (if symmetric) ${\tau }_{j,i}={\tau }_{i,j}$ 16:     if approach stagnation then 17:         pheromone smoothing                               ▹ Equation (10) 18:     end if 19: end while

Furthermore, at the end of each algorithm iteration, it is checked whether the algorithm is entering a stagnation situation (line 16). The criterion considered for triggering the pheromone smoothing strategy described by Equation (10) is when the standard deviation of the fitness of the 80% of ants tours of the iteration is zero. Hence, the pheromone smoothing is applied before the algorithm enters stagnation. Finally, once the termination condition is met (maximum number of iterations) the algorithm returns the global best tour.

Furthermore, as in symmetric TSP instances, it is assumed that ${\tau }_{i,j}={\tau }_{j,i}$$\forall (i,j)$; ACO algorithms ensure this by updating the symmetric pheromone element (line 15). Similarly, in the case of symmetric TSP, ${\nu }_{i,j}$ counts the number of ants that have traversed either $arc(i,j)$ or $arc(j,i)$ (line 8).

4. Experimental Results

This section analyses the performance of the proposed extension of Rank-based Ant System. First, the evaluation methodology is described, including the utilized benchmarks and the parameter settings. Next, the performance of the proposed ACO algorithm is analysed and compared with AS, the original AS${}_{Rank}$, and with MMAS and ACS, which are widely considered the best-performing ACO algorithms according to multiple sources (see, for instance, [14,15,16]).

4.1. TSP and SOP Benchmarks

The following combinatorial optimization problems are used during the analysis:

• Symmetric and Asymmetric Travelling Salesman Problem (TSP and ASTP) aim to find the Hamiltonian cycle of minimum length given a graph with n cities. In case the distances between the cities are independent of the direction of traversing the edges $d_{i,j}=d_{j,i}$, $\forall (i,j)$, the problem is known as symmetric TSP; otherwise—as asymmetric TSP.
• Sequential Ordering Problem (SOP) consists of finding a Hamiltonian path of the minimal length from node 1 to node n taking precedence constraints into account. The precedence constraints impose that some nodes have to be visited before some other nodes of the graph G.

The characteristics of TSP and SOP instances can be expressed by a distance matrix, where each element $d_{i,j}$ states the distance from node i to node j, or in SOP instances it may be equal to $-1$, indicating that node j must precede node i. For instance, as SOP imposes that all tours start at node 1 and end at node n, $d_{n,j}=-1$, $\forall j$. Additionally, in symmetric TSP instances, the matrix is symmetric as $d_{i,j}=d_{j,i}$, $\forall (i,j)$.

Table 1 lists the relevant information about the instances used for the analysis: their name, the type of optimization problem, the fitness of the optimal solution and the number of nodes (dimension of the problem instance). These instances belong to the TSPLIB benchmark library [38], which is accessible at http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/ (accessed on 24 October 2022).

Table 1. Problem instances used in this paper for the experiments and analysis.

Instance	Type	Optimal Solution	Dimension (n)
brazil58	TSP	25,395	58
kroA100	TSP	21,282	100
ch130	TSP	6110	130
tsp225	TSP	3916	335
gr48	TSP	5046	48
pr76	TSP	108,159	76
gr202	ATSP	40,160	202
ftv35	ATSP	1473	36
ftv64	ATSP	1839	65
ftv70	ATSP	1950	71
ESC78	SOP	18,230	80
ft70.1	SOP	39,313	71
p43.1	SOP	28,140	44
p43.4	SOP	83,005	44

4.2. Experimental Setup

Due to their stochastic nature, all ACO algorithms were run 30 times for each problem instance. During each run, the length of the best-found solution at each iteration is saved. This information is later used for comparing the performance of the algorithms by means of comparative tables and evolutionary curves (see Section 4.3 and Section 4.4 for details).

Regarding the parameter settings, typically recommended values, already used in several previous studies, were selected [11,13,14,18]. The following pheromone and heuristic influence parameters were set for all ACO algorithms; $\alpha =1,\beta =2$. The number of ants m was set equal to the number of cities n for all ACO algorithms with exception of ACS, leading to good algorithm performance (see [14] for details). In the case of ACS, the number of ants m per iteration was set equal to 10, as recommended in [12,14]. Regarding the values of ACS-specific parameters, the following recommended values were considered: $q_0=0.9$, $\xi =0.1$ [12,14]. Regarding Rank-based ACO variants, the following parameters were considered: $w=6$, $\rho =0.1$ and ${\tau }_0=m/f\left(s_{gb}\right)$, also selected in previous studies [14]. Furthermore, in the case of MMAS, the evaporation parameter is set to $\rho =0.02$, the iteration-best solution is considered for pheromone reinforcement, and pheromone trails reinitialization to ${\tau }_{max}$ is triggered whenever no improved tour has been found for more than 250 iterations [14].

With regard to the parameter settings of the proposed algorithm, the common parameters with $A{S}_{Rank}$ are set with the same values for a fair comparison. Additionally, the pheromone smoothing strategy rescales the pheromone table to $[0.1{\tau }_0,{\tau }_0]$ whenever the standard deviation of the lengths of the 80% of the ant tours of the iteration is zero. This criterion was chosen empirically, after observing that in most of the cases, AS${}_{Rank}$ is not able to find a better solution once 80% of the ants have followed the same path (i.e., have the same fitness). The results of the analysis are shown in Table 2, where for each problem instance, the number of simulations (from a total of 30 runs) is shown in which AS${}_{Rank}$ has been able to find a better solution after different percentages d of solutions (from d = 10%, 20%, …, to 100%) have reached null standard deviation (i.e., after the d% of the ants have had the same fitness). The objective of this analysis is to find a good balance, avoiding applying the smoothing mechanism too late (wasting a lot of algorithm iterations with little chance of improving the best solution found so far) or, on the contrary, applying the smoothing mechanism too early (where the pheromone information could still be further exploited to find a better solution). The results of Table 2 show that quite often, AS${}_{Rank}$ is able to find a better solution after 10% of the m solutions have the same fitness, e.g., 22 of the 30 runs for brazil58 instance, or 17 of the 30 runs in kroA100 instance. As we would expect, the higher percentage of solutions considered, the closer it gets to a stagnation situation and the harder it is for the algorithm to find a better solution. For instance, in the case of brazil58, the algorithm was able to find a better solution in 22 of 30 runs after 10% of the m solutions were the same, but only in 6 of the 30 runs after 30% of solutions were the same, and after all the solutions were the same at some iteration, the algorithm was no longer able to improve the best-found-solution in any of the 30 runs.

Table 2. Analysis of the number of times from the 30 runs that AS${}_{Rank}$ was able to find a better solution after different percentages of solutions (ants) have reached null standard deviation.

Instance	Percentage (%)
	10	20	30	40	50	60	70	80	90	100
brazil58	22	7	6	5	3	2	1	1	1	0
kroA100	17	12	9	7	4	3	3	2	2	1
ch130	18	11	8	6	5	4	3	3	3	0
tsp225	21	18	14	12	10	7	4	1	0	0
gr48	14	7	4	2	2	2	2	1	0	0
pr76	14	9	6	5	5	4	4	2	2	1
gr202	16	14	9	7	5	4	3	2	1	0
ftv35	18	14	10	7	4	4	4	3	3	3
ftv64	17	13	9	8	7	7	5	3	1	0
ftv70	21	15	5	4	2	2	1	1	0	0
ESC78	9	6	5	5	3	2	1	0	0	0
ft70.1	18	13	11	7	5	2	2	1	0	0
p43.1	15	12	8	6	6	5	3	2	1	0
p43.4	25	20	18	15	13	10	6	5	5	3

Moreover, for all ACO algorithms, a maximum number of iterations was considered as a stopping criterion; 800 iterations for problem instances with dimensions lower than 100 nodes and 1200 iterations for bigger instances. Additionally, it is worth mentioning that all implemented ACO algorithms do not consider local search, as the goal is to analyse the performance of the proposed approach. Hence, the results obtained could be improved by the consideration of local search strategies typically used for TSP (e.g., k-exchange neighbourhood), see [11]. This will be part of our future work in the field (see Section 5 for further details).

4.3. Analysis of the Proposed ACO Algorithm

With the purpose of analysing the benefits of the extended Rank-based Ant System with originality reinforcement and pheromone smoothing, denoted onwards as AS${}_{ORank}^{ps}$, with respect to the original AS${}_{Rank}$, this section compares their performance over several TSP and SOP instances. Furthermore, in order to analyse how each of the two new proposed strategies contributes to the performance of the algorithm, we also analyse the performance of the algorithm when only one of the two strategies is considered—either with the originality reinforcement (denoted as AS${}_{ORank}$), or with the pheromone smoothing strategy (denoted as AS${}_{Rank}^{ps}$).

The comparative results obtained by these four variants of Rank-based Ant System are shown in Table 3 for the symmetric and asymmetric TSP instances, and in Table 4 for the SOP instances. Both tables are organized in a similar way: the different instances are shown in the first column; for each instance, columns 2–8 show: the algorithm used for execution (second column), the mean length of the best-ant tours and its standard deviation over 30 independent runs of the algorithm (third and fourth columns, respectively), the fitness of the best solution found by the 30 runs (fifth column), the average percentage deviation of the solutions from the optimal solution given by PD${}_{avg}=(Avg-Opt)/Opt·100$ (sixth column) and the percentage deviation of the length of the best solution of the 30 runs from the optimal solution, given by PD${}_{best}=(Best-Opt)/Opt·100$ (seventh column) and computed according to [30], and lastly, the mean computational time over the independent runs of the algorithms in seconds (eighth column). Furthermore, for each problem instance, the best (lowest) average length tour (Avg.), best-found tour (Best), average (PD${}_{avg}$) and best (PD${}_{best}$) percentage deviation are highlighted in bold.

Table 3. Results for symmetric and asymmetric TSP instances obtained by Rank-based ACO variants. The best results for each problem instance are highlighted in bold.

Instance	Algorithm	Avg.	Std.	Best	PD${}_{\mathit{avg}}(\%)$	PD${}_{\mathit{best}}(\%)$	Time (s)
brazil58	AS${}_{Rank}$	25,628	126	25,400	0.92	0.02	14
	AS${}_{Rank}^{ps}$	25,480	118	25,395	0.33	0	14
	AS${}_{ORank}$	25,677	124	25,400	1.11	0.02	13
	AS${}_{ORank}^{ps}$	25,487	121	25,395	0.36	0	15
kroA100	AS${}_{Rank}$	21,683	252	21,306	1.89	0.11	45
	AS${}_{Rank}^{ps}$	21,357	100	21,282	0.35	0	45
	AS${}_{ORank}$	21,591	186	21,331	1.45	0.23	43
	AS${}_{ORank}^{ps}$	21,378	120	21,282	0.45	0	45
ch130	AS${}_{Rank}$	6235	39	6169	2.04	0.97	120
	AS${}_{Rank}^{ps}$	6193	47	6141	1.36	0.51	120
	AS${}_{ORank}$	6241	48	6154	2.14	0.72	115
	AS${}_{ORank}^{ps}$	6170	33	6136	0.98	0.43	120
tsp225	AS${}_{Rank}$	4026	31	3989	2.80	1.86	422
	AS${}_{Rank}^{ps}$	3949	23	3916	0.84	0	422
	AS${}_{ORank}$	4034	33	3978	3.02	1.58	407
	AS${}_{ORank}^{ps}$	3942	17	3916	0.65	0	424
gr48	AS${}_{Rank}$	5117	40	5066	1.40	0.40	9
	AS${}_{Rank}^{ps}$	5104	35	5054	1.15	0.16	9
	AS${}_{ORank}$	5135	39	5074	1.76	0.55	9
	AS${}_{ORank}^{ps}$	5091	28	5049	0.88	0.06	11
pr76	AS${}_{Rank}$	111,609	1064	109,392	3.19	1.14	60
	AS${}_{Rank}^{ps}$	110,357	1187	108,238	2.03	0.07	61
	AS${}_{ORank}$	111,507	810	110,100	3.10	1.79	60
	AS${}_{ORank}^{ps}$	109,922	900	108,159	1.63	0	64
gr202	AS${}_{Rank}$	41,803	435	40,960	4.09	1.99	324
	AS${}_{Rank}^{ps}$	41,095	255	40,609	2.33	1.12	325
	AS${}_{ORank}$	41,602	340	41,022	3.59	2.15	317
	AS${}_{ORank}^{ps}$	41,056	228	40,554	2.23	0.98	328
ftv35	AS${}_{Rank}$	1497	9	1473	1.65	0	5
	AS${}_{Rank}^{ps}$	1488	10	1473	0.98	0	5
	AS${}_{ORank}$	1497	11	1473	1.64	0	5
	AS${}_{ORank}^{ps}$	1483	11	1473	0.71	0	5
ftv64	AS${}_{Rank}$	1867	21	1848	1.50	0.49	17
	AS${}_{Rank}^{ps}$	1859	8	1848	1.07	0.49	17
	AS${}_{ORank}$	1862	14	1839	1.23	0	16
	AS${}_{ORank}^{ps}$	1858	9	1839	1.05	0	17
ftv70	AS${}_{Rank}$	2010	44	1957	3.10	0.36	21
	AS${}_{Rank}^{ps}$	1999	35	1957	2.49	0.36	21
	AS${}_{ORank}$	1989	30	1950	1.98	0	20
	AS${}_{ORank}^{ps}$	1989	37	1989	1.99	0.20	21

Table 4. Results for SOP instances obtained by Rank-based ACO variants. The best results for each problem instance are highlighted in bold.

Instance	Algorithm	Avg.	Std.	Best	PD${}_{\mathit{avg}}(\%)$	PD${}_{\mathit{best}}(\%)$	Time (s)
ESC78	AS${}_{Rank}$	18,609	147	18,415	2.08	1.01	183
	AS${}_{Rank}^{ps}$	18,470	43	18,405	1.32	0.96	185
	AS${}_{ORank}$	18,584	158	18,380	1.94	0.82	185
	AS${}_{ORank}^{ps}$	18,460	69	18,300	1.26	0.38	192
ft70.1	AS${}_{Rank}$	41,403	419	40,646	5.32	3.39	81
	AS${}_{Rank}^{ps}$	41,082	297	40,505	4.50	3.03	81
	AS${}_{ORank}$	41,053	331	40,529	4.43	3.09	80
	AS${}_{ORank}^{ps}$	40,768	341	40,092	3.70	1.98	81
p43.1	AS${}_{Rank}$	28,333	107	28,220	0.69	0.28	21
	AS${}_{Rank}^{ps}$	28,255	65	28,220	0.41	0.28	21
	AS${}_{ORank}$	28,330	107	28,220	0.63	0.28	21
	AS${}_{ORank}^{ps}$	28,236	34	28,220	0.34	0.28	22
p43.4	AS${}_{Rank}$	83,693	119	83,415	0.83	0.49	67
	AS${}_{Rank}^{ps}$	83,405	73	83,295	0.48	0.35	68
	AS${}_{ORank}$	83,620	120	83,405	0.74	0.48	67
	AS${}_{ORank}^{ps}$	83,416	113	83,265	0.49	0.31	68

The comparative results show that the proposed Rank-based extension AS${}_{ORank}^{ps}$ clearly outperforms the original AS${}_{Rank}$, obtaining lower mean path lengths in all TSP, ATSP and SOP instances. For example, in the case of the symmetric TSP instance ch130, AS${}_{Rank}$ obtained a mean path length of 6235, which corresponds to an average percentage of deviation from the optimal solution of PD${}_{agv}=2.04\%$, while AS${}_{ORank}^{ps}$ obtained a mean path length of 6170 and PD${}_{agv}=0.98\%$. Moreover, for the same problem instance, the fitness of the best solution found during the 30 runs by AS${}_{Rank}$ was 6169, which corresponds to a percentage of deviation from the optimal solution of PD${}_{best}=0.97\%$, while AS${}_{ORank}^{ps}$ obtained a path length of 6136 and PD${}_{best}=0.43\%$. Additionally, no significant differences are observed between the computational times.

Additionally, several conclusions can be drawn from the analysis of the AS${}_{ORank}$ and AS${}_{Rank}^{ps}$ variants. On the one hand, the results from Table 3 and Table 4 show that the pheromone smoothing strategy by itself (AS${}_{Rank}^{ps}$) clearly improves the performance of the Rank-based algorithm, showing better results than AS${}_{Rank}$ in all the problem instances. On the other hand, the inclusion of the originality reinforcement strategy in Rank-based Ant System showed an improvement in the results. AS${}_{ORank}$ variant obtained better results than AS${}_{Rank}$ in 7 of the 12 problem instances, worse in 4 problem instances (brazil58, ch130, gr48 and tsp95) and similar performance in (ftv35). However, the ACO variant that considers both the originality reinforcement and the pheromone smoothing (AS${}_{ORank}^{ps}$) obtained the best results out of all considered algorithms in the majority of the 12 instances, (with the exception of brazil58, kroA100 and p43.4 where AS${}_{Rank}^{ps}$ obtained better results). Therefore, we can conclude that the originality reinforcement strategy is clearly beneficial when combined with the pheromone smoothing strategy in the proposed AS${}_{ORank}^{ps}$.

To sum up, we can conclude that AS${}_{ORank}^{ps}$ outperformed the original AS${}_{Rank}$ in the fourteen problem instances thanks to both the pheromone smoothing and the originality reinforcement strategies.

4.4. Comparison with ACO Algorithms

The comparative Table 5 and Table 6, and the evolutionary curves in Figure 6 and Figure 7 show the performance of several ACO algorithms: Ant System (AS) [9], Rank-based Ant System (AS${}_{Rank}$) [10], Max-Min Ant System (MMAS) [11], Ant Colony System (ACS) [12] and the proposed extension of the Rank-based Ant System (AS${}_{ORank}^{ps}$).

Table 5. Results for symmetric and asymmetric TSP instances obtained by ACO algorithms. The best results for each problem instance are highlighted in bold.

Instance	Algorithm	Avg.	Std.	Best	PD${}_{\mathit{avg}}(\%)$	PD${}_{\mathit{best}}(\%)$	Time (s)
brazil58	AS	25,930	89	25,685	2.10	1.14	14
	AS${}_{Rank}$	25,628	126	25,400	0.92	0.02	14
	MMAS	25,622	51	25,480	0.89	0.33	14
	ACS	25,464	116	25,395	0.27	0	16
	AS${}_{ORank}^{ps}$	25,487	121	25,395	0.36	0	15
kroA100	AS	22,714	198	22,221	6.73	4.41	45
	AS${}_{Rank}$	21,683	252	21,306	1.89	0.11	45
	MMAS	21,462	173	21,330	0.85	0.23	45
	ACS	21,559	279	21,282	1.30	0	53
	AS${}_{ORank}^{ps}$	21,378	120	21,282	0.45	0	45
ch130	AS	6632	71	6482	8.54	6.09	120
	AS${}_{Rank}$	6235	39	6169	2.04	0.97	120
	MMAS	6202	34	6127	1.48	0.28	121
	ACS	6234	44	6145	2.03	0.57	145
	AS${}_{ORank}^{ps}$	6170	33	6136	0.98	0.42	120
tsp225	AS	4374	57	4166	11.69	6.38	424
	AS${}_{Rank}$	4026	31	3989	2.80	1.86	420
	MMAS	3998	20	3962	2.10	1.17	420
	ACS	4022	42	3929	2.72	0.33	504
	AS${}_{ORank}^{ps}$	3942	17	3916	0.65	0	424
gr48	AS	5227	36	5147	3.58	2.00	9
	AS${}_{Rank}$	5117	40	5066	1.40	0.40	9
	MMAS	5103	35	5063	1.13	0.34	9
	ACS	5095	35	5046	0.96	0	12
	AS${}_{ORank}^{ps}$	5091	28	5049	0.88	0.06	9
pr76	AS	115,664	793	113,911	6.94	5.32	60
	AS${}_{Rank}$	111,609	1064	109,392	3.19	1.14	60
	MMAS	110,521	1027	109,271	2.18	1.03	60
	ACS	110,157	1326	108,159	1.85	0	70
	AS${}_{ORank}^{ps}$	109,922	900	108,159	1.63	0	64
gr202	AS	45,746	482	44,368	13.90	10.48	327
	AS${}_{Rank}$	41,803	435	40,960	4.09	1.99	324
	MMAS	42,004	413	41,331	4.59	2.92	327
	ACS	41,646	340	40,720	3.70	1.39	387
	AS${}_{ORank}^{ps}$	41,056	228	40,554	2.23	0.98	328
ftv35	AS	1504	10	1487	2.11	0.95	5
	AS${}_{Rank}$	1497	9	1473	1.65	0	5
	MMAS	1493	8	1473	1.39	0	5
	ACS	1494	19	1473	1.45	0	6
	AS${}_{ORank}^{ps}$	1483	11	1473	0.71	0	5
ftv64	AS	1918	13	1902	4.31	3.43	17
	AS${}_{Rank}$	1867	21	1848	1.50	0.49	17
	MMAS	1857	7	1854	1.00	0.815	18
	ACS	1866	21	1842	1.85	0.16	21
	AS${}_{ORank}^{ps}$	1858	9	1839	1.05	0	17
ftv70	AS	2149	23	2051	10.20	5.18	21
	AS${}_{Rank}$	2010	44	1957	3.10	0.36	21
	MMAS	1988	30	1950	1.95	0	21
	ACS	2044	48	1967	4.83	0.87	25
	AS${}_{ORank}^{ps}$	1989	37	1954	1.99	0.20	21

Table 6. Results for SOP instances obtained by ACO algorithms. The best results for each problem instance are highlighted in bold.

Instance	Algorithm	Avg.	Std.	Best	PD${}_{\mathit{avg}}(\%)$	PD${}_{\mathit{best}}(\%)$	Time (s)
ESC78	AS	20,631	227	19,950	13.17	9.43	182
	AS${}_{Rank}$	18,609	147	18,415	2.08	1.01	184
	MMAS	18,464	28	18,405	1.29	0.96	187
	ACS	18,477	97	18,290	1.35	0.33	196
	AS${}_{ORank}^{ps}$	18,460	69	18,300	1.26	0.38	192
ft70.1	AS	44,110	469	43,221	12.20	9.94	81
	AS${}_{Rank}$	41,403	419	40,646	5.32	3.39	81
	MMAS	40,903	441	40,192	4.05	2.24	81
	ACS	42,562	715	41,014	8.27	4.33	87
	AS${}_{ORank}^{ps}$	40,768	341	40,092	3.70	1.98	81
p43.1	AS	28,776	64	28,615	2.26	1.69	21
	AS${}_{Rank}$	28,333	107	28,220	0.69	0.28	21
	MMAS	28,258	57	28,220	0.42	0.28	21
	ACS	28,461	88	28,245	1.40	0.37	24
	AS${}_{ORank}^{ps}$	28,236	34	28,220	0.34	0.28	22
p43.4	AS	84,218	115	83,950	1.46	1.14	68
	AS${}_{Rank}$	83,693	119	83,415	0.83	0.49	67
	MMAS	83,514	130	83,360	0.61	0.43	67
	ACS	83,601	146	83,270	0.72	0.32	69
	AS${}_{ORank}^{ps}$	83,416	113	83,265	0.49	0.31	68

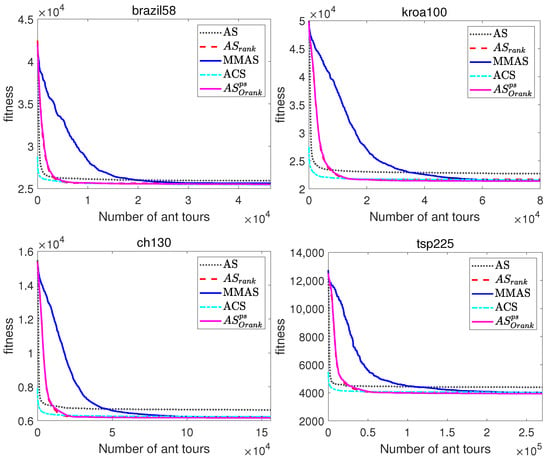
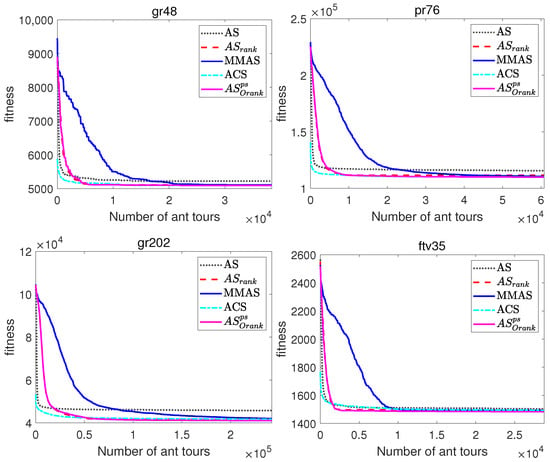
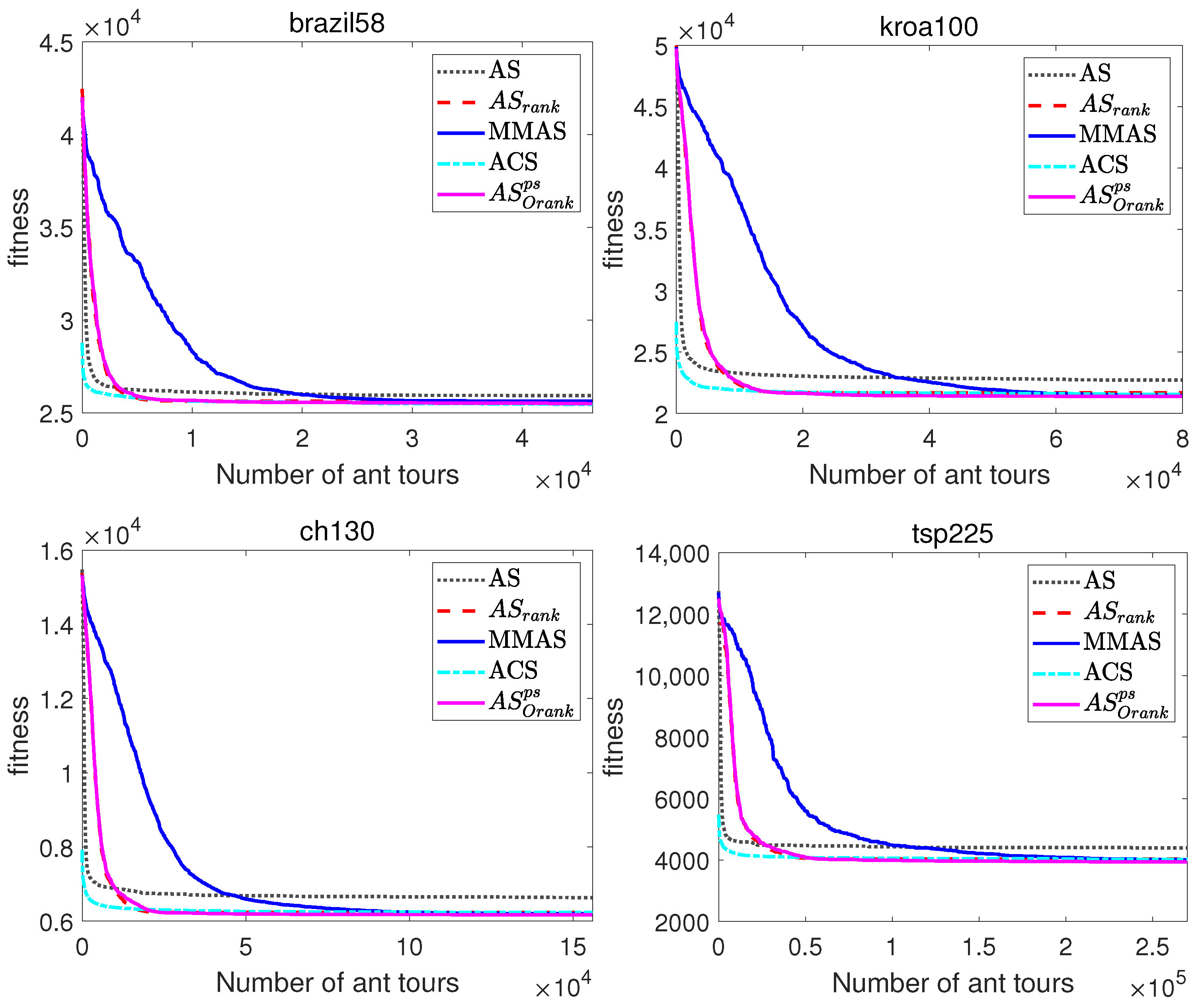
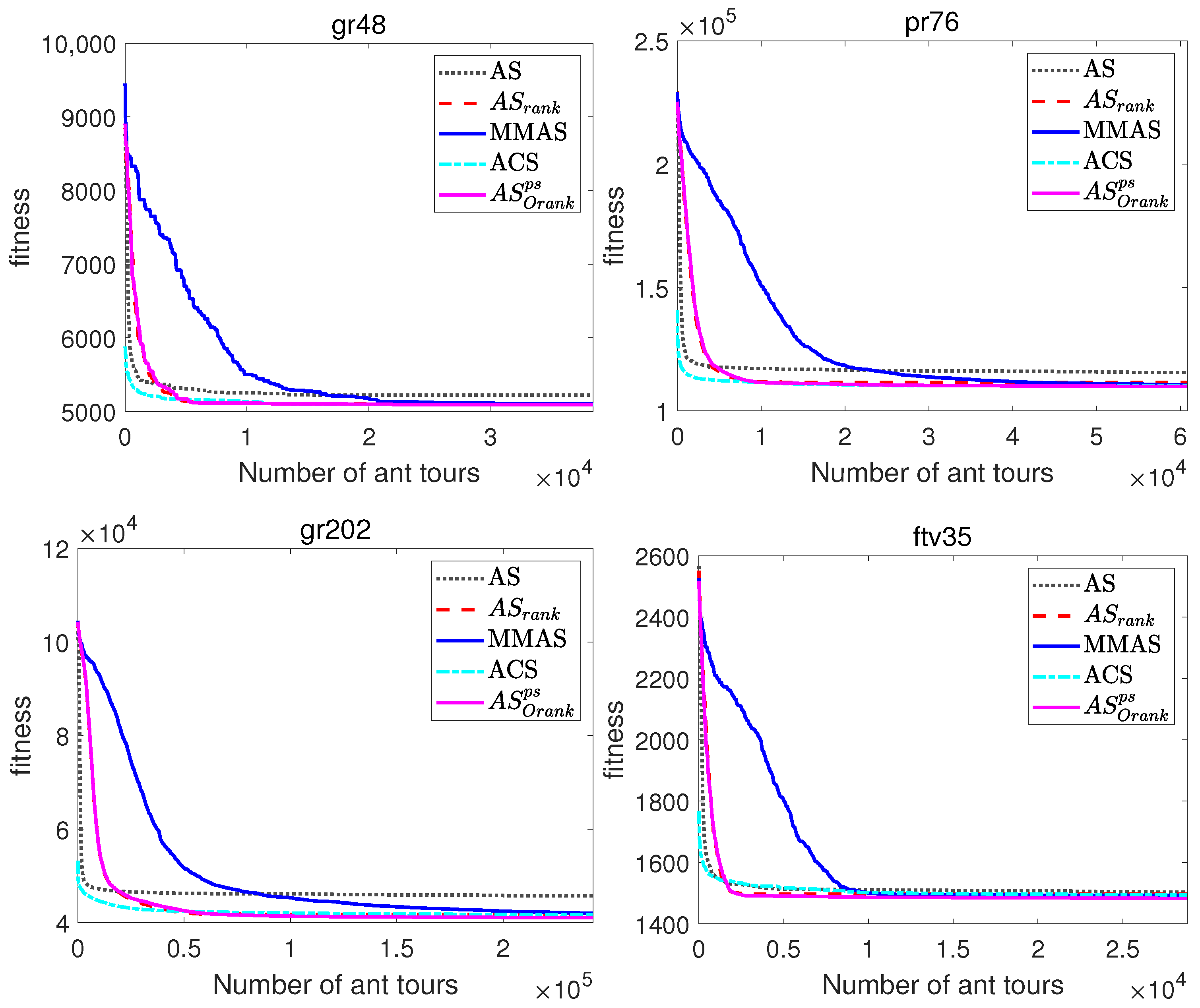
Figure 6. Evolutionary curves of ACO algorithms for symmetric and asymmetric TSP instances.

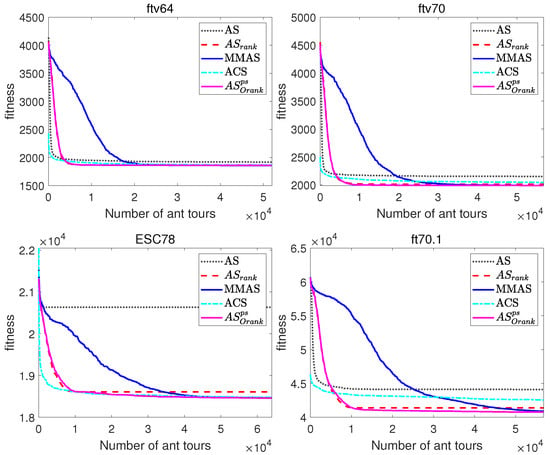
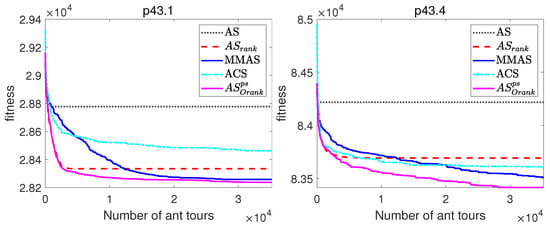
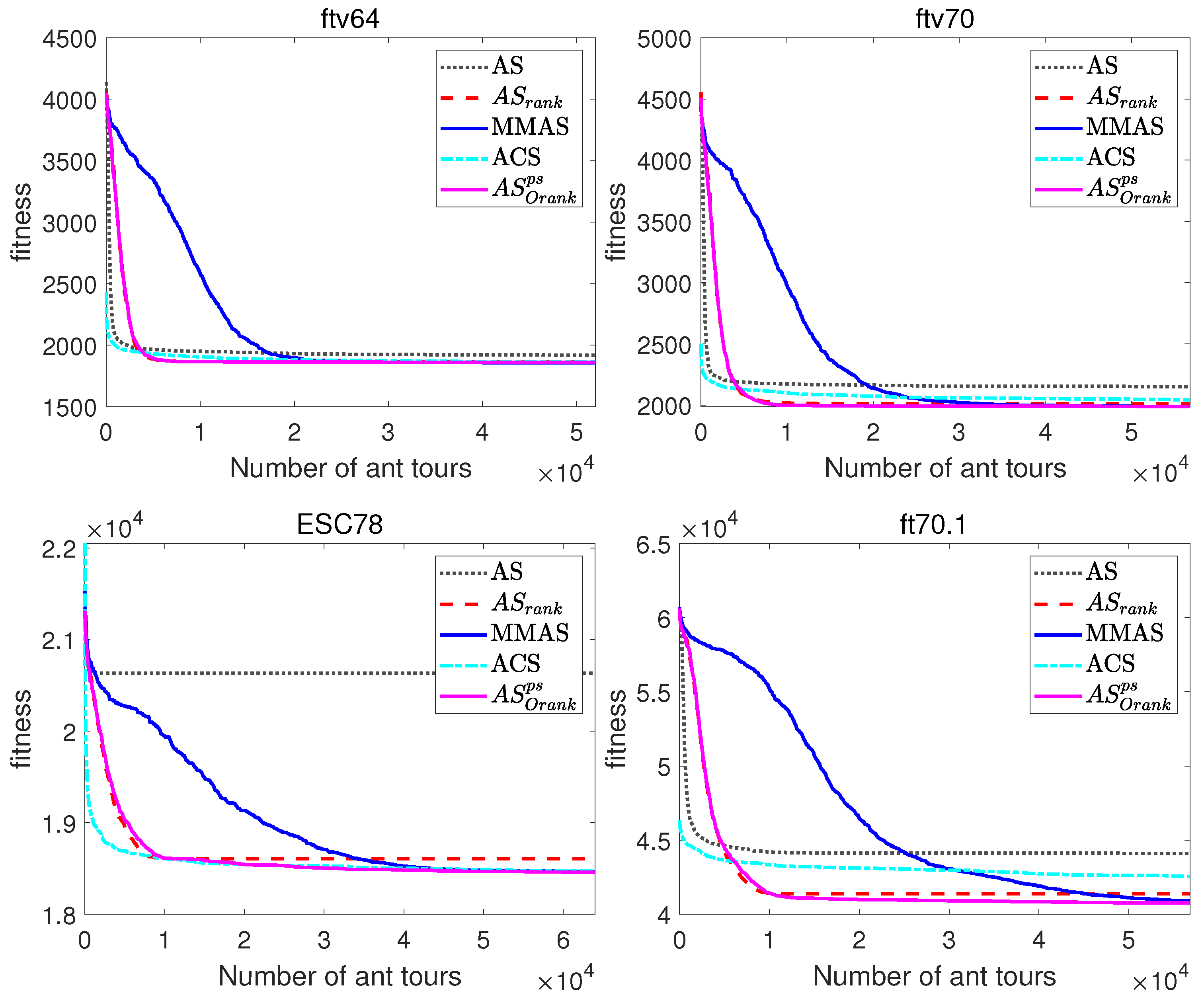
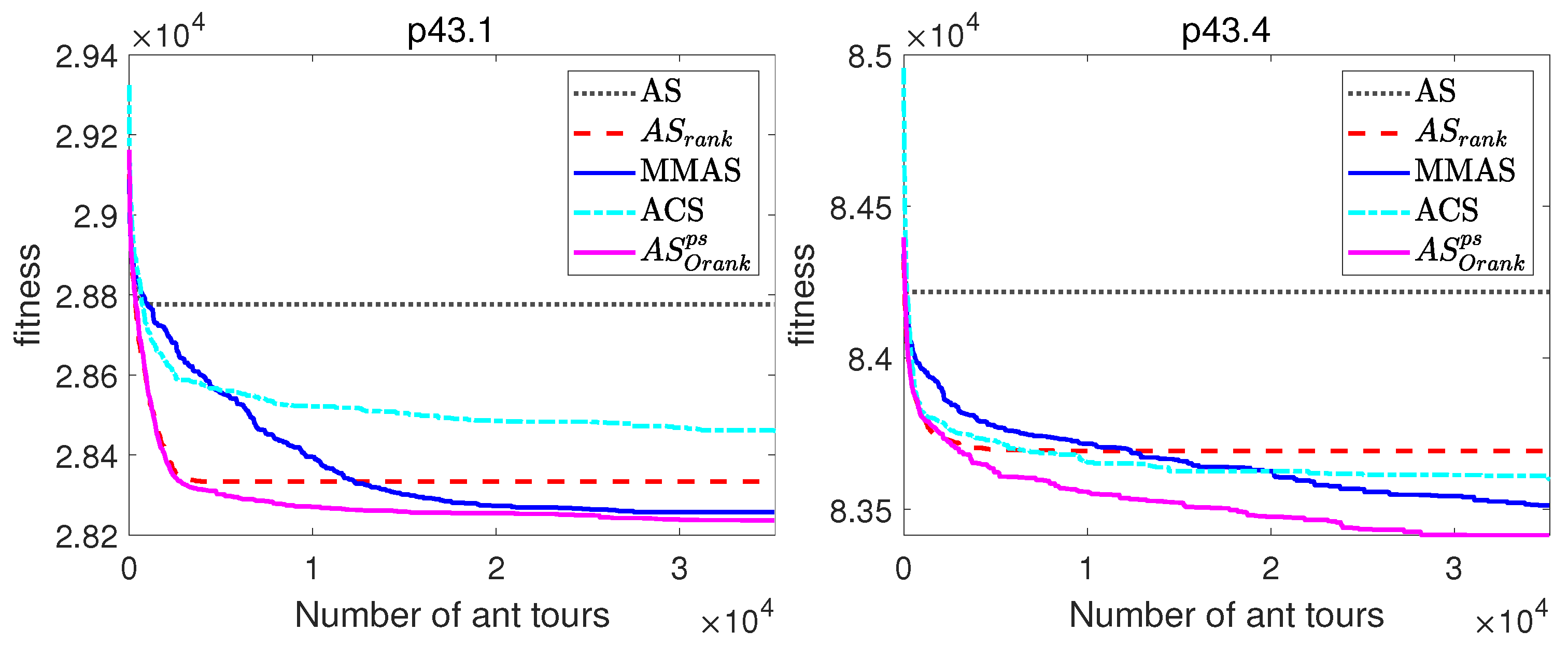
Figure 7. Evolutionary curves of ACO algorithms for asymmetric TSP instances (ftv64 and ftv70) and four SOP instances.

On the one hand, Table 5 and Table 6 allow the comparison of the final solutions obtained by the ACO algorithms, showing that AS${}_{ORank}^{ps}$ outperforms all analysed ACO algorithms, including MMAS and ACS which are the most widely used and often best performing ACO algorithms [14,15,16]. More concretely, AS${}_{ORank}^{ps}$ obtained better results than AS and AS${}_{Rank}$ in all problem instances, better results than ACS in all instances with the exception of brazil58, and better results than MMAS in all SOP instances, and all TSP instances with the exception of ftv64 and ftv70, where both algorithms obtained similar results. Regarding the computational times, ACS requires slightly longer computational times than the rest of the algorithms.

On the other hand, the evolutionary curves of Figure 6 and Figure 7, which represent the evolution of the average best-found tour lengths along the number of tours constructed, enable the comparison of the performance of the ACO algorithms along the runs of the algorithms, and not just the comparison of the fitness of final solutions. Note that these graphs allow to compare the performance of the algorithms at different iterations, but due to the scale, the comparison of the fitness of the final solutions is better observed in the comparative Table 5 and Table 6.

The evolutionary curves of Figure 6 and Figure 7 show that during the initial iterations, all ACO algorithms outperform MMAS, which presents a slower convergence to high-quality solutions. For example, at iteration 100 of the TSP instance brazil58, the mean percentage deviations from the optimal solution of AS${}_{Rank}$ and AS${}_{ORank}^{ps}$ are, respectively, 1.26% and 1.6%, while MMAS clearly presents a higher error equal to $26.2\%$. The reason for the observed behaviour is that, while MMAS relies on a high initial exploration of the search space in order to finally converge to high-quality solutions, AS${}_{ORank}^{ps}$ maintains the rapid convergence of AS${}_{Rank}$ and relies on search diversification of the originality reinforcement and pheromone smoothing mechanism to improve the quality of the solutions. The behaviour of AS${}_{ORank}^{ps}$ can be especially beneficial in those optimization problems where the available computational time is limited or not known beforehand, as its faster convergence would return a significantly better solution if the number of iterations is restricted.

To sum up the conclusions from comparative tables and evolutionary graphs, AS${}_{ORank}^{ps}$ is able to find higher-quality solutions than AS and AS${}_{Rank}$ in all the problem instances and in all except one instance when compared with ACS. Moreover, AS${}_{ORank}^{ps}$ showed a much faster convergence than MMAS, while being able to reach better final solutions in most of the problem instances.

5. Conclusions and Future Work

This work proposes an extension of the Rank-based Ant System that incorporates originality reinforcement and pheromone smoothing strategies in order to avoid early stagnation and improve the quality of the solutions. The performance of the approach is analysed and compared with AS, AS${}_{Rank}$, MMAS, and ACS, over TSP and SOP benchmarks showing very promising results. Contrary to the occasional reinitialization of pheromone trails employed by MMAS [14,17], the proposed algorithm relies strongly on search diversification through frequent smoothing of the pheromone trails. Therefore, the promising results obtained by the proposed approach are not due only to the pheromone smoothing mechanism, but also to the use of the proposed criterion for triggering the pheromone smoothing. Additionally, the comparative results show that the originality reinforcement strategy helps to improve the quality of the Rank-based Ant System when it is combined with the pheromone smoothing strategy. Together, they enable the proposed approach to maintain the rapid convergence to high-quality solutions during the first iterations of AS${}_{Rank}$, in addition to reaching higher-quality solutions in the long run. These features can be advantageous in those optimization problems where the available time for computation is limited or not known beforehand.

In this regard, we consider as an interesting future research line the adaptation of the proposed approach to dynamic optimization problems (where the search domain changes over time). For example, the rapid convergence of the proposed ACO algorithm could be advantageous in Dynamic TSP [14,39], where new cities can be added or removed during run time and the new shortest tour after each transition should be found as quickly as possible. We also consider the analysis of the proposed method with other combinatorial optimization problems such as the Vehicle Routing Problem and different modifications of the original TSP [14].

Other interesting potential extension of this work is its hybridization with local search strategies and/or other metaheuristics for better performance. As previously indicated in Section 4.2, the present method does not include any local search, since our primary goal is to enhance the pure state-of-the-art ACO algorithms without the addition of other heuristics. However, it has been remarked by several authors that adding sophisticated local search procedures to the ACO algorithms can improve their performance for certain problems significantly [17]. In line with this, we plan to combine our method with different local search strategies and analyse their performance for the TSP, SOP and other combinatorial optimization problems. We also plan to compare the performance of our method with other ACO implementations after they are all paired with those local search procedures, under the premise that the superior behaviour of our method with respect to best ACO performers without any local search should remain when the local search is added to all methods in a similar fashion. Other interesting extensions are the comparison of this new ACO algorithm with other powerful metaheuristics, such as genetic algorithms, particle swarm optimization or differential evolution, as well as analysing whether the performance of our method can be improved by its hybridization with some of those metaheuristics. These ideas are all part of our plans for future work in the field.