1. Introduction
In recent years, researchers have witnessed the great success of deep neural networks (DNNs) in many fields, e.g., image classification [
1] and target detection [
2]. However, the heavy computation cost and high requirements of memory and storage by DNNs block their application in resource-limited devices. For example, the VGG-16 model has 138.34 million parameters, which requires more than 500 MB of storage space. Therefore, it is impractical to deploy such a complex model on embedded devices. A feasible solution to this kind of problem is to compress a large DNN without a significant drop in the model accuracy. Network pruning is one of the effective compression technologies.
In order to avoid unnecessary manual operations in the pruning process and explore a larger network pruning space, automatic pruning [
3,
4] is favored. Automatic pruning uses a learnable agent to optimize the pruning scheme, i.e., the pruning rate for each layer of a DNN. During the auto-pruning process, the agent learns to prune in an iterative manner with feedback on model accuracy and complexity. Among all the automatic pruning methods, reinforcement learning (RL)-based approaches [
5] have attracted extensive attention due to their maturity, universality, and high performance. However, the time cost of an RL-based automatic pruning algorithm greatly limits its use.
The filter-level DCNN pruning method discussed in this paper mainly focuses on the following two problems: (1) The determination of the filter pruning rate in each layer and (2) the ordering of filters to be pruned, which is known as the filter-sorting problem. To solve these two problems, this paper proposes a filter-level DCNN pruning method based on RL, termed FPRL. In the proposed FPRL, the filter pruning rate determination problem is formulated as a Markov decision process (MDP), which is solved by a deep deterministic policy gradient (DDPG) algorithm. Furthermore, the Taylor expansion criterion is considered for filter ordering
The major contributions of this paper can be summarized as follows:
A DDPG-based automatic DCNN pruning method is proposed, which prunes the redundant filters in the network to compress the network.
The DDPG algorithm optimizes the pruning rate of each layer. A tailored reward function considering the change of both network accuracy and complexity before and after layer-wise pruning is developed for DDPG training.
A Taylor-expansion-based filter ranking criterion is considered for filter pruning in the FPRL method, which proves to be much more efficient than the widely used minimum-weight-based ranking criterion.
To illustrate the efficiency of the proposed method in DCNN pruning, extensive experiments have been conducted with several classical DCNNs including VGGNet and ResNet on CIFAR10 and CIFAR100 datasets. The results demonstrate that the FPRL can achieve more than 10× the parameter compression and 3× the FLOPs reduction while maintaining accuracy similar to the initial network.
2. Related Work
In this paper, a DRL-based automatic filter-level DCNN pruning method is proposed. In this section, the background of filter pruning is presented, which includes pruning, architecture search, and filter selection criteria.
2.1. Pruning
There are a variety of network compression methods such as network pruning, network distilling [
6], quantization [
7], network decomposition [
8], and compact network design [
9]. Among them, pruning is the most widely used method [
10,
11,
12], which can transform the original dense deep neural network into a sparse network without a significant reduction in the network accuracy. The pruning of DCNNs can be divided into two categories, including unstructured pruning and structured pruning.
Unstructured pruning, which is also known as sparse pruning, sets some weight values to 0 for the sparsity of the convolution matrix. Han et al. [
13] proposed an iterative method to cut the network weight below a certain threshold. Yang et al. [
14] proposed a convolution neural network clipping algorithm, which cuts the network in a layer-wise manner by using energy consumption as the ranking criterion and restores network accuracy by using the least-squares method for local fine-tuning of each layer.
Structured pruning removes convolution kernels, filters, channels, and layers in the network and eliminates redundant connections in the network. L1 regularization [
15] and L2 regularization [
16] have been used to assess the correlation between convolution kernel and network performance and determine the filters to be pruned. In [
17], scaling coefficient normalization in the batch normalization layer was used to guide the thinning and pruning of the neural network structure. Compared with traditional channel pruning, Huang et al. [
18] accelerated neural networks based on an acceleration-aware finer-grained channel pruning method. Hu et al. [
19] proposed a channel clipping method for ultra-deep CNN compression, in which the trimming of the channel was formulated as a search problem solved by a genetic algorithm. He et al. [
20] developed an effective channel-clipping method based on LASSO regression and least-squares reconstruction, which accelerated VGG-16 by five times with a 0.3% error increase. Li et al. [
21] proposed AdaPrune, which adaptively switches pruning between the input channel group and the output channel to accelerate deep neural networks.
The most important problem of network pruning is the determination of the redundant unit in the network, while there is no clear criterion to solve this problem. Most methods require repeated experiments, which results in high costs of human and material resources.
2.2. Architecture Search
The performance of DCNN highly depends on its architecture, which is a great challenge for DCNN architecture design. The pioneering study on automatic neural network architecture design can be traced back to the 1980s when the genetic algorithm was proposed to search the neural network architecture and weight. Modern architecture search methods produce state-of-the-art results for many tasks, but it usually takes a long time even on GPU to obtain high-performance architecture [
22]. The genetic algorithm has also been applied to architecture searches, such as evolving unsupervised DNNS (EUDNN) [
23], automatic evolving CNN (AE-CNN) [
24], and the evolving deep convolutional neural network (EvoCNN) [
25]. RL is also used to find compressed architecture from well-trained networks. Baker et al. [
26] designed the network architecture search algorithm based on Q-learning, conditionally sampled the network architecture through empirical knowledge, and automatically generated a high-performance CNN according to specific tasks. He et al. [
27] learned the compression rate of each layer of the network architecture through the DDPG algorithm, which, however, rewards the agent at the end of an episode resulting in thousands of hours on GPU for RL agent training.
2.3. Different Filter Selection Criteria
In filter pruning, the determination of which filters need to be pruned depends on the filter’s importance. The less important filters are, the more likely they are to be pruned. There are a few heuristic criteria to evaluate the importance of each filter.
Minimum weight. The activation of filters with a lower absolute sum of weight tends to be weaker. This makes the minimum weight an attractive criterion for filter importance ranking. Li et al. [
15] deployed minimum weight as a filtering sorting score for filtering pruning and the results illustrated that the minimum weight was a simple and effective criterion.
Average percentage of zeros. Hu et al. [
28] defined the average percentage of zeros (APoZ) to calculate each neuron’s sparsity of the model activated by the ReLU function. A filter with a high APoZ value indicates low importance. Pruning of these filters can achieve the same or even better performance than the original model.
Taylor expansion. Molchanov [
29] proposed a new criterion based on Taylor expansion, which approximates the change in cost function caused by network pruning.
3. Filter-Level Pruning Based on RL
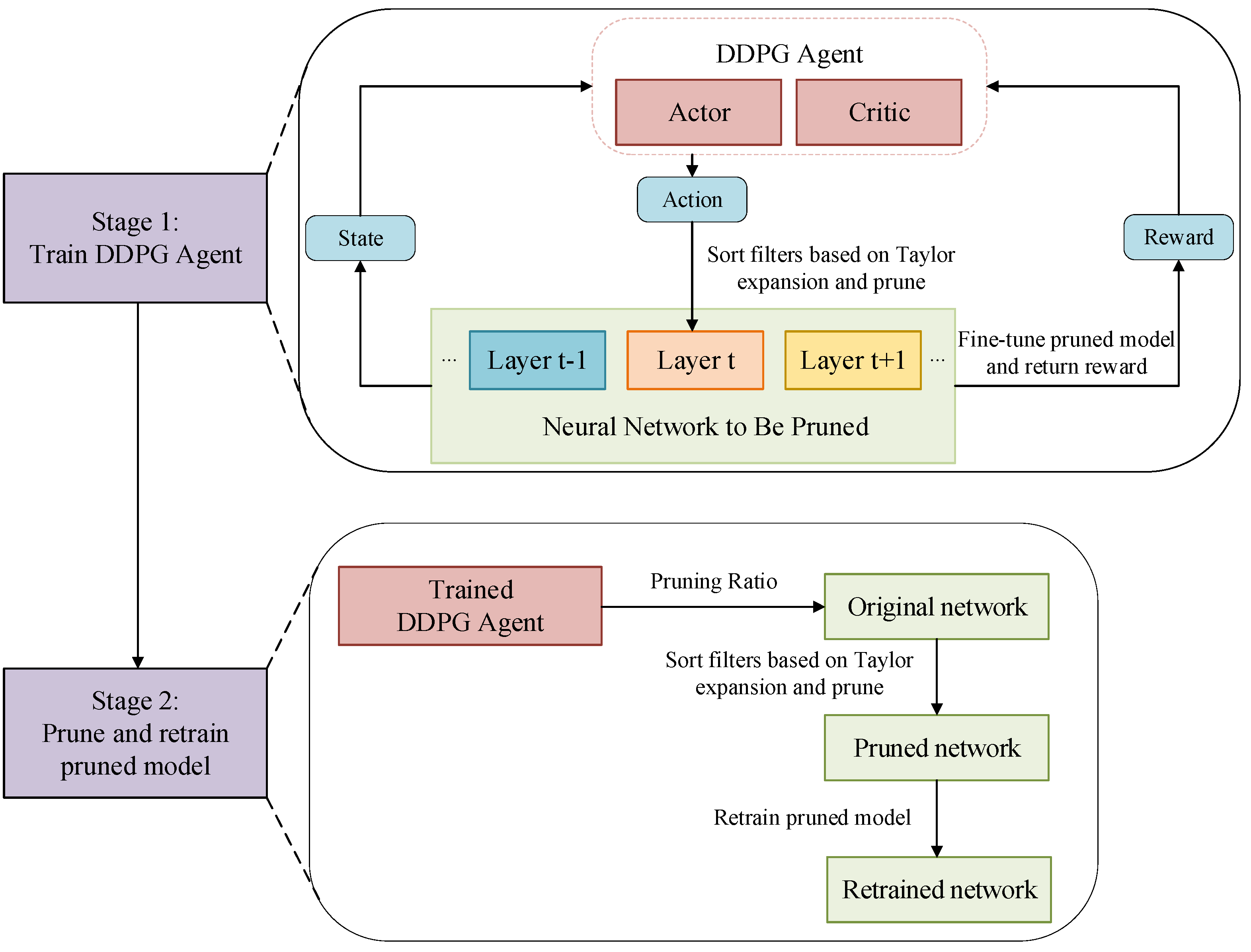
This section discusses the details of the proposed FPRL method for DCNN pruning via deep reinforcement learning. The optimization problem of the layer-wise filter pruning rate is formulated as an MDP, which is solved by the DDPG algorithm. Moreover, a Taylor-expansion-based criterion is further developed for filter importance evaluation. There are two stages in the proposed FPRL method shown in
Figure 1: (1) Training of DDPG for the optimization of the layer-wise filter pruning rate and (2) network pruning and retraining for accuracy reconstruction. In stage 1, the training of DDPG is performed in a recursive manner consisting of the following steps: (1) The DDPG agent offers the pruning rate, (2) filter sorting, (3) network pruning, (4) network fine-tuning, and (5) network evaluation, and sends feedback to the DDPG agent; (6) the DDPG policy is updated; (7) steps 1–6 are repeated until the stopping condition is met. In state 2, given the optimized layer-wise filter pruning rate from stage 1, the filter is sorted and prunes less important filters and the network is retrained to restore its accuracy.
3.1. DCNN Pruning as a Markov Decision Process
In filter pruning, the determination of which filters need to be pruned often depends on filter importance. The problem can be formulated as a Markov decision process (MDP) in the form of a tuple , where is the set of all possible states, is the set of available action in all states, is the reward function, is the transition probability, and is the discount factor.
The MDP provides a mathematical framework for decision-making in the stochastic environment. At each time step, the RL agent takes an action according to the current state , and receives a reward . Consequently, the state is updated to with transition . The target of the RL agent is to find an optimal policy that maximizes the expected cumulative rewards. In this paper, the task of filter-level pruning of DCNN is formulated as an MDP, which is later solved by the DDPG algorithm. The details of the modeling of MDP and DDPG are as follows.
3.1.1. State Representation
A tuple of features is used to represent the network state, i.e., , where is the index of the layer being pruned, is the number of filters, is the kernel size, is the network accuracy, and corresponds to the reduction rate of FLOPs.
3.1.2. Action Representation
The action refers to the filter pruning rate for the layer being pruned. The action
is bounded by (1):
where
pr_max denotes the maximum pruning rate at each convolutional layer and is set to 0.95 in this study.
3.1.3. State Transition and Reward Function
With the execution of action
given state
, a new state
can be observed by evaluating the performance of the pruned network. The reward is a feedback signal from the environment. A tailored reward function is developed to guide the evolution of the agent strategy. The goal of network compression is to maximize the compression rate while maintaining network accuracy. To consider both the network complexity and accuracy, the reward function in (2) is developed:
where
and
are weight parameters. The considered reward function by applying the minimization operation in the first term on the right of Equation (2) ensures the stability of the agent during the optimization process.
3.2. Optimization of Pruning Rate with DDPG
RL is rather effective in dealing with the sequential decision-making problem. The target of the RL agent is to find an optimal policy
to maximize the expected cumulative rewards, which is expressed as:
where
denotes the discount factor that represents the attenuation of the future rewards. Let
denote the state–action evaluate function, which measures the expected accumulative return by taking action
following policy π in state
as follows:
The
Q-value can be obtained in a recursive manner as in the Bellman Equation (5), which sets the foundation of RL.
In this paper, the DDPG algorithm is applied to solve the MDP problem, which is composed of an actor network and a critic network. The actor network parametrized by defines the policy, which maps the state to the action, i.e., . The critic network parametrized by approximates the Q-value function.
In deep reinforcement learning, the policy
determines the agent’s action
. Considering the deterministic policy, denoted as
, the
Q-value function can be written as
where
denotes the discount factor in the Bellman equation.
The critic net approximates the
Q-value function. The loss of the critic net in (7) is adopted to minimize the difference in the
Q-value.
where
represents the parameters in the deep
Q-network and
is defined as follows:
The actor net updates the policy with the aid of the critic net. The policy gradient in (9) is used for the optimization of actor network parameters, which strives to boost the
Q-value [
30].
where
represents the parameters of the online actor net.
In DDPG, it is important to balance exploration and exploitation for agent training. Hence, the exploration policy by adding Gaussian noise as in (10) is applied.
To facilitate the training of DDPG, an experience reply [
31] is considered whereby at each time step a mini-batch of samples is uniformly sampled for the update of network parameters. To stabilize the training process, target networks are used to evaluate target
Q-values, and a soft update strategy [
32] is used to update the parameters of target networks.
3.3. Filter Selection and Pruning
In this paper, the Taylor-expansion-based criterion is used for filter importance evaluation [
29].
To illustrate the idea of the Taylor-expansion-based filter sorting criterion, let
denote the cost value of the pruned feature map
, and
is the cost value without pruning
. Thereby, the change in the cost value before and after pruning
can be expressed as (11):
The approximation of
with first-order Taylor expansion is shown in (12).
where
R1 denotes the remainder of Taylor first-order expansion. The Taylor-expansion-based filter sorting criterion in (13) can be obtained by substituting (12) into (11) and ignoring the remainder.
This criterion tends to prune feature maps that have an almost flat gradient of the cost function.
Given the filter pruning rate and the Taylor-expansion-based sorting criterion considered, the network pruning process is summarized as follows:
Obtain the number of filters to be pruned in the current layer by multiplying the number of filters in the current layer and the pruning rate.
Sort filters according to the Taylor-expansion-based criterion.
Prune less important filters as determined by steps 1 and 2.
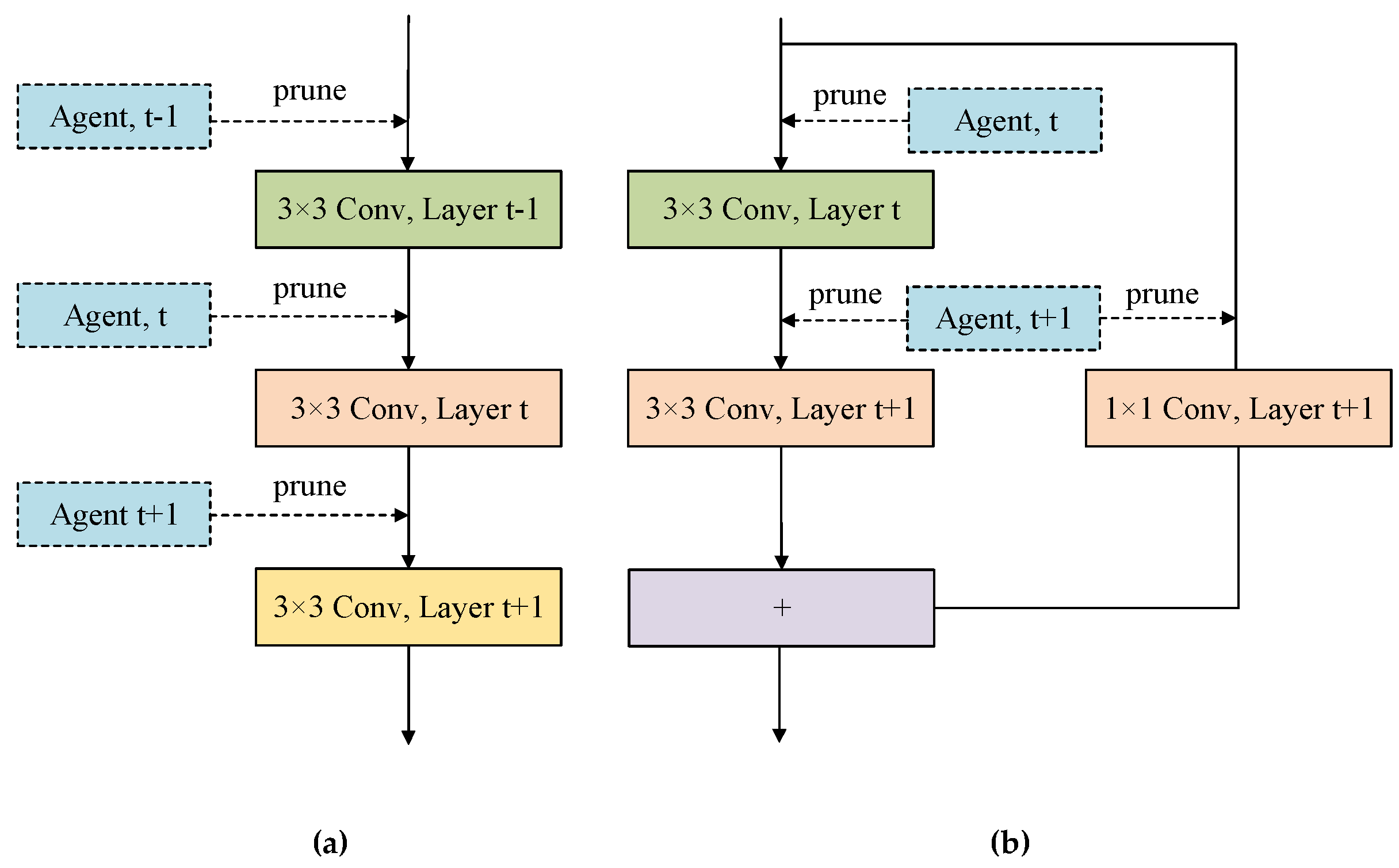
The network connectivity should be ensured with network pruning. Examples of filter pruning on VGGNet and ResNet are shown in
Figure 2.
3.4. The FPRL Algorithm
The framework of the proposed FPRL method is shown in
Figure 1, while the implementation of the filter-level DCNN pruning method is summarized in Algorithm 1, which is composed of two stages: (1) The training of DDPG to offer an optimized layer-wise filter pruning rate and (2) the pruning of a DCNN given the layer-wise filter pruning rate and network retraining for accuracy reconstruction. The main steps in Algorithm 1 are further explained as follows:
Observe the network state. This step obtains the characteristics of the current network layer, the compression rate, and the accuracy of the network as the state information of DDPG.
Network pruning. This step prunes less important filters given the filter pruning rate.
Fine-tuning. The pruned network is fine-tuned for several epochs to restore accuracy.
DDPG update. Use the rewards to update the actor and critic networks in DDPG.
| Algorithm 1. The FPRL method |
| 1: | Stage 1: Train DDPG agent |
| 2: | Initialize DDPG model |
| 3: | episodes 0 |
| 4: | Whileepisodesmax_episodesdo |
| 5: | network load original network |
| 6: | For each layer t in the network do |
| 7: | Observe network state ; |
| 8: | Select action according to the current policy in DDPG; |
| 9: | Determine the number of filters to be pruned given ; |
| 10: | Sort the filters of layer t based on Taylor expansion; |
| 11: | Prune the less important filters of layer t; |
| 12: | Fine-tune network; |
| 13: | Calculate reward and new state ; |
| 14: | Update actor network and critic network in DDPG; |
| 15: | episodes episodes + 1 |
| 16: | Stage 2: Prune and retrain network |
| 17: | network load original network |
| 18: | Prune network using the optimized pruning rate from well-trained DDPG based on Taylor expansion |
| 19: | Retrain pruned network |
4. Experiments and Analysis
To illustrate the efficiency of the proposed method, extensive experiments on state-of-the-art DCNNs and different datasets are conducted against benchmark methods.
4.1. Datasets and DCNNs
The proposed method is evaluated on widely used datasets, i.e., CIFAR10 and CIFAR100 [
33]. Specifically, the CIFAR10 dataset consists of 60,000 images with dimensions of 32 × 32 for the classification of 10 classes of natural objects. In addition, there are 50,000 images and 10,000 images in the training set and the testing set, respectively. The CIFAR100 dataset consists of the same number of images as CIFAR10 but has 100 class labels.
State-of-the-art DCNNs including VGG-16, VGG-19, ResNet-18, and ResNet-34 are considered [
34,
35]. VGG-16 is a 16-layer single-path convolutional neural network with 13 convolutional layers, while VGG-19 is a 19-layer single-path convolutional neural network with 16 convolutional layers. ResNet-18 is a residual network composed of a series of residual blocks with 17 convolutional layers, while ResNet-34 has 33 convolutional layers.
4.2. Experiment Setting
4.2.1. Hyperparameters Setting for VGGNet/ResNet
In order to train the initial VGGNet and ResNet for pruning, the random gradient descent optimizer with a batch size of 512, a momentum of 0.9, and a weight attenuation of 5 × 10
−4 is used. The learning rate is initialized to 0.1 and will be reduced by half every 25 epochs. The performance of VGGNet and ResNet on different datasets are shown in
Table 1, including the number of parameters (Params), FLOPs, and accuracy (Acc.).
4.2.2. Hyperparameters Setting for DDPG
The setting of DDPG is described below. There are two hidden layers in the actor net with 300 neurons in each layer. For the critic net, there are 200 neurons and 150 neurons for the two hidden layers. The learning rates of the actor net and the critic net are set to 0.002 and 0.01, respectively. These nets are trained for 200 epochs with a discount factor of 0.95. The initialized Gaussian noise is 0.5, and the noise’s decay factor is 0.96. The replay buffer’s capacity is set to 2000, and the size of mini-batch is set to 128.
4.2.3. Network Fine-Tuning
A compact network with lower accuracy is obtained after network pruning. Then the pruned network is fine-tuned for three epochs with a learning rate of 0.001.
4.3. Pruning Performance Analysis on Taylor-Expansion-Based Filter Sorting Criterion
To illustrate the pruning performance of the proposed FPRL method by adopting the Taylor-expansion-based filtering sorting criterion, a comparison study against the minimum-weight-based filter sorting criterion is conducted and the results are provided in
Table 2. The metrics on network accuracy and complexity including the top-1 accuracy (Acc), the change in accuracy before and after pruning (
), the compression rate of network parameters (Params.(×)), and the compression rate of FLOPs (FLOPs.(×)) are considered.
From
Table 2, it is observable that (1) generally, the FPRL achieves over 10× the parameter compression and over 3× the Flops reduction with small decreases in accuracy with both filter-sorting criteria on both datasets for all the networks. (2) Compared to CIFAR10, the classification task on CIFAR100 is more difficult and the decrease in accuracy is higher with both sorting criteria. (3) VGG-19 and ResNet-34 illustrate higher pruning rates than VGG-16 and ResNet-18, respectively. This demonstrates that the structures of VGG-19 and ResNet-34 are more redundant than that of VGG-16 and ResNet-18, respectively. (4) The Taylor-expansion-based filter sorting criterion improves the pruning performance in both network compression and accuracy. For the considered DCNNS, the Taylor-expansion-based pruning method generally achieves a higher compression rate in both Params.(×) and FLOPs.(×), but a smaller decrease in accuracy on both datasets.
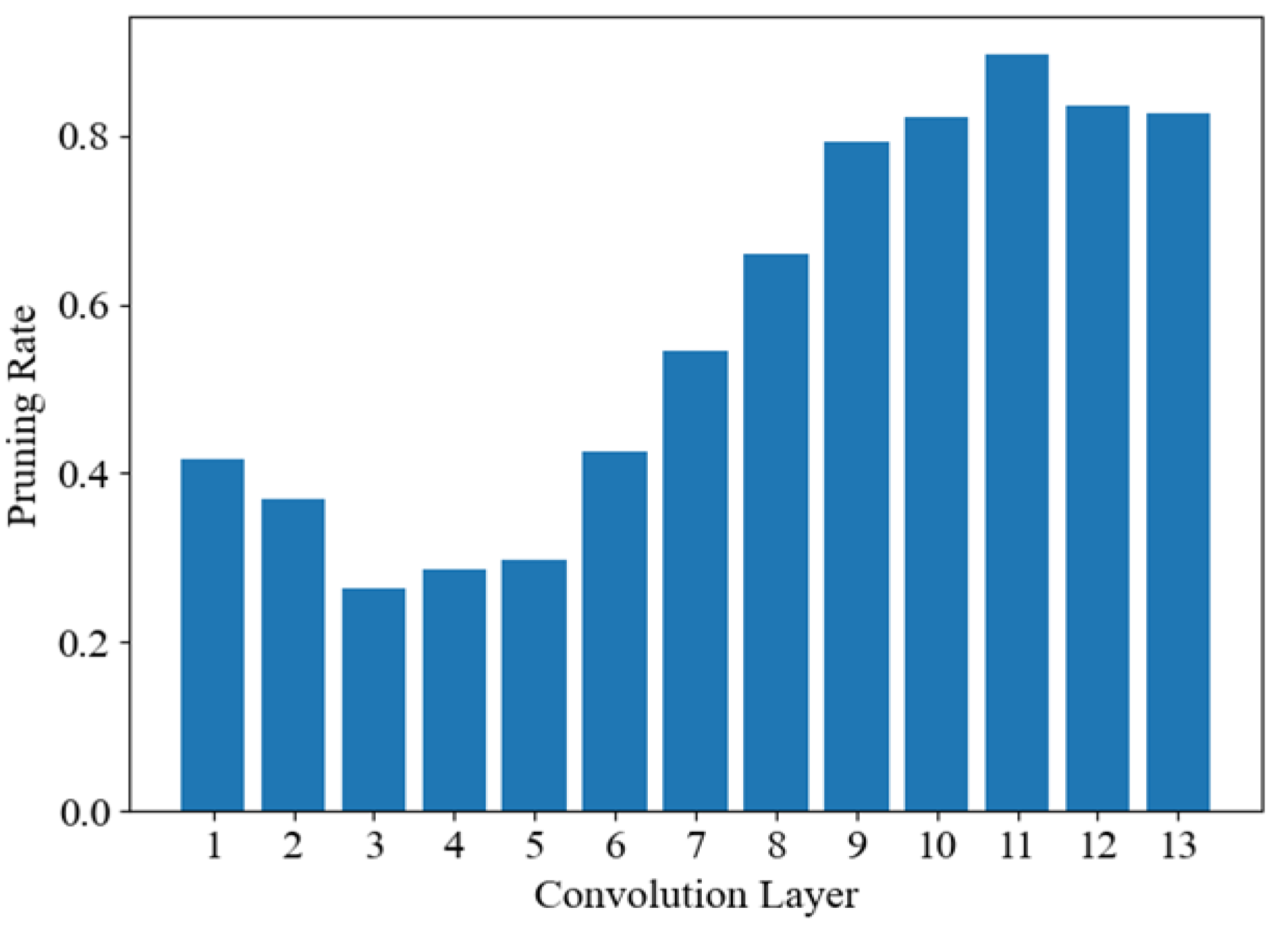
To further investigate how the proposed FPRL method works, the pruning rates for each layer are considered.
Figure 3 illustrates an example of the optimal layer-wise filter pruning rates for VGG-16 offered by the DDPG algorithm on the CIFAR10 dataset. It is observable that the third, fourth, and fifth convolution layers are more important, and the pruning rates are low. Pruning these layers will greatly affect the performance of the model. If filters are pruned too much in these layers, the accuracy of the model cannot be recovered even with fine-tuning or retraining. The redundancy of the 10th, 11th, 12th, and 13th convolution layers is serious as their pruning rates are more than 80%. This shows that the network does not learn much in deeper layers and these layers do not store much useful information. These layers can be greatly pruned without a significant impact on the model performance.
4.4. Pruning Performance Comparison
In order to further verify the efficiency of the FPRL method, the compression performance of the N2N [
36] method is used for comparative analysis. The results are shown in
Table 3.
From
Table 3, the proposed FPRL method achieves a much higher compression rate while reserving higher network accuracy after pruning than N2N on both datasets and all the networks. Taking the ResNet-18 network as an example, on the CIFAR100 dataset, N2N achieves 4.64× parameter compression and the accuracy is reduced by 4.21%, while FPRL achieves 10.93× parameter compression, and the network accuracy after pruning is only reduced by 2.04%. There are cases where the decrease in accuracy by the proposed FPRL method is greater than N2N. For example, on the CIFAR10 dataset, N2N achieves 11.10× parameter compression for the ResNet-18 network and the accuracy is increased by 0.18%. This is due to the fact that the base networks by N2N are under-fitted, resulting in very low initial accuracy. The comparison results highly support that the proposed FPRL method can efficiently compress DCNNs with only a small decrease in network accuracy.
5. Conclusions
In this paper, we propose an automatic filter-level DCNN pruning method FPRL based on the DDPG algorithm. FPRL can achieve over 10× parameter compression and 3× floating point operations (FLOPs) reduction while maintaining similar accuracy to the original network. The accuracy of pruned VGG-19, ResNet-18, and ResNet-34 is greater than 90% on CIFAR10. In the proposed FPRL method, the DDPG algorithm optimizes the layer-wise filter pruning rate, and the Taylor-expansion-based criterion is developed for filter importance sorting. To illustrate the effectiveness of the proposed FPRL method, extensive numerical studies are conducted with state-of-the-art DCNNs on large public datasets. The results demonstrate that the Taylor-expansion-based filter sorting criterion is more efficient than the widely used minimum-weight-based criterion. Moreover, the proposed FPRL method achieves a much higher compression rate while reserving higher network accuracy compared to the DRL-based benchmark method.
Author Contributions
Conceptualization and methodology, Y.F. and C.H.; software and writing—original draft preparation, Y.F.; writing—review and editing, L.W., X.L. and Q.L.; funding acquisition, C.H. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant 62002016, in part by the Guangdong Basic and Applied Basic Research Foundation under Grant 2020A1515110431, in part by the Interdisciplinary Research Project for Young Teachers of USTB (Fundamental Research Funds for the Central Universities) under Grant FRF-IDRY-GD21-001, and in part by the Scientific and Technological Innovation Foundation of Foshan under Grant BK20BF010, Grant BK21BF001, and Grant BK22BF009.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Guo, C.; Fan, B.; Zhang, Q.; Xiang, S.; Pan, C. AugFPN: Improving Multi-Scale Feature Learning for Object Detection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 12592–12601. [Google Scholar] [CrossRef]
- Lin, M.; Ji, R.; Zhang, Y.; Zhang, B.; Wu, Y.; Tian, Y. Channel Pruning via Automatic Structure Search. arXiv 2020, arXiv:2001.08565. [Google Scholar] [CrossRef]
- Liu, Z.; Mu, H.; Zhang, X.; Guo, Z.; Yang, X.; Cheng, K.T.; Sun, J. MetaPruning: Meta Learning for Automatic Neural Network Channel Pruning. arXiv 2019, arXiv:1903.10258. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep Reinforcement Learning: An Overview. In Proceedings of the SAI Intelligent Systems Conference (IntelliSys) 2016, London, UK, 21–22 September 2016; Bi, Y., Kapoor, S., Bhatia, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 16, pp. 426–440. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. Comput. Sci. 2015, 14, 38–39. [Google Scholar] [CrossRef]
- Son, S.; Nah, S.; Lee, K.M. Clustering Convolutional Kernels to Compress Deep Neural Networks. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11212, pp. 225–240. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, J.; He, K.; Sun, J. Accelerating Very Deep Convolutional Networks for Classification and Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1943–1955. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; IEEE: Boston, MA, USA, 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Wang, J.; Yu, S.; Yuan, Z.; Yue, J.; Yuan, Z.; Liu, R.; Wang, Y.; Yang, H.; Li, X.; Liu, Y. PACA: A Pattern Pruning Algorithm and Channel-Fused High PE Utilization Accelerator for CNNs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 5043–5056. [Google Scholar] [CrossRef]
- Wu, C.; Cui, Y.; Ji, C.; Kuo, T.-W.; Xue, C.J. Pruning Deep Reinforcement Learning for Dual User Experience and Storage Lifetime Improvement on Mobile Devices. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 3993–4005. [Google Scholar] [CrossRef]
- Huang, K.; Li, B.; Chen, S.; Claesen, L.; Xi, W.; Chen, J.; Jiang, X.; Liu, Z.; Xiong, D.; Yan, X. Structured Term Pruning for Computational Efficient Neural Networks Inference. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2016, arXiv:1510.00149. [Google Scholar] [CrossRef]
- Yang, T.-J.; Chen, Y.-H.; Sze, V. Designing Energy-Efficient Convolutional Neural Networks Using Energy-Aware Pruning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 6071–6079. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. arXiv 2017, arXiv:1608.08710. [Google Scholar] [CrossRef]
- He, Y.; Kang, G.; Dong, X.; Fu, Y.; Yang, Y. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks. arXiv 2018, arXiv:1808.06866. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks through Network Slimming. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Venice, Italy, 2017; pp. 2755–2763. [Google Scholar] [CrossRef]
- Huang, K.; Chen, S.; Li, B.; Claesen, L.; Yao, H.; Chen, J.; Jiang, X.; Liu, Z.; Xiong, D. Acceleration-Aware Fine-Grained Channel Pruning for Deep Neural Networks via Residual Gating. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 1902–1915. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, S.; Li, J.; Wang, X.; Gu, Q. A novel channel pruning method for deep neural network compression. arXiv 2018, arXiv:1805.11394. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Venice, Italy, 2017; pp. 1398–1406. [Google Scholar] [CrossRef]
- Li, J.; Louri, A. AdaPrune: An Accelerator-Aware Pruning Technique for Sustainable CNN Accelerators. IEEE Trans. Sustain. Comput. 2022, 7, 47–60. [Google Scholar] [CrossRef]
- Zoph, B.; Le, Q.V. Neural Architecture Search with Reinforcement Learning. arXiv 2017, arXiv:1611.01578. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. Evolving Unsupervised Deep Neural Networks for Learning Meaningful Representations. IEEE Trans. Evol. Computat. 2019, 23, 89–103. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Completely Automated CNN Architecture Design Based on Blocks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1242–1254. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving Deep Convolutional Neural Networks for Image Classification. IEEE Trans. Evol. Comput. 2020, 24, 394–407. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing Neural Network Architectures using Reinforcement Learning. arXiv 2017, arXiv:1611.02167. [Google Scholar] [CrossRef]
- He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.-J.; Han, S. AMC: AutoML for Model Compression and Acceleration on Mobile Devices. In Proceedings of the IEEE European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 784–800. [Google Scholar] [CrossRef]
- Hu, H.; Peng, R.; Tai, Y.-W.; Tang, C.-K. Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar] [CrossRef]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Inference. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017; pp. 1–17. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on International Conference on Machine Learning (PMLR), Beijing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ashok, A.; Rhinehart, N.; Beainy, F.; Kitani, K.M. N2N Learning: Network to Network Compression via Policy Gradient Reinforcement Learning. arXiv 2017, arXiv:1709.06030. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).