Abstract
To reveal the relationship between the center of mass (CoM) trajectory of a closed five-bow-shaped-bar linkage and its energy consumption, this paper presents a trajectory planning method based on the workspace of the CoM. Using different height points located on the symmetric centerline of the workspace of the CoM as via points, the CoM trajectory is planned by combining cubic polynomials with Bézier curves based on quadratic Bernstein polynomials. Herein, the system energy consumption is obtained by integrating the product of generalized velocity and generalized force versus time, where the generalized force is calculated by Lagrange’s equation including the Rayleigh dissipation function. Then, two schemes of dynamic rolling are proposed to compare, and the theoretical results show that the system consumes less energy under the sinusoid scheme when the via point height is lower and the via point of higher height is more suitable under the modified trapezoidal curve scheme. Furthermore, this paper combines the locomotion simulation software to design the locomotion of the mechanism’s CoM trajectory under two schemes in detail and verifies the correctness of the theoretical results.
1. Introduction
Mobile mechanisms have a variety of locomotion modes, commonly including walking, rolling, and crawling [1,2,3,4]. In the rolling mode, a class of mobile mechanisms, called structural morphing mechanisms, rolls forward by changing their shapes [5,6,7]. The closed five-bow-shaped-bar linkage is a structural morphing mechanism. The rolling locomotion of the mechanism is generated by making a certain offset of its CoM in the horizontal direction with respect to the contact point between the bow-shaped module and the ground. This mechanism was first investigated by our project team, and its favorable characteristics were demonstrated in speed, compliance, and continuity [8,9]. Then, the mechanism’s climbing capacity and the minimum coefficient of friction were analyzed [10]. Previous studies have mainly focused on the kinematic performance of the mechanism, neglecting the study of energy consumption. However, energy consumption is an essential research direction that can significantly reduce the operating costs of mechanisms. For the mechanism, the location of its CoM is closely related to energy consumption. Therefore, it is necessary to determine the relationship between the energy consumption of the mechanism and CoM trajectories, which can be used as a reference for locomotion planning.
Locomotion planning is an essential branch of mechanism research that studies how a mechanism moves from the initial position to the target position with less energy consumption [11]. Many studies have been carried out to improve and optimize the trajectory of mechanisms. A trajectory plan was generated by [12] based on a smooth point-to-point method to obtain continuous displacement, velocity, acceleration, and jerk of each joint and end-effector. An algorithm was established by [13], as well, based on cubic smoothing B-spline curves to represent the final trajectories that are collision-free. Zhou et al. [14] proposed an improved lazy Probabilistic Roadmap algorithm based on the online collision-free path planning method. Rybus et al. [15] raised a new method for the path planning of the robotic arm mounted on a free-floating unmanned spacecraft. Shi et al. [16] constructed an adaptive model predictive control trajectory tracking system that considers disturbances in the path curvature. Some studies used machine learning models [17,18] to optimize the trajectories of mechanisms. Chen et al. [19] presented a biological-inspired reinforcement learning control method to help the robot learn adaptive swimming actions. Yin et al. [20] proposed a machine learning-based energy efficient trajectory planning method for industrial robots. Ji et al. [21] obtained the optimal gait of a quadruped robot by using deep reinforcement learning. Furthermore, some studies have focused on reducing energy consumption by optimizing trajectories. The objective function was assumed to minimize the total consumed energy to find an optimum trajectory planning of the positioning manipulator [22]. A control architecture was developed to coordinate energy management with trajectory tracking control for hybrid UAVs [23]. Guo et al. [24] raised an efficient co-optimization strategy of unmanned hybrid electric tracked vehicles to achieve accurate path tracking and optimal energy management simultaneously. Jin and Huang [25] presented a new trajectory optimization scheme adopting dynamic programming, which combined the joint energy consumption with a particle swarm optimization algorithm. Some researchers have paid particular attention to the problem of mechanism workspace and its trajectory planning. The end-effector motion trajectory was planned based on the workspace of the weeding mechanism [26]. Li et al. [27] studied the reachable workspace of the robot body with shank-ground interferences, which helped to enhance the efficiency of foothold selection. Schreiber and Gosselin [28] proposed an analytic workspace determination method, and a simple algorithm for their trajectory planning was provided for prescribed Cartesian trajectories. Gosselin and Dion-Gauvin [29] presented a general framework for planning point-to-point motions that extended beyond the static workspace of six-degree-of-freedom cable-suspended parallel mechanisms.
Furthermore, Bézier curves are widely used in machine tool machining [30,31,32], CAD/CAM design [33,34], and trajectory optimization and prediction for mobile robots [35]. A path-smoothing technique was proposed using Bézier curves to ensure smoothness and continuity of spiking points [36]. A new strategy was developed to plan the smooth path for mobile robots through an improved PSO algorithm in combination with the continuous high-degree Bezier curve [37]. A novel path and velocity planning method for lane changing collision avoidance of intelligent vehicle based on cubic 3D Bezier curve was proposed to guarantee the flexibility of the path [38]. Xu et al. [39] proposed a new approach for the smooth path planning of mobile robots based on a new quartic Bezier transition curve and an improved particle swarm optimization algorithm. Dinçer and Çevik [40] presented a composite polynomial consisting of cubic polynomials and Bézier curves to obtain a smooth trajectory in the vicinity of the starting and ending points.
Inspired by the insights above, this study proposes a trajectory planning method based on the workspace of the CoM. Specifically, using different height points located on the symmetric centerline of the workspace of the CoM as via points, the CoM trajectory is planned by high-order differentiable composite polynomial functions. In addition, Lagrange’s equation, including the Rayleigh dissipation function, is established to consider the viscous friction in the joint. Then, the relationship between energy consumption and the height of the via point is identified, which provides a reference for reducing energy consumption during locomotion.
The structure and content of this paper are organized as follows. The mechanical structure, the kinematic model, and the CoM trajectories planning are elaborated in Section 2. The dynamics and energy consumption models under different CoM trajectories are described in Section 3. The analysis results of the kinematics simulation of the mechanism based on ADAMS are given to verify the correctness of the theoretical calculation results in Section 4. Finally, the conclusion and future work are discussed in Section 5.
2. Trajectory Planning of the Mechanism’s CoM
The trajectory of the mechanism’s CoM is planned under the condition that its workspace of the CoM is obtained. In this section, the mechanical structure and kinematics model are first analyzed to determine the workspace of the CoM, and then the CoM trajectory is planned by combining cubic polynomials with Bézier curves based on quadratic Bernstein polynomials.
2.1. Mechanical Structure of the Rolling Mechanism
As shown in Figure 1, the rolling mechanism is composed of five identical bow-shaped modules connected by revolute joints to form a closed chain linkage. The usage of the bow-shaped module can not only ensure the continuity of the rolling locomotion, but also prevent the mechanism from being subjected to impact force from the ground. The bow-shaped module mainly consists of left and right bow-shaped plates, support attachments, motors, transmission devices, and others. By introducing a counterweight, the CoM of each module can be located at the midpoint of the line that connects adjacent joints [8]. Additionally, the rolling locomotion is then generated by controlling the trajectory of the mechanism’s CoM to offset the grounded point in the horizontal direction.
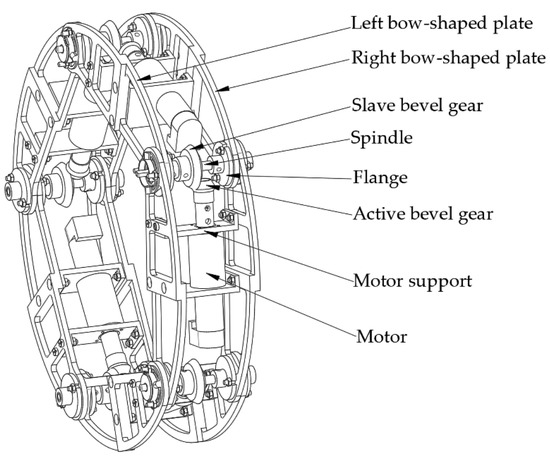
Figure 1.
Mechanical structure of the rolling mechanism.
2.2. Kinematics Model
According to the mechanical structure, the kinematics analytical model is established in Figure 2, in which coordinates and DH parameters [41] are also labeled. As shown in Figure 2, the contact point between the bow-shaped module and the ground is marked as P, while the joints used to connect adjacent modules are successively defined as A, B, C, D, and E. XOY represents the global coordinate system with the initial grounded point O that is consistent with joint A, while the X-axis is parallel to the ground and the Y-axis is perpendicular to the ground. The point o is located at the center of the curvature circle that is composed of the outer contour of the grounded module. Link coordinate systems are attached at the joints i of each module, and the directions of are consistent with the lines between adjacent joints. Then, the joint angle is defined to describe the rotation of link i with respect to link , and the rolling angle represents the angle between the lines and . Despite a range of [0, ] for the rolling course while different modules contact the ground in succession, we can only discuss the case of for any one is grounded due to the symmetrical configuration of the mechanical structure.
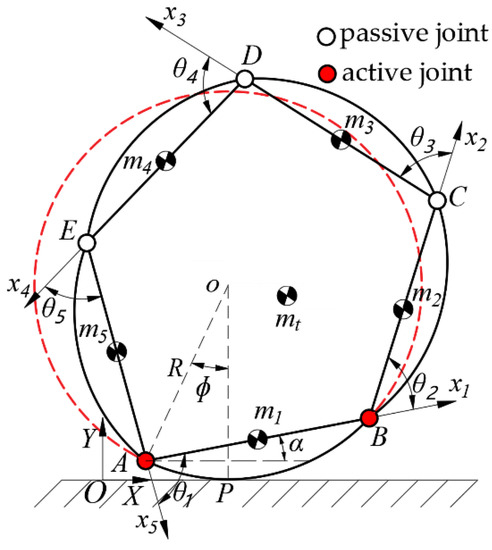
Figure 2.
Kinematics analytical model.
According to the geometrical relationship in Figure 2, the angle between the grounded module and the ground, denoted as , can be expressed as
The coordinates of joint A with respect to XOY can be denoted as
where R is the radius of the curvature circle that is composed of the outer contour of the grounded module, and and represent the coordinates of joint A in frame XOY. Additionally, then, based on [9], the homogeneous transformation matrixes of adjacent coordinate systems could be written as
where is the homogeneous transformation matrix of with respect to XOY; is a homogeneous transformation matrix representing the coordinate transformation from to ; represents the chord length of the bow-shaped module, and .
The coordinate of the CoM for module i with respect to XOY can be expressed as
where and denote the first and second components of the coordinate. Subsequently, the coordinate of the CoM for the whole rolling mechanism can be defined by [9].
where denotes the mass of module i, and . By substituting Equations (1)–(4) into Equation (5), the coordinates of the mechanism’s CoM can be described in another form as
During the rolling process, there is a singular configuration when the five chords of modules form a concave pentagon, which could cause a serious impact on the joint activities. Therefore, the mechanism should maintain a convex pentagon to avoid the generation of singular configurations. For this purpose, Wang et al. [8] proposed one point contact constraint model to limit the dynamic rolling locomotion and acquired the ranges of the joint angles by numerical method. However, the numerical method is not suitable for kinematics analysis. In order to obtain analytical formulas of the range of active joint angles, we establish geometrical models to discuss the two situations for and , i.e., and . The analytical models of the two situations are, respectively illustrated in Figure 3 and Figure 4.
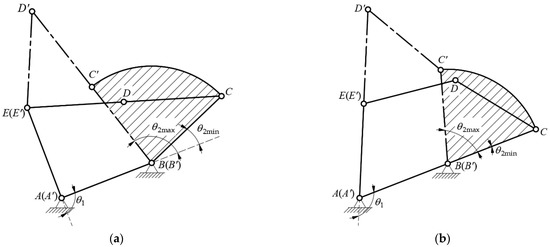
Figure 3.
Active joint angle analysis of rolling angle . (a) . (b) .
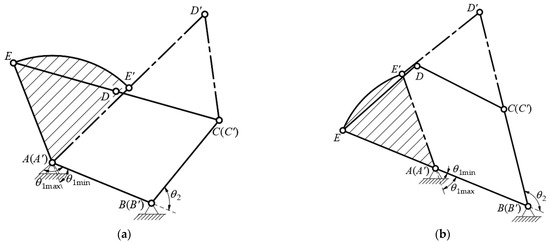
Figure 4.
Active joint angle analysis of rolling angle . (a) . (b) .
- (1)
- .
Under this situation of , the range of is from to , while is divided into two segments for discussion as in Figure 3a,b. According to the range of in Figure 3a,b, the corresponding can be obtained as Equations (7) and (8).
- (2)
- .
2.3. Trajectory Planning of the CoM
The shape of the mechanism is determined by its location of the CoM, while the component of the CoM in the vertical direction affects potential energy. The speed and acceleration are controlled by the offset of the mechanism’s CoM with respect to the grounded point in the horizontal direction. Because the position of the mechanism’s CoM is closely related to energy consumption, it is necessary to choose an appropriate CoM trajectory to reduce the energy consumption of the mechanism. Whereupon, the previous work of the trajectory planning is to acquire the workspace of the CoM.
In Section 2.2, the relationship between the active joint angles and the rolling angle was analyzed. The workspace of the CoM when (, k = 0, 1, 2 … 73) can be figured out by Equations (1)–(6). Then, the workspace of the CoM when is illustrated in Figure 5. As shown in Figure 5, the feasible region is encompassed by a red boundary which is formed by connecting outer boundary points.
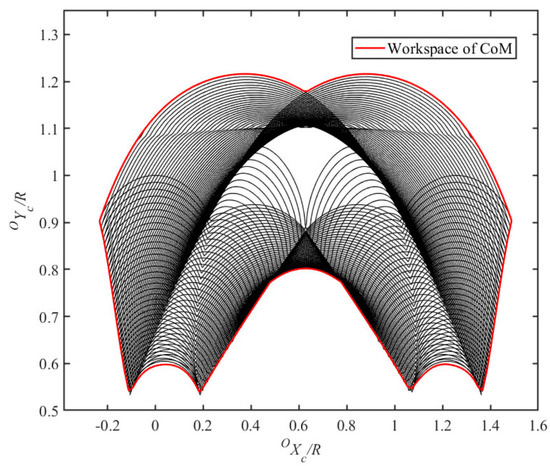
Figure 5.
The workspace of the CoM when the rolling angle is in the range of 0 to
.
The workspaces of the CoM of the rolling mechanism at the initial and end positions, i.e., and , are, respectively shown in Figure 6a,b. To ensure the continuity of the rolling locomotion during the alternation of grounded modules, the outer profile curve of the adjacent modules should be continuous. It means that the angle between two successive grounded modules should remain . Correspondingly, the mechanism’s CoM must be located on the red line in Figure 6.
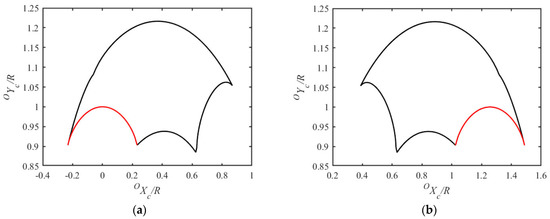
Figure 6.
The workspace of the mechanism’s CoM at the initial and end positions. (a) . (b) .
In order to avoid spontaneous rolling, the CoM of the mechanism and the grounded point P should be in the same vertical line at the initial position, while they also should be in the same vertical line to achieve periodic locomotion at the end position. Therefore, the coordinates of the CoM at the initial and end positions can be written as
It can be seen that both the workspace for and the workspace for and are symmetrical about in Figure 5 and Figure 6. Thus, points on the symmetry centerline of its workspace of the CoM are used as via points to plan CoM trajectories. The start point, via points, and end point are shown in Figure 7, where height of the via point, denoted as , ranges from 0.801R to 1.183R. The routes of the CoM are start-via-end (1-2-3), and the values of each variable are presented in Table 1.
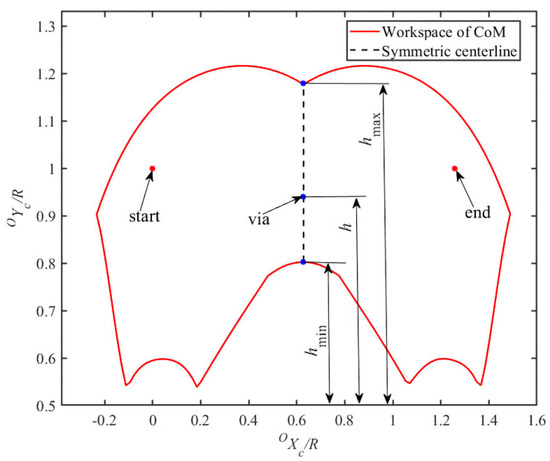
Figure 7.
Distribution of the initial point, via points, and end point for CoM trajectory planning.

Table 1.
The position defined for the trajectory planning.
Dinçer and Çevik [40] proposed a composite polynomial consisting of Bézier curves and cubic polynomials, exhibiting smoother position, velocity, and acceleration curves than the cubic spline method. In this paper, the quadratic Bézier curve is combined with a cubic polynomial to plan the trajectory of the CoM under the condition that the start, via, and end points have been determined. The direction and shape of the trajectory are specified by the via point, whether the via point is on this curve or not. The i-th Bernstein polynomials of degree m are defined by [42].
where is a binomial coefficient. When , the Bernstein polynomials can be expressed as
Using the Bernstein polynomials with a degree of 2 as a basis function, a Bézier curve of Bernstein polynomials can be defined as
The cubic polynomial [40] is constructed as
is the coordinate of i-th point that can be denoted as . Let the composite polynomial can be obtained as
where is the coordinate of the planned CoM trajectory, and are the X-axis coordinate and Y-axis coordinate of the planned CoM trajectory, respectively.
According to the composite polynomial Equation (16), the upper and lower limits of the CoM trajectories are obtained and illustrated in Figure 8.
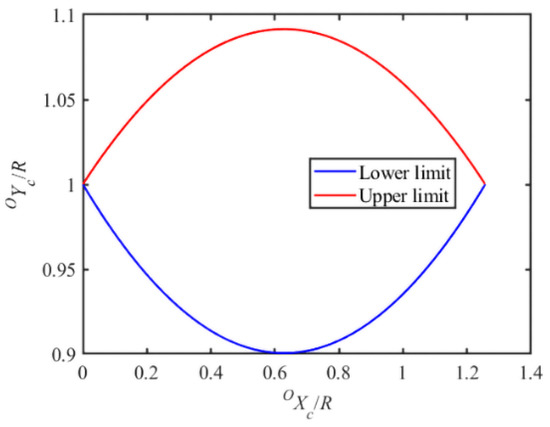
Figure 8.
The upper and lower limits of the CoM trajectories.
3. Dynamics and Energy Consumption Analysis
3.1. Dynamics Model
Wang et al. [9] analyzed the dynamics of the closed five-bow-shaped-bar linkage using Lagrange’s equation ignoring joint friction. However, during the rolling process, the revolute joints are affected by viscous damping, generating joint friction torque, which hinders the mechanism from rolling. Therefore, the influence of joint friction must be taken into account in the dynamics. Ostrowski [43] presented a method for modeling damping forces using Rayleigh’s dissipation function. Taking the viscous friction into consideration, the Rayleigh’s dissipation function [43] is defined as
where is the coefficient of viscous friction damping in the joint i.
The mechanism dynamics is modeled by the Lagrange’s equation including the dissipative function [43] as
where and represent the generalized coordinates and generalized velocity, respectively; represents the generalized force; represents the Lagrange capability.
To define the ground as the zero plane of potential energy, the mechanism’s potential energy can be expressed as
where g is the gravitational acceleration.
As a typical multi-rigid-body system, the mechanism’s kinetic energy consists of the kinetic energy of each component module. Thus, the mechanism’s kinetic energy can be denoted as
where is the angular velocity for the CoM of the bow-shaped module i; is the rotational inertia of the bow-shaped module i about its CoM; and are the first and second elements of the CoM coordinates of each module with respect to the global coordinate system.
Additionally, then, the Lagrange capability could be computed out by . Based on Equation (1), the angular velocity for the CoM of the I module can be given as
Substituting Equation (17) and Equations (19)–(21) into Equation (18), the Lagrange’s equation could be written as
where is the inertia matrix; is the moment matrix generated by the influence of Coriolis force and centripetal force terms; is the moment matrix generated by the influence of gravity; is the damping coefficient matrix; is the generalized force, and due to the passive degree of freedom of the rolling angle .
3.2. System Rolling Angle Acceleration Planning
In this paper, the locomotion of the mechanism is equivalent to pure rolling, i.e., there is no relative slipping between the mechanism and the ground, as shown in Figure 9. The grounded point P is the instantaneous center of velocity. The locomotion can be considered as rotation around the instantaneous axis that passes through point P and is perpendicular to the plane of locomotion. The rotational inertia of the mechanism [9] about the instantaneous axis can be denoted as
where denotes the rotational inertia of the bow-shaped module i about its CoM, and denotes the distance from the CoM of the bow-shaped module i to the grounded point P.
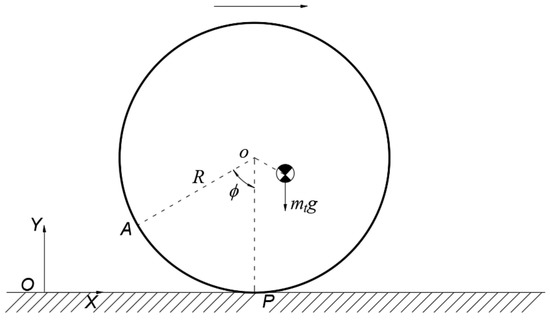
Figure 9.
Equivalent rolling motion.
During rolling locomotion, neglecting rolling resistances and considering the effect of the mechanism’s CoM, the relationship between gravity and acceleration [9] is written as
According to the research of Wang et al. [8], four types of curves were proposed as dynamic rolling schemes, and the simulation results showed that sinusoid and modified trapezoidal curves were more appropriate for the dynamic rolling of the mechanism. Therefore, the sinusoid and modified trapezoidal curves are used as the dynamic rolling schemes in this paper. To compare and analyze these two schemes, the time spending of the accelerating phase is , and the angular velocity and angular displacement are equal when at the final moment. Since the rolling angle is in the range of 0 to 2/5, the total angular displacement is . Furthermore, by setting the angular acceleration to be equal to zero that at both the initial and final moments, the dynamic rolling schemes [8] are shown as below.
Case (1): sinusoid acceleration
Case (2): modified trapezoidal curve acceleration
Using the rolling angular acceleration expressed by Equations (25) and (26), the velocity and displacement of the rolling angle can be obtained by the integral method. On this basis, the curves of the angular acceleration along with the time t and the curves of the angular velocity along with the time t are shown in Figure 10, which can meet the requirements of angular velocity and angular displacement above.
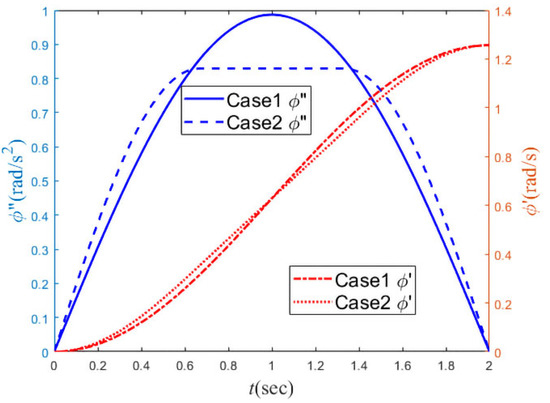
Figure 10.
The dynamic rolling schemes.
3.3. Energy Consumption Analysis
When the mechanism rolls in conformance with the CoM trajectory planned in Section 2.3, by substituting Equation (24), the rolling equation can be given as
where and are the X-axis coordinates and Y-axis coordinates of the planned CoM trajectory, respectively.
The active joints and can be calculated by substituting the acceleration and displacement of the rolling angle into Equation (27). Then, the energy consumption of the mechanism locomotion can be written as
where is the time spending of the accelerating phase, and and denote the instantaneous power of the active joints, respectively.
To set the parameters as R = 0.15 m, = 1.0 kg, g , , , . Combined with the above analysis, the relationship between the energy consumption and the height h of the via point can be obtained. As shown in Figure 11a, the lowest energy consumption of case 1 is when the height of the via point is 0.972R, and is the lowest energy consumption of case 2 when the height of the via point is 0.979R. Furthermore, the energy consumption decreases and then increases with the height h of the via point increasing in case 1 and case 2. Figure 11b shows that the energy consumption of case 1 is lower when the height h of the via points is less than 0.967R. On the contrary, in case 2, the energy is consumed less when h is higher than 0.967R.
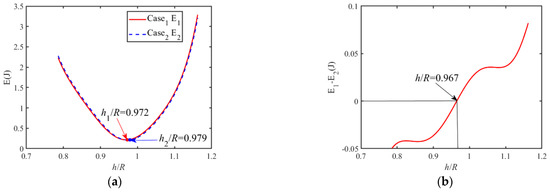
Figure 11.
The variation of energy consumption with the height h of via points. (a) Energy consumption under case 1 and case 2. (b) Energy Consumption Difference under Case 1 and Case 2.
4. Virtual Prototype Simulation
To verify the theoretical analysis above, the virtual prototype simulation was conducted, and the 3D model of the closed five-bow-shaped-bar linkage has been imported to ADAMS, as shown in Figure 12. There is a 0.70 N/(m/s) bushing force constraint at each joint, while contact forces are set between the bow-shaped module and the ground.
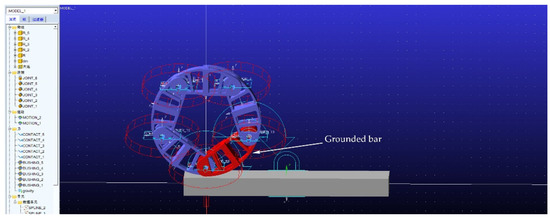
Figure 12.
Simulation of ADAMS.
In the virtual prototype simulation, three points with different heights h of 0.120 m, 0.145 m, and 0.177 m are studied, which are the lower limit point, lower energy consumption point, and upper limit point, respectively. Using the three points as the via points to plan the CoM trajectories, the corresponding angular displacements of the active joints are calculated by Equation (27), and shown in Figure 13. The theoretical values of angular displacements of the active joints are fitted by the CUBSPL function to drive the active joints. Additionally, then, the simulation data of the CoM trajectories and rolling angle paths are obtained under case 1 and case 2. Figure 14 shows the rolling angle paths when choosing the via points with different heights under case 1 and case 2. Figure 15, Figure 16 and Figure 17 show the theoretical and simulated trajectories of the CoM for h = 0.177 m, h = 0.145 m, and h = 0.120 m, respectively.
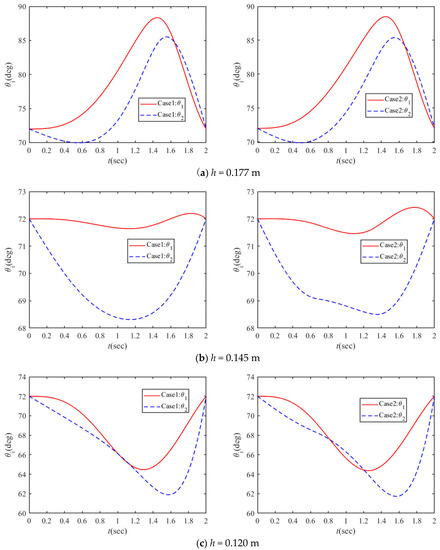
Figure 13.
The angular displacement of the active joint when choosing the via points with different heights h.
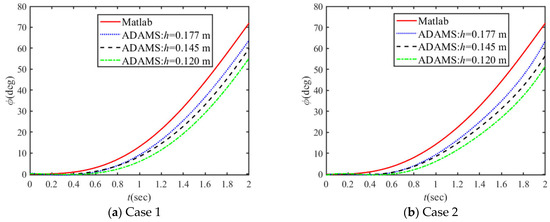
Figure 14.
Theoretical and simulated results of rolling angular displacement.
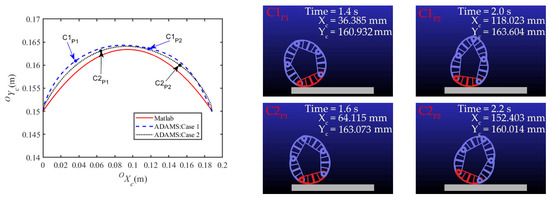
Figure 15.
Theoretical and simulated trajectories of the CoM at h = 0.177 m.
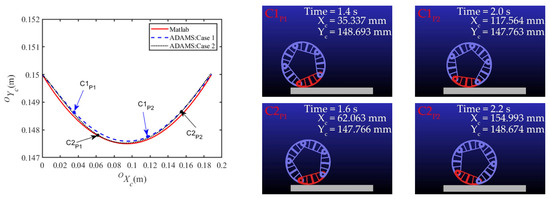
Figure 16.
Theoretical and simulated trajectories of the CoM at h = 0.145 m.
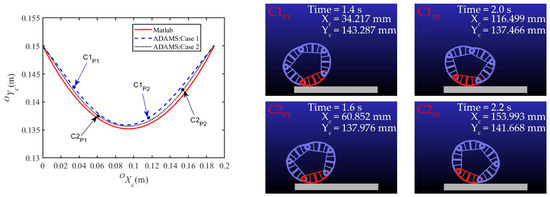
Figure 17.
Theoretical and simulated trajectories of the CoM at h = 0.120 m.
As shown in Figure 14, the theoretical and simulated results of the rolling angle displacement have the same increasing tendency with the time increasing. However, there is a slight time lag between the theoretical and simulated results due to neglect of the rolling resistance of the ground in theoretical calculation. Because of overcoming the rolling resistance at the beginning of dynamic rolling, the mechanism must change its shape to create a certain offset of the CoM. As illustrated in Figure 15, Figure 16 and Figure 17, although the simulation results of the CoM trajectory have some deviations from the theoretical calculations, the tendency is consistent. The reason is that the simulation model is not accurate enough, which affects the results. In Figure 15, the simulated CoM trajectory of case 2 is lower compared to case 1, and the simulated CoM trajectory of case 1 is higher compared than case 2 in Figure 16 and Figure 17, consistent with the theoretical results. In summary, the correctness of the relationship between energy consumption and height h of the via point is verified.
5. Conclusions
The workspace of the closed five-bow-shaped-bar linkage’s CoM with the rolling angle ranging from 0 to 2/5 was studied. Using different height points on the symmetric centerline of the workspace of the CoM as the via points, the CoM trajectory planning was planned by combining cubic polynomials with Bézier curves based on quadratic Bernstein polynomials. Additionally, then, the energy consumption of the rolling mechanism was investigated by the theoretical calculation through integrating the product of the generalized velocity and the generalized force versus time, where the generalized force was calculated by Lagrange’s equation including the Rayleigh dissipation function. Furthermore, the CoM trajectories and rolling angle paths were investigated by the theoretical calculation and the virtual prototype simulation, respectively. Based on above studies, the significant findings are listed below.
- The workspace of the closed five-bow-shaped-bar linkage’s CoM with the rolling angle ranging from 0 to 2/5 is symmetric about = 0.63R.
- By high-order differentiable composite polynomial functions to plan the CoM trajectory, the mechanism obtains smooth joint trajectories.
- The energy consumption decreases and then increases with the height h of the via point increasing in the schemes of sinusoid acceleration and modified trapezoidal curve acceleration, where the range of h is from 0.801R to 1.183R.
- The energy consumption of the sinusoid acceleration scheme is lowest when the height h of the via point is 0.972R, and the modified trapezoidal curve acceleration scheme is lowest when the height h of the via point is 0.979R.
- The energy consumption of the sinusoid acceleration scheme is lower when the height of the via point is less than 0.967R, and the modified trapezoidal curve acceleration scheme is lower when the height of the via point is higher than 0.967R.
This paper provides a reference for the mechanism to choose an appropriate via point, which can significantly reduce the energy consumption of the mechanism during rolling along a straight line.
Future research must include the energy consumption analysis of irregular terrains and obstacles based on the workspace of the CoM. Furthermore, to enhance the adaptability of the mechanism in complex environments, a scheme of the crawling and rolling integrated mechanism will be developed and applied practically.
Author Contributions
All authors contributed to this work. Conceptualization, Y.Z. and L.Y.; methodology, Y.Z. and L.Y.; software and funding acquisition, X.X. and Y.W.; validation, T.Z. and N.F.; writing—original draft, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the National Natural Science Foundation of China (grant number 52275007), Hubei Provincial Department of Education Science and Technology Research Project (grant number Q20201708), and Chongqing Science and Technology Commission of China (grant number cstc2020jcyj-msxmX0242).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, R.; Yao, Y.; Li, Y. Design and analysis of a deployable tetrahedron-based mobile robot constructed by Sarrus linkages. Mech. Mach. Theory 2020, 152, 103964. [Google Scholar] [CrossRef]
- Guffanti, D.; Brunete, A.; Hernando, M. Development and validation of a ROS-based mobile robotic platform for human gait analysis applications. Robot. Auton. Syst. 2021, 145, 103869. [Google Scholar] [CrossRef]
- Wang, W.; Wang, K.; Zhang, H. Crawling gait realization of the mini-modular climbing caterpillar robot. Prog. Nat. Sci. 2009, 19, 1821–1829. [Google Scholar] [CrossRef]
- Bruzzone, L.; Quaglia, G. Review article: Locomotion systems for ground mobile robots in unstructured environments. Mech. Sci. 2012, 3, 49–62. [Google Scholar] [CrossRef]
- Paskarbeit, J.; Beyer, S.; Engel, M.; Gucze, A.; Schröder, J.; Schneider, A. Ourobot—A sensorized closed-kinematic-chain robot for shape-adaptive rolling in rough terrain. Robot. Auton. Syst. 2021, 140, 103715. [Google Scholar] [CrossRef]
- Wang, J.; Fei, Y.; Liu, Z. Locomotion modeling of a triangular closed-chain soft rolling robot. Mechatronics 2019, 57, 150–163. [Google Scholar] [CrossRef]
- Wei, X.; Tian, Y.; Wen, S. Design and locomotion analysis of a novel modular rolling robot. Mech. Mach. Theory 2019, 133, 23–43. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Yu, L.; Mei, Y. Trajectory planning of a rolling robot of closed five-bow-shaped-bar linkage. Robot. Comput.-Integr. Manuf. 2018, 53, 81–92. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Yu, L.; Mei, Y. Dynamics of a rolling robot of closed five-arc-shaped-bar linkage. Mech. Mach. Theory 2018, 121, 75–91. [Google Scholar] [CrossRef]
- Yu, L.; Mei, Y.; Wang, Y.; Wu, C. Research on Slope Climbing Capacity of a Close Chain Five-Bow-Shaped-Bar Linkage. In Mechanism and Machine Science; Springer: Singapore, 2016; pp. 1365–1376. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Wang, H.; Wang, H.; Huang, J.; Quan, L. Smooth point-to-point trajectory planning for industrial robots with kinematical constraints based on high-order polynomial curve. Mech. Mach. Theory 2019, 139, 284–293. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Zhang, W.; Hao, L. Smooth and collision-free trajectory generation in cluttered environments using cubic B-spline form. Mech. Mach. Theory 2022, 169, 104606. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Xie, Z.; Gu, X. Online obstacle avoidance path planning and application for arc welding robot. Robot. Comput.-Integr. Manuf. 2022, 78, 102413. [Google Scholar] [CrossRef]
- Rybus, T.; Wojtunik, M.; Basmadji, F.L. Optimal collision-free path planning of a free-floating space robot using spline-based trajectories. Acta Astronaut. 2022, 190, 395–408. [Google Scholar] [CrossRef]
- Shi, J.; Sun, D.; Qin, D.; Hu, M.; Kan, Y.; Ma, K.; Chen, R. Planning the trajectory of an autonomous wheel loader and tracking its trajectory via adaptive model predictive control. Robot. Auton. Syst. 2020, 131, 103570. [Google Scholar] [CrossRef]
- Garg, A.; Aggarwal, P.; Aggarwal, Y.; Belarbi, M.O.; Chalak, H.D.; Tounsi, A.; Gulia, R. Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr. 2022, 30, 33–42. [Google Scholar]
- Garg, A.; Belarbi, M.O.; Tounsi, A.; Li, L.; Singh, A.; Mukhopadhyay, T. Predicting elemental stiffness matrix of FG nanoplates using Gaussian Process Regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem. 2022, 143, 779–795. [Google Scholar] [CrossRef]
- Chen, G.; Lu, Y.; Yang, X.; Hu, H. Reinforcement learning control for the swimming motions of a beaver-like, single-legged robot based on biological inspiration. Robot. Auton. Syst. 2022, 154, 104116. [Google Scholar] [CrossRef]
- Yin, S.; Ji, W.; Wang, L. A machine learning based energy efficient trajectory planning approach for industrial robots. Procedia CIRP 2019, 81, 429–434. [Google Scholar] [CrossRef]
- Ji, Q.; Fu, S.; Tan, K.; Muralidharan, S.T.; Lagrelius, K.; Danelia, D.; Andrikopoulos, G.; Wang, X.V.; Wang, L.; Feng, L. Synthesizing the optimal gait of a quadruped robot with soft actuators using deep reinforcement learning. Robot. Comput.-Integr. Manuf. 2022, 78, 102382. [Google Scholar] [CrossRef]
- Mohamed, K.; Elgamal, H.; Elsharkawy, A. Dynamic analysis with optimum trajectory planning of multiple degree-of-freedom surgical micro-robot. Alex. Eng. J. 2018, 57, 4103–4112. [Google Scholar] [CrossRef]
- Liu, H.; Yao, Y.; Wang, J.; Qin, Y.; Li, T. A control architecture to coordinate energy management with trajectory tracking control for fuel cell/battery hybrid unmanned aerial vehicles. Int. J. Hydrog. Energy 2022, 47, 15236–15253. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, X.; Zou, Y.; Han, L.; Du, G.; Guo, N.; Xiang, C. Co-optimization strategy of unmanned hybrid electric tracked vehicle combining eco-driving and simultaneous energy management. Energy 2022, 246, 123309. [Google Scholar] [CrossRef]
- Jin, Q.B.; Huang, J. The solar-tracking optimal trajectory planning research based on minimum energy consumption in SSPS. Aerosp. Sci. Technol. 2018, 76, 272–279. [Google Scholar] [CrossRef]
- Bo, B.; Zhang, S.; Liu, W.; Liu, L.; Shi, Y. Simulation of workspace and trajectory of a weeding mechanism. Alex. Eng. J. 2022, 61, 1133–1143. [Google Scholar] [CrossRef]
- Li, H.; Qi, C.; Gao, F.; Chen, X.; Zhao, Y.; Chen, Z. Mechanism design and workspace analysis of a hexapod robot. Mech. Mach. Theory 2022, 174, 104917. [Google Scholar] [CrossRef]
- Schreiber, L.T.; Gosselin, C. Kinematically redundant planar parallel mechanisms: Kinematics, workspace and trajectory planning. Mech. Mach. Theory 2018, 119, 91–105. [Google Scholar] [CrossRef]
- Dion-Gauvin, P.; Gosselin, C. Beyond-the-static-workspace point-to-point trajectory planning of a 6-DoF cable-suspended mechanism using oscillating SLERP. Mech. Mach. Theory 2022, 174, 104894. [Google Scholar] [CrossRef]
- Sharma, S.K.; Duvedi, R.K.; Bedi, S.; Mann, S. A multipoint tool positioning method for five-axis machining in the region of two intersecting tensor product Bézier surfaces. Int. J. Mach. Tools Manuf. 2019, 142, 42–53. [Google Scholar] [CrossRef]
- Sun, S.; Altintas, Y. A G3 continuous tool path smoothing method for 5-axis CNC machining. CIRP J. Manuf. Sci. Technol. 2021, 32, 529–549. [Google Scholar] [CrossRef]
- Fan, W.; Ji, J.; Wu, P.; Wu, D.; Chen, H. Modeling and simulation of trajectory smoothing and feedrate scheduling for vibration-damping CNC machining. Simul. Model. Pract. Theory 2020, 99, 102028. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.; Li, H.; Hu, X. Shape optimization of generalized developable H-Bézier surfaces using adaptive cuckoo search algorithm. Adv. Eng. Softw. 2020, 149, 102889. [Google Scholar] [CrossRef]
- Zhu, X.; Ji, Y.; Zhu, C.; Hu, P.; Ma, Z.D. Isogeometric analysis for trimmed CAD surfaces using multi-sided toric surface patches. Comput. Aided Geom. Des. 2020, 79, 101847. [Google Scholar] [CrossRef]
- Deng, X.; Li, R.; Zhao, L.; Wang, K.; Gui, X. Multi-obstacle path planning and optimization for mobile robot. Expert Syst. Appl. 2021, 183, 115445. [Google Scholar] [CrossRef]
- Duraklı, Z.; Nabiyev, V. A new approach based on Bezier curves to solve path planning problems for mobile robots. J. Comput. Sci. 2022, 58, 101540. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Chen, L.; Qin, D.; Xu, X.; Cai, Y.; Xie, J. A path and velocity planning method for lane changing collision avoidance of intelligent vehicle based on cubic 3-D Bezier curve. Adv. Eng. Softw. 2019, 132, 65–73. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.; Song, B. A new approach to smooth path planning of mobile robot based on quartic Bezier transition curve and improved PSO algorithm. Neurocomputing 2022, 473, 98–106. [Google Scholar] [CrossRef]
- Dinçer, Ü.; Çevik, M. Improved trajectory planning of an industrial parallel mechanism by a composite polynomial consisting of Bézier curves and cubic polynomials. Mech. Mach. Theory 2019, 132, 248–263. [Google Scholar] [CrossRef]
- Rocha, C.R.; Tonetto, C.P.; Dias, A. A comparison between the Denavit–Hartenberg and the screw-based methods used in kinematic modeling of robot manipulators. Robot. Comput.-Integr. Manuf. 2011, 27, 723–728. [Google Scholar] [CrossRef]
- Škrjanc, I.; Klančar, G. Optimal cooperative collision avoidance between multiple robots based on Bernstein–Bézier curves. Robot. Auton. Syst. 2010, 58, 1–9. [Google Scholar] [CrossRef]
- Ostrowski, J. Reduced equations for nonholonomic mechanical systems with dissipative forces. Rep. Math. Phys. 1998, 42, 185–209. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).