Forecasting of PM2.5 Concentration in Beijing Using Hybrid Deep Learning Framework Based on Attention Mechanism
Abstract
1. Introduction
- (1)
- Our model uses multi-channel 1D CNNs to process data from neighboring sites (i.e., pollutant data and meteorological data) to predict pollutant concentrations at the target site. This fully extracts the spatial characteristics among the stations and captures the spatiotemporal characteristics of the pollutant data and meteorological data.
- (2)
- The attention mechanism, as a lightweight module, does not consume too many resources of the computer. The attention mechanism matches the corresponding weights to the time series at different moments and concentrates the information that is more effective for prediction at different moments, thus improving the final prediction results.
- (3)
- Bi LSTM, as the prediction output layer, is more suitable for processing long time series spatiotemporal big data. Bi LSTM effectively utilizes the input forward and backward feature information to fully capture the long time series variation pattern of pollutant concentration.
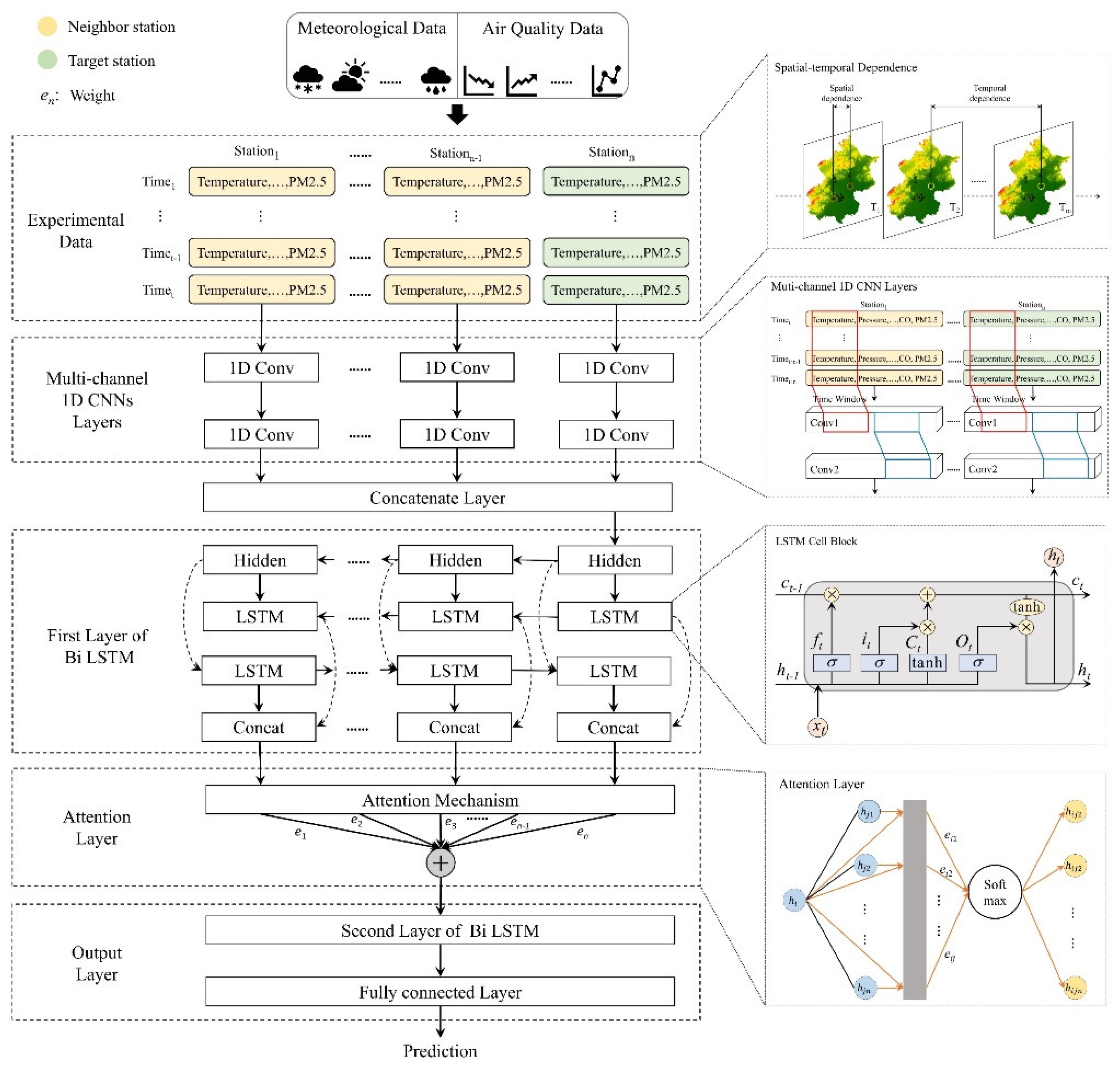
2. Research Method
2.1. Spatiotemporal Analysis
2.2. FPHFA Model
2.2.1. Multi-Channel 1D CNNs for Learning of Overall Spatial Features
2.2.2. Bi LSTM for Long-Term Series Learning
2.2.3. Attention Mechanism
3. Experimental Analysis
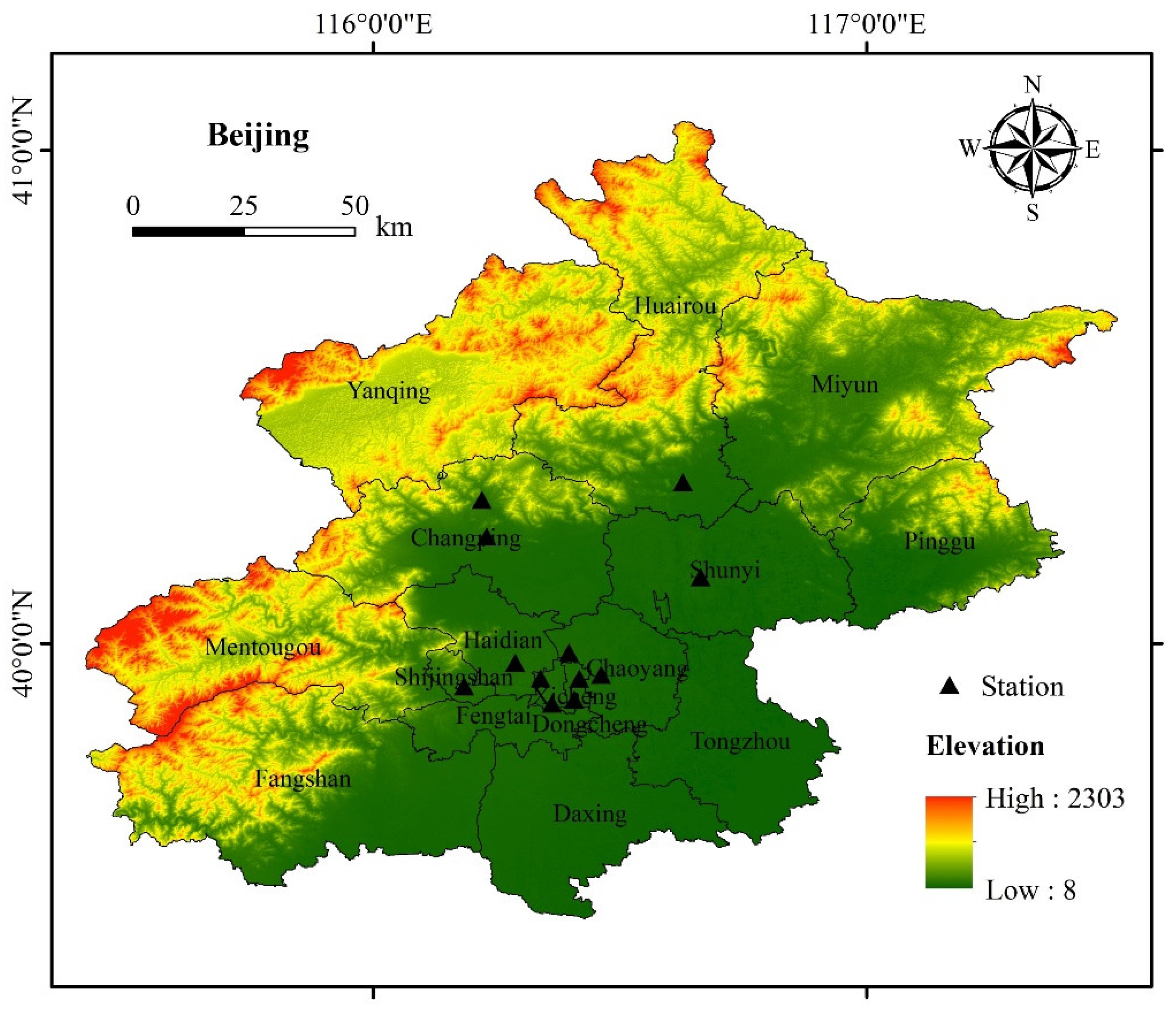
3.1. Research Area
3.2. Data Description and Preprocessing
3.3. Experimental Setup
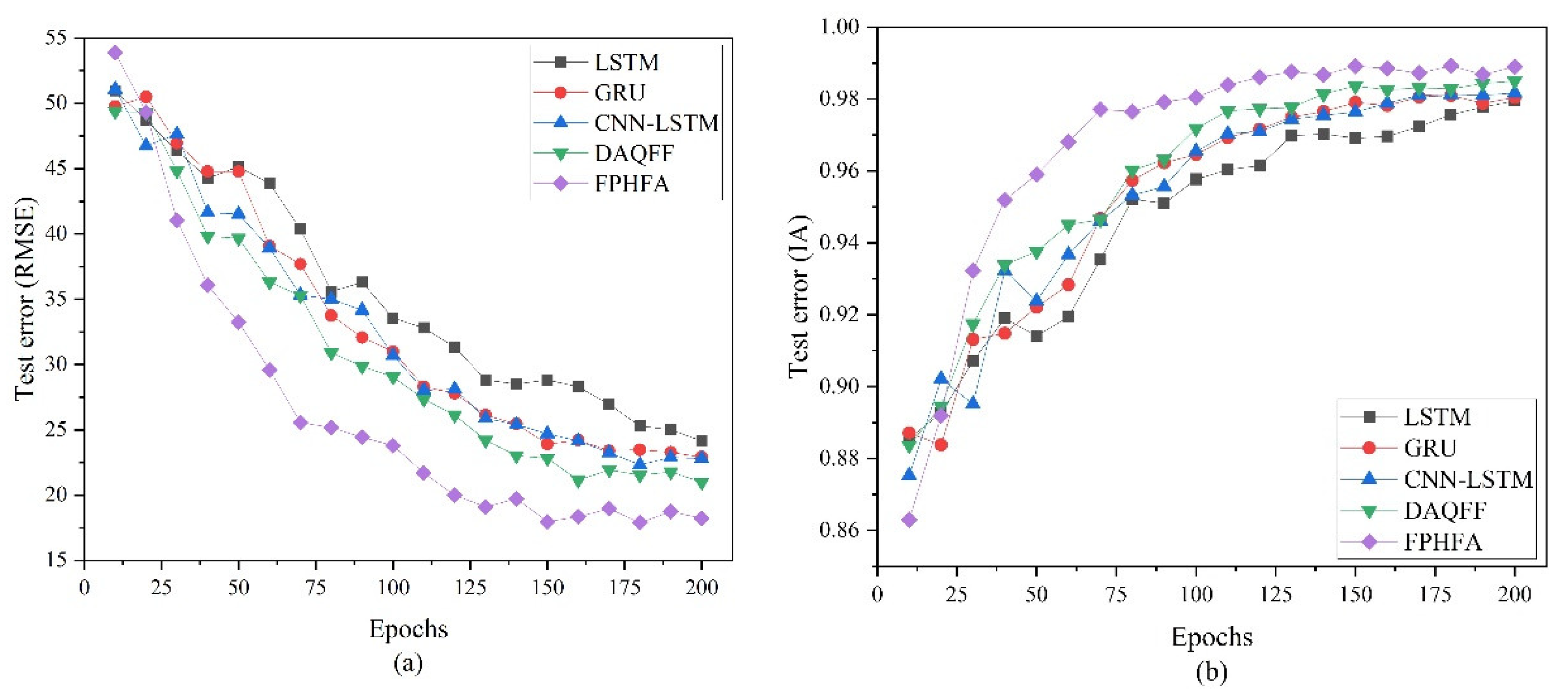
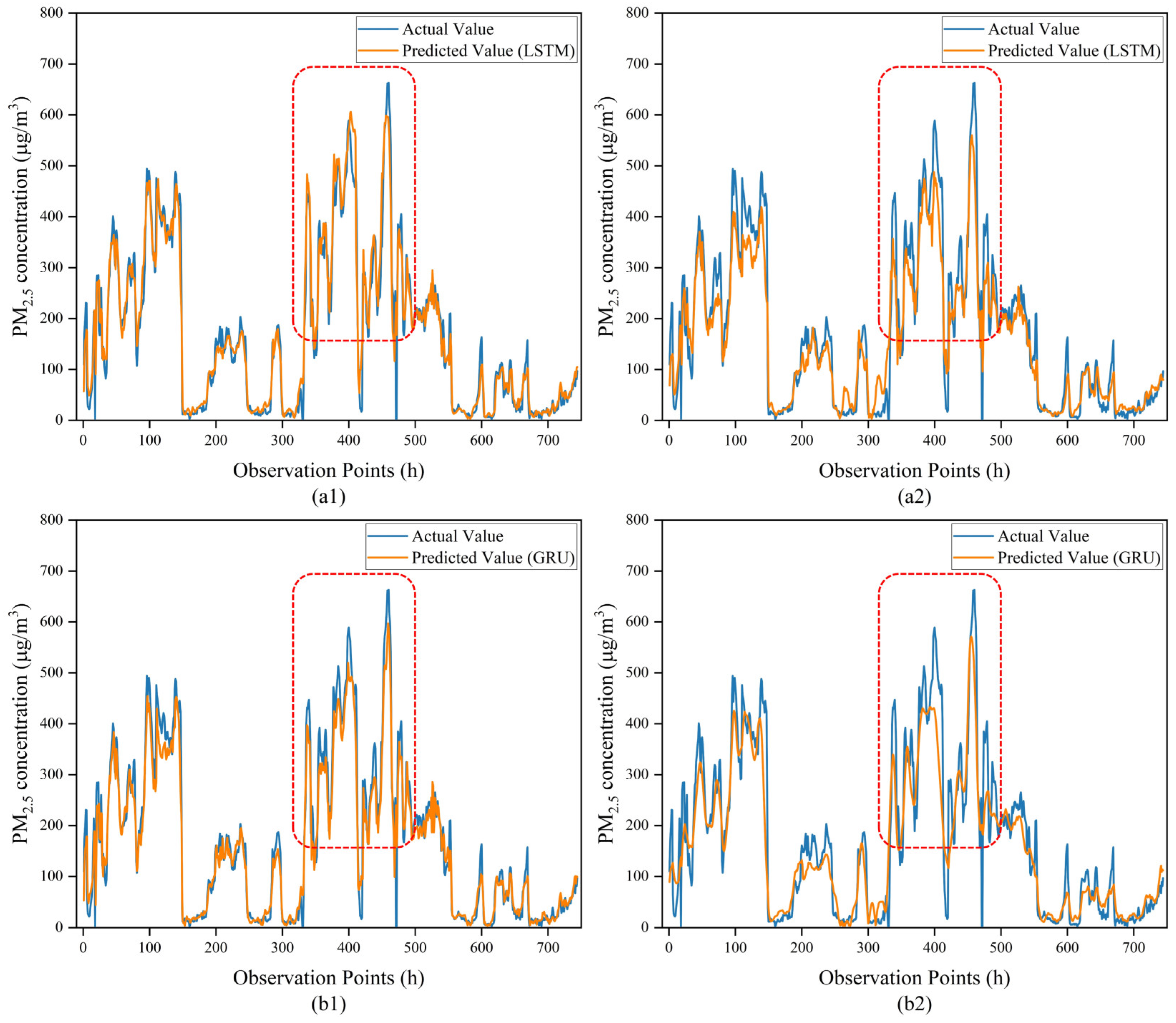
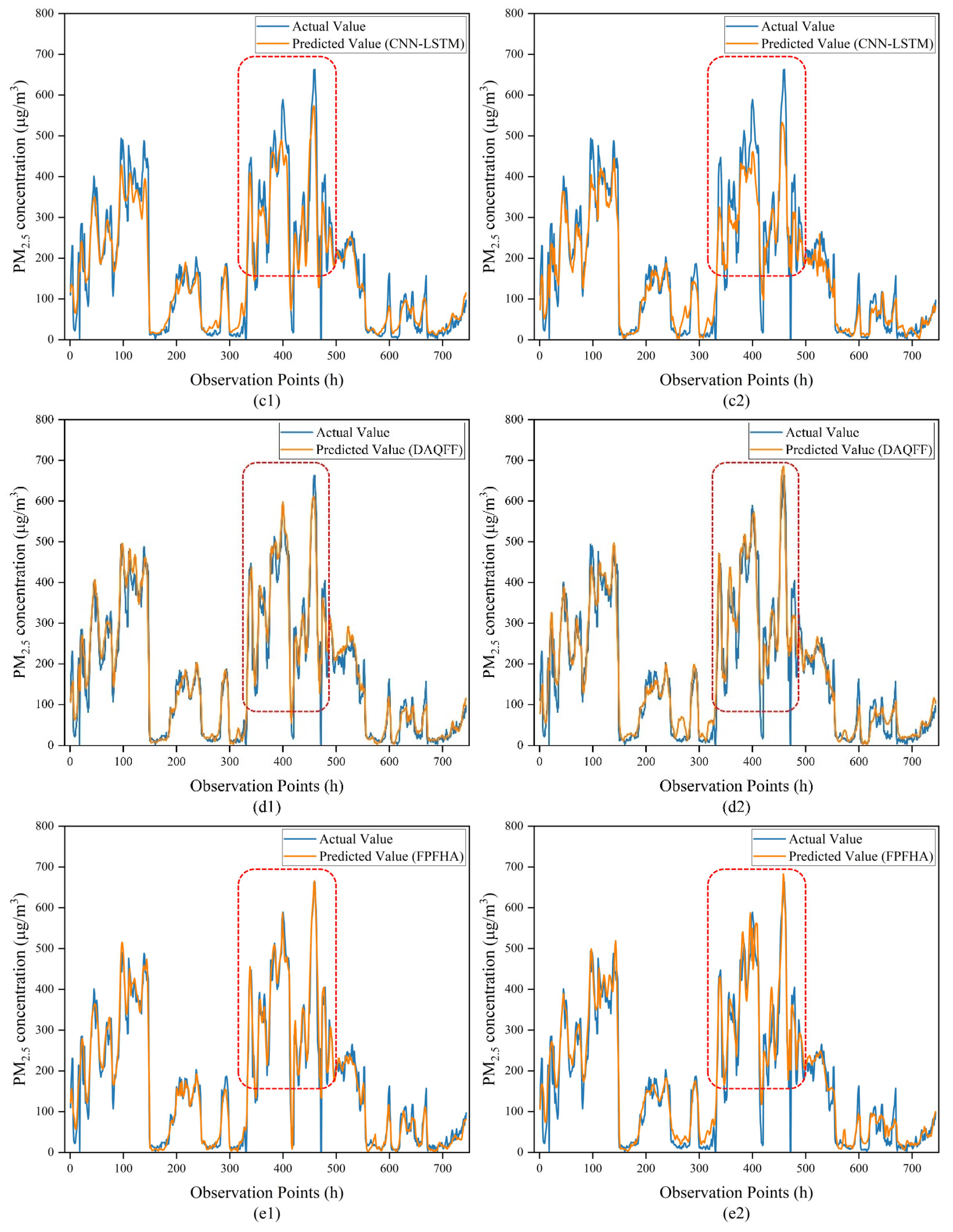
4. Results
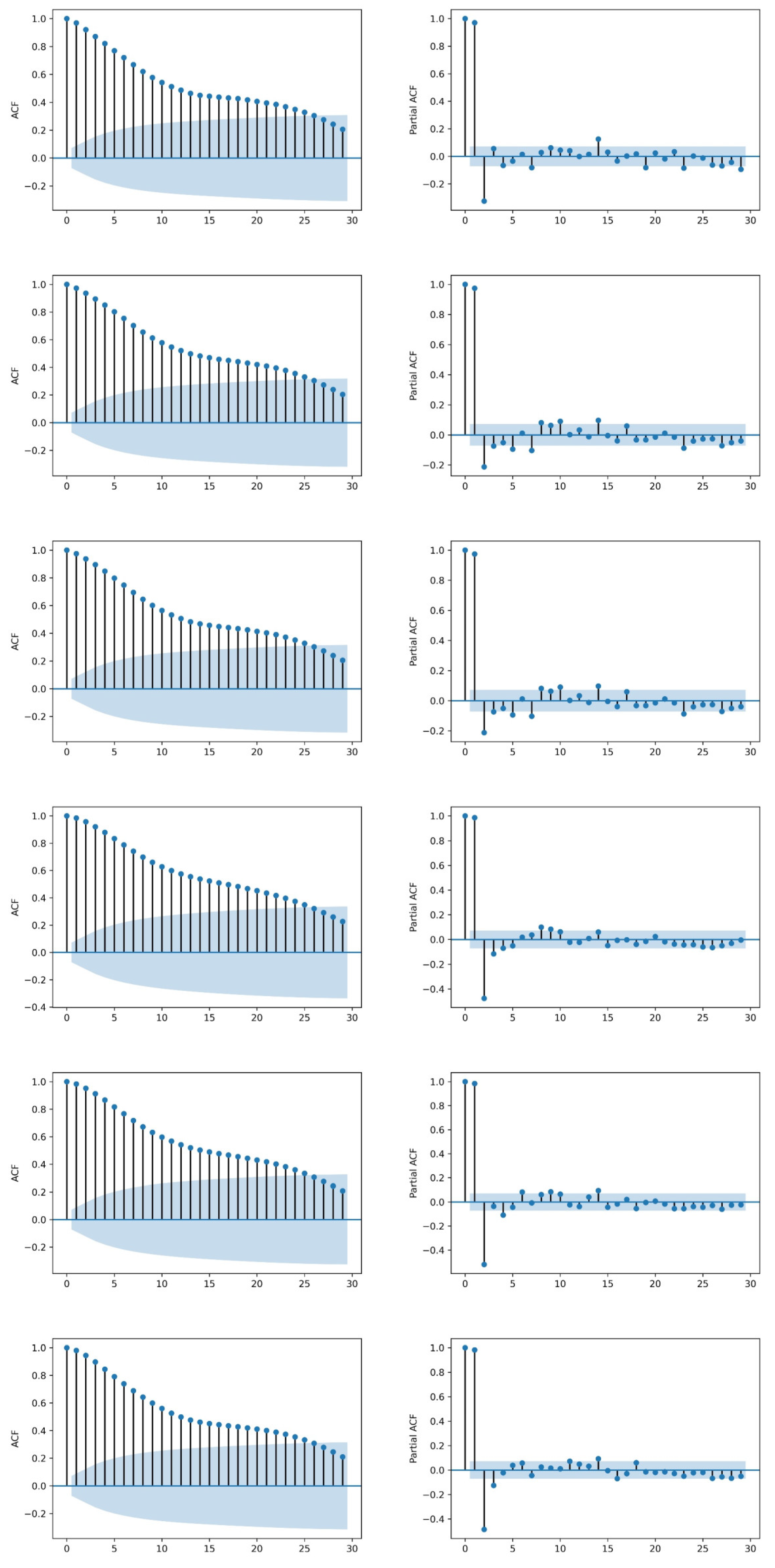
4.1. Spatial and Temporal Features of PM2.5 Concentration
4.2. Analysis of Short-Term Prediction Results
4.3. Analysis of Long-Term Prediction Result
5. Discussion
6. Conclusions and Future Work
- (1)
- This paper was the first attempt to combine multi-channel 1D CNNs, Bi LSTM, and attention mechanisms for hybrid fusion learning of PM2.5-related time series data, yielding a model which can capture spatial-temporal dependent features.
- (2)
- The attention mechanism in the FPHFA model was used to focus on information that is more useful for prediction for different instants, thus improving the final prediction outcomes.
- (3)
- We proved the effectiveness of FPHFA by conducting experiments on the Beijing historical air pollution dataset, and the experimental outcomes show that our model has excellent prediction capability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, S.; Li, T.; Yang, Y.; Horng, S.J. Deep Air Quality Forecasting Using Hybrid Deep Learning Framework. IEEE Trans. Knowl. Data Eng. 2018, 33, 2412–2424. [Google Scholar] [CrossRef]
- Zhang, B.; Zou, G.; Qin, D.; Lu, Y.; Wang, H. A novel Encoder-Decoder model based on read-first LSTM for air pollutant prediction. Sci. Total Environ. 2021, 765, 144507. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Chen, Z. Cost of economic growth: Air pollution and health expenditure. Sci. Total Environ. 2021, 755, 142543. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.B.; Fang, C.L. Spatial-temporal characteristics and determinants of PM2.5 in the Bohai Rim Urban Agglomeration. Chemosphere 2016, 148, 148–162. [Google Scholar] [CrossRef]
- Zhou, J.; Li, W.; Yu, X.; Xu, X.; Yuan, X.; Wang, J. Elman-Based Forecaster Integrated by AdaboostAlgorithm in 15 min and 24 h ahead Power OutputPrediction Using PM 2.5 Values, PV ModuleTemperature, Hours of Sunshine, and Meteorological Data. Pol. J. Environ. Stud. 2019, 28, 1999. [Google Scholar] [CrossRef]
- Mao, X.; Shen, T.; Feng, X. Prediction of hourly ground-level PM2.5 concentrations 3 days in advance using neural networks with satellite data in eastern China. Atmos. Pollut. Res. 2017, 8, 1005–1015. [Google Scholar] [CrossRef]
- Djalalova, I.; Delle Monache, L.; Wilczak, J. PM2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmos. Environ. 2015, 108, 76–87. [Google Scholar] [CrossRef]
- Zhu, B.; Akimoto, H.; Wang, Z.J.A.G.U. The Preliminary Application of a Nested Air Quality Prediction Modeling System in Kanto Area, Japan. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2005. [Google Scholar]
- Saide, P.E.; Carmichael, G.R.; Spak, S.N.; Gallardo, L.; Osses, A.E.; Mena-Carrasco, M.A.; Pagowski, M. Forecasting urban PM10 and PM2.5 pollution episodes in very stable nocturnal conditions and complex terrain using WRF–Chem CO tracer model. Atmos. Environ. 2011, 45, 2769–2780. [Google Scholar] [CrossRef]
- Vautard, R.; Builtjes, P.; Thunis, P.; Cuvelier, C.; Bedogni, M.; Bessagnet, B.; Honore, C.; Moussiopoulos, N.; Pirovano, G.; Schaap, M.; et al. Evaluation and intercomparison of ozone and PM10 simulations by several chemistry transport models over four European cities within the CityDelta project. Atmos. Environ. 2007, 41, 173–188. [Google Scholar] [CrossRef]
- Zhang, B.; Zou, G.; Qin, D.; Ni, Q.; Mao, H.; Li, M. RCL-Learning: ResNet and convolutional long short-term memory-based spatiotemporal air pollutant concentration prediction model. Expert Syst. Appl. 2022, 207, 118017. [Google Scholar] [CrossRef]
- Kumar, D. Evolving Differential evolution method with random forest for prediction of Air Pollution. Procedia Comput. Sci. 2018, 132, 824–833. [Google Scholar]
- Hong, Z.; Sheng, Z.; Ping, W.; Qin, Y.; Wang, H. Forecasting of PM 10 time series using wavelet analysis and wavelet-ARMA model in Taiyuan, China. J. Air Waste Manag. Assoc. 2017, 67, 776–788. [Google Scholar]
- Leong, W.C.; Kelani, R.O.; Ahmad, Z. Prediction of air pollution index (API) using support vector machine (SVM). J. Environ. Chem. Eng. 2019, 8, 103208. [Google Scholar] [CrossRef]
- Yu, Z.; Yi, X.; Ming, L.; Li, R.; Shan, Z. Forecasting Fine-Grained Air Quality Based on Big Data. In Proceedings of the 21th ACM SIGKDD International Conference, Sydney, Australia, 10–13 August 2015. [Google Scholar]
- Gu, K.; Qiao, J.; Li, X. Highly Efficient Picture-Based Prediction of PM2.5 Concentration. IEEE Trans. Ind. Electron. 2019, 66, 3176–3184. [Google Scholar] [CrossRef]
- Liu, Y.; Zhai, D.; Ren, Q. News Text Classification Based on CNLSTM Model with Attention Mechanism. Comput. Eng. 2019, 45, 303–308. [Google Scholar]
- Jan, F.; Shah, I.; Ali, S. Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis. Energies 2022, 15, 3423. [Google Scholar] [CrossRef]
- Chen, Y.; An, J. A novel prediction model of PM2.5 mass concentration based on back propagation neural network algorithm. J. Intell. Fuzzy Syst. 2019, 37, 3175–3183. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Xin, R.B.; Jiang, Z.F.; Li, N.; Hou, L.J. An Air Quality Predictive Model of Licang of Qingdao City Based on BP Neural Network. Adv. Mater. Res. 2013, 756–759, 3366–3371. [Google Scholar] [CrossRef]
- Fan, J.; Li, Q.; Hou, J.; Feng, X.; Lin, S. A Spatiotemporal Prediction Framework for Air Pollution Based on Deep RNN. Remote Sens. Spat. Inf. Sci. 2017, 4, 15. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Prihatno, A.T.; Nurcahyanto, H.; Ahmed, M.F.; Rahman, M.H.; Alam, M.M.; Jang, Y.M. Forecasting PM2.5 Concentration Using a Single-Dense Layer BiLSTM Method. Electronics 2021, 10, 1808. [Google Scholar] [CrossRef]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Li, F. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering. Expert Syst. Appl. 2020, 169, 114513. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, F.; Cai, Y.; Chen, J. Long short-term memory—Fully connected (LSTM-FC) neural network for PM 2.5 concentration prediction. Chemosphere 2019, 220, 486–492. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Li, S.; Xie, G.; Ren, J.; Guo, L.; Xu, X. Urban PM2.5 Concentration Prediction via Attention-Based CNN–LSTM. Appl. Sci. 2020, 10, 1953. [Google Scholar] [CrossRef]
- Zhou, Q.; Jiang, H.; Wang, J.; Zhou, J. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef]
- Guojian, Z.; Bo, Z.; Ruihan, Y.; Dongming, Q.; Qin, Z. FDN-learning: Urban PM 2.5-concentration Spatial Correlation Prediction Model Based on Fusion Deep Neural Network. Big Data Res. 2021, 26, 100269. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2012, 25, 84–90. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, B.; Huang, B.; Ma, Z.; Biswas, A.; Jiang, Y.; Shi, Z. Predicting annual PM2.5 in mainland China from 2014 to 2020 using multi temporal satellite product: An improved deep learning approach with spatial generalization ability. ISPRS J. Photogramm. Remote Sens. 2022, 187, 141–158. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and meteorological factors in China: Seasonal and regional variations. Int. J. Environ. Res. Public Health 2017, 12, 1510. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yan, R.; Nong, M.; Liao, J.; Li, F.; Sun, W. PM 2.5 concentrations forecasting in Beijing through deep learning with different inputs, model structures and forecast time. Atmos. Pollut. Res. 2021, 12, 101168. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, G.; Xu, C.; An, Z. The air pollution caused by the burning of fireworks during the lantern festival in Beijing. Atmos. Environ. 2007, 41, 417–431. [Google Scholar] [CrossRef]
- Wang, G.; Xue, J.; Zhang, J. Analysis of Spatial-temporal Distribution Characteristics and Main Cause of Air Pollution in Beijing-Tianjin-Hebei Region in 2014. Environ. Sci. 2016, 39, 34–42. [Google Scholar]
- Tian, Y.; Jiang, Y.; Liu, Q.; Xu, D.; Zhao, S.; He, L.; Liu, H.; Xu, H. Temporal and spatial trends in air quality in Beijing. Landsc. Urban Plan. 2019, 185, 35–43. [Google Scholar] [CrossRef]
- Xu, W.; Tian, Y.; Xiao, Y.; Jiang, W.; Liu, J. Study on the spatial distribution characteristics and the drivers of AQI in North China. Circumstantiae 2017, 8, 3085–3096. [Google Scholar]
- Zhu, Y.; Qi, L.I.; Hou, J.; Fan, J.; Feng, X. Spatio-temporal modeling and prediction of PM_(2.5) concentration based on Bayesian method. Sci. Surv. Mapp. 2016, 2, 44–48. [Google Scholar]
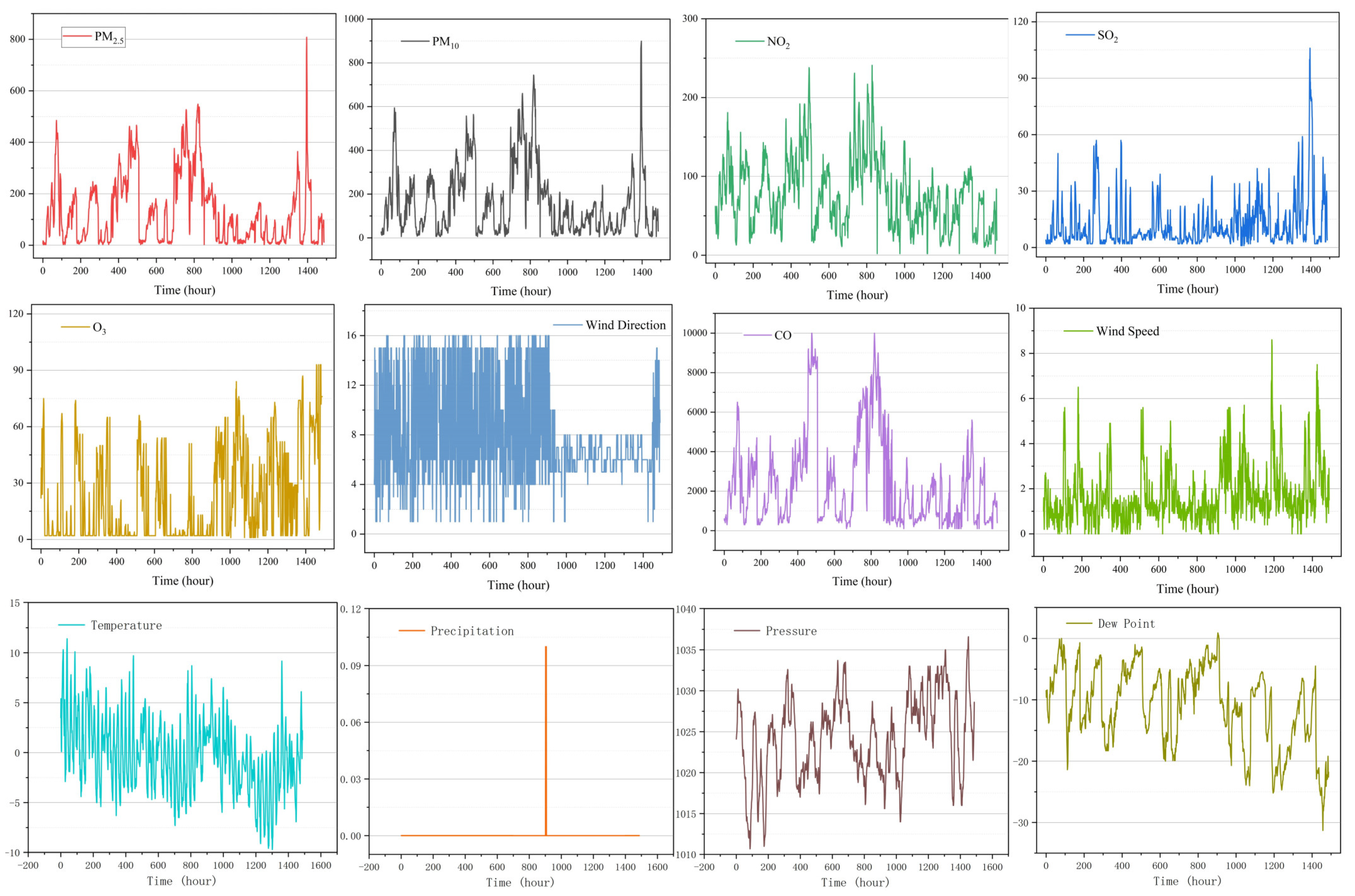








| Kind | Var. | Unit | Range |
|---|---|---|---|
| Air Pollutant Data | PM2.5 | μg/m3 | [2, 999] |
| PM10 | μg/m3 | [2, 999] | |
| SO2 | μg/m3 | [0.2856, 500] | |
| NO2 | μg/m3 | [1.0265, 290] | |
| CO | μg/m3 | [100, 10,000] | |
| O3 | μg/m3 | [0.2142, 1071] | |
| Meteorological Data | Temperature | °C | [−19.9, 41.6] |
| Pressure | hPa | [982.4, 1042.8] | |
| Dew Point | °C | [−43.4, 29.1] | |
| Precipitation | mm | [0, 72.5] | |
| Wind Direction | [N, ESE] | ||
| Wind Speed | m/s | [0, 13.2] |
| Models | RMSE | MAE | R2 | IA | MAPE |
|---|---|---|---|---|---|
| LSTM | 34.39 | 23.03 | 0.796 | 95.30% | 0.707 |
| GRU | 32.62 | 22.25 | 0.824 | 95.93% | 0.683 |
| CNN-LSTM | 31.69 | 21.81 | 0.832 | 96.15% | 0.672 |
| DAQFF | 30.12 | 21.02 | 0.849 | 96.47% | 0.669 |
| FPHFA | 28.15 | 19.19 | 0.877 | 97.04% | 0.561 |
| Models | RMSE | MAE | R2 | IA | MAPE |
|---|---|---|---|---|---|
| LSTM | 33.95 | 24.00 | 0.804 | 95.53% | 0.831 |
| GRU | 33.01 | 23.33 | 0.814 | 95.80% | 0.829 |
| CNN-LSTM | 31.32 | 22.14 | 0.830 | 96.17% | 0.746 |
| DAQFF | 29.15 | 20.57 | 0.864 | 96.83% | 0.691 |
| FPHFA | 22.12 | 15.27 | 0.932 | 98.30% | 0.438 |
| Models | Spring | Summer | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | IA | RMSE | MAE | R2 | IA | |
| LSTM | 24.58 | 17.53 | 0.856 | 96.63% | 21.78 | 16.19 | 0.668 | 92.72% |
| GRU | 22.45 | 15.76 | 0.873 | 97.12% | 19.87 | 14.79 | 0.716 | 93.90% |
| CNN-LSTM | 21.04 | 14.34 | 0.896 | 97.55% | 17.84 | 13.23 | 0.791 | 95.32% |
| DAQFF | 20.20 | 14.10 | 0.905 | 97.76% | 19.05 | 14.44 | 0.771 | 94.73% |
| FPHFA | 15.87 | 10.80 | 0.949 | 98.71% | 13.18 | 9.78 | 0.917 | 97.84% |
| Models | Autumn | Winter | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | IA | RMSE | MAE | R2 | IA | |
| LSTM | 23.74 | 17.09 | 0.896 | 97.50% | 32.44 | 21.34 | 0.928 | 98.29% |
| GRU | 23.39 | 16.84 | 0.890 | 97.48% | 33.43 | 22.01 | 0.915 | 98.08% |
| CNN-LSTM | 22.06 | 15.32 | 0.910 | 97.85% | 34.24 | 21.56 | 0.911 | 98.00% |
| DAQFF | 20.22 | 14.53 | 0.928 | 98.24% | 28.70 | 17.74 | 0.956 | 98.85% |
| FPHFA | 15.86 | 11.05 | 0.958 | 98.85% | 23.69 | 14.93 | 0.966 | 99.14% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Liu, J.; Zhao, Y. Forecasting of PM2.5 Concentration in Beijing Using Hybrid Deep Learning Framework Based on Attention Mechanism. Appl. Sci. 2022, 12, 11155. https://doi.org/10.3390/app122111155
Li D, Liu J, Zhao Y. Forecasting of PM2.5 Concentration in Beijing Using Hybrid Deep Learning Framework Based on Attention Mechanism. Applied Sciences. 2022; 12(21):11155. https://doi.org/10.3390/app122111155
Chicago/Turabian StyleLi, Dong, Jiping Liu, and Yangyang Zhao. 2022. "Forecasting of PM2.5 Concentration in Beijing Using Hybrid Deep Learning Framework Based on Attention Mechanism" Applied Sciences 12, no. 21: 11155. https://doi.org/10.3390/app122111155
APA StyleLi, D., Liu, J., & Zhao, Y. (2022). Forecasting of PM2.5 Concentration in Beijing Using Hybrid Deep Learning Framework Based on Attention Mechanism. Applied Sciences, 12(21), 11155. https://doi.org/10.3390/app122111155






