The Study of Machine Learning Assisted the Design of Selected Composites Properties
Abstract
1. Introduction
2. Work Methodology
- -
- by measuring, we will determine the absorption values of all material samples (VO_20_PVB_80_TF, VO_30_PVB_70_TF and VO_50_PVB_50_TF);
- -
- materials VO_20_PVB_80_TF and VO_50_PVB_50_TF will be tested in a climate chamber;
- -
- using the measured values, we will compile a training set of data in order to design models for the prediction of values for the material VO_30_PVB_70_TF, which is not tested in a climate chamber;
- -
- we will verify the results obtained through models for materials VO_20_PVB_80_TF and VO_50_PVB_50_TF separately by comparing them with their measured values;
- -
- the more favorable of the models will be applied to predict data for the material VO_30_PVB_70_TF.
2.1. Materials and Test Characterization
2.2. Methods and Tools Characterization
- Matlab Software Application Tools
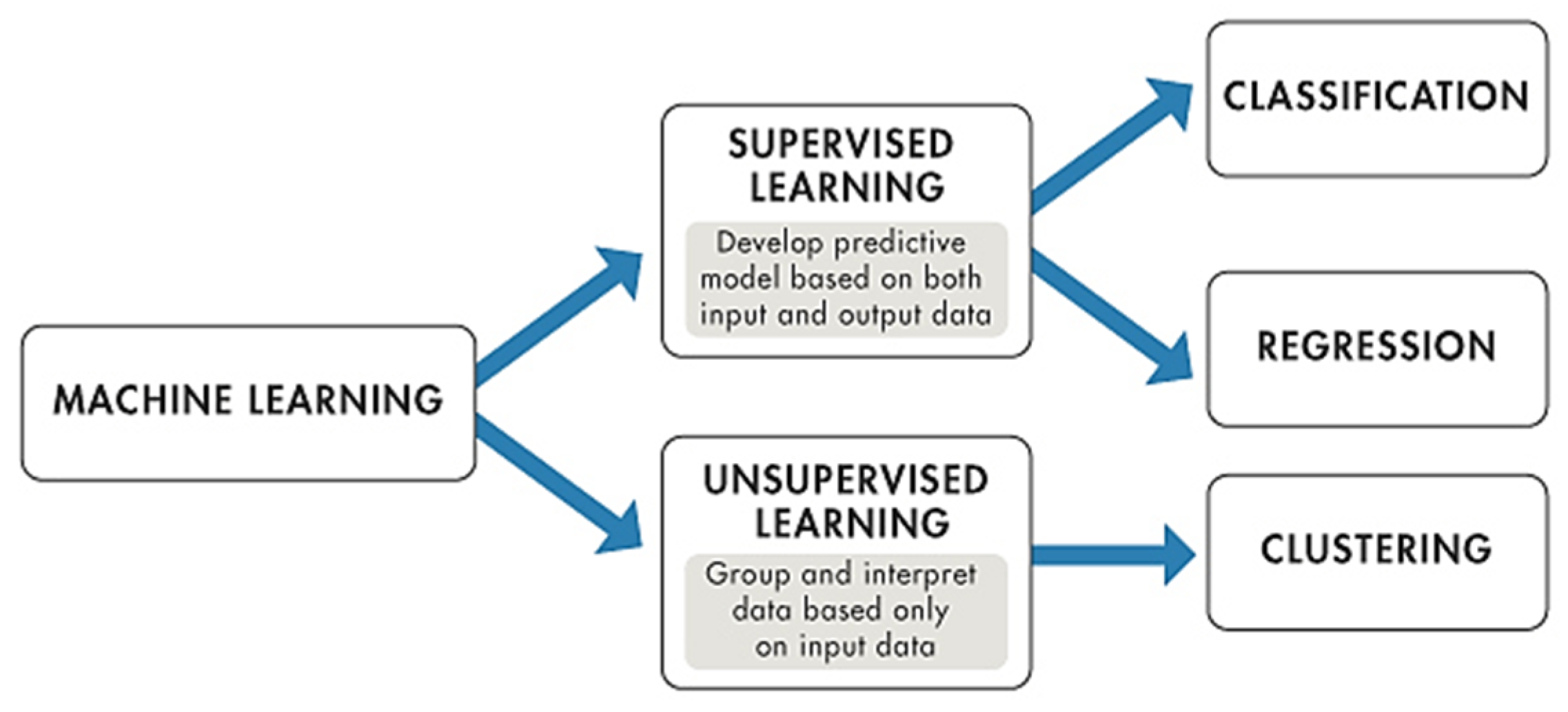
- Machine Learning
- Regression Analysis
- Qualitative Evaluation
3. Model Proposal
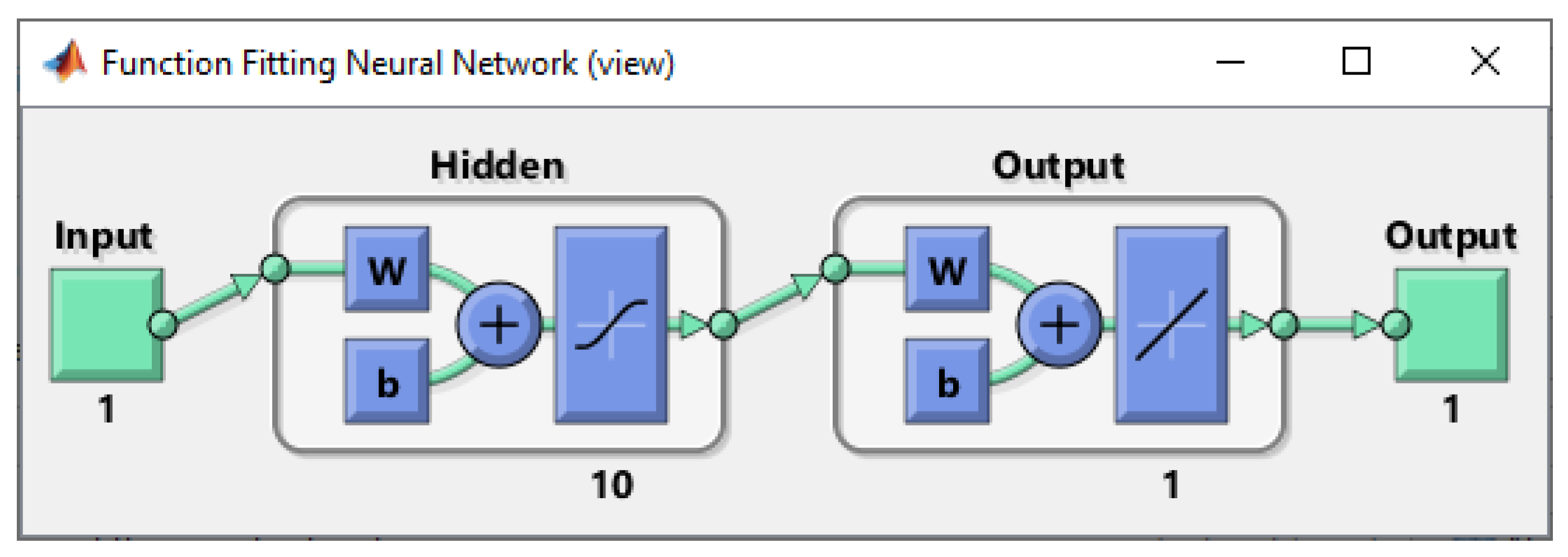
Neural Networks
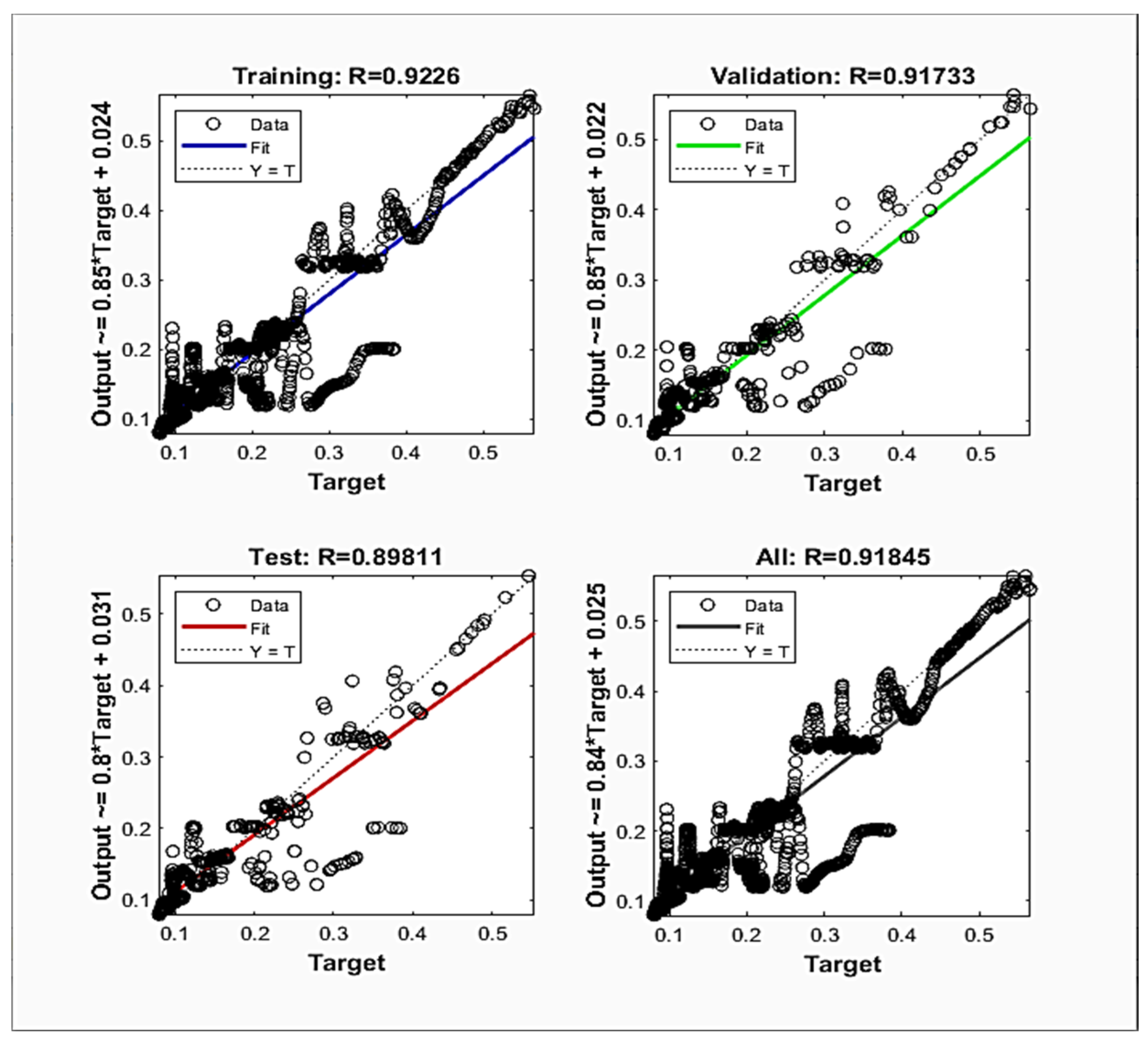
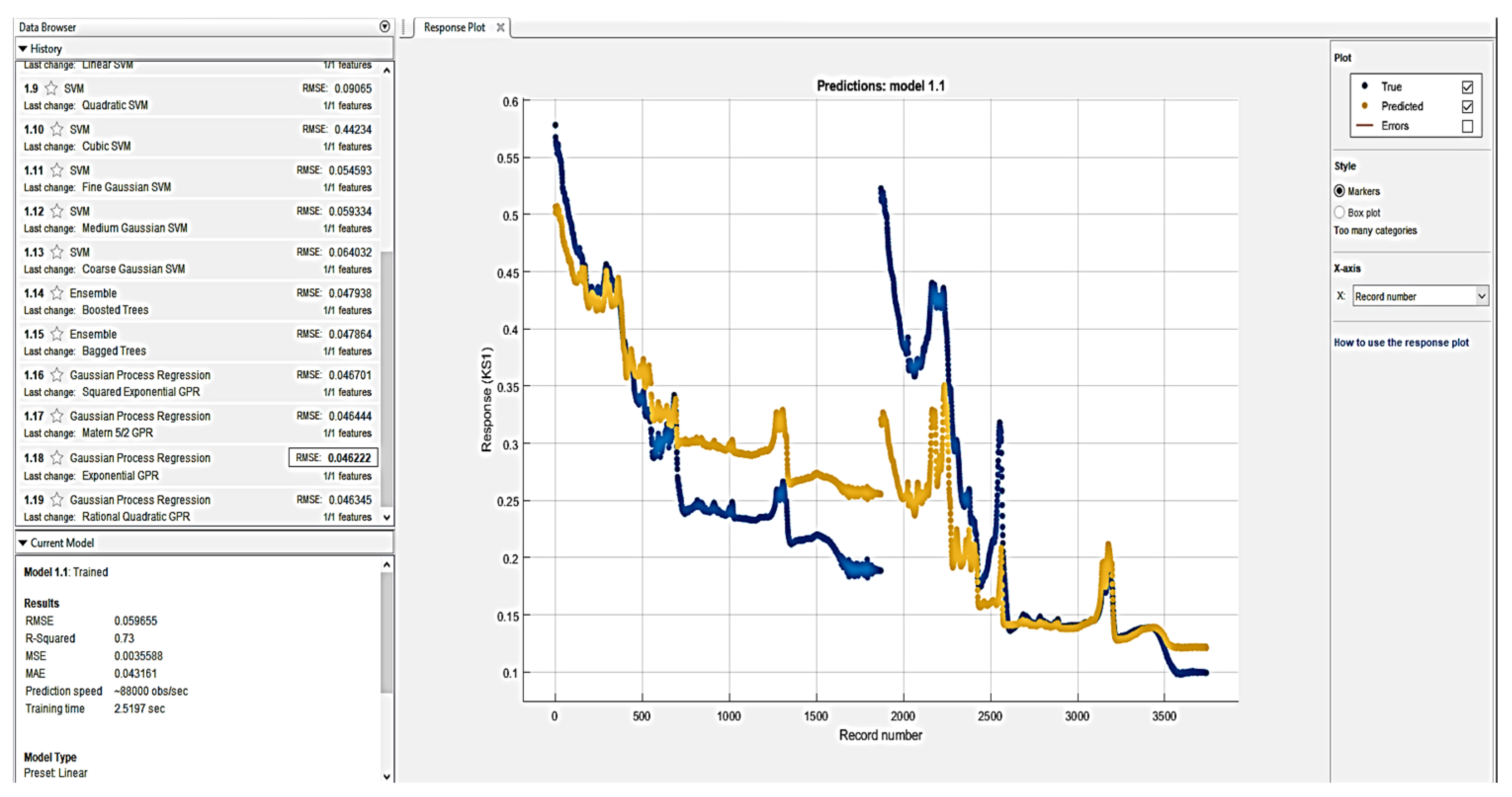
4. Results and Discussion
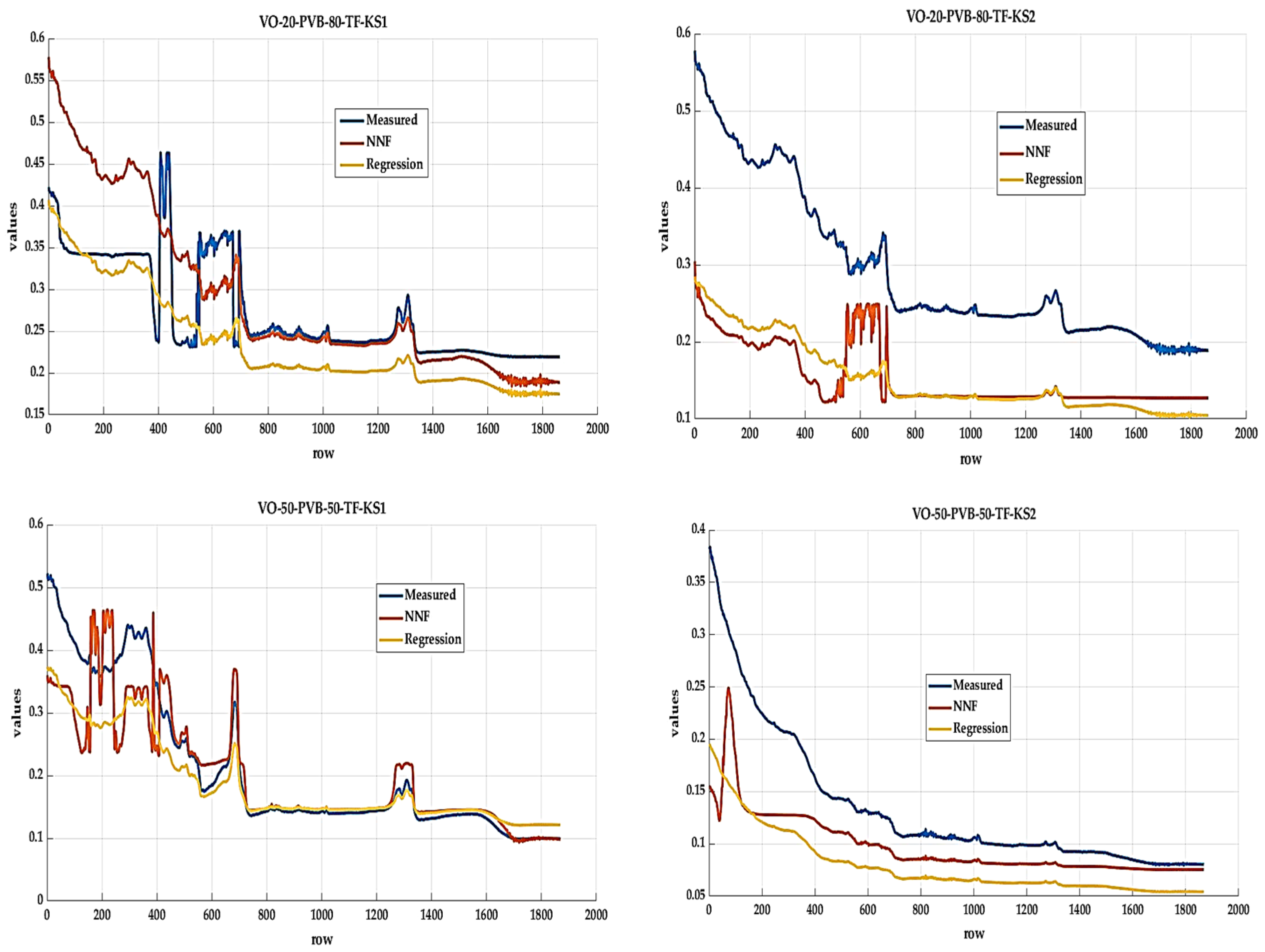
Application of Selected Model for VO_30_PVB_70_TF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.T.; Gu, G.X. Machine learning for composite materials. MRS Commun. 2019, 9, 556. [Google Scholar] [CrossRef]
- Breque, M.; de Nul, L.; Petridis, A. Industry 5.0, Towards a Sustainable, Human-Centric and Resilient European Industry; European Commission: Brussels, Belgium, 2021. [Google Scholar]
- Industry 5.0. Available online: https://research-and-innovation.ec.europa.eu/research-area/industry/industry-50_en (accessed on 15 September 2022).
- Rodríguez-Martín, M.; Fueyo, J.G.; Gonzalez-Aguilera, D.; Madruga, F.J.; García-Martín, R.; Muñóz, Á.L.; Pisonero, J. Predictive Models for the Characterization of Internal Defects in Additive Materials from Active Thermography Sequences Supported by Machine Learning Methods. Sensors 2020, 20, 3982. [Google Scholar] [CrossRef]
- Furtado, C.; Pereira, L.F.; Tavares, R.P.; Salgado, M.; Otero, F.; Catalanotti, G.; Arteiro, A.; Bessa, M.A.; Camanho, P.P. A methodology to generate design allowables of composite laminates using machine learning. Int. J. Solids Struct. 2021, 233, 111095. [Google Scholar] [CrossRef]
- Sharma, A.; Mukhopadhyay, T.; Rangappa, S.M.; Siengchin, S.; Kushvaha, V. Advances in Computational Intelligence of Polymer Composite Materials: Machine Learning Assisted Modeling, Analysis and Design. Arch. Comput. Methods Eng. 2022, 29, 3341–3385. [Google Scholar] [CrossRef]
- Hrehova, S. Quality Evaluation of Heating Process Control Using Matlab Tools. In Proceedings of the 19th International Carpathian Control Conference (ICCC), IEEE, Szilvasvarad, Hungary, 28–31 May 2018. [Google Scholar] [CrossRef]
- Mathworks. Machine Learning. Available online: https://www.mathworks.com/help/stats/machine-learning-in-matlab.html (accessed on 13 March 2022).
- Artificial Neural Networks Overview. Available online: https://www.dataversity.net/artificial-neural-networks-overview/# (accessed on 11 March 2022).
- Paluszek, M.; Thomas, S. Practical MATLAB Deep Learning; Apress: Berkeley, CA, USA, 2020; p. 270. [Google Scholar]
- Hošovský, A.; Piteľ, J.; Trojanová, M.; Židek, K. Computational Intelligence in the Context of Industry 4.0. Implementing Industry 4.0 in SMEs; Palgrave Macmillan: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Kalita, K.; Čep, R.; Chakraborty, S. A Comparative Analysis on Prediction Performance of Regression Models during Machining of Composite Materials. Materials 2021, 14, 6689. [Google Scholar] [CrossRef] [PubMed]
- Sinay, J.; Kotianova, Z.; Balazikova, M.; Dulebová, M.; Markulik, Š. Measurement of low-frequency noise during CNC machining and its assessment. Measurement 2018, 119, 190–195. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Evaluation of Regression Models: Model Assessment, Model Selection and Generalization Error. Mach. Learn. Knowl. Extr. 2019, 1, 521–551. [Google Scholar] [CrossRef]
- Inyurt, S.; Kashani, M.H.; Sekertekin, A. Ionospheric TEC forecasting using Gaussian Process Regression (GPR) and Multiple Linear Regression (MLR) in Turkey. Astrophys. Space Sci. 2020, 365, 99. [Google Scholar] [CrossRef]
- Nagyova, A.; Pacaiova, H.; Markulik, S.; Turisová, R.; Kozel, R.; Džugan, J. Design of a Model for Risk Reduction in Project Management in Small and Medium-Sized Enterprises. Symetry 2021, 13, 763. [Google Scholar] [CrossRef]
- Priya, K.S. Linear Regression Algorithm in Machine Learning through MATLAB. Int. J. Res. Appl. Sci. Eng. Technol. (IJRASET) 2021, 9, 12. [Google Scholar] [CrossRef]
- Hamidi, Y.K.; Berrado, A.; Altan, M.C. Machine learning applications in polymer composites. AIP Conf. Proc. 2020, 2205, 20031. [Google Scholar] [CrossRef]
- Anuar, M.A.R.B.K.; Ngamkhanong, C.; Wu, Y.; Kaewunruen, S. Recycled Aggregates Concrete Compressive Strength Prediction Using Artificial Neural Networks (ANNs). Infrastructures 2021, 6, 17. [Google Scholar] [CrossRef]
- Cvitic’, I.; Perakovic’, D.; Perisa, M.; Gupta, B.B. Ensemble machine learning approach for classification of IoT devices in smart home. Int. J. Mach. Learn. Cybern. Ensemble 2021, 12, 3179–3202. [Google Scholar] [CrossRef]
- Jierula, A.; Wang, S.; Oh, T.-M.; Wang, P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Appl. Sci. 2021, 11, 2314. [Google Scholar] [CrossRef]
- Straka, M.; Rosová, A.; Radim, L.; Petr, B.; Janka, Š. Principles of computer simulation design for the needs of improvement of the raw materials combined transport system. Acta Montan. Slovaca 2018, 23, 163–174. [Google Scholar]
- Malindzakova, M.; Straka, M.; Rosova, A.; Kanuchova, M.; Trebuna, P. Modeling the process for incineration of municipal waste. Przem. Chem. 2015, 94, 1260–1264. [Google Scholar] [CrossRef]
- Wicher, P.; Staš, D.; Karkula, M.; Lenort, R.; Besta, P. A computer simulation-based analysis of supply chains resilience in industrial environment. Metalurgija 2015, 54, 703–706. [Google Scholar]
- Szavai, S.; Kovacs, S.; Bezi, Z.; Kozak, D. Coupled Numerical Method for Rolling Contact Fatigue Analysis. Teh. Vjesn. Tech. Gaz. 2021, 28, 1560–1567. [Google Scholar] [CrossRef]
- Gupta, B.B.; Tewari, A.; Cvitic, I.; Perakovic, D.; Chang, X.J. Articial intelligence empowered emals classifier for Internet of Things based system in industry 4.0. Wirel. Netw. 2022, 28, 493–503. [Google Scholar] [CrossRef]
- Cvitic´, I.; Perakovic´, D.; Periša, M.; Botica, M. Novel approach for detection of IoT generated DDoS traffic. Wirel. Netw. 2019, 27, 1573–1586. [Google Scholar] [CrossRef]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. The Internet of Things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Georgala, K.; Kosmopoulos, A.; Paliouras, G. Spam filtering: An active learning approach using incremental clustering. In Proceedings of the 4th International Conference on Web Intelligence, Mining and Semantics, Thessaloniki, Greece, 2–4 June 2014. [Google Scholar]
- Xie, Z.; Peng, J.; Sorokina, M.; Zeng, H. Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold. Appl. Sci. 2022, 12, 10318. [Google Scholar] [CrossRef]
- Behunova, A.; Soltysova, Z.; Behun, M. Complexity Management and its impact on economy. TEM J. Technol. Educ. Manag. Inform. 2018, 7, 324–329. [Google Scholar] [CrossRef]
- Grabara, J.K.; Dima, I.C.; Kot, S.; Kwiatkowska, J. Case on in-house logistics modeling and simulation. Res. J. Appl. Sci. 2011, 6, 7–12. [Google Scholar] [CrossRef]
- Gor, M.; Dobriyal, A.; Wankhede, V.; Sahlot, P.; Grzelak, K.; Kluczyński, J.; Łuszczek, J. Density Prediction in Powder Bed Fusion Additive Manufacturing: Machine Learning-Based Techniques. Appl. Sci. 2022, 12, 7271. [Google Scholar] [CrossRef]
- Kot, S.; Slusarczyk, B. Process simulation in supply chain using logware software. Ann. Univ. Apulensis Ser. Oeconomica 2009, 11, 932. [Google Scholar]
- Schmid, J.; Trabesinger, S.; Brillinger, M.; Pichler, R.; Wurzinger, J.; Ciumasu, R. Tacit Knowledge Based Acquisition of Verified Machining Data. In Proceedings of the IEEE, 9th International Conference on Industrial Technology and Management (ICITM 2020), Oxford, UK, 11–13 February 2020; pp. 117–121. [Google Scholar]
- Yu, J.; Oh, S.J.; Baek, S.; Kim, J.; Lee, T. Predicting the Effect of Processing Parameters on Caliber-Rolled Mg Alloys through Machine Learning. Appl. Sci. 2022, 12, 10646. [Google Scholar] [CrossRef]

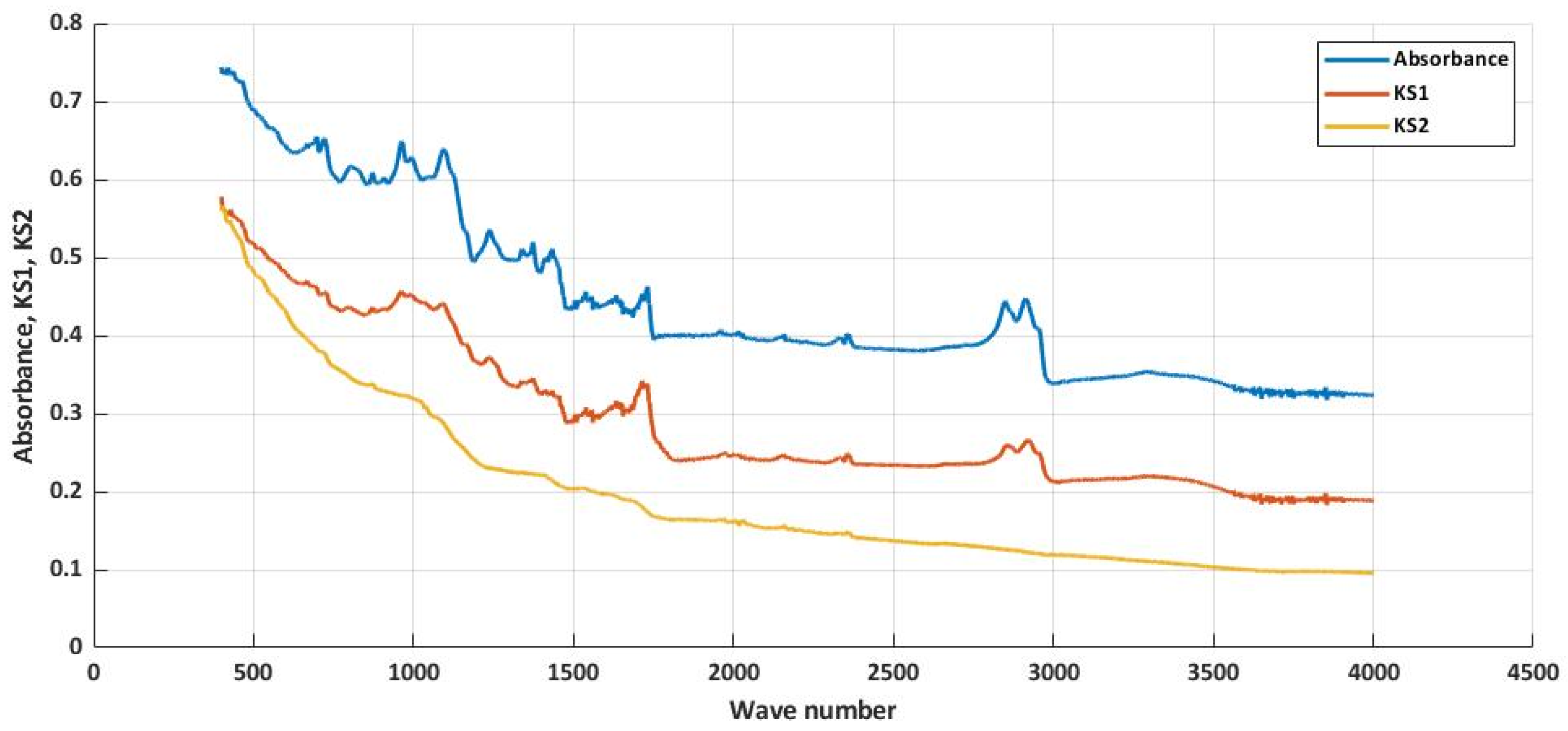
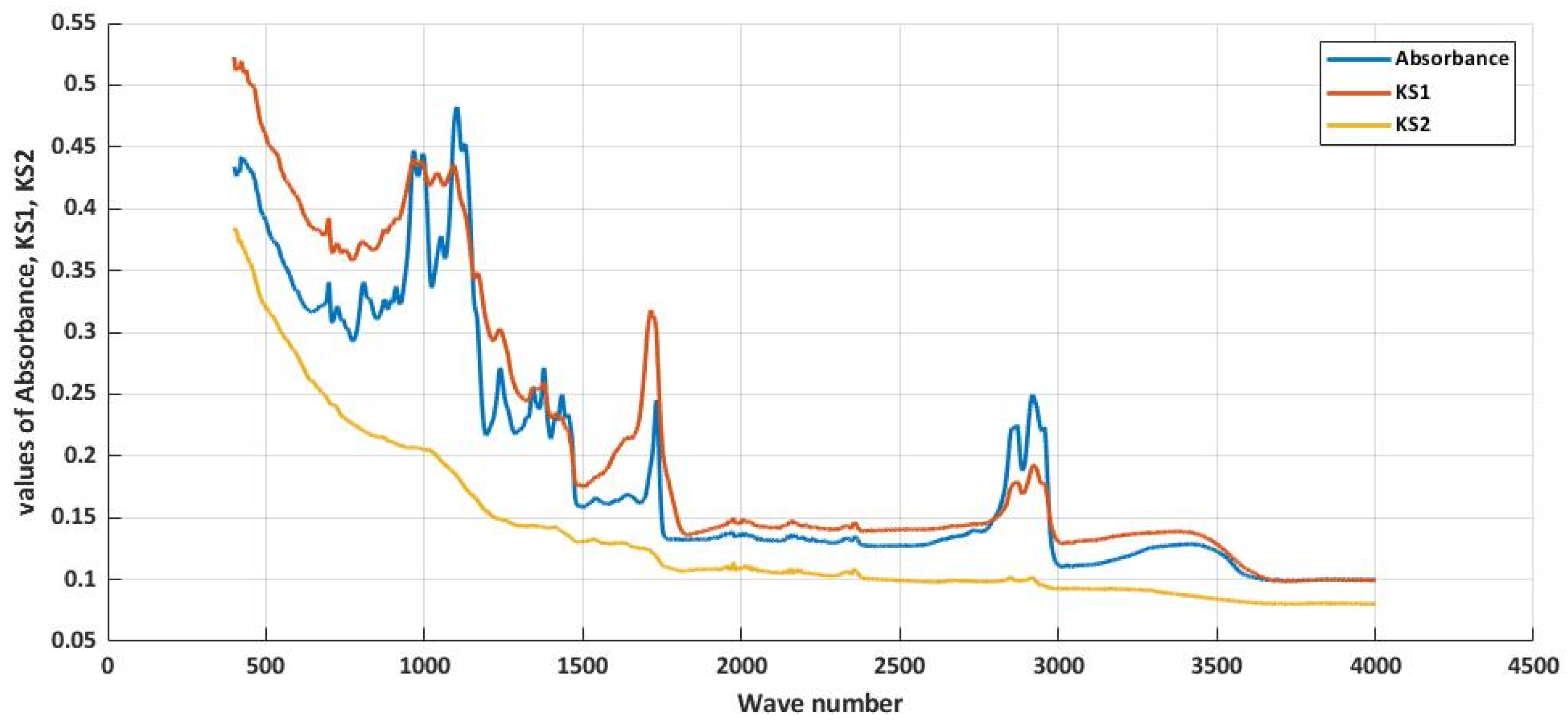

| Method | Neural Net Fitting | Regression Learner | ||||||
|---|---|---|---|---|---|---|---|---|
| Material | VO-20-PVB-80-TF | VO-50-PVB-50-TF | VO-20-PVB-80-TF | VO-50-PVB-50-TF | ||||
| State | KS1 | KS2 | KS1 | KS2 | KS1 | KS2 | KS1 | KS2 |
| R2 | 0.9052 | 0.9866 | 0.7302 | 0.8655 | 0.7617 | 0.6325 | 0.6448 | 0.5659 |
| MAPE | 8.56% | 11.21% | 12.04% | 15.37% | 14.92% | 27.11% | 18.64% | 29.45% |
| MSE | 0.00094 | 0.000708 | 0.00359 | 0.00209 | 0.00237 | 0.00432 | 0.00473 | 0.00188 |
| Values | ||||||||
|---|---|---|---|---|---|---|---|---|
| Wave | 399.19 | 401.12 | 403.05 | 404.97 | 406.90 | 408.83 | 410.76 | 412.69 |
| Absorbance | 0.774 | 0.778 | 0.777 | 0.769 | 0.762 | 0.757 | 0.762 | 0.772 |
| Values | ||||||||
|---|---|---|---|---|---|---|---|---|
| Absorbance | 0.774 | 0.778 | 0.777 | 0.769 | 0.762 | 0.757 | 0.762 | 0.772 |
| KS1 | 0.5702 | 0.5707 | 0.5705 | 0.5692 | 0.5676 | 0.5659 | 0.5675 | 0.5697 |
| KS2 | 0.6809 | 0.6865 | 0.6850 | 0.6702 | 0.6495 | 0.6288 | 0.6482 | 0.6759 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hrehova, S.; Knapcikova, L. The Study of Machine Learning Assisted the Design of Selected Composites Properties. Appl. Sci. 2022, 12, 10863. https://doi.org/10.3390/app122110863
Hrehova S, Knapcikova L. The Study of Machine Learning Assisted the Design of Selected Composites Properties. Applied Sciences. 2022; 12(21):10863. https://doi.org/10.3390/app122110863
Chicago/Turabian StyleHrehova, Stella, and Lucia Knapcikova. 2022. "The Study of Machine Learning Assisted the Design of Selected Composites Properties" Applied Sciences 12, no. 21: 10863. https://doi.org/10.3390/app122110863
APA StyleHrehova, S., & Knapcikova, L. (2022). The Study of Machine Learning Assisted the Design of Selected Composites Properties. Applied Sciences, 12(21), 10863. https://doi.org/10.3390/app122110863







