Dynamic Response of Rectangular Tunnels Embedded at Various Depths in Spatially Variable Soils
Abstract
1. Introduction
2. Random Field Theory
3. Finite Difference Model
4. Results and Discussion
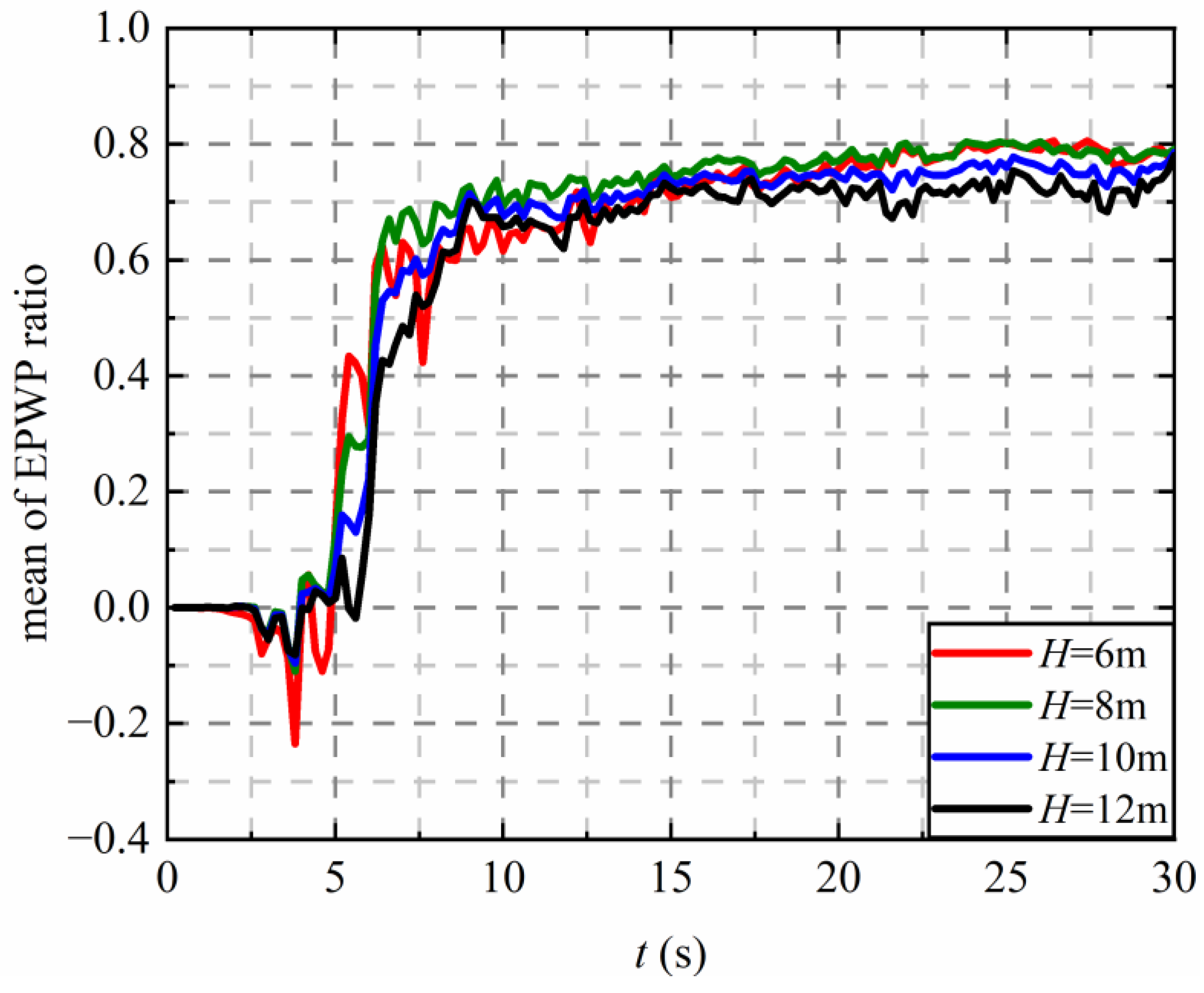
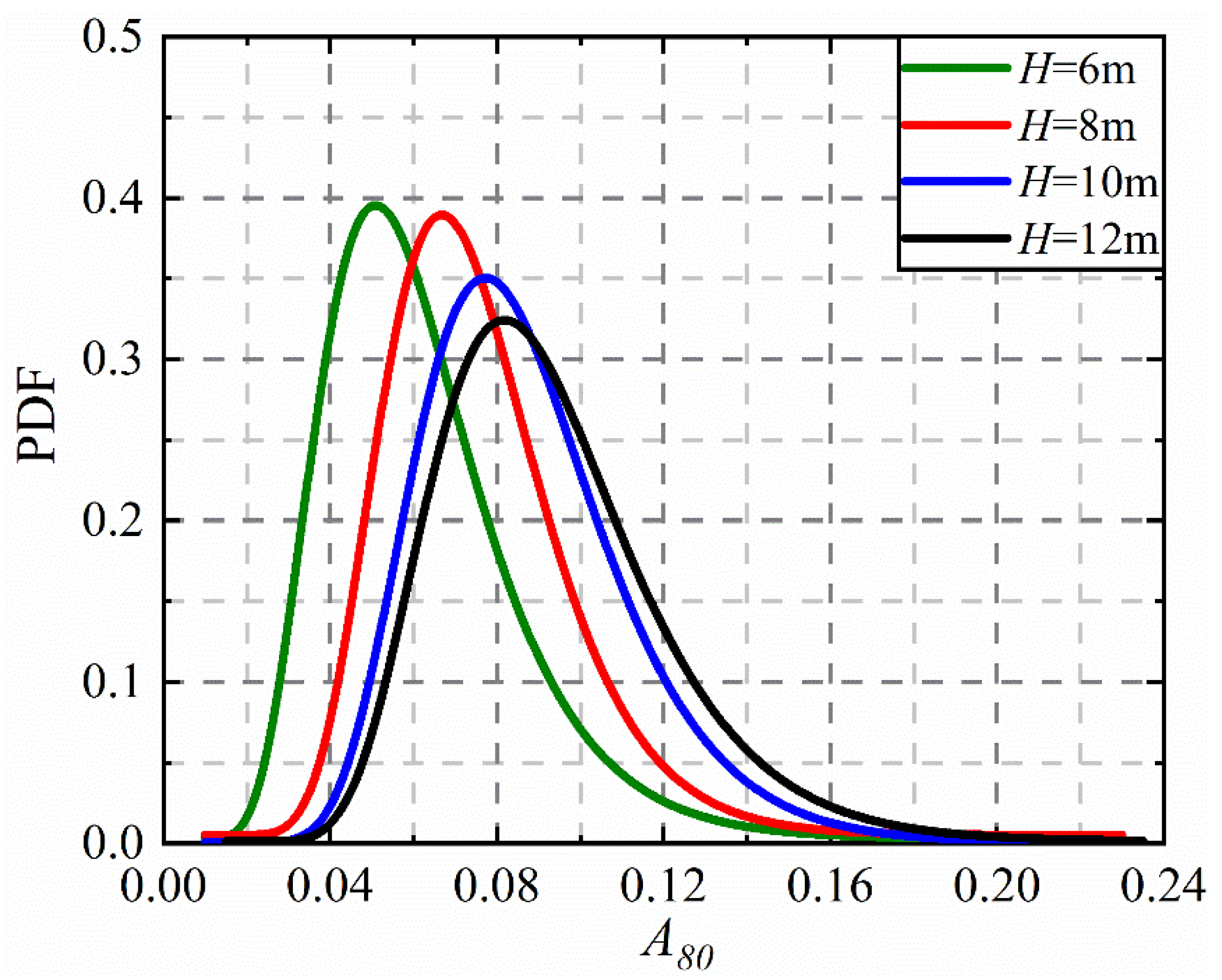
4.1. Effect of Tunnel Embedment Depth on Excess Pore Water Pressure (EPWP) Ratio
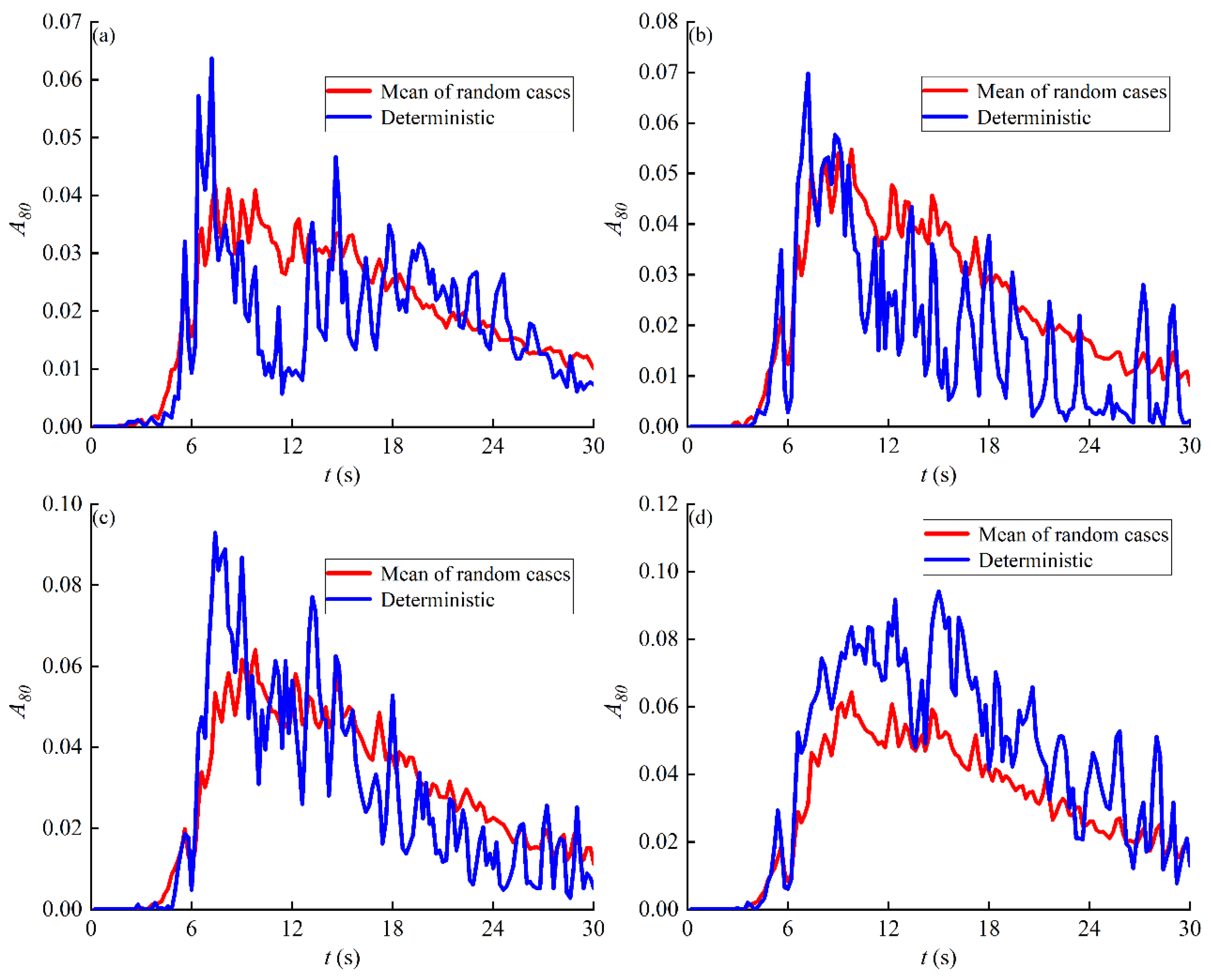
4.2. Effect of Tunnel Embedment Depth on Liquefied Zone
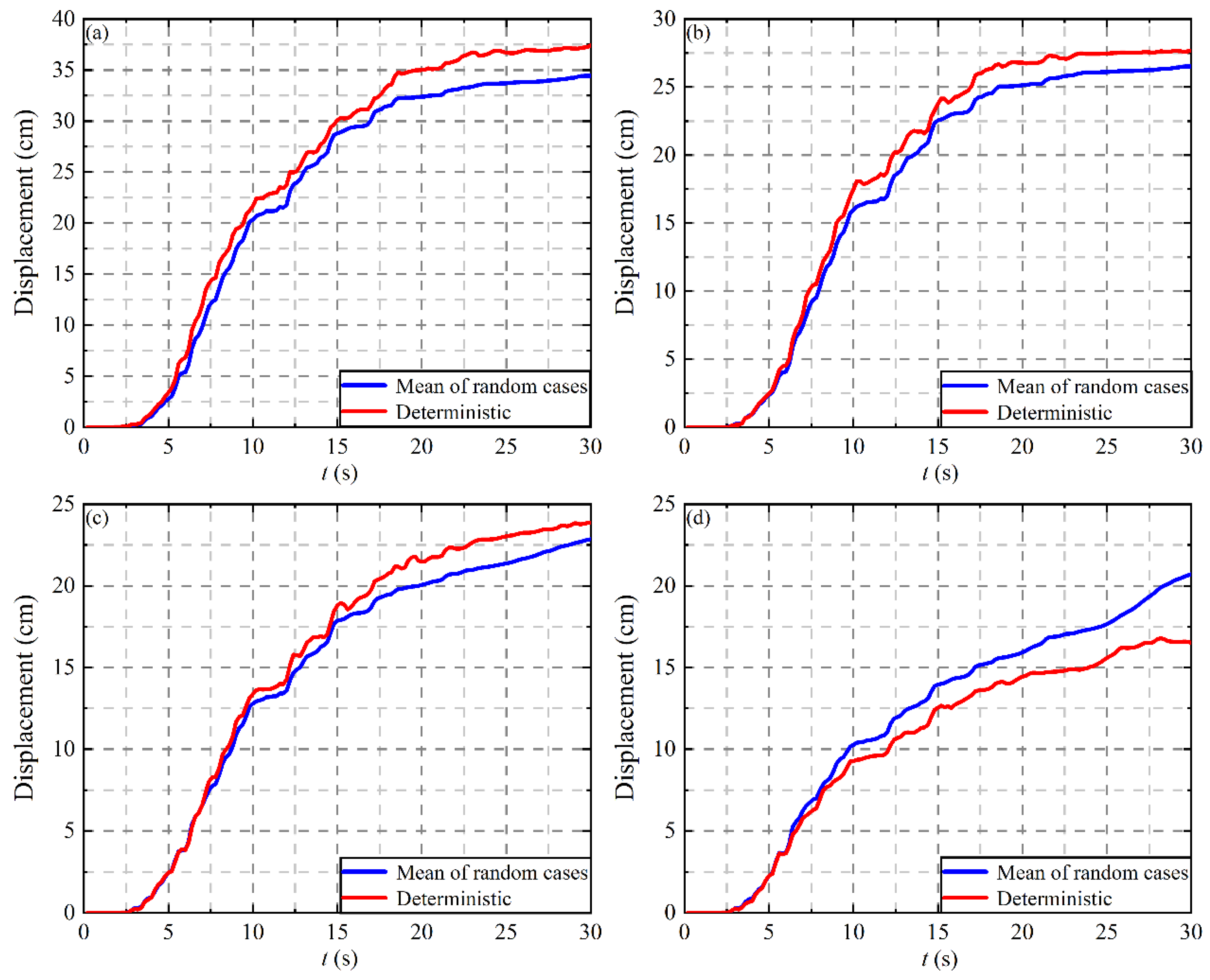
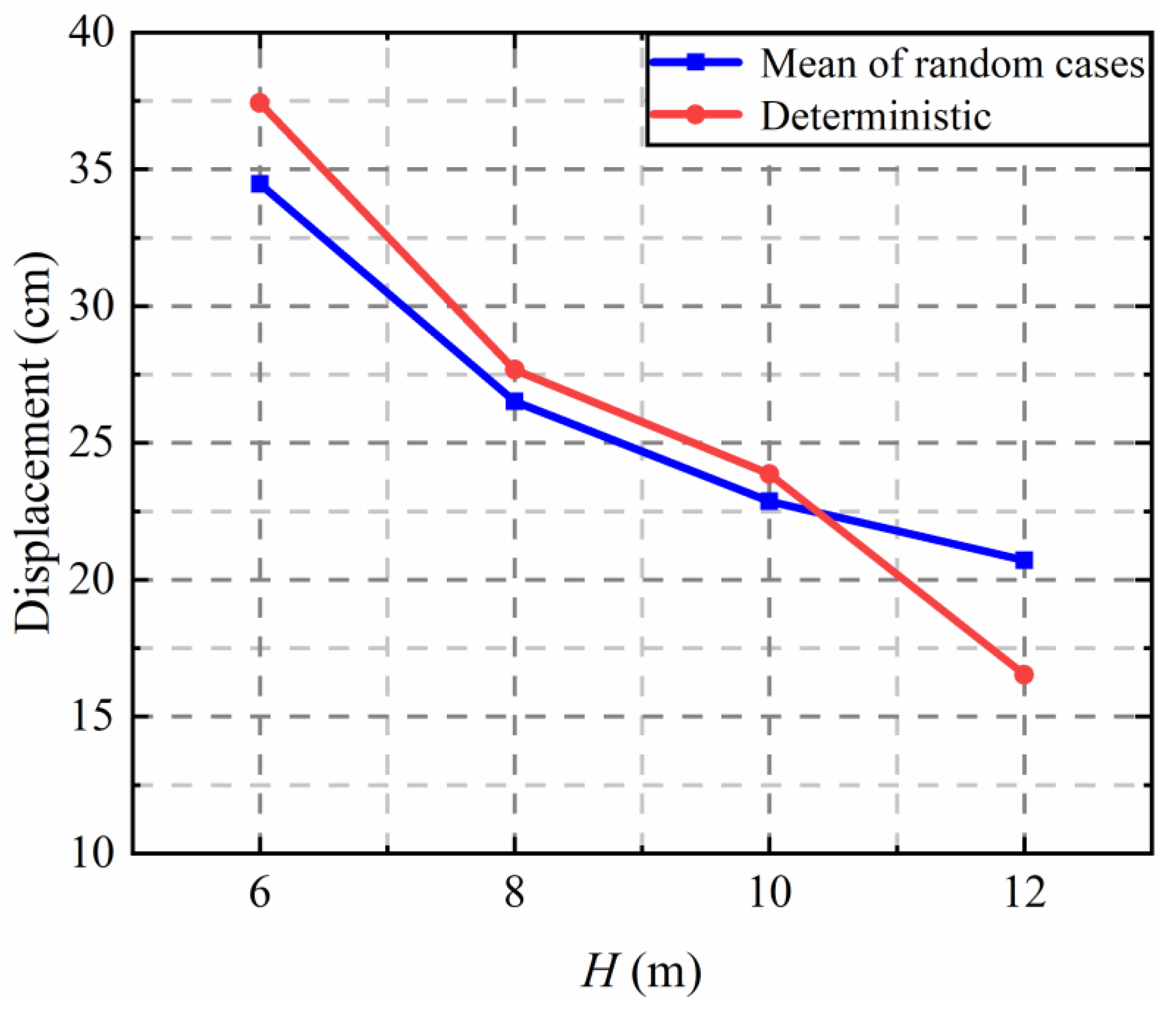
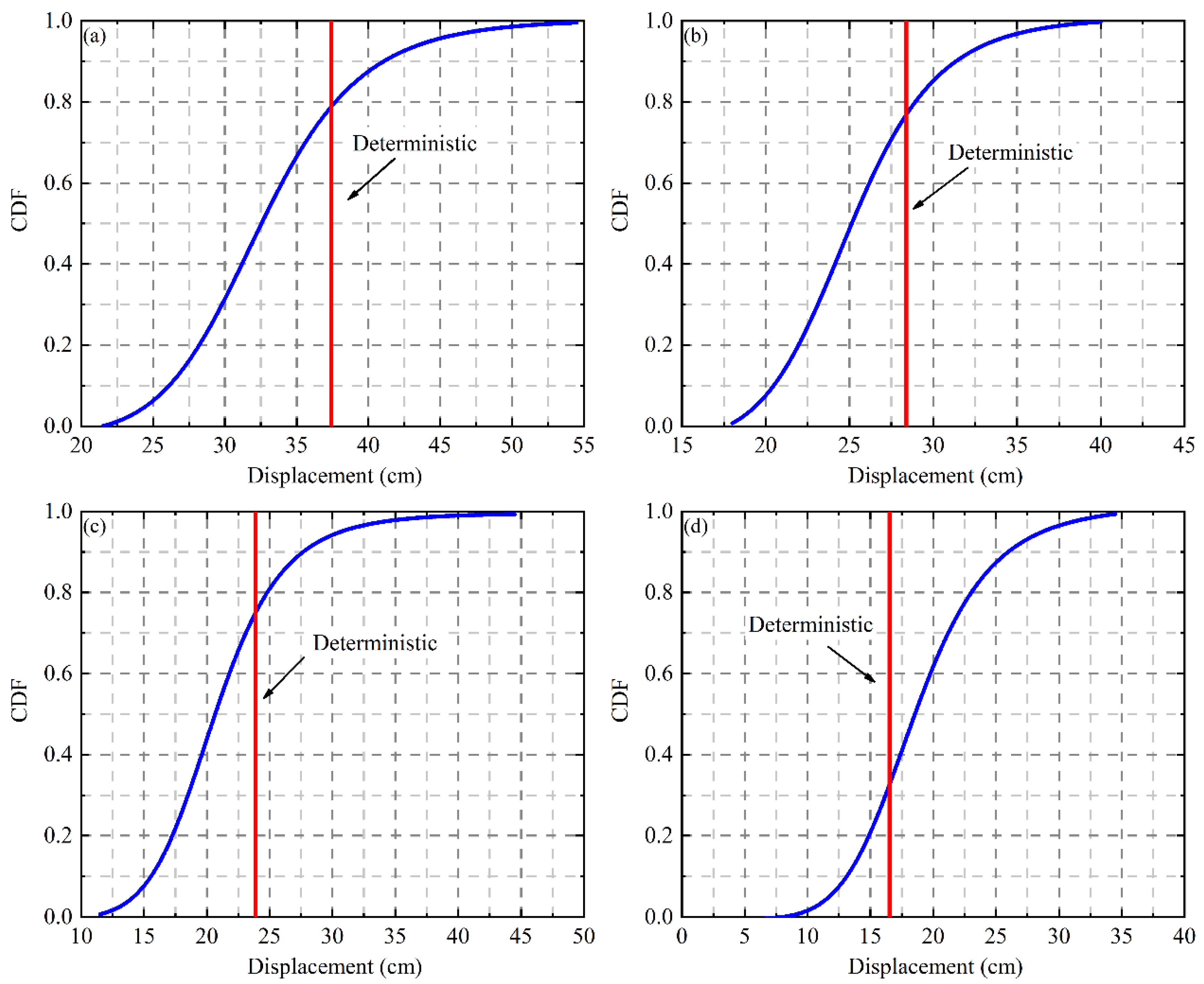
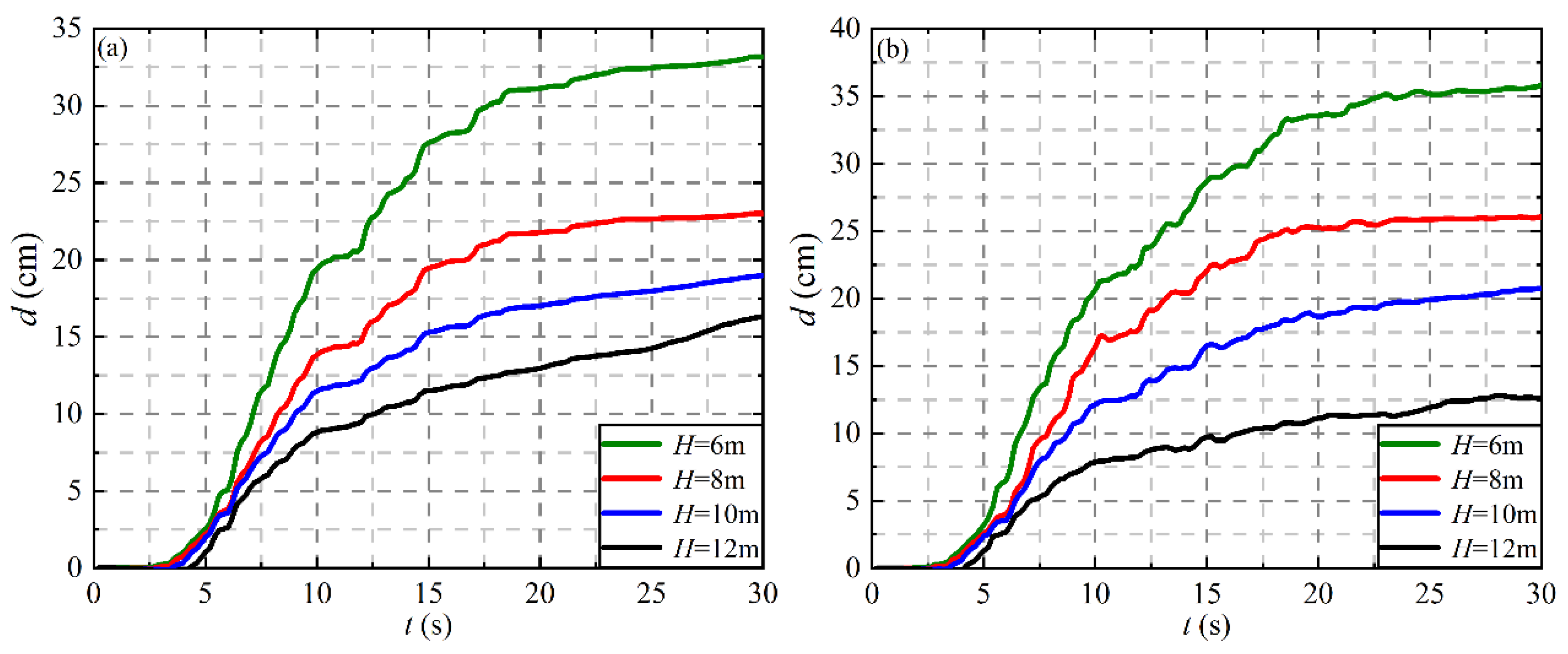
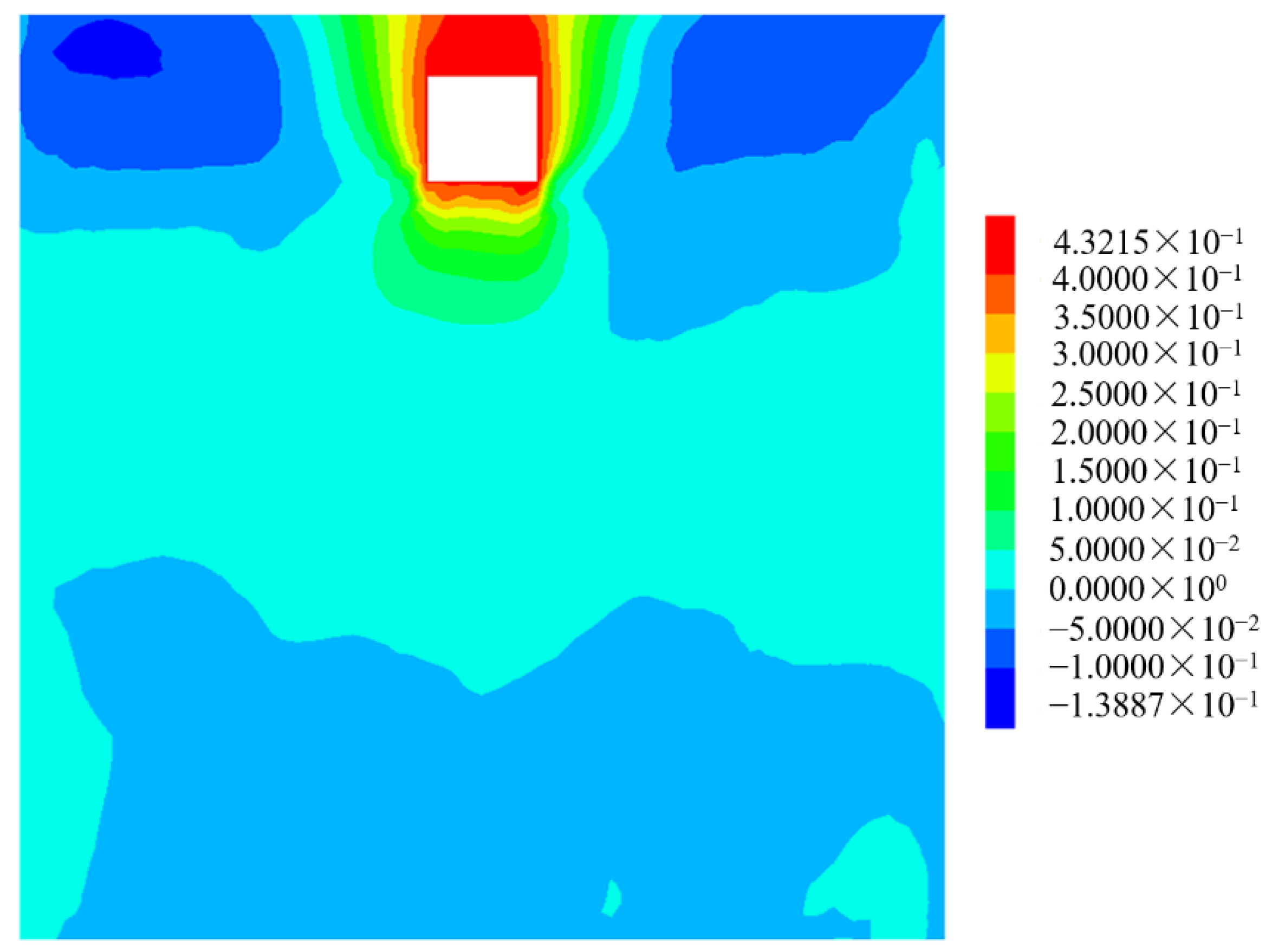
4.3. Effect of Tunnel Embedment Depth on Tunnel Displacement
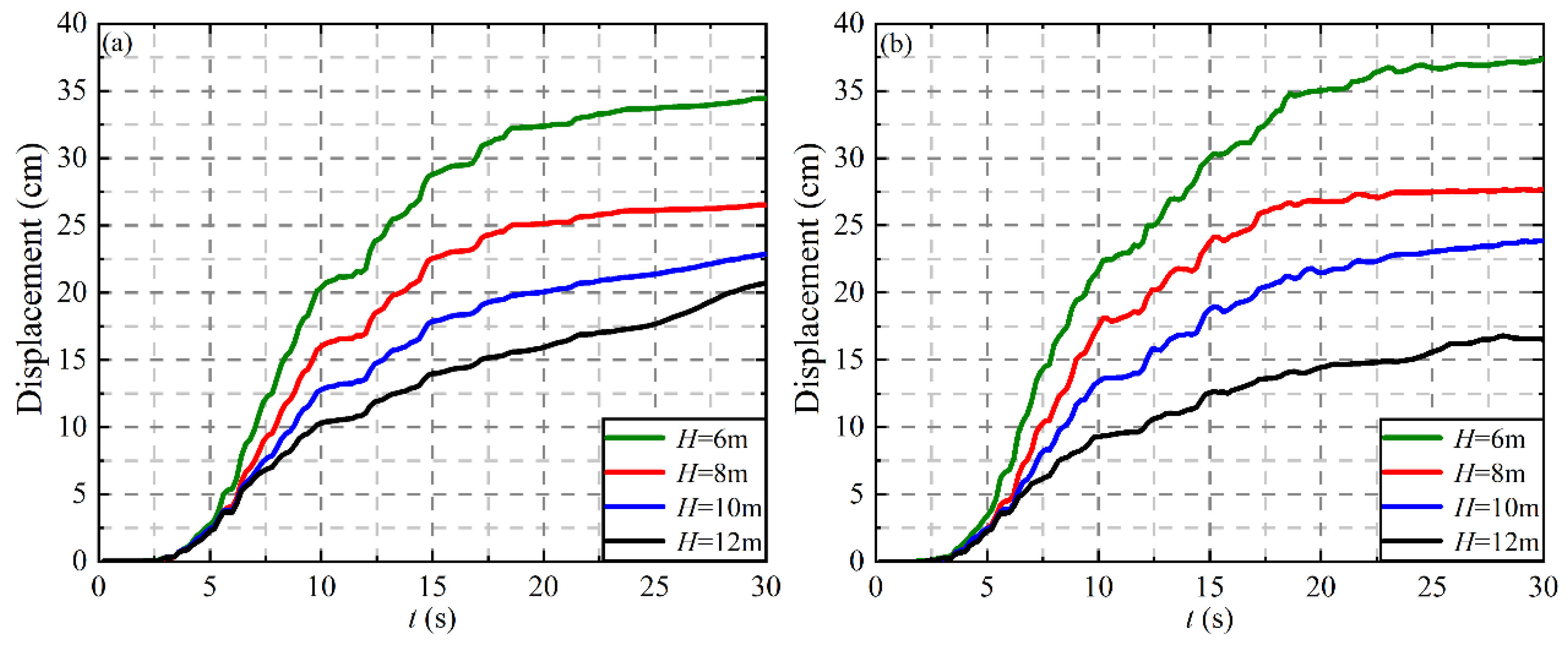
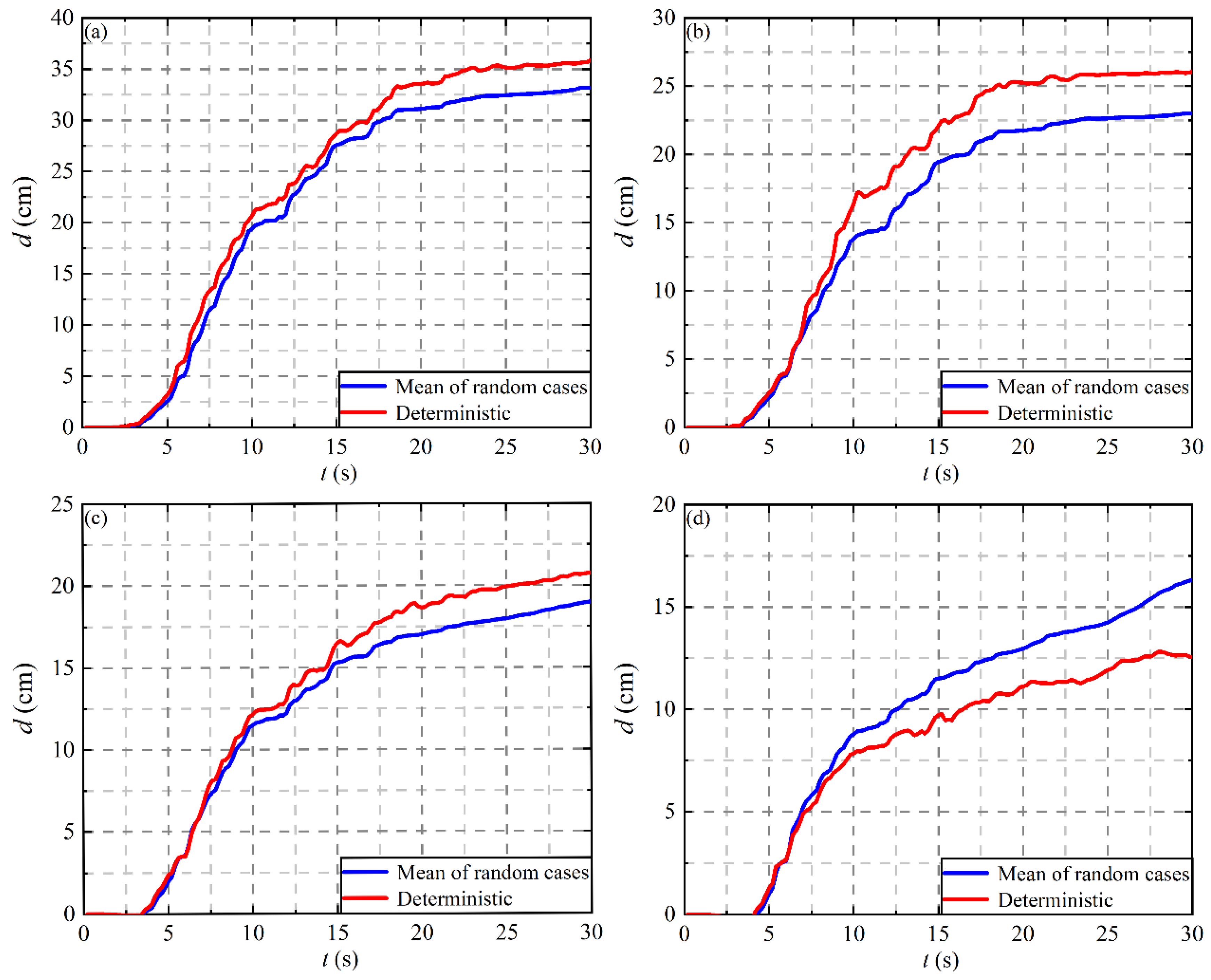
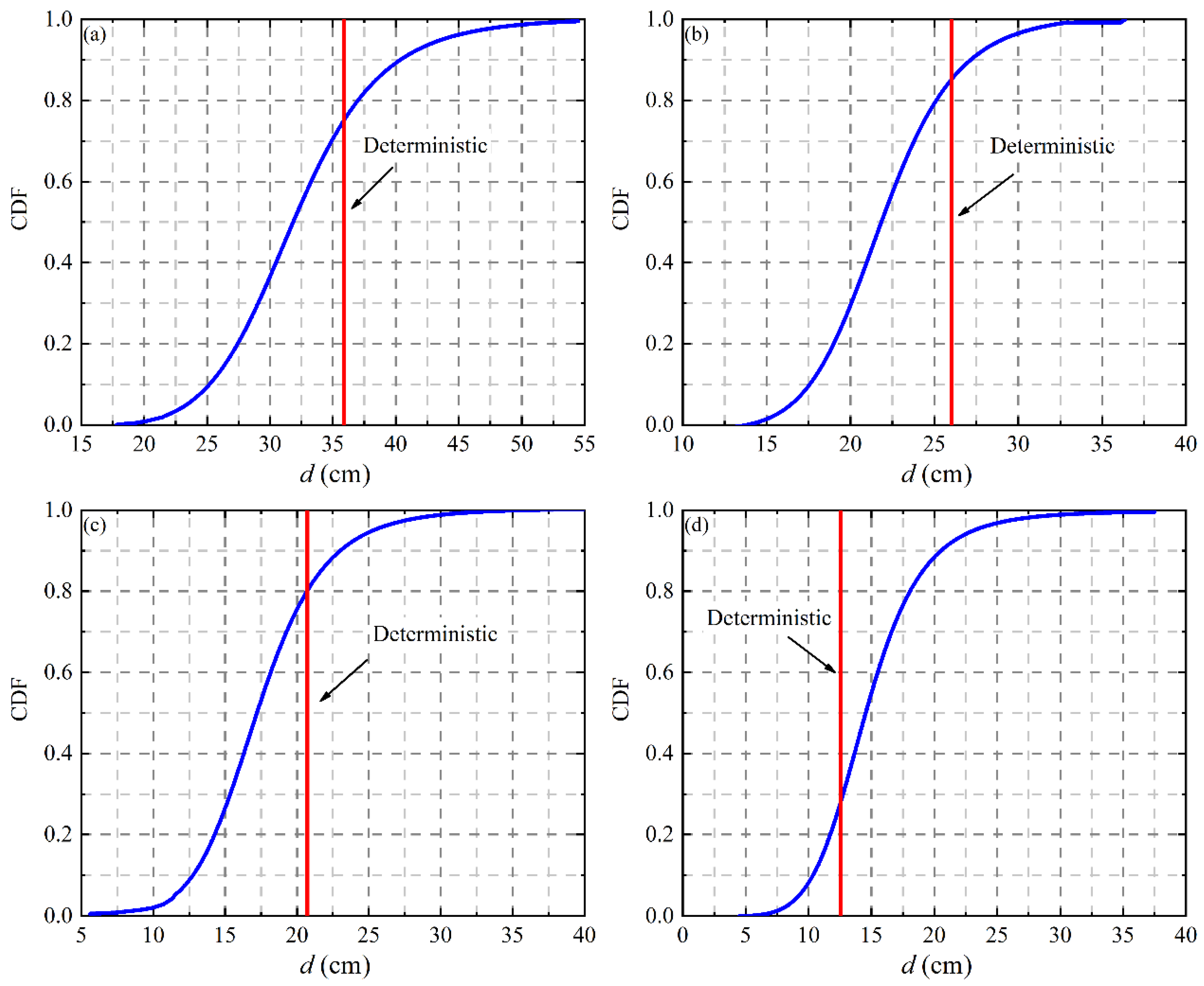
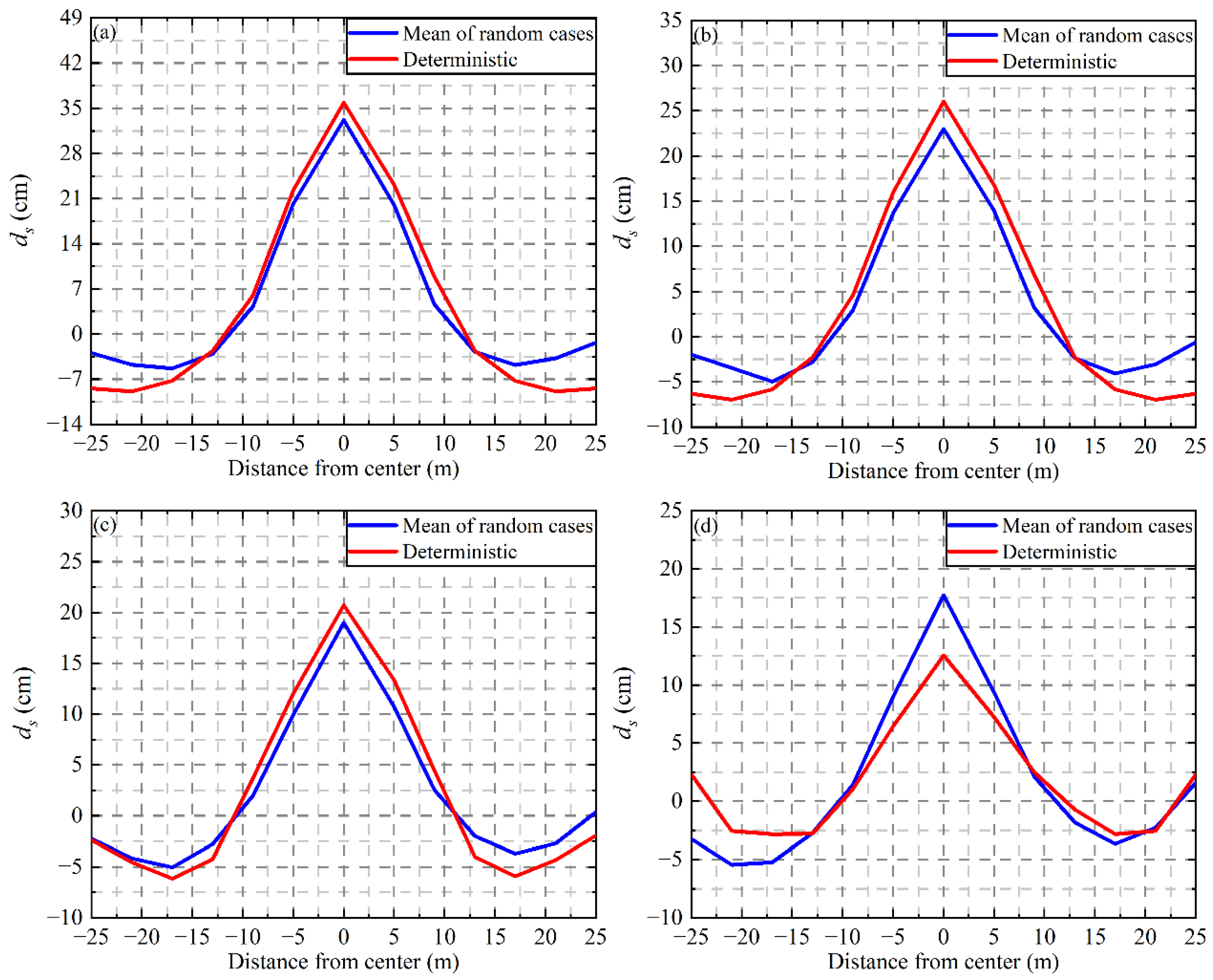
4.4. Effect of Tunnel Embedment Depth on Ground Displacement
5. Conclusions
- (1)
- The excessive static pore pressure ratio and soil liquefaction range are greatly affected by the change in the tunnel embedment depth. With depth increasing, the soil excess pore water pressure ratio under the tunnel gradually decreases and the liquefaction degree reduces. The peak value of the foundation liquefaction range increases with the increase of embedment depth, and the time history of the liquefaction range rises faster over time in the ascending stage, while decreasing faster over time in the descending stage.
- (2)
- The tunnel depth has the same effect on the maximum uplift displacement of the tunnel and the ground surface. With the increase of embedment depth, the thickness of the overlying soil and the gravity of the soil also increase, which leads to the decrease of the maximum displacement of the tunnel and the ground surface, and the decrease of the maximum settlement of soil far away from the tunnel area.
- (3)
- When considering the anisotropy random fields of soil shear modulus, the mean response of stochastic analysis is smaller than the deterministic calculation results when the tunnel embedment depth is less than 10 m. However, when H = 10 m, it will seriously overestimate the deformation of soil and tunnel structure if the soil is regarded as a uniform field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Notation | |
| x, z | transverse and vertical coordinates |
| , | mean and standard deviation of log field |
| standard deviation of the th term | |
| , | standard normally distributed random variables |
| , | frequency coordinate values |
| , | horizontal and vertical lag distances |
| , | horizontal and vertical scales of fluctuation |
| EPWP | excess pore water pressure |
| excess static pore pressure ratio in each element | |
| liquefied zone | |
| u(t) | EPWP at a time instant t |
| initial effective stress | |
| H | Embedment depth of tunnel |
| COV | Coefficient of variation |
| probability density function | |
| CDF | cumulative distribution function |
References
- Hamada, M.; Isoyama, R.; Wakamatsu, K. Liquefaction-induced ground displacement and its related damage to lifeline facilities. Soils Found 1996, 36, 81–97. [Google Scholar] [CrossRef]
- Uenishi, K.; Sakurai, S. Characteristic of the vertical seismic waves associated with the 1995 Hyogo-ken Nanbu (Kobe), Japan earthquake estimated from the failure of the Daikai Underground Station. Earthq. Eng. Struct. Dyn. 2000, 29, 813–821. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Chou, H.S.; Yang, C.Y.; Hsieh, B.J.; Chang, S.S. A study of liquefaction related damages on shield tunnels. Tunn. Undergr. Space Technol. 2001, 16, 185–193. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Miao, Y.; He, H.J.; Liu, H.B.; Wang, S.Y. Reproducing ground response using in-situ soil dynamic parameters. Earthq. Eng. Struct Dyn. 2022, 51, 2449–2465. [Google Scholar] [CrossRef]
- Chen, G.X.; Chen, S.; Qi, C.Z.; Du, X.L.; Wang, Z.H.; Chen, W.Y. Shaking table tests on a three-arch type subway station structure in a liquefiable soil. Bull. Earthq. Eng. 2015, 13, 1675–1701. [Google Scholar] [CrossRef]
- Yu, H.T.; Yan, X.; Bobet, A.; Yuan, Y.; Xu, G.P.; Su, Q.K. Multi-point shaking table test of a long tunnel subjected to non-uniform seismic loadings. Bull. Earthq. Eng. 2018, 16, 1041–1059. [Google Scholar] [CrossRef]
- Hou, C.; Jin, X.G.; Ge, Y.; He, J. Shaking table test on the seismic response of a frame-type subway station in composite soil. Int. J. Geomech. 2021, 21, 04021220. [Google Scholar] [CrossRef]
- Chian, S.C.; Madabhushi, S.P.G. Effect of embedment depth and diameter on uplift of underground structures in liquefied soils. Soil Dyn. Earthq. Eng. 2012, 41, 181–190. [Google Scholar] [CrossRef]
- Lanzano, G.; Bilotta, E.; Russo, G.; Silvestri, F. Experimental and numerical study on circular tunnels under seismic loading. Eur. J. Environ. Civ. Eng. 2015, 19, 539–563. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Li, Y.; Xu, C.S.; Du, X.L.; Dou, P.F.; Yan, G.Y. Study on seismic failure mechanism of shallow embedment underground frame structures based on dynamic centrifuge tests. Soil Dyn. Earthq. Eng. 2021, 150, 106938. [Google Scholar] [CrossRef]
- Yu, H.T.; Chen, J.T.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Miao, Y.; Yao, E.L.; Ruan, B.; Zhuang, H.Y. Seismic response of shield tunnel subjected to spatially varying earthquake ground motions. Tunn. Undergr. Space Technol. 2018, 77, 216–226. [Google Scholar] [CrossRef]
- Banerjee, S.K.; Chakraborty, D. Stability analysis of a circular tunnel underneath a fully liquefied soil layer. Tunn. Undergr. Space Technol. 2018, 78, 84–94. [Google Scholar] [CrossRef]
- Azadi, M.; Hosseini, S.M.M.M. The uplifting behavior of shallow tunnels within the liquefiable soils under cyclic loadings. Tunn. Undergr. Space Technol. 2010, 25, 158–167. [Google Scholar] [CrossRef]
- Song, K.I.; Cho, G.C.; Lee, S.W. Effects of spatially variable weathered rock properties on tunnel behavior. Probabilistic Eng. Mech. 2011, 26, 413–426. [Google Scholar] [CrossRef]
- Mahmoud, A.O.; Hussien, M.N.; Karray, M.; Chekired, M.; Bessette, C.; Jinga, L. Mitigation of liquefaction-induced uplift of underground structures. Comput. Geotech. 2020, 125, 103663. [Google Scholar] [CrossRef]
- Liu, H.B.; Song, E.R. Seismic response of large underground structures in liquefiable soils subjected to horizontal and vertical earthquake excitations. Comput. Geotech. 2005, 32, 223–244. [Google Scholar] [CrossRef]
- Azadi, M.; Hosseini, S.M.M.M. Analyses of the effect of seismic behavior of shallow tunnels in liquefiable grounds. Tunn. Undergr. Space Technol. 2010, 25, 543–552. [Google Scholar] [CrossRef]
- Bao, X.H.; Xia, Z.F.; Ye, G.L.; Fu, Y.B.; Su, D. Numerical analysis on the seismic behavior of a large metro subway tunnel in liquefiable ground. Tunn. Undergr. Space Technol. 2017, 66, 91–106. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, P.B.; Zhou, H.Z.; Zeng, C.F.; Yang, X.Y.; He, X.P.; Yu, X.X. Evaluation of the earthquake induced uplift displacement of tunnels using multivariate adaptive regression splines. Comput. Geotech. 2019, 113, 103099. [Google Scholar] [CrossRef]
- Huang, H.W.; Xiao, L.; Zhang, D.M.; Zhang, J. Influence of spatial variability of soil Young’s modulus on tunnel convergence in soft soils. Eng. Geol. 2017, 228, 357–370. [Google Scholar] [CrossRef]
- Li, K.S.; Lumb, P. Probabilistic design of slopes. Can. Geotech. J. 1987, 24, 520–535. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.M.; Tang, W.H. New methods for system reliability analysis of soil slopes. Can. Geotech. J. 2011, 48, 1138–1148. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic stability analysis of rainfall-induced landslides considering spatial variability of permeability. Eng. Geol. 2014, 171, 11–20. [Google Scholar] [CrossRef]
- Shu, S.; Ge, B.; Wu, Y.X.; Zhang, F. Probabilistic assessment on 3D stability and failure mechanism of undrained slopes. Int. J. Geomech. 2022; accepted. [Google Scholar] [CrossRef]
- Li, L.; Li, J.H.; Huang, J.S.; Liu, H.J.; Cassidy, M.J. The bearing capacity of spudcan foundations under combined loading in spatially variable soils. Eng. Geol. 2017, 227, 139–148. [Google Scholar] [CrossRef]
- Wu, Y.X.; Zhou, X.H.; Gao, Y.F.; Shu, S. Bearing capacity of embedment shallow foundations in spatially random soils with linearly increasing mean undrained shear strength. Comput. Geotech. 2020, 122, 103508. [Google Scholar] [CrossRef]
- Shu, S.; Gao, Y.F.; Wu, Y.X. Probabilistic bearing capacity analysis of spudcan foundation in soil with linearly increasing mean undrained shear strength. Ocean Eng. 2020, 204, 106800. [Google Scholar] [CrossRef]
- Wu, Y.X.; Zhang, H.L.; Shu, S. Probabilistic bearing capacity of spudcan foundations under combined loading in spatially variable soils. Ocean Eng. 2022, 248, 110738. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Gazetas, G.; Tadjbakhsh, I. Stochastic seismic sliding of rigid mass supported through non-symmetric friction. Earthq. Eng. Struct. Dyn. 1984, 12, 777–794. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Probabilistic analyses of tunneling-induced ground movements. Acta Geotech. 2013, 8, 181–199. [Google Scholar] [CrossRef]
- Eshraghi, A.; Zare, S. Face stability evaluation of a TBM-driven tunnel in heterogeneous soil using a probabilistic approach. Int. J. Geomech. 2015, 15, 04014095. [Google Scholar] [CrossRef]
- Miro, S.; Konig, M.; Hartmann, D.; Schanz, T. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study. Comput. Geotech. 2015, 68, 38–53. [Google Scholar] [CrossRef]
- Wu, Y.X.; Bao, H.; Wang, J.C.; Gao, Y.F. Probabilistic analysis of tunnel convergence on spatially variable soil: The importance of distribution type of soil properties. Tunn. Undergr. Space Technol. 2021, 109, 103747. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Huang, H.W.; Zhang, D.M.; Zhou, M.L.; Tang, C.; Liu, D.J. Effect of ground surface surcharge on deformational performance of tunnel in spatially variable soil. Comput. Geotech. 2021, 136, 104229. [Google Scholar] [CrossRef]
- Chen, Q.S.; Wang, C.F.; Juang, C.H. CPT-Based Evaluation of Liquefaction Potential Accounting for Soil Spatial Variability at Multiple Scales. J. Geotech. Geoenviron. 2016, 142, 04015077. [Google Scholar] [CrossRef]
- Wang, C.F.; Chen, Q.S.; Shen, M.F.; Juang, C.H. On the spatial variability of CPT-based geotechnical parameters for regional liquefaction evaluation. Soil Dyn. Earthq. Eng. 2017, 95, 153–166. [Google Scholar] [CrossRef]
- Juang, C.H.; Shen, M.F.; Wang, C.F.; Chen, Q.S. Random field-based regional liquefaction hazard mapping-data inference and model verification using a synthetic digital soil field. Bull. Eng. Geol. Environ. 2018, 77, 1273–1286. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, M.; Baise, L.G.; Kim, B. Local and regional evaluation of liquefaction potential index and liquefaction severity number for liquefaction-induced sand boils in pohang, South Korea. Soil Dyn. Earthq. Eng. 2021, 141, 106459. [Google Scholar] [CrossRef]
- Wang, Y.B.; Shu, S.; Wu, Y.X. Reliability Analysis of Soil Liquefaction Considering Spatial Variability of Soil Property. J. Earthq. Tsunami 2021, 16, 2250002. [Google Scholar] [CrossRef]
- Wang, Y.B.; He, J.J.; Shu, S.; Zhang, H.L.; Wu, Y.X. Seismic responses of rectangular tunnels in liquefiable soil considering spatial variability of soil properties. Soil Dyn. Earthq. Eng. 2022, 162, 107489. [Google Scholar] [CrossRef]
- Ali, A.; Lyamin, A.V.; Huang, J.S.; Sloan, S.W.; Cassidy, M.J. Undrained stability of a single circular tunnel in spatially variable soil subjected to surcharge load. Comput. Geotech. 2017, 84, 16–27. [Google Scholar] [CrossRef]
- Gong, W.P.; Juang, C.H.; Martin, J.R.; Tang, H.M.; Wang, Q.Q.; Huang, H.W. Probabilistic analysis of tunnel longitudinal performance based upon conditional random field simulation of soil properties. Tunn. Undergr. Space Technol. 2018, 73, 1–14. [Google Scholar] [CrossRef]
- Popescu, R.; Deodatis, G.; Nobahar, A. Effects of random heterogeneity of soil properties on bearing capacity. Probabilistic Eng. Mech. 2005, 20, 324–341. [Google Scholar] [CrossRef]
- Popescu, R.; Deodatis, G.; Prevost, J.H. Simulation of non-Gaussian homogeneous stochastic vector fields. Probabilistic Eng. Mech. 1998, 13, 1–13. [Google Scholar] [CrossRef]
- Wu, Y.X.; Li, R.; Gao, Y.F.; Zhang, N.; Zhang, F. Simple and efficient method to simulate homogenous multidimensional non-Gaussian vector field by the spectral representation method. J. Eng. Mech. 2017, 143, 06017016. [Google Scholar] [CrossRef]
- Stefanou, G.; Papadrakakis, M. Assessment of spectral representation and Karhunen-Loeve expansion methods for the simulation of Gaussian stochastic fields. Comput. Methods App. Mech. Eng. 2007, 196, 2465–2477. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, P.B.; Zhou, H.Z.; Zhang, W.B. The uplift response of rectangular tunnel in liquefiable soil. China Civ. Eng. J. 2019, 52, 257–264. [Google Scholar]
- Kang, G.C.; Tobita, T.; Iai, S. Seismic simulation of liquefaction-induced uplift behavior of a hollow cylinder structure buried in shallow ground. Soil Dyn. Earthq. Eng. 2014, 64, 85–94. [Google Scholar] [CrossRef]
- Chian, S.C.; Tokimatsu, K.; Madabhushi, S.P.G. Soil liquefaction-induced uplift of underground structures: Physical and numerical modeling. J. Geotech. Geoenviron. 2014, 140, 04014057. [Google Scholar] [CrossRef]
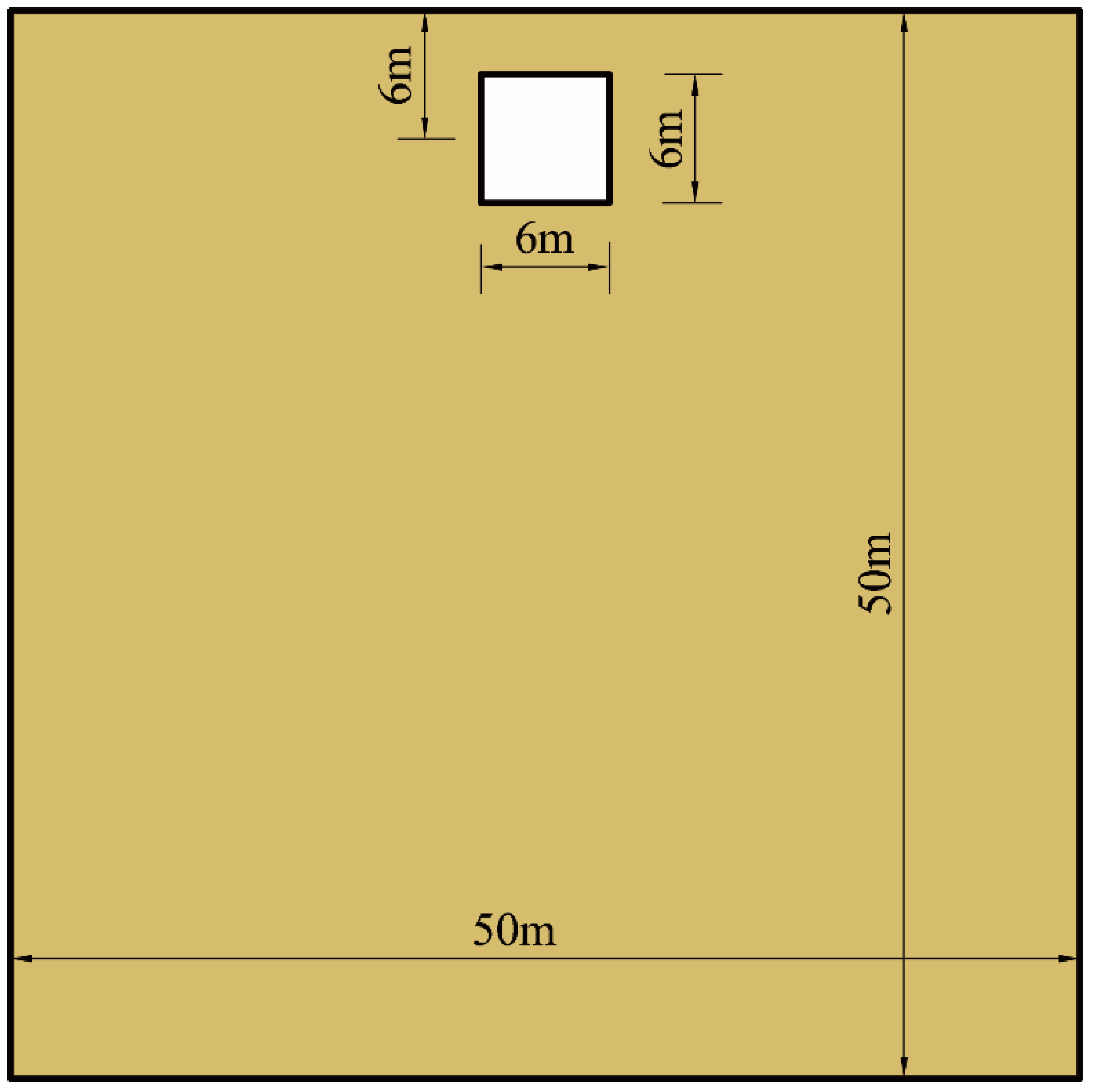


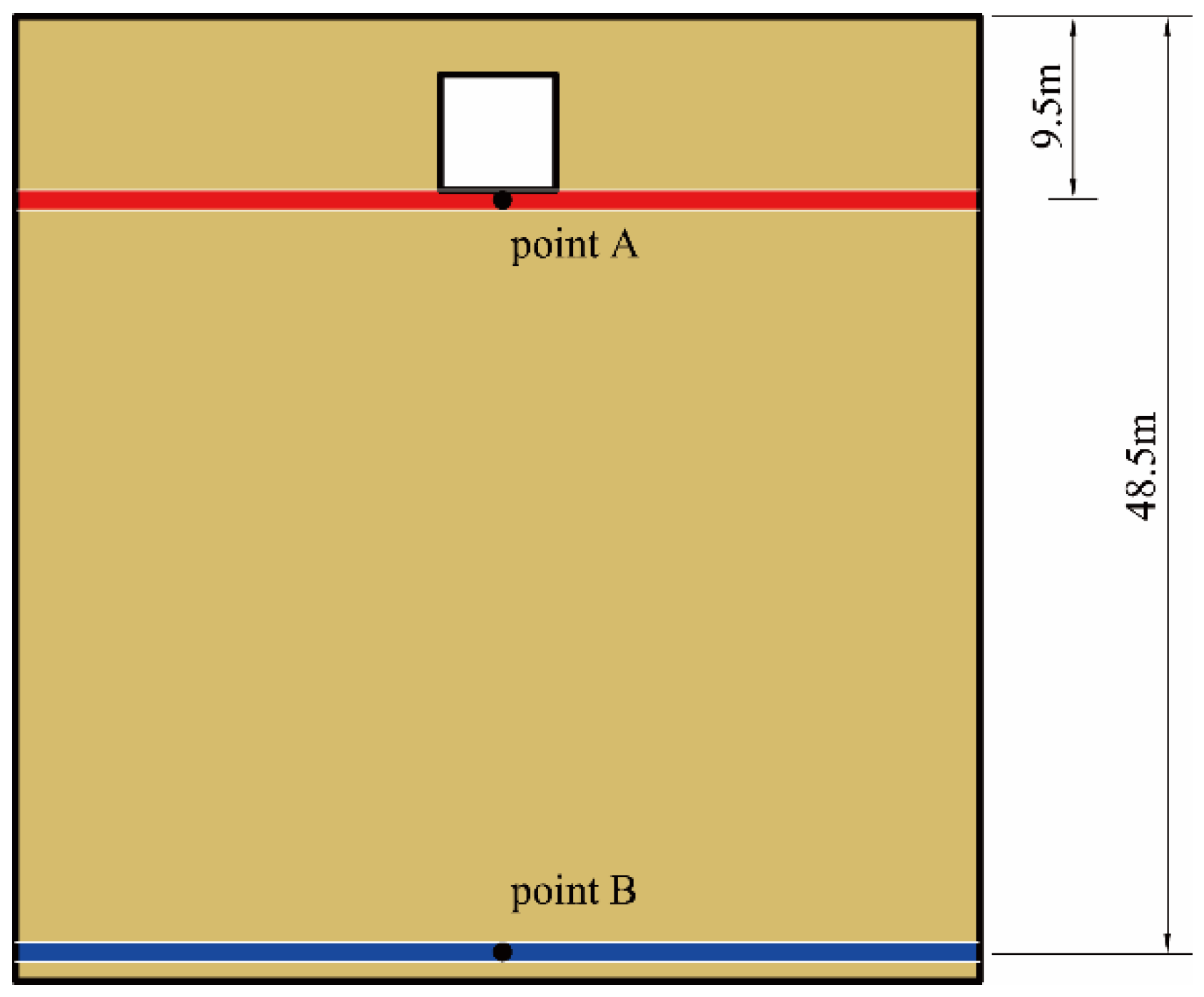





| Soil Parameters | Value | Lining Parameters | Value |
|---|---|---|---|
| Thickness () | 30 | Thickness () | 0.3 |
| Unit weight () | 15 | Unit weight () | 24 |
| Shear modulus () | 20 | Young’s modulus () | 30 |
| Bulk modulus () | 30 | Poisson ratio | 0.25 |
| Friction angle () | 25 | ||
| Cohesion () | 0 |
| Fluid Parameters | Value |
|---|---|
| Permeability coefficient () | 1.0 × 10−4 |
| Fluid density () | 1000 |
| Fluid modulus () | 200 |
| Void ratio | 0.5 |
| H | 6 m | 8 m | 10 m | 12 m |
|---|---|---|---|---|
| Mean of random cases | 96.3% | 86.7% | 83.1% | 78.8% |
| Deterministic case | 95.9% | 94.1% | 86.8% | 76.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, H.; Wu, Y. Dynamic Response of Rectangular Tunnels Embedded at Various Depths in Spatially Variable Soils. Appl. Sci. 2022, 12, 10719. https://doi.org/10.3390/app122110719
Zhang Y, Zhang H, Wu Y. Dynamic Response of Rectangular Tunnels Embedded at Various Depths in Spatially Variable Soils. Applied Sciences. 2022; 12(21):10719. https://doi.org/10.3390/app122110719
Chicago/Turabian StyleZhang, Yanjie, Houle Zhang, and Yongxin Wu. 2022. "Dynamic Response of Rectangular Tunnels Embedded at Various Depths in Spatially Variable Soils" Applied Sciences 12, no. 21: 10719. https://doi.org/10.3390/app122110719
APA StyleZhang, Y., Zhang, H., & Wu, Y. (2022). Dynamic Response of Rectangular Tunnels Embedded at Various Depths in Spatially Variable Soils. Applied Sciences, 12(21), 10719. https://doi.org/10.3390/app122110719





