Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines
Abstract
1. Introduction
2. Related Works
2.1. Existing Physics-Based Datasets
2.2. Magnetic Field Approximation
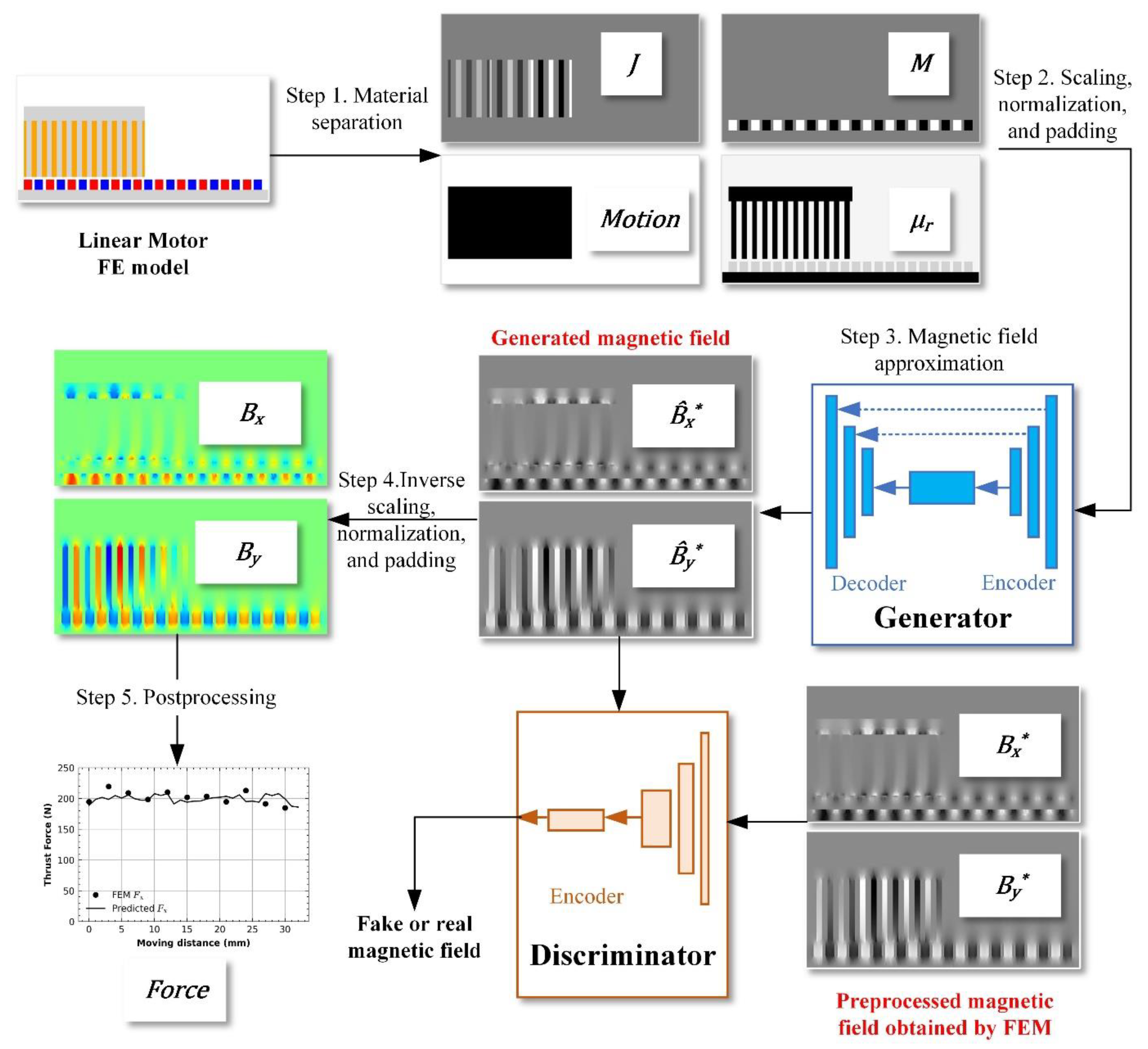
3. Physics-Informed GAN
3.1. Problem Definition for Magnetic Field Approximation
3.2. Structure and Workflow of the PIGAN
3.3. The Physics-Informed Loss Functions
4. The Linear Machine Dataset
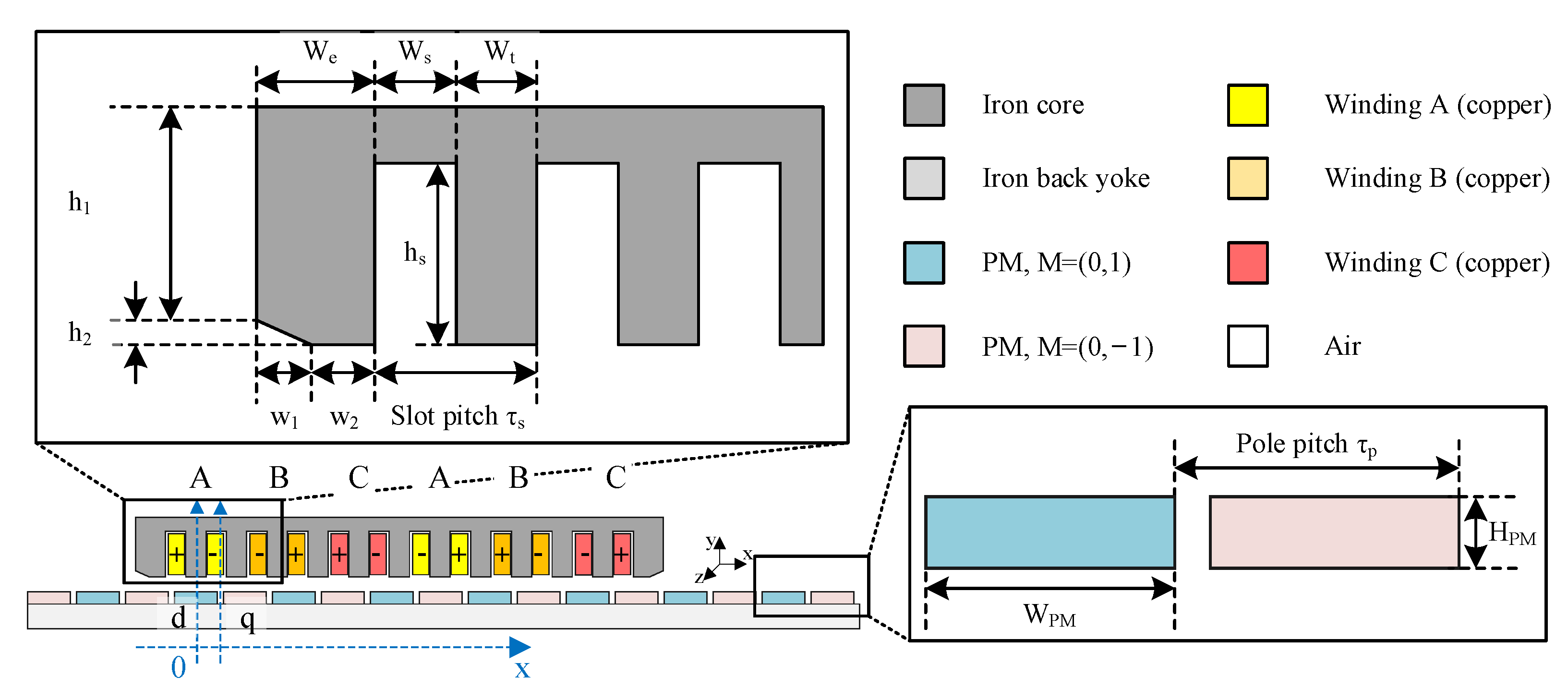
4.1. The Linear Machine Model
4.2. Definition of Physics-Based Channels
- 1.
- Current density (—The current excitation applied to the material on the mesh of the linear motor will be converted to the current density. The number of channels of current density is three in the 3-D problem. In the particular 2-D model, the number of channels of current density can be simplified to one (containing only the vertical direction, such as to ) or two (containing any two components, such as to ) to reduce the storage space occupation.
- 2.
- Magnetization of magnetic materials ()—The relative permeability of the magnetic material is close to one, and this material involves channels for the magnetization direction vector. The magnetization will have two channels in the 2-D problem and three in the 3-D problem. If the magnetization has only one direction in the 2-D problem, one channel will be added to reduce the space complexity.
- 3.
- Motion band ()—The moving part will be marked as 1, and the materials and approximated fields inside the moving band will be extracted after approximation. The number of channels of the motion band is 1.
- 4.
- Permeability of permeable materials ()—The relative permeability of the permeable material is larger than one. The value of channels of the permeable material is one when the material is isotropic. The anisotropy material will have two channels in 2-D problems and three in 3-D problems.
4.3. Dataset Generation
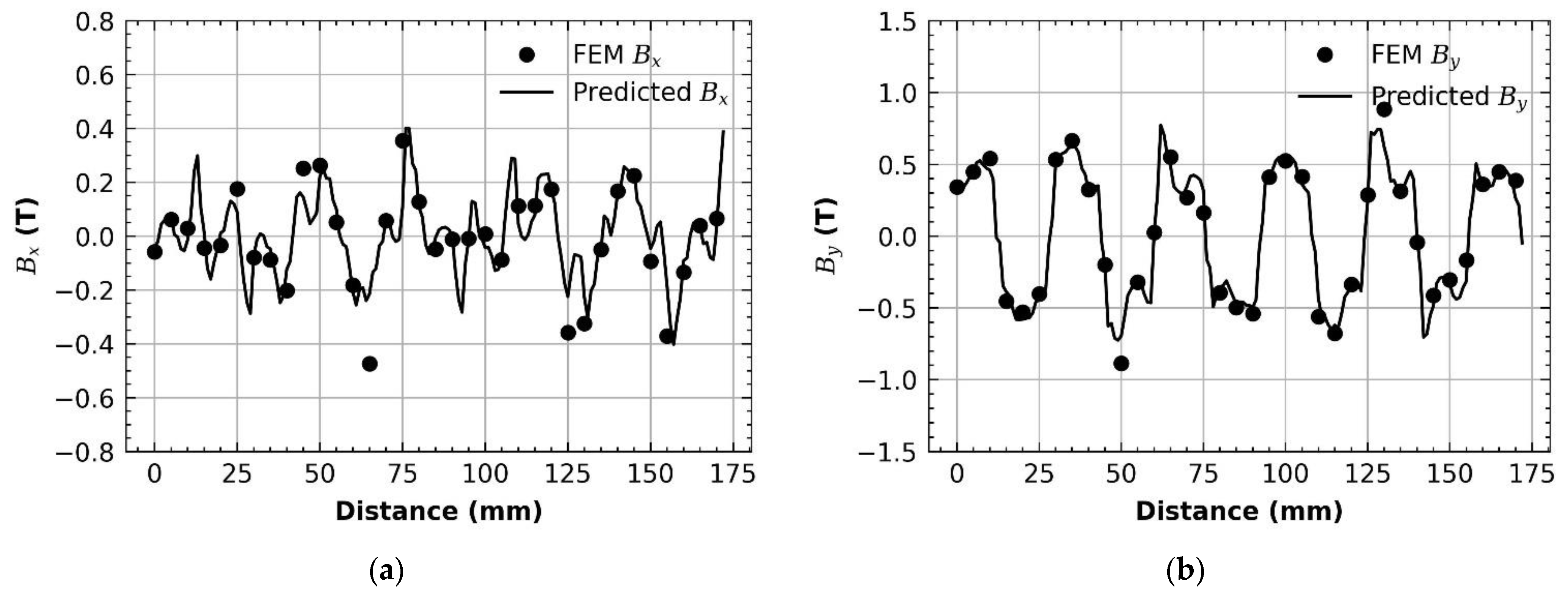
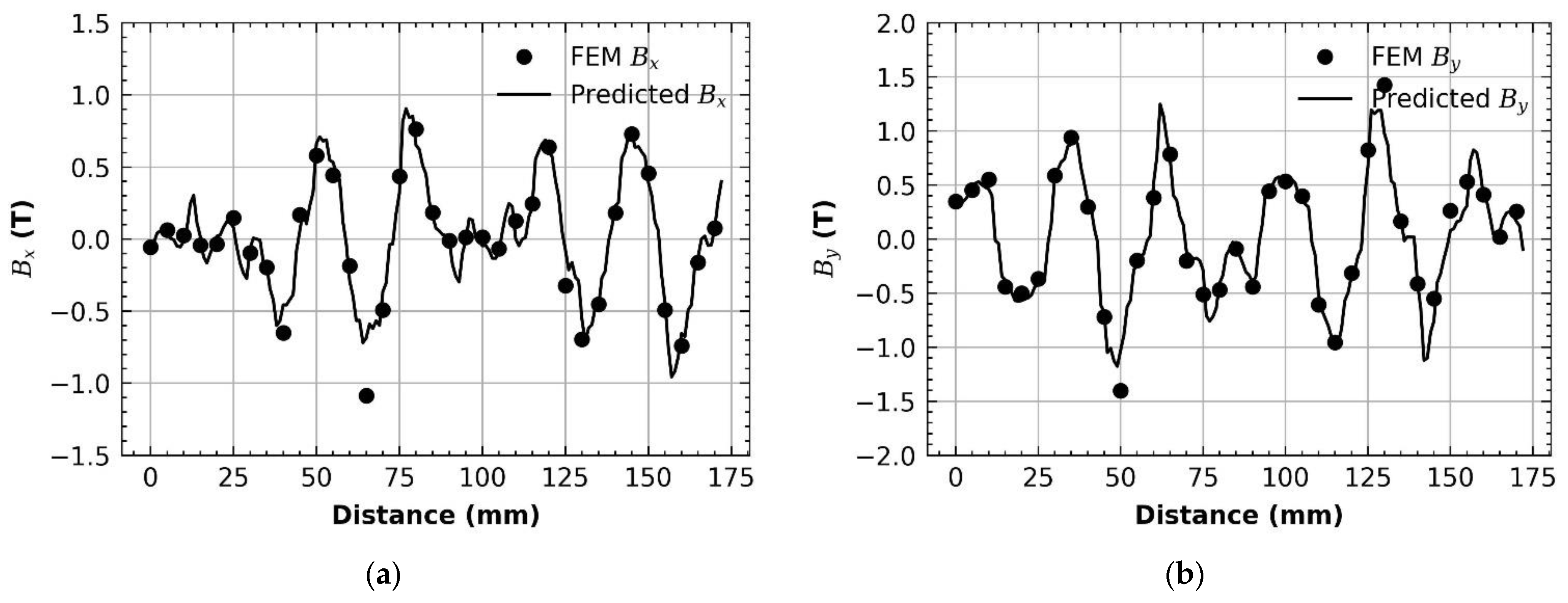
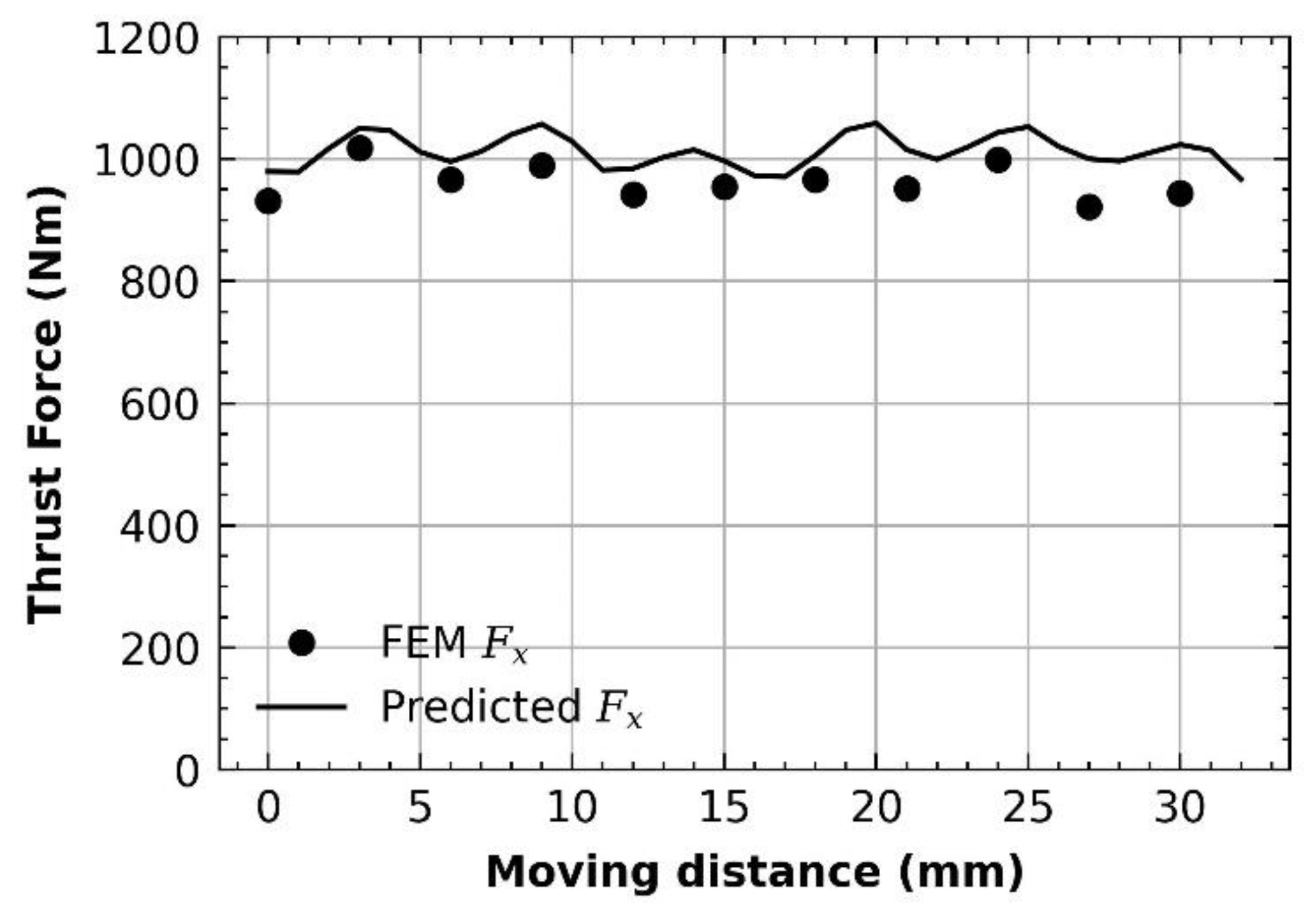
5. Results
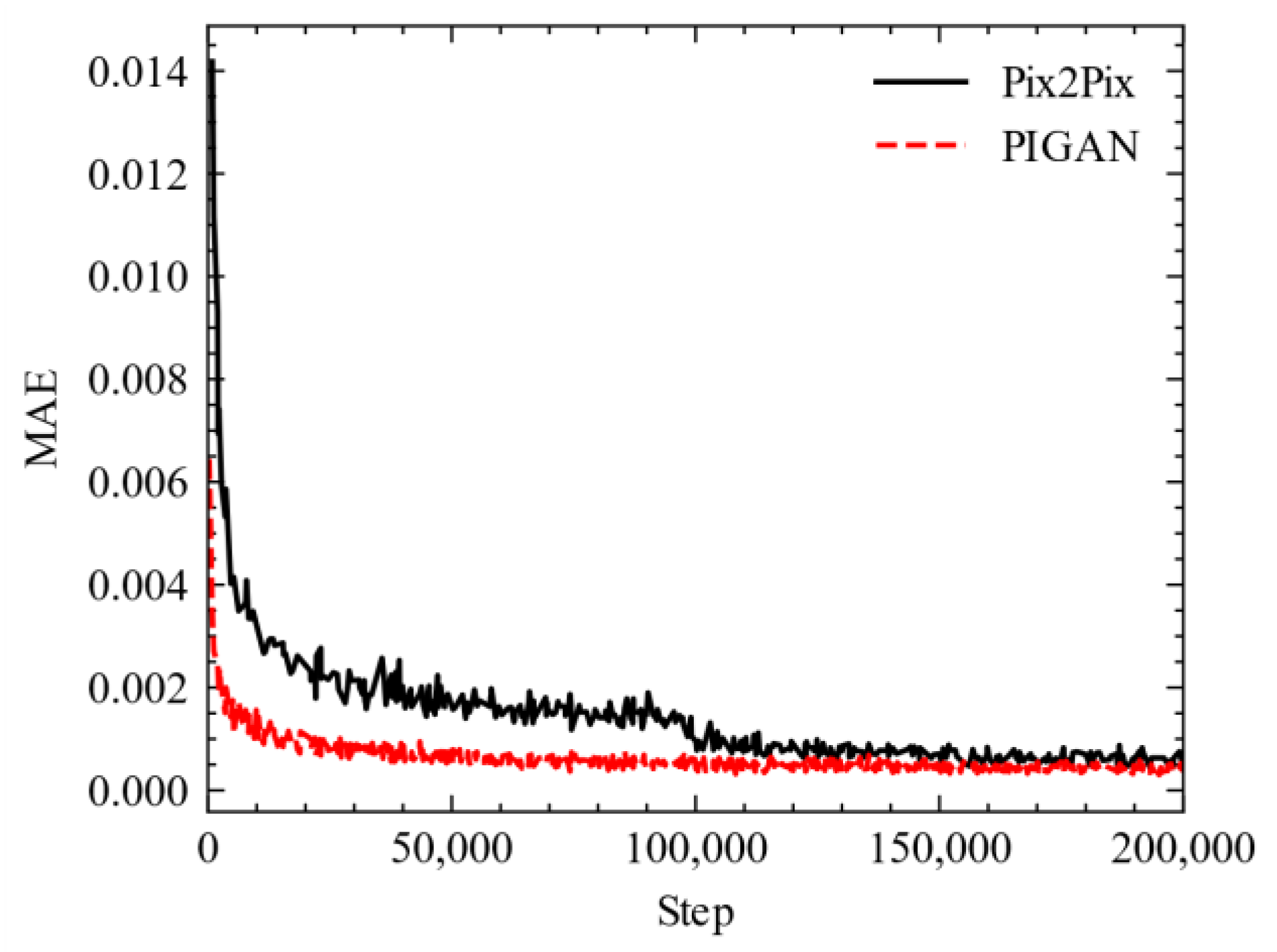
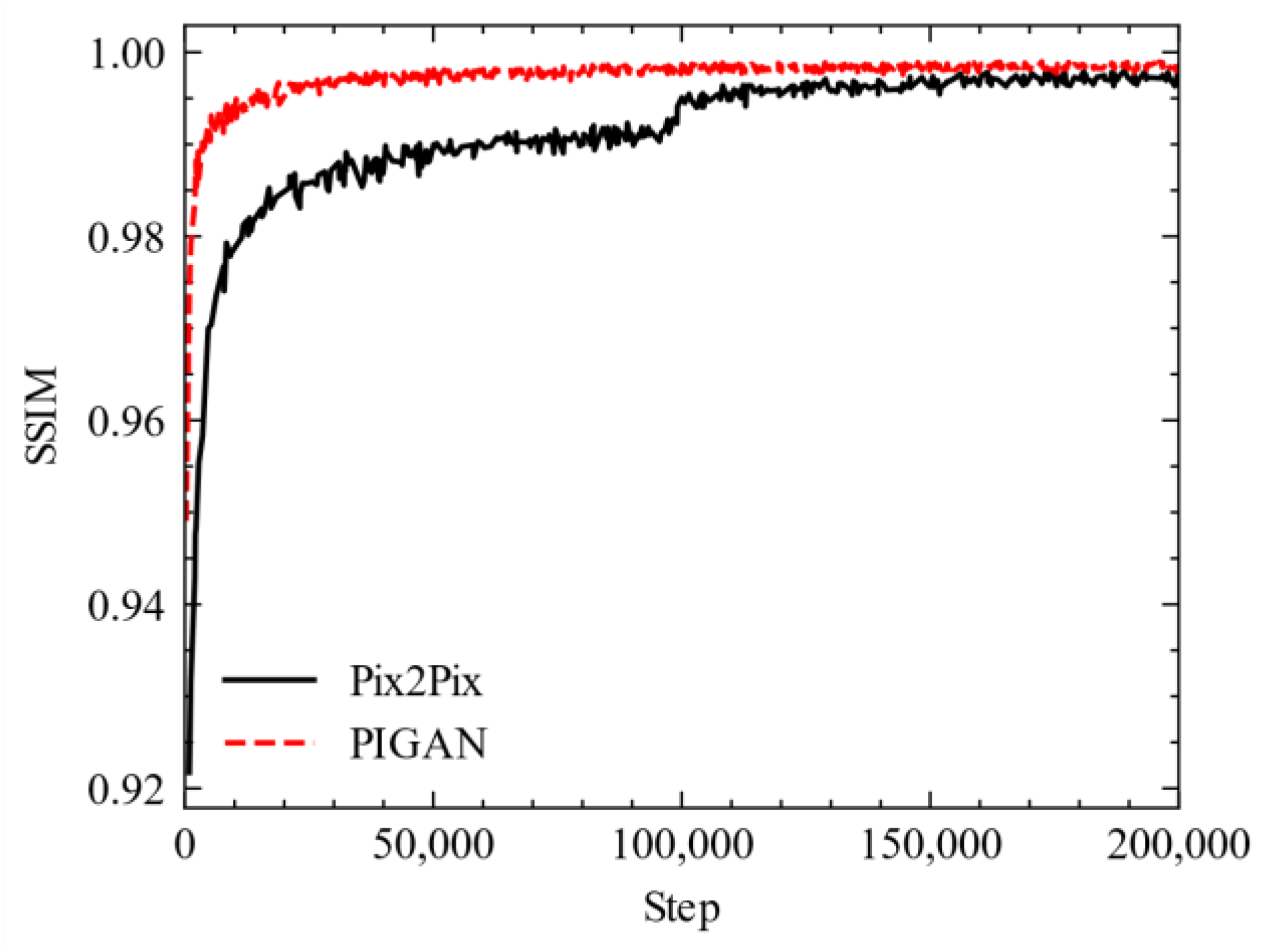
5.1. Evaluation Metrics
5.1.1. Image Synthesis Metrics
5.1.2. Electromagnetic Metric
5.2. Predicted Results of the Linear Machine
6. Discussion
- A.
- 3-D problem
- B.
- Materials
- C.
- Boundary conditions
- D.
- Integration error
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Lei, G.; Bramerdorfer, G.; Peng, S.; Sun, X.; Zhu, J. Machine Learning for Design Optimization of Electromagnetic Devices: Recent Developments and Future Directions. Appl. Sci. 2021, 11, 1627. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Yang, Y.; Liang, R.H.W.; Hui, S.Y. A Comparative Study on Overall Efficiency of 2-Dimensional Wireless Power Transfer Systems Using Rotational and Directional Methods. IEEE Trans. Ind. Electron. 2021, 69, 260–269. [Google Scholar] [CrossRef]
- Yang, H.; Qian, C.; Wang, W.; Lin, H.; Zhu, Z.Q.; Niu, S.; Liu, W.; Lyu, S. A Novel Asymmetric-Magnetic-Pole Interior PM Machine with Magnet-Axis-Shifting Effect. IEEE Trans. Ind. Appl. 2021, 57, 5927–5938. [Google Scholar] [CrossRef]
- Pata, J.; Duarte, J.; Vlimant, J.-R.; Pierini, M.; Spiropulu, M. MLPF: Efficient Machine-Learned Particle-Flow Reconstruction Using Graph Neural Networks. Eur. Phys. J. C 2021, 81, 381. [Google Scholar] [CrossRef]
- Jiang, H.; Nie, Z.; Yeo, R.; Farimani, A.B.; Kara, L.B. StressGAN: A Generative Deep Learning Model for Two-Dimensional Stress Distribution Prediction. J. Appl. Mech. Trans. ASME 2021, 88, 051005. [Google Scholar] [CrossRef]
- Tresser, S.; Dolev, A.; Bucher, I. Dynamic Balancing of Super-Critical Rotating Structures Using Slow-Speed Data via Parametric Excitation. J. Sound Vib. 2018, 415, 59–77. [Google Scholar] [CrossRef]
- Jha, D.; Smedsrud, P.H.; Riegler, M.A.; Johansen, D.; De Lange, T.; Halvorsen, P.; Johansen, H.D. ResUNet++: An Advanced Architecture for Medical Image Segmentation. In Proceedings of the 2019 IEEE International Symposium on Multimedia (ISM), San Diego, CA, USA, 9–11 December 2019; pp. 225–230. [Google Scholar] [CrossRef]
- Hanke, S.; Wallscheid, O.; Böcker, J. Data Set Description: Identifying the Physics Behind an Electric Motor—Data-Driven Learning of the Electrical Behavior (Part I). arXiv 2020, arXiv:2003.06268. [Google Scholar]
- Kirchgassner, W.; Wallscheid, O.; Bocker, J. Estimating Electric Motor Temperatures with Deep Residual Machine Learning. IEEE Trans. Power Electron. 2021, 36, 7480–7488. [Google Scholar] [CrossRef]
- Mcgregor, S.; Dhuri, D.; Berea, A.; Muñoz-Jaramillo, A. FlareNet: A Deep Learning Framework for Solar Phenomena Prediction. In Proceedings of the Workshop on Deep Learning for Physical Sciences (DLPS 2017), NIPS 2017, Long Beach, CA, USA, 8 December 2017; pp. 1–5. [Google Scholar]
- Mokhtar, F.; Kansal, R.; Diaz, D.; Duarte, J.; Pata, J.; Pierini, M.; Vlimant, J.-R. Explaining Machine-Learned Particle-Flow Reconstruction. arXiv 2021, arXiv:2111.12840. [Google Scholar]
- Ma, Z.; Xu, K.; Song, R.; Wang, C.-F.; Chen, X. Learning-Based Fast Electromagnetic Scattering Solver Through Generative Adversarial Network. IEEE Trans. Antennas Propag. 2020, 69, 2194–2208. [Google Scholar] [CrossRef]
- Gong, R.; Tang, Z. Investigation of Convolutional Neural Network U-Net under Small Datasets in Transformer Magneto-Thermal Coupled Analysis. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 959–970. [Google Scholar] [CrossRef]
- Wu, H.; Niu, S.; Zhang, Y.; Zhao, X.; Fu, W. Fast Magnetic Field Approximation Method for Simulation of Coaxial Magnetic Gears Using AI. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 1–9. [Google Scholar] [CrossRef]
- Weinkauf, T.; Theisel, H. Streak Lines as Tangent Curves of a Derived Vector Field. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1225–1234. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Ghorbanian, V.; Lowther, D. Deep Learning for Magnetic Field Estimation. IEEE Trans. Magn. 2019, 55, 7202304. [Google Scholar] [CrossRef]
- Brunton, S.L.; Budišić, M.; Kaiser, E.; Kutz, J.N. Modern Koopman Theory for Dynamical Systems. arXiv 2021, arXiv:2102.12086. [Google Scholar] [CrossRef]
- Essien, A.; Giannetti, C. A Deep Learning Model for Smart Manufacturing Using Convolutional LSTM Neural Network Autoencoders. IEEE Trans. Ind. Inform. 2020, 16, 6069–6078. [Google Scholar] [CrossRef]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep Learning for Universal Linear Embeddings of Nonlinear Dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.H.; Ghorbanian, V.; Lowther, D.A. A Data-Driven Approach for Design Knowledge Extraction of Synchronous Reluctance Machines Using Multi-Physical Analysis. In Proceedings of the 2018 23rd International Conference on Electrical Machines, ICEM 2018, Alexandroupoli, Greece, 3–6 September 2018; pp. 479–485. [Google Scholar] [CrossRef]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine Learning Accelerated Computational Fluid Dynamics. Proc Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
- Gong, R.; Tang, Z. Training Sample Selection Strategy Applied to CNN in Magneto-Thermal Coupled Analysis. IEEE Trans. Magn. 2021, 9464, 8–11. [Google Scholar] [CrossRef]
- Pollok, S.; Bjork, R.; Jorgensen, P.S. Inverse Design of Magnetic Fields Using Deep Learning. IEEE Trans. Magn. 2021, 57, 2101604. [Google Scholar] [CrossRef]
- Doi, S.; Sasaki, H.; Igarashi, H. Multi-Objective Topology Optimization of Rotating Machines Using Deep Learning. IEEE Trans. Magn. 2019, 55, 7202605. [Google Scholar] [CrossRef]
- Qi, S.; Wang, Y.; Li, Y.; Wu, X.; Ren, Q.; Ren, Y. Two-Dimensional Electromagnetic Solver Based on Deep Learning Technique. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 83–88. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Arora, S.; Ge, R.; Liang, Y.; Ma, T.; Zhang, Y. Generalization and Equilibrium in Generative Adversarial Nets (GANs). In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney Australia, 6–11 August 2017; Volume 1, pp. 322–349. [Google Scholar]
- Remy, G.; Krebs, G.; Tounzi, A.; Barre, P. Finite Element Analysis of a PMLSM (Part 1)—Meshing Techniques and Thrust Computations. In Proceedings of the 6th International Symposium on Linear Drives for Industrial Applications, Lille, France, 16–19 September 2007; pp. 2–5. [Google Scholar]
- Remy, G.; Krebs, G.; Tounzi, A.; Barre, P. Finite Element Analysis of a PMLSM (Part 2)—Cogging Force and End-Effect Force Calculations. In Proceedings of the 6th International Symposium on Linear Drives for Industrial Applications, Lille, France, 16–19 September 2007; pp. 2–5. [Google Scholar]
- Remy, G.; Krebs, G.; Tounzi, A.; Barre, P.J. Detent Force Calculations of a PMLSM Using the Finite Element Method. IEEJ Trans. Ind. Appl. 2009, 129, 462–469. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Le, M.; Pham, C.T.; Lee, J. Deep Neural Network for Simulation of Magnetic Flux Leakage Testing. Meas. J. Int. Meas. Confed. 2021, 170, 108726. [Google Scholar] [CrossRef]
- Pan, J.; Liu, Y.; Dong, J.; Zhang, J.; Ren, J.; Tang, J.; Tai, Y.W.; Yang, M.H. Physics-Based Generative Adversarial Models for Image Restoration and Beyond. arXiv 2018. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Pollok, S.; Olden-Jørgensen, N.; Jørgensen, P.S.; Bjørk, R. Magnetic Field Prediction Using Generative Adversarial Networks. arXiv 2022, arXiv:2203.07897. [Google Scholar]



| Parameter | Value | Unit |
|---|---|---|
| Winding type | Concentrate Winding | - |
| Number of turns | 380 | - |
| Residual flux density of the PMs | 1.23 | T |
| Number of slots | 12 | - |
| Airgap length | 0.8 | mm |
| Edge Height (h1) | 17.4 | mm |
| Edge Height (h2) | 2.0 | mm |
| Edge Width (w1) | 4.5 | mm |
| Edge Width (w2) | 5.2 | mm |
| Variable | Min. | Max. | Unit | |
|---|---|---|---|---|
| We | Edge of the PMLSM | 5 | 20 | mm |
| Ws | Width of the slot | 5 | 11 | mm |
| hs | Height of the slot | 8 | 15 | mm |
| Wt | Width of the teeth | 5 | 11 | mm |
| τp | Pole pitch | 12 | 16 | mm |
| WPM | PM length | 10 | 20 | mm |
| irms | Input current | 1 | 16 | A |
| Parameter | Value | Unit | |
|---|---|---|---|
| We | Edge of the PMLSM | 9.7 | mm |
| Ws | Width of the slot | 6.6 | mm |
| hs | Height of the slot | 14.8 | mm |
| Wt | Width of the teeth | 6.6 | mm |
| τp | Pole pitch | 16 | mm |
| WPM | PM length | 14 | mm |
| Time = 0 s | Time = 15 s | Time = 30 s | |||
|---|---|---|---|---|---|
| Model |  |  |  | ||
| Input | Motion |  |  |  |  |
 |  |  |  | ||
| M |  |  |  | 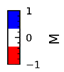 | |
| J | 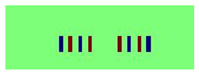 |  |  |  | |
| Output | Bx |  |  |  |  |
| By |  | 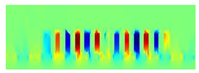 |  | 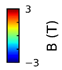 |
| FEM | Prediction | Absolute Error (%) | |||
|---|---|---|---|---|---|
| Pix2Pix | PIGAN | Pix2Pix | PIGAN | ||
| Continuous force @ 2.23 A | 190 N | 150 N | 192 N | 21.05% | 1.05% |
| Peak force @ 15.5 A | 950 N | 800 N | 980 N | 15.79% | 3.16% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Niu, S.; Zhang, Y.; Fu, W. Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines. Appl. Sci. 2022, 12, 10426. https://doi.org/10.3390/app122010426
Wu H, Niu S, Zhang Y, Fu W. Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines. Applied Sciences. 2022; 12(20):10426. https://doi.org/10.3390/app122010426
Chicago/Turabian StyleWu, Huihuan, Shuangxia Niu, Yunpeng Zhang, and Weinong Fu. 2022. "Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines" Applied Sciences 12, no. 20: 10426. https://doi.org/10.3390/app122010426
APA StyleWu, H., Niu, S., Zhang, Y., & Fu, W. (2022). Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines. Applied Sciences, 12(20), 10426. https://doi.org/10.3390/app122010426







