Assessment of the Influence of Astronomical Cyclicity on Sedimentation Processes in the Eastern Paratethys Based on Paleomagnetic Measurements Using Discrete Mathematical Analysis
Abstract
1. Introduction
2. Materials and Methods
- Time series analysis, including spectral analysis (Fourier, spectrogram, and wavelet analysis), autocorrelation, cross-correlation, smoothing, filtering, and extremum search.
- Multivariate data analysis, including multivariate distributions and cluster analysis.
- Statistical methods, such as statistical distributions, correlation, regression, and chi-square tests.
- Neural networks (including deep learning neural networks).
2.1. Classical Spectral Methods
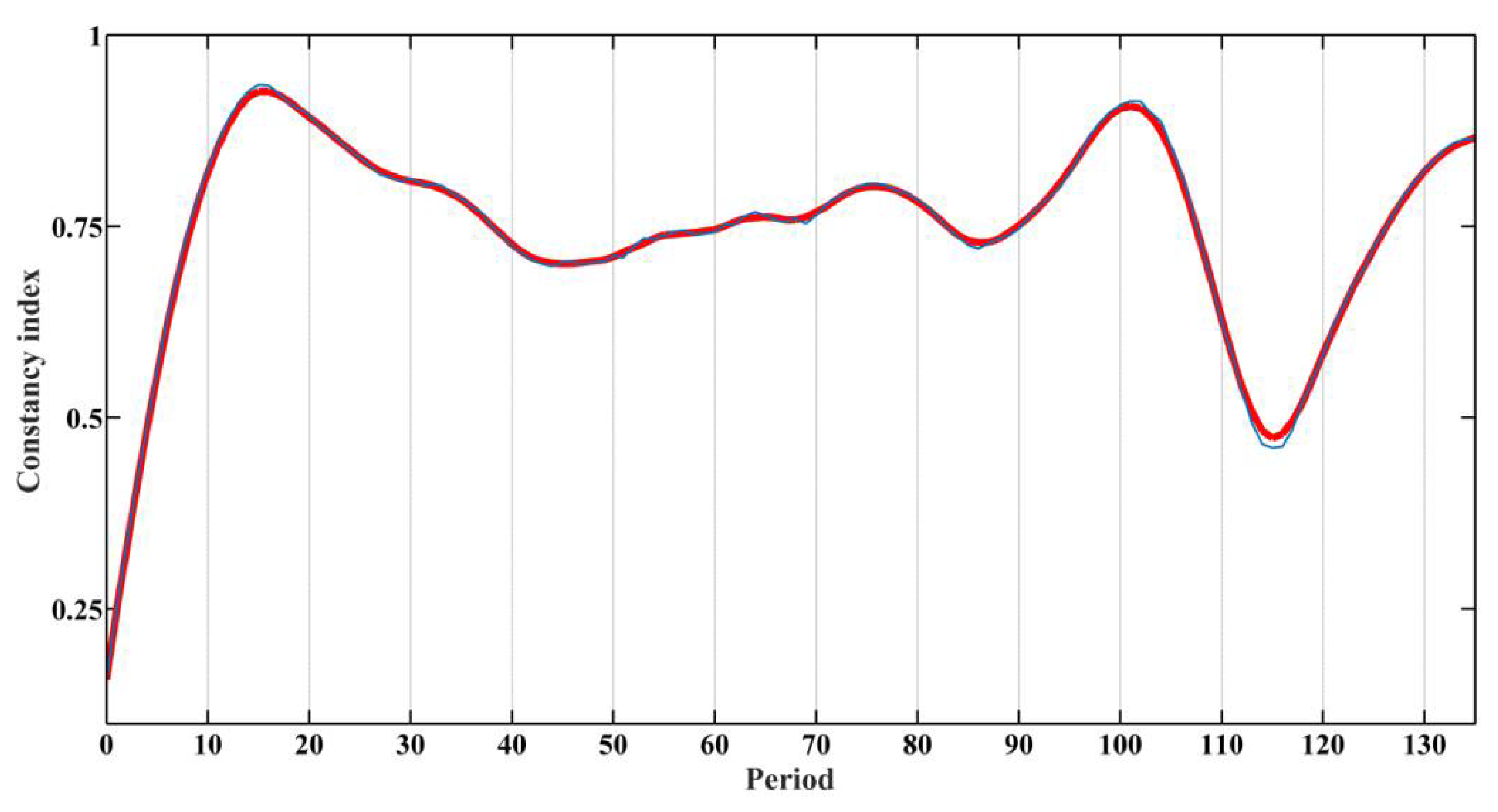
2.2. DMA-Algorithm for the Identification of Periods in Data Arrays
2.3. Time Series for the Demonstration of the Efficiency of the Algorithm
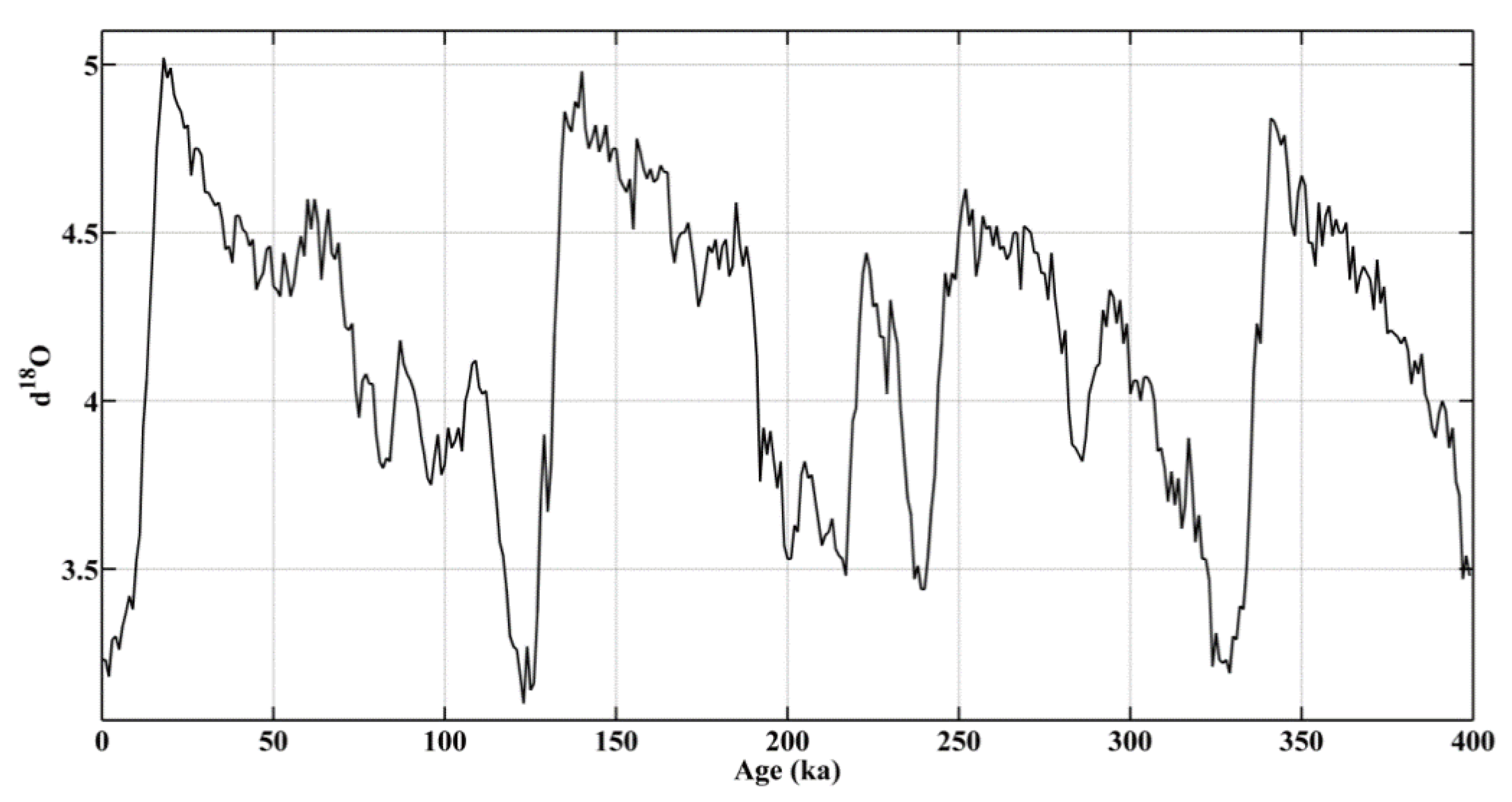
2.4. Magnetic Susceptibility Data of Zhelezny Rog Cape
3. Results
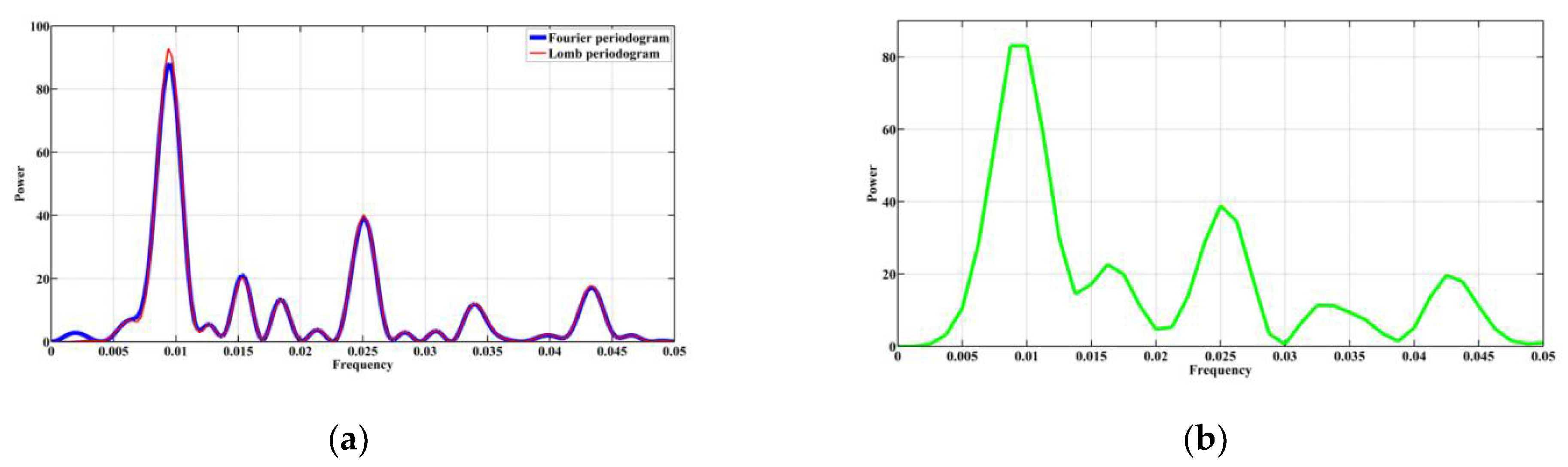
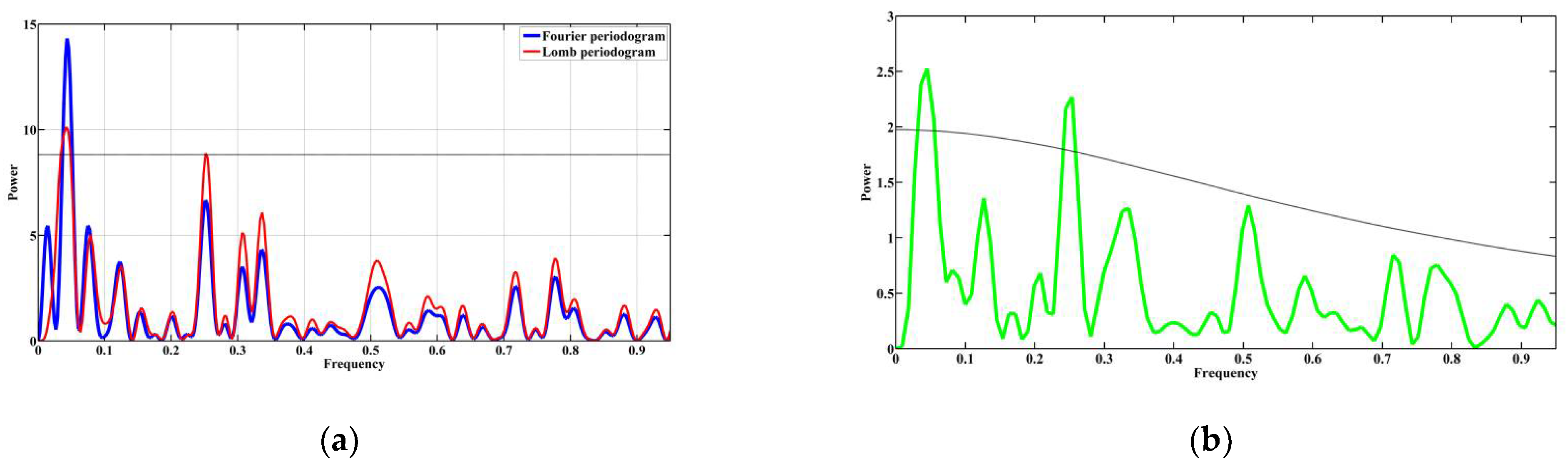
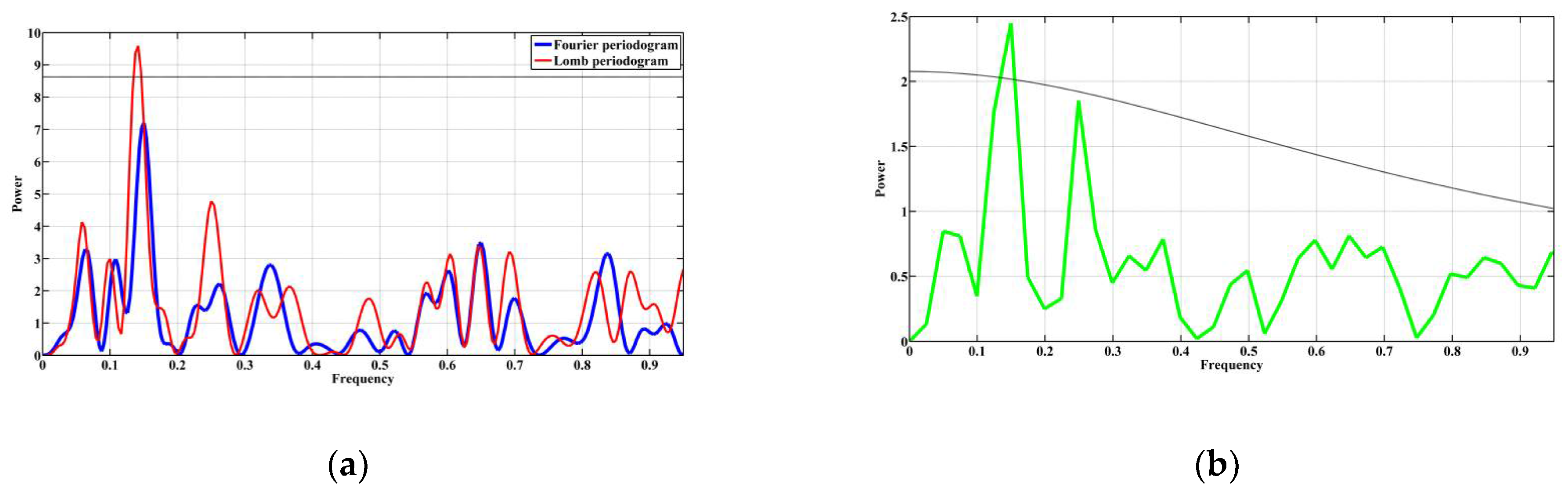
3.1. Demonstration of the Efficiency of the Algorithms
3.2. Identification of Periods in Magnetic Susceptibility Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwarzacher, W. Mathematical geology and the development of cyclostratigraphy. Geoinformatics 1993, 4, 353–356. [Google Scholar] [CrossRef][Green Version]
- Foucault, A. Sedimentary record of orbital cycles, methodology, results and perspectives. Bull. Soc. Geol. Fr. 1992, 163, 325–335. [Google Scholar]
- Strasser, A.; Hilgen, F.J.; Heckel, P.H. Cyclostratigraphy—Concepts, definitions and applications. Newsl. Stratigr. 2006, 42, 75–114. [Google Scholar] [CrossRef]
- Agayan, S.M.; Bogoutdinov, S.R.; Krasnoperov, R.I. Short introduction into DMA. Russ. J. Earth Sci. 2018, 18, ES2001. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R.; Soloviev, A.A. Discrete mathematical analysis and applications in geology and geophysics. Vestn. KRAUNTs Nauk. Zemle 2010, 2, 109–125. [Google Scholar]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R. Discrete mathematical analysis and monitoring of volcanoes. Inzh. Ekol. 2008, 5, 26–31. [Google Scholar]
- Widiwijayanti, C.; Mikhailov, V.; Diament, M.; Deplus, C.; Louat, R.; Tikhotsky, S.; Gvishiani, A. Structure and evolution of the Molucca Sea area: Constraints based on interpretation of a combined sea-surface and satellite gravity dataset. Earth Planet. Sci. Lett. 2003, 215, 135–150. [Google Scholar] [CrossRef]
- Bogoutdinov, S.R.; Gvishiani, A.D.; Agayan, S.M.; Soloviev, A.A.; Kihn, E. Recognition of disturbances with specified morphology in time series. Part 1: Spikes on magnetograms of the worldwide INTERMAGNET network. Izv. Phys. Solid Earth 2010, 46, 1004–1016. [Google Scholar] [CrossRef]
- Gvishiani, A.; Soloviev, A.; Krasnoperov, R.; Lukianova, R. Automated Hardware and Software System for Monitoring the Earth’s Magnetic Environment. Data Sci. J. 2016, 15, 18. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Bogoutdinov, S.R.; Agayan, S.M.; Gvishiani, A.D.; Kihn, E. Detection of hardware failures at INTERMAGNET observatories: Application of artificial intelligence techniques to geomagnetic records study. Russ. J. Earth Sci. 2009, 11, ES2006. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Lukianova, R.Y. Geoinformatics and observations of the Earth’s magnetic field: The Russian segment. Izv. Phys. Solid Earth 2015, 51, 157–175. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Mikhailov, V.O.; Agayan, S.M.; Bogoutdinov, S.R.; Graeva, E.M.; Diament, M.; Galdeano, A. Artificial intelligence algorithms for magnetic anomaly clustering. Izv. Phys. Solid Earth 2002, 38, 545–559. [Google Scholar]
- Gvishiani, A.D.; Dzeboev, B.A.; Agayan, S.M. FCAZm intelligent recognition system for locating areas prone to strong earth-quakes in the Andean and Caucasian mountain belts. Izv. Phys. Solid Earth 2016, 52, 461–491. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R.; Zlotnicki, J.; Bonnin, J. Mathematical methods of geoinformatics. III. Fuzzy comparisons and recognition of anomalies in time series. Cybern. Syst. Anal. 2008, 44, 309–323. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Schulz, M.; Mudelsee, M. REDFIT: Estimating red-noise spectra directly from unevenly spaced paleoclimatic time series. Comput. Geosci. 2002, 28, 421–426. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic δ 18O records. Paleoceanography 2005, 20, 1–17. [Google Scholar] [CrossRef]
- Rybkina, A.I.; Rostovtseva, Y.V. Astronomically-tuned cyclicity in Upper Maeotian deposits of the Eastern Paratethys (Zheleznyi Rog Section, Taman). Mosc. Univ. Geol. Bull. 2014, 69, 341–346. [Google Scholar] [CrossRef]
- Rostovtseva, Y.V.; Rybkina, A.I. The Messinian event in the Paratethys: Astronomical tuning of the Black Sea Pontian. Mar. Pet. Geol. 2017, 80, 321–332. [Google Scholar] [CrossRef]
- Hammer, Ø.; Harper, D.A.T. Paleontological Data Analysis; Blackwell Publishing: Hoboken, NJ, USA, 2005; Volume 351. [Google Scholar] [CrossRef]
- Carbonell, M.; Oliver, R.; Ballester, J.L. Power spectra of gapped time series: A comparison of several methods. Astron. Astrophys. 1992, 264, 350–360. [Google Scholar]
- Zgurovsky, M.Z.; Pankratova, N.D. System Analysis: Theory and Applications (Data and Knowledge in a Changing World); Springer: Berlin/Heidelberg, Germany, 2007; Volume 447. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzeboev, B.A.; Odintsova, A.A.; Rybkina, A.I.; Dzeranov, B.V. Assessment of the Influence of Astronomical Cyclicity on Sedimentation Processes in the Eastern Paratethys Based on Paleomagnetic Measurements Using Discrete Mathematical Analysis. Appl. Sci. 2022, 12, 580. https://doi.org/10.3390/app12020580
Dzeboev BA, Odintsova AA, Rybkina AI, Dzeranov BV. Assessment of the Influence of Astronomical Cyclicity on Sedimentation Processes in the Eastern Paratethys Based on Paleomagnetic Measurements Using Discrete Mathematical Analysis. Applied Sciences. 2022; 12(2):580. https://doi.org/10.3390/app12020580
Chicago/Turabian StyleDzeboev, Boris A., Anastasia A. Odintsova, Alena I. Rybkina, and Boris V. Dzeranov. 2022. "Assessment of the Influence of Astronomical Cyclicity on Sedimentation Processes in the Eastern Paratethys Based on Paleomagnetic Measurements Using Discrete Mathematical Analysis" Applied Sciences 12, no. 2: 580. https://doi.org/10.3390/app12020580
APA StyleDzeboev, B. A., Odintsova, A. A., Rybkina, A. I., & Dzeranov, B. V. (2022). Assessment of the Influence of Astronomical Cyclicity on Sedimentation Processes in the Eastern Paratethys Based on Paleomagnetic Measurements Using Discrete Mathematical Analysis. Applied Sciences, 12(2), 580. https://doi.org/10.3390/app12020580






