Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach
Abstract
1. Introduction
2. Methodology
3. Experimental Campaigns
4. Result Analysis and Discussion
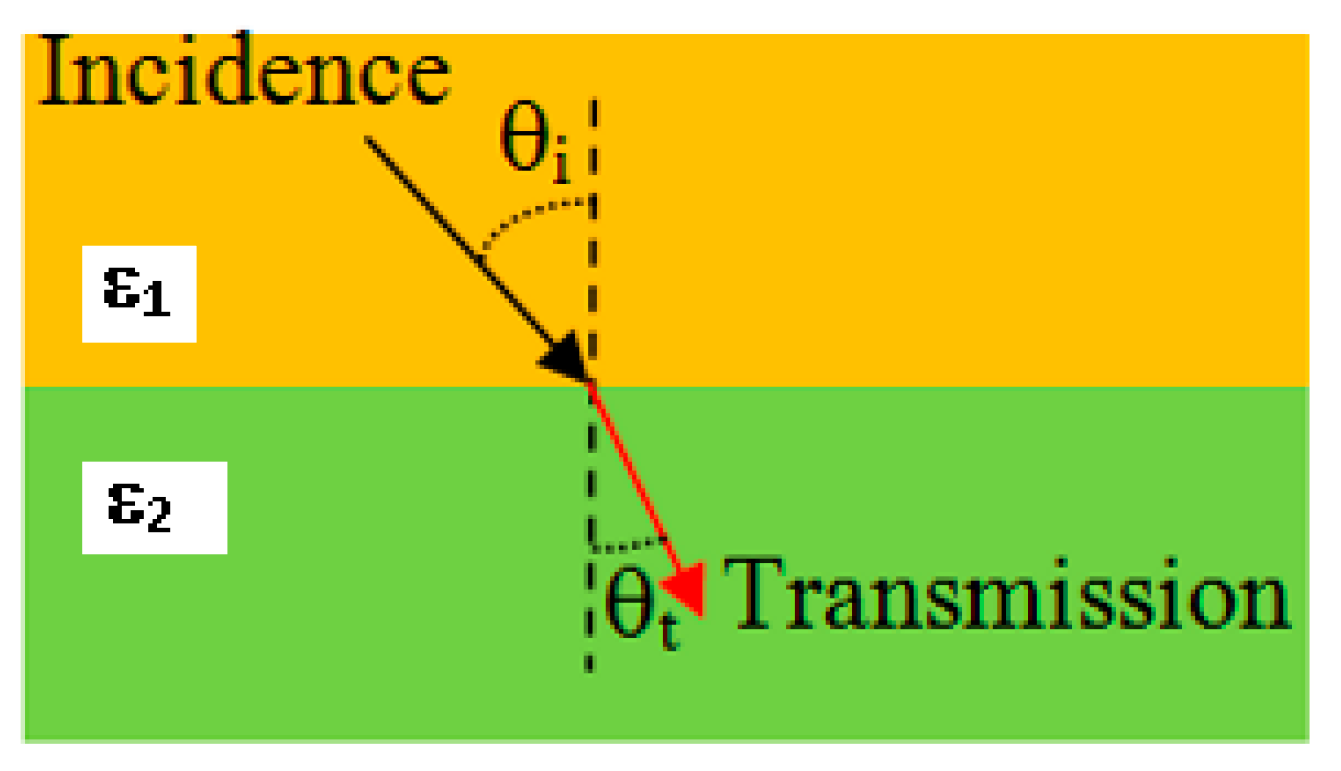
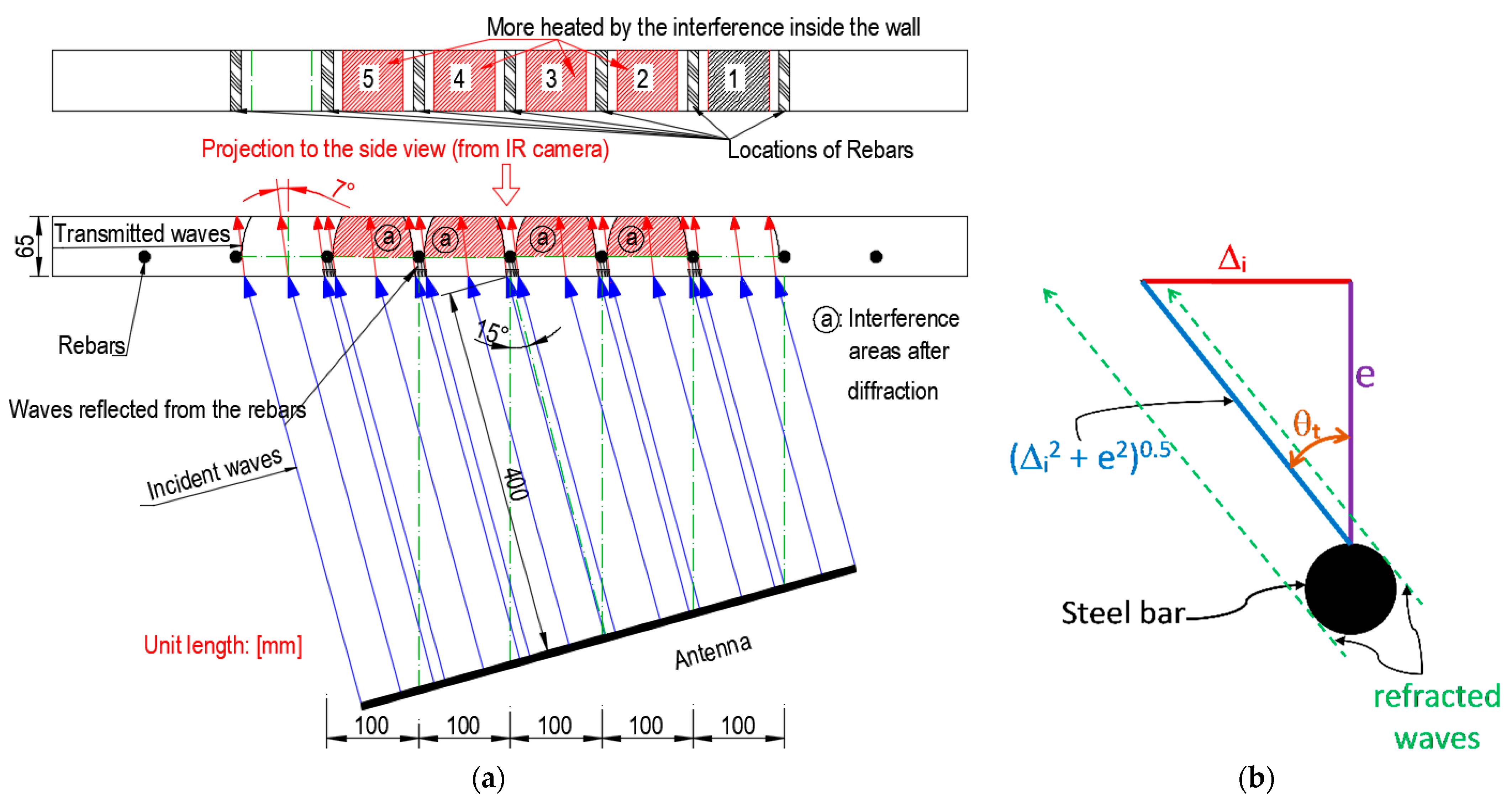
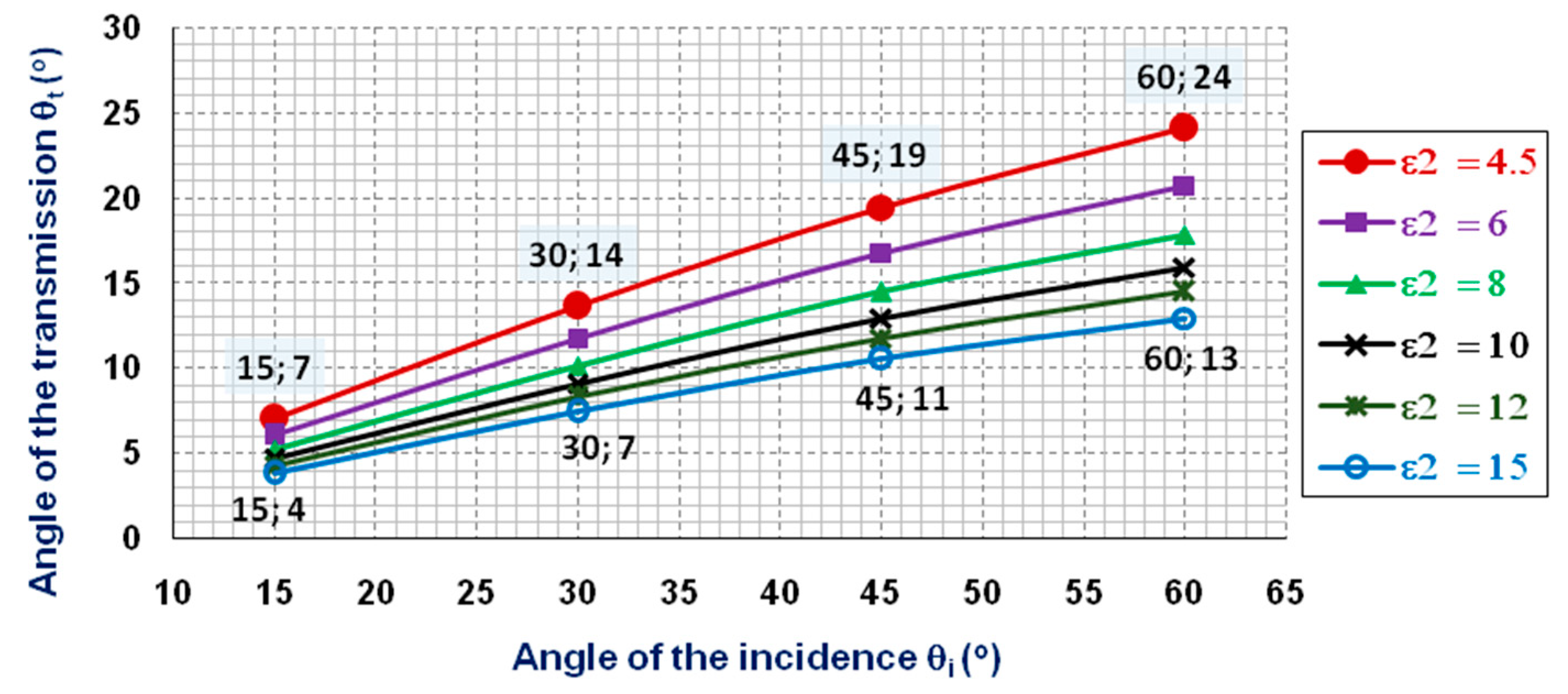
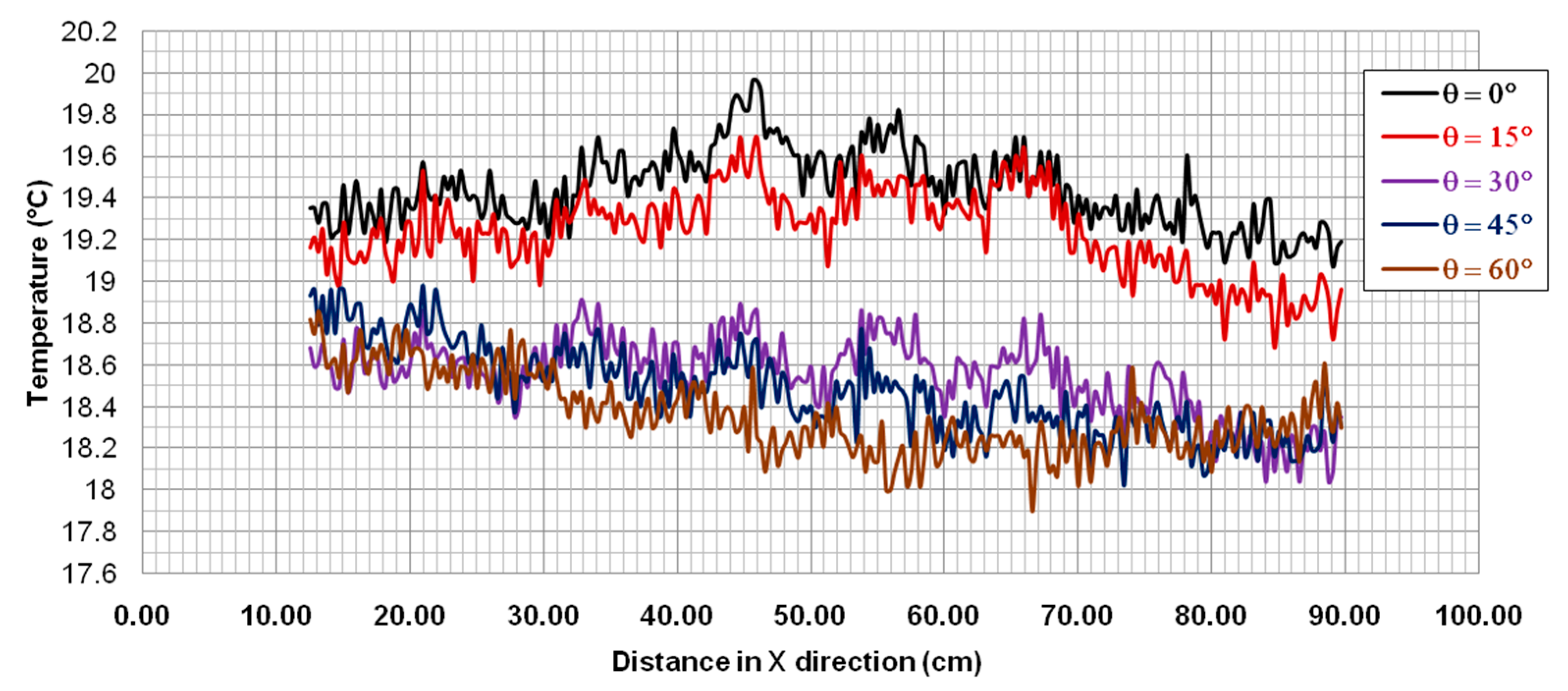
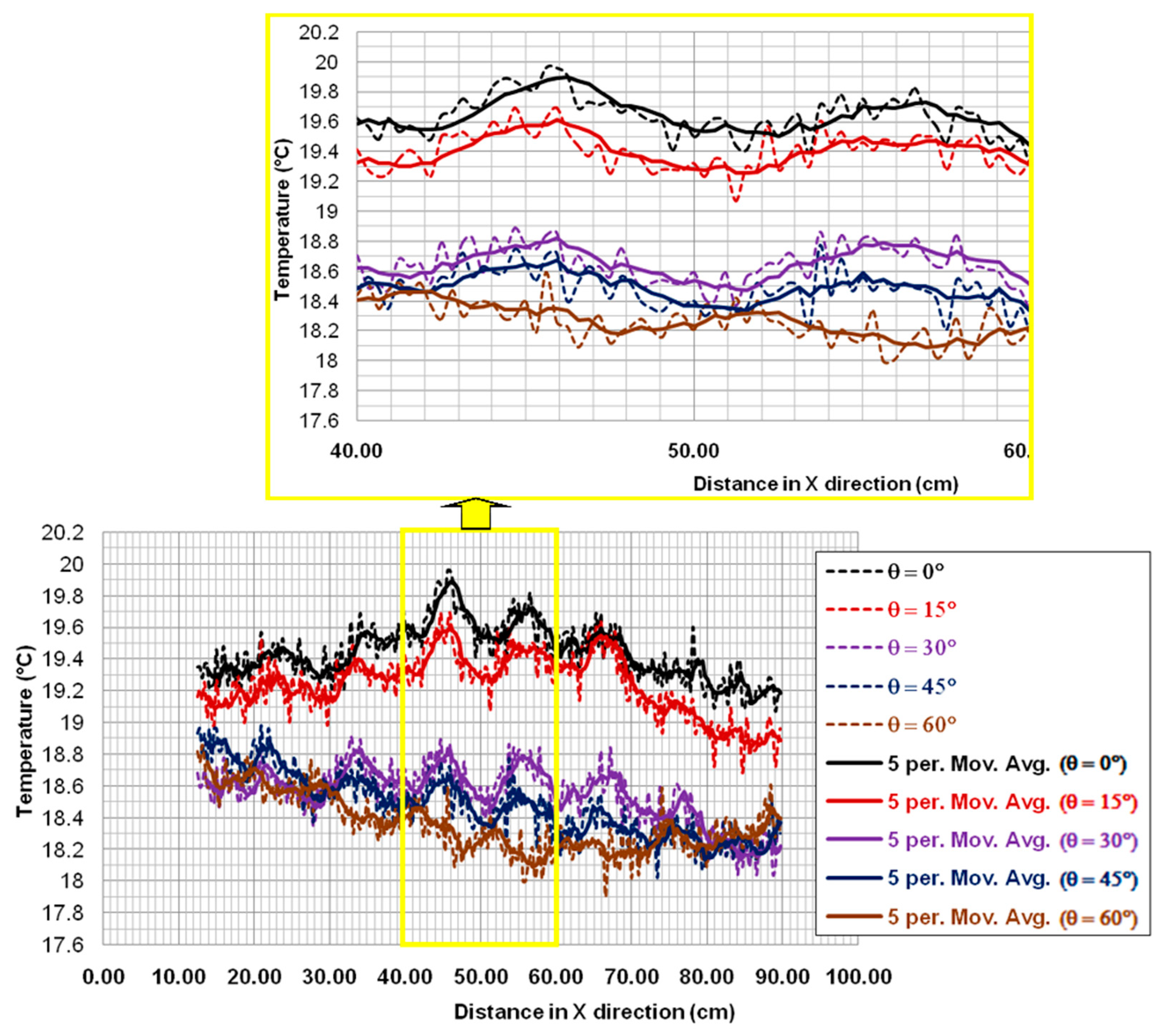
4.1. Angles of Transmitted Waves
4.2. Determination of the Shifts’ Values (Δi) from the Thermograms
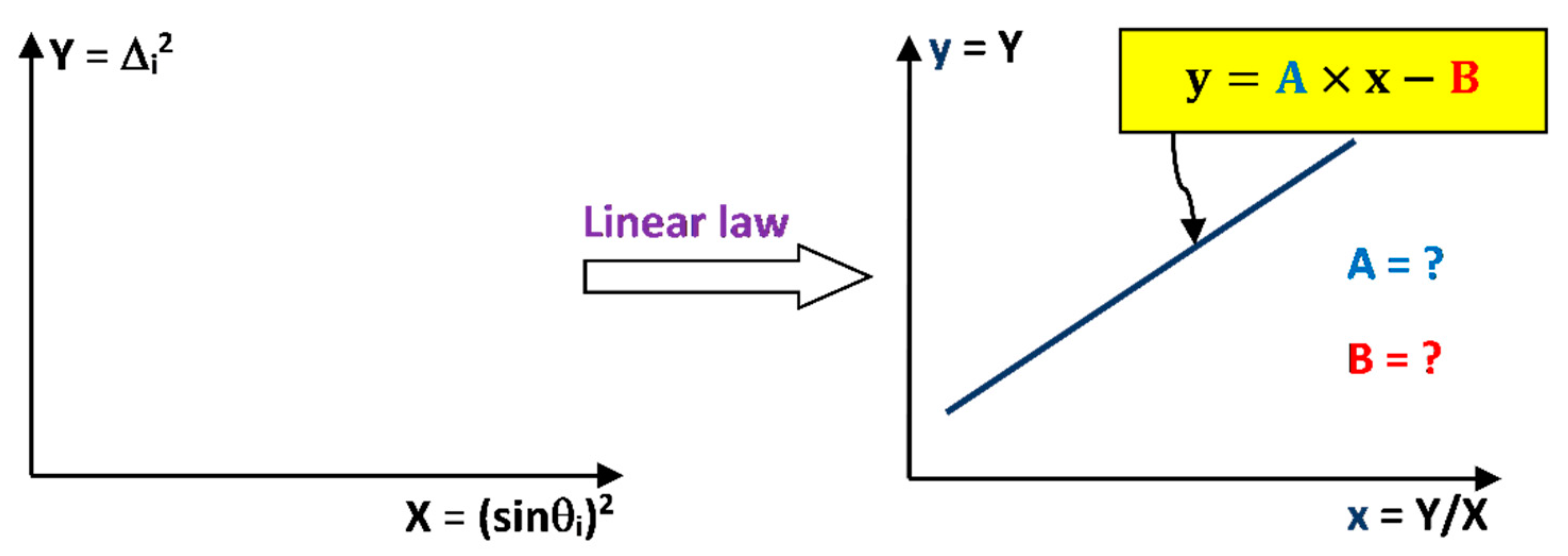
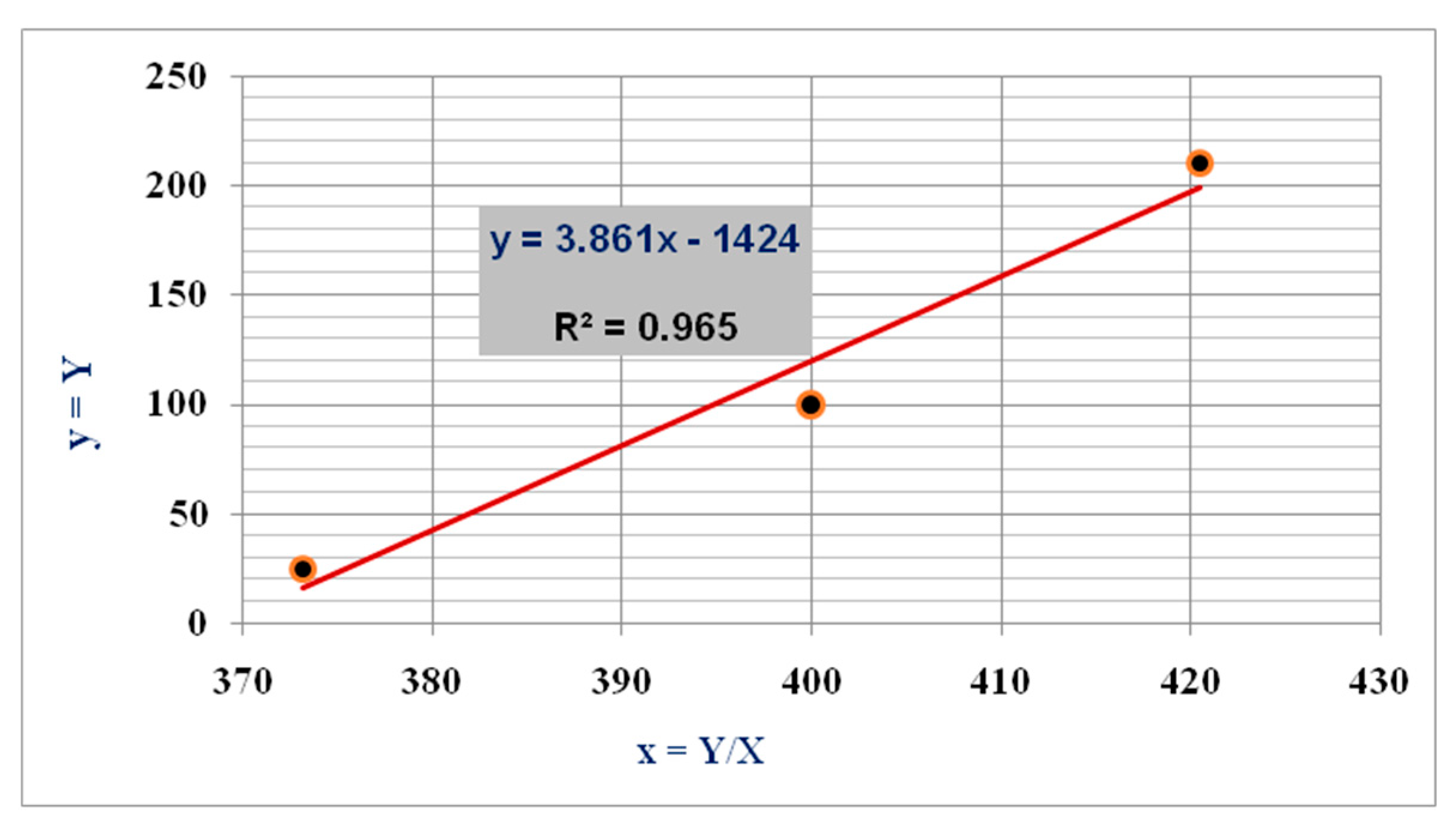
4.3. Deduction of Concrete Cover Thickness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Civil Engineering Association of France (AFGC). Conception des bétons pour une durée de vie donnée des ouvrages—Indicateurs de durabilité: Conception des bétons pour une durée de vie donnée des ouvrages—Indicateurs de durabilité; Research Report in French; Civil Engineering Association of France (AFGC): Paris, France, 2004; p. 252. [Google Scholar]
- Klysz, G.; Balayssac, J.-P.; Laurens, S. Spectral Analysis of Radar Surface Waves for Non-Destructive Evaluation of Cover Concrete. NDT E Int. 2004, 37, 221–227. [Google Scholar] [CrossRef]
- Dérobert, X.; Iaquinta, J.; Klysz, G.; Balayssac, J.-P. Use of Capacitive and GPR Techniques for the Non-Destructive Evaluation of Cover Concrete. NDT E Int. 2008, 41, 44–52. [Google Scholar] [CrossRef]
- Agred, K. Localisation automatique des aciers et caractérisation de la teneur en eau du béton armé par radar double-offset à grand rendement. Ph.D. Thesis, Université Toulouse 3 Paul Sabatier, Toulouse, France, 2017. (In French). [Google Scholar]
- Agred, K.; Klysz, G.; Balayssac, J.-P. Location of Reinforcement and Moisture Assessment in Reinforced Concrete with a Double Receiver GPR Antenna. Constr. Build. Mater. 2018, 188, 1119–1127. [Google Scholar] [CrossRef]
- Sbartaï, Z.M.; Laurens, S.; Viriyametanont, K.; Balayssac, J.P.; Arliguie, G. Non-Destructive Evaluation of Concrete Physical Condition Using Radar and Artificial Neural Networks. Constr. Build. Mater. 2009, 23, 837–845. [Google Scholar] [CrossRef]
- Du Plooy, R.; Villain, G.; Palma Lopes, S.; Ihamouten, A.; Dérobert, X.; Thauvin, B. Electromagnetic Non-Destructive Evaluation Techniques for the Monitoring of Water and Chloride Ingress into Concrete: A Comparative Study. Mater. Struct. 2015, 48, 369–386. [Google Scholar] [CrossRef]
- Sbartaï, Z.-M.; Laurens, S.; Breysse, D. Concrete Moisture Assessment Using Radar NDT Technique—Comparison between Time and Frequency Domain Analysis. In Proceedings of the Non-Destructive Testing in Civil Engineering (NDTCE’09), Nantes, France, 30 June–3 July 2009; p. 9. [Google Scholar]
- Maldague, X.P.V. Theory and Practice of Infrared Technology for Nondestructive Testing. In Wiley Series in Microwave and Optical Engineering; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Deane, S.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Williamson, A.A.; Withers, S.; Zolotas, A.; Maldague, X.P.V.; Ahmadi, M.; Pant, S.; Genest, M.; et al. Development of a Thermal Excitation Source Used in an Active Thermographic UAV Platform. Quant. InfraRed Thermogr. J. 2022, 1–32. [Google Scholar] [CrossRef]
- Dahlberg, P.; Ziegeler, N.J.; Nolte, P.W.; Schweizer, S. Design and Construction of an LED-Based Excitation Source for Lock-In Thermography. Appl. Sci. 2022, 12, 2940. [Google Scholar] [CrossRef]
- Geng, C.; Shi, W.; Liu, Z.; Xie, H.; He, W. Nondestructive Surface Crack Detection of Laser-Repaired Components by Laser Scanning Thermography. Appl. Sci. 2022, 12, 5665. [Google Scholar] [CrossRef]
- Lee, S.; Chung, Y.; Kim, W. Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography. Appl. Sci. 2022, 12, 6006. [Google Scholar] [CrossRef]
- Lubkowska, A.; Pluta, W. Infrared Thermography as a Non-Invasive Tool in Musculoskeletal Disease Rehabilitation—The Control Variables in Applicability—A Systematic Review. Appl. Sci. 2022, 12, 4302. [Google Scholar] [CrossRef]
- Sultan, A.A.; Washer, G. A Pixel-by-Pixel Reliability Analysis of Infrared Thermography (IRT) for the Detection of Subsurface Delamination. NDT E Int. 2017, 92, 177–186. [Google Scholar] [CrossRef]
- Bagavac, P.; Krstulović-Opara, L.; Domazet, Ž. Infrared Thermography of Steel Structure by FFT. Mater. Today Proc. 2019, 12, 298–303. [Google Scholar] [CrossRef]
- Bu, C.; Liu, G.; Zhang, X.; Tang, Q. Debonding Defects Detection of FMLs Based on Long Pulsed Infrared Thermography Technique. Infrared Phys. Technol. 2020, 104, 103074. [Google Scholar] [CrossRef]
- Verspeek, S.; Ribbens, B.; Maldague, X.; Steenackers, G. Spot Weld Inspections Using Active Thermography. Appl. Sci. 2022, 12, 5668. [Google Scholar] [CrossRef]
- Keo, S.A.; Brachelet, F.; Defer, D.; Breaban, F. Defects Detection by Infrared Thermography with a New Microwave Excitation System. Mech. Ind. 2014, 15, 509–516. [Google Scholar] [CrossRef]
- Zheng, H.; Zhou, L.; Marks, R.; Happonen, T.; Kraft, T.M. Defect Recognition of Roll-to-Roll Printed Conductors Using Dark Lock-in Thermography and Localized Segmentation. Appl. Sci. 2022, 12, 2005. [Google Scholar] [CrossRef]
- Keo, S.-A.; Defer, D.; Breaban, F.; Brachelet, F. Comparison between Microwave Infrared Thermography and CO2 Laser Infrared Thermography in Defect Detection in Applications with CFRP. Mater. Sci. Appl. 2013, 4, 600–605. [Google Scholar] [CrossRef][Green Version]
- Keo, S.A.; Brachelet, F.; Breaban, F.; Defer, D. Defect Detection in CFRP by Infrared Thermography with CO2 Laser Excitation Compared to Conventional Lock-in Infrared Thermography. Compos. Part B Eng. 2015, 69, 1–5. [Google Scholar] [CrossRef]
- Keo, S.-A.; Brachelet, F.; Breaban, F.; Defer, D. Development of an Infrared Thermography Method with CO2 Laser Excitation, Applied to Defect Detection in CFRP. Int. J. Civ. Environ. Eng. 2013, 7, 5. [Google Scholar]
- Yumnam, M.; Gupta, H.; Ghosh, D.; Jaganathan, J. Inspection of Concrete Structures Externally Reinforced with FRP Composites Using Active Infrared Thermography: A Review. Constr. Build. Mater. 2021, 310, 125265. [Google Scholar] [CrossRef]
- Dragan, R.G.; Rosca, I.-C.; Keo, S.-A.; Breaban, F. Active Thermography Method Using an CO2 Laser for Thermal Excitation, Applied to Defect Detection in Bioceramic Materials. In Proceedings of the 2013 E-Health and Bioengineering Conference (EHB), Iasi, Romania, 21–23 November 2013; IEEE: Iasi, Romania, 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Keo, S.A. Développement d’une méthode de thermographie infrarouge active par excitation micro-ondes appliquée au contrôle non destructif. Ph.D. Thesis, Université d’Artois, Béthune, France, 2013. (In French). [Google Scholar]
- Keo, S.A. Nouvelles Méthodes de Contrôle Non Destructif (CND) en Génie Civil Développement de la Méthode de Thermographie Infrarouge par Excitation Micro-onde et Laser CO2; Presses Académiques Francophones: Sarrebruck, Germany, 2014. [Google Scholar]
- Keo, S.A.; Brachelet, F.; Breaban, F.; Defer, D. Steel Detection in Reinforced Concrete Wall by Microwave Infrared Thermography. NDT E Int. 2014, 62, 172–177. [Google Scholar] [CrossRef]
- Szymanik, B.; Frankowski, P.; Chady, T.; John Chelliah, C. Detection and Inspection of Steel Bars in Reinforced Concrete Structures Using Active Infrared Thermography with Microwave Excitation and Eddy Current Sensors. Sensors 2016, 16, 234. [Google Scholar] [CrossRef] [PubMed]
- Szymanik, B.; Chady, T.; Frankowski, P. Inspection of Reinforcement Concrete Structures with Active Infrared Thermography. AIP Conf. Proc. 2017, 1806, 100013. [Google Scholar] [CrossRef]
- Hong, C.R.; Buyukozturk, O. Electromagnetic Properties of Concrete at Microwave Frequency Range. ACI Mater. J. 1998, 95, 262–271. [Google Scholar]
- Jamil, M.; Hassan, M.K.; Al-Mattarneh, H.M.A.; Zain, M.F.M. Concrete Dielectric Properties Investigation Using Microwave Nondestructive Techniques. Mater. Struct. 2013, 46, 77–87. [Google Scholar] [CrossRef]
- Makul, N.; Rattanadecho, P.; Agrawal, D.K. Applications of Microwave Energy in Cement and Concrete—A Review. Renew. Sustain. Energy Rev. 2014, 37, 715–733. [Google Scholar] [CrossRef]
- Mai, T.C. Evaluation non destructive des matériaux de construction par technique électromagnétique aux fréquences radar—Modélisation et Expérimentation en laboratoire. Ph.D. Thesis, Université de Bordeaux, Bordeaux, French, 2015. (In French). [Google Scholar]
- Keo, S.-A.; Yune, C.-Y.; Dragan, R.G.; Defer, D.; Breaban, F. Analysis of Effects of Diffraction and Interference on Detection by Microwave Thermography. J. Civ. Struct. Health Monit. 2019, 9, 153–167. [Google Scholar] [CrossRef]


| θi (°) | sin(θi) | Δi (mm) |
|---|---|---|
| 0 | 0 | 0 |
| 15 | 0.259 | 5 |
| 30 | 0.500 | 10 |
| 45 | 0.707 | 14.5 |
| 60 | 0.866 | 60 |
| θi (°) | X = (sinθi)2 | y = Y = Δi2 (mm2) | x = Y/X (mm2) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 15 | 0.067 | 25 | 373.205 |
| 30 | 0.250 | 100 | 400 |
| 45 | 0.500 | 210.25 | 420.5 |
| 60 | 0.750 | 3600 | 4800 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keo, S.A.; Brachelet, F.; Defer, D.; Breaban, F. Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach. Appl. Sci. 2022, 12, 9865. https://doi.org/10.3390/app12199865
Keo SA, Brachelet F, Defer D, Breaban F. Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach. Applied Sciences. 2022; 12(19):9865. https://doi.org/10.3390/app12199865
Chicago/Turabian StyleKeo, Sam Ang, Franck Brachelet, Didier Defer, and Florin Breaban. 2022. "Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach" Applied Sciences 12, no. 19: 9865. https://doi.org/10.3390/app12199865
APA StyleKeo, S. A., Brachelet, F., Defer, D., & Breaban, F. (2022). Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach. Applied Sciences, 12(19), 9865. https://doi.org/10.3390/app12199865








