Abstract
Renewable energy generation and nonlinear load devices will generate harmonics and reactive power to power grids, resulting in current distortion and low power factors. To solve the power quality problems, the LC-coupling hybrid active power filter (LC-HAPF) is proposed, with lower DC-link voltage and lower cost compared with conventional active power filters (APFs). The LC-HAPF requires a controller to operate, therefore, hysteresis current control (HCC) and proportional current control (PCC) were proposed. However, they both result in significant steady-state error. Hence, linear quadratic regulator control (LQRC) with integral action (LQRIC) is proposed for the LC-HAPF in this paper to mitigate the steady-state error. The d-q-0 coordinate state-space model of the LQRIC-controlled LC-HAPF is derived, and a detailed design guideline of the weighting matrices Q and R of LQRIC is given. By the state-space model and weighting matrices, the gain matrix K of LQRIC can be acquired by MATLAB, thus a good steady-state performance can be ensured. Finally, the simulation results of different controllers for the LC-HAPF under 40V and 50V DC-link voltages are given to verify the effectiveness of the proposed LQRIC. The experimental results of LQRIC-controlled LC-HAPF are also given to verify the feasibility of the proposed LQRIC.
1. Introduction
In recent years, clean and renewable energy, such as solar power and wind power, has been vigorously promoted and applied [1,2,3]. However, the photovoltaic (PV) systems [1] and typical wind power systems [2] require inverters to operate. They cause power quality issues such as a low power factor and current harmonic pollution, which result in the failure of electrical equipment, the interference of communication circuits, etc., bringing economic losses to societies [4,5].
In order to solve the power quality problem, capacitor bank (CB) was proposed and used for reactive power compensation in the 1900s. In the 1940s, passive power filter (PPF) was proposed to achieve both reactive power and harmonic compensation [6]. However, it can only compensate fixed harmonic frequency and suffers from resonance problems. Therefore, the active power filter (APF), which combines the voltage source inverter (VSI) and inductor, was proposed in 1976 [7]. It overcomes the shortcomings of CB and PPF, and can achieve dynamic compensation. However, APF has the problem of high cost due to the high DC-link voltage. The hybrid active power filter (HAPF) was proposed to overcome the disadvantages of PPF and APF. It can reduce the operation cost by reducing the DC-link voltage [8,9,10]. There are different topologies of HAPF. Among them, the LC-coupling hybrid active power filter (LC-HAPF), which has an LC branch and a voltage source inverter (VSI) in series, was proposed in 2003. It can achieve harmonic current and reactive power compensation [8,9,10,11]. The thyristor-controlled LC-coupling hybrid active power filter (TCLC-HAPF) was proposed in 2014 [12], and can provide a wide range of reactive power compensation for both capacitive and inductive loads in the medium-voltage-level power system. However, it also increases the control complexity and power consumption. Next, LCLC-coupling hybrid active power filter (LCLC-HAPF) was proposed in 2020 [13]. It has a good high-order harmonic attenuation characteristic and lower inductor cost. However, it has stability problems and needs the assistance of active damping control. Therefore, considering the complexity and the system stability, the LC-HAPF is mainly focused on in this paper.
In addition to the topology of the LC-HAPF, the controller design also plays an important role in the compensation performance. Hysteresis current control (HCC) is the most widely used control method and provides fast transient response and acceptable steady-state performance [14]. However, due to its varied switching frequency, it generates harmonic current in a wide frequency range, resulting in a large output current ripple. Thus, the classical fixed switching frequency control, proportional current control (PCC), is proposed [15] to mitigate the current ripple for a better current tracking ability comparing with the HCC. However, the control gain optimization of PCC requires a trial-and-error process, therefore retaining a certain degree of steady-state error.
To obtain a lower steady-state error, a linear quadratic regulator control (LQRC) [16,17,18,19,20,21,22,23] was proposed for APF, HAPF and other applications due to the good steady-state performance. Moreover, some research suggests that LQRC with integral action (LQRIC) [24,25,26,27] is able to achieve a better steady-state performance because of the integral term. Therefore, this paper proposes the LQRIC for the LC-HAPF to achieve superior steady-state performance, and the LQRC for the LC-HAPF for the comparative study. Moreover, the gain matrix K of LQRC and LQRIC is obtained from the cost function of state errors, weighting matrices and system state space model. It results in a better steady-state performance than the PCC, whose gain optimization is just the trial-and-error process.
The objective of this paper is to design a LQRIC for the LC-HAPF to improve the steady-state performance under low DC-link voltage. Figure 1 is the graphical abstract of this paper.

Figure 1.
The graphical abstract.
The contributions of this paper are summarized as follows:
- (1)
- A LQRIC for the three-phase four-wire LC-HAPF is proposed to obtain a superior compensation performance.
- (2)
- Design the state-space model in d-q-0 coordinate of a LQRIC-controlled LC-HAPF.
- (3)
- Study the design of the weighting matrices, Q and R, of the LQRIC for LC-HAPF to ensure a good compensation performance.
- (4)
- Compare the simulation results with HCC, PCC and LQRC under different DC-link voltage conditions and verify the effectiveness of the proposed LQRIC for the LC-HAPF.
- (5)
- The experimental results for LQRIC under different DC-link voltages are given to verify the feasibility of the proposed LQRIC.
The arrangement of this paper is shown below. Section 2 establishes the system configuration of the three-phase four-wire LC-HAPF, and also gives the system model and introduces the parameter design. Then, Section 3 introduces the design of the proposed LQRC and LQRIC. The state-space model of LC-HAPF in d-q-0 coordinate and the design method of the weighting matrices, Q and R, are also given. Section 4 provides the overall control block diagram of the different controllers for the LC-HAPF. Section 5 provides the simulation results for verifying the effectiveness of the proposed LQRIC. Section 6 provides the experimental results for verifying the feasibility of the proposed LQRIC. The overall performance of different controllers is discussed in Section 7. Finally, the paper is concluded in Section 8.
2. Circuit Configuration of LC-HAPF
2.1. Circuit Configuration and System Modeling
Figure 2 shows a three-phase four-wire LC-HAPF with a balanced nonlinear load [9,10,11]. The subscript x indicates the phase a, b, c and n. vsx, isx, vx and iLx are the source voltage, source current, the point of common coupling (PCC) voltage, and load current for each phase, respectively. icx, vcx and vinvx are the compensation current, compensation capacitor voltage and inverter output voltage, respectively. LLx, RLx and CLx are the inductor, resistor and capacitor of the nonlinear loads, which are the full-bridge rectifier. Lcx, Ccx and Rcx are the inductor, capacitor and equivalent resistance of the coupling PPF. T1x and T2x are the trigger signals for IGBTs. The upper and lower DC-link capacitor voltage, VdcU and VdcL, satisfy VdcU = VdcL = 0.5Vdc, where Vdc is the DC-link voltage of VSI.
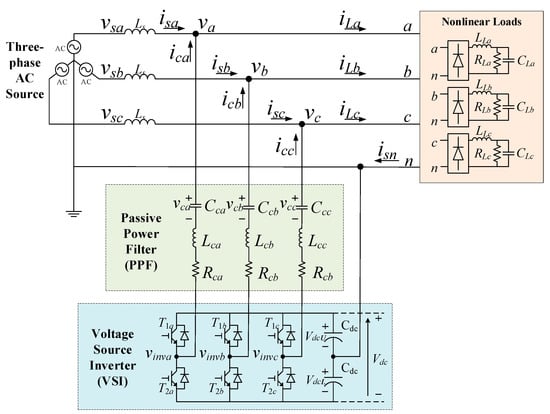
Figure 2.
The circuit configuration of a three-phase four-wire LC-HAPF with balanced nonlinear load.
The PPF and VSI consist of LC-HAPF, which generate icx to compensate the grid harmonics and reactive power. The differential equations for LC-HAPF are set up by (1).
Based on (1), the state-space model of LC-HAPF is set up by (2).
where e, u, z and y indicate state, control, disturbance and output variable matrix, and they are expressed as , , and . T indicates the transpose of the matrix.
The upper equation in (2) is the system state differential equation of the LC-HAPF, the matrix A, B and E are state, control and disturbance matrix. The lower equation in (2) is the output equation of the LC-HAPF, which includes the output state matrix, C, and the output control matrix, D. The value of the A, B, C, D and E matrices for LQRC and LQRIC will be discussed in Section 3.
2.2. Parameter Design
The value design of Lcx and Ccx are based on the root-mean-square of PCC voltage Vx_rms and the reactive power for the load QLx in (3), where XCc and XLc are the reactance of Lcx and Ccx and (4) shows the relation between Lcx and Ccx. ω1 is the fundamental angular frequency, ωm is the harmonic angular frequency and the subscript m is the harmonic order.
The full-bridge rectifier load will generate odd order (m = 3, 5, 7, …) harmonic. As the main harmonic current of full bridge rectifier are the 3rd and 5th orders [28,29], in this paper, the 5th order harmonic is chosen to reduce the structure size and cost.
3. Proposed LQRC and LQRIC for LC-HAPF
3.1. Linear Quadratic Regulator Control (LQRC) for LC-HAPF
3.1.1. State-Space Model for LQRC-Controlled LC-HAPF
Based on (4), the small-signal state-space model is proposed for the LQRC, and the detail derivation is given as follows. In order to extract the reactive power and harmonics from the three-phase power grid, the d-q-0 synchronous rotating coordinate system is applied. Through the a-b-c to d-q-0 conversion, the active power, harmonics, reactive power and three-phase unbalance convert into d-axis DC component, d-axis AC component, q-axis and 0-axis, respectively. The a-b-c to d-q-0 conversion is achieved by the Park transform matrix H given in (5). After the reference current calculation in the d-q-0 coordinate, the calculated reference compensation current will convert back to an a-b-c coordinate by inverse Park transform H−1.
where ω1t is the fundamental phase angle and is obtained by phase locked loop (PLL). With the help of (5), icx, vinvx, vx and vcx in the d-q-0 coordinate can be obtained. They are shown as:
From (1), (2), (5) and (6), the state differential equations for the LC-HAPF in d-q-0 coordinate are given by (7), and the outputs of the LC-HAPF in the d-q-0 coordinate are given by (8).
For the steady state system in (7), overlaying perturbations , , and are given by (9), where the subscript h indicates the phase d, q and 0. [16] and the ‘~’ denotes the perturbation value.
where Ich, Vinvh, Vh and Vch are the steady state values of compensation current, inverter voltage, PCC voltage and compensation capacitor voltage.
Based on (7)–(9), the small-signal state-space model of the LC-HAPF with LQRC-controlled is then set up and shown in (10).
where , , and are expressed as , , and . The matrices A, B, C, D and E are expressed as:
So far, the small-signal state-space model of the LQRC-controlled LC-HAPF is established for the derivation process of the LQRC for the LC-HAPF. And it applies in the following section.
3.1.2. LQRC for LC-HAPF
The objective of optimal control is to find a control system under the given constraint conditions so as to minimize the cost function, J. LQRC, which is an optimal control, has good tracking control ability, and calculates the gain by the cost function, weighting matrices and state-space model. Generally, LQRC takes the minimum value of the cost function (11) in time interval [t0, tf] [17], where t0 and tf represent the initial time and final time, respectively.
Q is a state weighting matrix, which is defined as a diagonal semi-positive matrix (), and measures the importance of each phase state variable for the LQRC. R is an input weighting matrix, which is diagonal positive definite () and measures the importance level of each phase control variable. They are given by (12) and (13).
when e and u indicate the error and input, qqi (i = 1, 2, 3, …) represents the weighting value of corresponding e, and rqi represents the weighting value of corresponding u. The larger value of qqi means take more effect on corresponding state variable in certain phase, so as rqi.
The physical meaning of minimizing the cost function (11) is to minimize the tracking error and control cost (DC-link voltage of the inverter) by minimizing the corresponding terms and .
To solve the optimal control problem for this dynamical system, the Hamiltonian function F with Lagrange multipliers λ in (14) is constructed.
Then, (15) is used to calculate the minimum value of F, i.e., the minimum value of the cost function, J.
As R is positive and symmetrical, by (15), the optimal control variable solution u* is calculated by:
In order to realize feedback control, the positive-definite transformation matrix, P, is introduced to evaluate the λ.
and the matrix P is the solution of Algebraic Riccati equation (ARE):
From (16) and (17), we have:
where K is the gain matrix for LQR optimal control. Every combination of Q and R matrices can obtain a unique solution for K, which can satisfy the minimum cost of (11).
From (19) and (20), the controlled system is expressed as:
and the design of Q and R matrices is based on Bryson’s rule [30], which provides the reasonable weighting elements qqi and rqi that are shown in below:
The overall design process of LQRC is shown as follows:
- Select Q and R matrices based on Bryson’s rule;
- Substitute the A, B, Q and R matrices to (18) and obtain the P matrix;
- Using the R, B and P matrices to obtain the optimal control gain K matrix.
3.2. LQRC with Integral Action (LQRIC) for LC-HAPF
The LQRIC adds the integral term of each state variable on the basis of LQRC, which aims to reduce the steady state error of the system. Thus, for the small-signal state-space model of LQRIC-controlled LC-HAPF, the state variable is upgraded and shown in (23), whereas the control variable , disturbance variable , and output variable of the LQRIC remain the same as the LQRC.
The matrices A, B, C, D and E for the LQRIC-controlled LC-HAPF are modified accordingly and expressed as:
For LQRIC, the R matrix remains the same as LQRC, whereas the Q matrix has three additional integral weighting elements, qq4, qq5 and qq6, which are shown below:
For the design of the Q matrix for LQRIC, the integral weighting elements are designed larger than the corresponding proportional weighting elements qq1, qq2 and qq3, i.e., , in order to achieve a better steady-state performance compared with the LQRC. Finally, based on the updated variable and matrices A, B, C, D, E, Q and R, the optimal control gain K matrix of the LQRIC can be obtained by the design process of LQRC in Section 3.1.2, and therefore the controlled system in (21) of LQRIC can be acquired.
4. Overall Control Strategy of LC-HAPF
Figure 3 shows the overall control block diagram of the LQRC and LQRIC for the LC-HAPF. Firstly, both iLx and icx are transformed into d-q-0 coordinates by Park transformation, where the ω1t is obtained by the PLL. The reference compensation current in the d-axis is derived from the high pass filter (HPF). Then, the compensation current error εh is obtained by εh = ich − ich*. After that, the εh can be transformed into vinvh* by the LQRC or LQRIC, and the vinvh* is converted back into the a-b-c coordinate, which is vinvx*. It will be applied into the PWM so as to generate the inverter trigger signals T1x and T2x to control the IGBTs in the VSI of LC-HAPF. Finally, the VSI outputs vinvx to the PPF branch in Figure 1, in which icx injects into the power grid and compensates the reactive power and harmonics current.

Figure 3.
The overall block diagram of LQRC and LQRIC for LC-HAPF.
In this paper, a comparative study of the compensation for LC-HAPF with different controllers will be demonstrated in order to verify the effectiveness of the LQRCI for LC-HAPF. The HCC and PCC are applied to the LC-HAPF for the comparative study, and their control block diagrams and parameter designs will be mentioned in the following sections.
4.1. Hysteresis Current Control (HCC)
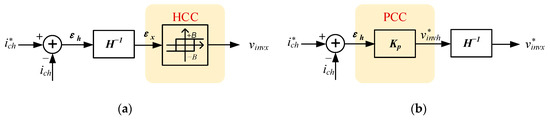
Figure 4.
Control block diagram of (a) HCC; (b) PCC.
The design of the hysteresis band B needs to satisfy (26).
where fsw is the switching frequency.
4.2. Proportional Current Control (PCC)
The control block diagram of PCC [15] is shown in Figure 4b. The PCC is expressed by:
where Kp is the proportional gain and the Kp can be designed by:
where Ts is the sampling time.
5. Simulation Result
The system parameters and control parameters of different controllers for simulation are shown in Table 1. MATLAB/Simulink is used to simulate the compensation results of the different current controllers for the three-phase four-wire LC-HAPF. The simulation results before and after HCC, PCC, LQRC and LQRIC-controlled LC-HAPF under 50 V and 40 V DC-link voltage conditions are shown in Figure 5 and Figure 6, and the values are summarized in Table 2 and Table 3.

Table 1.
System parameters and control parameters of different controllers for simulation.

Figure 5.
Simulation results of three-phase PCC voltage, source current and neutral current before and after LC-HAPF compensation with (a) HCC; (b) PCC; (c) LQRC; and (d) LQRIC under 50 V DC-link voltage. (For each graph, the blue lines are the waveforms of source voltage, the red lines are the waveforms of source current, and the peacock blue lines are the waveforms of neutral current.)

Figure 6.
Simulation results of three-phase PCC voltage, source current and neutral current before and after the LC-HAPF compensation with (a) HCC; (b) PCC; (c) LQRC; and (d) LQRIC under 40 V DC-link voltage. (For each graph, the blue lines are the waveforms of source voltage, the red lines are the waveforms of source current, and the peacock blue lines are the waveforms of neutral current.)

Table 2.
Simulation results before and after LC-HAPF compensation under 50V DC-link voltage.

Table 3.
Simulation results before and after the LC-HAPF compensation under 40V DC-link voltage.
5.1. Hysteresis Current Control (HCC)
After compensation, the simulation results of HCC under 50V DC-link voltage conditions are shown in Figure 5a and Table 2. The harmonic currents are compensated, and the total source current harmonic distortion (THDisx) is reduced from 33.7% to about 11.3%. Also, the compensated isn is 0.49 Arms and the compensated isx is around 2.50 Arms. Additionally, the three-phase power factors (PFs) are the same and increase to 0.99, and the QTotal reduces to 4.2 var. The total switching loss (total SW loss) of HCC is 25.0 W.
The simulation results of HCC under 40V DC-link voltage conditions are shown in Figure 6a and Table 3. The THDisx reduces to about 15.9%. Also, the compensated isn is 0.79 Arms and the compensated isx is around 2.49 Arms. Additionally, the three-phase PFs are the same and increase to 0.99, and the QTotal reduces to 10.0 var. The total SW loss of HCC is 12.3 W.
5.2. Proportional Current Control (PCC)
The simulation results of the LC-HAPF with PCC under 50V DC-link voltage conditions are shown in Figure 5b and Table 2. The THDisx reduces to about 8.7% after compensation. The compensated isn is 0.44 Arms and the compensated isx is around 2.48 Arms. Moreover, the three-phase PFs are equal to 1, and the QTotal reduces to 3.8 var. The total SW loss of PCC is 26.3 W.
The simulation results of the LC-HAPF with PCC under 40V DC-link voltage conditions are shown in Figure 6b and Table 3. The THDisx reduces to about 15.0% after compensation. The compensated isn is 0.77 Arms and the compensated isx is around 2.45 Arms. Moreover, the three-phase PFs increase to 0.99, and the QTotal reduces to 9.7 var. The total SW loss of PCC is 13.8 W.
5.3. Linear Quadratic Regulator Control (LQRC)
Figure 5c and Table 2 show the simulation results of the LC-HAPF with LQRC under 50V DC-link voltage conditions. After compensation, the THDisx reduces to about 8.1%. The compensated isn is 0.41 Arms and the compensated isx is around 2.47 Arms. The three-phase PFs are equal to 1, and the QTotal reduces to 2.8 var. The total SW loss of LQRC is 26.6 W.
Figure 6c and Table 3 show the simulation results of the LC-HAPF with LQRC under 40V DC-link voltage conditions. After compensation, the THDisx reduces to about 8.2%. The compensated isn is 0.41 Arms and the compensated isx is around 2.46 Arms. The three-phase PFs are equal to 1, and the QTotal reduces to 3.6 var. The total SW loss of LQRC is 15.9 W.
5.4. Proposed LQR Control with Integral Action Control (LQRIC)
The simulation results of the LC-HAPF with proposed LQRIC under 50V DC-link voltage conditions are shown in Figure 5d and Table 2. After compensation, the THDisx reduces to about 6.8%. The compensated isn is 0.38 Arms and the compensated isx is around 2.46 Arms. The three-phase PFs are equal to 1, and the QTotal reduces to 2.1 var. The total SW loss of LQRC is 27.0 W.
The simulation results of the LC-HAPF with proposed LQRIC under 40V DC-link voltage conditions are shown in Figure 6d and Table 3. After compensation, the THDisx reduces to about 7.1%. The compensated isn is 0.36 Arms and the compensated isx is around 2.46 Arms. The three-phase PFs are equal to 1, and the QTotal reduces to 2.9 var. Hence, the proposed LQRIC can achieve the smallest steady-state error. The total SW loss of LQRC is 15.9 W.
6. Experimental Result
To verify the feasibility of proposed LQRIC, a 110 V–5 kVA three-phase four-wire LC-HAPF experimental prototype was constructed and is shown in Figure 7. A digital signal processor TMS320F2812 is applied and works in a 10 kHz sampling frequency. The Mitsubishi IGBT intelligent power module PM300DSA60 is used as the power switch in the VSI.

Figure 7.
Experimental prototype of 110 V–5 kVA LC-HAPF.
This paper takes IEEE Standard 519-2014 [31] as a reference. At small experimental rated 110 V–5 kVA prototypes and ISC/IL in the range of 100 < 1000 scale, the acceptable total demand distortion (TDD) is less than or equal to 15%. Considering the worst case, the rated current is equal to the fundamental load current and results in THD = TDD ≤ 15%. Therefore, THD ≤ 15% is used as a criterion to evaluate the LC-HAPF current harmonic compensation performance.
The experimental results before and after the LC-HAPF compensation with LQRC and LQRIC under 50V and 40V DC-link voltage conditions are shown in Figure 8 and Figure 9 and Table 4.
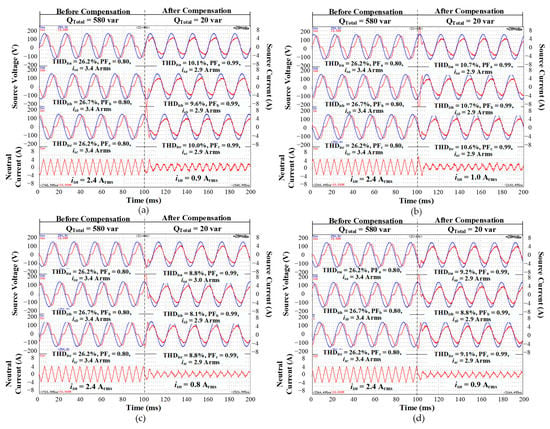
Figure 8.
Experimental results of three-phase PCC voltage, source current and neutral current before and after the LC-HAPF compensation with (a) LQRC under 50V DC-link voltage; (b) LQRC under 40V DC-link voltage; (c) LQRIC under 50 V DC-link voltage and (d) LQRIC under 40 V DC-link voltage. (For each graph, the blue lines are the waveforms of source voltage, the red lines in the 1st, 2nd and 3rd tunes are the waveforms of source current, and the red lines in last tune are the waveforms of neutral current.)

Figure 9.
Experimental results of THDisx after the LC-HAPF compensation with (a) LQRC under 50 V DC-link voltage; (b) LQRC under 40 V DC-link voltage; (c) LQRIC under 50V DC-link voltage and (d) LQRIC under 40 V DC-link voltage.

Table 4.
Experimental results before and after the LC-HAPF compensation with LQRC and LQRIC.
6.1. Linear Quadratic Regulator Control (LQRC)
After compensation, the experimental results of LQRC under 50V DC-link voltage conditions are shown in Figure 8a and Figure 9a and Table 4. The THDisx reduces to about 10.1%. Also, the compensated isn is 0.9 Arms and the compensated isx is 2.9 Arms. Additionally, the three-phase PFs are the same and increase to 0.99, and the QTotal reduces to 20 var. The total SW loss is 29.6 W.
The experimental results of LQRC under 40V DC-link voltage conditions are shown in Figure 8b and Figure 9b and Table 4. The harmonic currents are compensated, and the THDisx reduces to about 10.7%. Also, the compensated isn is 1.0 Arms and the compensated isx is 2.9 Arms. Moreover, the three-phase PFs are equal and increase to 0.99, and the QTotal reduces to 20 var. The total SW loss is 19.5 W.
6.2. Proposed LQR Control with Integral Action Control (LQRIC)
The experimental results of LQRIC under 50V DC-link voltage conditions are shown in Figure 8c and Figure 9c and Table 4. The THDisx reduces to about 8.8% after compensation. The compensated isn is 0.8 Arms and the compensated isx is around 2.9 Arms. Additionally, the three-phase PFs are the same and increase to 0.99, and the QTotal reduces to 20 var. The total SW loss is 30.2 W.
The experimental results of LQRIC under 40V DC-link voltage conditions are shown in Figure 8d and Figure 9d and Table 4. The THDisx reduces to about 9.2% after compensation. The compensated isn is 0.9 Arms and the compensated isx is around 2.9 Arms. Moreover, the three-phase PFs are equal and increase to 0.99, and the QTotal reduces to 20 var. The total SW loss is 20.3 W.
7. Discussion
7.1. Simulation Results Comparison of Different Controllers
From the simulation results shown in Figure 5 and Table 2, all controllers can compensate the reactive power and current harmonics. Comparing four controllers, HCC shows the worst THDisx, the largest neutral current isn and the largest reactive power after compensation, the current after HCC compensation still exists as a large current ripple. The PCC shows a lower THDisx, isn and QTotal than HCC with the fixed switching frequency, whereas the Kp gain of PCC is obtained by trial and error. LQRC shows a better harmonic, reactive power and neutral current compensation capability compared with PCC, as its control gain matrix K is optimized using the LQR method. LQRIC has the best harmonic and reactive power compensation capability with the lowest THDisx, QTotal and isn because an integral action is added to perform the error correction and the control gain K is also optimized by the LQR method.
7.2. Optimal Control of LQRC and LQRIC
From the simulation results shown in Figure 6 and Table 3, when the supplied DC-link voltage is reduced from 50V to 40V, the compensation performances of HCC and PCC become worse. A large steady-state error and reactive power exists after the HCC- and PCC-controlled LC-HAPF compensation, whereas the LQRC maintains a good harmonic and reactive power compensation performance. The LQRIC still shows the lowest THDisx, isn and QTotal, which verifies the optimal control of the proposed LQRIC.
7.3. Feasibility of LQRC and LQRIC Controllers
The experimental results in Figure 8, Figure 9 and Table 4 verify the feasibility of LQRC and LQRIC for LC-HAPF under 50V and 40V DC-link voltage. Followed by the IEEE standard [31], the LQRC- and LQRIC-controlled LC-HAPF can compensate the THDisx to less than 15%, while the reactive power and neutral current are small after compensation. These results show that both LQRC and LQRIC can achieve optimal control and can compensate harmonics and reactive power even in low DC-link voltage conditions. The proposed LQRIC also shows a better steady-state and reactive power compensation performance compared with the LQRC.
8. Conclusions
In this paper, a LQRIC for the three-phase four-wire LC-HAPF is proposed and designed to ensure a good steady-state performance even under low DC-link voltage. The state-space model in the d-q-0 coordinate of the LQRIC-controlled LC-HAPF is established and helps to obtain the reference current. The detailed design process of the weighting matrices, Q and R, of the LQRIC for the LC-HAPF based on Bryson’s rule is also given in this paper. Then, the control gain K matrix is calculated through the LQR method by using MATLAB. Finally, the obtained K matrix is applied and the feasibility of LQRC and LQRIC for the LC-HAPF are verified by the simulation and experimental results. The results show that LQRC- and LQRIC-controlled LC-HAPF can achieve a good compensation performance even under low DC-link voltage. Moreover, the proposed LQRIC shows superior steady-state performance compared with the harmonic compensation, neutral current compensation and reactive power compensation with HCC, PCC and LQRC.
Author Contributions
Formal analysis, Q.-R.H.; Methodology, Q.-R.H. and C.G.; Software, Q.-R.H., P.-I.C. and W.-K.S.; Supervision, C.-S.L.; Validation, Q.-R.H.; Writing—original draft, Q.-R.H.; Writing—review and editing, Q.-R.H., P.-I.C., W.-K.S. and C.-S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Science and Technology Development Fund, Macau SAR (FDCT) (File no. 0027/2021/A1, 025/2017/A1, 0028/2020/A1, SKL-AMSV(UM)-2020-2022); and in part by the University of Macau (File no. MYRG2017-00090-AMSV).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farhoodnea, M.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Power Quality Impact of Grid-Connected Photovoltaic Generation System in Distribution Networks. In Proceedings of the 2012 IEEE Student Conference on Research and Development (SCOReD), Penang, Malaysia, 5–6 December 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Bose, B.K. Power Electronics, Smart Grid, and Renewable Energy Systems. Proc. IEEE. 2017, 105, 2011–2018. [Google Scholar] [CrossRef]
- Di Paolo, M. Analysis of Harmonic Impact of Electric Vehicle Charging on the Electric Power Grid, Based on Smart Grid Regional Demonstration Project—Los Angeles. In Proceedings of the 2017 IEEE Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 6–7 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Anu, G.; Fernandez, F.M. Identification of Harmonic Injection and Distortion Power at Customer Location. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Subjak, J.S.; McQuilkin, J.S. Harmonics-Causes, Effects, Measurements, and Analysis: An Update. IEEE Trans. Ind. Appl. 1990, 26, 1034–1042. [Google Scholar] [CrossRef]
- Das, J.C. Passive Filters-Potentialities and Limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. Frequency Response Analysis of Current Controllers for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Ind. Electron. 2009, 56, 337–347. [Google Scholar] [CrossRef]
- Lam, C.-S.; Wong, M.-C.; Choi, W.-H.; Cui, X.-X.; Mei, H.-M.; Liu, J.-Z. Design and Performance of an Adaptive Low-DC-Voltage-Controlled LC-Hybrid Active Power Filter with a Neutral Inductor in Three-Phase Four-Wire Power Systems. IEEE Trans. Ind. Electron. 2014, 61, 2635–2647. [Google Scholar] [CrossRef]
- Sou, W.-K.; Choi, W.-H.; Chao, C.-W.; Lam, C.-S.; Gong, C.; Wong, C.-K.; Wong, M.-C. A Deadbeat Current Controller of LC-Hybrid Active Power Filter for Power Quality Improvement. IEEE Trans. Emerg. 2020, 8, 3891–3905. [Google Scholar] [CrossRef]
- Gong, C.; Sou, W.-K.; Lam, C.-S. Design and Analysis of Vector Proportional–Integral Current Controller for LC-Coupling Hybrid Active Power Filter with Minimum DC-Link Voltage. IEEE Trans. Ind. Electron. 2021, 36, 9041–9056. [Google Scholar] [CrossRef]
- Chan, P.-I.; Sou, W.-K.; Lam, C.-S. Improved Model Predictive Control with Signal Correction Technique of LC-Coupling Hybrid Active Power Filter. IEEE Trans. Emerg. Sel. Top. Power Electron. 2022, 10, 4650–4664. [Google Scholar] [CrossRef]
- Sou, W.-K.; Chao, C.-W.; Gong, C.; Lam, C.-S.; Wong, C.-K. Analysis, Design, and Implementation of Multi-Quasi-Proportional-Resonant Controller for Thyristor-Controlled LC-Coupling Hybrid Active Power Filter (TCLC-HAPF). IEEE Trans. Ind. Electron. 2022, 69, 29–40. [Google Scholar] [CrossRef]
- Xiang, Z.; Pang, Y.; Wang, L.; Wong, C.-K.; Lam, C.-S.; Wong, M.-C. Design, Control and Comparative Analysis of an LCLC Coupling Hybrid Active Power Filter. IET Power Electron. 2020, 13, 1207–1217. [Google Scholar] [CrossRef]
- Lam, C.-S.; Wong, M.-C.; Han, Y.-D. Hysteresis current control of hybrid active power filters. IET Power Electron. 2012, 5, 1175–1187. [Google Scholar] [CrossRef]
- Ye, T.; Dai, N.; Lam, C.-S.; Wong, M.-C.; Guerrero, J.M. Analysis, Design, and Implementation of a Quasi-Proportional-Resonant Controller for a Multifunctional Capacitive-Coupling Grid-Connected Inverter. IEEE Trans. Ind Appl. 2016, 52, 4269–4280. [Google Scholar] [CrossRef]
- Ahmed, M.; Alsokhiry, F.; Abdel-Khalik, A.S.; Ahmed, K.H.; Al-Turki, Y. Improved Damping Control Method for Grid-Forming Converters Using LQR and Optimally Weighted Feedback Control Loops. IEEE Access 2021, 9, 87484–87500. [Google Scholar] [CrossRef]
- Fan, L.; Liu, P.; Teng, H.; Qiu, G.; Jiang, P. Design of LQR Tracking Controller Combined with Orthogonal Collocation State Planning for Process Optimal Control. IEEE Access 2020, 8, 223905–223917. [Google Scholar] [CrossRef]
- Huerta, F.; Pizarro, D.; Cobreces, S.; Rodriguez, F.J.; Giron, C.; Rodriguez, A. LQG Servo Controller for the Current Control of LCL Grid-Connected Voltage-Source Converters. IEEE Trans. Ind. Electron. 2012, 59, 4272–4284. [Google Scholar] [CrossRef]
- Panigrahi, R.; Subudhi, B.; Panda, P.C. A Robust LQG Servo Control Strategy of Shunt-Active Power Filter for Power Quality Enhancement. IEEE Trans. Power Electron. 2016, 31, 2860–2869. [Google Scholar] [CrossRef]
- Ufnalski, B.; Kaszewski, A.; Grzesiak, L.M. Particle Swarm Optimization of the Multioscillatory LQR for a Three-Phase Four-Wire Voltage-Source Inverter with an LC Output Filter. IEEE Trans. Ind. Electron. 2015, 62, 484–493. [Google Scholar] [CrossRef]
- De Almeida, P.M.; Ribeiro, A.S.B.; Souza, I.D.N.; de Fernandes, M.C.; Fogli, G.A.; Ćuk, V.; Barbosa, P.G.; Ribeiro, P.F. Systematic Design of a DLQR Applied to Grid-Forming Converters. IEEE J. Emerg. Sel. Top. Ind. Electron. 2020, 1, 200–210. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Liang, H.; Luo, Y. LQR-Based Optimal Distributed Cooperative Design for Linear Discrete-Time Multiagent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 599–611. [Google Scholar] [CrossRef]
- Gokcek, C.; Kabamba, P.T.; Meerkov, S.M. An LQR/LQG Theory for Systems with Saturating Actuators. IEEE Trans. Autom. Control 2001, 46, 1529–1542. [Google Scholar] [CrossRef]
- Kedjar, B.; Al-Haddad, K. LQR with Integral Action to Enhance Dynamic Performance of Three-Phase Three-Wire Shunt Active Filter. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1138–1144. [Google Scholar] [CrossRef]
- Arab, N.; Vahedi, H.; Al-Haddad, K. LQR Control of Single-Phase Grid-Tied PUC5 Inverter with LCL Filter. IEEE Trans. Ind. Electron. 2020, 67, 297–307. [Google Scholar] [CrossRef]
- Kedjar, B.; Al-Haddad, K. DSP-Based Implementation of an LQR With Integral Action for a Three-Phase Three-Wire Shunt Active Power Filter. IEEE Trans. Ind. Electron. 2009, 56, 2821–2828. [Google Scholar] [CrossRef]
- Kedjar, B.; Al-Haddad, K. LQ Control of a Three-Phase Four-Wire Shunt Active Power Filter Based on Three-Level NPC Inverter. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 6–7 May 2008; pp. 1297–1302. [Google Scholar] [CrossRef]
- Santiprapan, P.; Areerak, K.; Areerak, K. Dynamic Model of Active Power Filter in Three-Phase Four-Wire System. In Proceedings of the 2014 11th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Nakhon, Thailand, 14–17 May 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Busatto, T.; Rönnberg, S.; Bollen, M.H.J. Comparison of Models of Single-Phase Diode Bridge Rectifiers for Their Use in Harmonic Studies with Many Devices. Energies 2022, 15, 66. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 6th ed.; Pearson: Upper Saddle River, NJ, USA, 2010; ISBN 978-0-13-601969-5. [Google Scholar]
- IEEE Std 519-2014 (Revision of IEEE Std 519-1992); Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Hoboken, NJ, USA, 2014; pp. 1–29. [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).