Potential of Computer-Aided Engineering in the Design of Ground-Improvement Technologies
Abstract
:1. Introduction
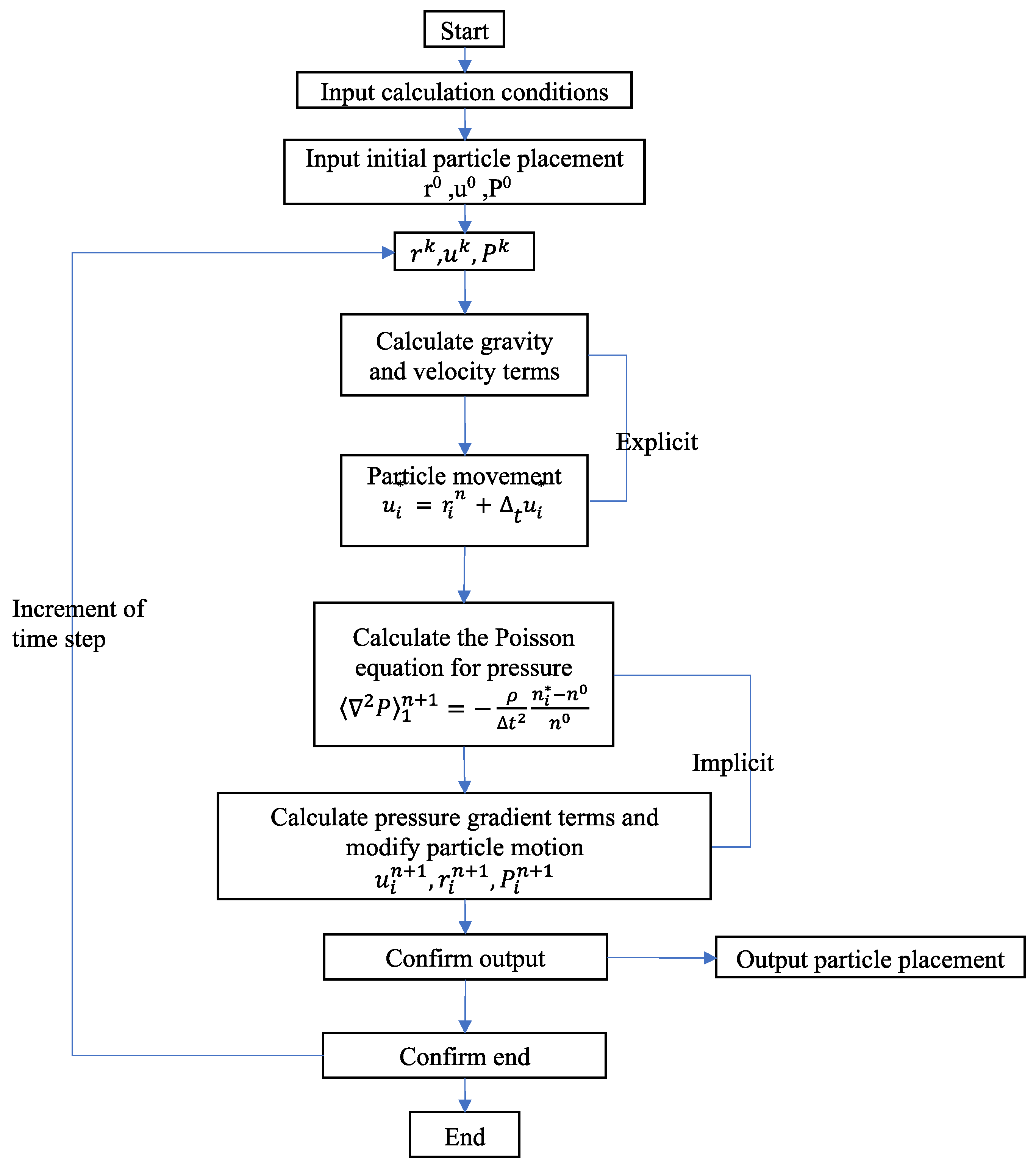
2. CAE_MPS Method
2.1. Computer-Aided Engineering (CAE)
2.2. Particle Methods and Moving Particle Semi-Implicit (MPS) Method
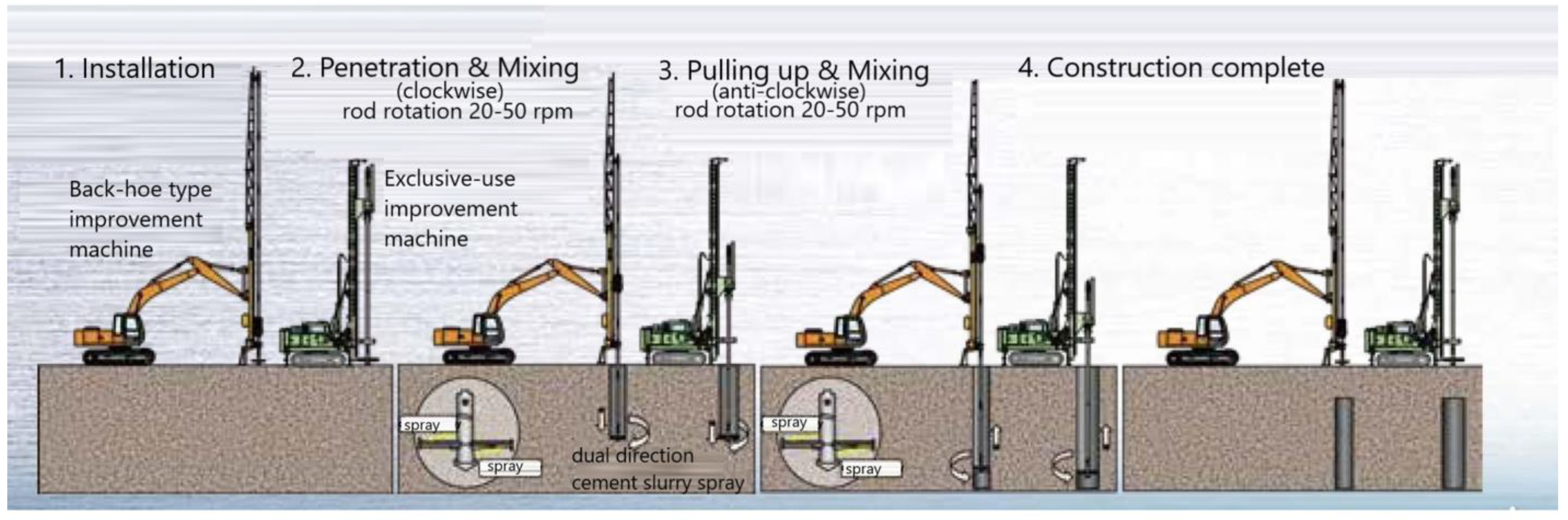
3. Outline of Middle-Pressure Jet-Grouting Method
4. Methodology
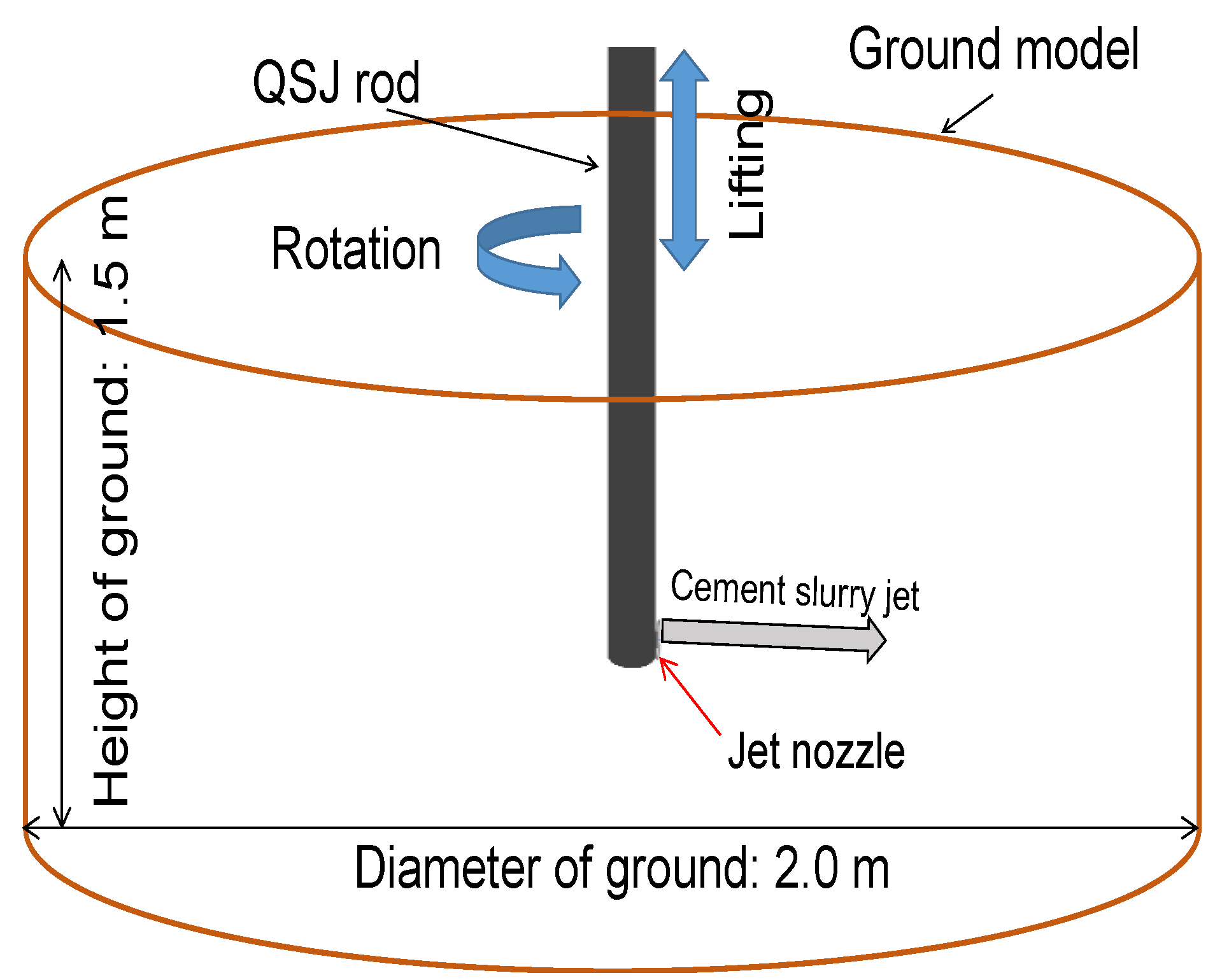
4.1. Ground Modelling
4.2. Analysis Conditions
4.3. Material Parameters
4.4. Setting Probe Region and Boundaries
5. Results and Discussion
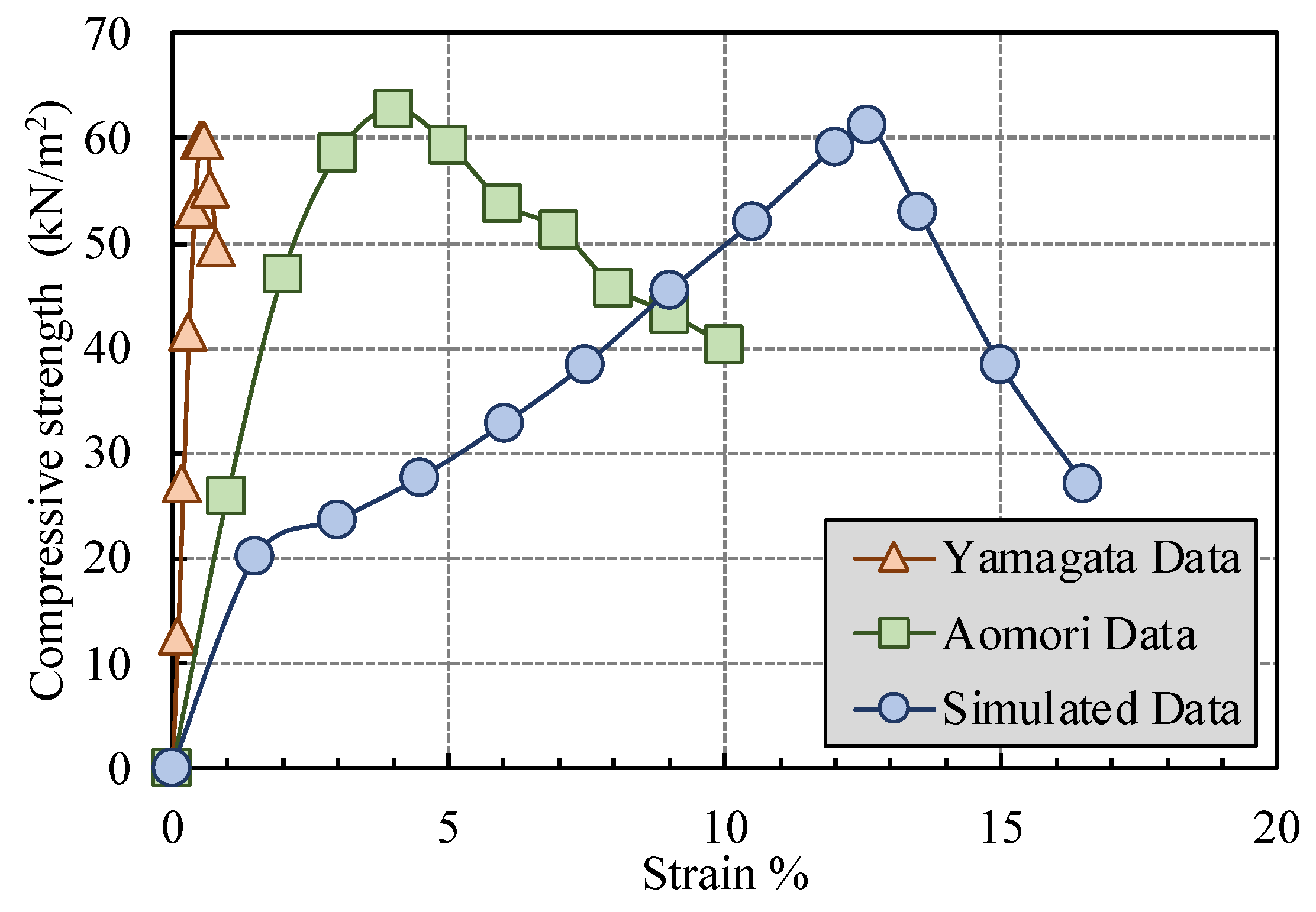
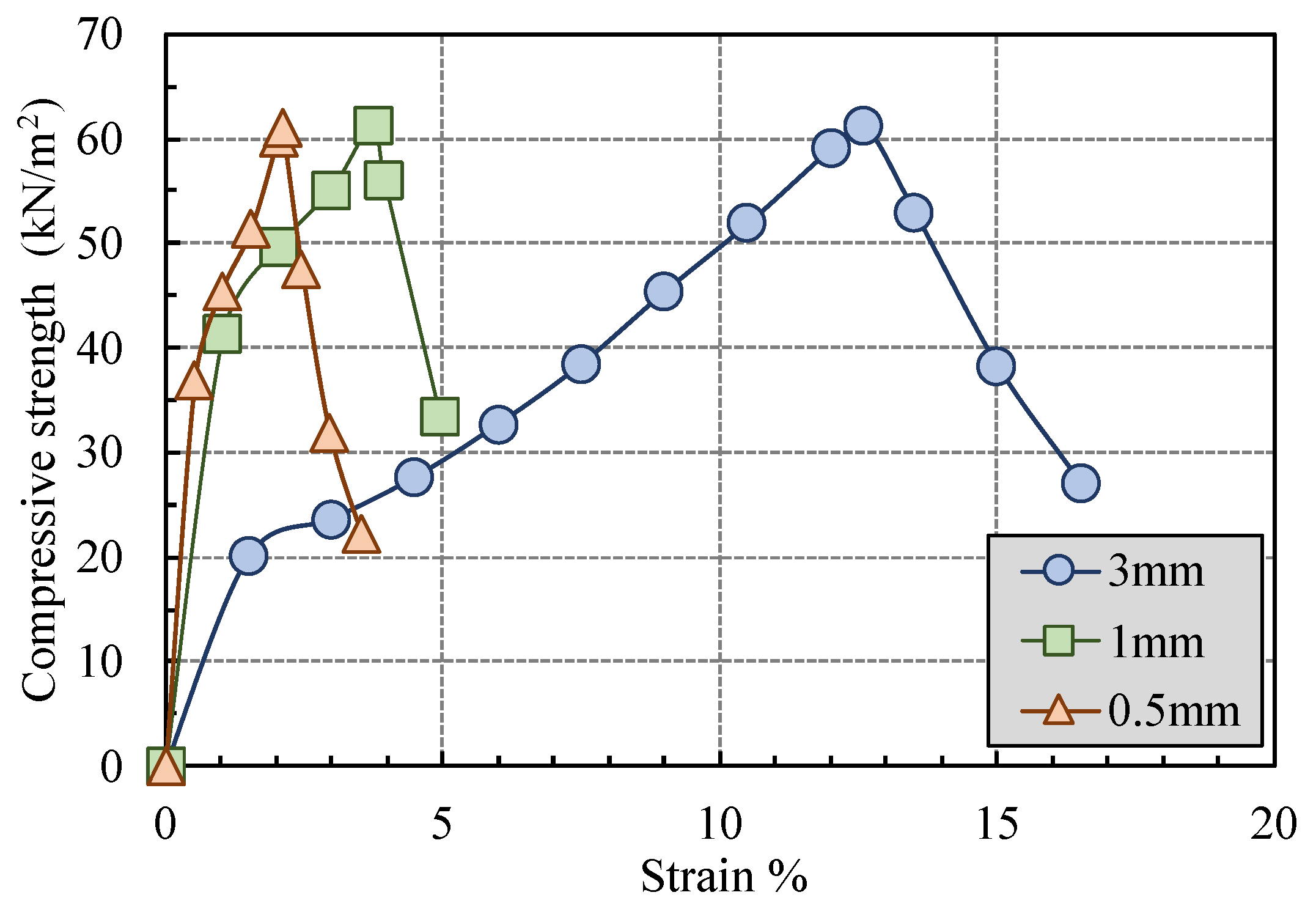
5.1. Validation of Analytical Ground Model
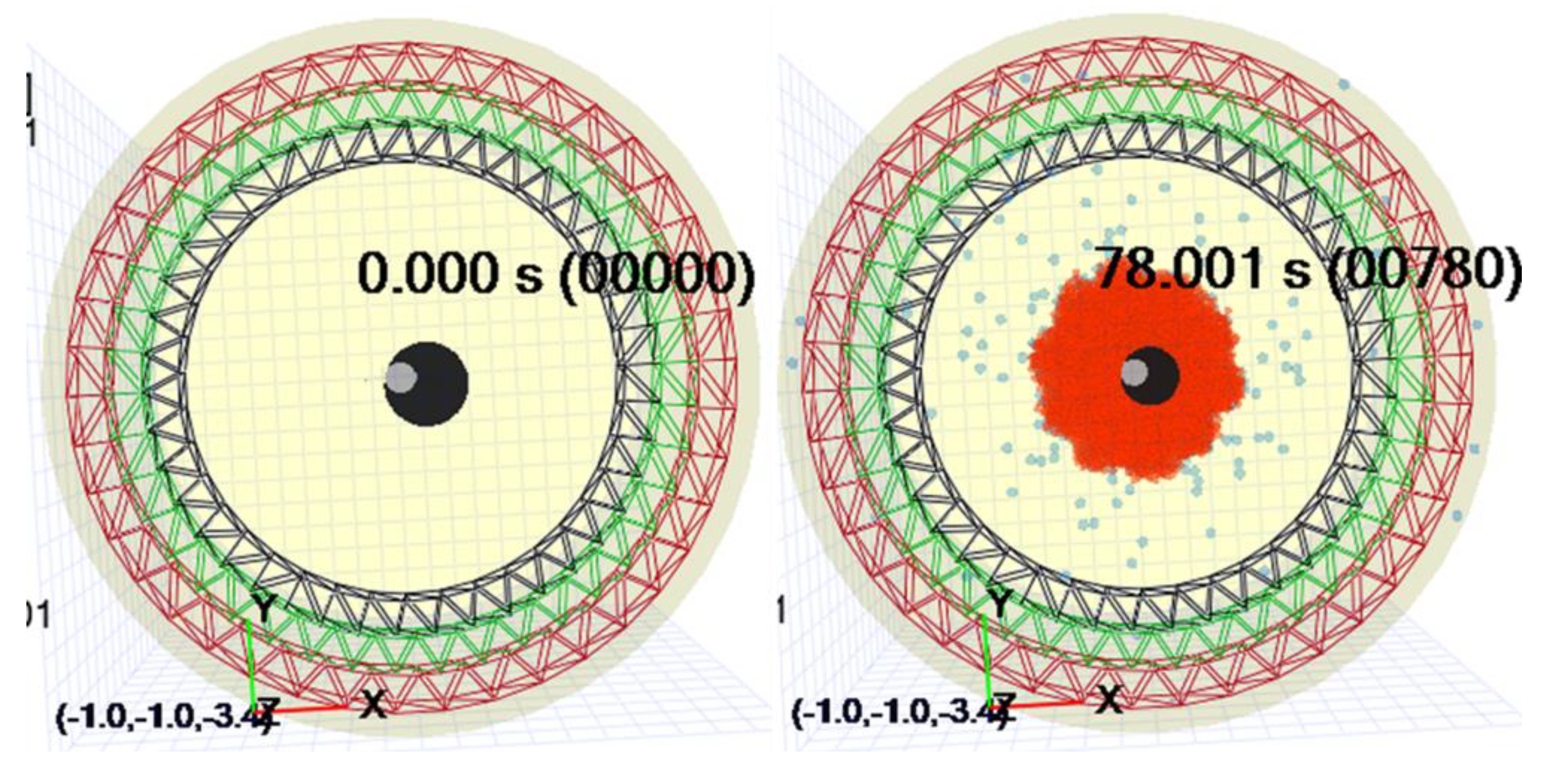
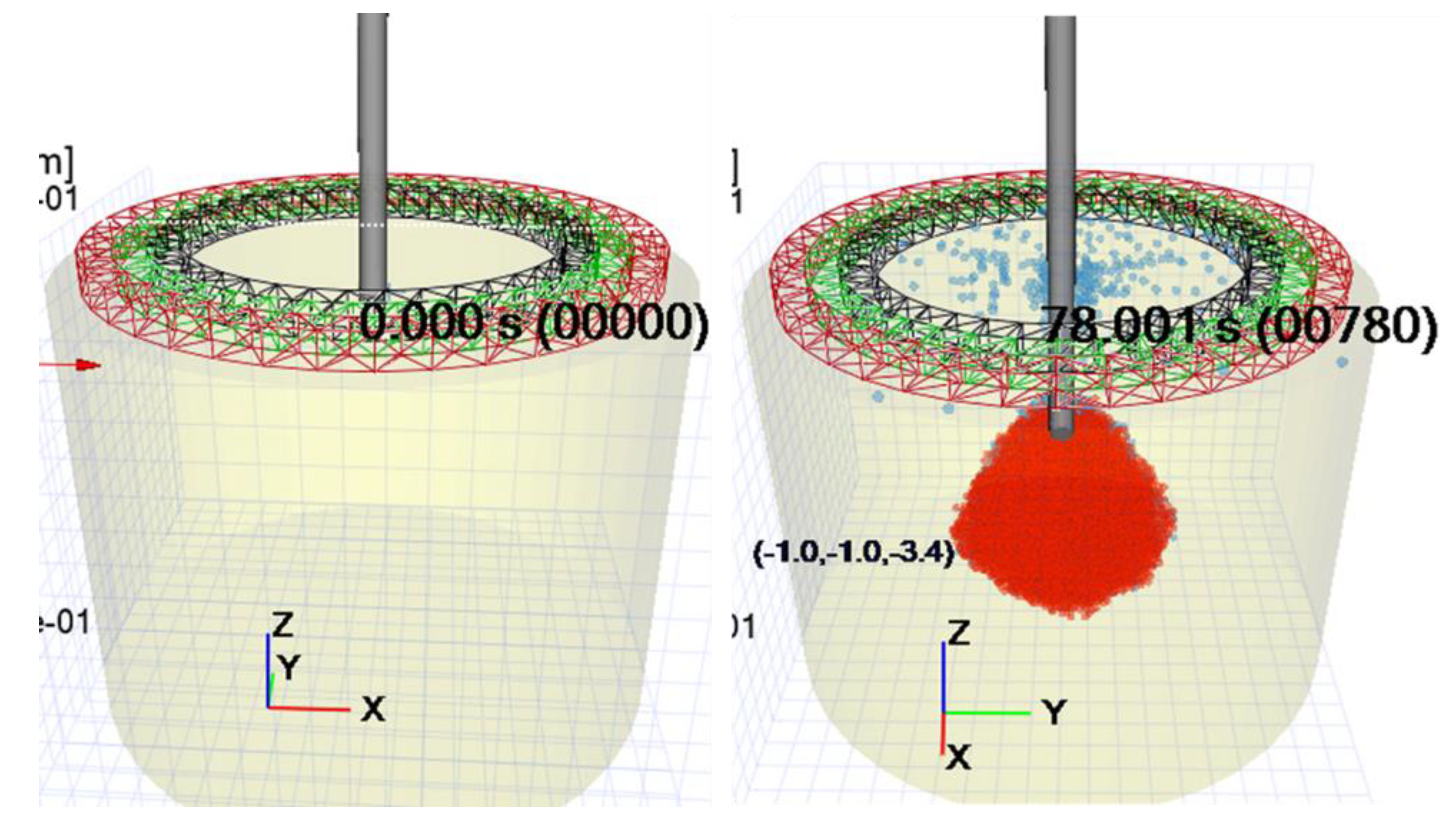
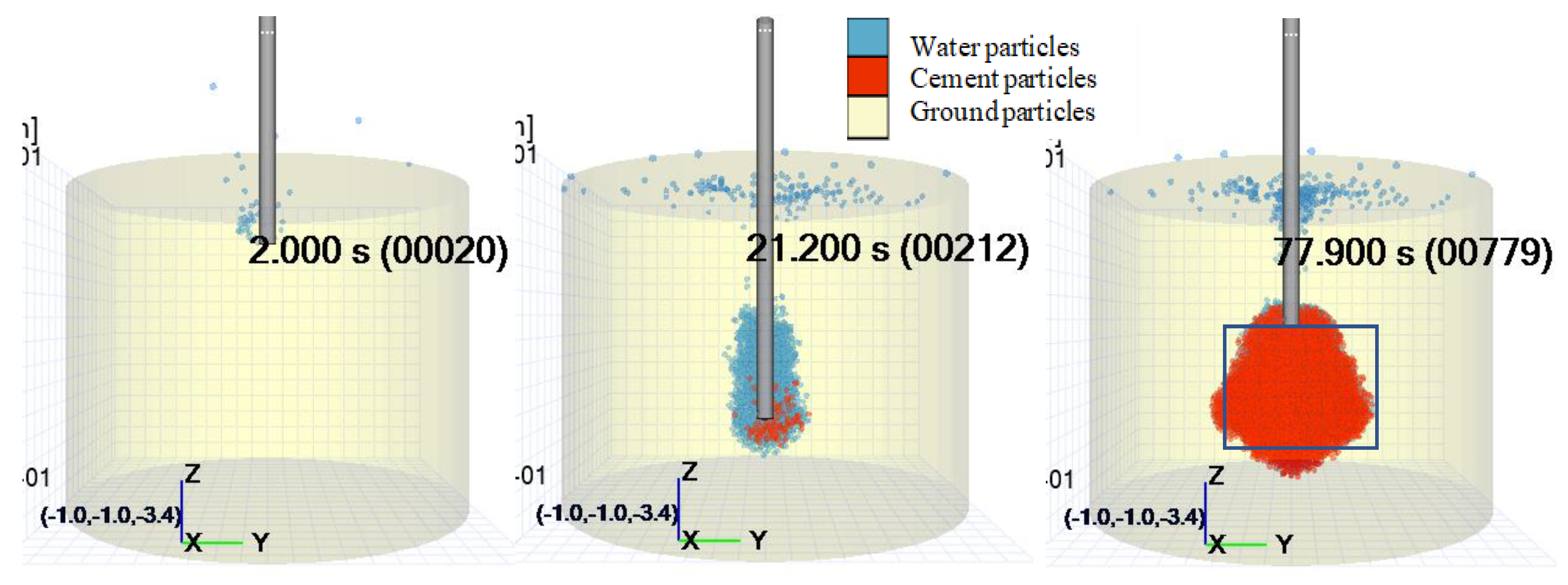
5.2. Reproduction of Development Situation of Columnar Soil-Improved Body
5.3. Computation of Mud Discharge Quantity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burke, G.K. Jet grouting systems: Advantages and disadvantages. In Proceedings of the GeoSupport 2004: Innovation and Cooperation in the Geo-Industry, Orlando, FL, USA, 29–31 January 2003; pp. 875–886. [Google Scholar]
- Harada, K.; Ohbayashi, J.; Matsumoto, J.; Kubo, Y.; Akima, T. New ground improvement technologies under restricted conditions in Japan. In Proceedings of the 15th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Kyushu, Japan, 9–13 November 2015; Volume 2, pp. 1165–1170. [Google Scholar] [CrossRef]
- Pinto, A.; Tomásio, R.; Marques, G. Ground improvement with jet grouting solutions at the new cruise terminal in Lisbon, Portugal. Procedia Eng. 2016, 143, 1495–1502. [Google Scholar] [CrossRef]
- You, W.; Lin, L.; Jingpei, L.; De’an, S. Jet-grouting in ground improvement and rotary grouting pile installation: Theoretical analysis. Geomech. Eng. 2020, 21, 279–288. [Google Scholar] [CrossRef]
- Wang, Z.F.; Bian, X.; Wang, Y.Q. Numerical approach to predict ground displacement caused by installing a horizontal jet grout column. Mar. Georesources Geotechnol. 2017, 35, 970–977. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, X.; Li, X.; Wang, X.; Zhao, X. Impacts of free-floating bikesharing system on public transit ridership. Transp. Res. Part D Transp. Environ. 2019, 76, 100–110. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Modoni, G.; Croce, P.; Mongiovì, L. Theoretical modelling of jet grouting. Géotechnique 2016, 56, 335–347. [Google Scholar] [CrossRef]
- Modoni, G.; Lidia, W.; Joanna, B.; Gaspare, G.; Angelo, L. Numerical analysis of submerged flows for jet grouting. Ground Improv. 2016, 169, 42–53. [Google Scholar] [CrossRef]
- Nakanishi, W.; Nakazawa, J. The process of development on jet grouting methods and their future. Soil Mech. Found. Eng. 2006, 54, 10–12. [Google Scholar]
- Njock, A.; Guy, P.; Shen, S.L.; Modoni, G.; Arulrajah, A. Recent advances in horizontal jet grouting (HJG): An overview. Arab. J. Sci. Eng. 2018, 43, 1543–1560. [Google Scholar] [CrossRef]
- Njock, P.G.A.; Chen, J.; Modoni, G.; Arulrajah, A.; Kim, Y.H. A review of jet grouting practice and development. Arab. J. Geosci. 2018, 11, 459. [Google Scholar] [CrossRef]
- Pinto, A.; Falcão, J.; Pinto, F.; Ribeiro, J. Ground improvement solutions using jet grouting columns. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 1249–1252. [Google Scholar] [CrossRef]
- Shen, S.L.; Njock, P.G.A.; Zhou, A.; Lyu, H.M. Dynamic prediction of jet grouted column diameter in soft soil using Bi-LSTM deep learning. Acta Geotech. 2021, 16, 303–315. [Google Scholar] [CrossRef]
- Shen, S.L.; Wang, Z.F.; Yang, J.; Ho, C.E. Generalized approach for prediction of jet grout column diameter. J. Geotech. Geoenvironmental Eng. 2013, 139, 2060–2069. [Google Scholar] [CrossRef]
- Zhang, W.; Hong, L.; Li, Y.; Zhang, R.; Goh, A.T.C.; Liu, H. Effects of jet grouting slabs on responses for deep braced excavations. Undergr. Space 2021, 6, 185–194. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Goh, A.T.C.; Zhang, R. Numerical study of the performance of jet grout piles for braced excavations in soft clay. Comput. Geotech. 2020, 124, 103631. [Google Scholar] [CrossRef]
- Komaki, T.; Fukada, S.; Shimano, A.; Nakanishi, Y. Efficient of mechanical mixing method with middle pressure injection by high performance fluidizing agent. In Proceedings of the 13th National Symposium on Ground Improvement, Kyoto, Japan, 24–26 October 2018; pp. 375–378. [Google Scholar]
- Komaki, T.; Fukada, S.; Sumi, K.; Nakanishi, Y.; Tanaka, N. Demonstration experiment of evolution technology by combination mixing slurry of middle pressure injection total system. In Proceedings of the 53th Japan National Conference on Geotechnical Engineering, Takamatsu, Japan, 24–26 July 2018; pp. 835–836. [Google Scholar]
- Inazumi, S.; Shakya, S.; Komaki, T.; Nakanishi, Y. Numerical analysis on performance of middle-pressure jet grouting method for ground improvement. Geosciences 2021, 11, 313. [Google Scholar] [CrossRef]
- Hattori, M. An attempt to apply mathematical foundation of Moving Particle Simulation to the MPS software “Particleworks”. Proc. Symp. Educ. Appl. Inf. Technol. 2015, 9, 59–62. [Google Scholar]
- Shakibaeini, A.; Jin, Y.C. MPS mesh-free particle method for multiphase flows. Comput. Methods Appl. Mech. Eng. 2012, 229–232, 13–26. [Google Scholar] [CrossRef]
- Tanaka, M.; Cardoso, R.; Bahai, H. Multi-resolution MPS method. J. Comput. Phys. 2018, 359, 106–136. [Google Scholar] [CrossRef]
- Chang, K.H. Product Design Modeling using CAD/CAE: The Computer Aided Engineering Design Series; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hamri, O.; Léon, J.C.; Giannini, F.; Falcidieno, B. Software environment for CAD/CAE integration. Adv. Eng. Softw. 2010, 41, 1211–1222. [Google Scholar] [CrossRef]
- Inazumi, S.; Kuwahara, S.; Jotisankasa, A.; Chaiprakaikeow, S. MPS-CAE simulation on dynamic interaction between steel casing and existing pile when pulling out existing piles, International Journal of GEOMATE: Geotechnique. Constr. Mater. Environ. 2020, 18, 68–73. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, X.; Teng, R.; Cao, X. Computer-aided design-while-engineering technology in topdown modeling of mechanical product. Comput. Ind. 2016, 75, 151–161. [Google Scholar] [CrossRef]
- Yang, P.; Zang, M.; Zeng, H. DEM-FEM simulation of tire-sand interaction based on improved contact model. Comput. Part. Mech. 2020, 7, 629–643. [Google Scholar] [CrossRef]
- Inazumi, S.; Komaki, T.; Nakanishi, Y.; Hashida, H.; Suzuki, M. Qualities evaluation on high pressure Jet mixing ground improvement methods by distinct element method (DEM). In Proceedings of the 13th National Symposium on Ground Improvement, Kyoto, Japan, 24–26 October 2018; pp. 211–216. [Google Scholar]
- Shimano, A.; Yamazaki, J.; Shinsaka, T. The study about work progress control of jet grouting method. In Proceedings of the 12th National Symposium on Ground Improvement; JSMS: Tokyo, Japan, 2016; pp. 455–458. [Google Scholar]
- Shinsaka, T.; Yamazaki, J.; Nakanishi, Y.; Komiya, K. Quality control and shape control techniques in jet grouting. In Proceedings of the IFCEE 2018: Innovations in Ground Improvement for Soils, Pavements, and Subgrades, Orlando, FL, USA, 5–10 March 2018. [Google Scholar] [CrossRef]
- Güllü, H. A new prediction method to rheological behavior of grout with bottom ash for jet grouting columns. Soils Found. 2017, 57, 384–396. [Google Scholar] [CrossRef]
- Güllü, H.; Cevik, A.; Ezzi, A.K.M.A.; Gülsan, M.E. On the rheology of using geopolymer for grouting: A comparative study with cement-based grout included fly ash and cold bonded fly ash. Constr. Build. Mater. 2019, 196, 594–610. [Google Scholar] [CrossRef]
- Kamalova, Z.; Hatanaka, S. Moving particle simulation for a simplified permeability model of pervious concrete. Comput. Concr. 2019, 24, 571–578. [Google Scholar]

| Target Material | Ground | |
|---|---|---|
| Ground Model Dimension | 2 m ø | 1.5 m Height |
| Jet materials | Water *1 | Cement slurry *2 |
| Spraying time | 20 s | 58 s |
| Penetration length while blanking (m) | 0.5 | 0 *2 |
| Penetration length while improving soil (m) | 0.5 | 0.5 |
| Jet amount (L/min) | 80 | 90 |
| Jet pressure (MPa) | 9.4 | 18.0 |
| Jet velocity (m/s) | 137.5 | 155.0 |
| Penetration velocity while blanking (m/min) | 3.0 | - |
| Penetration velocity while improving soil (m/min) | 3.0 | - |
| Lifting velocity while improving soil (m/min) | - | 0.52 *2 |
| Rotation speed (rpm) | 20 *1 | 20 |
| Material | Density (kg/m3) | w/c | Yield Value (Pa) | Plastic Viscosity (Pa·s) | Yield Parameter (-) | Surface Tension (N/m) | Fluid Model |
|---|---|---|---|---|---|---|---|
| Water | 1000 | - | - | - | - | 0.10 | Newtonian fluid |
| Cement slurry | 1500 | 1.0 | 10 | 0.28 | 0.0001 | 0.10 | Bingham fluid |
| Ground | 1600 | - | 60000 | 17000 | 0.0001 | 0.002 | Bingham fluid |
| Time after the Start of Construction (s) | 20 | 30 | 40 | 50 | 60 | 78 | |
|---|---|---|---|---|---|---|---|
| Number of particles for probe diameter of 1.8 m | Cement grout | 0 | 0 | 0 | 0 | 0 | 0 |
| Ground | 64 | 168 | 462 | 591 | 596 | 859 | |
| Water | 5 | 4 | 0 | 4 | 5 | 5 | |
| Number of particles number for probe diameter of 1.6 m | Cement grout | 0 | 0 | 0 | 0 | 0 | 0 |
| Ground | 209 | 320 | 532 | 533 | 538 | 892 | |
| Water | 4 | 4 | 3 | 4 | 4 | 4 | |
| Number of particles for probe diameter of 1.4 m | Cement grout | 0 | 0 | 0 | 0 | 0 | 0 |
| Ground | 364 | 440 | 466 | 466 | 498 | 878 | |
| Water | 8 | 7 | 6 | 8 | 8 | 8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakya, S.; Inazumi, S.; Nontananandh, S. Potential of Computer-Aided Engineering in the Design of Ground-Improvement Technologies. Appl. Sci. 2022, 12, 9675. https://doi.org/10.3390/app12199675
Shakya S, Inazumi S, Nontananandh S. Potential of Computer-Aided Engineering in the Design of Ground-Improvement Technologies. Applied Sciences. 2022; 12(19):9675. https://doi.org/10.3390/app12199675
Chicago/Turabian StyleShakya, Sudip, Shinya Inazumi, and Supakij Nontananandh. 2022. "Potential of Computer-Aided Engineering in the Design of Ground-Improvement Technologies" Applied Sciences 12, no. 19: 9675. https://doi.org/10.3390/app12199675
APA StyleShakya, S., Inazumi, S., & Nontananandh, S. (2022). Potential of Computer-Aided Engineering in the Design of Ground-Improvement Technologies. Applied Sciences, 12(19), 9675. https://doi.org/10.3390/app12199675






