A Distributed Bi-Behaviors Crow Search Algorithm for Dynamic Multi-Objective Optimization and Many-Objective Optimization Problems
Abstract
:1. Introduction
- Each problem (MOP, MaOP, DMOP) has a fitness function F(X), which can be minimized or maximized with simultaneously performed M objectives.
- Each problem has a set of solutions, X, presented by a set of bounded decision variables, X, with a d-dimensional search space generated between the minimum (X) and the maximum (X) boundaries.
- The search space of each problem can be limited by a set of inequality and equality constraint.
- For the MOP and the DMOP, the number of objectives (M) is fixed to 2 or 3 and is upper than 3 for MaOP .
- However, the DMOP has a time-varying decision variables, objectives and/or constraints, and is presented in Equation (2).
- The DMOP has M dynamic objective functions F(X, t) and a set of time-varying variables , which are subject to different bounded constraints, limiting the search space.
- This contribution presents a novel Distributed Bi-behaviours Crow Search Algorithm (DB-CSA) to solve both Dynamic Multi-Objective Optimization Problems (DMOPs) and static Many-Objective Optimization Problems (MaOPs), which have not yet been performed using the standard CSA algorithm.
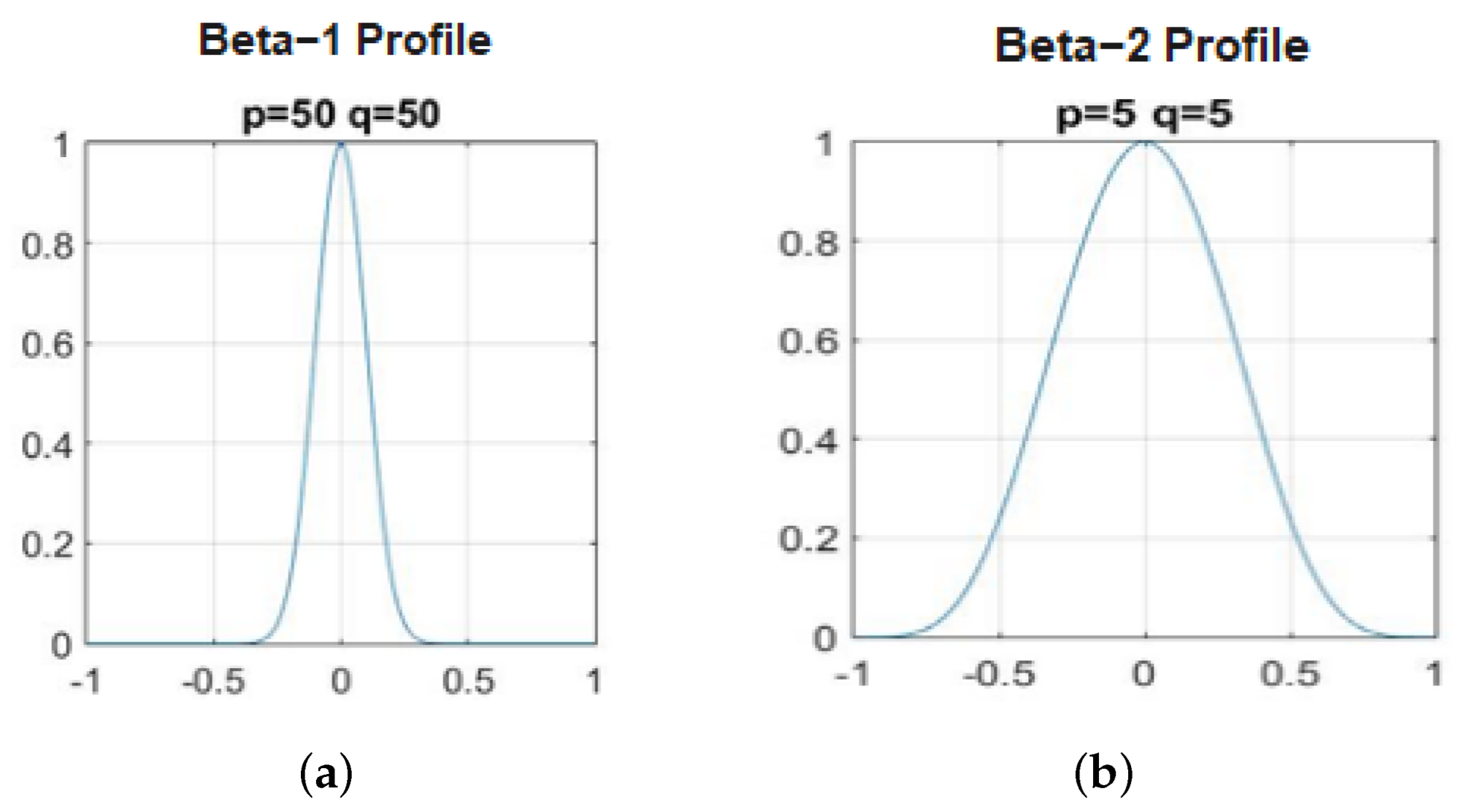
- The main difference between the original CSA algorithm and the new DB-CSA algorithm is as follows: the proposed DB-CSA approach presents two new chasing profiles, denoted by Beta Distribution profiles over the large Gaussian Beta-1 function for diversity enhancement and the narrow Gaussian Beta-2 function for convergence improvements.
- The proposed approach tends to achieve a dynamic balance between exploitation and exploration at each iteration during the optimization process, which makes it more suitable for both dynamic multi-objective optimization and many-objective optimization.
- A dynamic optimization mechanism is considered within the proposed DB-CSA algorithm when solving DMOPs to detect the time-varying POS and POF, effectively reacts to the dynamic changes and is denoted by the second variant (DB-CSA-II). This process aims to manage and control the dynamic change in a time-varying search space.
2. State-of-the-Art on Evolutionary Multi-Objective Optimization
2.1. Dynamic Multi-Objective Optimization Methods
| Diversity-Based Approaches | DNSGA-II [1] |
| Memory-Based Approaches | SGEA [11] |
| Prediction-Based methods | PPS [14] |
| Parallel Approaches | MOEA/D [13] |
| dCOEA [12] | |
| Transfer Learning-Based Methods | MMTL-MOEA/D [15] |
| RI-MOEA/D [15] | |
| SVR-MOEA/D [16] | |
| Tr-MOEA/D [17] | |
| KF-MOEA/D [18] |
2.2. Many-Objective Optimization Methods
| Decomposition-based approaches | MSOPS [20] and MSOPS-II [19] |
| MOEA/D [13] | |
| MOEA/DD [25] | |
| TSEA [57] | |
| MPEA-MP and MPEA*-MA [54] | |
| Indicator-based approaches | HypE [27] |
| Diversity-based selection criterion | NSGA-III [24] |
| SPEA/SDE [39] | |
| KnEA [40] | |
| SPEAR [56] | |
| Modified dominance relation-based approaches | GrEA [35] |
| VaEA [52] | |
| -DEA [36] | |
| NSGA-II/SDR [53] | |
| AnD[55] | |
| Preference-based approaches | RVEA [22] |
| PICEA-g[41] | |
| Two_Arch2 [43] |
2.3. Existing Crow Search-Based Methods
3. The Proposed Distributed Bi-Behaviors Crow Search Algorithm
3.1. The Standard Crow Search Algorithm
| Algorithm 1 The Standard Crow Search Algorithm (CSA) |
|
- The first state is when the crow i ignores being followed, and simply continues its search, considering what it previously found
- The second state is when the crow is aware of being followed; in this case, the crow will simply hide its food source and undergo a completely random search.
- These two position updates are detailed in Equation (3).
3.2. The Distributed Bi-Behaviours Crow Search Algorithm (DB-CSA)
- For MaOPs, the original meta-heuristics, such as the CSA algorithm [9] suffer from a robust mechanism to optimize a problem with a high number of objectives (more than three), which are optimized at the same time.
- For DMOPs, most of the existing approaches cannot manage the dynamic change in decision variables and objective values in the POS and the POF, respectively.
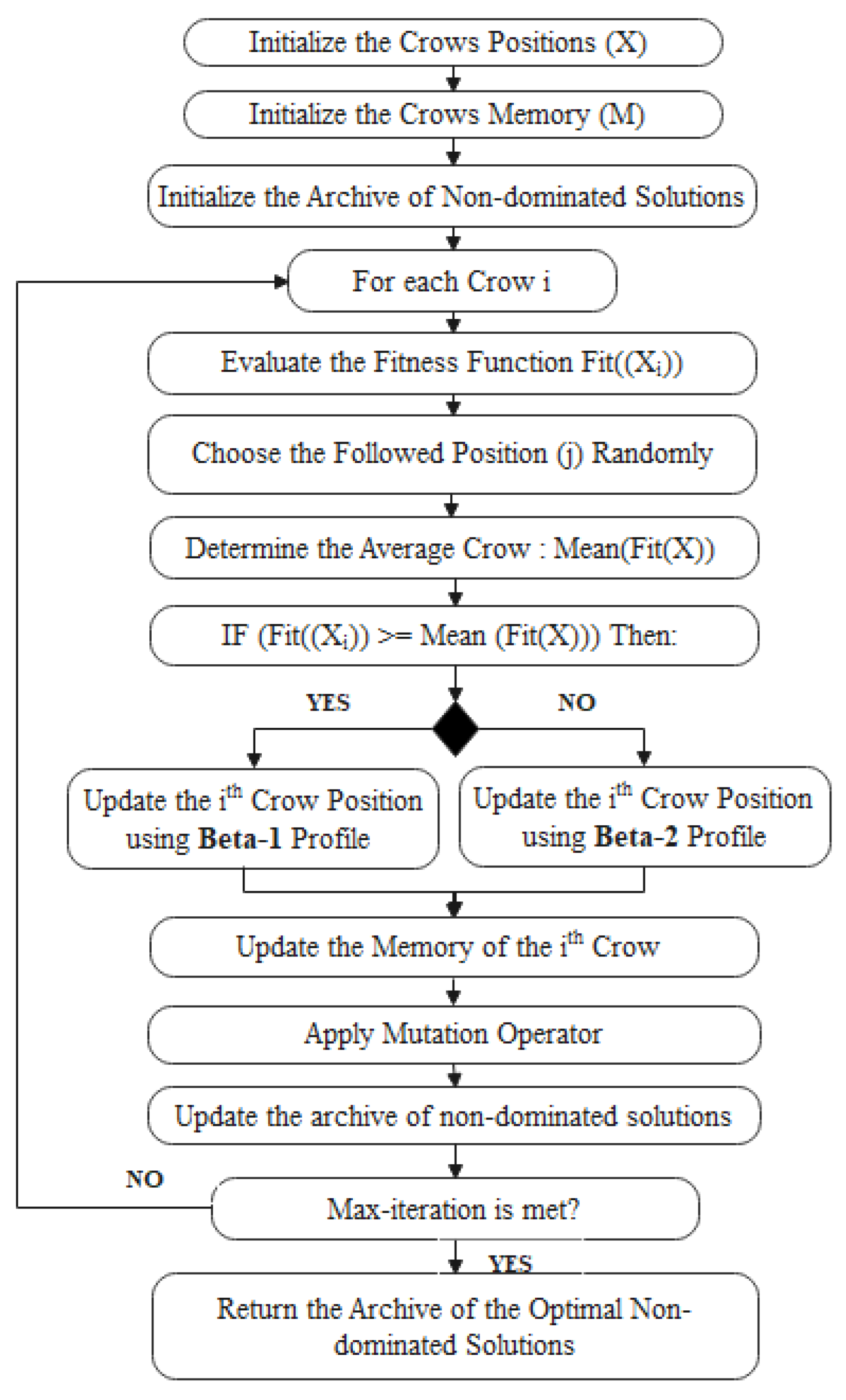
- The first variant (DB-CSA) has the same optimization process as the standard CSA algorithm [9] where the main difference is provided in the convergence and the diversity enhancement during the optimization process. A modified rules are considered in the first CSA algorithm to update the position of each crow. The first version of the proposed DB-CSA algorithm is developed to solve static MaOPs. The general flowchart is shown in Figure 1, and in the pseudo-code is given in Algorithm 2. More details are presented in Section 3.2.1.
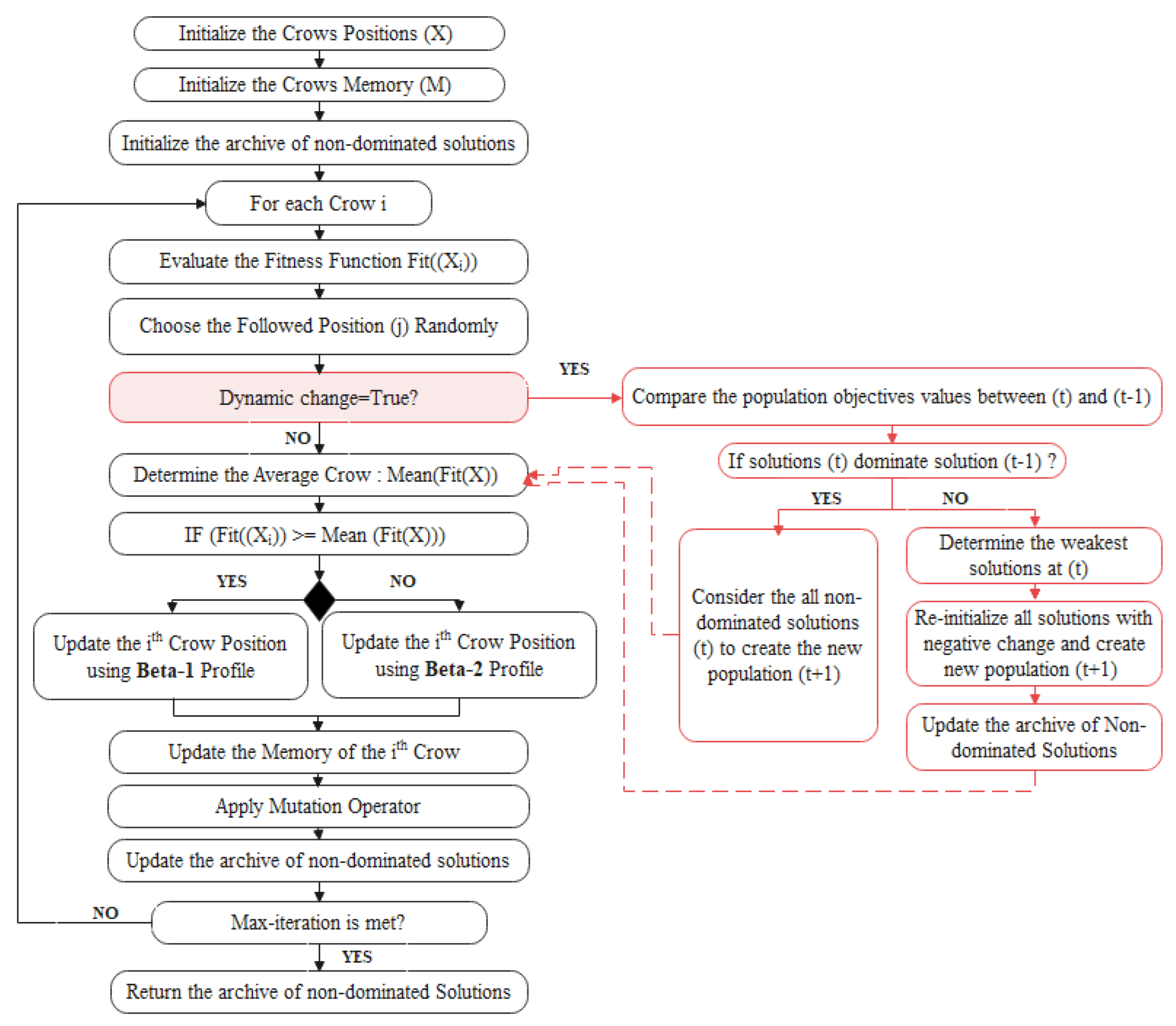
- The second variant (DB-CSA-II) is proposed based on the first DB-CSA algorithm. The main difference is that this investigates the dynamic optimization mechanism to efficiently detect and react to the change when solving DMOPs with a time-varying Pareto Optimal Set (POS) and dynamic Pareto Optimal Front (POF). The general flowchart of the second version is shown in Figure 2 and the pseudo-code is presented by Algorithm 3. More details are presented in Section 3.2.2.
| Algorithm 2 The pseudo-code of the proposed Distributed Bi-behaviours Crow Search Algorithm (DB-CSA) |
|
3.2.1. First Variant: DB-CSA for Static MaOPs
- 1.
- Initialization of population positions and their memories: In DB-CSA algorithm, each crow i is presented as a potential solution in the search space. The DB-CSA starts with a random initialization of position (X) and the memory (Mem) of the flock of N crows when each crow i has presented a potential solution in the search space.
- 2.
- Initialization of the archive of the non-dominated solutions: the archive (A) is initially created to store all the non-dominated solutions during the optimization process. After that, all the following steps are executed until a predefined number of iterations is reached.
- 3.
- Fitness Function Evaluation: for each crow i, the fitness function is evaluated.
- 4.
- Determine the followed crow i: at each iteration, one of the main behaviors of crow i is to determine one crow i to follow by selecting a random position value between zero and the size of the flock of best crows.
- 5.
- Determine the average crow i: the aggregated value of K objectives are computed as the fitness function of each crow i; then, the average value of all fitness functions is selected to determine the mean solution.
- 6.
- Update the crow position using the bi-behaviours’ beta-distribution profiles
- 7.
- 8.
- Apply the mutation operators
- 9.
- Update the archive of non-dominated solutions: at each time t of the optimization procedure, all the non-dominated solutions are stored in the archive (A) based on the operator.
- 10.
- Generate OUTPUT = the best Pareto solutions from the archive (A).
| Algorithm 3 The DB-CSA-II Algorithm with Dynamic Optimization Process |
|
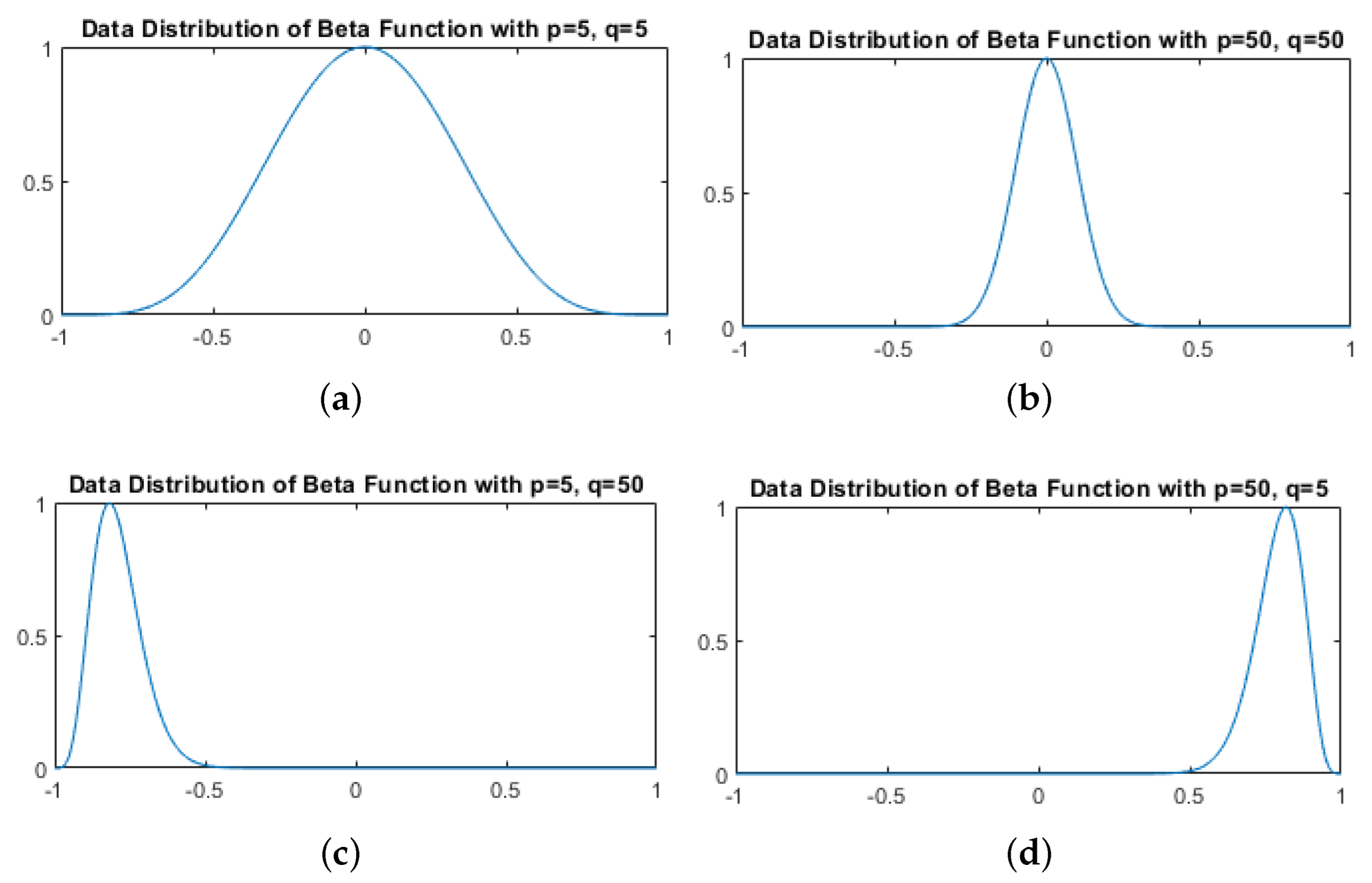
- The first large Gaussian Beta-1 exploitation profile is used to update the crows positions which is characterized by a large standard deviation pushing the population to achieve good diversity in the search space with p and q variables of the beta-function in Equation (8), which are equal to 5.
- The second narrow Gaussian Beta-2 exploration profile adapts a limited standard deviation to update the crows positions with p and q in Equation (8), which are equal to 50 allowing for a good convergence to the optimal solution over time.
3.2.2. The Second Variant: DB-CSA for DMOPs, DB-CSA-II
- Check dominance condition (2): the is strictly better than , for at least one objective.
- Check the dynamic change: if the current solution dominates the previous based on both conditions (1) and (2), so the dynamic change is successfully detected. The next step aims to effectively react to the dynamic change and to enhance all deterioration in the time-varying search space.
- React to the dynamic change: all non-dominated are considered to create the next population at iteration (t + 1), and all deteriorated solutions are randomly re-initialized. Then, all non-dominated solutions in the archive (A) are updated. This process aims to enhance the convergence and diversity of crows in a dynamic search space. The general flowchart of the second version of DB-CSA algorithm is shown in Figure 2.
3.3. The Complexity Analysis of the Proposed DB-CSA Approach
4. Experimental Study
- The first was to compare the new proposed DB-CSA-II to a set of DMOEAs designed for Dynamic Multi-Objective Optimization Problems (DMOPs).
- The second was for Many-Objective Optimization Problems (MaOPs).
4.1. Quality Indicators
4.2. Tested Benchmarks
4.3. Experimental Settings
4.3.1. Comparative Study (1) for DMOPs
4.3.2. Comparative Study (2) for MaOPs
4.3.3. Taguchi Method for Orthogonal Experimental Design
- The swarm size is fixed with two-level factors (N), for DMOPs and MaOPs .
- The maximum number of iterations is fixed with two-level factors, for DMOPs for severe and moderate change and for MaOPs .
- Both parameters of the Beta-1 function (p1) and (q1) are fixed to 5 or 50.
- Both parameters of the Beta-2 function (p2) and (q2) are fixed to 5 or 50.
4.4. Results Analysis and Discussion
- Step 1: define the null hypothesis (): the means of the paired approaches are the same.
- Step 2: define ix, the alternative hypothesis (): the means of the paired approaches are different.
- Step 3: compute the difference between the mean values.
- Step 4: assign a rank for the results obtained in step 3.
- Step 5: compute the number of ranks with negative values () and positive values ().
- Step 6: compute the probability (p-value) that the null hypothesis is true and is computed based on the test statistic value (z-score) produced by the Wilcoxon Rank–Sum test.
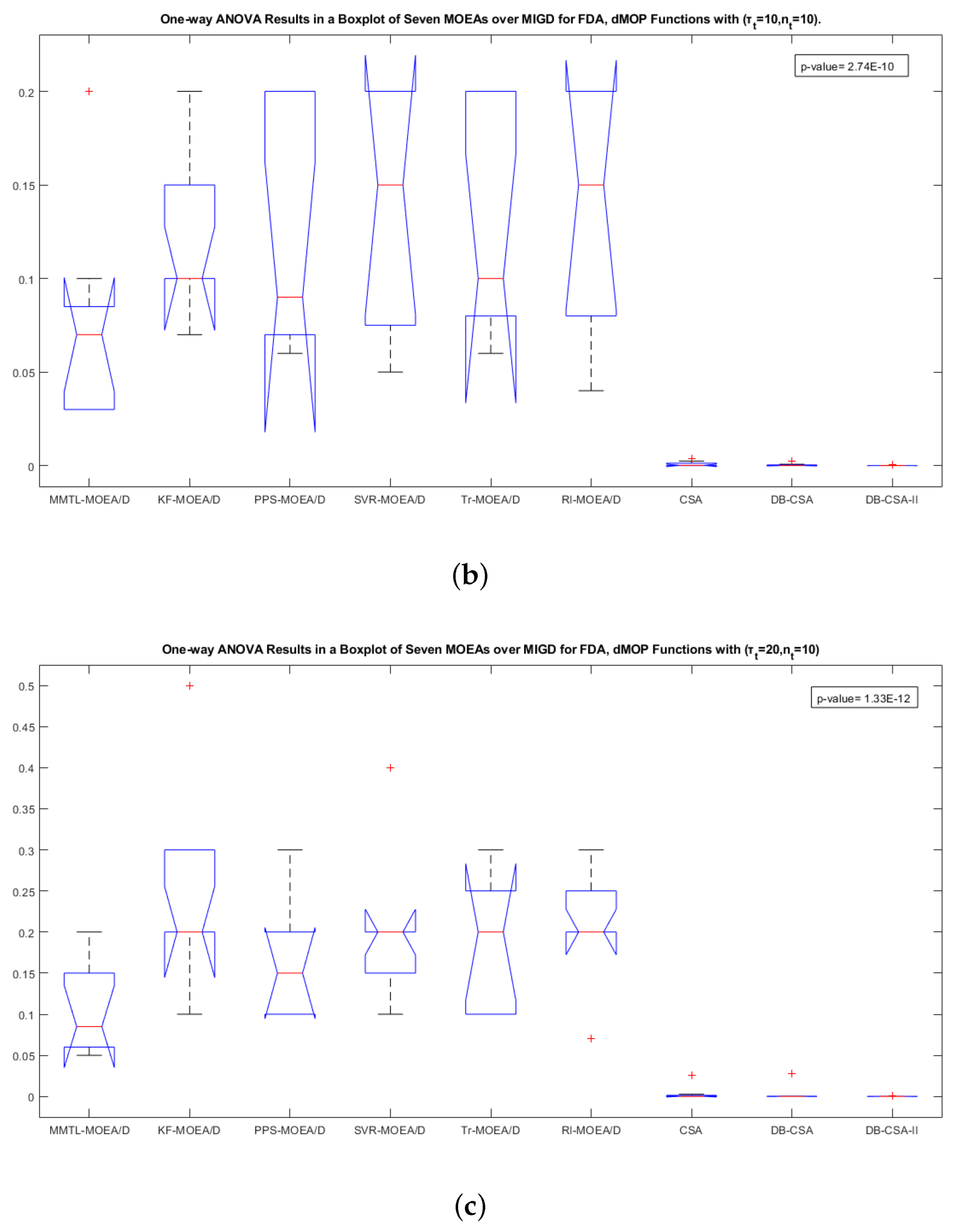
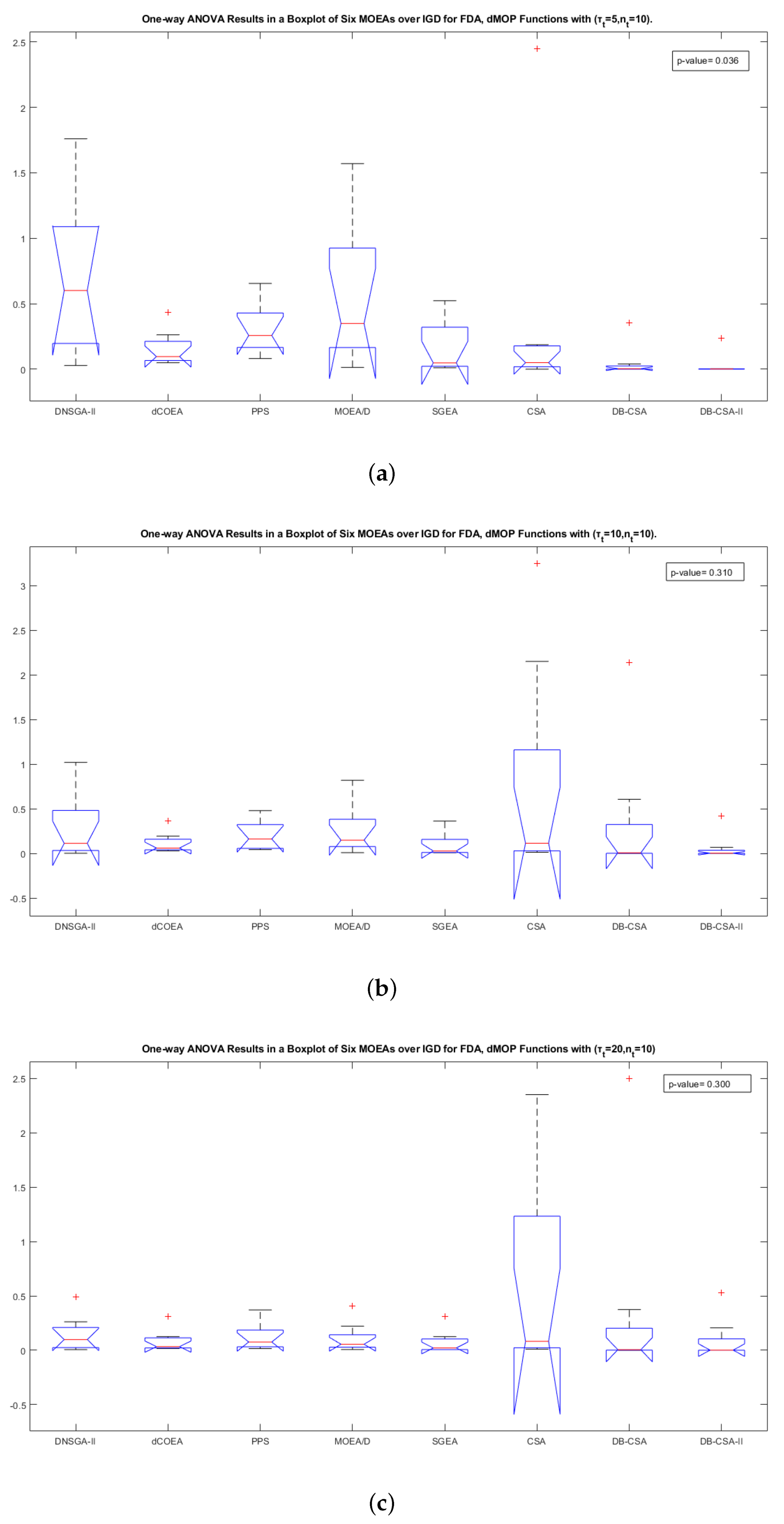
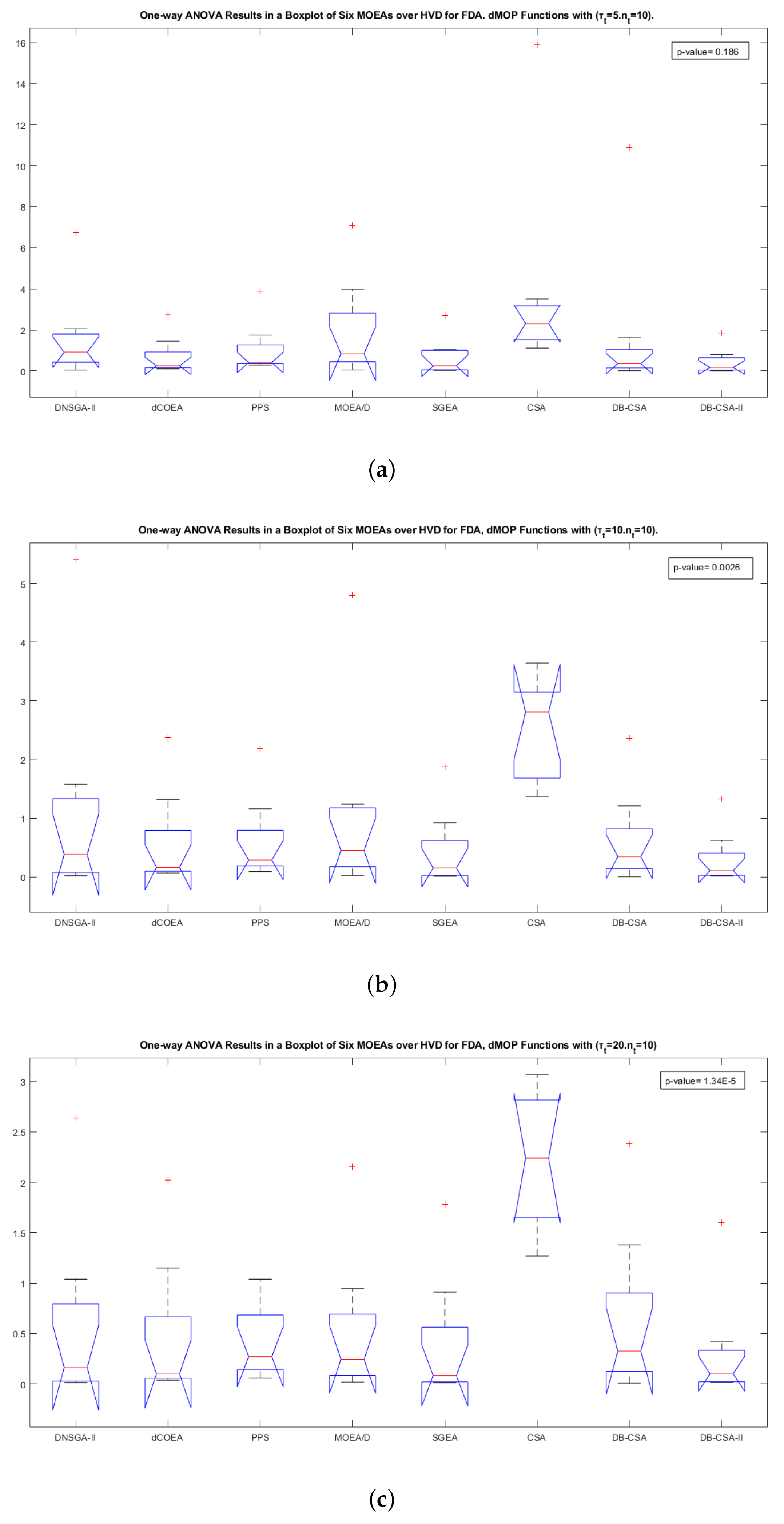
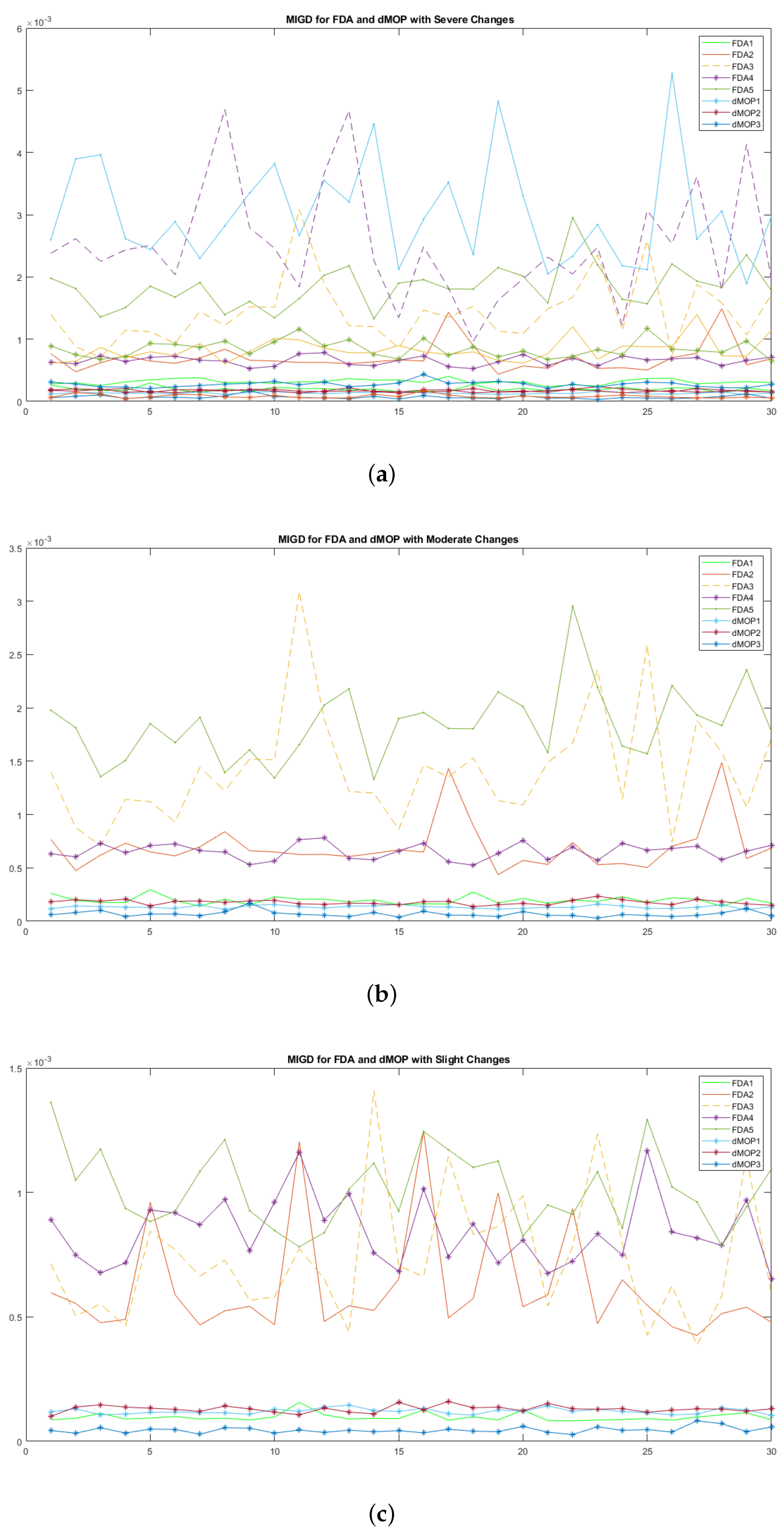
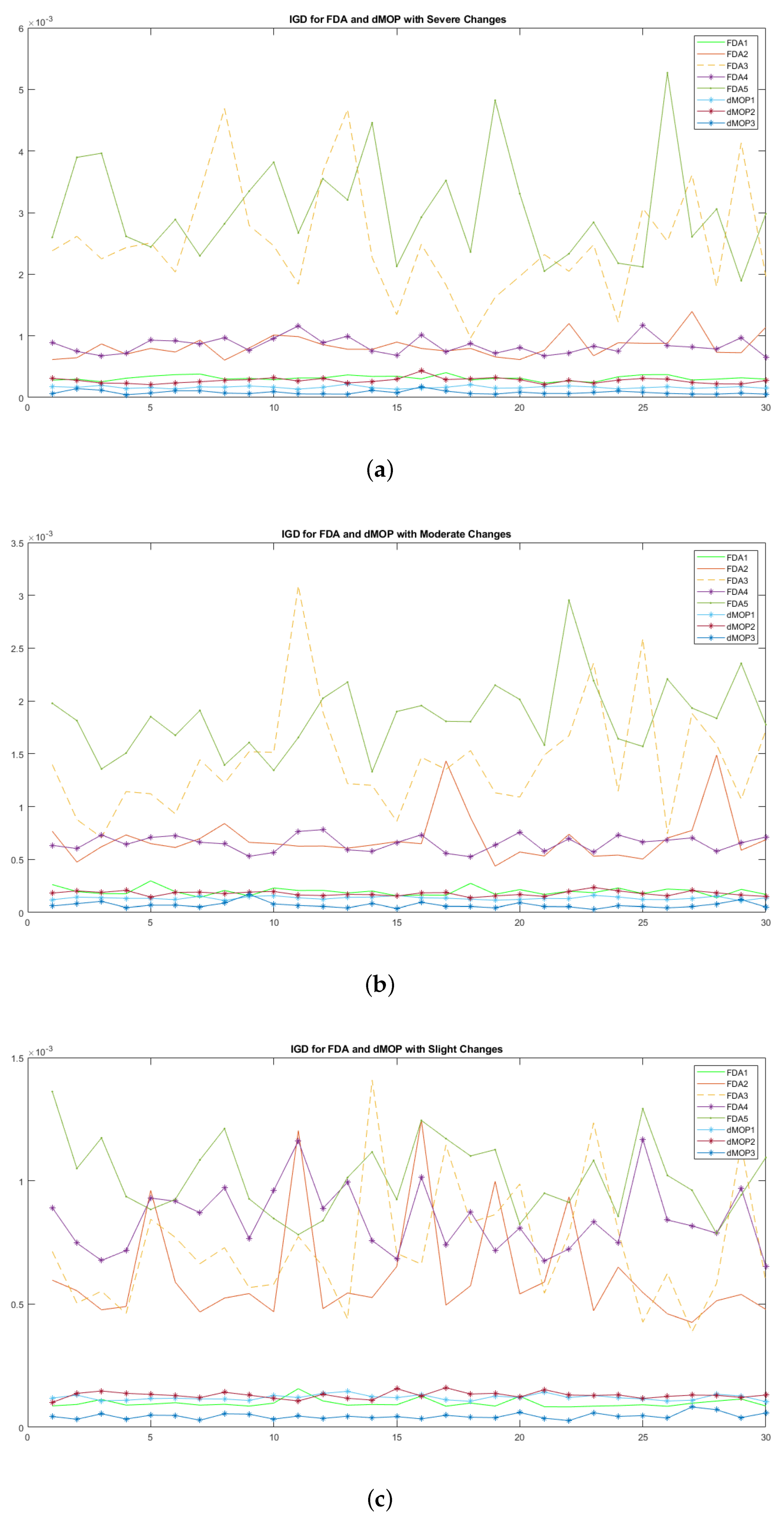
4.4.1. Analysis of the Comparative Study (1) for FDA and dMOP Problems
4.4.2. Analysis of the Comparative Study (1) for UDF and F Problems
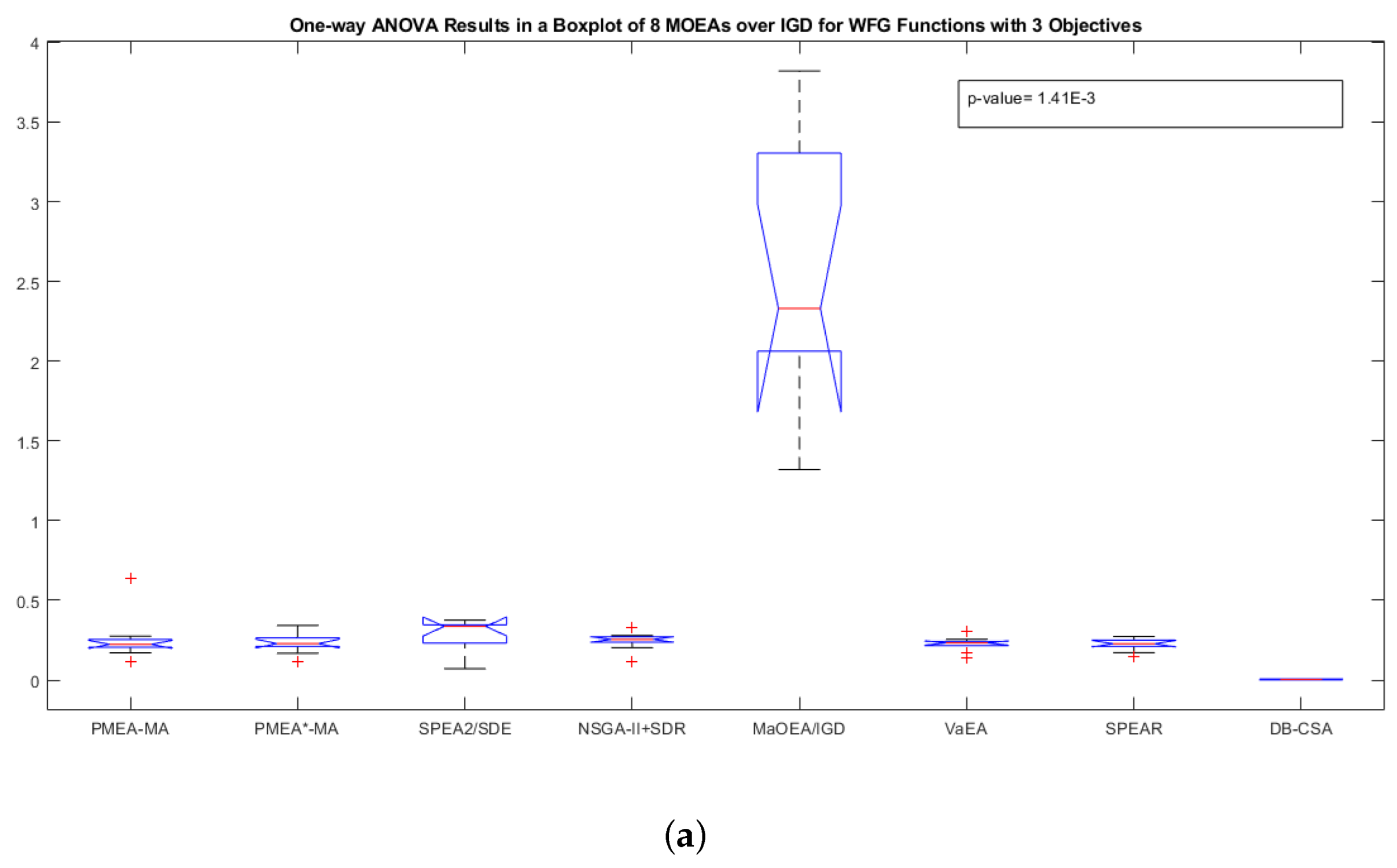
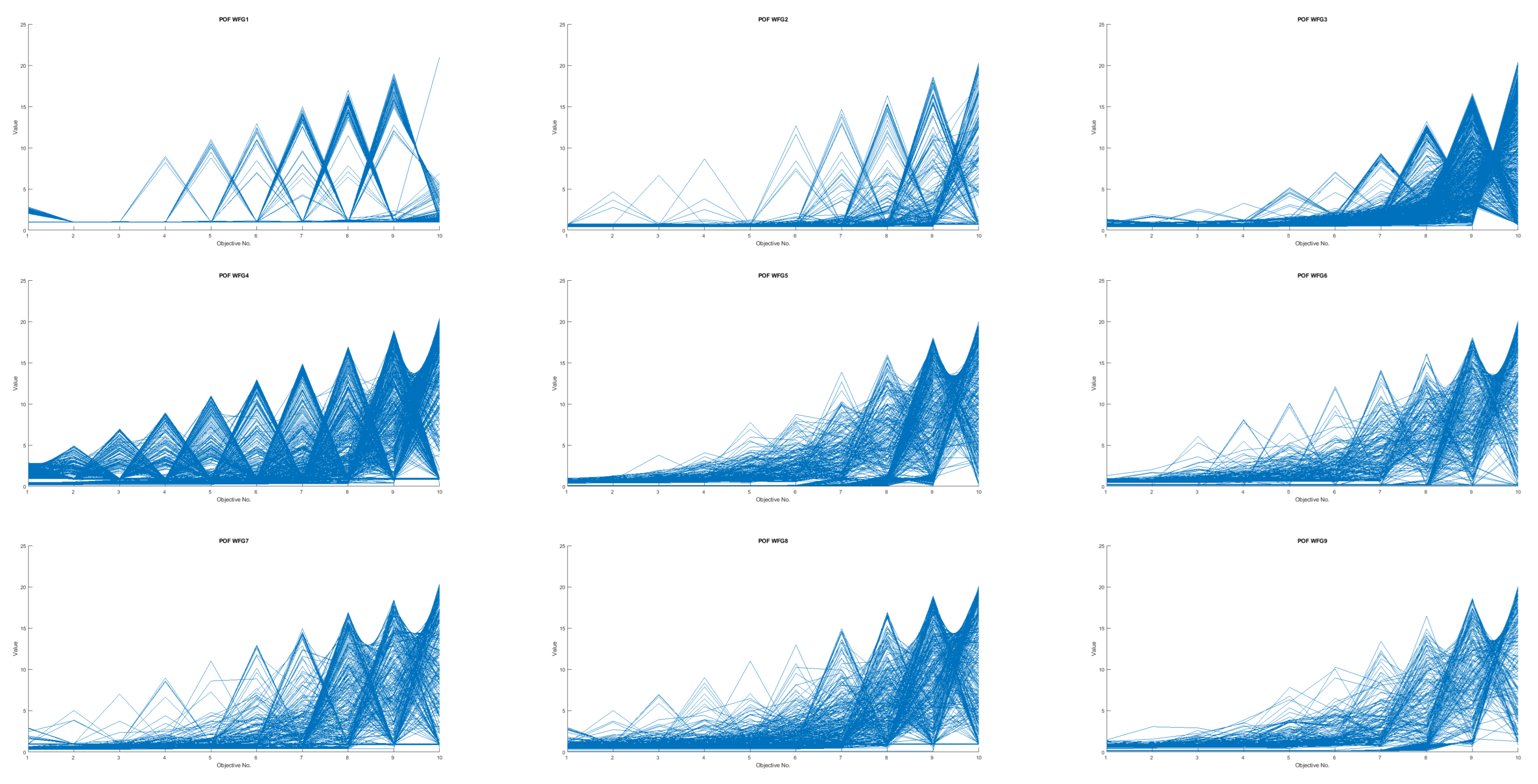
4.4.3. Analysis of the comparative study (2) for MaF and WFG problems with 2, 3 and 7 objectives
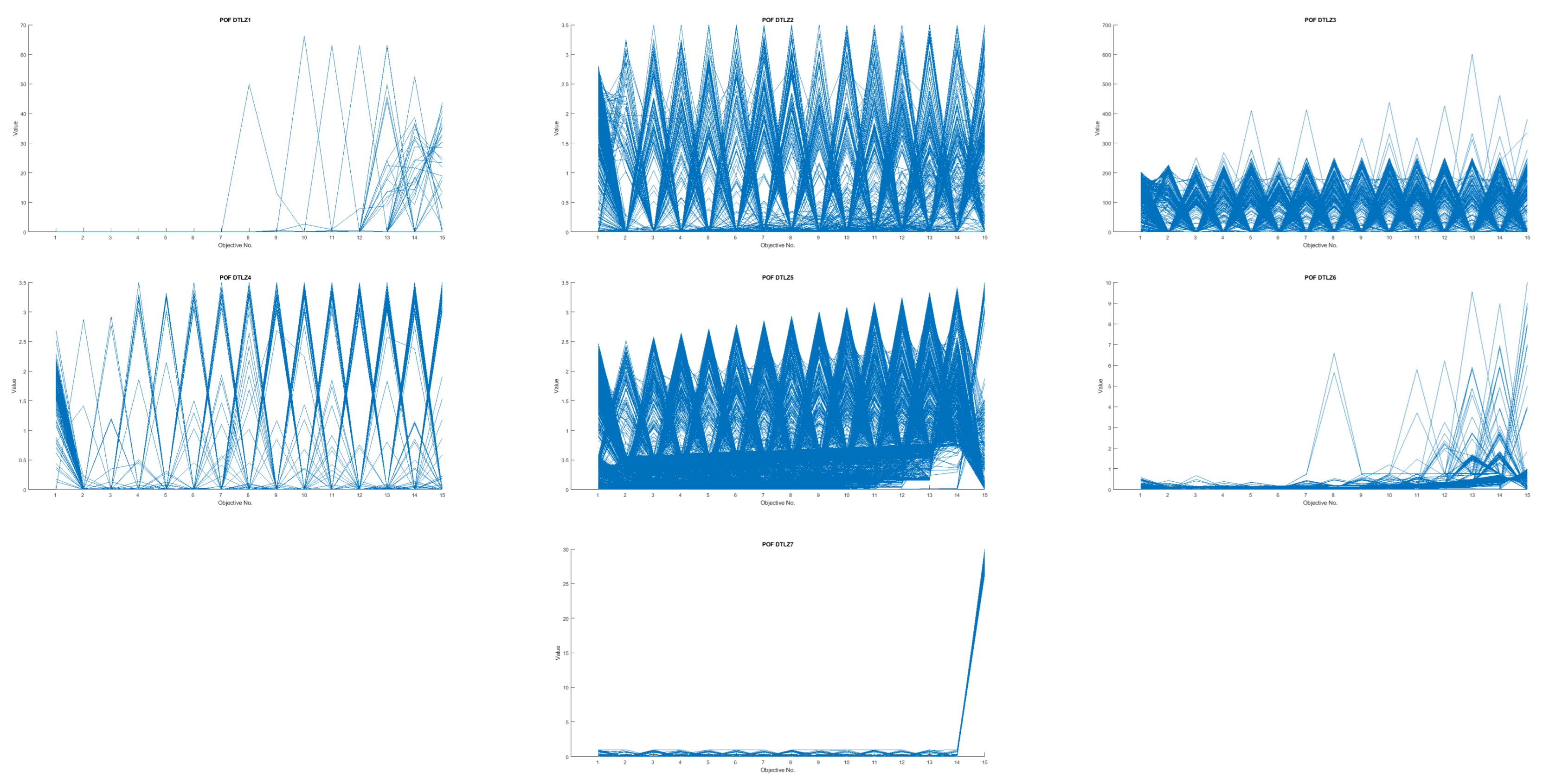
4.4.4. Analysis of the comparative study (2) for DTLZ and WFG problems with 3, 5, 8, 10 and 15 objectives
4.4.5. Time Processing Cost
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deb, K.; Rao N, U.B.; Karthik, S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: A case study on hydro-thermal power scheduling. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2007; pp. 803–817. [Google Scholar] [CrossRef]
- Aboud, A.; Fdhila, R.; Alimi, A. Dynamic Multi Objective Particle Swarm Optimization Based on a New Environment Change Detection Strategy. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2017; Volume 10637, pp. 258–268. [Google Scholar] [CrossRef]
- Aboud, A.; Fdhila, R.; Alimi, A. MOPSO for dynamic feature selection problem based big data fusion. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2016—Conference Proceedings, Budapest, Hungary, 9–12 October 2016; pp. 3918–3923. [Google Scholar] [CrossRef]
- Aboud, A.; Rokbani, N.; Fdhila, R.; Qahtani, A.M.; Almutiry, O.; Dhahri, H.; Hussain, A.; Alimi, A.M. DPb-MOPSO: A dynamic Pareto bi-level Multi-objective Particle Swarm Optimization Algorithm. App. Soft Comput. 2022, 109622. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Farina, M.; Deb, K.; Amato, P. Dynamic multiobjective optimization problems: Test cases, approximations, and applications. IEEE Trans. Evol. Comput. 2004, 8, 425–442. [Google Scholar] [CrossRef]
- Ou, J. A pareto-based evolutionary algorithm using decomposition and truncation for dynamic multi-objective optimization. Appl. Soft Comput. 2019, 85, 105673. [Google Scholar] [CrossRef]
- Zou, J.; Li, Q.; Yang, S.; Bai, H.; Zheng, J. A prediction strategy based on center points and knee points for evolutionary dynamic multi-objective optimization. Appl. Soft Comput. 2017, 61, 806–818. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Geem, Z.; Kim, J.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A Steady-State and Generational Evolutionary Algorithm for Dynamic Multiobjective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 65–82. [Google Scholar] [CrossRef]
- Goh, C.; Tan, K. A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization. IEEE Trans. Evol. Comput. 2009, 13, 103–127. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zhou, A.; Jin, Y.; Zhang, Q. A Population prediction strategy for evolutionary dynamic multiobjective optimization. IEEE Trans. Cybern. 2014, 44, 40–53. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Z.; Qiu, L.; Guo, S.; Gao, X.; Tan, K. A Fast Dynamic Evolutionary Multiobjective Algorithm via Manifold Transfer Learning. IEEE Trans. Cybern. 2020, 51, 3417–3428. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Xu, L.; Goodman, E.; Bao, C.; Zhu, S. Evolutionary Dynamic Multiobjective Optimization Assisted by a Support Vector Regression Predictor. IEEE Trans. Evol. Comput. 2020, 24, 305–319. [Google Scholar] [CrossRef]
- Jiang, M.; Huang, Z.; Qiu, L.; Huang, W.; Yen, G. Transfer Learning-Based Dynamic Multiobjective Optimization Algorithms. IEEE Trans. Evol. Comput. 2018, 22, 501–514. [Google Scholar] [CrossRef]
- Muruganantham, A.; Tan, K.; Vadakkepat, P. Evolutionary Dynamic Multiobjective Optimization Via Kalman Filter Prediction. IEEE Trans. Cybern. 2016, 46, 2862–2873. [Google Scholar] [CrossRef]
- Purshouse, R.; Fleming, P. On the evolutionary optimization of many conflicting objectives. IEEE Trans. Evol. Comput. 2007, 11, 770–784. [Google Scholar] [CrossRef]
- Hughes, E.J. Multiple single objective Pareto sampling. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, Australia, 8–12 December 2003; Volume 4, pp. 2678–2684. [Google Scholar] [CrossRef]
- Hughes, E.J. MSOPS-II: A general-purpose many-objective optimiser. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, CEC 2007, Singapore, 25–28 September 2007; pp. 3944–3951. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Liu, H.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2014, 18, 450–455. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Lu, X.; Tan, Y.; Zheng, W.; Meng, L. A Decomposition Method Based on Random Objective Division for MOEA/D in Many-Objective Optimization. IEEE Access 2020, 8, 103550–103564. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics; Springer: Berlin/ Heidelberg, Germany, 2004; Volume 3242, pp. 832–842. [Google Scholar] [CrossRef]
- Feng, S.; Wen, J. An Evolutionary Many-Objective Optimization Algorithm Based on IGD Indicator and Region Decomposition. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security, CIS 2019, Macau, China, 13–16 December 2019; pp. 206–210. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.; Yi, Z. IGD Indicator-Based Evolutionary Algorithm for Many-Objective Optimization Problems. IEEE Trans. Evol. Comput. 2019, 23, 173–187. [Google Scholar] [CrossRef]
- Zou, X.; Chen, Y.; Liu, M.; Kang, L. A new evolutionary algorithm for solving many-objective optimization problems. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 2008, 38, 1402–1412. [Google Scholar] [CrossRef]
- Hadka, D.; Reed, P. Borg: An auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef]
- Gaoping, W.; Huawei, J. Fuzzy-dominance and its application in evolutionary many objective optimization. In Proceedings of the CIS Workshops 2007, 2007 International Conference on Computational Intelligence and Security Workshops, Harbin, China, 15–19 December 2007; pp. 195–198. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A New Dominance Relation-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]
- Pierro, F.; Khu, S.; Savić, D. An investigation on preference order ranking scheme for multiobjective evolutionary optimization. IEEE Trans. Evol. Comput. 2007, 11, 17–45. [Google Scholar] [CrossRef]
- Adra, S.; Fleming, P. Diversity management in evolutionary many-objective optimization. IEEE Trans. Evol. Comput. 2011, 15, 183–195. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Shift-based density estimation for pareto-based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2015, 19, 761–776. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.; Fleming, P. Preference-inspired coevolutionary algorithms for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 474–494. [Google Scholar] [CrossRef]
- Praditwong, K.; Yao, X. A new multi-objective evolutionary optimisation algorithm: The two-archive algorithm. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, ICCIAS 2006, Guangzhou, China, 3–6 November 2006; Volume 1, pp. 286–291. [Google Scholar] [CrossRef]
- Wang, H.; Jiao, L.; Yao, X. Two Arch2: An Improved Two-Archive Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2015, 19, 524–541. [Google Scholar] [CrossRef]
- Carvalho, A.; Pozo, A. Measuring the convergence and diversity of CDAS Multi-Objective Particle Swarm Optimization Algorithms: A study of many-objective problems. Neurocomputing 2012, 75, 43–51. [Google Scholar] [CrossRef]
- Castro, O.; Pozo, A. A MOPSO based on hyper-heuristic to optimize many-objective problems. In Proceedings of the 2014 IEEE Symposium on Swarm Intelligence, Proceedings, Orlando, FL, USA, 9–12 December 2014; pp. 251–258. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Y.; Liu, Y.; Gong, D. Indicator-based set evolution particle swarm optimization for many-objective problems. Soft Comput. 2016, 20, 2219–2232. [Google Scholar] [CrossRef]
- Hu, W.; Yen, G.; Luo, G. Many-Objective Particle Swarm Optimization Using Two-Stage Strategy and Parallel Cell Coordinate System. IEEE Trans. Cybern. 2017, 47, 1446–1459. [Google Scholar] [CrossRef] [PubMed]
- Maltese, J.; Ombuki-Berman, B.; Engelbrecht, A. Pareto-based many-objective optimization using knee points. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, CEC 2016, Vancouver, BC, Canada, 24–29 July 2016; pp. 3678–3686. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Chen, Z.; Zhang, J. A Many-Objective Particle Swarm Optimizer with Leaders Selected from Historical Solutions by Using Scalar Projections. IEEE Trans. Cybern. 2020, 50, 2209–2222. [Google Scholar] [CrossRef]
- Leung, M.; Coello, C.; Cheung, C.; Ng, S.; Lui, A. A hybrid leader selection strategy for many-objective particle swarm optimization. IEEE Access 2020, 8, 189527–189545. [Google Scholar] [CrossRef]
- Ma, L.; Huang, M.; Yang, S.; Wang, R.; Wang, X. An Adaptive Localized Decision Variable Analysis Approach to Large-Scale Multiobjective and Many-Objective Optimization. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A Vector Angle-Based Evolutionary Algorithm for Unconstrained Many-Objective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 131–152. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Su, Y.; Jin, Y. A Strengthened Dominance Relation Considering Convergence and Diversity for Evolutionary Many-Objective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 331–345. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, N.; Li, M. Solving Many-Objective Optimization Problems by a Pareto-Based Evolutionary Algorithm with Preprocessing and a Penalty Mechanism. IEEE Trans. Cybern. 2020, 51, 5585–5594. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Zhang, T.; Ishibuchi, H. Evolutionary Many-Objective Optimization: A Comparative Study of the State-of-The-Art. IEEE Access 2018, 6, 26194–26214. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A strength pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 329–346. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, R.; Pedrycz, W.; Jin, Y. Solving Many-Objective Optimization Problems via Multistage Evolutionary Search. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3552–3564. [Google Scholar] [CrossRef]
- Meraihi, Y.; Gabis, A.; Ramdane-Cherif, A.; Acheli, D. A comprehensive survey of Crow Search Algorithm and its applications. Artif. Intell. Rev. 2021, 54, 2669–2716. [Google Scholar] [CrossRef]
- Nobahari, H.; Bighashdel, A. MOCSA: A Multi-Objective Crow Search Algorithm for Multi-Objective optimization. In Proceedings of the 2nd Conference on Swarm Intelligence and Evolutionary Computation, CSIEC 2017–Proceedings, Kerman, Iran, 7–9 March 2017; pp. 60–65. [Google Scholar] [CrossRef]
- John, J.; Rodrigues, P. MOTCO: Multi-objective Taylor Crow Optimization Algorithm for Cluster Head Selection in Energy Aware Wireless Sensor Network. Mob. Netw. Appl. 2019, 24, 1509–1525. [Google Scholar] [CrossRef]
- Souza, R.; Coelho, L.; MacEdo, C.; Pierezan, J. A V-Shaped Binary Crow Search Algorithm for Feature Selection. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Laabadi, S.; Naimi, M.; Amri, H.; Achchab, B. A Binary Crow Search Algorithm for Solving Two-dimensional Bin Packing Problem with Fixed Orientation. Procedia Comput. Sci. 2020, 167, 809–818. [Google Scholar] [CrossRef]
- Coelho, L.S.; Richter, C.; Mariani, V.; Askarzadeh, A. Modified crow search approach applied to electromagnetic optimization. In Proceedings of the 2016 IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 13–16 November 2016. [Google Scholar] [CrossRef]
- Gupta, D.; Rodrigues, J.; Sundaram, S.; Khanna, A.; Korotaev, V.; Albuquerque, V. Usability feature extraction using modified crow search algorithm: A novel approach. Neural Comput. Appl. 2020, 32, 10915–10925. [Google Scholar] [CrossRef]
- Mohammadi, F.; Abdi, H. A modified crow search algorithm (MCSA) for solving economic load dispatch problem. Appl. Soft Comput. J. 2018, 71, 51–65. [Google Scholar] [CrossRef]
- Cuevas, E.; Espejo, E.B.; Enríquez, A.C. A modified crow search algorithm with applications to power system problems. In Studies in Computational Intelligence; Springe: Cham, Switzerland, 2019; Volume 822, pp. 137–166. [Google Scholar] [CrossRef]
- Huang, K.W.; Girsang, A.S.; Wu, Z.X.; Chuang, Y.W. A Hybrid Crow Search Algorithm for Solving Permutation Flow Shop Scheduling Problems. Appl. Sci. 2019, 9, 1353. [Google Scholar] [CrossRef]
- Díaz, P.; Pérez-Cisneros, M.; Cuevas, E.; Avalos, O.; Gálvez, J.; Hinojosa, S.; Zaldivar, D. An Improved Crow Search Algorithm Applied to Energy Problems. Energies 2018, 11, 571. [Google Scholar] [CrossRef]
- Meddeb, A.; Amor, N.; Abbes, M.; Chebbi, S. A Novel Approach Based on Crow Search Algorithm for Solving Reactive Power Dispatch Problem. Energies 2018, 11, 3321. [Google Scholar] [CrossRef]
- Javidi, A.; Salajegheh, E.; Salajegheh, J. Enhanced crow search algorithm for optimum design of structures. Appl. Soft Comput. J. 2019, 77, 274–289. [Google Scholar] [CrossRef]
- Bhullar, A.; Kaur, R.; Sondhi, S. Enhanced crow search algorithm for AVR optimization. Soft Comput. 2020, 24, 11957–11987. [Google Scholar] [CrossRef]
- Cuevas, E.; Gálvez, J.; Avalos, O. An Enhanced Crow Search Algorithm Applied to Energy Approaches. In Studies in Computational Intelligence; Springer: Cham, Switzerland, 2020; Volume 854, pp. 27–49. [Google Scholar] [CrossRef]
- Moghaddam, S.; Bigdeli, M.; Moradlou, M.; Siano, P. Designing of stand-alone hybrid PV/wind/battery system using improved crow search algorithm considering reliability index. Int. J. Energy Environ. Eng. 2019, 10, 429–449. [Google Scholar] [CrossRef]
- Arora, S.; Singh, H.; Sharma, M.; Sharma, S.; Anand, P. A New Hybrid Algorithm Based on Grey Wolf Optimization and Crow Search Algorithm for Unconstrained Function Optimization and Feature Selection. IEEE Access 2019, 7, 26343–26361. [Google Scholar] [CrossRef]
- Huang, K.W.; Wu, Z.X. CPO: A Crow Particle Optimization Algorithm. Int. J. Comput. Intell. Syst. 2019, 12. [Google Scholar] [CrossRef]
- Gaddala, K.; Raju, P. Merging Lion with Crow Search Algorithm for Optimal Location and Sizing of UPQC in Distribution Network. J. Control. Autom. Electr. Syst. 2020, 31, 377–392. [Google Scholar] [CrossRef]
- Alimi, A. Beta Neuro-Fuzzy Systems. Task Q. 2003, 7, 23–41. [Google Scholar]
- Rokbani, N.; Slim, M.; Alimi, A.M. The Beta distributed PSO, β-PSO, with application to Inverse Kinematics. In Proceedings of the National Computing Colleges Conference (NCCC), Taif, Saudi Arabia, 27–28 March, 2021; 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Garzelli, A.; Capobianco, L.; Nencini, F. Fusion of multispectral and panchromatic images as an optimisation problem. In Image Fusion; Elsevier: Amsterdam, The Netherlands, 2008; pp. 223–250. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Biswas, S.; Das, S.; Suganthan, P.; Coello, C. Evolutionary multiobjective optimization in dynamic environments: A set of novel benchmark functions. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, CEC 2014, Beijing, China, 6–11 July 2014; pp. 3192–3199. [Google Scholar] [CrossRef]
- Durillo, J.; Nebro, A. JMetal: A Java framework for multi-objective optimization. Adv. Eng. Softw. 2011, 42, 760–771. [Google Scholar] [CrossRef]
- Genichi, T.; Rajesh, J.; Shin, T. Computer-based Robust Engineering: Essentials for DFSS; ASQ Quality Press: Milwaukee, WI, USA, 2004; p. 217. [Google Scholar]
- Rokbani, N. Bi-heuristic ant colony optimization-based approaches for traveling salesman problem. Soft Comput. 2021, 25, 3775–3794. [Google Scholar] [CrossRef]
- Dordevic, M. Statistical analysis of various hybridization of evolutionary algorithm for traveling salesman problem. In Proceedings of the IEEE International Conference on Industrial Technology, Melbourne, Australia, 13–15 February 2019; pp. 899–904. [Google Scholar] [CrossRef]





| Parameters | Comparative Study (1) for DMOPs | |
|---|---|---|
| Comparable DMOEAs | Five MOEAs [11] | Six transfer learning-based methods [15] |
| DNSGA-II [1] SGEA [11] dCOEA [12] PPS [14] MOEA/D [13] | MMTL-MOEA/D [15] RI-MOEA/D [15] PPS-MOEA/D [15] SVR-MOEA/D [16] Tr-MOEA/D [17] KF-MOEA/D [18] | |
| Quality indicators | IGD and HVD | MIGD |
| Testbeds (DMOPs) | FDA, dMOP, UDF, F | FDA, dMOP |
| Number of Objectives (M) | 2 and 3 | 2 and 3 |
| Population size | 100 | |
| Max-Iteration () | 3 × × + 50 | |
| Independent runs | 30 | |
| Parameters | Comparative Study (2) for DMOPs | |
|---|---|---|
| Comparable MaOEAs | Thirteen MOEAs [55] | Seven MaOEAs [54] |
| MSOPS-II [21] MOEA/D [13] HypE [27] picea-G [41] SPEA/SDE [39] GrEA [35] NSGA-III [24] KnEA [40] RVEA [22] Two_Arch2 [41] -dea [36] MOEA/DD ] [25] AnD [55] | PMEA-MA [54] PMEA*-MA [54] SPEA2/SDE [39] NSGA-II/SDR [53] MaOEA/IDG [31] VaEA [52] spea [56] | |
| Quality indicators | IGD | IGD |
| Benchmarks | WFG, MaF | WFG, DTLZ |
| Number of Objectives (M) | 2, 3, and 7 | 3, 5, 8, 10, and 15 |
| Population size | 100 | 92, 224, 164, 280, and 152 |
| Max-Iteration (Max) | 25.000 | 300: WFG1-9 and DTLZ 2,4,5,6, 1000: DTLZ 1,3,6 |
| Independent runs | 31 | 30 |
| DMOPs | D | M | Properties | |
|---|---|---|---|---|
| Dynamic Multi Objective Optimization Problems (DMOPs) | FDA1 | 20 | 2 | Type I, convex, POS: sinusoidal and vertical shift |
| FDA2 | 15 | 2 | Type II, POF: convex to concave, dynamic density, POS: sinusoidal and vertical shift | |
| FDA3 | 30 | 2 | Type II, POF: convex, dynamic spread, POS: sinusoidal and vertical shift | |
| FDA4 | 12 | 3 | Type I, POF: concave, dynamic spread, POS: sinusoidal and vertical shift | |
| FDA5 | 12 | 3 | Type II, POF: concave, dynamic spread, POS: sinusoidal and vertical shift | |
| dMOP1 | 10 | 2 | Type III, POF: convex to concave, POS: no change | |
| dMOP2 | 10 | 2 | Type II, POF: convex to concave, POS: sinusoidal and vertical shift | |
| dMOP3 | 10 | 2 | Type I, POF: convex, dynamic spread, POS: sinusoidal and vertical shift | |
| F5, F6, F7 | 20 | 2 | Type II, POF: convex to concave, POS: | |
| F9, F10 | 20 | 2 | Type II, POF: convex to concave, POS: | |
| F8 | 20 | 3 | trigonometric and vertical | |
| UDF1 | 10 | 2 | Type I, POF: linear continuous, POS: trigonometric and vertical shift | |
| UDF2 | 10 | 2 | Type I, POF: linear continuous, POS: polynomial and vertical shift | |
| UDF3 | 10 | 2 | Type III, POF: discontinuous, POS: trigonometric and no variation | |
| UDF4 | 10 | 2 | Type II, convex to concave, POS: trigonometric and horizontal shift | |
| UDF5 | 10 | 2 | Type II, convex to concave, POS: polynomial + vertical shift | |
| UDF6 | 10 | 2 | Type III, discontinuous, POS: trigonometric and no variation | |
| UDF7 | 10 | 3 | Type III, POF: 3D radius concave, POS: trigonometric and no variation | |
| Many Objective Optimization Problems (MaOPs) | MaF1 | Linear | ||
| MaF2 | 11 | 2 | Concave | |
| MaF3 | 12 | 3 | Convex, multimodal | |
| MaF4 | 16 | 7 | Concave, multimodal | |
| MaF5 | Convex, biased | |||
| MaF6 | Concave, degenerate | |||
| MaF7 | 21 | 2 | Mixed | |
| 22 | 3 | Disconnected | ||
| 26 | 7 | Multimodal | ||
| Many Objective Optimization Problems (MaOPs) | WFG1 | 11 | 2 | Convex, unimodal |
| WFG2 | 12 | 3 | Convex, disconnected | |
| WFG3 | 16 | 7 | Linear, unimodal | |
| WFG4 | Concave, multimodal | |||
| WFG5 | 12 | 3 | Concave, deceptive | |
| WFG6 | 14 | 5 | Concave, unimodal | |
| WFG7 | 17 | 8 | Concave, unimodal | |
| WFG8 | 19 | 10 | Concave, unimodal | |
| WFG9 | 24 | 15 | Concave, multimodal | |
| DTLZ1 | 7 | 3 | Linear | |
| 9 | 5 | |||
| 12 | 8 | |||
| 14 | 10 | |||
| 19 | 15 | |||
| DTLZ2 | 12 | 3 | Concave | |
| DTLZ3 | 14 | 5 | Concave | |
| DTLZ4 | 17 | 8 | Concave | |
| DTLZ5 | 19 | 10 | Degenerate | |
| DTLZ7 | 22 | 3 | Disconnected |
| Problems | ID Run | Population Size | Max-Iteration | Parameters of Beta Function | |||
|---|---|---|---|---|---|---|---|
| p1 | p2 | q1 | q2 | ||||
| DMOPs | 1 | 100 | 250 | 5 | 5 | 5 | 5 |
| 2 | 100 | 250 | 5 | 50 | 5 | 50 | |
| 3 | 200 | 250 | 50 | 5 | 50 | 5 | |
| 4 | 200 | 250 | 50 | 50 | 5 | 50 | |
| 5 | 100 | 350 | 50 | 5 | 5 | 50 | |
| 6 | 100 | 350 | 50 | 50 | 50 | 5 | |
| 7 | 200 | 350 | 5 | 50 | 5 | 50 | |
| 8 | 200 | 350 | 5 | 50 | 5 | 5 | |
| MaOPs | 1 | 100 | 100 | 5 | 5 | 5 | 5 |
| 2 | 100 | 100 | 5 | 50 | 50 | 50 | |
| 3 | 100 | 25.000 | 50 | 5 | 5 | 50 | |
| 4 | 100 | 25.000 | 5 | 50 | 5 | 50 | |
| 5 | 300 | 100 | 50 | 5 | 50 | 5 | |
| 6 | 300 | 100 | 50 | 50 | 5 | 50 | |
| 7 | 300 | 25.000 | 5 | 5 | 50 | 50 | |
| 8 | 300 | 25.000 | 5 | 50 | 5 | 5 | |
| Problems | Population Size | Max-Iteration | Parameters of Beta Function | Best Mean Values | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p1 | p2 | q1 | q2 | MIGD | IGD | HVD | ||||
| DMOPs with Severe Change | FDA1 | 100 | 250 | 5 | 50 | 5 | 50 | |||
| FDA2 | 100 | 250 | 5 | 50 | 5 | 50 | ||||
| FDA3 | 100 | 250 | 5 | 50 | 5 | 50 | ||||
| FDA4 | 100 | 250 | 5 | 50 | 5 | 50 | ||||
| FDA5 | 200 | 250 | 50 | 5 | 50 | 5 | ||||
| dMOP1 | 100 | 250 | 5 | 50 | 5 | 50 | ||||
| dMOP2 | 200 | 250 | 50 | 50 | 5 | 50 | ||||
| dMOP3 | 200 | 250 | 50 | 50 | 5 | 50 | ||||
| DMOPs with Moderate change | FDA1 | 100 | 350 | 5 | 50 | 5 | 50 | |||
| FDA2 | 100 | 350 | 5 | 50 | 5 | 50 | ||||
| FDA3 | 100 | 350 | 5 | 50 | 5 | 50 | ||||
| FDA4 | 100 | 350 | 5 | 50 | 5 | 50 | ||||
| FDA5 | 100 | 350 | 5 | 50 | 5 | 50 | ||||
| dMOP1 | 100 | 350 | 5 | 50 | 5 | 50 | ||||
| dMOP2 | 100 | 350 | 50 | 5 | 5 | 50 | ||||
| dMOP3 | 200 | 350 | 5 | 50 | 5 | 50 | ||||
| MaOPs with 7 objectives | WFG1 | 100 | 25.000 | 5 | 50 | 5 | 50 | - | - | |
| WFG2 | 100 | 25.000 | 50 | 5 | 5 | 50 | - | - | ||
| WFG3 | 100 | 25.000 | 5 | 50 | 5 | 50 | - | - | ||
| WFG4 | 100 | 25.000 | 50 | 5 | 5 | 50 | - | - | ||
| WFG5 | 100 | 25.000 | 50 | 5 | 5 | 50 | - | - | ||
| WFG6 | 100 | 25.000 | 50 | 5 | 5 | 50 | - | - | ||
| WFG7 | 100 | 25.000 | 50 | 5 | 5 | 50 | - | - | ||
| WFG8 | 100 | 25.000 | 5 | 50 | 5 | 50 | - | - | ||
| WFG9 | 100 | 25.000 | 5 | 50 | 5 | 50 | - | - | ||
| DB-CSA-II (with Dynamic Process) vs. | QI | Prob. | R− | R+ | p-Value | Best Method |
|---|---|---|---|---|---|---|
| MMTL-MOEA/D | MIGD | FDA & dMOP | 300 | 0 | 0.000018 | DB-CSA-II |
| KF-MOEA/D | 300 | 0 | 0.000018 | |||
| PPS-MOEA/D | 300 | 0 | 0.000018 | |||
| SVR-MOEA/D | 300 | 0 | 0.000018 | |||
| Tr-MOEA/D | 300 | 0 | 0.000018 | |||
| RI-MOEA/D | 300 | 0 | 0.000018 | |||
| CSA | 300 | 0 | 0.000018 | |||
| DB-CSA | 275 | 25 | 0.000355 |
| DB-CSA-II (with Dynamic Process) vs. | Prob. | QI | R− | R+ | p-Value | Best Method |
|---|---|---|---|---|---|---|
| DNSGA-II | FDA & dMOP | IGD | 235 | 65 | 0.015158 | DB-CSA-II |
| dCOEA | 213 | 87 | 0.071861 | ≅ | ||
| PPS | 241 | 59 | 0.009322 | DB-CSA-II | ||
| MOEA/D | 231 | 69 | 0.020652 | DB-CSA-II | ||
| SGEA | 204 | 96 | 0.122865 | ≅ | ||
| CSA | 300 | 0 | 0.000018 | DB-CSA-II | ||
| DB-CSA | 275 | 25 | 0.000355 | DB-CSA-II | ||
| DNSGA-II | FDA & dMOP | HVD | 222 | 78 | 0.039672 | DB-CSA-II |
| dCOEA | 206 | 94 | 0.109599 | ≅ | ||
| PPS | 219 | 81 | 0.048675 | DB-CSA-II | ||
| MOEA/D | 223 | 77 | 0.037005 | DB-CSA-II | ||
| SGEA | 205 | 95 | 0.116083 | ≅ | ||
| CSA | 289 | 11 | 0.000071 | DB-CSA-II | ||
| DB-CSA | 240 | 60 | 0.010128 | DB-CSA-II | ||
| DNSGA-II | UDF & F | IGD | 91 | 0 | 0.001474 | DB-CSA-II |
| dCOEA | 90 | 0 | 0.001871 | DB-CSA-II | ||
| PPS | 86 | 5 | 0.004649 | DB-CSA-II | ||
| MOEA/D | 91 | 0 | 0.001474 | DB-CSA-II | ||
| SGEA | 85 | 6 | 0.005772 | DB-CSA-II | ||
| CSA | 90 | 1 | 0.001871 | DB-CSA-II | ||
| DB-CSA | 91 | 0 | 0.001474 | DB-CSA-II | ||
| DNSGA-II | UDF & F | HVD | 36 | 55 | 0.506746 | ≅ |
| dCOEA | 34 | 57 | 0.421579 | ≅ | ||
| PPS | 35 | 56 | 0.463071 | ≅ | ||
| MOEA/D | 36 | 55 | 0.506746 | ≅ | ||
| SGEA | 35 | 56 | 0.463071 | ≅ | ||
| CSA | 69 | 22 | 0.100525 | ≅ | ||
| DB-CSA | 71 | 20 | 0.074735 | ≅ |
| DB-CSA vs. | QI | Prob. | R− | R+ | p-Value | Best Method |
|---|---|---|---|---|---|---|
| MSOPS-II | IGD | WFG | 378 | 0 | 0.000006 | DB-CSA |
| MOEA/D | 378 | 0 | 0.000006 | |||
| HypE | 374 | 4 | 0.000009 | |||
| PICEA-g | 378 | 0 | 0.000006 | |||
| SPEA/SDE | 376 | 2 | 0.000007 | |||
| GrEA | 378 | 0 | 0.000006 | |||
| NSGA-III | 373 | 5 | 0.000010 | |||
| KnEA | 378 | 0 | 0.000006 | |||
| RVEA | 378 | 0 | 0.000006 | |||
| Two_Arch2 | 374 | 4 | 0.000009 | |||
| -DEA | 376.5 | 1.5 | 0.000007 | |||
| MOEA/DD | 377 | 1 | 0.000006 | |||
| AnD | 378 | 0 | 0.000006 | |||
| CSA | 378 | 0 | 0.000006 | |||
| MSOPS-II | IGD | MaF | 231 | 0 | 0.000060 | DB-CSA |
| PMEA*-MA | 1035 | 0 | 0.000006 | |||
| MOEA/D | 231 | 0 | 0.000060 | |||
| HypE | 231 | 0 | 0.000060 | |||
| PICEA-g | 231 | 0 | 0.000060 | |||
| SPEA/SDE | 231 | 0 | 0.000060 | |||
| GrEA | 231 | 0 | 0.000060 | |||
| NSGA-III | 231 | 0 | 0.000060 | |||
| KnEA | 231 | 0 | 0.000060 | |||
| RVEA | 231 | 0 | 0.000060 | |||
| Two_Arch2 | 231 | 0 | 0.000060 | |||
| -DEA | 231 | 0 | 0.000060 | |||
| MOEA/DD | 231 | 0 | 0.000060 | |||
| AnD | 231 | 0 | 0.000060 | |||
| CSA | 231 | 0 | 0.000060 | |||
| PMEA-MA | IGD | WFG | 1035 | 0 | DB-CSA | |
| PMEA*-MA | 1035 | 0 | ||||
| SPEA2/SDE | 1035 | 0 | 5. | |||
| NSGA-II/SDR | 1035 | 0 | ||||
| MaOEA/IGD | 1035 | 0 | ||||
| VaEA | 1035 | 0 | ||||
| SPEA | 1035 | 0 | ||||
| CSA | 1035 | 0 | ||||
| PMEA-MA | IGD | DTLZ | 629 | 1 | DB-CSA | |
| PMEA*-MA | 1035 | 0 | ||||
| PMEA*-MA | 629 | 1 | ||||
| SPEA2/SDE | 630 | 0 | ||||
| NSGA-II/SDR | 630 | 0 | ||||
| MaOEA/IGD | 630 | 0 | ||||
| VaEA | 629 | 1 | ||||
| SPEA | 630 | 0 |
| DMOPs | MMTL-MOEA/D | KF-MOEA/D | PPS-MOEA/D | SVR-MOEA/D | Tr-MOEA/D | DB-CSA-II |
|---|---|---|---|---|---|---|
| FDA1 | 5.83 | 3.55 | 3.11 | 4.85 | 42.54 | 10.32 |
| FDA2 | 5.40 | 3.46 | 3.08 | 4.63 | 45.27 | 12.86 |
| FDA3 | 5.09 | 3.92 | 3.64 | 4.78 | 57.71 | 14.96 |
| FDA4 | 10.06 | 9.78 | 13.32 | 9.66 | 132.59 | 21.92 |
| FDA5 | 9.94 | 10.24 | 14.83 | 11.52 | 115.52 | 19.85 |
| dMOP1 | 7.05 | 7.25 | 8.96 | 8.34 | 80.23 | 9.05 |
| dMOP2 | 7.74 | 4.02 | 4.93 | 4.47 | 73.53 | 9.29 |
| dMOP3 | 5.63 | 3.52 | 4.15 | 4.61 | 75.55 | 9.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboud, A.; Rokbani, N.; Neji, B.; Al Barakeh, Z.; Mirjalili, S.; Alimi, A.M. A Distributed Bi-Behaviors Crow Search Algorithm for Dynamic Multi-Objective Optimization and Many-Objective Optimization Problems. Appl. Sci. 2022, 12, 9627. https://doi.org/10.3390/app12199627
Aboud A, Rokbani N, Neji B, Al Barakeh Z, Mirjalili S, Alimi AM. A Distributed Bi-Behaviors Crow Search Algorithm for Dynamic Multi-Objective Optimization and Many-Objective Optimization Problems. Applied Sciences. 2022; 12(19):9627. https://doi.org/10.3390/app12199627
Chicago/Turabian StyleAboud, Ahlem, Nizar Rokbani, Bilel Neji, Zaher Al Barakeh, Seyedali Mirjalili, and Adel M. Alimi. 2022. "A Distributed Bi-Behaviors Crow Search Algorithm for Dynamic Multi-Objective Optimization and Many-Objective Optimization Problems" Applied Sciences 12, no. 19: 9627. https://doi.org/10.3390/app12199627
APA StyleAboud, A., Rokbani, N., Neji, B., Al Barakeh, Z., Mirjalili, S., & Alimi, A. M. (2022). A Distributed Bi-Behaviors Crow Search Algorithm for Dynamic Multi-Objective Optimization and Many-Objective Optimization Problems. Applied Sciences, 12(19), 9627. https://doi.org/10.3390/app12199627









