Assembly Deviation Analysis of New Integrated TBM Disc Cutter and Design of the Supporting Cutter-Changing Robot End-Effector
Abstract
1. Introduction
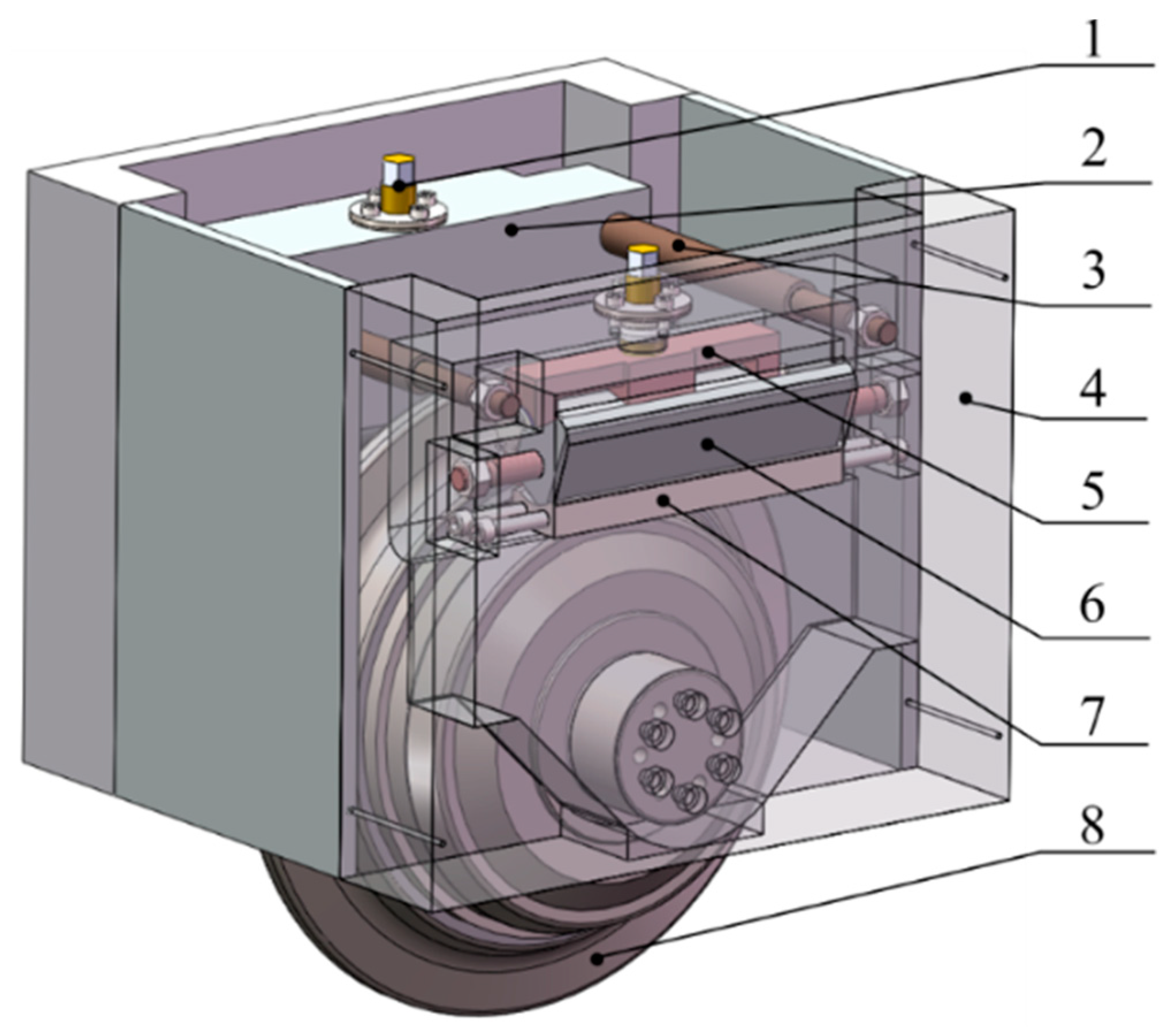
2. New Integrated TBM Disc Cutter
3. Deviation Analysis of New Integrated TBM Disc Cutter
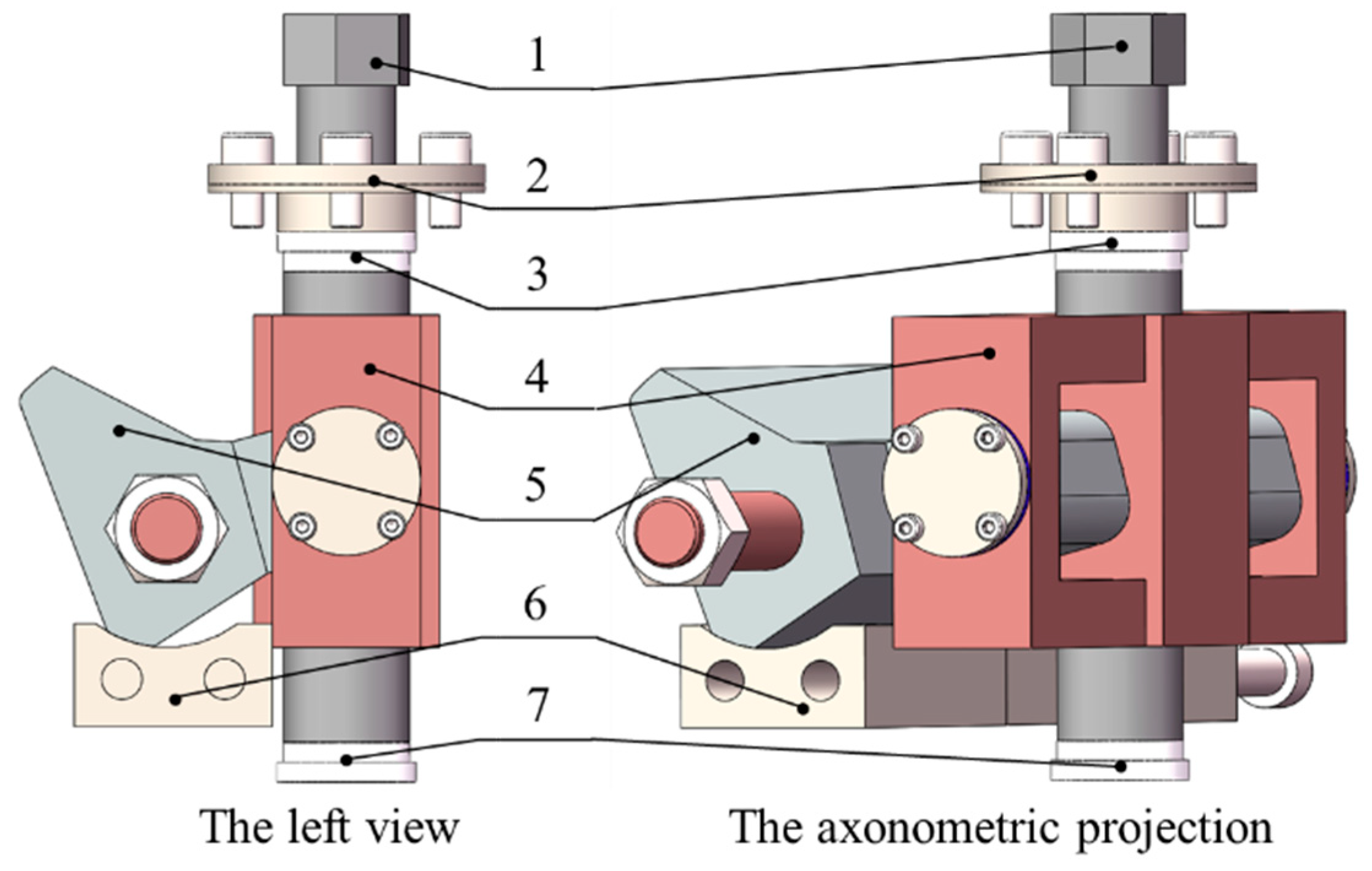
3.1. Analysis of Assembly Deviation of Threaded Fastening System
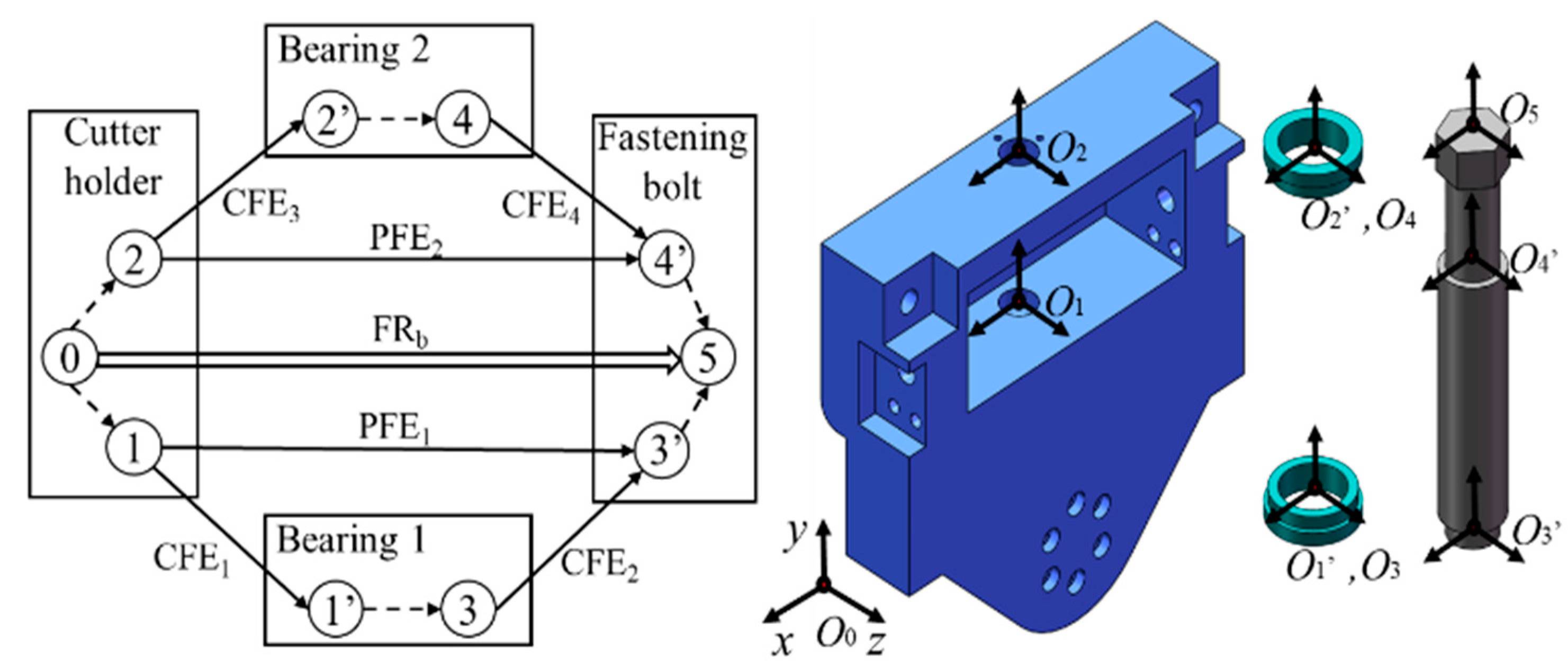
3.1.1. Establishing the Dimensional Chain of the Threaded Fastening System
3.1.2. Spinor Representation of Tolerance Zone of the Dimension Chains
- (1)
- Dimension chain 1
- (2)
- Dimension chain 2
3.1.3. Establish Jacobian–Torsor Model
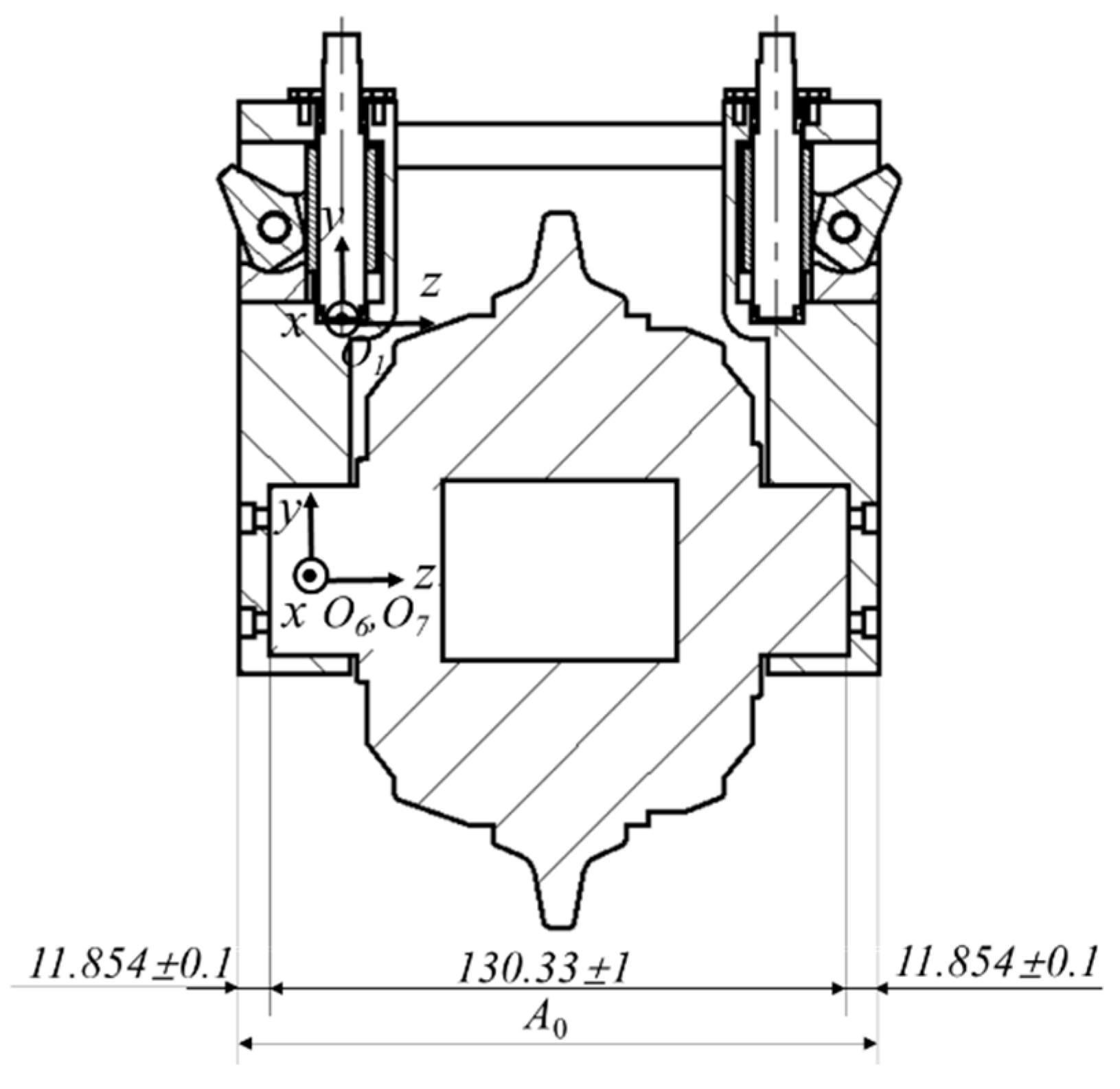
3.2. Calculation of Assembly Deviation between Disc Cutter and Cutter Holders
3.3. Calculation of Assembly Deviation between Cutter Holders and Cutter Box
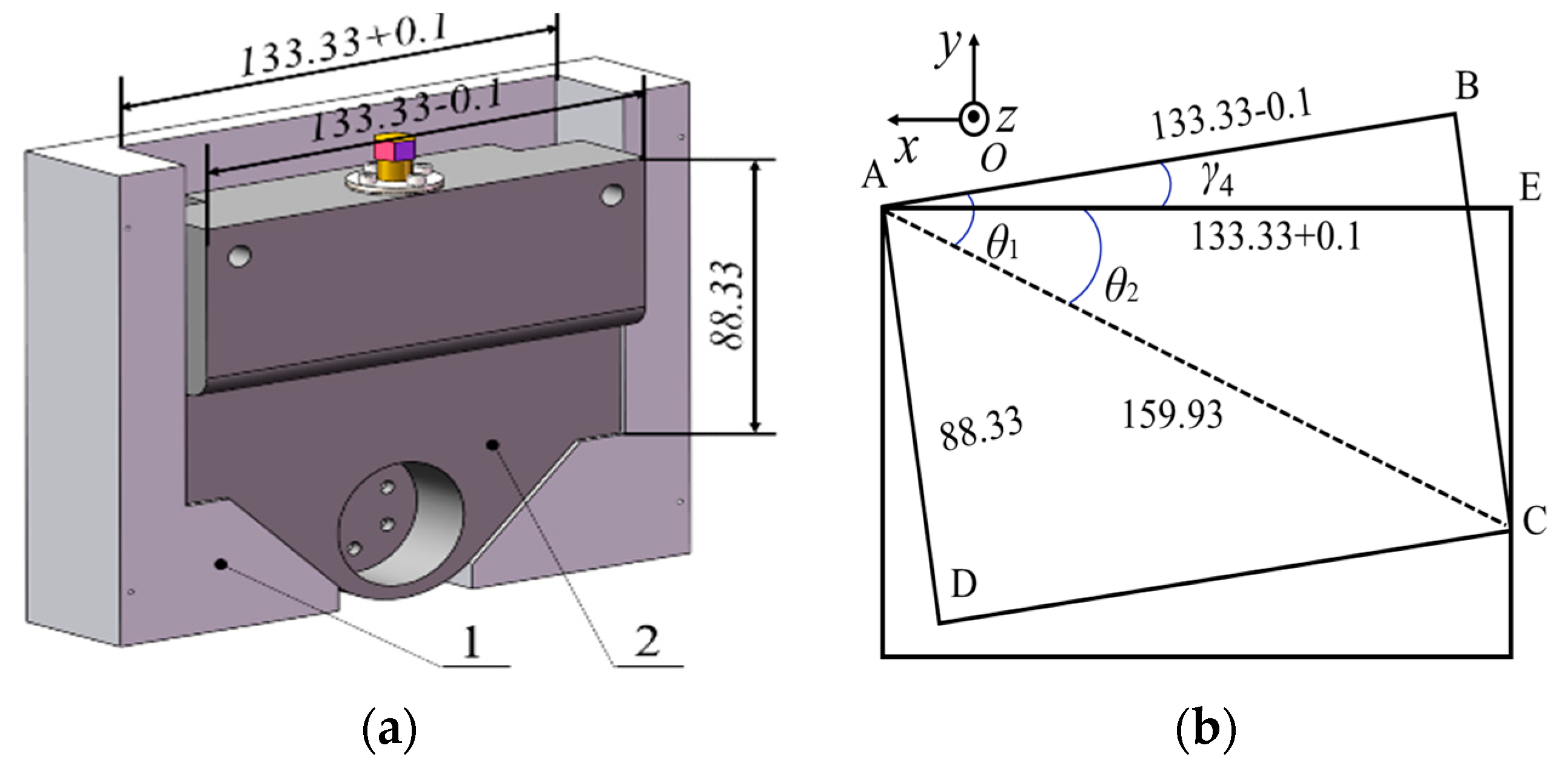
3.4. Calculation of Welding Deviation between Cutter Box and Cutter Head
3.5. Calculation of Comprehensive Deviation of Fastening Bolt
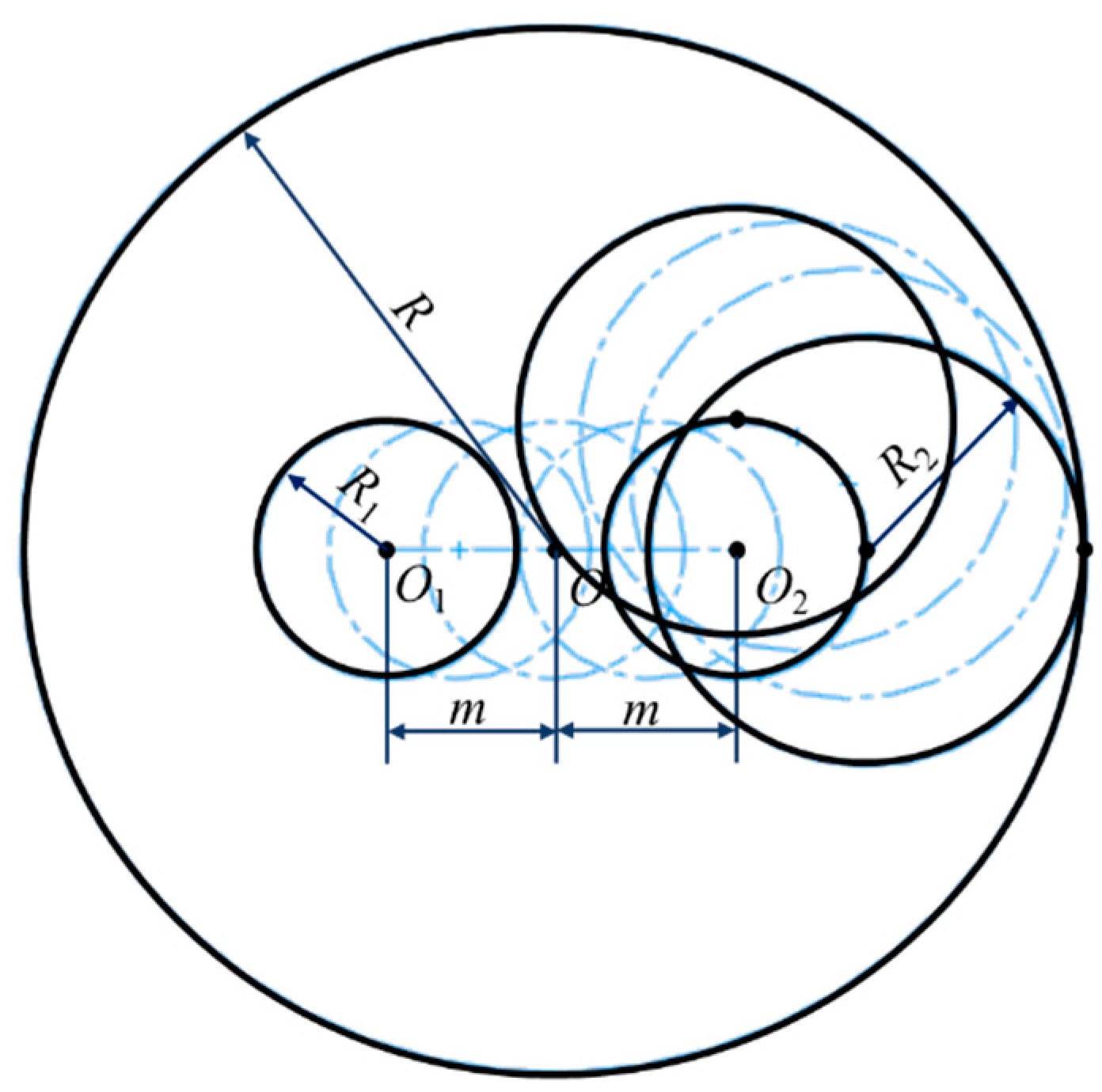
3.6. Comprehensive Deviation Envelope Circle of Fastening Bolt Head
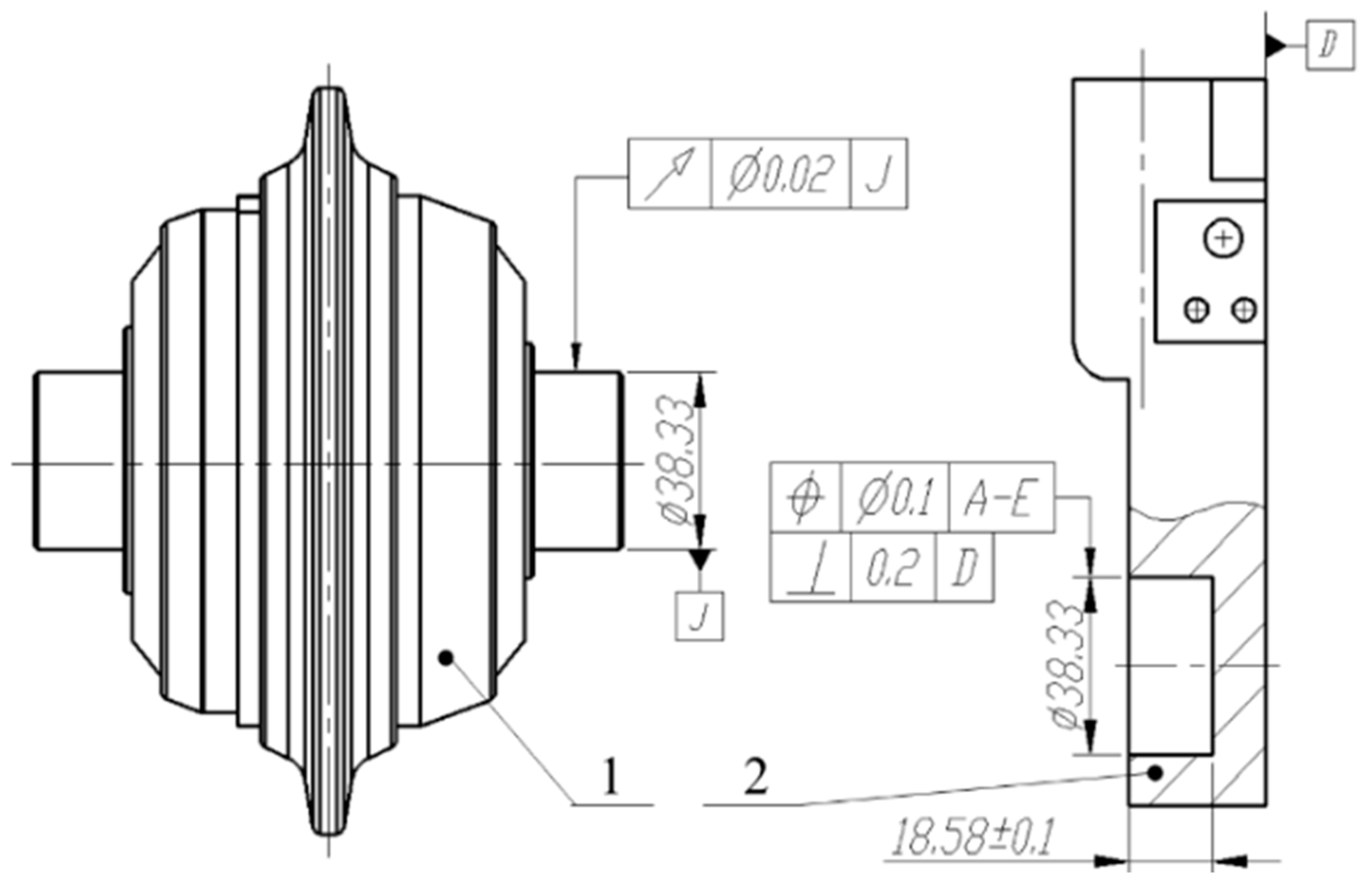
3.7. The Measurement of the Position Deviation of the Fastening Bolts of the New Integrated Disc Cutter System
4. Design of the End-Effector of Supporting Cutter-Changing Robot
4.1. Overall Structure Design of End Effector of Cutter-Changing Robot
4.2. Parametric Design of End-Effector of Supporting Cutter-Changing Robot
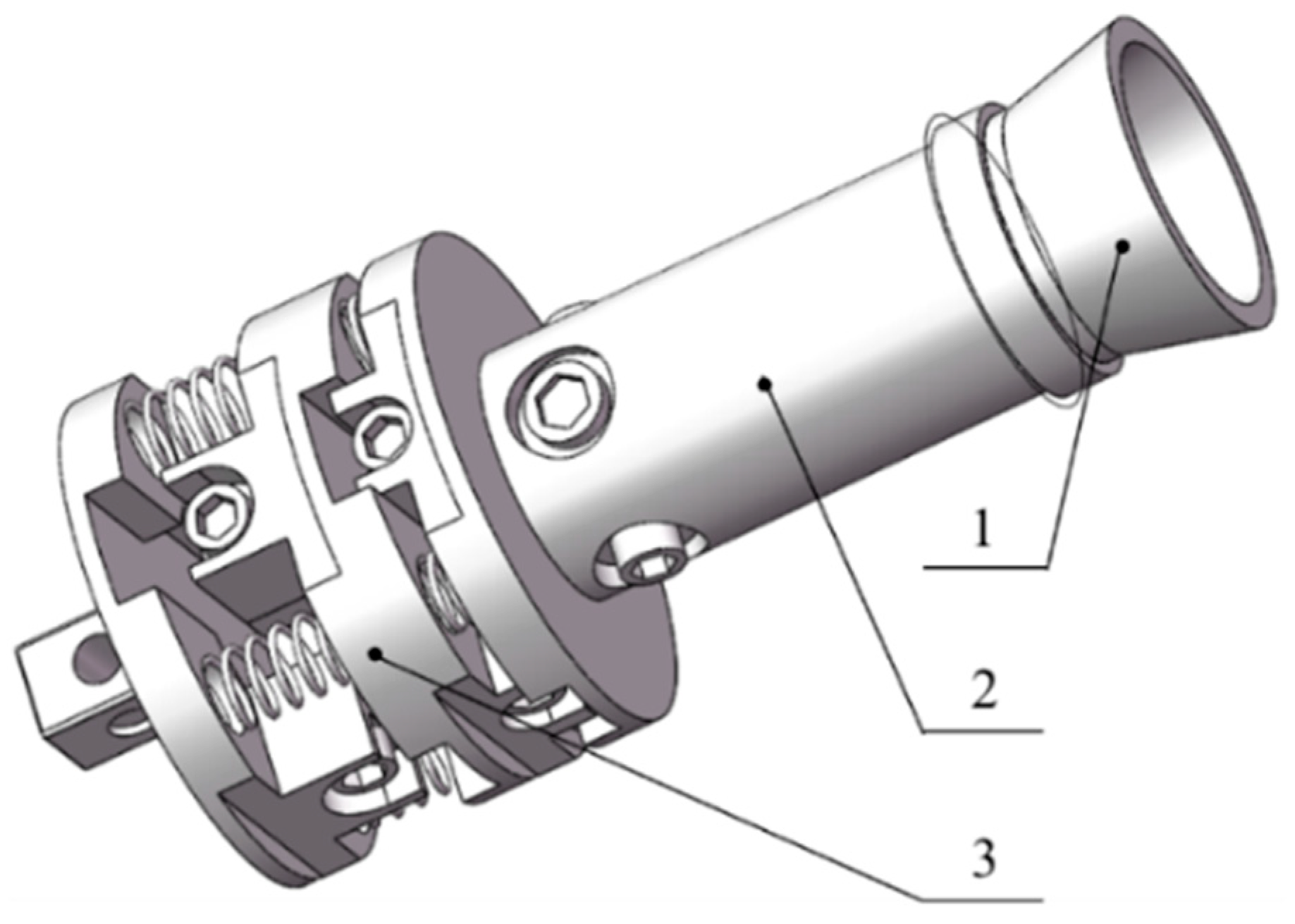
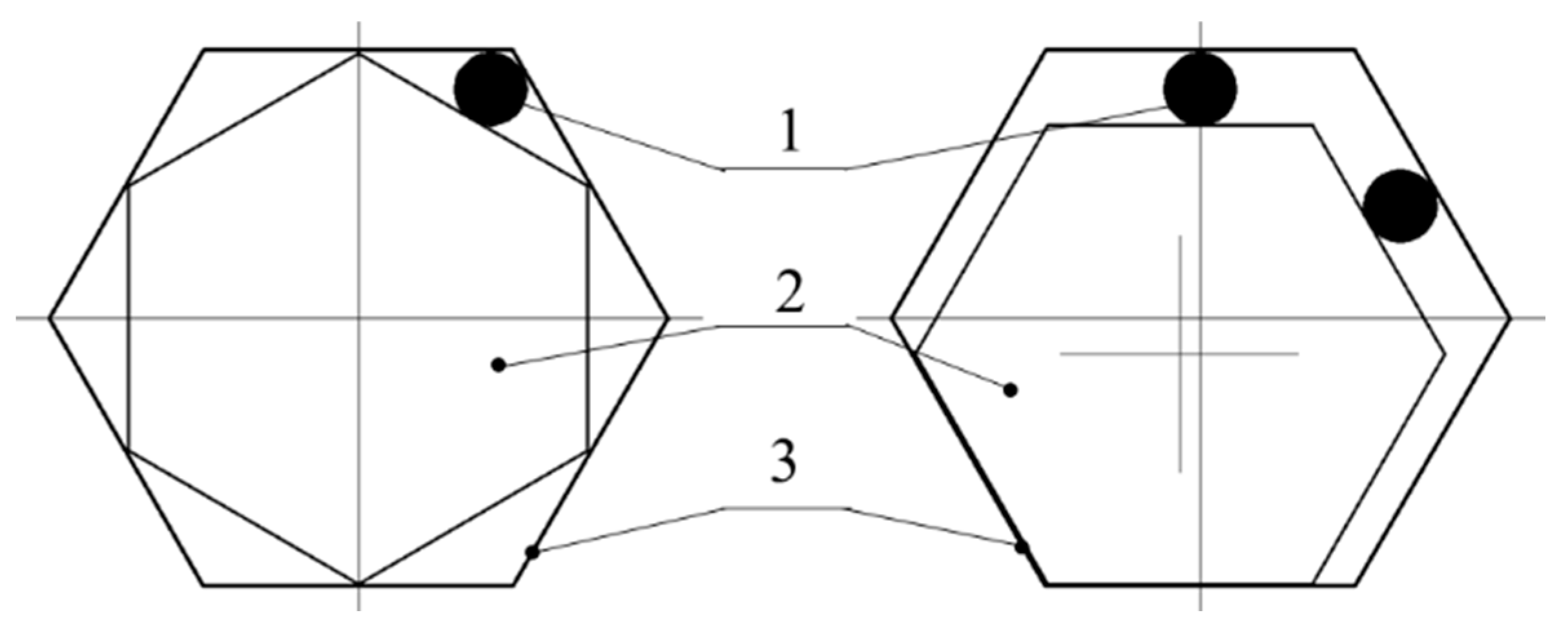
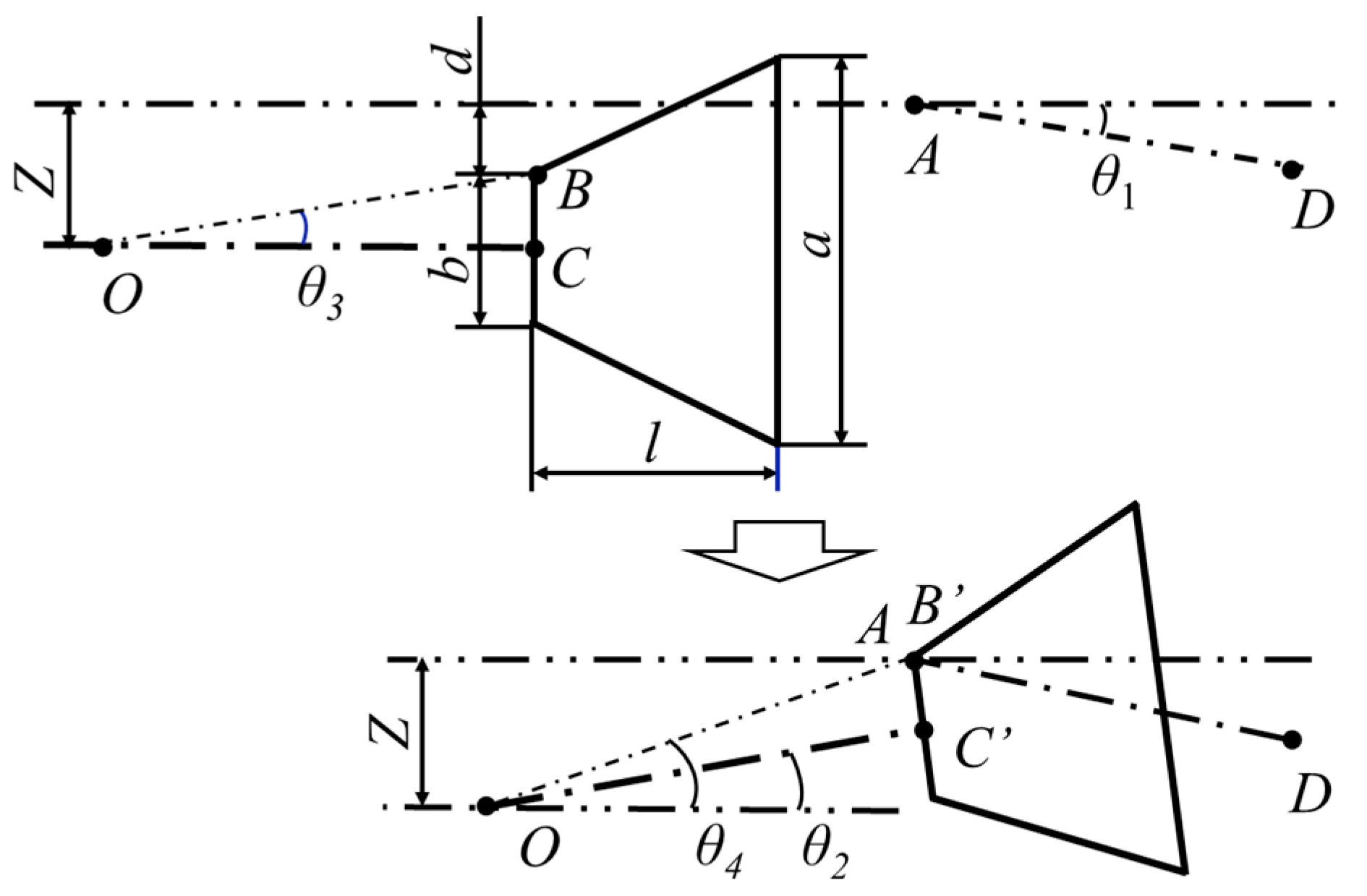
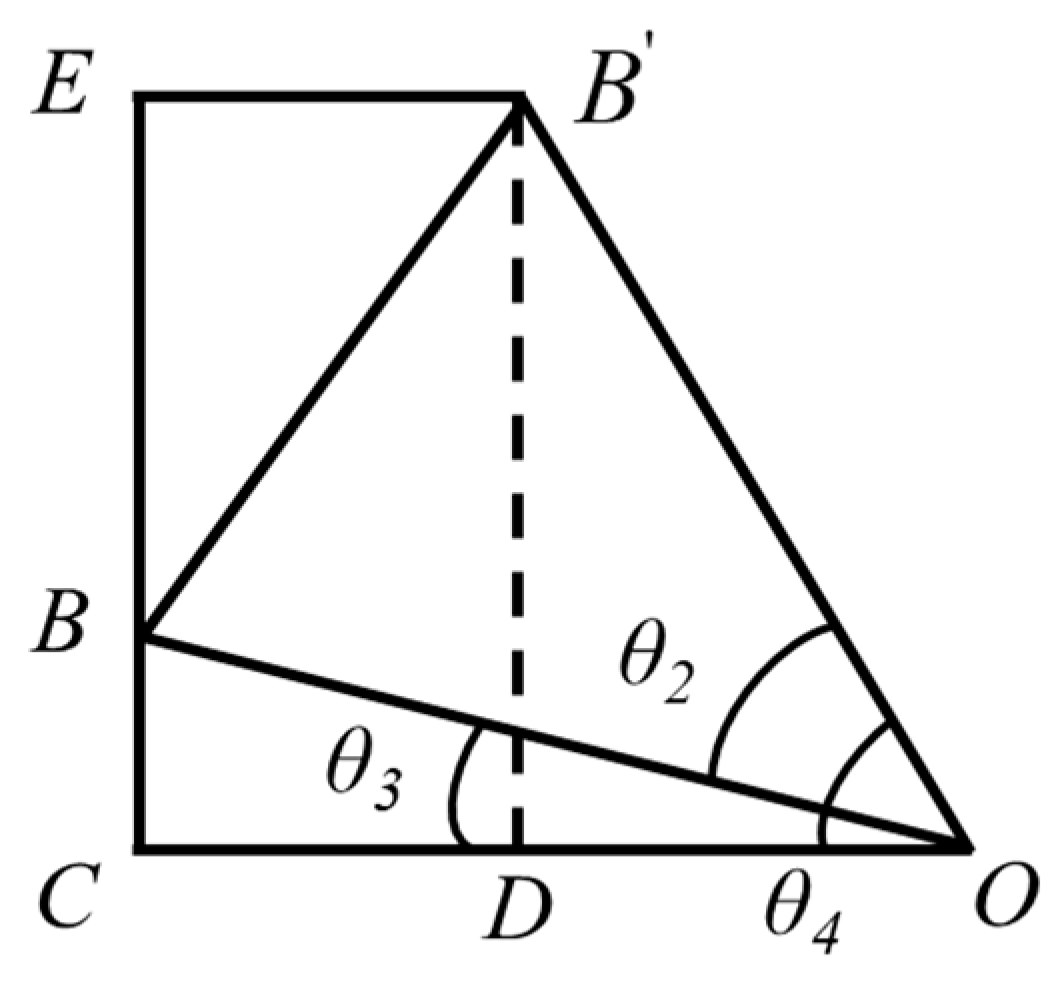
4.2.1. Parametric Design of the Guiding Mechanism
- (1)
- The diameter of the big end a
- (2)
- The diameter of the small end b
- (3)
- The length of the guiding mechanism l
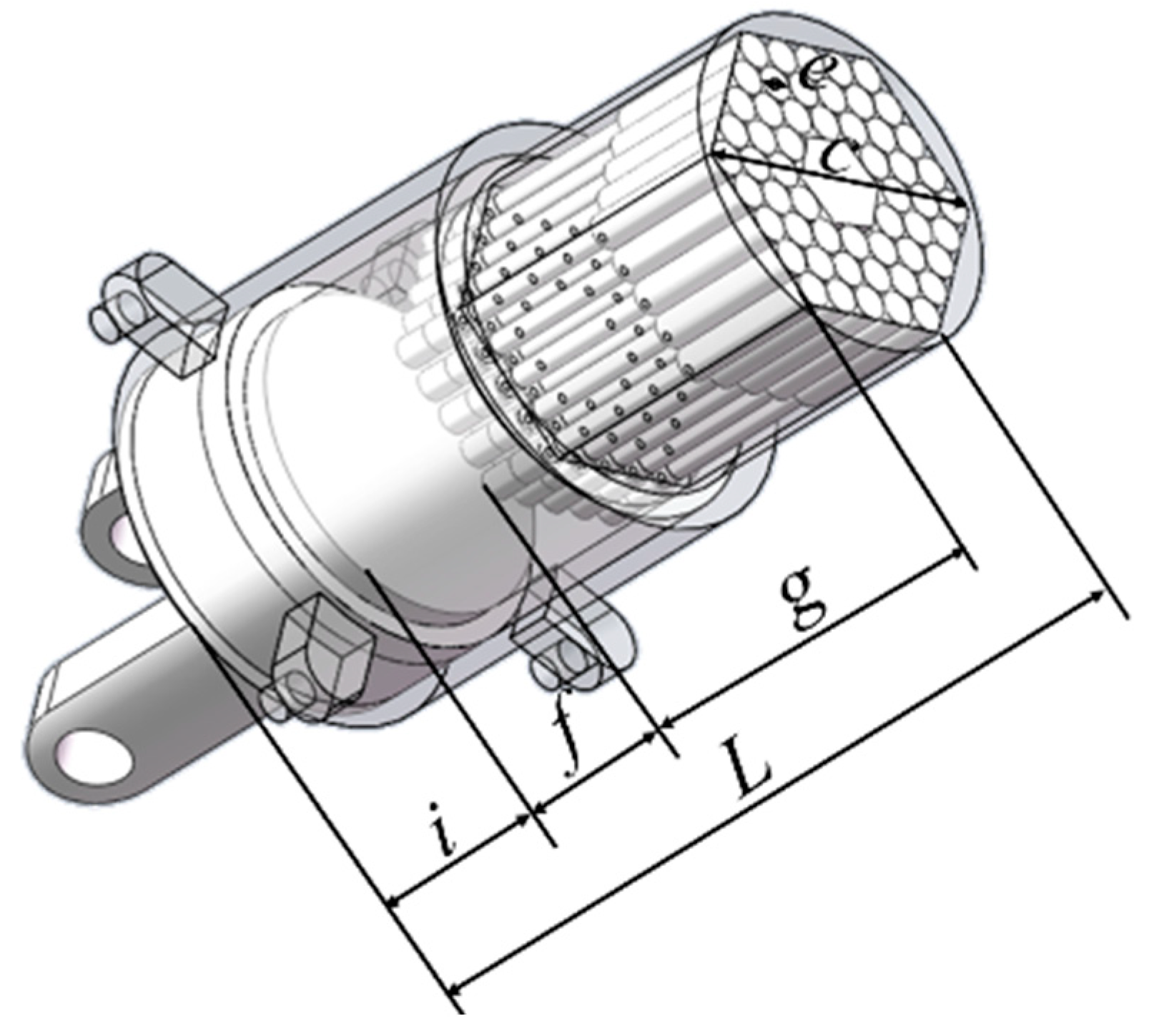
4.2.2. Parametric Design of the Universal Wrench
- (1)
- The diameter of the circumscribed circle of the hexagonal inner hole, c
- (2)
- The diameter of the steel bar, e
- (3)
- The working depth of the steel bar, f
- (4)
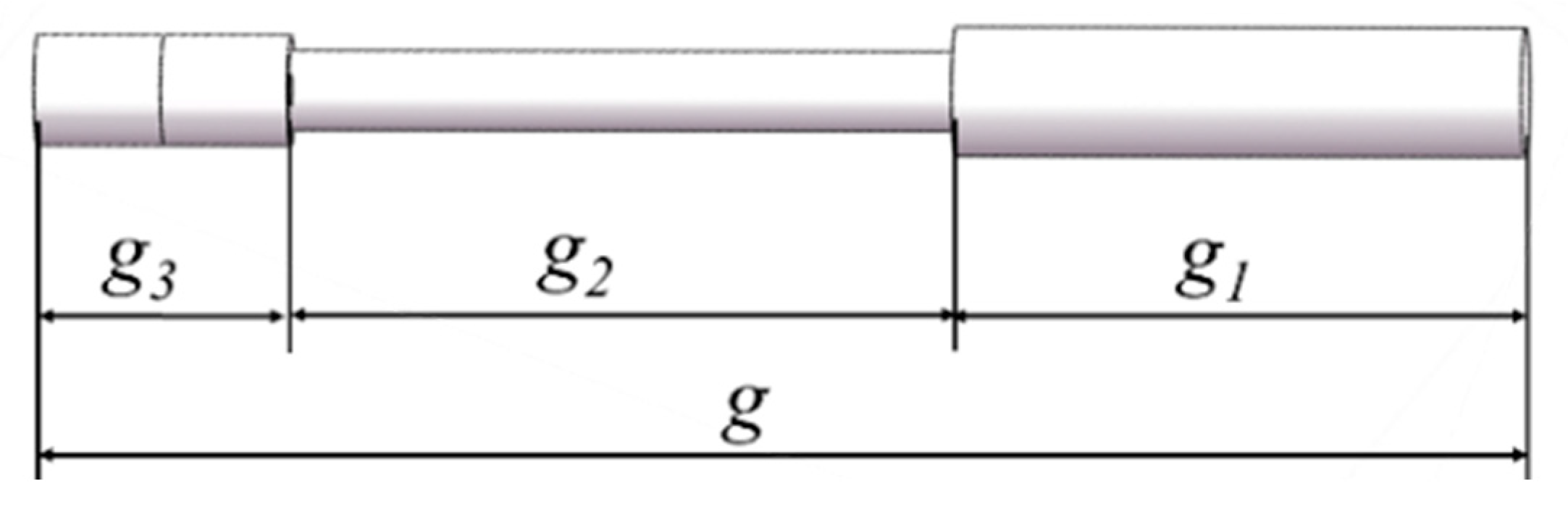
- The telescopic distance of the steel bar, h
- (5)
- The length of the steel bar, g
- (6)
- The height of the base, i
- (7)
- The total length of the universal wrench, L
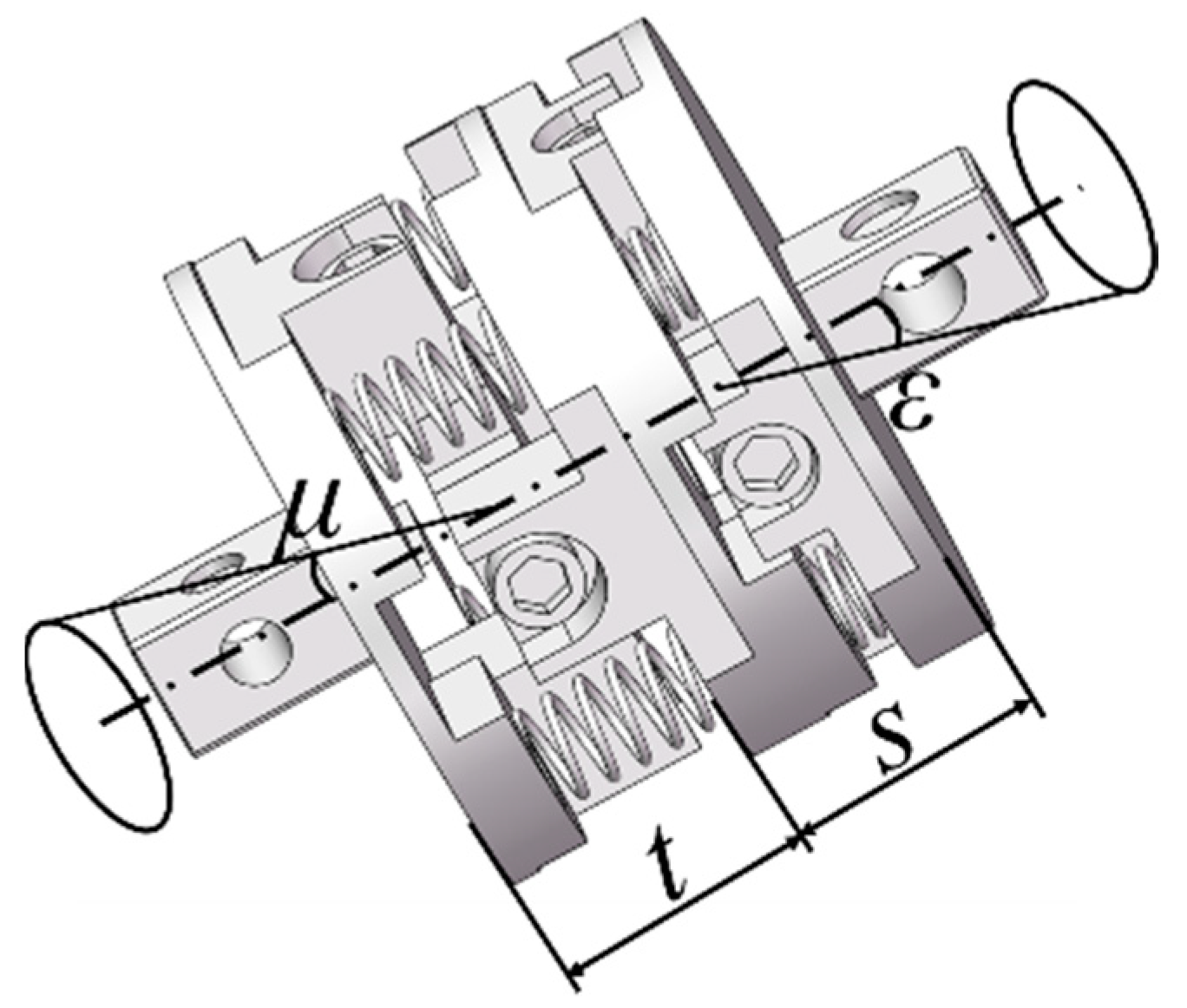
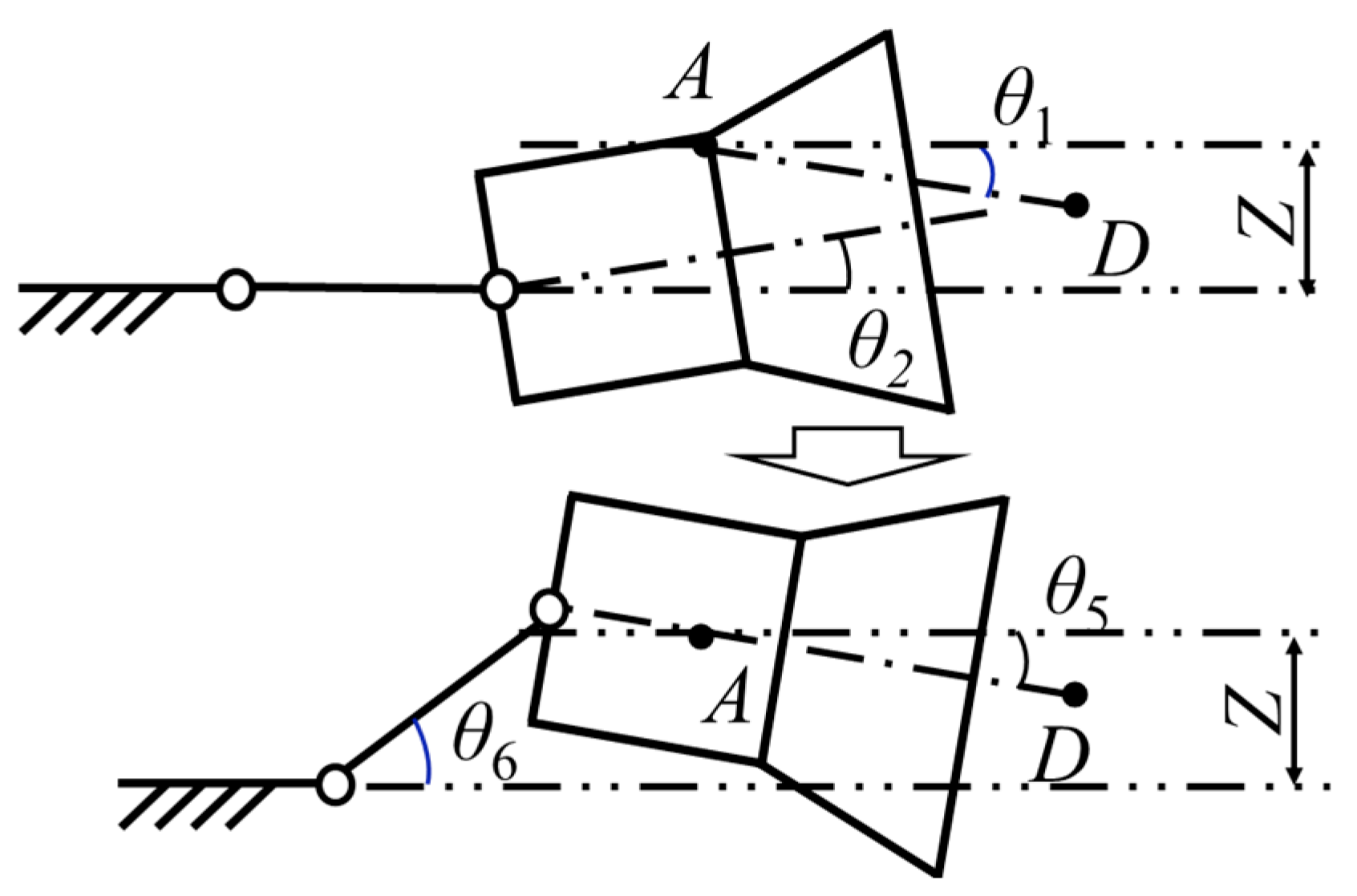
4.2.3. Parametric Design of the Flexible Connecting Mechanism
- (1)
- Determination of the rotation angle of the universal joint 1, ε
- (2)
- Determination of the rotation angle of the universal joint 2, μ
4.3. The Simulation Analysis of End-Effector of the Cutter-Changing Robot
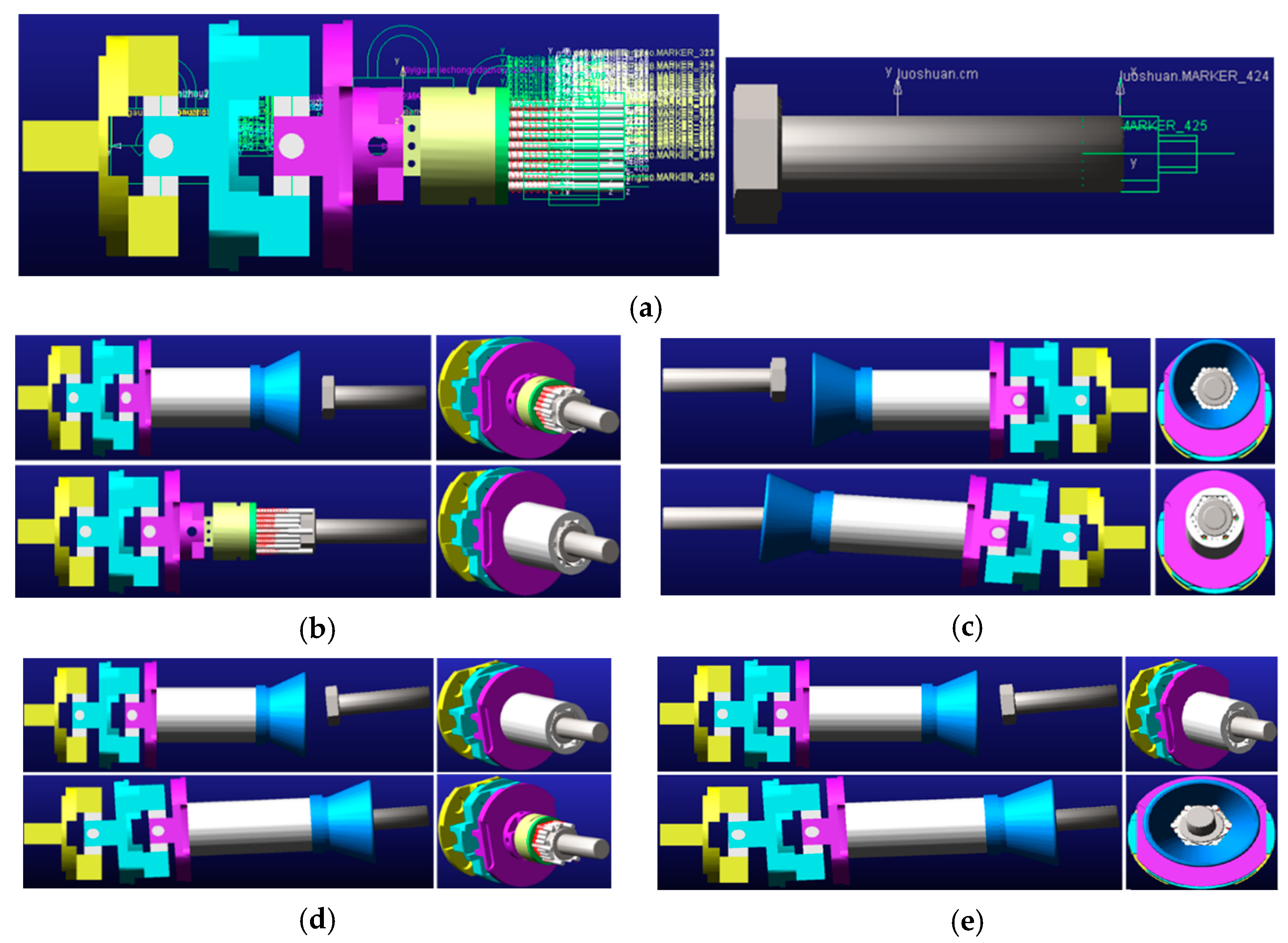
4.3.1. Function Simulation Analysis of End Effector
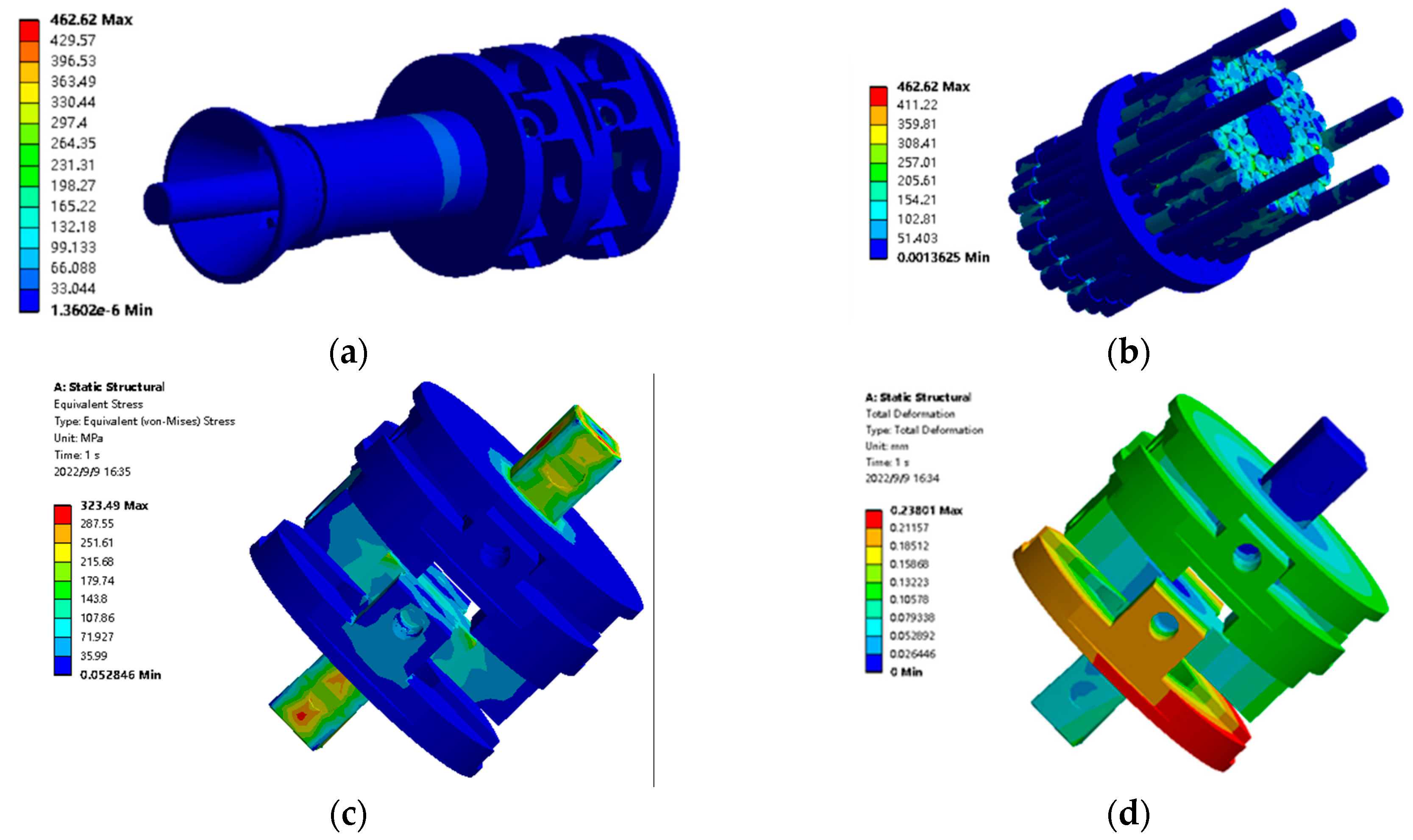
4.3.2. Simulation Analysis of Mechanical Properties of Key Structures
4.4. The Universal Wrench Performance Test
5. Conclusions
- (1)
- In this paper, the improved Jacobian–Torsor model is used to analyze the deviation of a new integrated disc cutter system of TBM developed by our research group. The experiment results show that the deviation analysis method is reasonable and accurate. Among the 10 deviation components tested, only one exceeds the theoretical calculation range by 5%.
- (2)
- Based on deviation analysis of the new integrated TBM disc cutter, an end-effector of a cutter-changing robot matched was designed, and a scaled-down sample was made for the test. The functions of each part of the end-effector of the cutter-changing robot can meet the expected requirements. The scaled-down cutter-changing robot end-effector can accommodate a radial deviation of 3.55 mm and an angular deviation of 11°.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Camus, T.; Manacorda, G. European Project NeTTUN–Making it happen. In ITA WTC 2015 Congress and 41st General Assembly; Lacroma Valamar Congress Center: Dubrovnik, Croatia, 2015. [Google Scholar]
- Derycke, J.N.; Rubrecht, S. Method for Replacing a Tunnel Boring Machine Disk Cutter, Handling Device and Disk Cutter Suited to Such a Method. U.S. Patent US20130045055A1, 30 August 2016. [Google Scholar]
- Mansard, N.; Khatib, O.; Kheddar, A. A unified approach to integrate unilateral constraints in the stack of tasks. IEEE Trans. Robot. 2009, 25, 670–685. [Google Scholar] [CrossRef]
- Camus, T.; Moubarak, S. Maintenance robotics in TBM tunnelling. In ISARC. Proceedings of the International Symposium on Automation and Robotics in Construction; IAARC Publications: Berlin, Germany, 2015. [Google Scholar]
- Chu, B.; Jung, K.; Ko, K.H.; Hong, D. Mechanism and analysis of a robotic bolting device for steel beam assembly. In Proceedings of the ICCAS 2010, Gyeonggi-do, Korea, 27–30 October 2010. [Google Scholar]
- Zhang, Q.; Xie, Z.; Liu, Y.; Liu, H. Development of Bolt Screwing Tool Based on Pneumatic Slip Ring. In 12th International Conference on Intelligent Robotics and Applications (ICIRA); Springer International Publishing Ag: Shenyang, China, 2019. [Google Scholar]
- Li, R.; Pham, D.T.; Huang, J.; Tan, Y.; Qu, M.; Wang, Y.; Kerin, M.; Jiang, K.; Su, S.; Ji, C.; et al. Unfastening of Hexagonal Headed Screws by a Collaborative Robot. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1455–1468. [Google Scholar] [CrossRef]
- DiFilippo, N.M.; Jouaneh, M.K. A System Combining Force and Vision Sensing for Automated Screw Removal on Laptops. IEEE Trans. Autom. Sci. Eng. 2018, 15, 887–895. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, Z.; Liu, Y.; Zhao, X.; Gu, Y.; Liu, H. A novel approach for flexible manipulator conducting screwing task based on robot-environment contact classification. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2021, 235, 1357–1367. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.; Lai, X. A comprehensive study of three dimensional tolerance analysis methods. Comput.-Aided Des. 2014, 53, 1–13. [Google Scholar] [CrossRef]
- Hong, Y.; Chang, T. A comprehensive review of tolerancing research. Int. J. Prod. Res. 2002, 40, 2425–2459. [Google Scholar] [CrossRef]
- Clement, A.; Riviere, A. Tolerancing versus nominal modeling in next generation CAD/CAM system. In Proceedings of the 3rd CIRP Seminar on Computer Aided Tolerancing, ENS de Cachan, Cachan, France, 27–28 April 1993. [Google Scholar]
- Laifa, M.; Sai, W.B.; Hbaieb, M. Evaluation of machining process by integrating 3D manufacturing dispersions, functional constraints, and the concept of small displacement torsors. Int. J. Adv. Manuf. Technol. 2014, 71, 1327–1336. [Google Scholar] [CrossRef]
- Davidson, J.; Mujezinovic, A.; Shah, J. A new mathematical model for geometric tolerances as applied to round faces. J. Mech. Des. 2002, 124, 609–622. [Google Scholar] [CrossRef]
- Jaishankar, L.N.; Davidson, J.K.; Shah, J.J. Tolerance analysis of parallel assemblies using tolerance-maps® and a functional map derived from induced deformations. In ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE); American Society of Mechanical Engineers: Portland, OR, USA, 2013. [Google Scholar]
- Barbero, B.R.; Azcona, J.P.; Pérez, J.G. A tolerance analysis and optimization methodology. The combined use of 3D CAT, a dimensional hierarchization matrix and an optimization algorithm. Int. J. Adv. Manuf. Technol. 2015, 81, 371–385. [Google Scholar] [CrossRef][Green Version]
- Jin, S.; Chen, H.; Li, Z.; Lai, X. A small displacement torsor model for 3D tolerance analysis of conical structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2514–2523. [Google Scholar] [CrossRef]
- Zeng, W.; Rao, Y.; Wang, P.; Yi, W. A solution of worst-case tolerance analysis for partial parallel chains based on the Unified Jacobian-Torsor model. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2017, 47, 276–291. [Google Scholar] [CrossRef]
- Gao, J.; Chase, K.W.; Magleby, S.P. Generalized 3-D tolerance analysis of mechanical assemblies with small kinematic adjustments. IIE Trans. 1998, 30, 367–377. [Google Scholar] [CrossRef]
- Liu, Y. Typical Russian space docking mechanism and its characteristics. Spacecr. Eng. 1994, 3, 33–38. [Google Scholar]
- Günther, H.; Knoop, H.U. Implication and usefulness of spacecraft servicing at the ISS using the pilot case of the large X-ray facility XEUS. Acta Astronaut. 2003, 53, 645–650. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, J.; Zhou, H. Analysis and Optimization of Force Transmissibility and Kinematic Performance of Low Impact Docking Mechanism. Manned Spacefl. 2015, 21, 462–467. [Google Scholar]
- Liu, W. Mechanism Analysis of Deviation Sourcing and Propagation for Mechanical Assembly. J. Mech. Eng. 2012, 48, 156–168. [Google Scholar] [CrossRef]




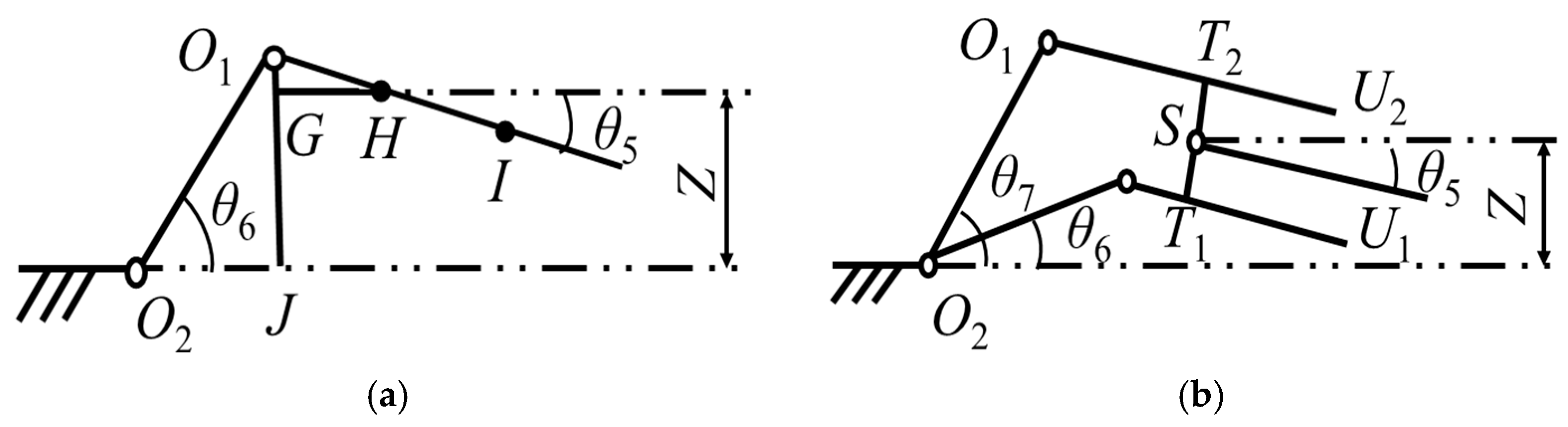



| Parameter | Tolerance Zone |
|---|---|
| CFE1 | |
| CFE2 | |
| CFE3 | |
| CFE4 | |
| PFE1 | |
| PFE2 |
| Parameters | Physical Significance | Tolerance Zone |
|---|---|---|
| FRb | Assembly deviation between fastening bolt and cutter holder | |
| FRt | Assembly deviation between disc cutter and cutter holders | |
| A0 | The deviation between cutter holders and disc cutter in the direction of cutter shaft | |
| FRh | Assembly deviation between cutter holders and cutter box | |
| N | Welding deviation between cutter box and cutter head |
| Density (kg/m3) | Elastic Modulus (GPa) | Poisson Ratio | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| 7800 | 207 | 0.25 | 1080 | 835 |
| Density (kg/m3) | Elastic Modulus (GPa) | Poisson Ratio | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| 7850 | 210 | 0.3 | 1080 | 835 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Li, H.; Huo, J.; Yang, B.; Yang, F. Assembly Deviation Analysis of New Integrated TBM Disc Cutter and Design of the Supporting Cutter-Changing Robot End-Effector. Appl. Sci. 2022, 12, 9549. https://doi.org/10.3390/app12199549
Chen H, Li H, Huo J, Yang B, Yang F. Assembly Deviation Analysis of New Integrated TBM Disc Cutter and Design of the Supporting Cutter-Changing Robot End-Effector. Applied Sciences. 2022; 12(19):9549. https://doi.org/10.3390/app12199549
Chicago/Turabian StyleChen, Hao, Hao Li, Junzhou Huo, Bowen Yang, and Fan Yang. 2022. "Assembly Deviation Analysis of New Integrated TBM Disc Cutter and Design of the Supporting Cutter-Changing Robot End-Effector" Applied Sciences 12, no. 19: 9549. https://doi.org/10.3390/app12199549
APA StyleChen, H., Li, H., Huo, J., Yang, B., & Yang, F. (2022). Assembly Deviation Analysis of New Integrated TBM Disc Cutter and Design of the Supporting Cutter-Changing Robot End-Effector. Applied Sciences, 12(19), 9549. https://doi.org/10.3390/app12199549




