Abstract
To control the level of tensile stress in the section of reinforced concrete arch cantilever construction, a construction control method of temporary prestressing reinforcement is proposed in this study. The influence law of temporary prestressing on the arch ring section stress is revealed based on the engineering background (Shatuo Special Bridge in Guizhou). Meanwhile, a temporary prestressing test is carried out on the ring section of the main arch to verify the effectiveness of the method. The results show that the prestressing configuration during the construction of the main arch ring of the suspension arch bridge has obvious influence on the control of tensile stress. The method can also effectively improve the force uniformity of the buckle cables, reduce the variation range of cable forces during construction, and improve the safety of arch ring construction.
1. Introduction
Reinforced concrete arch bridges are highly respected in the construction of mountain bridges because of their good force performance and low post-maintenance costs [1,2,3], and the site-specific diagonal buckle cantilever casting construction method has increasingly become the mainstream of construction methods for large-span reinforced concrete arch bridges [4,5,6,7,8,9]. The first cantilever-cast reinforced concrete arch bridge was the 246 m main span Sibenik Bridge, which was completed in Croatia (former Yugoslavia) in 1966. Several world-record reinforced concrete arch bridges have been built abroad using this construction method, which also makes cantilever-cast reinforced concrete arch bridges widely promoted and applied, and the world’s largest cantilever-cast reinforced concrete arch bridge with a main span of 384 m is the Almonte railroad bridge completed in 2016 [5]. The cantilever casting method for reinforced concrete arch bridges was applied in China at a late stage. The first reinforced concrete arch bridge constructed by cantilever casting method in China was the 150 m main span of Baishaigou No. 1 bridge built in 2007 on the Xichang-Panzhihua highway in Sichuan [10]. So far, China has used the cantilever casting method to build the Mupeng Bridge (completed in 2013, the main span of 165 m), the Xinmidi Bridge (completed in 2013, the main span of 182 m), the Horseshoe River Bridge (completed in 2015, the main span of 180 m), Ganyu Bridge (completed in 2015, the main span of 200 m), Shatuo Bridge (completed in 2019, the main span of 240 m), Jieming Three Provinces Bridge (completed in 2020, the main span of 180 m) and other seven reinforced concrete arch bridge [11,12,13]. Among them, Shatuo Bridge is the largest span cantilever cast reinforced concrete arch bridge completed in China. At present, the largest span of cantilever cast reinforced concrete in China is the main span of the Shuiluo River Bridge with 335 m under construction in Gulin County, Sichuan Province. The typical cantilever cast reinforced concrete arch bridges of more than 200 m at home and abroad are summarized in Table 1.

Table 1.
Summary of typical reinforced concrete arch bridges built using the cantilever casting method in the world (L0 ≥ 200 m).
As the main arch ring of reinforced concrete arch bridge relies only on the multi-point elastic support of temporary buckle anchor cables to ensure the structural force and stability safety of the arch ring during cantilever construction, the construction control risk is large [14]. With the increasing span of the bridge, the number of sections and the number of buckled anchor cables increases, the tensile and compressive stresses in the top and bottom flanges of the arch section change alternately, and the difficulty of construction control becomes higher and higher. The control of arch section stress during the cantilever casting construction of the main arch ring is more concerned by related scholars. Granata et al. [15] proposed a partial elastic method for solving the construction cable force of a suspended concrete arch bridge based on the idea of multi-point elastic support and zero-displacement method control, and carried out numerical calculations with a concrete arch bridge as an example, and compared the initial cable force calculated by the partial elastic method with the calculation results of the traditional method, and the results showed that the partial elastic method has a good effect on the control of the arch ring alignment, internal force, and buckle force during the construction of a concrete arch bridge. Au et al. [1] used a concrete arch bridge with a main span of 180 m cantilever assembly construction as a basis and used the stress balance and influence matrix method to optimize the cable force during the construction of the arch segment assembly to ensure that the arch alignment and force during construction meet the safety control requirements. Li et al. [16] determined the initial cable force of a large-span steel pipe concrete arch bridge based on the influence matrix and linear programming method. Dai and Wang [17] proposed an optimal calculation method to optimize the initial cable force of a cable-stayed arch bridge for the cantilever erection of arch ribs. Tian et al. [14] used the stress balance and influence matrix method to determine the initial cable force of a concrete arch bridge. The stress balance equation and influence matrix for the critical section of the arch rib were established to determine the range of buckle forces. The engineering application examples show that the stress balance and influence matrix method for determining the initial cable force are feasible and reliable.
Most of the existing research on stress control of the main arch ring during the construction period is to ensure the safety of the arch ring by optimizing the initial tensioning force of the buckle cable, while the actual construction process of the buckle cable to regulate the stress of the arch ring section has certain limitations, the adjustable range is small, and due to the uncertainty of temporary load and the control accuracy of actual tensioning force on site, the actual stress of the arch ring is different from the theoretically calculated stress. In this paper, to reduce the risk of exceeding the tensile stress limit in the arch section during the construction of cantilever-casting concrete arch bridges, temporary prestressing tendons are introduced into the cantil process of arch sections to control the tensile stress in the arch section by drawing on the method of arranging prestressing tendons in the main girders of concrete cable-stayed bridges and girder bridges to resist the tensile stress generated by the loads. A few Chinese scholars have discussed the method of configuring prestressing tendons in the arch ring during the construction of cantilever cast arch bridges, and Zhou et al. [18] analyzed the effect of configuring prestressing in the arch ring on the internal force and deformation of arch construction using the zero-order optimization method that comes with the Ansys program. Wu et al. [19] analyzed the effect of temporary prestressing on the stress in the arch section of cantilever cast RC arch bridges based on the stress index control method, and the calculation results confirmed that temporary short beam prestressing can effectively reduce the maximum tensile stress level during the construction of the arch section, while a comparative analysis of the sensitivity of the prestressing effect parameters was conducted. Wu and Tian [20] compared and analyzed the effects of prestressing effect on key factors such as arch section stress, deformation, cable force, tower deflection, and local stress during the construction of a cantilever cast arch bridge. The calculation results show that the prestressing effect can effectively reduce the peak stress of the cross-section and improve the cross-sectional force, and at the same time, it can increase the arch ring stiffness and reduce the buckle anchor cable stress amplitude to a certain extent, and the prestressing effect has no significant effect on the tower deflection.
However, the existing research on the configuration of temporary prestressing tendons in the arch section is mostly a theoretical concept, lacking the support of the basic theory, corresponding engineering practice, and test data. In this paper, we propose a construction control method for temporary prestressing tendons in the arch section, by deriving the formula for calculating the stress in the arch section under the joint action of prestressing force and cable force, and using Matlab and Ansys program as the development platform to prepare an iterative optimization solution program to study the influence law of temporary prestressing on the stress in the arch section, and compare it with the real bridge test of temporary prestressing in the main arch section to verify it. This study provides an effective reference for stress control in the main arch ring of reinforced concrete arch bridges.
2. Stress Analysis Method of the Arch Ring Section
This section aims to study the stress distribution law in the top and bottom flanges of each arch ring section after the main arch ring control sections are equipped with prestressing tendons. The detailed derivation of stress formulae for the top and bottom flanges under different conditions is derived in the following.
2.1. Analysis of the Initial Stress State of the Arch Ring Section Considering Prestressing Effect
The prestressing effect analysis is carried out for reinforced concrete arches equipped with prestressing, and the formula for calculating the stresses at the top and bottom flanges of each section of the arch section is derived by combining the diagonal tension buckle cantilever casting process. The following assumptions are made before the derivation of the formula.
- (1)
- Flat section assumption.
- (2)
- The neutral layer and the neutral axis assumptions.
- (3)
- The assumption of linear elasticity by Hooke’s law.
- (4)
- The arch ring segments with straight lines instead of curves, ignoring the effect of curvature.
- (5)
- The arch ring section is straight instead of curved to ignore the effect of bending.
The formulae for the calculation of the post-tensioning prestressing effect in the “Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts” (JTG3362-2018) [21] were used to analyze the stresses at the top and bottom flanges of the arch section caused by the prestressing force. The stresses in the cross-section of the concrete member generated by the prestressing force are at the top flanges and at the bottom flanges. The specific expressions are shown in Equation (3) and Equation (4), respectively. The simplified calculation model of prestressing concrete members is shown in Figure 1.

Figure 1.
Simplified calculation model of prestressing concrete members.
Eccentric distance:
The top flanges:
The bottom flanges:
where is the net cross-sectional area, is the combined force of prestressing and common reinforcement in post-tensioned members, is the secondary bending moment generated by the prestressing force, is a super-stationary structure such as a prestressed concrete continuous beam, is the net cross-sectional moment of inertia, is the distance from the center of gravity of the net cross-section to the point of the combined force of prestressing and common reinforcement in the body, is the distance from the center of gravity of the net section to the calculation fiber, , is the distance from the point of the combined force of prestressing bars in the tension zone and compression zone to the axis of the center of gravity of the net section, , is the effective prestressing stress of prestressing bars in the tension zone and compression zone, , is the cross-sectional area of prestressing reinforcement in the tension and compression zones, is the stress at the top flange of the main arch rim section under the prestressing effect, and is the stress at the bottom flange of the main arch rim section under the prestressing effect.
During the construction of the cantilever cast arch bridge, the structural system is relatively complex, and the calculation of stress at the top and bottom flanges of the main arch section is more complicated considering the prestressing effect, and the coupling effect of cable force and prestressing will occur after buckle tensioning. Three crucial construction conditions are highlighted during the process of cantilever casting of the main arch ring considering prestressing: concrete casting, prestressing tensioning and buckle cable tensioning, and the stress formula of the top and bottom flanges of the arch ring section after prestressing tensioning and the stress formula of the top and bottom flanges of the arch ring section after buckle cable tensioning under the coupling effect of cable force and prestressing are derived. The detailed derivation and analysis process is as follows.
Condition 1: Prestressing tensioning condition
As shown in Figure 2, any two arch ring sections are selected for structural analysis, and the stress distribution at the top and bottom flanges of the section after prestressing tensioning is analyzed for sections and in the figure.
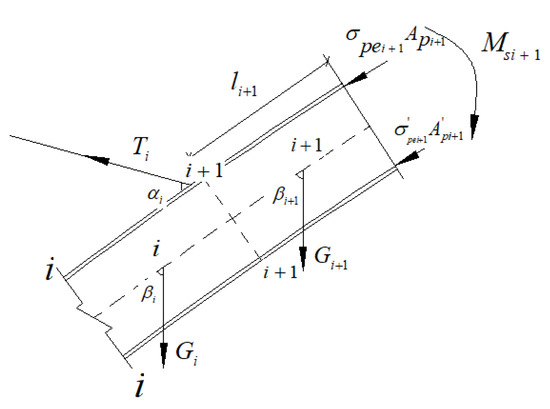
Figure 2.
Structural calculation model of the arch ring prestressing tensioning working condition.
According to the calculation and analysis model of the arch ring section, the stresses at the top and bottom flanges of section can be calculated as follows.
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
The stresses at the top and bottom flanges of the section can be calculated as follows.
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
Condition 2: Buckle cable tensioning condition
As shown in Figure 3, any two arch ring sections are selected for structural analysis, and the stress distribution at the top and bottom flanges of the arch ring sections under the action of buckle and stress coupling after buckle tensioning is analyzed with the i and sections in the figure. The analysis of the calculation model of the arch ring section in Figure 3 is described.
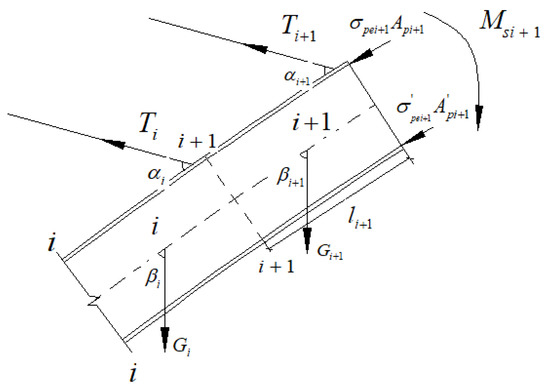
Figure 3.
Simplified mathematical model of main arch ring buckle tensioning condition.
The stresses at the top and bottom flanges of section i+1 can be calculated as follows.
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
The stresses at the top and bottom flanges of section i can be calculated as follows.
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
The stress calculation of the top and bottom flanges of the arch ring section for the two sections can be extended to the stress calculation of the top and bottom flanges of the arch ring section for any section under any construction stage. The structural calculation model is shown in Figure 4. The analysis of the prestressing tensioning condition of any arch section and the coupling action of the cable force and prestressing force after tensioning of the buckled cable can derive the formula of the stress on the top and bottom flanges of the section of any arch section.
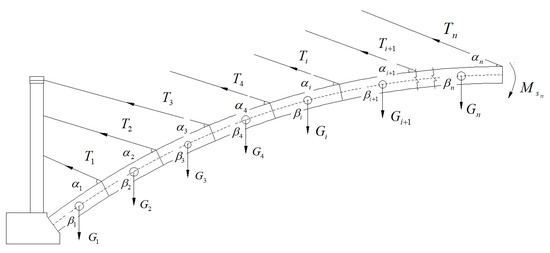
Figure 4.
Simplified mathematical model of prestressing tensioning condition of the main arch ring.
Condition 1: Prestressing tensioning condition
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
Condition 2: Buckle cable tensioning condition
Axial force:
Bending moment:
Eccentric distance:
The top flanges:
The bottom flanges:
where is the axial pressure of the section i of the arch ring, is the bending moment of the section i of the arch ring, is the temporary bending moment load at the section i, generally considered as hanging basket and formwork load, is the self-weight load of the segment i, is the distance from the center of gravity of the net section to the point of the combined force of prestressing and normal reinforcement in the body, is the stress at the top flange of the arch ring of section i of segment i, is the stress at the bottom flange of the arch ring of section i of segment i, is the angle from the position of the j-th buckle cable and buckle point to the straight line of the shaped center point of the calculated section, is the angle from the position of the center of gravity point of segment j to the straight line of the shaped center point of the calculated section to the vertical direction, and is the length of segment j, l is the length of the segment, h is the height of the section.
Found from the formula analysis that the formula can solve the stress at the top and bottom flanges of each section of the main arch construction process in the forward direction and can solve the cable force of each section in the reverse direction under the premise of controlling the number of prestressing force unchanged. The formula can also solve the number of prestressing tendons in each section under the condition of controlling the cable force unchanged.
Since the formula assumptions and the actual bridge conditions have a certain amount of deviation, the formula solution results are used as the proposed initial state of the structure, and then the precise analysis and adjustment of the stresses in the control section of the arch ring are carried out by the joint method of Matlab and ANSYS. The specific analysis and research process are detailed in the following.
2.2. The Arch Ring Section Stress Optimization Method
To improve the efficiency of calculation and analysis, Matlab is used to prepare the stress solution program for the top and bottom flanges of the arch ring section, and the basic parameters required for the calculation are imported through the interface between the large finite element software Ansys and its interface, and the method of combining Matlab and Ansys programs is used to solve the stress of the main arch ring by using the formula for calculating the stress of the main arch ring under the joint action of buckle and prestressing in the previous section through the preparation of a circular iterative program in Matlab.
2.2.1. Ansys-Based Objective Optimization Algorithm Flow
In Ansys, there are two types of objective optimization algorithms: zero-order optimization and first-order optimization. The zero-order optimization method is based on the idea of “limit approximation”, in which the accuracy of the calculation results is limited. The first-order optimization method is based on solving the minimum value to achieve the optimization procedure with high computational accuracy [22]. Ansys’ first-order optimization function module is applied to study the joint effect of temporary prestressing and buckle force. The main procedure is as follows.
- (1)
- Determining parameters such as objective function, design variables, and state variables.
- (2)
- Establishing a finite element parametric model to load and solve.
- (3)
- Entering the Design Opt first-order optimization module, setting the optimization initial sequence, specifying the loop control parameters, and invoking the Batch batch start mode.
- (4)
- Optimization iterative analysis and calculation: determining reasonable iterative convergence conditions, and entering the post-processing module to view the results after the program converges.
According to the optimization target and the actual construction situation, the parameters are selected as follows.
Objective function: To control the peak tensile stress in the cross-section of the arch ring sections during construction, the maximum tensile stress at the top and bottom flanges of the cross-section of each section of the main arch ring during construction is now taken as the objective function: .
Design variables: the buckle cable force and the quantity of prestressing are selected as design variables, and the cable force and prestressing are optimally solved based on the influence matrix, where the quantity of prestressing is expressed in the form of area function.
Constraints: the design value of tensile strength of the main arch ring material is used to customize the maximum tensile stress constraint index of the top and bottom flanges during the construction of the main arch ring as constraint 1: ; the buckle cable safety factor of 2.5 is used as constraint 2: ; the buckle tower offset of 40 mm is used as constraint 3.
2.2.2. Matlab-Based Solution of Buckle and Prestressing Influence Matrix
First, taking two buckle ropes of any section of the arch ring as a group, and tension the group of buckle ropes with the unit rope force value (for the convenience of analysis, the buckle force of each rope of the group is 10 kN as the unit rope force value) as the applied amount. Second, using the Ansys model for operational analysis, calculating the effective value of each parameter (the value does not include the parameter effect value under the action of constant load alone) and integrating the difference to obtain the effect array of the rope on each parameter. Similarly, we can obtain the effect array of each other buckle ropes on the parameters. Last, combining all the buckle ropes to obtain the effect matrix of the buckle force on each parameter. Similarly, we can also obtain the effect matrix of the temporary to prestressing on each parameter.
Considering the complexity of calculating the sample, the LinProg toolbox in Matlab is used to solve the influence matrix. The influence coefficients of buckle force and temporary prestressing effect are determined, which takes the stress at the top and bottom flanges of the main arch ring in each construction stage state as the planning target.
The influence coefficients of buckle force and temporary prestressing effect are determined in the maximum cantilever condition of the arch ring as an example. The mathematical expression is: , where solving the minimized linear programming of the objective function , and are constraints, the variables are x, and the upper and lower bounds of x are defined.
Given a large amount of data, the surfaces of the influence of the buckle force on the stress and the bending moment of the arch ring are shown in Figure 5 and Figure 6.
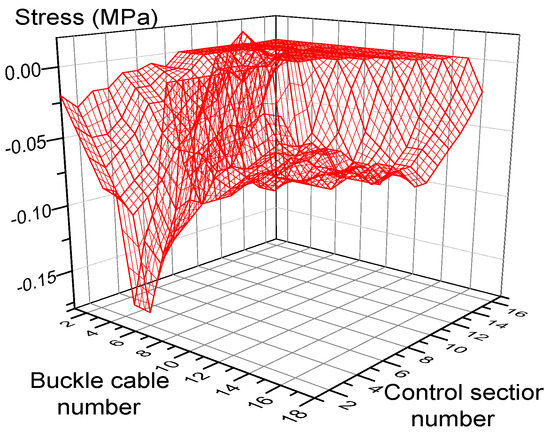
Figure 5.
Surface diagram of stress influence coefficient of the main arch ring.
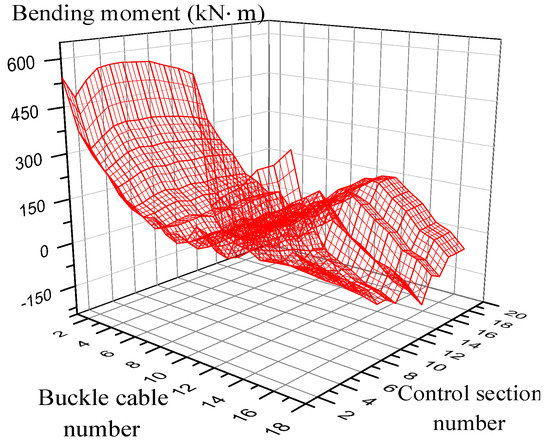
Figure 6.
Surface diagram of bending moment influence coefficient of the main arch circle.
Figure 5 shows the surface diagram of the influence of the buckle force on the stress of the control section of the arch ring, and the control section is each end section of the arch ring. The closer to the buckle change, the more obvious the change of the stress of the arch ring section, and the change of the buckle force near 1/4 of the arch ring has a greater influence on the stress of the section. Figure 6 shows the surface diagram of the influence of the buckle force on the bending moment of the control section of the arch ring, and the control section is selected as the end section of each section. The change of the buckle force has the most obvious influence on the bending moment of the section of the front section, and the amount of influence of the buckle force is smaller as the cantilever section increases, and the fitting results are consistent with the actual situation.
2.3. Programming of the Arch Ring Stress Solutions
Combining Matlab and Ansys to jointly analyze the stress distribution at the top and bottom flanges of each section of the main arch ring during the construction process, Matlab is used to prepare the calculation procedure of the stress formula derived in Section 2.1 for the top and bottom flanges of the main arch ring, and the iterative optimization solution of the cable force and pre-stress quantity using the influence matrix in Section 2.2. The specific implementation process is as follows. The flow chart of the main arch ring stress optimization solution procedure is shown in Figure 7.

Figure 7.
Flow chart of the main arch ring stress optimization solution procedure.
- (1)
- Customizing the stress control index at the top and bottom flanges of each section of the arch ring during the construction of the main arch ring.
- (2)
- Using Matlab to prepare the calculation program of the stress formula for the top and bottom flanges of the main arch ring derived in Section 2.1. Based on the formula derived in Section 2.1, establishing the corresponding multi-order matrix to prepare the forward solving subroutine 1 for the stresses at the top and bottom flanges of each section during the construction of the main arch ring. Based on the multi-order matrix, preparing the reverse solving subroutine 2 for the cable force of each section under the premise of controlling the number of pre-stress; and under the condition of controlling the constant cable force subroutine 3 for solving the prestressing quantity of each section in the reverse direction under constant control of the cable force.
- (3)
- Solving the initial cable force value for each section buckle according to the custom stress control index for each section using subroutine 2 in process step 1. Then, solving the stress for the top and bottom flanges of each section of the arch ring during construction according to the solid model of the whole bridge established by Ansys, and using the parameters of the interface with Matlab imported into Ansys for the construction phase analysis of the whole bridge.
- (4)
- Solving the initial prestressing quantity for each section of the main arch ring based on the difference between the stress and the stress indicator for each section of the main arch ring using subroutine 3 in process step 1.
- (5)
- Solving the matrix of the influence of the cable force on the stress in the main arch ring and the matrix of the influence of the amount of prestressing on the stress in the main arch ring during each construction stage of the main arch ring construction process using the solution method of the influence matrix of the cable force and prestressing in Section 2.2.
- (6)
- According to the initial cable force values of the buckle cables of each section of the main arch ring and the initial prestressing quantity of each section of the main arch ring as found in process steps (2) and (3), numerical simulation analysis is imported into Ansys to obtain the stresses at the top and bottom flanges of each section of the main arch ring for the whole construction process of the main arch ring.
- (7)
- If ≤, it means that the stress at the top and bottom flanges of each section of the main arch ring under the combined action of the cable force and the prestressing quantity has reached the custom stress index for each section, and the design of each parameter meets the requirements, and the program is terminated; if >, it means that the stress at the top and bottom flanges of each section of the main arch ring under the combined action of the cable force and the prestressing quantity has not reached the custom stress index for each section, and the analysis proceeds to the next step.
- (8)
- Calculating the stress difference = − between the top and bottom flanges of each section of the main arch ring, and solving for the buckle cable force through the influence matrix , and solving for the stress at the top and bottom flanges of each section of the main arch ring according to step 6.
- (9)
- Calculating the stress difference = − at the top and bottom flanges of each section of the main arch ring, and solving for the prestressing quantity via the influence matrix , and overwriting the cable force data with the data and replacing the with the data.
- (10)
- Executing the process steps (5) to (10).
- (11)
- Until ≤ , end the program loop.
3. Engineering Background and Numerical Simulation Modeling
3.1. Background of Dependency Project
Shatuo Bridge is located in Yanhe County, Guizhou Province, and is a reinforced concrete arch bridge across the Wu River, whose arch ring is built with a skewed buckle cantilever casting process. The main arch of the bridge is a reinforced concrete box structure with equal height cantilever lines, with a net span diameter of 240 m, a net vector height of 40 m, a net vector-to-span ratio of and an arch axis coefficient of . The span layout of the main bridge is shown in Figure 8. The arch ring section is a single box double chamber structure, box width of 10 m, height of 4.5 m. The thickness of top and bottom of the arch rib section is both 80 cm, and the thickness of three webs is all 65 cm, as shown in Figure 9a. In the L/4 section of the arch rib, the thickness of the top and bottom of the arch rib section is both 35 cm, and the thickness of three webs is all 40 cm, as shown in Figure 9b. In the L/2 section of the arch rib, the thickness of top and bottom of the arch rib section is 50 cm and 35 cm, respectively, and the thickness of three webs is all 50 cm, as shown in Figure 9c. The longitudinal section of the arch ring is divided into 37 sections, among which section No.1 at the position of the arch foot on both banks is a bracket cast-in-place section, a hanger cast-in-place section is set at the top of the arch, and the remaining 34 sections are cantilever cast-in-place sections with diagonal pulling buckle hanging baskets. After the arch ring sections are cast and reach the design strength, they are anchored on the junction pier or buckle tower with buckle cables, and the longitudinal deflection of the junction pier and buckle tower is adjusted with the anchor cables to control the structural deformation. Construction layout of the buckled anchor cable of Shatuo Bridge is shown in Figure 10.

Figure 8.
Effect drawing of main span layout of Shatuo Bridge.
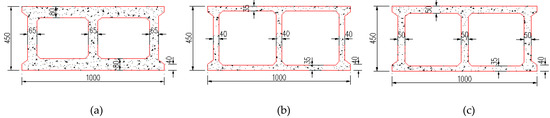
Figure 9.
Typical cross-section of the main arch circle of Shatuo Bridge (unit: cm): (a) Arch foot section, (b) L/4 section, (c) L/2 section.
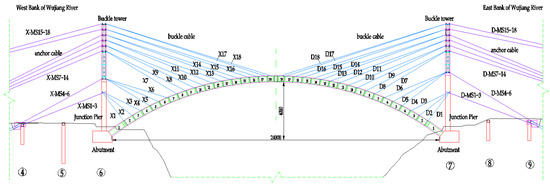
Figure 10.
Construction layout of the buckled anchor cable of Shatuo Bridge (unit: cm).
3.2. Numerical Simulation Model Building
Ansys/APDL is used to build the finite element parametric model of the whole bridge, in which the main arch ring is modeled by SOLID65 3D beam unit; considering that the optimization model needs to be solved iteratively at a later stage, LINK10 nonlinear rod unit is used for the buckle cable, and the modulus of elasticity of the buckle cable is modified based on Ernst’s formula to account for the geometric nonlinear effect; the restraint between the buckle cable and the main arch ring is achieved by MPC184 unit (activated rigid beam characteristic); the arch footing end face is solidified by face restraint and the node joint degrees of freedom between arch ring i and i + 1 segments. The buckle tension is applied by applying real constants (initial strain), and the “cell life and death” function is introduced to simulate the construction process of cantilever casting of the arch ring. To simplify the calculation process and improve the calculation efficiency, the constraint equations are established between the concrete unit nodes and the force reinforcement unit nodes by the “ceintf” command. The “ceintf” command automatically selects several nodes of the concrete unit and establishes the constraint equation with one node of the force reinforcement within the tolerance range and connects the force reinforcement unit and concrete unit as a whole through multiple sets of constraint equations. Ignoring the prestressing loss case, the prestressing design parameters are completed by setting the array about the area function. The specific finite element model is shown in Figure 11. The prestressing beam distribution is shown in Figure 12, Figure 13 and Figure 14.

Figure 11.
ANSYS finite element model diagram.
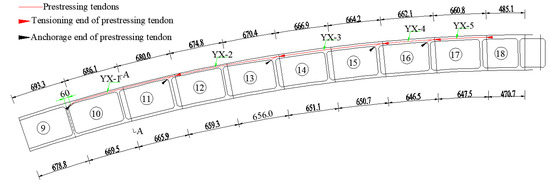
Figure 12.
Schematic diagram of the overall elevation of the prestressing tendon arrangement on the west bank.
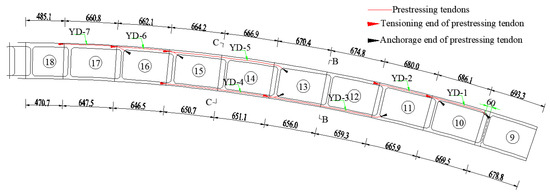
Figure 13.
Schematic diagram of the overall elevation of the prestressing tendons on the east bank.
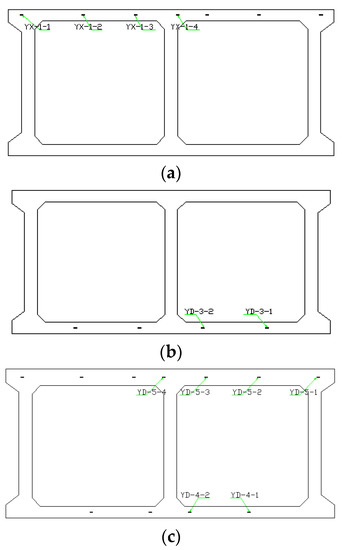
Figure 14.
Schematic diagram of the arrangement of prestressing beams in the section of the arch ring: (a) Single top slab with prestressing tendons, A-A cross-section, (b) Single bottom slab with prestressing tendons, B-B cross-section, (c) Top and bottom slabs with prestressing tendons at the same time, C-C cross-section.
To study the effect of temporary prestressing on the stress regulation of the arch ring section, it is assumed that the stress control indexes [13] of sections 10#~17# are given in Table 2. The corresponding section prestressing quantities are obtained by the iterative solution of the procedure in Section 2.3 given in Table 3.

Table 2.
Section stress control index [13].

Table 3.
Calculation table of temporary prestressing quantity.
4. Temporary Prestressing Control the Arch Ring Stress Results Analysis
4.1. Comparative Analysis of Buckle Force
In the presence of the temporary prestressing effect (hereinafter referred to as working condition 2), the initial tension of each buckle cable during cantilever casting and the maximum cable force during construction were extracted and compared with the results without the configuration of prestressing tendons (hereinafter referred to as working condition 1). The comparison after the convergence of the objective function iteration is summarized in Figure 15, Figure 16, Figure 17 and Figure 18, which is based on the West Coast buckle cable force.
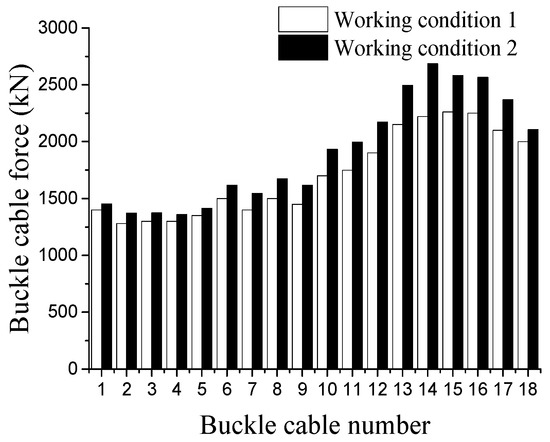
Figure 15.
Comparison of the initial tension of the buckle cable.
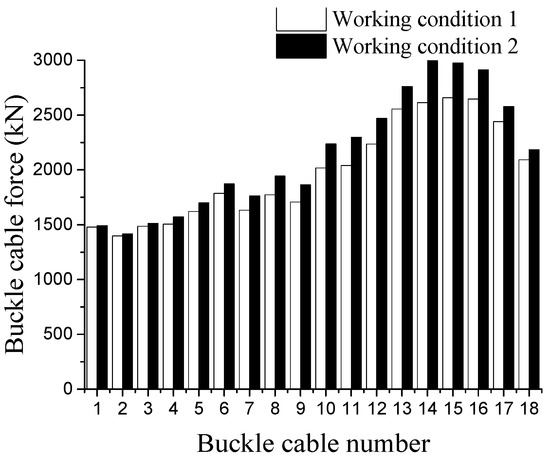
Figure 16.
Comparison of the maximum cable force during construction.
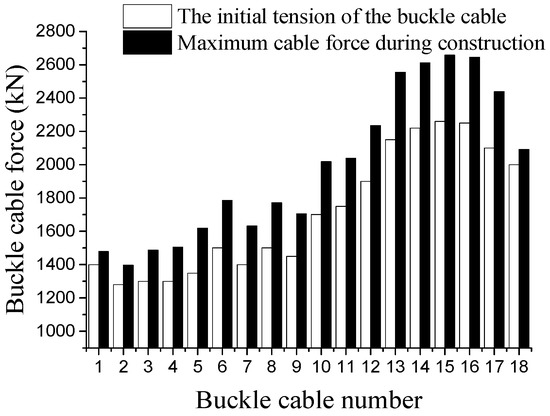
Figure 17.
Comparison of initial tension and maximum cable force of the buckle cable in working condition 1.
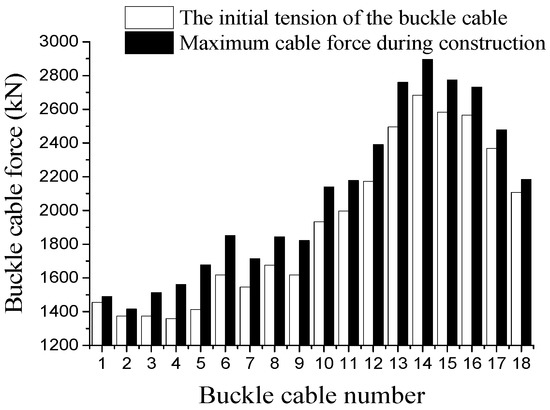
Figure 18.
Comparison of initial tension and maximum cable force of the buckle cable in working condition 2.
The optimization results show that the maximum value of initial tension of the original design buckle in West Bank is 2260 kN, while the maximum value of initial tension of buckle with the introduction of temporary prestressing is 2684 kN; and the initial tension value of X12~X17 buckle with the introduction of temporary prestressing increases significantly compared with that without prestressing, especially the X14, which has the largest increase rate of 21% and with an increase of 464 kN. The initial tensile force of introducing temporary prestressing is larger than that of no prestressing, but it reduces the variation of the maximum force and the initial tension of the corresponding buckle during the construction process. The average variation of the maximum force and the initial tension of the corresponding buckle during the construction process without prestressing is 15.7%, while the average variation is 9.3% after introducing prestressing, and the distribution of the force is more uniform. The change of each buckle cable force becomes more stable during the construction after the temporary prestress is introduced, which reduces the change of arch stress caused by the excessive change of cable force during the construction process.
4.2. Comparative Analysis of Stress in the Arch Ring Section
Under the joint action of buckle force and temporary prestressing force (hereinafter referred to as working condition 2), the maximum tensile stress results of each section of the top and bottom slab of the main arch ring in the process of cantilever pouring were extracted and analyzed, and compared with the stress results of each section of the main arch ring in each section from 10# to 17# without the configuration of prestressing tendons (hereinafter referred to as working condition 1), and the comparison of the specific results under the two working conditions is shown in Figure 19, Figure 20, Figure 21 and Figure 22. In the resultant data, negative stresses indicate compressive stresses and positive stresses indicate tensile stresses.
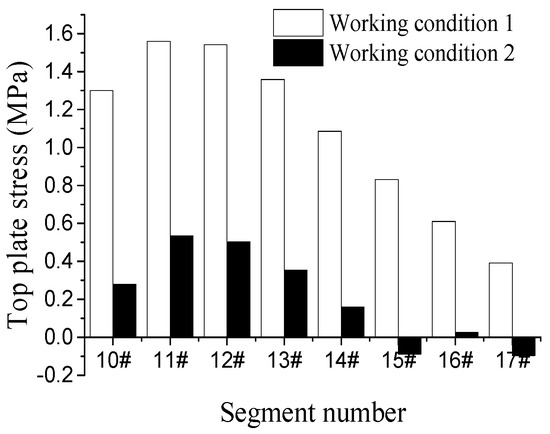
Figure 19.
Comparison diagram of the top flange stress of the west bank under different working conditions.
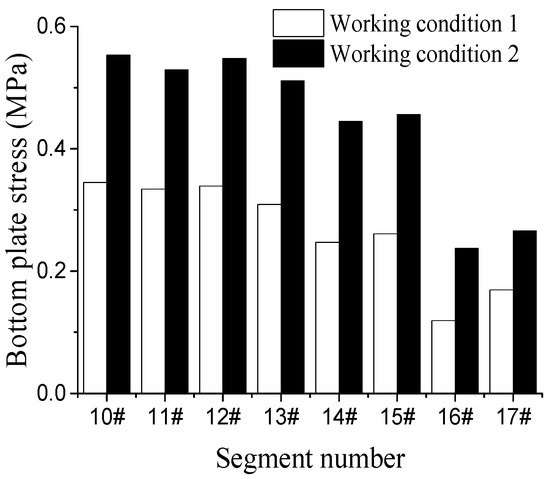
Figure 20.
Comparison diagram of the bottom flange stress of the west bank under different working conditions.
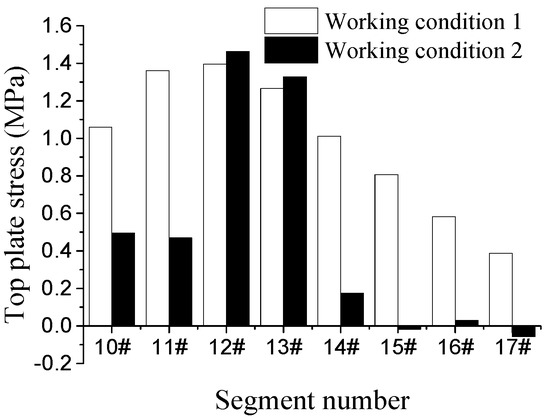
Figure 21.
Comparison diagram of the top flange stress of the east bank under different working conditions.
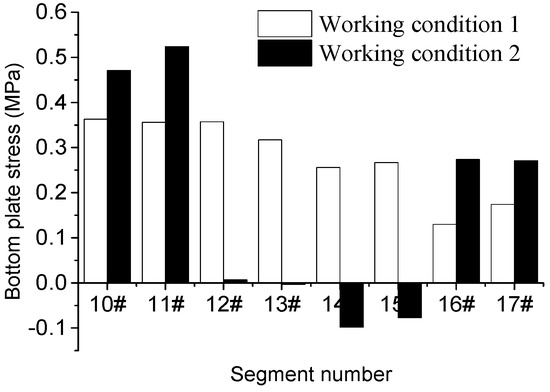
Figure 22.
Comparison diagram of the bottom flange stress of the east bank under different working conditions.
The comparison of the stress results shows that after the introduction of temporary prestressing, the maximum values of tensile stresses in the top and bottom flanges of each configuration of prestressing sections of the main arch ring during construction were within the range of the control index, the peak tensile stresses in the top flange were significantly reduced, and the growth of tensile stresses in the bottom flange is low. The results are reasonable. The introduction of temporary prestressing during cantilever casting construction changed the internal stress distribution of the arch ring, and the peak tensile stresses were all maintained at a low level, and the increase of compressive stress reserve also ensured good crack resistance and durability of the main arch ring during the construction process.
At the same time, due to the addition of pre-stress, the stress distribution in the top and bottom flanges is more balanced, which improves the utilization rate of the arch ring material strength and effectively reduces the risk of excessive tensile stress in the arch ring section during the construction process.
5. Results of Real Bridge Tests on Prestressing Arrangement of the Arch Ring Sections
The effect of temporary short beam prestressing on the stress regulation of the arch section during the cantilever casting of the main arch of the reinforced concrete arch bridge was investigated by burying vibrating string type strain transducers on site in the arch ring sections from 10# to 17# where temporary short beam prestressing is arranged. The strains in the control section of the arch ring during the suspension casting of the main arch ring are monitored to obtain sufficient sample data on the stress in the arch ring section during the whole construction of the arch ring section. The site prestressing beam arrangement is shown in Figure 23, and the site strain gauge arrangement is shown in Figure 24.
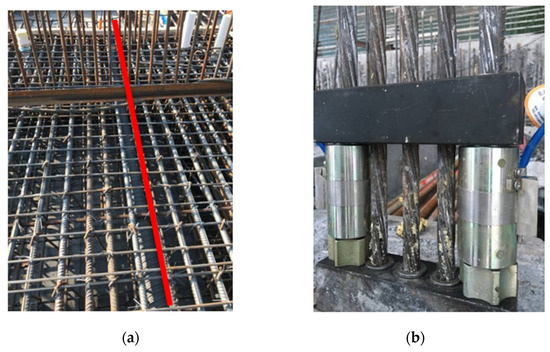
Figure 23.
Site layout of temporary prestressing tendons: (a) Site drawing of a longitudinal arrangement of prestressing tendons; (b) Site drawing of prestressing tendon section layout.

Figure 24.
Field sensor layout: (a) Site map of the arrangement of strain sensors on the roof of the arch ring; (b) Site map of the arrangement of strain sensors on the arch ring floor.
During the cantilever casting construction of the arch ring, the strain monitoring data of the arch ring section configured with temporary short beam prestressing was extracted for analysis, and the maximum tensile stress value of the section during construction was reasonably screened and compared with the theoretically calculated value, and the results of the comparison of the maximum tensile stress of each section during the construction of the main arch ring on the east and west banks are shown in Figure 25 and Figure 26.
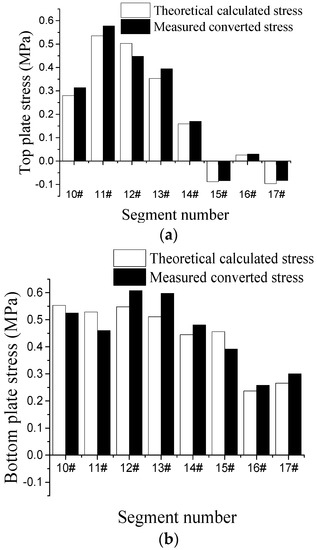
Figure 25.
Comparison of theoretical calculation and measured conversion stress of the arch ring section in the west bank: (a) Arch ring top flange, (b) Arch ring bottom flange.
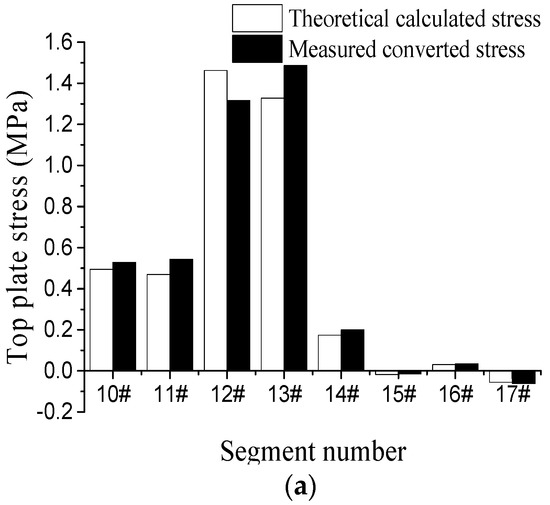
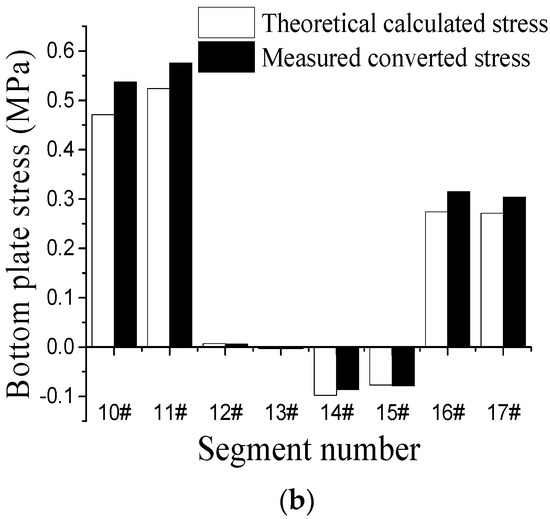
Figure 26.
Comparison of theoretical calculation and measured conversion stress of the arch ring section in the east bank: (a) Arch ring top flange, (b) Arch ring bottom flange.
From the comparison of measured and theoretical results, it can be seen that the measured maximum tensile stresses in the top and bottom flanges of the west bank are closer to the theoretical calculation results, and the average deviation of the maximum tensile stresses in the top flange is 10.4% and the maximum deviation is 15.4%; the average deviation of the maximum tensile stresses in the bottom flange is 11.3% and the maximum deviation is 17%. The average deviation between the measured conversion and the theoretical maximum tensile stress in the top and bottom flanges of the east bank is 11.4%, and the maximum deviation is 16%; the average deviation of stress in the bottom flange is 10%, and the maximum deviation is 15%.
Considering the discrete influence of data and concrete materials, it shows that the theoretical calculation results are more realistic and credible. It effectively verifies the feasibility of configuring temporary prestressing tendons to regulate the tensile stress level of the section during the construction process, and also confirms the correctness of the stress optimization algorithm of the arch section with the introduction of temporary prestressing in this study.
6. Conclusions
A construction control method of temporary prestressing reinforcement is proposed in this study to control the level of tensile stress in the section of reinforced concrete arch cantilever construction. The equation for calculating the stress in the arch section under the joint action of prestressing and buckle forces was derived. The iterative optimization solution procedure was prepared. The effect of temporary prestressing on the regulation of arch section stress was studied, and the theoretical analysis was verified by field real bridge tests. The main conclusions were obtained as follows.
- (1)
- The initial tension of the buckled cable with the introduction of temporary prestressing has increased to a certain extent compared with that without prestressing. However, the difference between the maximum force and the initial force during construction is significantly reduced, and the force distribution is more uniform. It avoids the large change of cable force during the construction process and alleviates the fatigue effect of the buckled cable during the construction period.
- (2)
- Temporary prestressing can effectively control the maximum tensile stress in the top and bottom flanges of the arch section within the control index, increase the compressive stress reserve in the arch section, improve the utilization rate of the arch ring material, and significantly reduce the risk of section cracking caused by the excess tensile stress in the arch section.
- (3)
- According to the comparison between the measured data and the theoretical analysis, the deviation between the measured stress and the theoretical calculation value is about 10%. Considering the discrete errors of data and concrete materials, the measured results are in good agreement with the theoretical analysis. The successful application of temporary prestressing in Shatuo Bridge provides novel ideas for the stress regulation of key sections during the construction of cantilever cast arch ring and can provide technical support for the breakthrough of cantilever cast arch bridges to larger spans.
Author Contributions
Conceptualization, Z.T., Z.Z., and W.P.; methodology, Z.Z. and W.P.; software, Z.Z.; validation, Z.Z. and W.P.; formal analysis, Z.Z.; investigation, Z.Z., W.P., Y.D., Y.C., and B.X.; resources, Z.T.; writing—original draft preparation, Z.Z. and W.P.; writing—review and editing, Z.T.; supervision, Z.T.; project administration, W.P.; funding acquisition, Z.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China, grant number 51478049; the National Nature Science Foundation of China, grant number 52078058; the Hunan Nature Science Foundation of China, grant number 14JJ2075; the Hunan Natural Science Foundation of China, grant number 2022JJ50323; the Major Technological Achievements Transformation Program of Hunan Strategic emerging industries of China, grant number 2017GK4034; the Hunan Long-span Bridge Construction Technology and Assembly Engineering Technology Research Center of China, grant number 2018TP2058; the Postgraduate Research and Innovation Project of Hunan, grant number CX20190660.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Au, F.T.K.; Wang, J.J.; Liu, G.D. Construction Control of Reinforced Concrete Arch Bridges. J. Bridg. Eng. 2003, 8, 39–45. [Google Scholar] [CrossRef]
- Chen, K.; Song, J.Y. Survey and Analysis of Exiting Reinforced Concrete Ribbed Arch Bridges. Adv. Mater. Res. 2011, 255–260, 1187–1191. [Google Scholar] [CrossRef]
- Salonga, J.; Gauvreau, P. Comparative Study of the Proportions, Form, and Efficiency of Concrete Arch Bridges. J. Bridg. Eng. 2014, 19, 04013010. [Google Scholar] [CrossRef]
- Chen, B.C.; ŠAVOR, Z.; Huang, Q.W. Material performance for long span concrete arch bridges: Higher is better//JAN B P. In Proceedings of the 8th International Conference on Arch Bridges, Wrocław, Poland, 5–7 October 2016; Springer Nature: Basel, Switzerland, 2016; pp. 85–102. [Google Scholar]
- Chen, B.C.; Liu, J.P. Review of construction and technology development of arch bridges in the world. J. Traffic Transp. Eng. 2020, 20, 27–41. [Google Scholar] [CrossRef]
- Arenas, J.J.; Capellán, G.; García, P.; Meana, I. Viaduct over River Almonte-conceptual design // ARCH’. In Proceedings of the 2016—8th Proceedings of 8th International Conference on Arch Bridges, Wrocław, Poland, 5–7 October 2016; pp. 313–322. [Google Scholar]
- DERIĆ, Ž.; RUNJIĆ, A.; HRELJA, G. Design and construction of Cetina river arch bridge // ARCH’07. In Proceedings of the 5th International Conference on Arch Bridges, Funchal, Madeira, Portugal, 12–14 September 2007; pp. 745–750. [Google Scholar]
- Cruz, P.J.S.; Cordeiro, J.M.L. Innovative and Contemporary Porto Bridges. Pract. Period. Struct. Des. Constr. 2004, 9, 26–43. [Google Scholar] [CrossRef]
- Wei, J.G.; Chen, B.C. Application and Research Progress of Foreign Long-Span Concrete Arch Bridges; World Bridges: Oak Brook, IL, USA, 2009; pp. 4–8. [Google Scholar]
- Li, X.B. Research on Construction Control and Model Test of Cantilever Casting for Long-Span Reinforced Concrete Arch Bridges. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Lu, Y.G.; Peng, W.P.; Tian, Z.C. Construction control study of overhanging buckle hanging of large span reinforced concrete box arch. J. China Foreign Highw. 2013, 33, 189–192. [Google Scholar] [CrossRef]
- Ouyang, C.W. Rational Bridge State and Optimal Construction Cable Force of the Horseshoe River Bridge. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2016. [Google Scholar]
- Peng, W.P. Research on Cable Force Optimization and Arch Ring Stress Control during Construction of Long-Span Cantilevered Concrete Arch Bridges. Ph.D. Thesis, Changsha University of Science and Technology, Changsha, China, 2020. [Google Scholar] [CrossRef]
- Tian, Z.-C.; Peng, W.-P.; Zhang, J.-R.; Jiang, T.-Y.; Deng, Y. Determination of initial cable force of cantilever casting concrete arch bridge using stress balance and influence matrix methods. J. Cent. South Univ. 2019, 26, 3140–3155. [Google Scholar] [CrossRef]
- Granata, M.F.; Margiotta, P.; Recupero, A.; Arici, M. Partial Elastic Scheme Method in Cantilever Construction of Concrete Arch Bridges. J. Bridg. Eng. 2013, 18, 663–672. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.-L.; Ge, S.-S. Optimum Calculation Method for Cable Force of Concrete-Filled Steel Tube Arch Bridge in Inclined Cable-Stayed Construction. J. Highw. Transp. Res. Dev. (Engl. Ed.) 2017, 11, 42–48. [Google Scholar] [CrossRef]
- Yu-Wen, D.; You-Yuan, W. A Research to Cable Force Optimizing Calculation of Cablestayed Arch Bridge. Procedia Eng. 2012, 37, 155–160. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, S.X.; Li, X.Q.; Feng, Y.S. Research on mechanical properties of cantilever pouring construction of concrete arch bridges. Chongqing Jiaotong Univ. Chin. J. (Nat. Sci. Ed.) 2018, 37, 9–13. [Google Scholar]
- Wu, X.; Wang, Q.S.; Zhang, Z.J. Analysis of temporary prestressing effect during cantilever casting of large-span RC arch bridges. Highw. Eng. 2019, 44, 11–16. [Google Scholar] [CrossRef]
- Wu, X.M.; Tian, Z.C. Analysis of the influence of key parameters in the suspension casting stage of a long-span RC arch bridge considering prestress. Highw. Eng. 2019, 44, 15–20+103. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts: JTG 3362-2018; People’s Communications Publishing House Co., Ltd.: Beijing, China, 2018. [Google Scholar]
- Hao, S.; Wang, X.; Xie, J.; Yang, Z. Rigid framework section parameter optimization and optimization algorithm research. Trans. Can. Soc. Mech. Eng. 2019, 43, 398–404. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).