The Effect of the Petrography, Mineralogy, and Physical Properties of Limestone on Mode I Fracture Toughness under Dry and Saturated Conditions

Sajad Safari Farrokhad; Gholam Reza Lashkaripour; Nasser Hafezi Moghaddas; Saeed Aligholi; Mohanad Muayad Sabri Sabri

doi:10.3390/app12189237

,

and

¹

Department of Geology, Faculty of Science, Ferdowsi University of Mashhad, Mashhad 9177948974, Iran

²

Institute of Innovation, Science and Sustainability, Federation University Australia, Ballarat, VIC 3350, Australia

³

Peter the Great St. Petersburg Polytechnic University, 195251 St. Petersburg, Russia

^*

Author to whom correspondence should be addressed.

Appl. Sci.2022, 12(18), 9237;https://doi.org/10.3390/app12189237

This article belongs to the Special Issue Mechanical Properties and Fracture Behavior of Rocks

Version Notes

Order Reprints

Review Reports

Abstract

Determining the fracture toughness of rock materials is a challenging, costly, and time-consuming task, as fabricating a sharp crack in rock specimens will lead to failure of the specimen, and preparing specimens for determining the rock fracture toughness requires special equipment. In this paper, the relationship between mode I fracture toughness (K_IC) with the rock index properties, mineralogy, and petrography of limestone is investigated using simple nonlinear and simple/multiple linear regression analyses to provide alternative methods for estimating the fracture toughness of limestones. The cracked chevron notched Brazilian disk (CCNBD) method was applied to 30 limestones with different petrographic and mineralogical characteristics under both dry and saturated conditions. Moreover, the index properties of the same rocks, including the density, porosity, electrical resistivity, P and S wave velocities, Schmidt rebound hardness, and point load index, were determined. According to the statistical analyses, a classification based on the petrography of the studied rocks was required for predicting the fracture toughness from index properties. By classifying the limestones based on petrography, reliable relationships with high correlations can be introduced for estimating the fracture toughness of different limestones using simple tests.

Keywords:

mode I fracture toughness; limestone; petrography; rock index properties

1. Introduction

Fracture toughness is defined as material resistance against crack growth [1]. The development and coalescence of cracks are the most important factors of rock failure with quasi-brittle behavior. Therefore, for analyzing the failure of rock materials, determining the fracture toughness is essential. This parameter is widely used in the fields of rock blasting, underground space stability, hydraulic fracturing, earthquake dynamic analysis, rock slope stability, and for evaluation of the drill-ability of rock masses.

Different studies have recently been conducted to develop some models for predicting the mechanical properties [2,3,4,5,6,7,8,9,10,11,12,13,14] and fracture toughness [15,16,17,18,19,20] of rock materials, including limestone. Akram et al. [21] reported a reverse relationship between mechanical properties and the percentages of sparite and allochems, and a direct relationship between the mechanical properties and the percentages of micrite and dolomite of limestone. Aligholi et al. [22] provided some relationship between the mechanical properties with the basic physical and dynamic characteristics of igneous rocks. Roy et al. [23] showed that the strength of sedimentary rocks decreased when the water content increased; consequently, the mechanical properties are strongly influenced by the percentage of water saturation. In addition, they estimated the rock fracture toughness using Young’s modulus and the Brazillian tensile strength. By investigating the effect of limestone texture on its mechanical behavior, Ajalloeian et al. [24] concluded that the best model for predicting Young’s modulus of carbonate rocks is multiple regression, by using some petrographic characteristics such as dolomitic percentage, the average grain size, and the percentage of allochems and carbonate. Zhixi et al. [25] reported a close relationship between K_IC and the physicomechanical properties of rock materials. According to Saeidi et al. [26], K_IC can be predicted using brittleness index. Some empirical relationships to predict K_IC from the index properties are outlined in Table 1.

Table 1. Some empirical relationships between K_IC and index properties.

In this study, the effect of the saturation condition on the fracture toughness of limestone has been investigated, considering the types of petrography. Moreover, because of the complexity of measuring fracture toughness, the index characteristics of the limestones studied were determined, and their correlations with fracture toughness were examined. As the determination of K_IC is one of the most destructive, time consuming, and costly tests, it is very useful to predict it using non-destructive and simple test methods, which is one of the main aims of this study.

2. Materials and Methods

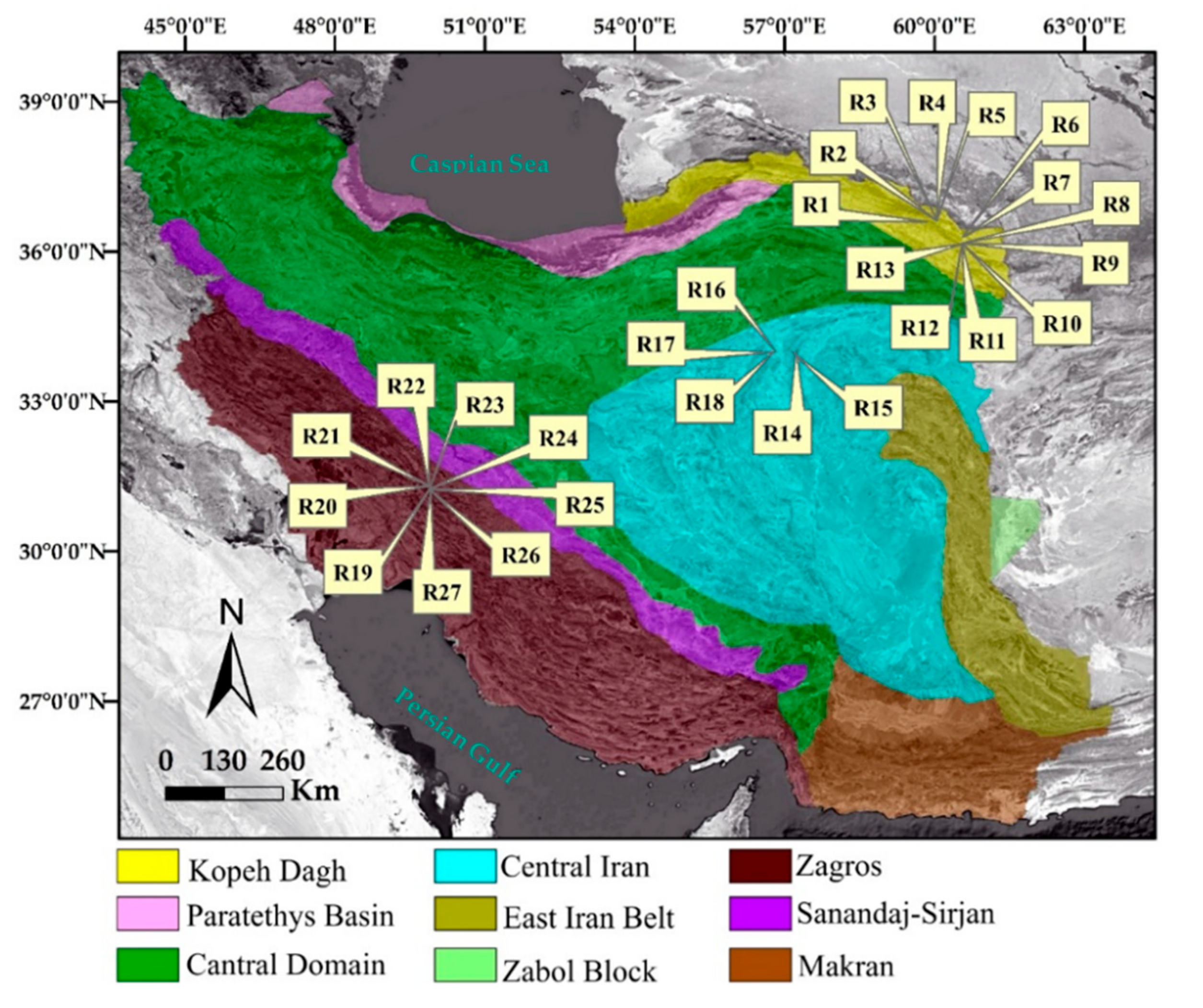
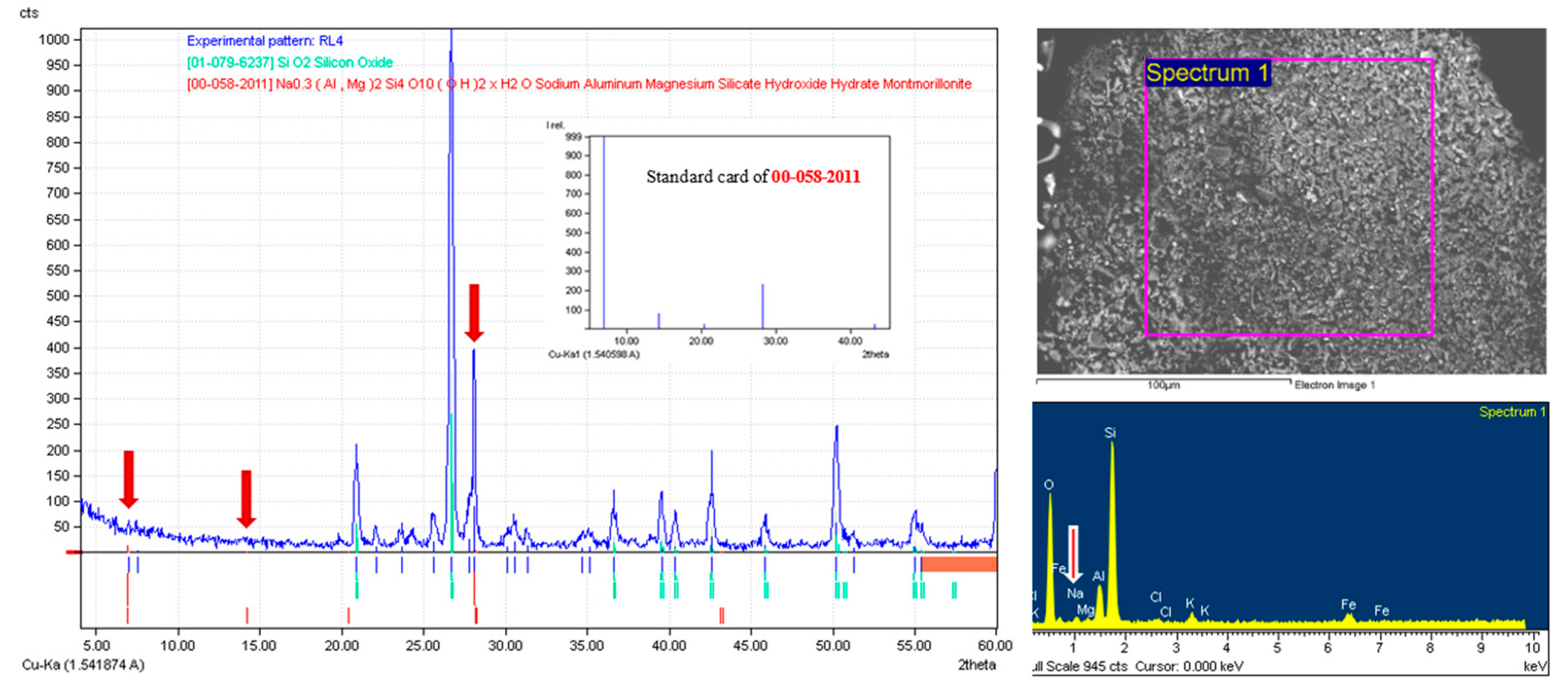
2.1. Materials

Thirty limestone blocks collected from different regions of Iran were studied (Figure 1). Some photomicrographs of the studied samples are represented in Figure 2. The locations, formation ages, and petrographic classification [31,32] of the studied limestones are summarized in Table 2. Among the studied formations, Asmari is the youngest, which belongs to the Oligo–Miocene era, while Jamal is the oldest formation with the age of early Gzhelian to Asselian.

Figure 1. Main sedimentary structural zones of Iran (modified from Aghanabati 2004 [33]) and the location of the studied rock samples.

Figure 2. Some photomicrographs of the studied samples: Packstone- R23 (A), Grainstone- R13 (B), Dolostone- R16 (C), and Dolo Mudstone- R28 (D).

Table 2. Age, sampling zone, and type of rocks.

2.2. Physicomechanical Tests

Different standard tests have been employed to determine the physical, mechanical, and dynamic properties of the studied limestones. Cylindrical cores with a diameter of 54 mm (NX) were extracted from limestone blocks for such a purpose. The physical properties, including the dry density and porosity, were determined according to the ISRM suggested method [34]. The electrical resistance was measured using a portable digital device (Figure 3A). In this method, the resistivity value was measured based on the following relationship between the electrical resistance and geometrical features of the sample, including the radius, length, and cross sectional area of the rock cores (Equation (1)).

R = ρ_{e} \frac{L}{A}

(1)

Figure 3. Simple test methods: electrical resistivity (A), vacuum saturation (B), ultrasonic wave velocity (C), and point load index (D).

The samples were fully saturated with water in a vacuum state for conducting tests under a saturated condition. Moreover, the specimens were placed in an oven at 105 °C for 24 h for conducting tests under a dry condition. Then, they were placed in a desiccator containing calcium silicate powder in a vacuum state for 3 h (Figure 3B). The ultrasonic wave velocity of the samples was determined using a portable digital device, as per the ISRM suggested method [35] (Figure 3C). The point load index was measured using a digital device, according to the ISRM suggested method [36] (Figure 3D). The point load experiments tests were carried out under both dry and saturated conditions on cylindrical cores axially with a length to diameter ratio of 0.3. The measured physical and mechanical properties of the studied rocks are presented in Table 3.

Table 3. Engineering characteristics of the studied rocks.

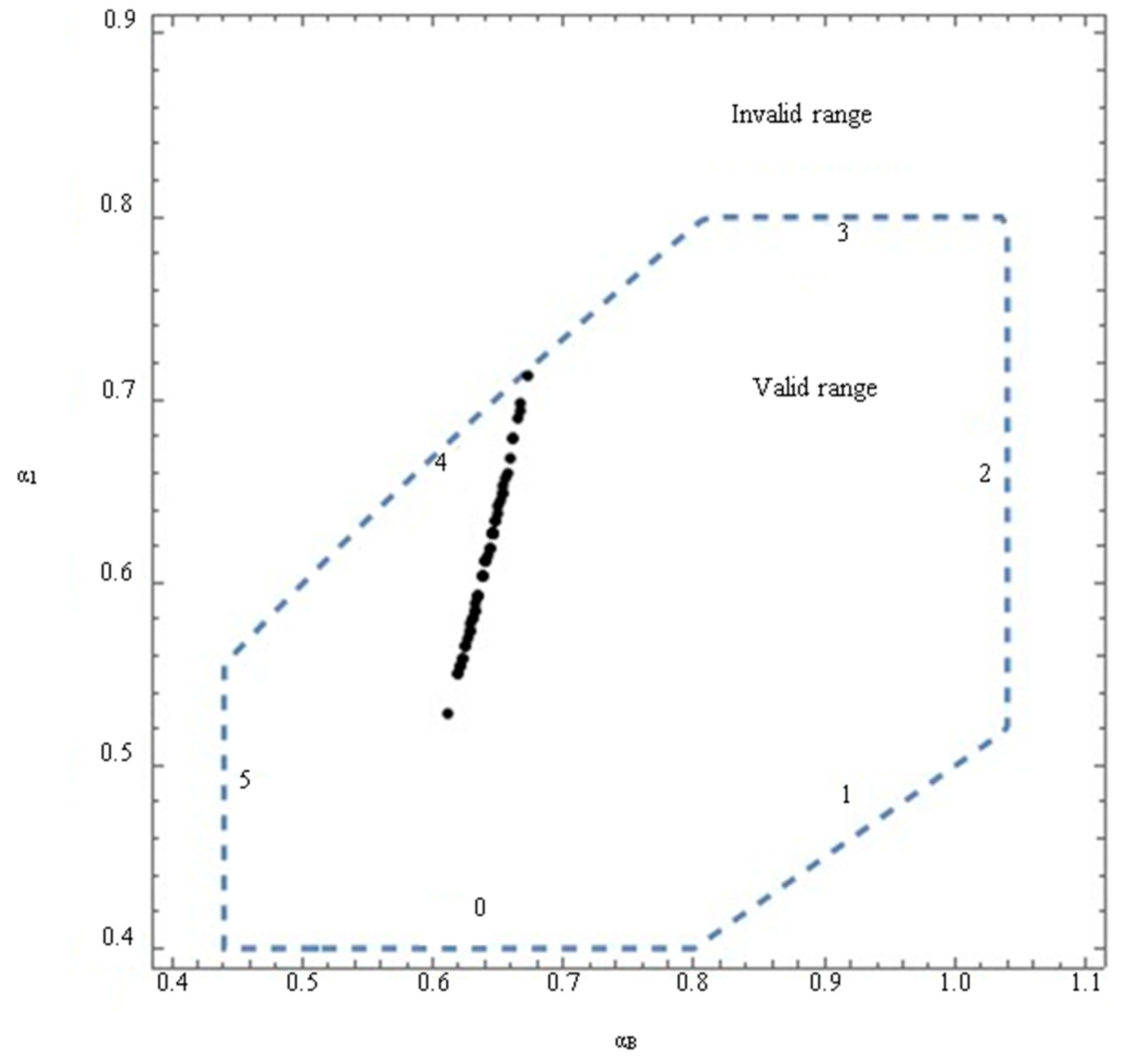
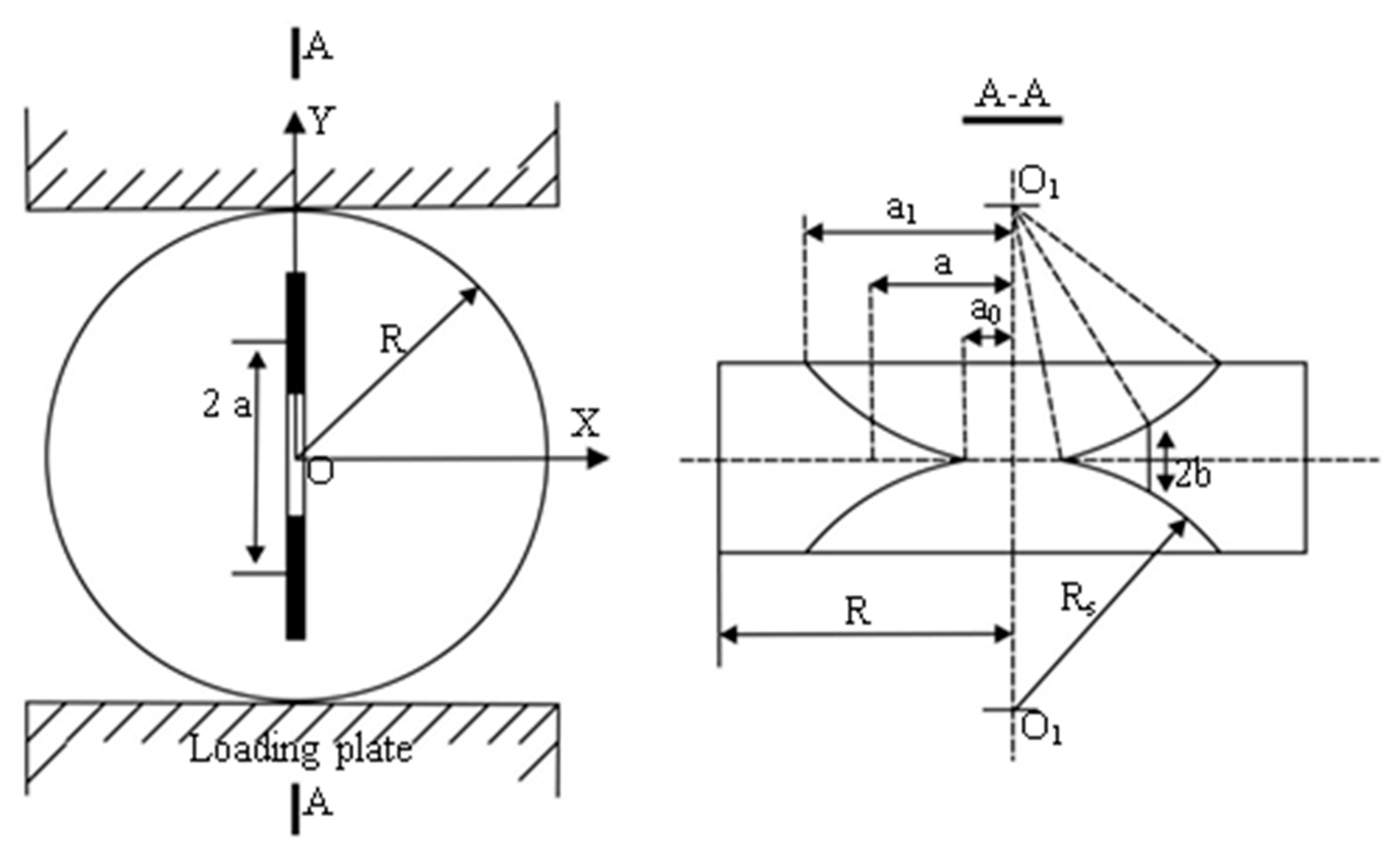
2.3. Mode I Fracture Toughness Tests

Several methods have been proposed to measure the K_IC of quasi-brittle materials [19,37,38,39,40,41,42,43]. In this study, CCNBD specimens were used. The K_IC of the studied specimens was determined under dry and saturated conditions according to the ISRM suggested method [35]. Based on this method, the results of the fracture toughness tests are acceptable for samples that are located in the valid range, according to Figure 4. To determine the position of the samples in the valid range, the geometric characteristics of the samples shown in Figure 5 and the following formulas (Equations (2) to (5)) were used. The valid ranges are the space enclosed by the graphs of Equations (6) to (11), as shown in Figure 4.

α_{0} = \frac{a_{0}}{R}

(2)

α_{1} = \frac{a_{1}}{R}

(3)

α_{B} = \frac{B}{R}

(4)

α_{s} = \frac{R_{s}}{R}

(5)

Line 0 \to α_{1} \geq 0.4

(6)

Line 1 \to α_{1} \geq \frac{α_{B}}{2}

(7)

Line 2 \to α_{B} \leq 1.04

(8)

Line 3 \to α_{1} \leq 0.8

(9)

Line 4 \to α_{B} \leq 1.1729 \times α_{1}^{1.6666}

(10)

Line 5 \to α_{B} \geq 0.44

(11)

Figure 4. Position of the samples in the valid geometrical range.

Figure 5. Geometry and loading condition of the CCNBD specimen [40].

The notch opening width of the specimens was less than 1 mm (Figure 6). The chevron notch crack cross-section under loading mode I are represented in Figure 6C,D before and after failure, respectively. For all of the samples, the parameters of

α_{0} = 0.2428

and R = 26.5 mm were constant. The value of αs was 0.7679. The values of α₁ and α_B were different, and were determined based on the position of each sample in the given valid range (Figure 5). The value of α1 is calculated using Equation (12).

α_{1} = \sqrt{α_{s}^{2} - {(\sqrt{α_{s}^{2} - α_{0}^{2}} - \frac{α_{B}}{2})}^{2}}

(12)

Figure 6. Wideness of the chevron crack (A), cross-section of the chevron notch (B), loading mode-I before failure (C), and loading mode-I after failure (D).

To determine K_IC, the methods presented by Atkinson et al. [44], Fowell [45], and Wang et al. [46] were used (Equations (13) and (14)). The resulting K_IC values are presented in Table 3. A_i is determined using Equations (15) to (19), and T_i is determined in terms of the a/R ratio in Atkinson’s proposed method.

K_{IC} = \frac{P_{Max}}{RB} \sqrt{\frac{α}{π}} \sqrt{\frac{α_{1} - α_{0}}{α - α_{0}}} N_{I}

(13)

N_{I} = \sum_{i = 1}^{n} T_{i} {(\frac{a}{R})}^{2 i - 2} A_{i} (θ)

(14)

A_{1} = 1 - 4 {Sin}^{2} θ

(15)

A_{2} = 8 {Sin}^{2} θ (1 - 4 {Cos}^{2} θ)

(16)

A_{3} = - 4 {Sin}^{2} θ (3 - 36 {Cos}^{2} θ + 48 {Cos}^{2} θ)

(17)

A_{4} = - 16 {Sin}^{2} θ (- 1 + 24 {Cos}^{2} θ - 80 {Cos}^{4} θ + 64 {Cos}^{6} θ)

(18)

A_{5} = - 20 {Sin}^{2} θ (1 - 4 {Cos}^{2} θ + 240 {Cos}^{4} θ - 448 {Cos}^{6} θ + 256 {Cos}^{8} θ)

(19)

The value of u and ν in equations provided by Fowell (Equations (20)–(21)) are determined using α₀ and α_S. Although the u and ν values are different in the Wang method, Equations (20)–(21) are similarly used [27,39,47].

K_{IC} = \frac{P_{Max}}{B \sqrt{D}} γ_{\min}^{*}

(20)

γ_{\min}^{*} = u \cdot e^{v \cdot α_{1}}

(21)

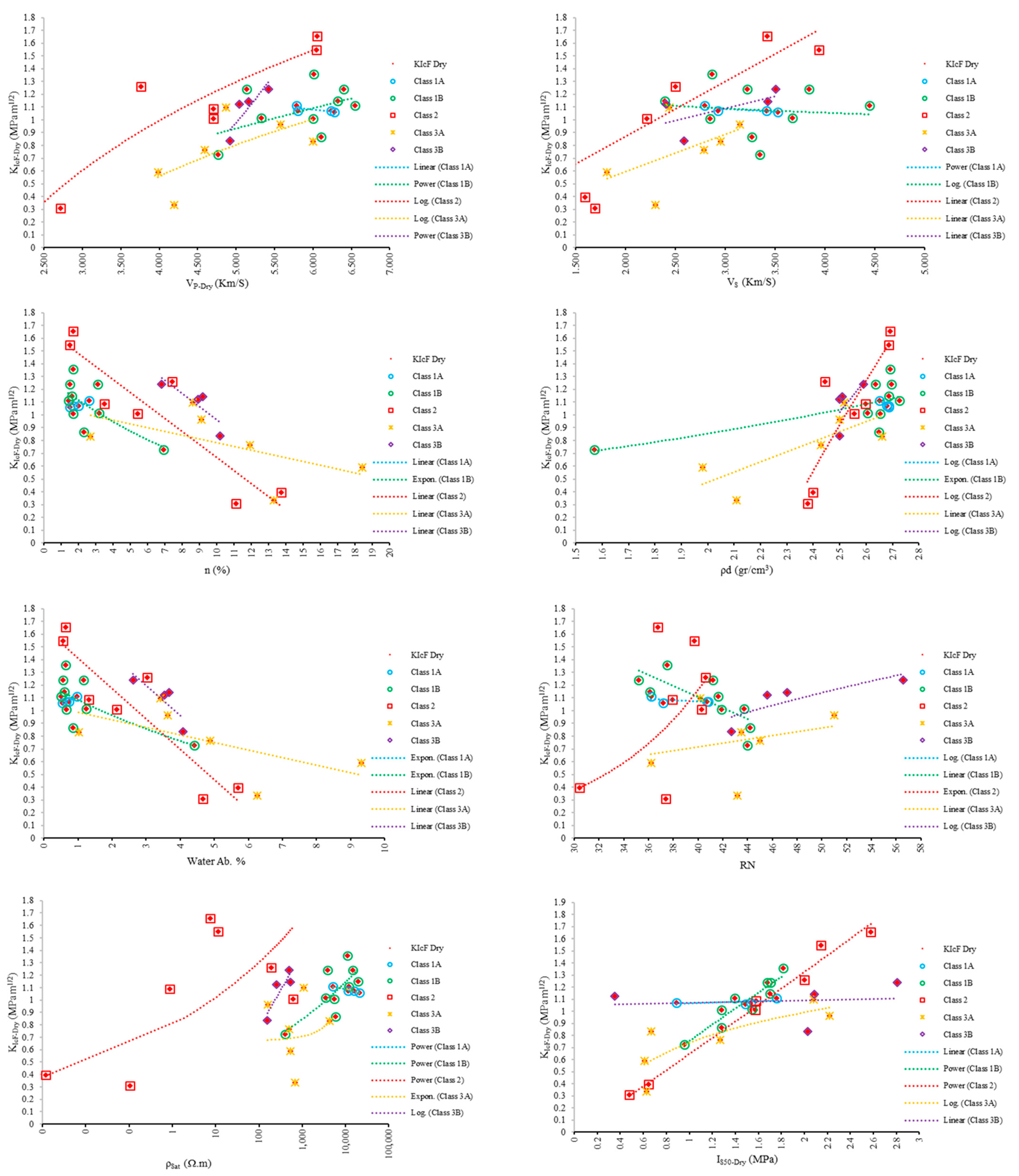
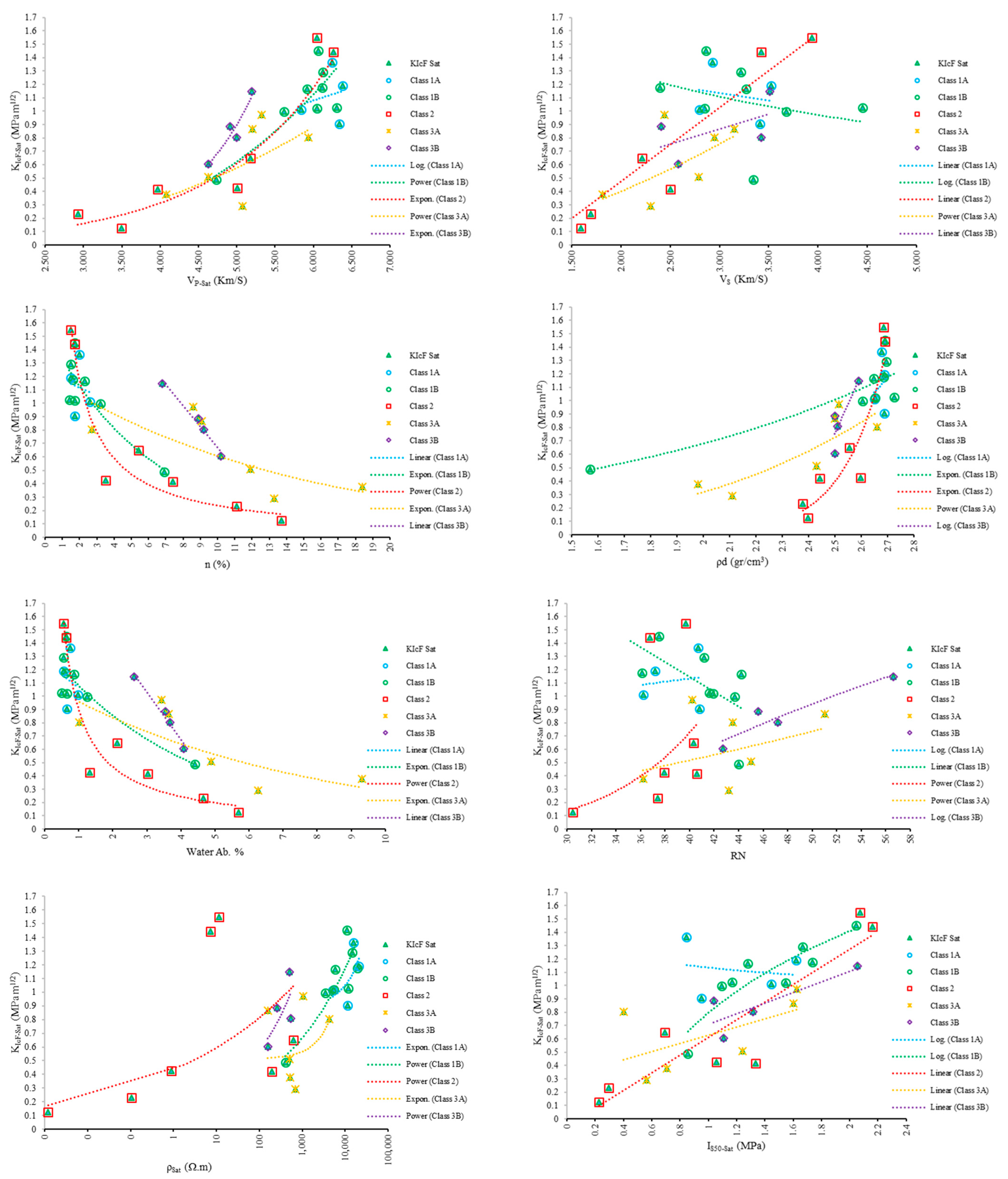
3. Results and Discussion

3.1. Analyzing the Behavior of Samples under Dry and Saturated States

After conducting the fracture toughness test on the selected limestones, it was observed that in most of the samples, including sandy limestones, dolomite limestones, floatstones, and mudstones, the fracture toughness was lower in the saturated state than in the dry condition. However, the toughness values of the wackeston, packstone, grainstone, and framestone samples did not show any dependency on the saturation state. To investigate this, factors such as the porosity, petrography of thin sections, and mineralagy of the samples were examined.

Samples R20 and R18 were two wackeston samples and both contained kaolinite. If the presence of this clay mineral had an effect on the toughness value in a saturated or dry state, we would have seen the same behavior in these samples as well, i.e., less fracture toughness under a saturation condition. Thus, it can be somehow concluded that the presence of kaolinite had no effect on the variations of toughness as a function of the saturation state. The porosity of the R20 and R18 samples was equal to 1.5 and 2.6, respectively. In general, it was observed that porosity was the most dominant factor affecting the variations of fracture toughness for wakestone, packstone, grainstone, and framestone, which did not show any particular trend considering the saturation state. In the samples with a porosity of more than 2.5%, the fracture toughness decreased under the saturated state, while the samples with a porosity less than 2.5% showed a higher fracture toughness under a saturated state.

Samples R15, R4, and R23 were placed in packston category in terms of petrography. According to the XRD and EDS analyses, the R15 sample contained the montmorillonite clay mineral (Figure 7). It is notable that, in this sample, the fracture toughness was higher under a saturated state. The porosity of the R15, R4, and R23 samples was 1.5, 2.3, and 6.9, respectively. Again, it was observed that, irrespective of mineralogy, porosity is the main factor controlling the fracture toughness as a function of the saturation state. In the studied packstone samples, if the porosity was higher than 2.5%, the fracture toughness was higher under a dry state, but if the porosity was less than 2.5%, the fracture toughness was higher under a saturated state.

Figure 7. Result of XRD and EDS experiments for R15.

Samples R14, R3, R6, and R13 were categorized as grainstone according to their petrography, and their porosity values were equal to 1.6, 1.7, 1.7, and 3.2 respectively. R14 contained broken particles (Figure 8), R3 contained glauconite clay mineral, and R6 contained both glauconite clay mineral and broken particles, as well as microcracks. All of these samples showed higher fracture toughness values under the saturated state, and the only common parameter in these samples was a lower porosity.

Figure 8. Thin section photomicrographs of some of the studied samples: R20 (A) and R14 (B).

Therefore, the presence of water-sensitive clay minerals in the samples of wackeston, packston, and grainstone had no effect on the variations of fracture toughness as a function of the saturation state, and the only factor affecting it was the porosity of the sample. It should also be mentioned that the R1, R2, and R10 rock samples contained glauconite; the R11, R29, and R30 rock samples contained montmorillonite; R18 contained kaolinite; and sample R9 contained palygorcite. According to our analyses, because of the high porosity values of these rock samples, which were more than 2.5%, their fracture toughness values were lower under a saturated state.

3.2. Normality Test of the Data

Normality of errors was considered by default, and because the dependent variables were associated with errors, data normality should be examined. Initially, the histograms, normal curves, and box diagrams for the dependent variable were plotted (Figure 9). Then, the skewness and kurtosis of the data were determined. Skewness represented symmetry or asymmetry of the data, and kurtosis indicate if the data have heavy/light tails in comparison with the normal distribution. In general, if the skewness and kurtosis were between −2 to 2, the data will have normal distribution. In addition, by using the box diagram, the scattered data were detected. In a usual plotting box diagram, if data have a significant difference compared with the rest, it are identified as scattered data and are treated in different ways. Generally, that data are deleted and replaced with the mean or the first or third quartile. Regarding the skewness and kurtosis values, dependent variables are normal.

Figure 9. Histograms and boxplots of the dependent variable.

3.3. Simple Regression

Linear/nonlinear simple regression with a 95% confidence level is used to determine the correlation between the fracture toughness and index properties. According to the results of the Pearson correlation, there is a high correlation among the K_IC calculated using the Atkinson et al. [44], Fowell [45], and Wang et al. [46] methods for the dry (Table 4) and saturated states (Table 5). Therefore, only the results of the Fowell method are used to determine the relationship between the K_IC and index properties.

Table 4. Correlation among K_IC determined from three different methods under a dry condition.

Table 5. Correlation among K_IC determined from three different methods under a saturated state.

Firstly, the correlation between the fracture toughness of the dry and saturated states with the index properties was investigated for all of the samples. The simple linear regression showed poor results. This is because limestone has a wide range of textural and petrological features. Therefore, according to the textural diversity of limestone, petrographic studies of the samples were conducted using optical microscopy and the samples were classified in five classes accordingly (Table 6). Mud supported limestones were placed in class 1A, grain supported samples were categorized as class 1B, sandy limestones were placed in class 2, coarse crystal dolomite limestones were placed in class 3A, and microcrystalline dolomite limestones were placed in class 3B.

Table 6. Rock classes based on petrographic study.

By applying this classification, more meaningful correlations were obtained between the fracture toughness and physical characteristics of the studied limestones (Table 7). The relationship between the K_IC and index properties for each class were determined under dry (Figure 10) and saturated conditions (Figure 11). The best relationship was determined for each class as well as for all of the rock samples based on simple linear/nonlinear regression analyses (Table 8). Classification of the samples according to petrographic studies showed acceptable relationships obtained from simple linear/nonlinear regression. Fracture toughness is generally inversely related to porosity and water absorption percentage, and is directly related to the ultrasonic wave velocity, density, and point load index. It is clear from Table 8 that by applying petrographic classification to the data, better correlations between fracture toughness and index properties were obtained.

Table 7. Linear correlation between the index properties and dry and saturated fracture toughness for all of the limestones and individual classes.

Figure 10. K_IC versus different engineering properties for each petrographic class under a dry state.

Figure 11. K_IC versus different engineering properties for each petrographic class under a saturated state.

Table 8. Statistical parameters of the simple linear/nonlinear regression between K_IC and the index properties.

3.4. Multiple Linear Regression

Multiple linear regression examines the simultaneous effect of several independent variables on a dependent variable. Various combinations of rock index properties were used to predict the K_IC of the studied rocks. In addition, for verifying the accuracy of the results, statistical accuracy controllers, including root mean squared error (RMSE), VIF, R², R² Adjust, and p-Value, were used. Initially, the p-value index was used to control the overall validity of the proposed models. A proposed model was considered to be statistically correct if its p-value was less than 0.05. The closer to zero, the more efficient the model. Then, the validity of each of the dependent variables was determined using the VIF criterion and the p-value. The value of the VIF criterion for each variable used in the model should be less than 10. The closer the RMSE indicator is to zero, the more functional the model. The most reliable models according to the statistical controllers are presented in Table 9. From this table, it can be clearly seen that by taking into account the petrographic characteristics of the studied limestones, their fracture toughness can be successfully estimated by means of their index properties.

Table 9. Statistical parameters of the multiple linear regression between the K_IC and index properties.

4. Conclusions

In this study, the effect of the petrogeraphical, mineralogical, and physical properties of different limestones on fracture toughness is investigated under both dry and saturated conditions. Some statistical relationships are stablished to determine the correlation between fracture toughness and these properties, which can be determined using simple methods. The main conclusions of the conducted statistical analyses are listed as follows:

The fracture toughness of the studied limestones decreased under a saturated state, except for the samples that were be categorized as wacketon, packstone, grainstone, and framestone, which indicates a complex behavior. In these limestone classes, porosity is the main factor affecting the ratio of dry to saturated fracture toughness. In the samples with a porosity of less than 2.5%, fracture toughness is higher under saturated condition, while in samples with a porosity more than 2.5%, fracture toughness is higher under dry condition.
No meaningful relationship between clay content with the ratio of saturated to dry fracture toughness is found.
The value of K_IC calculated from the different methods proposed by Atkinson, Fowell, and Wang were similar and showed perfect correlations.
K_ICsat and K_ICdry of the limestone could be predicted with a high accuracy from index tests if careful classification based on their petrography was utilized.

Author Contributions

Conceptualization, S.S.F. and G.R.L.; data curation, S.S.F.; formal analysis, S.S.F. and S.A.; funding acquisition, M.M.S.S.; investigation, S.S.F., S.A. and G.R.L.; methodology, S.S.F. and G.R.L.; project administration, G.R.L. and N.H.M.; resources, G.R.L. and N.H.M.; software, S.S.F. and M.M.S.S.; supervision, G.R.L. and N.H.M.; validation, S.S.F., S.A. and M.M.S.S.; visualization, S.S.F.; writing—original draft, S.S.F. and G.R.L.; writing—review and editing, G.R.L., N.H.M., S.A. and M.M.S.S. All authors have read and agreed to the published version of the manuscript.

Funding

The research is partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program “Priority 2030” (Agreement 075-15-2021-1333 dated 30 September 2021).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Data can be accessed by contacting the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

$a_{0}$	Half initial crack length	$α_{0}$	Normalized initial crack length
$a_{1}$	Half final crack length	$α_{1}$	Normalized final crack length
B	Specimen thickness	$α_{B}$	Normalized specimen thickness
R_S	Saw radius	$α_{S}$	Normalized saw diameter
$a_{}$	Half crack length	$α$	Normalized crack length
R	Specimen radius	D	Specimen diameter
P_M_ax	Maximum load	N_I	Auxiliary variable
$γ_{\min}^{*}$	Minimum normalized stress intensity factor	K_IC	Mode I fracture toughness
CCNBD	Cracked chevron notched Brazilian disc	L	Specimen length
ISRM	International Society for Rock Mechanics	ρSat	Electrical resistivity
A	Cross section area	n	Porosity
ρ	Dry density	V_P	P-Wave velocity
W.A.	Water Absorption	V_S	S-Wave velocity
V_P-Dry	P-Wave velocity under dry state	RN	Schmidt rebound number
V_P-Sat	P-Wave velocity under saturated state	R²	Correlation coefficient
XRD	X-ray diffraction	VIF	Variance inflation factor
EDS	Energy dispersive spectroscopy
RMSE	Root mean square error
R² Adjust	Adjusted correlation coefficient
p-Value	Probability value
I_S50-Dry	Point load strength index under a dry state
I_S50-Sat	Point load strength index under a saturated state
K_ICF-Dry	Mode I fracture toughness calculated using the Fowell method under a dry state
K_ICF-Sat	Mode I fracture toughness calculated using the Fowell method under a saturated state
K_ICW-Dry	Mode I fracture toughness calculated using the Wang method under a dry state
K_ICW-Sat	Mode I fracture toughness calculated using the Wang method under a saturated state
K_IC-Dry	Mode I fracture toughness calculated using the Atkinson method under a dry state
K_IC-Sat	Mode I fracture toughness calculated using the Atkinson method under a saturated state

References

Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 3rd ed.; CRC press: Boca Raton, FL, USA, 2005. [Google Scholar]
Çobanoğlu, İ.; Çelik, S.B. Estimation of uniaxial compressive strength from point load strength, Schmidt hardness and P-wave velocity. Bull. Eng. Geol. Environ. 2008, 67, 491–498. [Google Scholar] [CrossRef]
Karakul, H. Investigation of saturation effect on the relationship between compressive strength and Schmidt hammer rebound. Bull. Eng. Geol. Environ. 2017, 76, 1143–1152. [Google Scholar] [CrossRef]
Kılıç, A.; Teymen, A. Determination of mechanical properties of rocks using simple methods. Bull. Eng. Geol. Environ. 2008, 67, 237. [Google Scholar] [CrossRef]
Mousavi, E.; Cheshomi, A.; Ashtari, M. Estimating elasticity modulus and uniaxial compressive strength of sandstone using indentation test. J. Pet. Sci. Eng. 2018, 169, 157–166. [Google Scholar] [CrossRef]
Shalabi, F.I.; Cording, E.J.; Al-Hattamleh, O.H. Estimation of rock engineering properties using hardness tests. Eng. Geol. 2007, 90, 138–147. [Google Scholar] [CrossRef]
Vasanelli, E.; Colangiuli, D.; Calia, A.; Sileo, M.; Aiello, M.A. Ultrasonic pulse velocity for the evaluation of physical and mechanical properties of a highly porous building limestone. Ultrasonics 2015, 60, 33–40. [Google Scholar] [CrossRef]
Tang, S. The effects of water on the strength of black sandstone in a brittle regime. Eng. Geol. 2018, 239, 167–178. [Google Scholar] [CrossRef]
Ng, I.-T.; Yuen, K.-V.; Lau, C.-H. Predictive model for uniaxial compressive strength for Grade III granitic rocks from Macao. Eng. Geol. 2015, 199, 28–37. [Google Scholar] [CrossRef]
Yao, Q.; Chen, T.; Tang, C.; Sedighi, M.; Wang, S.; Huang, Q. Influence of moisture on crack propagation in coal and its failure modes. Eng. Geol. 2019, 258, 105156. [Google Scholar] [CrossRef]
Aligholi, S.; Lashkaripour, G.R.; Ghafoori, M. Estimating engineering properties of igneous rocks using semi-automatic petrographic analysis. Bull. Eng. Geol. Environ. 2019, 78, 2299–2314. [Google Scholar] [CrossRef]
Jamei, M.; Mohammed, A.S.; Ahmadianfar, I.; Sabri, M.M.S.; Karbasi, M.; Hasanipanah, M. Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model. Appl. Sci. 2022, 12, 7101. [Google Scholar] [CrossRef]
Huang, J.; Zhou, M.; Yuan, H.; Sabri, M.M.S.; Li, X. Prediction of the Compressive Strength for Cement-Based Materials with Metakaolin Based on the Hybrid Machine Learning Method. Materials 2022, 15, 3500. [Google Scholar] [CrossRef]
Aligholi, S.; Lashkaripour, G.R.; Ghafoori, M.; Azali, S.T. Evaluating the Relationships Between NTNU/SINTEF Drillability Indices with Index Properties and Petrographic Data of Hard Igneous Rocks. Rock Mech. Rock Eng. 2017, 50, 2929–2953. [Google Scholar] [CrossRef]
Hua, W.; Dong, S.; Fan, Y.; Pan, X.; Wang, Q. Investigation on the correlation of mode II fracture toughness of sandstone with tensile strength. Eng. Fract. Mech. 2017, 184, 249–258. [Google Scholar] [CrossRef]
Bao, H.; Wu, F.; Niu, J. Effects of test procedures and lithology on estimating the mode I fracture toughness of rocks using empirical relations: Einfluss der Prüfverfahren und der Lithologie auf die Bestimmung der Mode I-Bruchzähigkeit von Steinen mittels empirischer Beziehungen. Mater. Und Werkst. 2018, 49, 951–962. [Google Scholar] [CrossRef]
Zhou, Z.; Cai, X.; Ma, D.; Cao, W.; Chen, L.; Zhou, J. Effects of water content on fracture and mechanical behavior of sandstone with a low clay mineral content. Eng. Fract. Mech. 2018, 193, 47–65. [Google Scholar] [CrossRef]
Wang, J.-J.; Zhu, J.-G.; Chiu, C.; Zhang, H. Experimental study on fracture toughness and tensile strength of a clay. Eng. Geol. 2007, 94, 65–75. [Google Scholar] [CrossRef]
Aligholi, S.; Ponson, L.; Torabi, A.R.; Zhang, Q.B. A new methodology inspired from the Theory of Critical Distances for determination of inherent tensile strength and fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2022, 152, 105073. [Google Scholar] [CrossRef]
Jia, B.; Xian, C.-G. Permeability measurement of the fracture-matrix system with 3D embedded discrete fracture model. Pet. Sci. 2022. [Google Scholar] [CrossRef]
Akram, M.; Farooq, S.; Naeem, M.; Ghazi, S. Prediction of mechanical behaviour from mineralogical composition of Sakesar limestone, Central Salt Range, Pakistan. Bull. Eng. Geol. Environ. 2017, 76, 601–615. [Google Scholar] [CrossRef]
Aligholi, S.; Lashkaripour, G.R.; Ghafoori, M. Strength/brittleness classification of igneous intact rocks based on basic physical and dynamic properties. Rock Mech. Rock Eng. 2017, 50, 45–65. [Google Scholar] [CrossRef]
Roy, D.G.; Singh, T.; Kodikara, J.; Das, R. Effect of water saturation on the fracture and mechanical properties of sedimentary rocks. Rock Mech. Rock Eng. 2017, 50, 2585–2600. [Google Scholar]
Ajalloeian, R.; Mansouri, H.; Baradaran, E. Some carbonate rock texture effects on mechanical behavior, based on Koohrang tunnel data, Iran. Bull. Eng. Geol. Environ. 2017, 76, 295–307. [Google Scholar] [CrossRef]
Zhixi, C.; Mian, C.; Yan, J.; Rongzun, H. Determination of rock fracture toughness and its relationship with acoustic velocity. Int. J. Rock Mech. Min. Sci. 1997, 34, 49.e1–49.e11. [Google Scholar] [CrossRef]
Saeidi, O.; Torabi, S.R.; Ataei, M.; Hoseinie, S. Prediction of rock fracture toughness modes I and II utilising brittleness indexes. Int. J. Min. Mineral. Eng. 2012, 4, 163–173. [Google Scholar] [CrossRef]
Chang, S.-H.; Lee, C.-I.; Jeon, S. Measurement of rock fracture toughness under modes I and II and mixed-mode conditions by using disc-type specimens. Eng. Geol. 2002, 66, 79–97. [Google Scholar] [CrossRef]
Brown, G.; Reddish, D. Experimental relations between rock fracture toughness and density. Int. J. Rock Mech. Min. Sci. 1997, 34, 153–155. [Google Scholar] [CrossRef]
Roy, D.G.; Singh, T.; Kodikara, J.; Talukdar, M. Correlating the mechanical and physical properties with Mode-I fracture toughness of rocks. Rock Mech. Rock Eng. 2017, 50, 1941–1946. [Google Scholar]
Gunsallus, K.t.; Kulhawy, F. A comparative evaluation of rock strength measures. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1984, 21, 233–248. [Google Scholar] [CrossRef]
Dunham, R.J. Classification of carbonate rocks according to depositional textures. AAPG Bull. 1962, 308, 108–121. [Google Scholar]
Embry, A.F.; Klovan, J.E. A late Devonian reef tract on northeastern Banks Island, N. W.T. Bull. Can. Pet. Geol. 1971, 19, 730–781. [Google Scholar]
Aghanabati, A. Geology of Iran; Geological Survey of Iran: Tehran, Iran, 2004. [Google Scholar]
ISRM. Rock Characterization, Testing and Monitoring; Pergamon press: Oxford, UK, 1981. [Google Scholar]
ISRM. The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974–2006. Suggested Methods Prepared by the Commission on Testing Methods; Ulusay, R., Hudson, J.A., Eds.; International Soc. for Rock Mechanics, Commission on Testing Methods: Ankara, Turkey, 2007. [Google Scholar]
ISRM. Suggested method for determining point load strength. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 35, 51–60. [Google Scholar]
Chong, K.; Kuruppu, M. New specimen for fracture toughness determination for rock and other materials. Int. J. Fract. 1984, 26, R59–R62. [Google Scholar] [CrossRef]
Guo, H.; Aziz, N.; Schmidt, L. Rock fracture-toughness determination by the Brazilian test. Eng. Geol. 1993, 33, 177–188. [Google Scholar] [CrossRef]
Sheity, D.K.; Rosenfield, A.R.; Duckworth, W.H. Fracture toughness of ceramics measured by a chevron-notch diametral-compression test. J. Am. Ceram. Soc. 1985, 68, C-325–C-327. [Google Scholar] [CrossRef]
Szendi-Horvath, G. Fracture toughness determination of brittle materials using small to extremely small specimens. Eng. Fract. Mech. 1980, 13, 955–961. [Google Scholar] [CrossRef]
Wang, Q.-Z.; Xing, L. Determination of fracture toughness KIC by using the flattened Brazilian disk specimen for rocks. Eng. Fract. Mech. 1999, 64, 193–201. [Google Scholar] [CrossRef]
Awaji, H.; Sato, S. Combined mode fracture toughness measurement by the disk test. J. Eng. Mater. Technol. 1978, 100, 175–182. [Google Scholar] [CrossRef]
Kuruppu, M.D.; Obara, Y.; Ayatollahi, M.R.; Chong, K.P.; Funatsu, T. ISRM-Suggested Method for Determining the Mode I Static Fracture Toughness Using Semi-Circular Bend Specimen. Rock Mech. Rock Eng. 2014, 47, 267–274. [Google Scholar] [CrossRef]
Atkinson, C.; Smelser, R.; Sanchez, J. Combined mode fracture via the cracked Brazilian disk test. Int. J. Fract. 1982, 18, 279–291. [Google Scholar] [CrossRef]
Fowell, R.; Hudson, J.; Xu, C.; Zhao, X. Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 322A. [Google Scholar] [CrossRef]
Wang, Q.; Fan, H.; Gou, X.; Zhang, S. Recalibration and clarification of the formula applied to the ISRM-suggested CCNBD specimens for testing rock fracture toughness. Rock Mech. Rock Eng. 2013, 46, 303–313. [Google Scholar] [CrossRef]
Amrollahi, H.; Baghbanan, A.; Hashemolhosseini, H. Measuring fracture toughness of crystalline marbles under modes I and II and mixed mode I–II loading conditions using CCNBD and HCCD specimens. Int. J. Rock Mech. Min. Sci. 2011, 48, 1123–1134. [Google Scholar] [CrossRef]