Tight Maneuvering for Path Planning of Hyper-Redundant Manipulators in Three-Dimensional Environments
Abstract
:1. Introduction
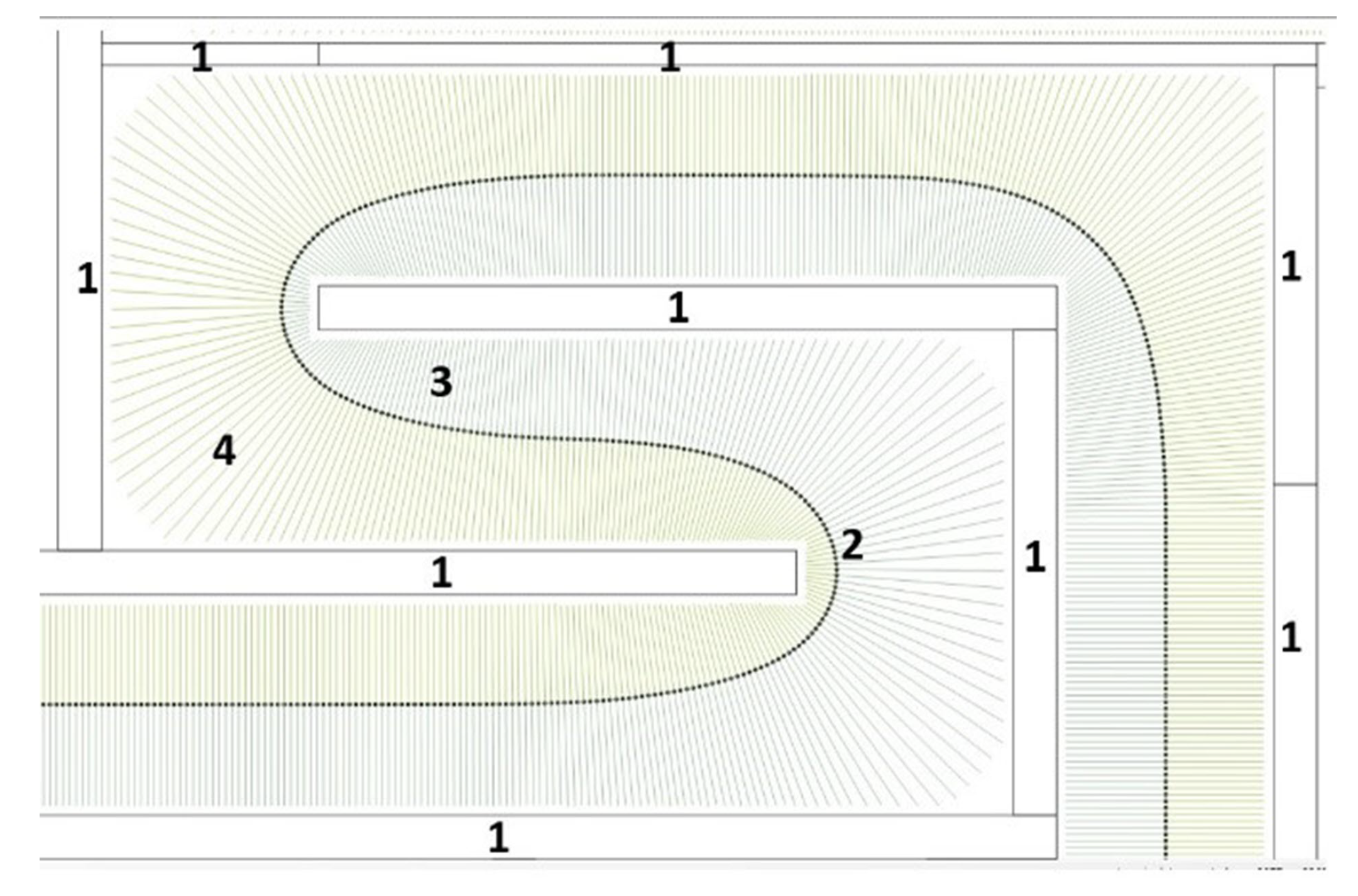
2. Potential Fields: Generating the Global Middle Path
3. Benchmark Environment
4. The Algorithm
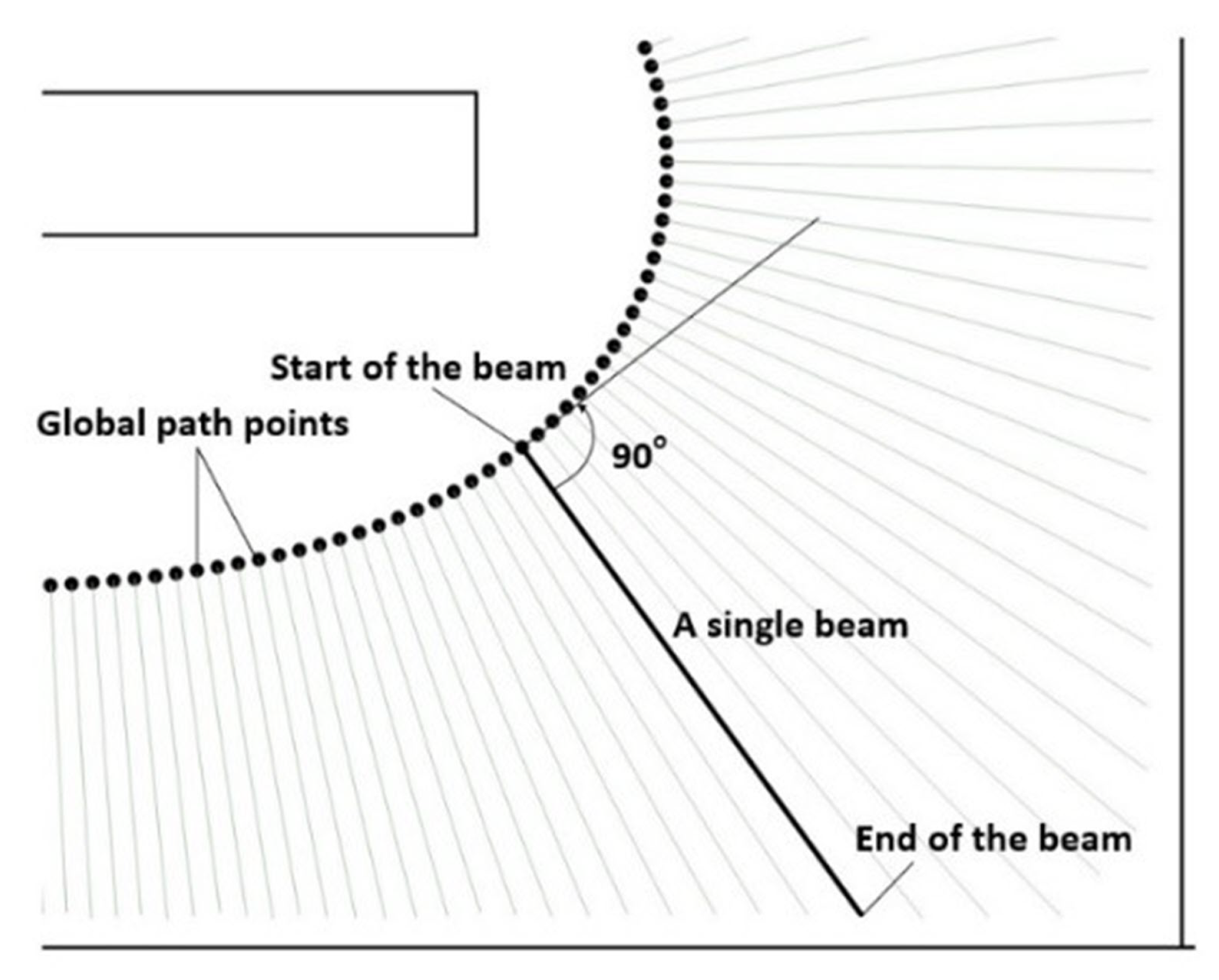
4.1. Obtaining the Global Middle Path and the Beams
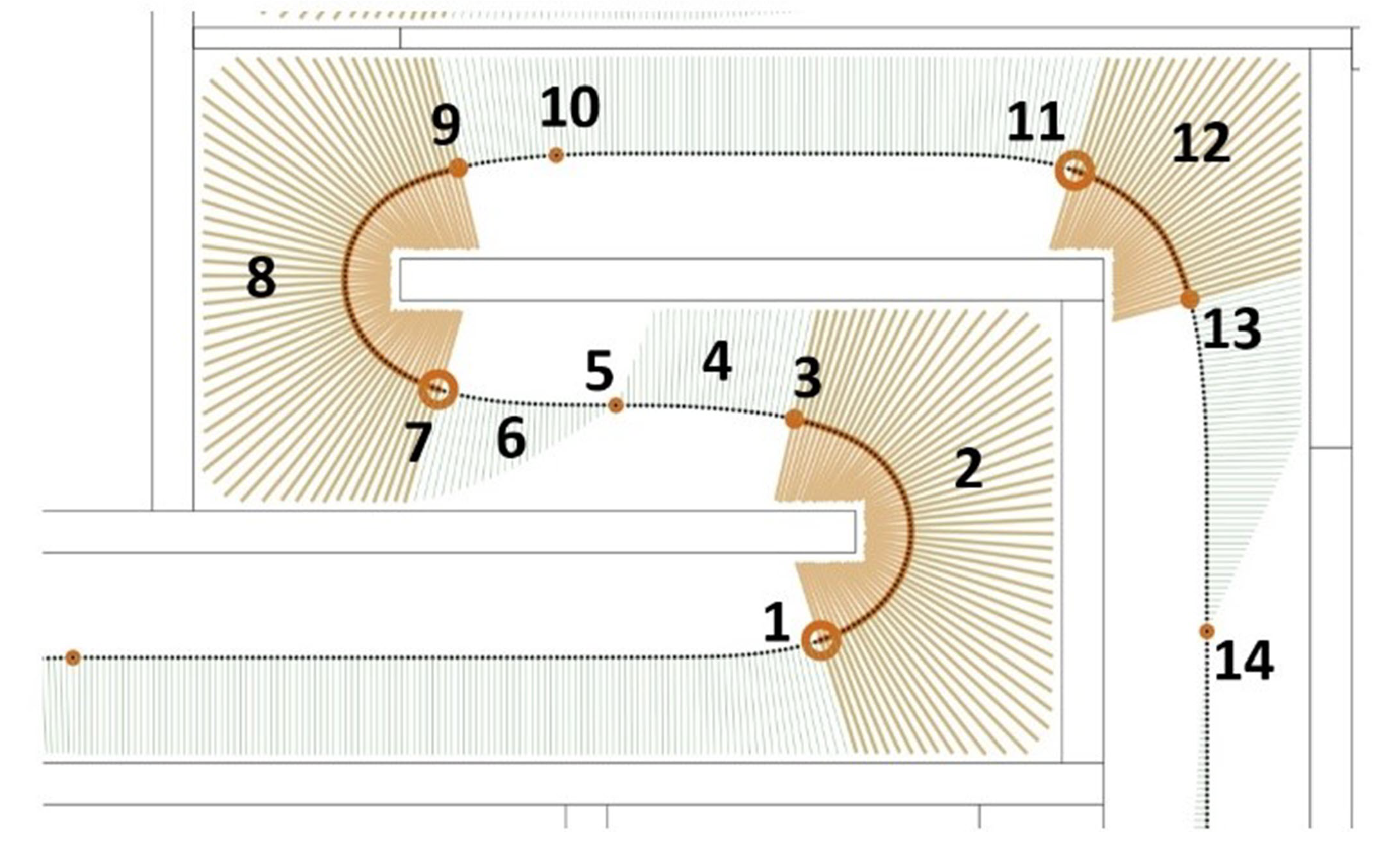
4.2. Determining Critical Regions
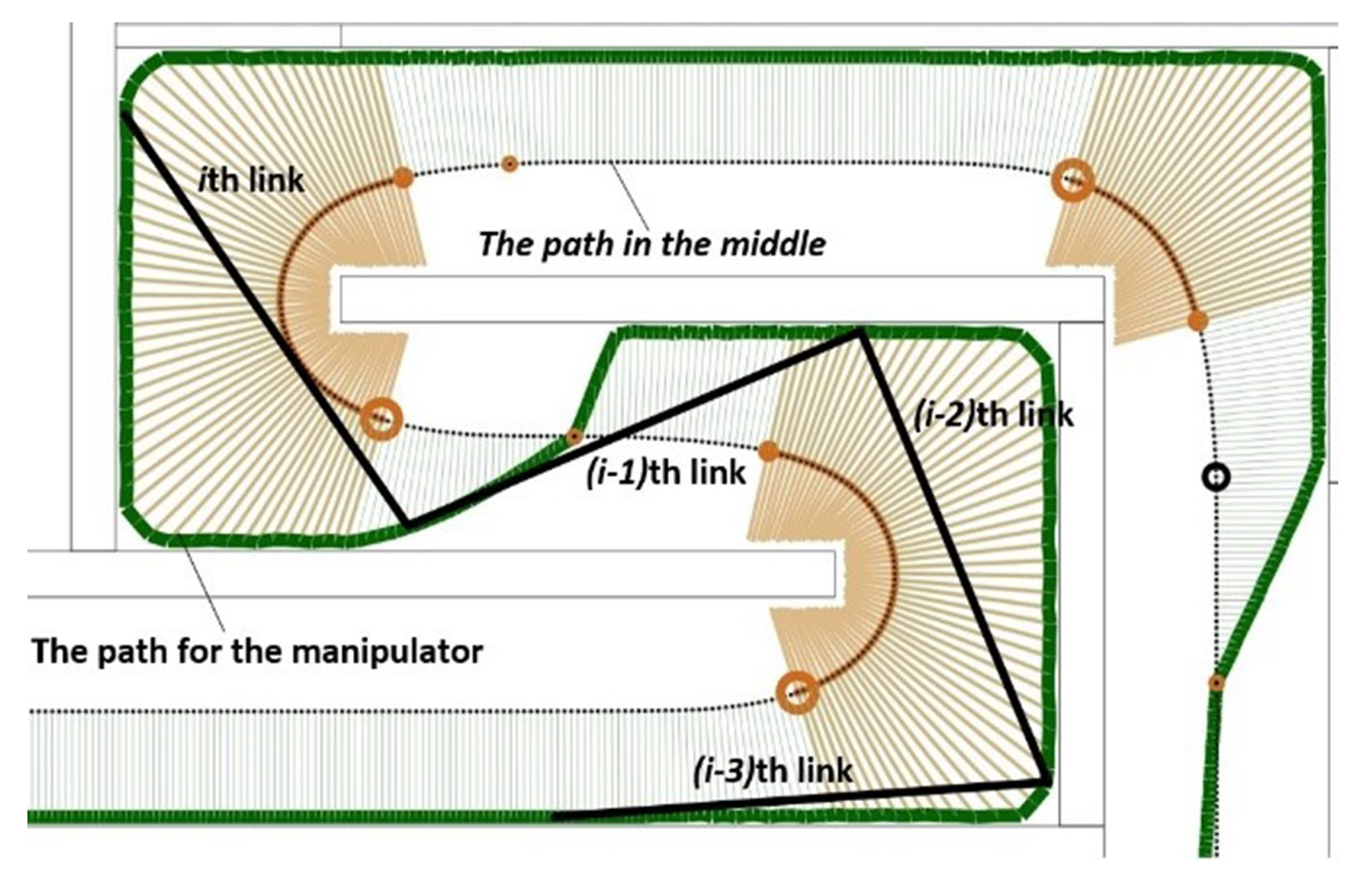
4.3. Determining the Path for the Manipulator
4.4. Control Strategy
4.5. Beams in 3D
4.6. Determining Critical Areas and Switching Directions
4.7. Determining Beam Couple Switching Points and the Manipulator Path
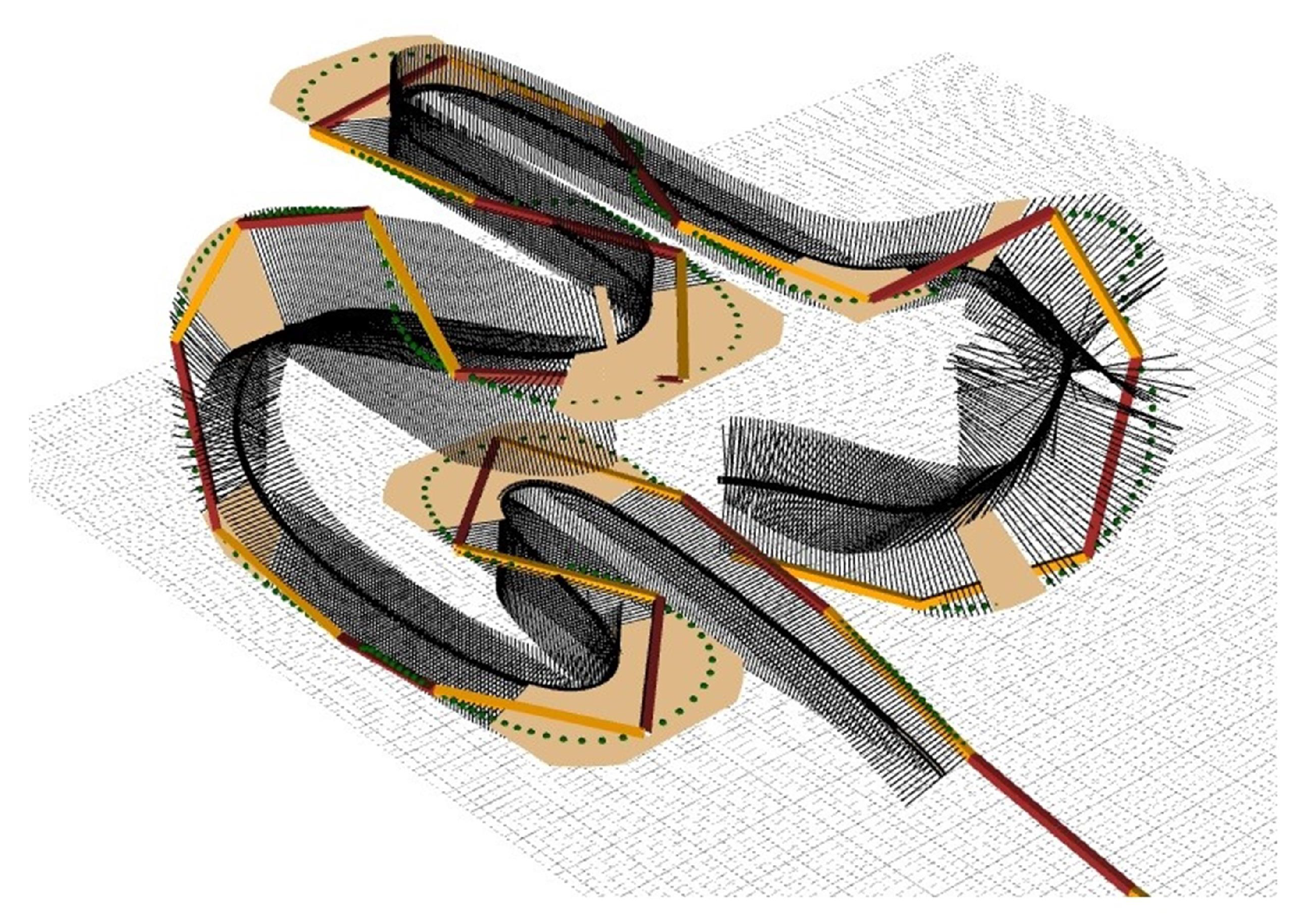
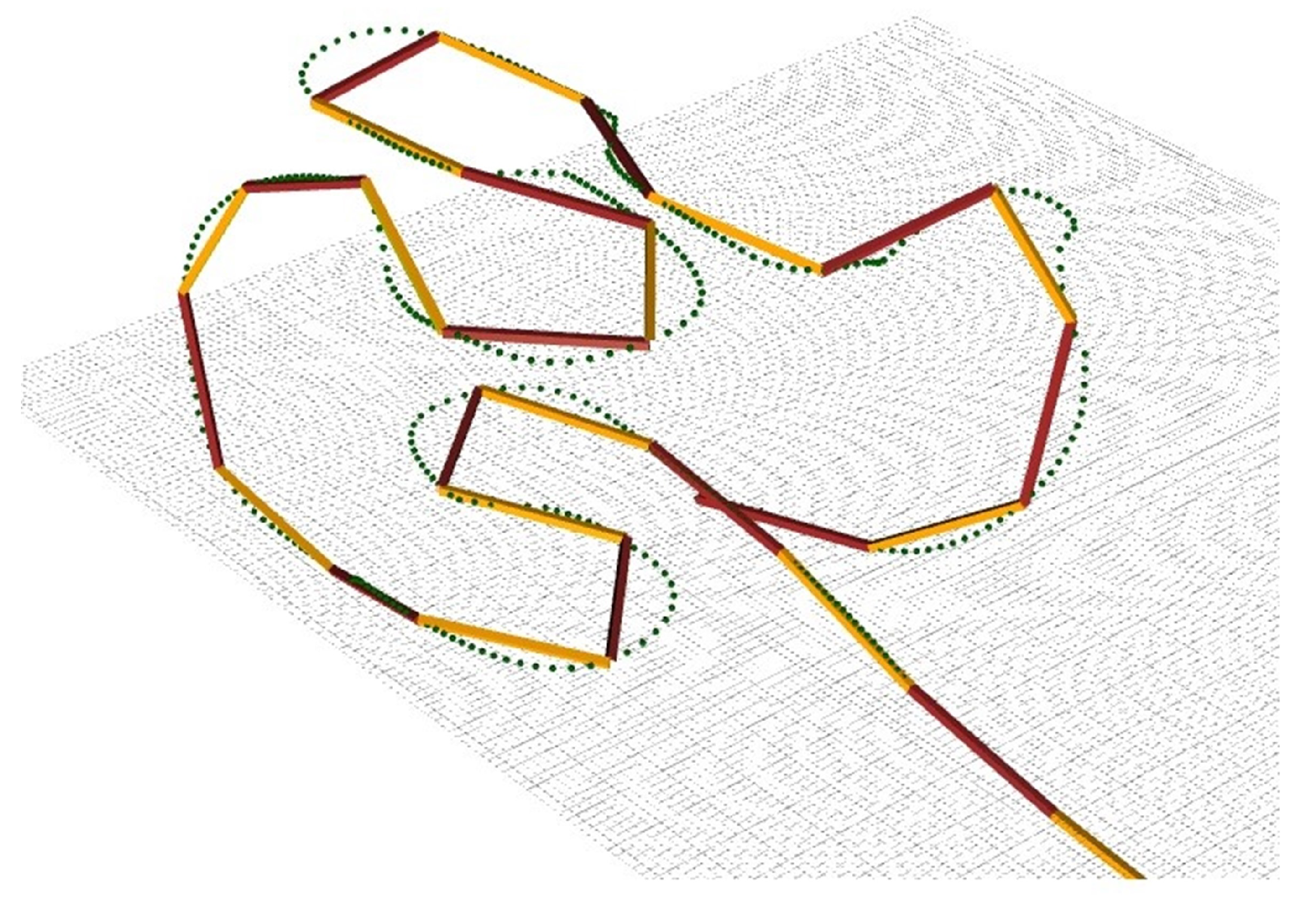
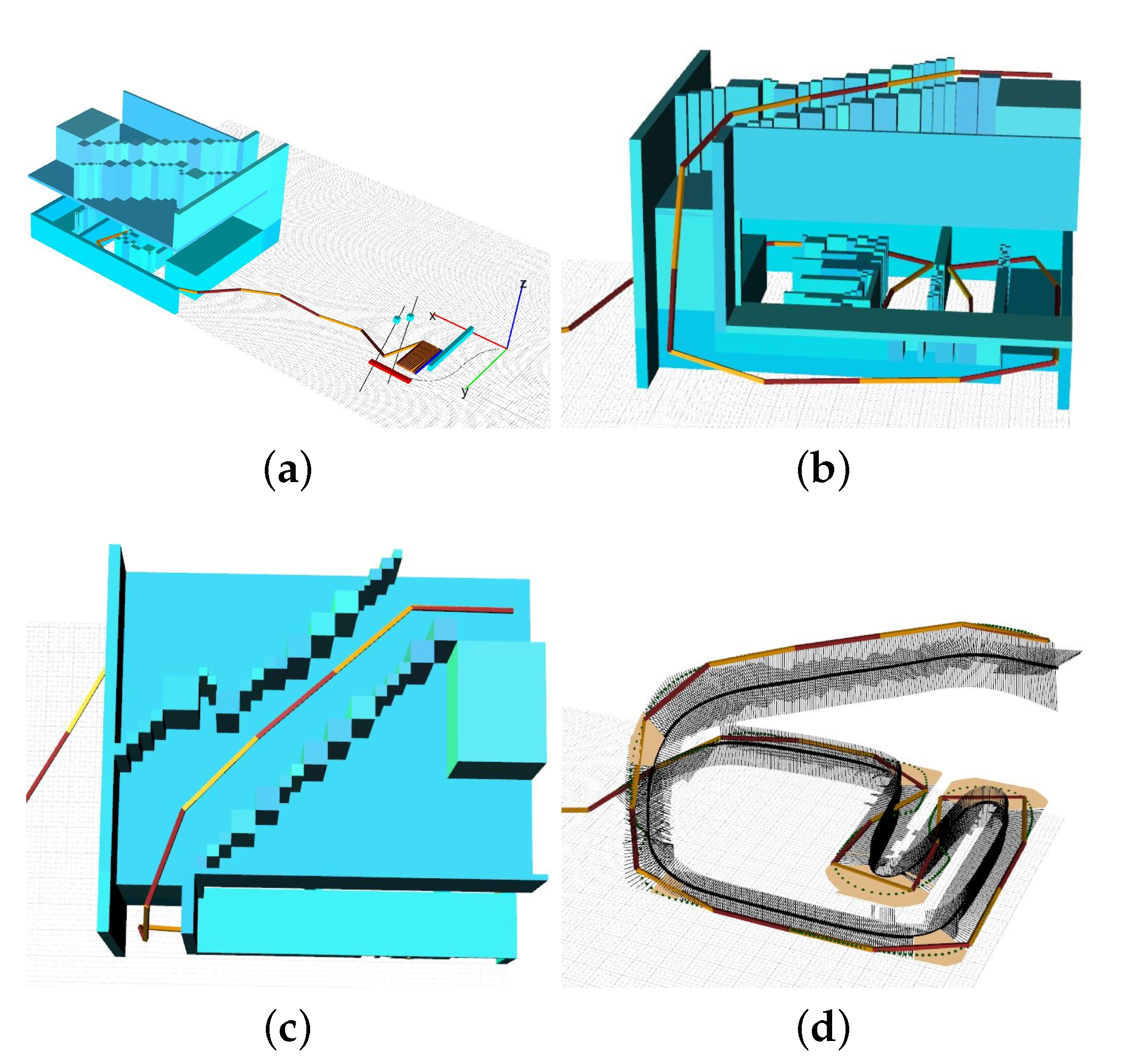
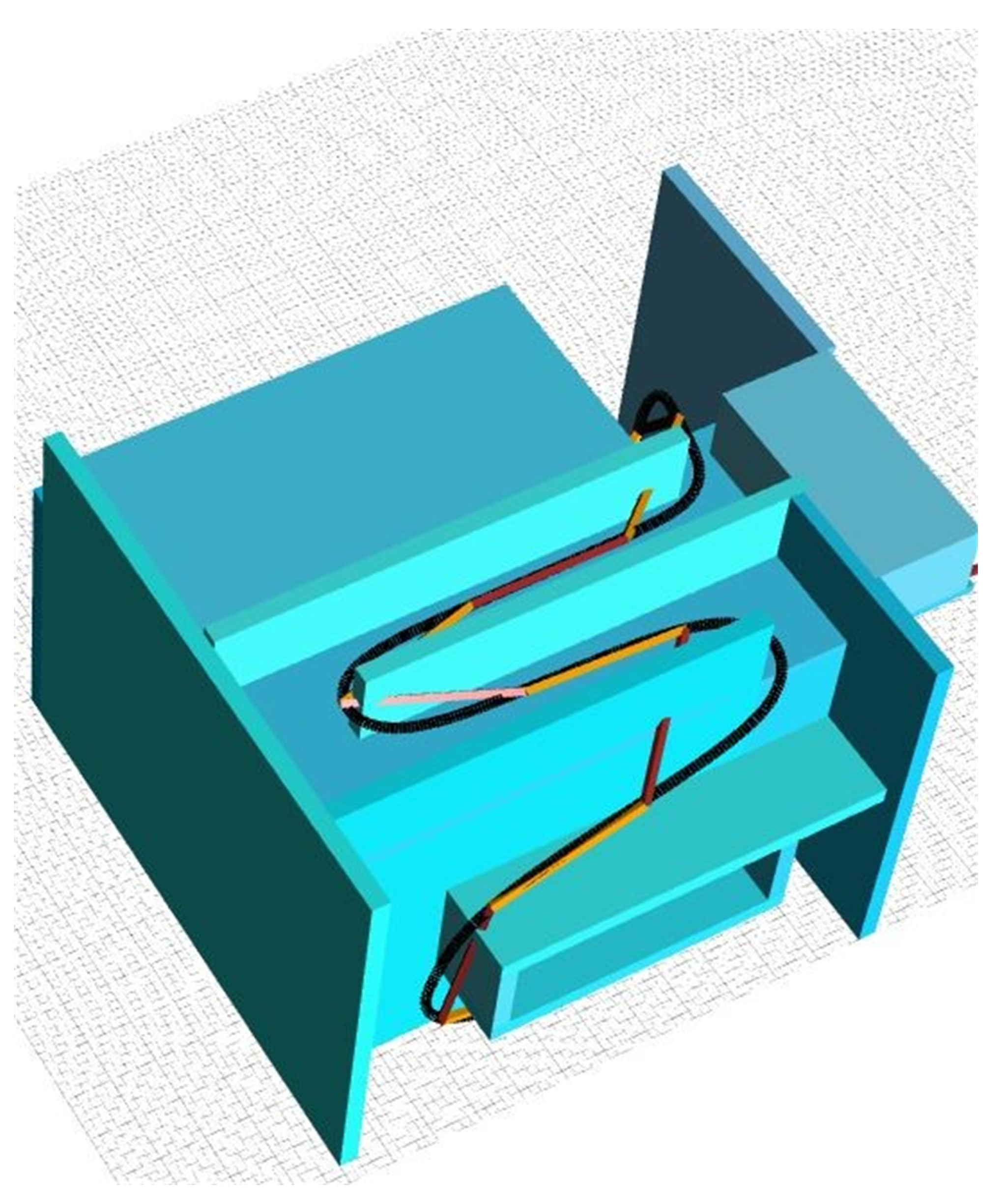
5. 3D Simulations
6. Discussion and Future Work
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| CPU | Central Process Unit |
| DOF | Degrees of Freedom |
| GA | Genetic Algorithm |
| RAM | Random Access Memory |
| RRT | Rapidly-Exploring Random Tree |
| USA | United States of America |
| WPF | Windows Presentation Foundation |
References
- Conkur, E.S.; Buckingham, R. Clarifying the definition of redundancy as used in robotics. Robotica 1997, 15, 583–586. [Google Scholar]
- Chiacchio, P.; Chiaverini, S.; Sciavicco, L.; Sicilliano, B. Closed-loop inverse kinematics schemes for constrained redundant manipulators with task space augmentation and task priority strategy. Int. J. Robot. Res. 1991, 10, 410–425. [Google Scholar]
- Nakamura, Y. Advanced Robotics: Redundancy and Optimization; Addison-Wesley Publishing Company: Boston, MA, USA, 1991; pp. 125–150. [Google Scholar]
- Ma, S.; Hirose, S.; Yoshinada, H. Development of a hyper-redundant multijoint manipulator for maintenance of nuclear reactors. Adv. Robot. 1994, 9, 281–300. [Google Scholar]
- Seereeram, S.; Wen, J.T. A global approach to path planning for redundant manipulators. IEEE Trans. Robot. Autom. 1995, 11, 152–160. [Google Scholar]
- Schilling, R.J.; Read, R.; Lovass-nagy, V.; Walker, G. Path tracking with the links of a planar hyper-redundant robotic manipulator. J. Robot. Syst. 1995, 12, 189–197. [Google Scholar]
- Takahashi, O.; Schilling, R.J. Motion planning in a plane using generalized Voronoi diagrams. IEEE Trans. Robot. Autom. 1989, 5, 143–150. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar]
- Motahari, A.; Zohoor, H.; Korayem, M.H. A new obstacle avoidance method for discretely actuated hyper-redundant manipulators. Sci. Iranica B 2012, 19, 1081–1091. [Google Scholar]
- Machmudah, A.; Parman, S.; Abbasi, A.; Solihin, M.I.; Manan, T.S.A.; Beddu, S.; Ahmad, A.; Rasdi, N.W. Cyclic path planning of hyper-redundant manipulator using whale optimization algorithm. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 677–686. [Google Scholar]
- Wei, H.; Zheng, Y.; Gu, G. RRT-based path planning for follow-the-leader motion of hyper-redundant manipulators. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3198–3204. [Google Scholar]
- Latombe, J.C. Robot Motion Planning; Springer: Boston, MA, USA, 1991; pp. 54–104. [Google Scholar]
- Conkur, E.S. Path following algorithm for highly redundant manipulators. Robot. Auton. Syst. 2003, 45, 1–22. [Google Scholar]
- Tang, L.; Zhu, L.M.; Zhu, X.Y.; Gu, G. Confined spaces path following for cable-driven snake robots with prediction lookup and interpolation algorithms. Sci. China Technol. Sci. 2020, 63, 255–264. [Google Scholar]
- Chirikjian, G.S.; Burdick, J.W. An obstacle avoidance algorithm for hyper-redundant manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Cincinnati, OH, USA, 13–18 May 1990; pp. 625–631. [Google Scholar]
- Graham, A.; Buckingham, R. Real-time collision avoidance of manipulators with multiple redundancy. Mechatronics 1993, 3, 89–106. [Google Scholar]
- McLean, A.; Cameron, S. Snake-based path planning for redundant manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 2–6 May 1993; pp. 275–282. [Google Scholar]
- Wang, W.; Zhu, M.; Wang, X.; He, S.; He, J.; Xu, Z. An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. Int. J. Robot. Syst. 2018, 15, 1–13. [Google Scholar]
- Lin, C.-C.; Chuang, J.-H. A potential-based path planning algorithm for hyper-redundant manipulators. J. Chin. Inst. Eng. 2010, 33, 415–427. [Google Scholar]
- Fahimi, F.; Ashrafiuon; Nataraj, C. Obstacle avoidance for spatial hyper-redundant manipulators. In Proceedings of The First Asian Conference on Multibody Dynamics (ACMD), Iwaki, Fukushima, Japan, 31 July–2 August 2002; pp. 247–254. [Google Scholar]
- Xidias, E.K.; Aspragathos, N.A. Time sub-optimal path planning for hyper redundant manipulators amidst narrow passages in 3D workspaces. In Advances on Theory and Practice of Robots and Manipulators, Mechanisms and Machine Science; Ceccarelli, M., Glazunov, V.A., Eds.; Springer: Cham, Switzerland, 2014; pp. 445–452. [Google Scholar]
- Xidias, E.K. Time-optimal trajectory planning for hyper-redundant manipulators in 3D workspaces. Robot. Comput.-Integr. Manuf. 2018, 50, 286–298. [Google Scholar]
- Choset, H.; Henning, W. A follow-the-leader approach to serpentine robot motion planning. J. Aerosp. Eng. 1999, 12, 65–73. [Google Scholar]
- Ayten, K.K.; Sahinkaya, M.N.; Dumlu, A. Real time optimum trajectory generation for redundant/hyperredundant serial industrial manipulators. Int. J. Robot. Syst. 2017, 14, 1–14. [Google Scholar]
- Ananthanarayanan, H.; Ordonez, R. A fast converging optimal technique applied to path planning of hyper-redundant manipulators. Mech. Mach. Theory 2017, 14, 231–246. [Google Scholar]
- Reznik, D.; Lumelsky, V. Sensor-based motion planning in three dimensions for a highly redundant snake robot. Adv. Robot. 1994, 9, 255–280. [Google Scholar]
- Azariadis, P.N.; Aspragathos, N.A. Obstacle representation by Bump-surfaces for optimal motion-planning. Robot. Auton. Syst. 2005, 51, 129–150. [Google Scholar]
- Islam, M.N.; Tamura, S.; Murata, T.; Yanase, T. Evaluation of a new backtrack free path planning algorithm for manipulators. IEEJ Trans. Electron. Inf. Syst. 2008, 128, 1293–1302. [Google Scholar]
- Chu, X.; Hu, Q.; Zhang, J. Path planning and collision avoidance for a multi-arm space maneuverable robot. IEEE Trans. Aerosp. Elect. Syst. 2018, 54, 217–232. [Google Scholar]
- Miao, Y.; Gao, F.; Zhang, Y. Gait fitting for snake robots with binary actuators. Sci. China Technol. Sci. 2014, 57, 181–191. [Google Scholar]
- Jamali, A.; Khan, M.R.; Osman, M.S.; Rahman, M.M.; Ashari, M.F.; Jamaludin, M.S.; Junaidi, E. Collision free control of variable length hyper redundant robot manipulator. Appl. Mech. Mater. 2014, 541–542, 1107–1114. [Google Scholar]
- Collins, T.; Shen, W.M. PASO: An Integrated, Scalable PSO-Based Optimization Framework for Hyper-Redundant Manipulator Path Planning and Inverse Kinematics. Available online: https://www.isi.edu/division3/robots/prl/collins2016-ISI-TR-697.pdf (accessed on 17 July 2022).
- Tappe, S.; Pohlmann, J.; Kotlarski, J.; Ortmaier, T. Towards a follow-the-leader control for a binary actuated hyper-redundant manipulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3195–3201. [Google Scholar]
- Zheng, Y.; Wu, B.; Chen, Y.; Zeng, L.; Gu, G.; Zhu, X. Design and validation of cable-driven hyper-redundant manipulator with a closed-loop puller-follower controller. Mechatronics 2021, 78, 102605. [Google Scholar]
- Tang, L.; Huang, J.; Zhu, L.-M.; Zhu, X.; Gu, G. Path tracking of a cable-driven snake robot with two-level motion planning method. IEEE/ASME Trans. Mechatronics 2019, 24, 935–946. [Google Scholar]
- Tang, L.; Zhu, L.M.; Zhu, X.; Gu, G. A serpentine curve based motion planning method for cable-driven snake robots. In Proceedings of the 25th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Stuttgart, Germany, 20–22 November 2018; pp. 5–10. [Google Scholar]
- Lin, Y.; Wang, J.; Xiao, X.; Qu, J.; Qin, F. A snake-inspired path planning algorithm based on reinforcement learning and self-motion for hyper-redundant manipulators. Int. J. Robot. Syst. 2022, 19, 1–13. [Google Scholar]
- Xu, W.; Mu, Z.; Liu, T.; Liang, B. A modified modal method for solving the mission-oriented inverse kinematics of hyper-redundant space manipulators for on-orbit servicing. Acta Astronaut. 2017, 139, 54–66. [Google Scholar]
- Jia, L.; Huang, Y.; Chen, T.; Guo, Y.; Yin, Y.; Chen, J. MDA + RRT: A general approach for resolving the problem of angle constraint for hyper-redundant manipulator. Exp. Syst. Appl. 2022, 193, 116379. [Google Scholar]
- Qin, G.; Wu, H.; Cheng, Y.; Pan, H.; Zhao, W.; Shi, S.; Song, Y.; Ji, A. Adaptive trajectory control of an under-actuated snake robot. App. Math. Mod. 2022, 106, 756–769. [Google Scholar]
- Duan, J.; Wang, B.; Cui, K.; Dai, Z. Path planning based on NURBS for hyper-redundant manipulator used in narrow space. Appl. Sci. 2022, 12, 1314. [Google Scholar]
- Conkur, E.S.; Buckingham, R. Manoeuvring highly redundant manipulators. Robotica 1997, 15, 435–447. [Google Scholar]
- Bulut, Y.; Conkur, E.S. A real-time path-planning algorithm with extremely tight maneuvering capabilities for hyper-redundant manipulators. Eng. Sci. Technol. Int. J. 2021, 24, 247–258. [Google Scholar]
- Conkur, E.S.; Buckingham, R.; Harrison, A. The beam analysis algorithm for path planning for redundant manipulators. Mechatronics 2005, 15, 67–94. [Google Scholar]
- Conkur, E.S. Path planning using potential fields for highly redundant manipulators. Robot. Auton. Syst. 2005, 52, 209–228. [Google Scholar]

| Example | (pixels) | (pixels) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (ms) | (ms) | (ms) | (ms) | (ms) | (ms) | (ms) | (ms) | |||
| First | 13,128 | 13,280 | 32,500 | 281 | 30,251 | 6564 | 13,022 | 15,738 | 117 | 14,623 |
| Second | 14,592 | 14,722 | 32,763 | 123 | 39,264 | 7296 | 13,822 | 15,124 | 56 | 29,578 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minnetoglu, O.; Conkur, E.S. Tight Maneuvering for Path Planning of Hyper-Redundant Manipulators in Three-Dimensional Environments. Appl. Sci. 2022, 12, 8882. https://doi.org/10.3390/app12178882
Minnetoglu O, Conkur ES. Tight Maneuvering for Path Planning of Hyper-Redundant Manipulators in Three-Dimensional Environments. Applied Sciences. 2022; 12(17):8882. https://doi.org/10.3390/app12178882
Chicago/Turabian StyleMinnetoglu, Okan, and Erdinc Sahin Conkur. 2022. "Tight Maneuvering for Path Planning of Hyper-Redundant Manipulators in Three-Dimensional Environments" Applied Sciences 12, no. 17: 8882. https://doi.org/10.3390/app12178882
APA StyleMinnetoglu, O., & Conkur, E. S. (2022). Tight Maneuvering for Path Planning of Hyper-Redundant Manipulators in Three-Dimensional Environments. Applied Sciences, 12(17), 8882. https://doi.org/10.3390/app12178882







