Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid
Abstract
:1. Introduction
- The implementation and simulation of a DQN-based EMS conducted based on Reinforcement Learning Toolbox of MATLAB/Simulink R2021a developed by MathWorks®.
- Defining a suitable design of the reward functions and neural networks to ensure the convergence during training process, and the trained EMS is able to respond precisely under all different weather conditions and load demand.
- Verifying the efficiency and stability of the proposed EMS system on an isolated HRES, which is designed based on HOMER software with practical data from Basco island.
- Conducting a performance comparison between the proposed method and the pre-determined-rule conventional dispatch (CD) control for validation.
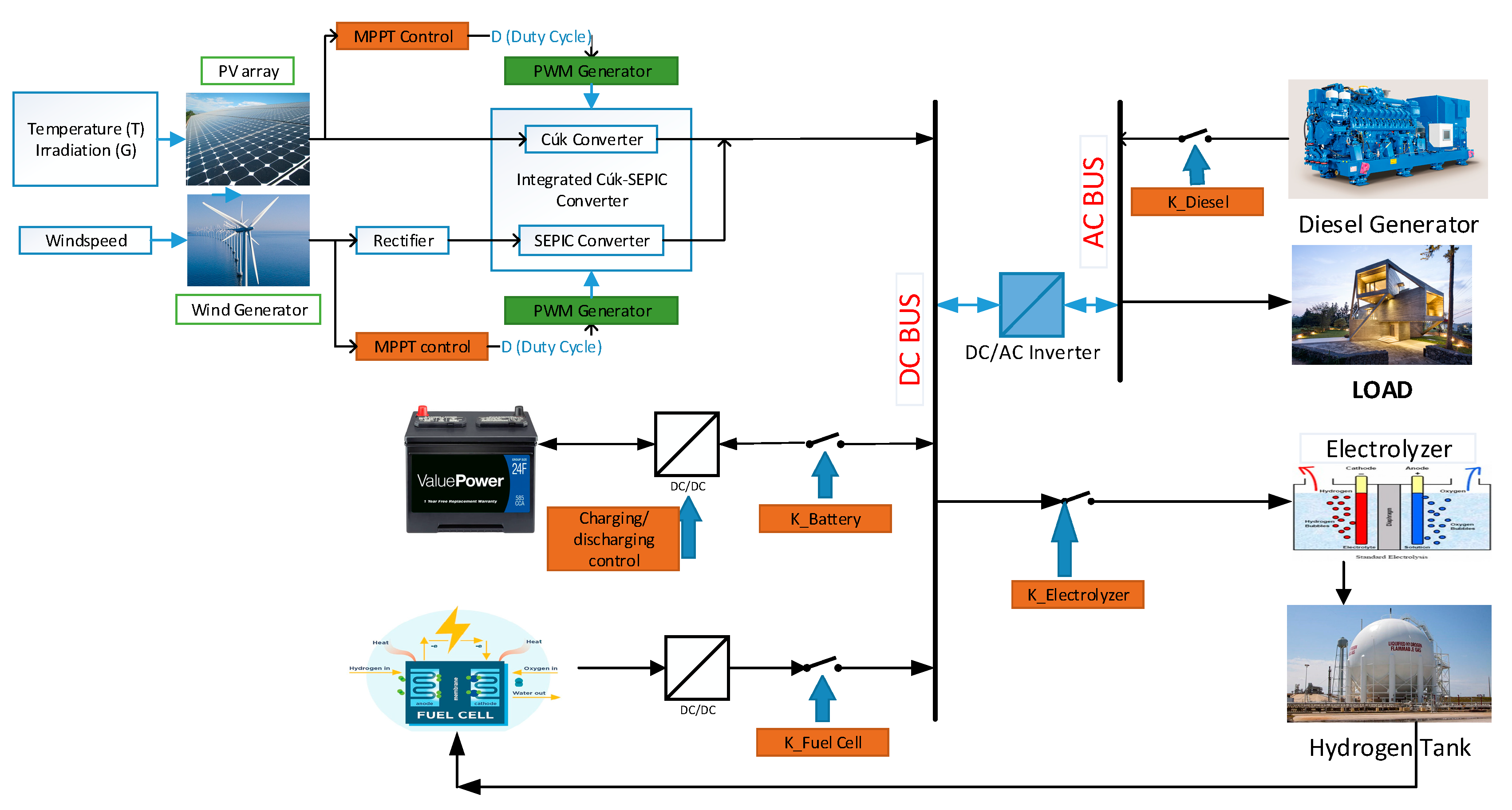
2. Mathematical Models of the System Components
2.1. PV System
2.2. Wind Turbine System
2.3. Battery Storage System
2.4. Diesel Generator
2.5. Fuel Cell
2.6. Electrolyzer
2.7. Hydrogen Tank
2.8. Power Balance
3. Energy Management of an HRES Based on Deep Q-Network
3.1. Introduction of the Proposed HRES
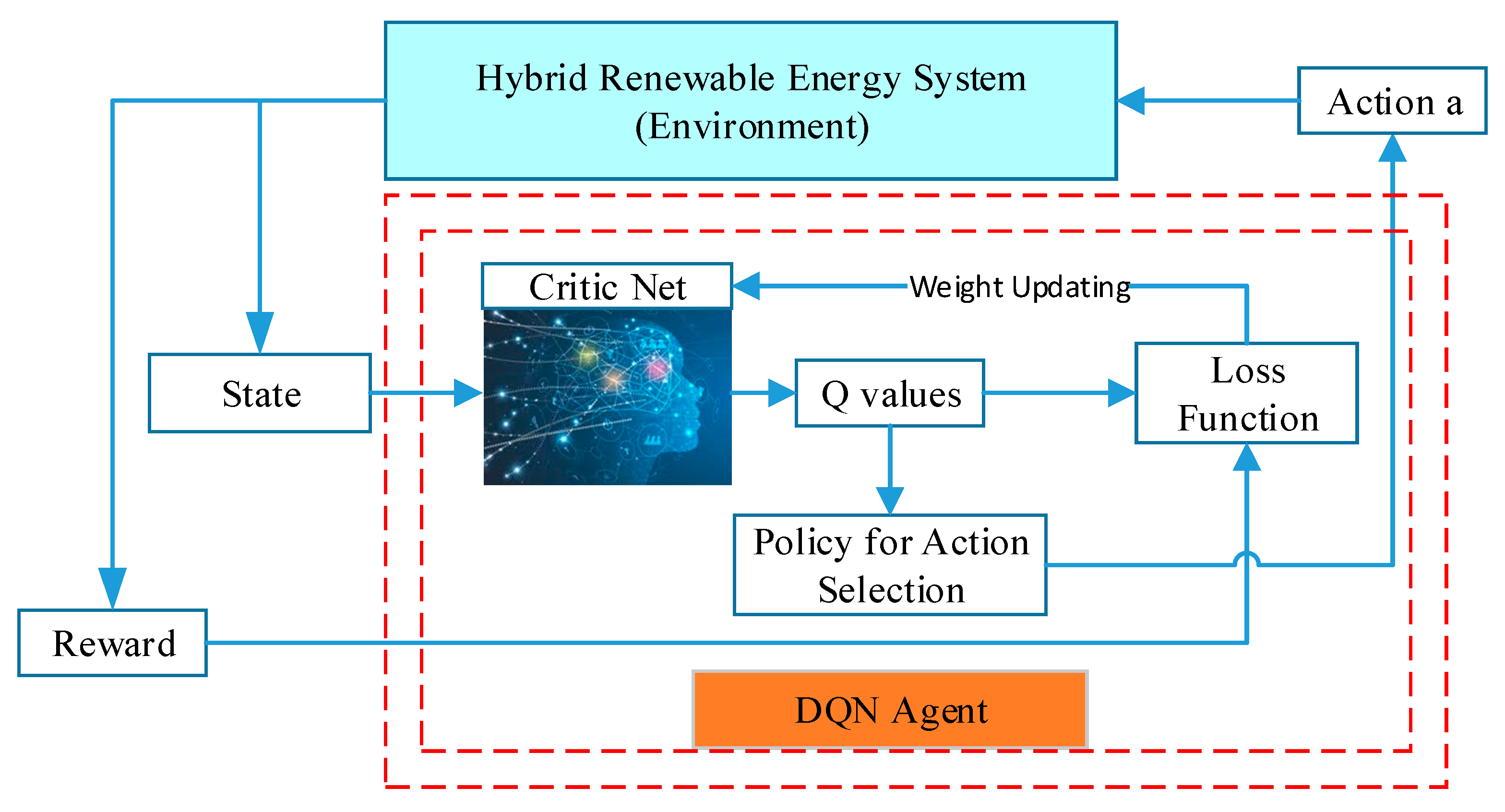
3.2. Markov Decision Process Model for the EMS
3.2.1. States and State Variables
3.2.2. Actions and Action Variables
3.2.3. Transition Probability
3.2.4. Rewards
3.3. Methodology of the DQN-Based EMS
3.4. Methodology of the Conventional Dispatch-Based EMS
4. Results and Discussion
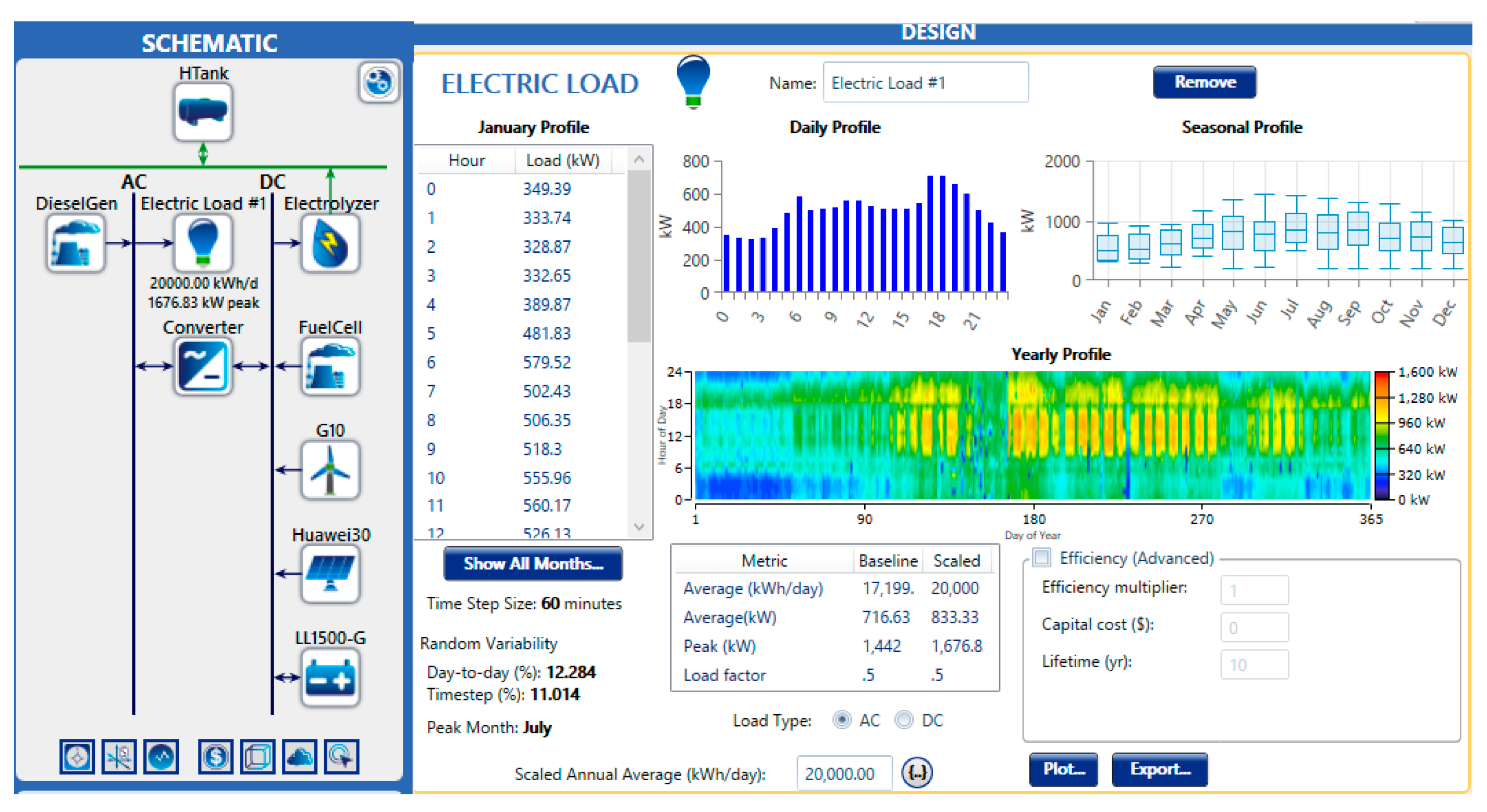
4.1. Site Description
4.2. Implementation of DQN-Based EMS in MATLAB/Simulink
4.3. Training Result
4.4. Performance under Various Conditions
4.4.1. Scenario 1
4.4.2. Scenario 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- The Renewable Energy Support Programme for ASEAN (RESP) Team. ASEAN Renewable Energy Policies; ASEAN Centre for Energy (ACE): Jakarta, Indonesia, 2016. [Google Scholar]
- Krishan, O.; Suhag, S. Techno-economic analysis of a hybrid renewable energy system for an energy poor rural community. J. Energy Storage 2019, 23, 305–319. [Google Scholar] [CrossRef]
- Lin, C.E.; Phan, B.C. Optimal Hybrid Energy Solution for Island Micro-Grid. In Proceedings of the 2016 IEEE International Conferences on Big Data and Cloud Computing (BDCloud), Social Computing and Networking (SocialCom), Sustainable Computing and Communications (SustainCom) (BDCloud-SocialCom-SustainCom), Atlanta, GA, USA, 8–10 October 2016. [Google Scholar]
- Vivas, F.J.; De Las Heras, A.; Segura, F.; Andújar Márquez, J.M. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Indragandhi, V.; Subramaniyaswamy, V.; Logesh, R. Resources, configurations, and soft computing techniques for power management and control of PV/wind hybrid system. Renew. Sustain. Energy Rev. 2017, 69, 129–143. [Google Scholar]
- Heymann, B.; Bonnans, J.F.; Martinon, P.; Silva, F.J.; Lanas, F.; Jiménez-Estévez, G. Continuous optimal control approaches to microgrid energy management. Energy Syst. 2018, 9, 59–77. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.; Ghias, A.M.Y.M. Energy Management and Control System for Laboratory Scale Microgrid Based Wind-PV-Battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Chen, Z.; Luo, A.; Wang, H.; Chen, Y.; Li, M.; Huang, Y. Adaptive sliding-mode voltage control for inverter operating in islanded mode in microgrid. Int. J. Electr. Power Energy Syst. 2015, 66, 133–143. [Google Scholar] [CrossRef]
- Wang, F.-C.; Kuo, P.-C.; Chen, H.-J. Control design and power management of a stationary PEMFC hybrid power system. Int. J. Hydrogen Energy 2013, 38, 5845–5856. [Google Scholar] [CrossRef]
- Jayalakshmi, N.S.; Gaonkar, D.; Nempu, P.B. Power Control of PV/Fuel Cell/Supercapacitor Hybrid System for Stand-Alone Applications. Int. J. Renew. Energy Res. 2016, 6, 672–679. [Google Scholar]
- Roumila, Z.; Rekioua, D.; Rekioua, T. Energy management based fuzzy logic controller of hybrid system wind/photovoltaic/diesel with storage battery. Int. J. Hydrogen Energy 2017, 42, 19525–19535. [Google Scholar] [CrossRef]
- Varghese, N.; Reji, P. Battery charge controller for hybrid stand alone system using adaptive neuro fuzzy inference system. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016. [Google Scholar]
- Battery charge controller for hybrid stand alone system using adaptive neuro fuzzy inference system Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [CrossRef]
- Luo, L.; Abdulkareem, S.S.; Rezvani, A.; Miveh, M.R.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal scheduling of a renewable based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K.; Isa, D. Hybrid energy storage systems and control strategies for stand-alone renewable energy power systems. Renew. Sustain. Energy Rev. 2016, 66, 174–189. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, H.; Gu, J.; Chen, H.; Deng, W. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism. Eng. Appl. Artif. Intell. 2022, 114, 105139. [Google Scholar] [CrossRef]
- An, Z.; Wang, X.; Li, B.; Xiang, Z.; Zhang, B. Robust visual tracking for UAVs with dynamic feature weight selection. Appl. Intell. 2022. [Google Scholar] [CrossRef]
- Wu, D.; Wu, C. Research on the Time-Dependent Split Delivery Green Vehicle Routing Problem for Fresh Agricultural Products with Multiple Time Windows. Agriculture 2022, 12, 793. [Google Scholar] [CrossRef]
- Chen, H.; Miao, F.; Chen, Y.; Xiong, Y.; Chen, T. A Hyperspectral Image Classification Method Using Multifeature Vectors and Optimized KELM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Hua, H.; Qin, Y.; Hao, C.; Cao, J. Optimal energy management strategies for energy Internet via deep reinforcement learning approach. Appl. Energy 2019, 239, 598–609. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Zhao, J.; Zhang, G.; Zhang, B.; Liu, Z.; Chen, Z.; Blaabjerg, F. Reinforcement learning and its applications in modern power and energy systems: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1029–1042. [Google Scholar] [CrossRef]
- Hsu, R.C.; Liu, C.-T.; Chen, W.-Y.; Hsieh, H.-I.; Wang, H.-L. A Reinforcement Learning-Based Maximum Power Point Tracking Method for Photovoltaic Array. Int. J. Photoenergy 2015, 2015, 496401. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602 . [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-line building energy optimization using deep reinforcement learning. IEEE Trans. Smart Grid 2018, 10, 3698–3708. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.; Liu, D. A self-learning scheme for residential energy system control and management. Neural Comput. Appl. 2013, 22, 259–269. [Google Scholar] [CrossRef]
- Leo, R.; Milton, R.S.; Sibi, S. Reinforcement learning for optimal energy management of a solar microgrid. In Proceedings of the 2014 IEEE Global Humanitarian Technology Conference-South Asia Satellite (GHTC-SAS), Trivandrum, India, 26–27 September 2014. [Google Scholar]
- Raju, L.; Sankar, S.; Milton, R. Distributed Optimization of Solar Micro-grid Using Multi Agent Reinforcement Learning. Procedia Comput. Sci. 2015, 46, 231–239. [Google Scholar] [CrossRef]
- Kim, H.-M.; Lim, Y.; Kinoshita, T. An Intelligent Multiagent System for Autonomous Microgrid Operation. Energies 2012, 5, 3347–3362. [Google Scholar] [CrossRef]
- Eddy, Y.S.F.; Gooi, H.B.; Chen, S.X. Multi-Agent System for Distributed Management of Microgrids. IEEE Trans. Power Syst. 2015, 30, 24–34. [Google Scholar] [CrossRef]
- Kofinas, P.; Vouros, G.; Dounis, A.I. Energy Management in Solar Microgrid via Reinforcement Learning. In Proceedings of the 9th Hellenic Conference on Artificial Intelligence, Thessaloniki, Greece, 18–20 May 2016; ACM: Thessaloniki, Greece, 2016; pp. 1–7. [Google Scholar]
- Kofinas, P.; Vouros, G.; Dounis, A.I. Energy management in solar microgrid via reinforcement learning using fuzzy reward. Adv. Build. Energy Res. 2017, 30, 97–115. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.; Vouros, G. Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids. Appl. Energy 2018, 219, 53–67. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.-C.; Lin, C.E. A Deep Reinforcement Learning-Based MPPT Control for PV Systems under Partial Shading Condition. Sensors 2020, 20, 3039. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Ahangari Hassas, M.; Pourhossein, K. Control and Management of Hybrid Renewable Energy Systems: Review and Comparison of Methods. J. Oper. Autom. Power Eng. 2017, 5, 131–138. [Google Scholar]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Optimal energy management system for stand-alone wind turbine/photovoltaic/hydrogen/battery hybrid system with supervisory control based on fuzzy logic. Int. J. Hydrogen Energy 2013, 38, 14146–14158. [Google Scholar] [CrossRef]
- Skarstein, Ø.; Uhlen, K. Design consideration with respect to long term diesel saving in wind/diesel plants. Wind. Eng. 1989, 13, 72–87. [Google Scholar]
- Ismail, M.; Moghavvemi, M.; Mahlia, T.M.I. Techno-economic analysis of an optimized photovoltaic and diesel generator hybrid power system for remote houses in a tropical climate. Energy Convers. Manag. 2013, 69, 163–173. [Google Scholar] [CrossRef]
- Kaabeche, A.; Ibtiouen, R. Techno-economic optimization of hybrid photovoltaic/wind/diesel/battery generation in a stand-alone power system. Sol. Energy 2014, 103, 171–182. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Z.; Xie, Y.; Yang, Z. A Theoretical Analysis of Deep Q-Learning. arXiv 2019, arXiv:1901.00137. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.-C. Control Strategy of a Hybrid Renewable Energy System Based on Reinforcement Learning Approach for an Isolated Microgrid. Appl. Sci. 2019, 9, 4001. [Google Scholar] [CrossRef] [Green Version]










| Specifications | Value |
|---|---|
| Memory capacity | |
| Batch size | 64 |
| Discount factor (γ) | 0.9 |
| Exploration rate (ε) | 1 |
| Decay of exploration rate | 0.001 |
| Minimum exploration rate (εmin) | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phan, B.C.; Lee, M.-T.; Lai, Y.-C. Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid. Appl. Sci. 2022, 12, 8721. https://doi.org/10.3390/app12178721
Phan BC, Lee M-T, Lai Y-C. Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid. Applied Sciences. 2022; 12(17):8721. https://doi.org/10.3390/app12178721
Chicago/Turabian StylePhan, Bao Chau, Meng-Tse Lee, and Ying-Chih Lai. 2022. "Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid" Applied Sciences 12, no. 17: 8721. https://doi.org/10.3390/app12178721
APA StylePhan, B. C., Lee, M.-T., & Lai, Y.-C. (2022). Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid. Applied Sciences, 12(17), 8721. https://doi.org/10.3390/app12178721









