Abstract
Pruning and quantization are core techniques used to reduce the inference costs of deep neural networks. Among the state-of-the-art pruning techniques, magnitude-based pruning algorithms have demonstrated consistent success in the reduction of both weight and feature map complexity. However, we find that existing measures of neuron (or channel) importance estimation used for such pruning procedures have at least one of two limitations: (1) failure to consider the interdependence between successive layers; and/or (2) performing the estimation in a parametric setting or by using distributional assumptions on the feature maps. In this work, we demonstrate that the importance rankings of the output neurons of a given layer strongly depend on the sparsity level of the preceding layer, and therefore, naïvely estimating neuron importance to drive magnitude-based pruning will lead to suboptimal performance. Informed by this observation, we propose a purely data-driven nonparametric, magnitude-based channel pruning strategy that works in a greedy manner based on the activations of the previous sparsified layer. We demonstrate that our proposed method works effectively in combination with statistics-based quantization techniques to generate low precision structured subnetworks that can be efficiently accelerated by hardware platforms such as GPUs and FPGAs. Using our proposed algorithms, we demonstrate increased performance per memory footprint over existing solutions across a range of discriminative and generative networks.
1. Introduction
The performance of deep neural networks (DNNs) has been shown to scale with the size of both the training dataset and model architecture [1]; however, the resources required to deploy larger networks for inference can be prohibitive as they often exceed the compute and storage budgets of resource-constrained platforms such as mobile or edge devices [2,3]. Therefore, as the usage of deep learning has proliferated in real-time applications with tight energy consumption budgets and low latency requirements, the field of research focused on reducing inference costs while maintaining model performance has rapidly expanded in recent years. Of the many techniques studied to accomplish this task, pruning and quantization are the most widely used and are often complementary to other approaches such as network distillation [4] and neural architecture search [5,6].
Pruning (i.e., the process of removing identified redundant elements from a neural network) and quantization (i.e., the processing of reducing their precision) are often considered to be independent problems [7,8]; however, recent work has begun to study the application of both in either a joint [2,6,9,10] or unified [11,12] setting. Unified algorithms typically use mixed precision quantization and integrate pruning by reducing the precision of an element (or a set of elements) to 0. On the other hand, joint algorithms combine separate optimization objectives for pruning and quantization under one learning framework, often using the standard “prune-then-quantize” paradigm [2]. In this work, we study the joint application of pruning and quantization under this paradigm across both discriminative and generative tasks for the purpose of learning low-precision structured subnetworks that can be efficiently accelerated by highly-parallelized hardware platforms.
Motivated by our observation that data-driven measures of neuron importance strongly depend on the activation distribution of the preceding layer, we design a greedy layerwise channel pruning algorithm that is heuristically guided by nonparametric estimates. We evaluate the performance of our algorithm using various pruning schedules and alternative measures of neuron importance based on pre-existing literature and observe that our greedy layerwise algorithm yields consistent benefits. Intuitively, our results suggest that, by allowing a given layer to adjust to abrupt shifts to its input activation distribution before pruning, the heuristics used to rank order neurons by importance become more effective, which leads to improved network performance. Furthermore, when combined with our moving average statistics-based uniform quantization procedure, we are able to learn low-precision structured subnetworks with minimal performance degradation for both discriminative and generative tasks. Our joint pruning and quantization algorithm is visualized in Figure 1, where we depict the sequence of pruning and quantization steps used during training. As further described in Section 4, our framework uses data-driven importance measures to guide our greedy layerwise channel pruning algorithm before our quantization operator is activated to reduce the precision of both the weights and activations for each layer . The pruning mask for each layer i is evaluated for steps before moving to layer . After all layers are pruned to a target sparsity, we activate the quantization operators and fine-tune for steps. It is important to note that, while only the pruning mask of one layer is tuned every steps, the weights in all layers are updated through gradient descent in every step, and latent operators act as identity functions until activated.
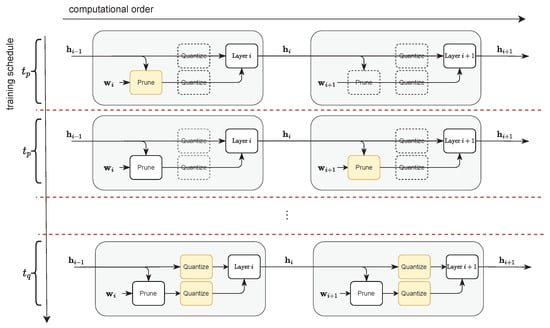
Figure 1.
We introduce a joint layerwise channel pruning and uniform quantization framework built from algorithms formulated using moving average statistics. Here, yellow blocks denote operators actively being evaluated, clear blocks with dotted lines denote latent operators that have yet to be activated, and white blocks denote activated operators that have already been evaluated.
The primary contributions of our work are as follows:
- We design a greedy layerwise channel pruning strategy using a nonparametric data-driven importance measure built without invoking any distributional assumptions.
- We build a fully data-driven nonparametric framework to learn performant low-precision structured subnetworks by combining our layerwise channel pruning algorithm with quantization-aware training.
- We evaluate our algorithm using alternative pruning schedules and neuron importance measures and demonstrate clear advantages over pre-existing approaches.
- We demonstrate increased performance per memory footprint over existing solutions across a wide range of discriminative and generative computer vision tasks.
The outline of the rest of the paper is as follows. In Section 2, we review prior work in neural network pruning and quantization. In Section 3, we motivate our intuition for data-driven layerwise pruning using nonparametric measures of correlation and distance between rank orderings of neuron importance. In Section 4, we describe our layer-by-layer channel pruning and moving average statistics-based quantization-aware training algorithms. In Section 5, we evaluate the performance results of our joint channel pruning and uniform quantization framework using discriminative and generative networks. In Section 6, we conclude the paper and discuss directions for future work.
2. Background
Our work explores the joint application of channel pruning and uniform quantization on both the weights and activations of deep neural networks. Here, we motivate our selected configurations for both.
2.1. Pruning
Neural network pruning techniques aim to reduce the inference costs of overparameterized models by identifying subnetworks that minimize memory requirements while maintaining task performance. In practice, pruning is often performed by setting the values of identified elements to zero, and the proportion of zero-valued elements is referred to as sparsity, where higher values correspond to fewer non-zero elements. Given a target sparsity, there are a variety of criteria used to identify which elements to prune; the most important of which are the topology constraints on the resulting subnetwork, the measure used to rank elements by importance, and the schedule in which elements are pruned.
Topology constraints for pruning techniques can be divided into structured or unstructured approaches. Structured pruning techniques introduce sparsity in varying levels of granularity (e.g., entire kernels or channels), whereas unstructured pruning techniques impose no constraint on the topology of the sparsity scheme, as shown in Figure 2. Due to their inherent flexibility, unstructured pruning techniques can offer high compression rates with minimal accuracy degradation [2,13]; however, they bring little hardware efficiency due to poor data locality caused by irregular sparsity patterns, which create minimal opportunities for parallelism [14,15]. Alternatively, structured pruning techniques offer more hardware-friendly implementations, often by removing entire channels. This not only reduces the compute workload in a manner that is easily accelerated by most computing platforms [14] but also reduces energy consumption as activations dominate data transfer costs for both discriminative [16] and generative [17] models. Therefore, we focus on channel pruning in this work.
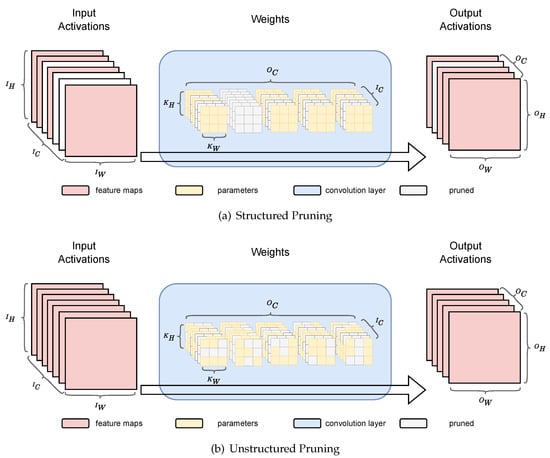
Figure 2.
We depict the differences between structured (a) structured pruning and (b) unstructured pruning.
Various measures have been proposed to heuristically determine the relative importance of channels in a neural network. Weight magnitude has become the standard importance measure used to guide unstructured pruning algorithms [2,13,18], intuitively suggesting that larger magnitudes have greater influence in the network. Thus, weight magnitude can be extended to rank order channels using the -norm of channel weights [19]. We refer to such importance measures as data-free, as they do not require a data distribution to estimate neuron importance. Alternatively, purely data-driven approaches such as [20] prioritize removing redundancy from the information (i.e., hidden activations) propagated through the network from the input data. This class of techniques has shown tremendous promise in finding performant structured subnetworks by heuristically guiding pruning algorithms to minimize feature reconstruction error [15], remove underutilized channels [20], or minimize the mutual information between successive layers [21]. However, we find that these approaches are limited by one or two key oversights:
- They do not consider the interdependence between successive layers in a neural network when measuring neuron importance, as in the case of [19,20,22].
- They either use a parametric setting or invoke distributional assumptions on the activation data that may not hold true for all network architectures, as in the case of [15,21,23,24].
In this paper, using a completely nonparametric framework, we design a layerwise channel pruning algorithm using a data-driven measure of channel importance. Using targeted statistical experiments, we focus on some important differences between data-driven and data-free approaches when constructing our pruning algorithms. These experiments, further discussed in Section 3, also motivate the rationale for our layerwise approach.
2.2. Quantization
We are interested in quantization for the purpose of accelerating our structured subnetworks on mobile or edge devices; thus, we construct our “quantization” and “dequantization” operators from the standard uniform affine mapping from a high precision real number r to a low-precision quantized number q using a scaling factor s and zero-point z, as given by Equation (1). Although more complex non-uniform and non-linear mappings have been considered [4,25], their utility and practicality are often circumstantial as they require dequantization before performing computation in the high precision real domain and are thus far less efficient on resource-constrained hardware [26].
As is standard practice, our quantizer (Equation (2)) and dequantizer (Equation (3)) are parameterized by scaling factor s and zero-point z. Here, s is a strictly positive real scaling factor and z is an integer value that maps to the real zero such that the real zero is exactly representable in the quantized domain. This ensures the numerical fidelity of common operations such as zero-padding [27,28]. Here, denotes the half-way rounding function and clip, where n and p are the clipping limits defined by the bitwidth b. For signed integers, and . For unsigned integers, and . As is standard practice, we use per-tensor scaling factors on the activations and per-channel scaling factors on only the weights [29].
As reported in previous studies, eliminating zero points in the quantization mapping such that reduces the computational overhead of cross-terms when executing inference using integer-only arithmetic [29,30]. This strategy is commonly referred to as symmetric quantization, with asymmetric quantization as its alternative. To demonstrate the computational overhead of cross-terms introduced by asymmetric quantization, consider the real values for input activation x, weight w, and output activation y mapping to quantized values , , and , respectively. The arithmetic for their product, , becomes the following:
where , , and represent their respective scaling factors and , , and represent their respective zero points. This simplifies to the following:
These cross-terms often require non-trivial optimizations to remain efficient; however, by constraining the quantization scheme of all weights in a DNN to be symmetric (i.e., ), we can mask the overhead of asymmetric quantization on the activations without any additional hardware or software optimizations as the arithmetic simplifies to Equation (6), where l denotes layer in a neural network with L sequential layers.
Note that, when using a symmetric quantizer on both the inputs and outputs to the neural network (i.e., and , respectively), we can freely use asymmetric quantization on the hidden layers without any overhead caused by the cross terms in Equation (5). While previous works have alluded to this optimization [26], we are not aware of any research that has explicitly exploited it as we do. In our work, we focus on uniform affine quantization, where we apply symmetric, per-channel quantization to the weights and asymmetric, per-tensor quantization to the activations.
3. Motivation
To demonstrate the interdependence between successive layers in a neural network, we inject structured sparsity into the input activations of a given layer within the network and evaluate how this leads to a shift in output channel importance rankings with respect to the dense input activations (i.e., when there is no input sparsity). To rank order output channels by importance, we use two measures: (1) the mean -norm of the output activations generated by each channel, and (2) the -norm of the learned weights for each output channel. For a given layer i with hidden activations and output channels, we denote the importance estimates for each channel as where . In order to compare two sets of rankings, we use the following nonparametric measures:
- Kendall’s Coefficient of Rank Correlation [31]:For a given layer i with outputs channels, let the rank orderings of two sets of importance estimates and be given by and , respectively. The Kendall’s coefficient of rank correlation measures the similarity between and . The statistic (referred to as Kendall’s Tau) is given below in Equation (7), where is given by Equation (8). Here, is a perfect relationship, is no relationship at all, and is a perfect negative relationship.
- Levenshtein Distance [32]:For a given layer i with outputs channels, let the rank orderings of two sets of importance estimates and be given by and , respectively. The Levenshtein distance between these two sequences of ranks, which we denote as , is defined as the minimum number of single element edits required to change to . The distance is formally defined using recursion as given by Equations (9) and (10). The function tail of an ordered set of n elements returns all but the first element of the string such that and tail, where we denote element j of ranked set as . Here, will have a low value close to 0 if and are very similar; otherwise, it will have a high value.
To perform our evaluation for a discriminative task, we train LeNet5 [33] models to classify MNIST [34] images. For a generative task, we train convolutional variational autoencoders (VAEs) to generate MNIST images1. For each case, we independently train 30 models using different random seeds. Our 30 LeNet5 models have an average test accuracy of 98.2% with a standard deviation of 0.003%, and our 30 VAEs have a mean Fréchet inception distance (FID) [35] of 9.81 with a standard deviation of 0.725. In Figure 3, we provide sampled images generated from a randomly selected VAE. These metrics and images are provided as supporting evidence that we use fully trained models in our statistical analysis, which forms the basis of our conclusions in this section.

Figure 3.
We provide random images generated from one of our VAEs trained on MNIST [34].
For LeNet5, we evaluate the importance of the 16 output channels of the second layer when iteratively pruning its six input channels. For the VAE, we evaluate the importance of the 16 output channels of the second layer of our decoder, which has 32 input channels. We increase the sparsity of the input channels using the rank ordering of the original unpruned network as determined by the mean -norm of its activations when estimated over the test dataset. We denote the importance estimate of the preceding layer as and the respective rank ordering as . Note that for LeNet5 and for our VAE. For each level of input sparsity, which we denote as s, we then rank order the output channels using the mean -norm over their respective activations also estimated over the test dataset. We denote the rank ordering of output channel activations by importance measure for a given sparsity level (s) as . Note that this sparsity level is over the input of our activation distribution, not the layer being evaluated, and the importance estimates of the evaluated layer i is for both LeNet5 and our VAE.
To evaluate the interdependence between successive layers, we iteratively increase the sparsity (s) of the input activations according to for both our discriminative and generative models and measure the Kendall coefficient and Levenshtein distance between (i.e., the rank order of the output channels of layer i by importance measure when input activations have a sparsity of ) and (i.e., the rank order of output channels of layer i by importance measure when input activations have no sparsity). We visualize the results in Figure 4. For brevity in the titles of our plots, we use sparse activations to refer to the rank order of the output channels of layer i when using the mean -norm of the output channel activations as the importance measure when input activations have a sparsity of s (i.e., ); alternatively, we use dense activations when input activations have no sparsity (i.e., ). We use dense weights to refer to the rank order of the output channels of layer i when using the -norm of the channel weights as the importance measure (i.e., ). We observe that as the input activation sparsity s increases from 0 to 100%, the correlation between and gradually decreases and the Levenshtein distance gradually increases. We repeat this process using the -norm of our channel weights as our measure of importance, which we will denote as ; however, the -norm of our channel weights is a data-free measure that is by definition invariant to this sparsity injection. Therefore, when iteratively increasing the sparsity of the input activations according to , we measure the relationship between our data-driven rankings and data-free ranking . We observe that the correlation between and is much weaker, and their relationship is not as severely affected by the sparsity of the input activations.
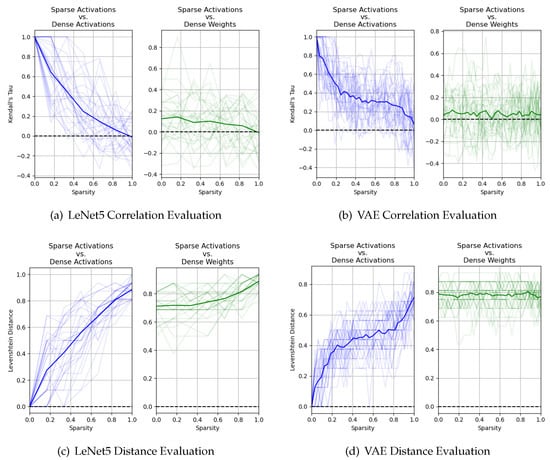
Figure 4.
As discussed in Section 3, we evaluate the Kendall coefficient of rank correlation (top row) and the Levenshtein distance (bottom row) over 30 independently trained discriminative models (left column) and generative models (right column). We plot the correlation and distance between and in blue, and the correlation and distance between and in green.
From these experiments, we draw the following conclusions. First, data-driven channel importance rankings (e.g., the rankings of output channels by the -norm of activation distributions) are heavily impacted by the sparsity of the preceding input activation distribution2. Given this, we hypothesize that we can increase the effectiveness of data-driven pruning criterion by allowing a given layer to adjust to shifts in its input activation before applying pruning. Second, data-driven and data-free channel importance measurements are weakly correlated. Therefore, when used to heuristically guide channel pruning algorithms, we expect that these two importance measurements will behave differently under extreme levels of sparsity. It is important to note that we cannot conclude which ranking is necessarily “correct”, as these experiments only demonstrate that they are “different”. In Section 5, we empirically evaluate the performance of these neuron importance measurements using various pruning schedules to provide further insights.
4. Algorithms
For the purpose of describing our pruning and quantization algorithms, we first introduce our notation. We denote the input data to a neural network with L layers as and, for discriminative tasks, its associated output label as . We denote the activations of the network as , where denotes the activations of hidden layer i and for convenience. The set of weights of each layer are denoted as , where is the set of weights for layer i with output channels, which we refer to as neurons. Finally, we denote the binary mask used to prune each layer as and the importance estimates of each neuron as , where and are, respectively, a scalar value for the binary mask and non-negative importance estimate for each neuron c in layer i, where .
4.1. Greedy Layerwise Channel Pruning Using Nonparametric Statistics
When viewing the input data as a random variable, neural networks are sometimes interpreted as Markov chains, where every hidden layer i defines the conditional probability [21,36]. Such a formulation motivates our observations that the effectiveness of neuron importance measurements relying on is dependent on the stability of input activation distribution . In Section 3, we show that iteratively increasing the sparsity of the input activations of a given layer results in a monotonic decorrelation between the rank orderings of its output activations when using sparse versus dense input activations. Thus, we hypothesize that by allowing a given layer to adjust to these abrupt shifts in its input activation distribution before pruning , we can increase the effectiveness of the heuristics used to rank order neurons by importance. As such, we design an iterative channel pruning algorithm that greedily traverses the topology of a feedforward neural network, starting from the first hidden layer and ending at the final hidden layer .
Our layerwise iterative channel pruning algorithm is summarized in Algorithm 1.
| Algorithm 1: Our proposed layerwise channel pruning algorithm, using per-channel -norm of activations to measure importance. All channel masks are initialized to 1 and all importance measurements are initialized to 0. We update learned weights of all layers in the network at every step using backpropagation, but only update the mask for layer i at step i. |
 |
We first initialize the values of all masks to 1 and the values of all importance measurements to 0. Note that the mask for a given neuron is a binary value that prunes the neuron when , and is a non-negative value where is interpreted as neuron one being more important than neuron two in layer i. When pruning layer i, we estimate the importance of each neuron c using the moving average of the -norm of activations over channel c from over steps. We evaluate our pruning mask every steps, where , at which point we prune neurons according to the using a pre-defined sparsity target . The entire network is pruned to the given target sparsity once all L layers are processed. As is standard practice, we do not prune visible activations (i.e., the input and output activations and , respectively). In practice, we apply this procedure on a pre-trained network and continue to fine-tune our structured subnetwork for T more epochs after pruning. As we greedily increase the sparsity of the network layer-by-layer, we refer to this iterative pruning schedule as “layerwise” channel pruning. Throughout our algorithm, we continue to update the weights of each layer using gradient descent such that all weights are updated for gradient steps.
The concept of using an iterative pruning schedule to alleviate the impact of abruptly removing neurons has been explored in prior work [11,23,37,38]; however, they iteratively introduce sparsity globally at each step. Because these pruning schedules gradually introduce sparsity according to a per-step heuristic, we refer to this class of algorithms as “stepwise” pruning. We visualize the differences in these algorithms in Figure 5. Unlike our layerwise pruning schedule, which determines only after has stabilized, stepwise pruning schedules determine and jointly. As discussed in Section 3, this could lead to less effective measures of neuron importance. In Section 5, we compare our layerwise pruning schedule against the standard stepwise approach.
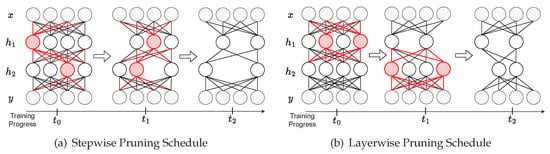
Figure 5.
We depict the differences between the standard stepwise pruning schedule (a) and our layerwise pruning schedule (b). While stepwise pruning algorithms iteratively increase sparsity globally in the network with each step, our layerwise pruning algorithm iteratively increases sparsity layer-by-layer with each step. Throughout the training progress (horizontal flow), gray nodes denote visible neurons that are not pruned, red nodes denote hidden neurons that have been identified to be pruned in a given step, and white nodes denote hidden neurons that remain active.
4.2. Uniform Quantization-Aware Training
To train our structured subnetworks for low-precision quantization, we use the straight-through estimator (STE) [39] to approximate the gradients of our rounding function such that , but . To apply asymmetric quantization to our hidden activations , we adaptively fit our per-tensor scaling factor and zero-point . To apply symmetric quantization to our weights , we adaptively fit our per-channel scaling factor where denotes the scaling factor for channel . For each layer i, we estimate the upper and lower bounds of activation and the maximum magnitude of weight using moving average statistics, similar to our technique in Algorithm 1. Following the work of [28], we summarize the adaptive asymmetric and symmetric quantization algorithms used in this paper in Algorithms 2 and 3, respectively.
| Algorithm 2: Our adaptive asymmetric quantization algorithm for our activations using per-tensor scaling factors. We use moving average statistics over hidden activation to estimate the bounds on its dynamic range for the purpose of deriving scaling factor and zero-point for layer i. |
| Input: estimated bounds on hidden activation at time step t Output: Quantized activation ; Updated bounds 1 2 3 4 5 |
| Algorithm 3: Our adaptive symmetric quantization algorithm for the set of weights for layer i using per-channel scaling factors. We use moving average statistics to estimate the maximum weight magnitude for each channel c to derive our per-channel scaling factors . |
 |
5. Experiments
In Section 3, we present our hypothesis that, by allowing a given layer to adjust to abrupt shifts to its input distribution before pruning its channels, the heuristics used to rank order neurons by importance become more effective. Here, we compare our greedy layerwise channel pruning algorithm against alternative pruning schedules and importance measures to demonstrate the increased performance of our approach versus existing baselines. For the purpose of enabling inference acceleration on resource-constrained hardware such as mobile and edge devices, we combine the use of our channel pruning algorithm with moving average statistics-based uniform quantization, as described in Section 4. We evaluate the performance of our algorithms using the following discriminative and generative computer vision tasks:
- Image classification with DenseNet121 [40], and MobileNetV2 [41] on CIFAR100 [42]
- Semantic segmentation with UNet [43], and FRRNet [44] on Cityscape [45]
- Image style transfer with CycleGAN [46] on Cityscape
We implement our pruning algorithms using the PyTorch deep learning framework [47] and create a custom neural network pruning module to compute neuron importance estimates and derive binary masks using local buffers3. Example usage of the functions in this repository is provided in Appendix A. For each task, our baselines are built using the existing open-source implementations provided by the respective original authors. To the extent possible, we use the same weight initialization techniques, network architecture, and hyperparameter configurations as reported in the original papers. All models are trained through Nautilus—a distributed research compute infrastructure from the Pacific Research Platform (PRP) [48]. Single-GPU training time for each model ranges from 3 hours (e.g., MobileNetV2 on CIFAR100) to 12 hours (e.g., CycleGAN on Cityscape) depending on the complexity of the task. Furthermore, for the style transfer task, CycleGAN uses a cycle consistency loss that includes two mappings: (1) generator , parameterized by , maps input image to the target domain ; and (2) generator , parameterized by , maps back to the original image . During training, we only prune the forward mapping into the target domain , as we are only interested in accelerating inference, and the reverse transform is discarded at inference time. Given an input label map, the forward mapping of our pruned and quantized CycleGAN model generates realistic 128 × 128 images in the first-person driving view, as shown in Figure 6.

Figure 6.
(a) Input, (b) Output (Baseline), (c) Output (P50%), (d) Output (P75%), (e) Output (P50%, W8A8), (f) Output (P75%, W8A8). We provide examples of images generated from CycleGAN given the same input (left). Here, P50% and P75% denote 50% and 75% channel pruning, respectively. We use “W8A8” to denote that the weights and activations have both been quantized to 8 bits.
5.1. Evaluating Pruning Schedules and Importance Measures
Here, we evaluate the importance of our layerwise iterative pruning schedule by comparing it to three alternative pruning schedules:
- Training from scratch. Prior work has demonstrated that, in some cases, there is no need to implement a pruning schedule because pre-defined structured subnetwork architectures can be trained from scratch to match or surpass the performance of the original larger network [38]. As such, we evaluate our pruning algorithm against this baseline.
- One-shot. We compare against the common “prune then fine-tune” strategy [20], where we train a fully connected baseline, and then prune the converged model to our target sparsity in one step before fine-tuning to heal the network.
- Stepwise. Unlike one-shot pruning schedules, which jump to the target sparsity in one step, stepwise pruning schedules iteratively increase the sparsity in the network over many steps throughout training. We benchmark against the state-of-the-art iterative pruning schedule proposed by Zhu and Gupta [23].
In Table 1, we report the performance of each of these algorithms with target sparsity levels of 50% and 75% across our discriminative and generative tasks. Each entry is the averaged result over three independent runs. We use the same learning rate schedule and optimizer for each experiment to ensure an even comparison. We use top-1 accuracy to evaluate image classification models, mean intersection-over-union (mIOU) to evaluate semantic segmentation models, and Fréchet inception distance (FID) [35] to measure the difference between real images and images generated from our CycleGAN. Based on these metrics, we observe that our layerwise channel pruning algorithm performs stronger at more extreme levels of sparsity in a majority of cases.

Table 1.
Comparing pruning schedules across discriminative and generative tasks. With higher levels of sparsity, our greedy layerwise channel pruning algorithm performs better than existing baselines across both discriminative and generative tasks. Note that for top-1 accuracy and mIOU, higher is better, but for FID, lower is better.
Next, we compare the performance of data-driven and data-free neuron importance measures when used to guide our greedy layerwise channel pruning algorithm. In Table 2, we compare the performance of our algorithm when using the -norm of the channel activations against using the -norm of the channel weights. Although prior work had experimented with using the -norm as a data-driven importance measure [20], we do not compare against this as not all layers in our baselines are followed by a ReLU. We observe that using the -norm of the output activation channels yields superior results than using the -norm of channel weights in a majority of cases. Furthermore, we also observe that using the -norm of channel weights to guide our greedy layerwise pruning algorithm often yields better results than other pruning schedules reported in Table 1.

Table 2.
Comparing data-free vs. data-driven neuron importance measures across discriminative and generative tasks using our greedy layerwise channel pruning algorithm, we observe that the mean -norm of the output activations (i.e., “Layerwise (A)”) performs better than the -norm of channel weights (i.e., “Layerwise (W)”).
The results reported in Table 1 and Table 2 suggest that we can increase the effectiveness of nonparametric data-driven pruning criteria by only pruning a given layer after its preceding layer has been fully pruned, which supports our motivating hypothesis. Our experiments in Section 3 show that the rank ordering of channels for a given layer i is strongly impacted by the sparsity of the input activations to that layer. Equation-based pruning schedules such as [23] gradually introduce sparsity throughout the network with each step, as shown in Figure 5. Thus, at time t, they approximate the neuron importance with respect to the target sparsity using the neuron importance with respect to the current sparsity , where and . As such, this class of algorithms uses rankings to heuristically guide pruning. Furthermore, one-shot pruning schedules approximate the neuron importance with respect to the target sparsity using estimates at step 0, when the input activations have no sparsity. As such, this class of algorithms uses rankings to heuristically guide pruning. In contrast, our layerwise pruning schedule directly uses the neuron importance measure with respect to the target sparsity , where we use to heuristically guide pruning. As the sparsity target increases to more extreme levels, there is a gradual decorrelation between and , as shown in Section 3. Our results given in Table 1 show that directly using within our greedy layerwise framework increases the effectiveness of data-driven rankings. We conjecture this is because our greedy layerwise channel pruning algorithm allows an unpruned layer to freely adjust to abrupt shifts in its input activation distribution caused by pruning the channels of its preceding layer.
5.2. Evaluation of Joint Pruning and Quantization
We evaluate our greedy layerwise channel pruning algorithm when jointly used with the quantization algorithms detailed in Section 4.2 to learn low-precision structured subnetworks through joint pruning and quantization. As discussed in Section 2, we apply symmetric, per-channel quantization to the weights of our deep neural networks and asymmetric, per-tensor quantization to the activations. To implement Algorithms 2 and 3, we create another custom quantization PyTorch module that accumulates the respective per-tensor or per-channel moving average statistics. As is standard practice, our modules produce a “fake quantized” output using the derived scale s and zero-point z [27,28]. We apply these modules to every hidden activation and set of weights in the network to prepare our models for integer-only inference [27]. We follow the standard “prune-then-quantize” training paradigm and activate the quantization operators only after the completion of layerwise pruning. Figure 1 shows both the training schedule and computational order of our joint pruning and quantization pipeline.
In Table 3, we report our joint pruning and quantization results for 50% and 75% sparsity when training 4-bit and 8-bit models. We use “W4A8” to denote quantizing weights to 4 bits and activations to 8 bits. For all networks except for CycleGAN, we quantize the weights of all layers to the specified bitwidth, including the first and last layer and quantize the activations of all layers to the specified bitwidth except for network input and output . For CycleGAN, we always quantize the weights and input activation of the last layer to 8-bit regardless of global bitwidth configuration, as is standard practice [49]. For each experiment reported in Table 3, we use our greedy layerwise pruning algorithm with the -norm of the output channel activations as our importance measure.

Finally, we apply our joint layerwise channel pruning and uniform quantization framework to train ResNet-32 [37] on the CIFAR10 dataset with sparsity ratios of 25%, 40% and 50%, and uniform bitwidths of 8 and 4. We compare against existing solutions and summarize the results in Table 4. Here, and denote the average number of bits used to quantize weights or activations, respectively, and and denote the global weight and activation sparsity, respectively. Note that, as discussed in Section 2.1, channel pruning reduces both the storage and operating memory4 requirements of both the weights and activations, while unstructured weight pruning only reduces the memory storage requirements of the weights. Therefore, structured pruning can result in lower operating memory requirements, despite lower compression ratios with respect to unstructured pruning. To compare different approaches across these configurations, we compute the performance per operating memory size (i.e., performance density) for each model, as listed in the last column. For existing solutions, we summarize the results reported in prior work. For solutions that do not apply quantization to the weights or activations, we estimate their precision at 16 bits per element rather than 32 since neural networks can be quantized to 16-bit fixed-point through post-training quantization without significant accuracy degradation [50].

Table 4.
We demonstrate the superior performance per memory footprint (i.e., performance density) of our framework when compared to existing image classification solutions trained on CIFAR10. By jointly applying uniform quantization and unstructured pruning to both the weights and activations of the DNN, we achieve a higher performance density (PD) with higher compression rates than existing solutions and comparable network performance.
Table 4 shows that our method is able to achieve a higher performance density (8.92) than the highest of previous solutions (8.59) while having very competitive performance (92.53% versus 91.66% top-1 accuracy). When applying 50% pruning and 4-bit quantization, our method achieves the smallest memory footprint and highest performance density of 25.25, three times larger than the existing highest, while still maintaining sufficient accuracy (87.3%). Moreover, unlike methods such as [12,51], our framework provides direct control over the target bitwidth and sparsity, which is more useful in practical scenarios under tight design constraints, as is the case when deployed on edge GPUs or FPGAs [52,53,54].
6. Conclusions and Future Work
In this work, we demonstrate that, when using data-driven measures of neuron importance, the rank orderings of the output channels of a given layer strongly depend on the sparsity level of the preceding layer. In Section 3, we show that as we increase the sparsity of the input activations for a given layer, the correlation trends toward zero when comparing: (1) the rank order of its output channels using input activations with no sparsity; versus (2) the rank order of its output channels when the input activations have sparsity . Informed by this observation, we propose a data-driven nonparametric, magnitude-based channel pruning algorithm that works in a greedy manner based on the activations of the previous sparsified layer, as detailed in Section 4. For the purpose of learning low-precision structured subnetworks, we demonstrate that our proposed algorithm works effectively in combination with statistics-based uniform quantization. As demonstrated in Section 5, our joint layerwise channel pruning and uniform quantization framework yields increased performance per memory footprint over existing solutions across a range of discriminative and generative networks. The resulting neural networks can be efficiently accelerated by resource-constrained hardware platforms such as edge GPUs and FPGAs. In future work, we aim to focus more closely on applying our framework to generative models and explore advanced quantization-aware training techniques to work jointly with our nonparametric greedy layerwise channel pruning algorithm.
Author Contributions
Software and experiments—X.Z.; writing, formal analysis, and visualization—X.Z., I.C. and S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found in [42,45]. Pre-trained models and configuration files are provided at: https://github.com/mlzxy/mdpi2022 (accessed on 30 June 2022).
Acknowledgments
This work was supported in part by NSF awards CNS1730158, ACI-1540112, ACI-1541349, OAC-1826967, the University of California Office of the President, and the California Institute for Telecommunications and Information Technology’s Qualcomm Institute (Calit2-QI).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Software Library
The code for each algorithm introduced in this paper can be found in our Python library, qsparse, at https://github.com/mlzxy/qsparse (accessed on 30 June 2022). In Listing A1, we provide an example of how to use our algorithms for quantization and pruning as PyTorch modules [47].
Listing A1. Examples of our software interface for quantization and pruning on activations.

The majority of existing model compression Python libraries provide either quantization [62,63,64] or pruning [18] support. In contrast, the simplicity of our framework enables an efficient software interface that supports a wide range of neural network architectures for both pruning and quantization. To improve the library flexibility, we introduce a technique that directly transforms the weight attribute of the input layer into a pruned or quantized version at runtime, as shown in Listing A2. Thus, our library is layer-agnostic and can work with any PyTorch module as long as their parameters can be accessed from their weight attribute, as is standard practice [47].
Listing A2. An illustration of the technique we use to create weight-quantized modules without modifying the internal implementation of specific modules. By injecting the weight property, we are able to automatically apply quantization or pruning at each access of weight. By chaining transformations for both prune and quantize, we create modules with weights that are jointly pruned and quantized.

Based on our custom modules and transformation technique, we provide the network conversion function, as shown in Listing A3, in which we traverse the entire network and automatically modify the computational graph to the aim of pruning and quantization. For each network in our experiments, we apply different conversions on top of the baseline network to the requirements of evaluation.
Listing A3. An example usage of our software interface for converting the computational graph of a pre-defined full-precision network to a quantized one by injecting the quantize module after each ReLU and transforming each Conv2d to its weight-quantized version without the need to modify the implementation of the original network.

Notes
| 1 | We use a network architecture comparable to LeNet for the purpose of a reasonably symmetric evaluation across discriminative and generative tasks. Our encoder uses two convolution layers, each followed by a ReLU and max pooling layer. Our decoder uses three deconvolution layers, each followed by a ReLU except for the final deconvolution layer, which is followed by a sigmoid. |
| 2 | We repeated these experiments using the -norm of the output activations and saw very similar results. |
| 3 | The code for the algorithms discussed in this paper can be found at https://github.com/mlzxy/mdpi202 (accessed on 30 June 2022). |
| 4 | We define operating memory as the aggregate hardware storage area used for weights and activations of the network during inference, all of which are required to be kept so they can be readily accessed. |
References
- Hestness, J.; Narang, S.; Ardalani, N.; Diamos, G.; Jun, H.; Kianinejad, H.; Patwary, M.; Ali, M.; Yang, Y.; Zhou, Y. Deep learning scaling is predictable, empirically. arXiv 2017, arXiv:1712.00409. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Network with Pruning, Trained Quantization and Huffman Coding. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Gale, T.; Elsen, E.; Hooker, S. The state of sparsity in deep neural networks. arXiv 2019, arXiv:1902.09574. [Google Scholar]
- Polino, A.; Pascanu, R.; Alistarh, D. Model compression via distillation and quantization. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Dong, X.; Yang, Y. Network pruning via transformable architecture search. arXiv 2019, arXiv:1905.09717. [Google Scholar]
- Wang, T.; Wang, K.; Cai, H.; Lin, J.; Liu, Z.; Wang, H.; Lin, Y.; Han, S. Apq: Joint search for network architecture, pruning and quantization policy. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 2078–2087. [Google Scholar]
- Paupamah, K.; James, S.; Klein, R. Quantisation and pruning for neural network compression and regularisation. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 1–6. [Google Scholar]
- Liang, T.; Glossner, J.; Wang, L.; Shi, S.; Zhang, X. Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing 2021, 461, 370–403. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, X.; Bates, D.; Mullins, R.; Xu, C.Z. Focused quantization for sparse CNNs. arXiv 2019, arXiv:1905.09717. [Google Scholar]
- Yu, P.H.; Wu, S.S.; Klopp, J.P.; Chen, L.G.; Chien, S.Y. Joint Pruning & Quantization for Extremely Sparse Neural Networks. arXiv 2020, arXiv:2010.01892. [Google Scholar]
- Colbert, I.; Kreutz-Delgado, K.; Das, S. AX-DBN: An approximate computing framework for the design of low-power discriminative deep belief networks. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–9. [Google Scholar]
- Van Baalen, M.; Louizos, C.; Nagel, M.; Amjad, R.A.; Wang, Y.; Blankevoort, T.; Welling, M. Bayesian bits: Unifying quantization and pruning. Adv. Neural Inf. Process. Syst. 2020, 33, 5741–5752. [Google Scholar]
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Mao, H.; Han, S.; Pool, J.; Li, W.; Liu, X.; Wang, Y.; Dally, W.J. Exploring the Granularity of Sparsity in Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel pruning for accelerating very deep neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 1389–1397. [Google Scholar]
- Jha, N.K.; Mittal, S.; Avancha, S. Data-type aware arithmetic intensity for deep neural networks. Energy 2021, 120, x109. [Google Scholar]
- Colbert, I.; Kreutz-Delgado, K.; Das, S. An Energy-Efficient Edge Computing Paradigm for Convolution-Based Image Upsampling. IEEE Access 2021, 9, 147967–147984. [Google Scholar] [CrossRef]
- Blalock, D.; Gonzalez Ortiz, J.J.; Frankle, J.; Guttag, J. What is the state of neural network pruning? Proc. Mach. Learn. Syst. 2020, 2, 129–146. [Google Scholar]
- Chen, T.; Chen, X.; Ma, X.; Wang, Y.; Wang, Z. Coarsening the Granularity: Towards Structurally Sparse Lottery Tickets. In Proceedings of the International Conference on Machine Learning, Baltimore, MA, USA, 17–23 July 2022. [Google Scholar]
- Hu, H.; Peng, R.; Tai, Y.W.; Tang, C.K. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar]
- Dai, B.; Zhu, C.; Guo, B.; Wipf, D. Compressing neural networks using the variational information bottleneck. In Proceedings of the International Conference on Machine Learning. PMLR, 2018, Stockholm, Sweden, 10–15 July 2018; pp. 1135–1144. [Google Scholar]
- Molchanov, P.; Mallya, A.; Tyree, S.; Frosio, I.; Kautz, J. Importance estimation for neural network pruning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11264–11272. [Google Scholar]
- Zhu, M.; Gupta, S. To Prune, or Not to Prune: Exploring the Efficacy of Pruning for Model Compression. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Luo, J.H.; Wu, J.; Lin, W. Thinet: A filter level pruning method for deep neural network compression. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 5058–5066. [Google Scholar]
- Wang, Y.; Lu, Y.; Blankevoort, T. Differentiable joint pruning and quantization for hardware efficiency. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 259–277. [Google Scholar]
- Wu, H.; Judd, P.; Zhang, X.; Isaev, M.; Micikevicius, P. Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation. arXiv 2020, arXiv:2004.09602. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar]
- Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A survey of quantization methods for efficient neural network inference. arXiv 2021, arXiv:1806.08342. [Google Scholar]
- Jain, S.; Gural, A.; Wu, M.; Dick, C. Trained quantization thresholds for accurate and efficient fixed-point inference of deep neural networks. Proc. Mach. Learn. Syst. 2020, 2, 112–128. [Google Scholar]
- Knight, W.R. A computer method for calculating Kendall’s tau with ungrouped data. J. Am. Stat. Assoc. 1966, 61, 436–439. [Google Scholar] [CrossRef]
- Levenshtein, V.I. Binary codes capable of correcting deletions, insertions, and reversals. In Soviet Physics—Doklady; 1966; Volume 10, pp. 707–710. Available online: https://nymity.ch/sybilhunting/pdf/Levenshtein1966a.pdf (accessed on 30 June 2022).
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y. The MNIST Database of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 30 June 2022).
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE information theory workshop (itw), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–20 June 2016; pp. 770–778. [Google Scholar]
- Liu, Z.; Sun, M.; Zhou, T.; Huang, G.; Darrell, T. Rethinking the Value of Network Pruning. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv 2013, arXiv:1308.3432. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the International Conference on Machine Learning, PMLR, 2018, Stockholm, Sweden, 10–15 July 2018; pp. 4510–4520. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 30 June 2022).
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical image computing and computer-assisted intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Pohlen, T.; Hermans, A.; Mathias, M.; Leibe, B. Full-resolution residual networks for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21—26 July 2017; pp. 4151–4160. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA; pp. 2223–2232.
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Nautilus. 2022. Available online: https://ucsd-prp.gitlab.io/ (accessed on 30 June 2022).
- Thomas, M.M.; Vaidyanathan, K.; Liktor, G.; Forbes, A.G. A reduced-precision network for image reconstruction. ACM Trans. Graph. Tog 2020, 39, 1–12. [Google Scholar] [CrossRef]
- Rezk, N.M.; Nordström, T.; Ul-Abdin, Z. Shrink and Eliminate: A Study of Post-Training Quantization and Repeated Operations Elimination in RNN Models. Information 2022, 13, 176. [Google Scholar] [CrossRef]
- Yang, H.; Gui, S.; Zhu, Y.; Liu, J. Automatic neural network compression by sparsity-quantization joint learning: A constrained optimization-based approach. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2178–2188. [Google Scholar]
- Zhang, X. A Design Methodology for Efficient Implementation of Deconvolutional Neural Networks on an FPGA; University of California: San Diego, CA, USA, 2017. [Google Scholar]
- Biookaghazadeh, S.; Zhao, M.; Ren, F. Are {FPGAs} Suitable for Edge Computing? In Proceedings of the USENIX Workshop on Hot Topics in Edge Computing (HotEdge 18), Boston, MA, USA, 10 July 2018. [Google Scholar]
- Colbert, I.; Daly, J.; Kreutz-Delgado, K.; Das, S. A competitive edge: Can FPGAs beat GPUs at DCNN inference acceleration in resource-limited edge computing applications? arXiv 2021, arXiv:2102.00294. [Google Scholar]
- Choi, Y.; El-Khamy, M.; Lee, J. Towards the Limit of Network Quantization. In Proceedings of the International Conference on Learning Representations, oulon, France, 24–26 April 2017. [Google Scholar]
- Achterhold, J.; Koehler, J.M.; Schmeink, A.; Genewein, T. Variational network quantization. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Zhao, C.; Ni, B.; Zhang, J.; Zhao, Q.; Zhang, W.; Tian, Q. Variational convolutional neural network pruning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2780–2789. [Google Scholar]
- Xiao, X.; Wang, Z. Autoprune: Automatic network pruning by regularizing auxiliary parameters. Adv. Neural Inf. Process. Syst. (NeurIPS 2019) 2019, 32. [Google Scholar]
- Dettmers, T.; Zettlemoyer, L. Sparse networks from scratch: Faster training without losing performance. arXiv 2019, arXiv:1907.04840. [Google Scholar]
- Paupamah, K.; James, S.; Klein, R. Quantisation and pruning for neural network compression and regularisation. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 1–6. [Google Scholar]
- Choi, Y.; El-Khamy, M.; Lee, J. Universal deep neural network compression. IEEE J. Sel. Top. Signal Process. 2020, 14, 715–726. [Google Scholar] [CrossRef] [Green Version]
- Pappalardo, A. Xilinx/Brevitas. Available online: https://zenodo.org/record/5779154#.YujQyepBxPY (accessed on 30 June 2022).
- torch.nn.qat — PyTorch 1.9.0 Documentation. 2021. Available online: https://pytorch.org/docs/stable/torch.nn.qat.html (accessed on 30 June 2022).
- Coelho, C.N., Jr.; Kuusela, A.; Zhuang, H.; Aarrestad, T.; Loncar, V.; Ngadiuba, J.; Pierini, M.; Summers, S. Ultra low-latency, low-area inference accelerators using heterogeneous deep quantization with QKeras and hls4ml. arXiv 2020, arXiv:2006.10159. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).