An Adaptive Dempster-Shafer Theory of Evidence Based Trust Model in Multiagent Systems

Abstract

Multiagent systems (MASs) have a wide range of industrial applications due to agents’ advantages. However, because of the agents’ dynamic behaviors, it is a challenge to ensure the quality of service they present. In this paper, to address this problem, we propose an adaptive agent trust estimation model where agents may decide to go from genuine to malicious or the other way around. In the proposed trust model, both direct trust and indirect reputation are used. However, the indirect reputation derived from the direct experience of third-party agents must have reasonable confidence to be useful. The proposed model introduces a near-perfect measure that utilizes consistency, credibility, and certainty to capture confidence. Moreover, agents are incentivized to contribute correct information (to be honest) through a credit mechanism in the proposed model. Simulation experiments are conducted to evaluate the proposed model’s performance against some of the previous trust models reported in the literature.

1. Introduction

Trust and reputation estimation is typical daily social behavior. Before purchasing particular items, rational customers accumulate information to determine the product’s quality. The decision-maker would highly rely on the comprehensive trustworthiness of the product provider. Similarly, the same mechanism fits MASs, especially for MASs with deceptive agents in a distributed environment.

Numerous protocols have been used to accentuate the trustworthiness issue in MASs. Generally, four models associated with trusted systems are commonly applied. The logical models describe how one agent trusts another according to mathematical logic. The social-cognitive models decide agents’ trustworthiness inspired by human psychology. Organizational models maintain trust through personal relationships in the system, whereas numerical models understand trust from a mathematical probability perspective [1,2]. Each of the four models has advantages for trust estimation.

In the numerical models, an agent’s trustworthiness is represented by a real number, signifying the possibility that the interaction with it is a success. The service provider with a high degree of trust is more likely to be selected. To obtain the honesty of an agent, trust models need to collect some information concerning possible cooperation. In general, the trust estimation mainly comes from the following types of information: direct trust, which is based on experience from its direct interactions [3,4]; indirect reputation, which is based on the testimonial presented by third-party agents [2,5]. In addition, social cognitive information and organizational knowledge are other essential aspects [6,7,8]. However, the collected information from the third-party agents must involve significant uncertainty; therefore, the collected information must have rational confidence to be serviceable.

In terms of distinguishing reliable information collected from third-party agents, some assume that the majority of agents are dependable [2]. Some identify dishonest agents through personal direct experience [9] or filter out the unreliable recommendation and discount their evidence by assigning adaptive weights [9,10,11,12]. Although some of them have excellent security features, most assume that service providers have a list of static performance. That is to say, service providers are all trusted and maintain their honest behavior consistently. What is more, the testimony provided by the third party is always reliable. However, there is no guarantee that service providers and witnesses would always present static behavior. They might decide to go from genuine to malicious or the other way around. Thus, the general assumption might be insufficient due to the dynamic behavior of agents in MASs. Furthermore, most systems that we reviewed only consider reliability, certainty, or consistency as separate models in MASs. These models do not exploit an integrated model concerning all aspects of trust for trustworthiness estimation.

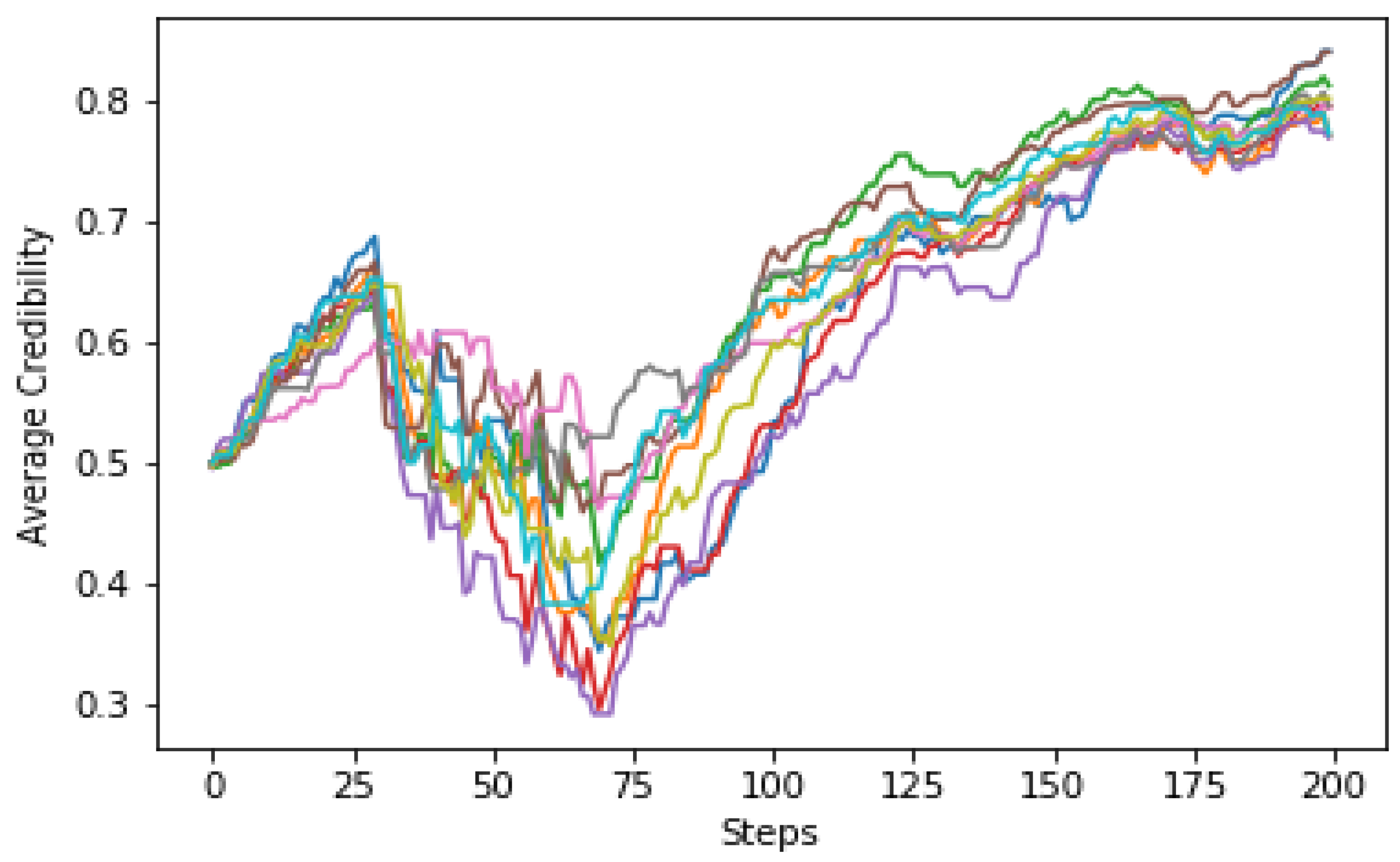
In summary, agents, both resource providers and third-party agents, can change their performances in MASs. In the numerical models, much information is collected to evaluate direct trust and indirect reputation. However, much uncertainty stems from incompleteness, randomness, fading, and so forth in direct trust, whereas the collected information from third-party agents must have rational confidence to be serviceable. This paper proposes an adaptive trust model in MASs where agents’ behaviors might differ over time. Agents in this model can be service providers, as well as witnesses who give testimony for trust estimation. The Dempster-Shafer theory of evidence is adopted to capture direct trust. Dynamic adaptive weights that depend on the quality of the collected information, the witness’s credibility, and the certainty are used to characterize confidence for modifying the indirect reputation. The ultimate trust combines both direct trust and indirect reputation. Our model presents customer agents with a measure to decide with which agent to interact. The rest of the paper is organized as follows. Some related work is introduced in Section 2. The primary tool, the Dempster-Shafer theory of evidence, is discussed in Section 3. Section 4 explains the proposed trust model in detail. Comparisons and conclusions are given in the last section.

2. Related Work

Trust, a subjective judgment, refers to the confidence in some aspect or another of a relationship in most of our reviewed articles [4]. It was first introduced in computer science as a measure of an agent in 1994 [13]. Trust can be classified into three types [14,15]. The first type of trust refers to truth and belief, which means trusting the behavior or quality of the other object. Next, trust implies that a declaration is correct. Finally, “Trust as commerce” indicates the ability or the intention of a buyer to purchase in the future. In this paper, we adopt the first class, that is to say, trust can be interpreted by believing the behavior and quality of the identity.

The literature is plentiful with various approaches to trust estimation in MASs [2,15,16,17,18,19]. In general, trust should be based on evidence consisting of positive and negative experiences with it [15,20,21]. Jøsang, A and Ismail, R capture trust in MASs based on the beta probability density functions that rely on the number of negative and positive interactions [2]. The probability expectation is used to express the trust value. The literature [22] provides a systematic study on when it is beneficial to combine direct trust and indirect reputation. TRAVOS [9] models trustworthiness probabilistically through a beta distribution computed from the outcomes of all the interactions a truster has observed, and it uses the probability of successful interaction between two agents to capture the value of trustworthiness. Fortino, Giancarlo, et al. studied trust and reputation in the Internet of Things [23]. In addition, some references evaluate trustworthiness by taking advantage of recent performances. In the literature [12,24], they achieve trust by evaluating recent performance and historical evaluations. However, trust evaluation might encounter uncertainty deviated from cognitive impairment, inefficient evidence, randomness, and incomplete information [25,26]. Wang and Singh use evidence theory to present uncertainty for trust estimation [27,28,29]. In Zuo and Liu’s model [30], they adopt a three-value opinion (belief, disbelief, uncertainty) in the opinion-based model for trust estimation. However, these models are questionable for trust estimation in a MAS with deceptive agents involved. At the same time, most of them define uncertainty by the medium evaluations. However, as explained, uncertainty stems from cognitive impairment, inefficient evidence, randomness, and incomplete information [25,26]. Therefore, a more exhaustive exploration that exploits the uncertainty needs to be carried out.

It is natural and reasonable to query for third-party information whenever the direct experience is insufficient. However, it is risky to make a final decision relying entirely and directly on the gathered information in a distributed MAS, especially with deceptive agents involved. Thus, we need to ensure that the accumulated information is reliable before being used. Therefore, the concept of confidence is adopted to capture the reliability of gathered information [9,12,15,20,24,28,31]. We define confidence as a probability that the trust is applicable, supported by evidence, consistency, credibility, and certainty. However, most of these models only take some aspects into consideration as a separate trust model in MASs.

First, some trust models assume that most third -party agents are reliable [2]. Thus, those opinions that are consistent with the majority can be regarded as reliable [2,32]. Others identify unreliable agents by comparing them with direct experience [9,28]. Here in this paper, we define this property as consistency. Consistency displays the differences or similarities with other evidence. It is helpful, especially for those agents whose trust and certainty are unknown. However, most of our reviewed articles did not pay much attention to consistency for trust estimation in MASs.

Credibility is widely applied in distributed MASs to capture confidence. In most circumstances, credibility can be interpreted as a weight indicating how much the agent could be reliable [12]. It is updated according to the provided information and the interactive feedback [12,24,28,29]. However, in the literature [12,28], the credibility of the third party agents decreases gradually; that is to say, the truster will no longer believe the agents with sufficient interactions. In the literature [29], the Dempster-Shafer theory of evidence is used to reach trust. However, the credibility of the third-party agents increases if the feedback is a success, and the other way around. In dynamic MASs, false information might also be reliable, and it can be caused by changing performance. Thus, improving agents’ credibility through current interactions can be questionable and not enough.

Certainty is “a measure of confidence that an agent may place in the trust information” [15]. Measuring certainty can filter out reliable information efficiently [33]. As previously stated, trust always involves uncertainty caused by the lack of certainty, a lack of right and complete information, or randomness [34]. Thus, the information that comes from a different degree of certainty may affect the confidence of that agent. For instance, agent A always trusts agent B, yet agent B is uncertain about its information towards some event. Thus, agent A would hesitate at the collected information from agent B. In the literature [31], the trust model uses fuzzy sets and assigns certainty to each evaluation. In [15], the model analyzed certainty to capture confidence. Most trust models believe that certainty and trust are independent. However, we consider trust as the rate of successful interaction. Thus, uncertainty comes from the conflict between successful and failed interactions, and certainty should depend on evidence.

In summary, the influential factors and their explanations for trust estimation in MASs are listed in

Table 1. Influential factors for trust estimation in MASs.

	Definition	Why the Factor Is Influential
Uncertainty (Direct trust)	Uncertainty caused by fading, randomness, incompleteness, etc.	To ensure trust accuracy in dynamic MASs
Consistency (Confidence)	The degree of similarity with third-party testimony	To tell high-quality evidence; Avoid sudden change
Credibility (Confidence)	The credibility degree of third-party witnesses	To distinguish trusted witnesses and avoid group deception
Certainty (Confidence)	The certainty degree of third-party testimony	To capture the certainty of testimony
Motivation	Inspire witnesses to be honest	Ensure the system runs correctly

. As we can see, from our perspective, we value uncertainty, evidence consistency, witness’ credibility, and certainty and the motivation for a witness, and they are influential factors for trust estimation in MASs. In what follows, we will display some of the recent trust estimation models that are related to confidence estimation.

FIRE is an integrated trust and reputation model for open MASs according to interaction trust (IT), role-based trust (RT), witness trust (WT), and certified trust (CT) [35]. It is direct trust calculated by direct experience; RT, WT, and CT are about witness experience. FIRE presents good performance. However, the model does not stress uncertainty and assumes that all agents provide accurate information. In addition, many static parameters must be used in the model, which limits its application [24,36]. SecuredTrust is a dynamic trust computation model in MASs [32]. The model addresses many factors, including differences and similarities. However, feedback credibility generated from similarity is used to capture the degree of accuracy of the feedback information, which is the same as consistency. However, certainty and personal credibility are not well stressed. At the same time, an incentive mechanism should be used to encourage agents to be reliable. The actor–critic model selects reliable witnesses by reinforcement learning [37]. It dynamically selects credible witnesses as well as the parameters associated with the direct and indirect trust evidence based on interactive feedback. Nevertheless, when only one known witness is available for the indirect reputation, bootstrapping errors occur [38]. What is more, capturing uncertainty in a perfect trust estimation model in a dynamic system is necessary. By analyzing uncertainty, we can obtain a degree of certainty and filter out reliable agents efficiently. An adaptive trust model for mobile agent systems is established. The model combines direct trust and indirect reputation and also assesses the credibility of witnesses. Moreover, the model considers that uncertainty when generating direct trust is reasonable. However, witnesses’ certainty is necessary for a trust model, especially a dynamic trust model. Despite the advantages presented by the models noted above, these trust models are still imperfect and can be extended. This paper proposes an evidence theory-based trust model. It first improves the inappropriate witness credibility updating approach in previous articles. When capturing direct trust, the model manages uncertainty from the perspective of cognitive impairment, inefficient evidence, randomness, and incomplete information [25,26]. What is more, consistency, credibility, and certainty are declared to achieve confidence. An encouragement mechanism is used to inspire agents to provide reliable information.

3. Dempster-Shafer Theory of Evidence

The Dempster-Shafer theory of evidence, proposed by Dempster and Shafer to handle uncertainty [39,40], has a wide range of applications in risk assessments, medical diagnosis, and target recognition [41,42,43]. It is a typical method of uncertainty information fusion because of its adjustability in uncertainty modeling [44]. Some preliminaries are introduced below.

Definition 1.

The frame of discernment and BPAs.

Evidence theory is defined in the frame of discernment denoted by $\Omega$, which consists of n mutually exclusive and collectively exhaustive elements; $2^{\Omega }$ is the set of all subsets of $\Omega$, which is represented by $2^{\Omega }=\{\varnothing ,\left\{{\theta }_1\right\},\left\{{\theta }_2\right\},\dots ,$$\left\{{\theta }_n\right\},\{{\theta }_1,{\theta }_2\},\dots ,$$\{{\theta }_1,{\theta }_2,\dots ,$${\theta }_n\left\}\right\}$. Mathematically, a basic probability assignment (BPA, also known as mass function) is $2^{\Omega }\to [0,1]$, with the following conditions satisfied:

$$\left\{\begin{array}{c}\sum _{A\in 2^{\Omega }}m(A)=1;\hfill \\ m(\varnothing )=0,\hfill \end{array}\right.$$

(1)

where ∅ is the empty set, the subsets $A\in 2^{\Omega }$ such that $m(A)>0$ is named as focus element, and the set of all focus elements is called core. The other two functions (belief function and plausibility function) are defined as follows.

Definition 2.

Belief function.

The belief function Bel of BPA m is defined as follows:

$$Be{l}_m(A)=\sum _{B\in 2^{\Omega }:B\subseteq A}m(B)$$

(2)

Definition 3.

Plausibility function.

The plausibility function Pl of BPA m is defined as follows:

$$P{l}_m(A)=\sum _{B\in 2^{\Omega }:B\bigcap A\ne \varnothing }m(B)$$

(3)

In the Dempster-Shafer theory of evidence, Dempster’s combination rule can be used to combine multiple pieces of evidence to reach the final evaluation. Given two BPAs $m_1$ and $m_2$, the Dempster’s combination rule denoted by $m=m_1\oplus m_2$ can fuse them as follows.

Definition 4.

Dempster’s combination rule.

$$m(A)=\left\{\begin{array}{cc}\frac{1}{1-K}\sum _{B\cap C=A}{m}_1(B)m_2(C),\hfill & A\ne \varnothing ;\hfill \\ 0,\hfill & A=\varnothing ;\hfill \end{array}\right.$$

(4)

with $K={\sum }_{B\cap C=\varnothing }{m}_1(B)m_2(C)$, A, B, and C are elements in $2^{\Omega }$. The normalization constant K shows the conflicting degree between defined BPAs. If $K=1$, the two pieces of evidence totally conflict, and Dempster’s combination rule is not applicable. If $K=0$, the two pieces of evidence are non-conflicting.

Definition 5.

Evidence distance.

With the full application of evidence theory, the study of the distance of evidence has attracted increasing interest. The distance measure of evidence can represent the dissimilarity between two BPAs, and several definitions of distance in evidence theory have also been proposed, such as Jousselme’s distance [45], Wen’s cosine similarity [46], and Smets’ transferable belief model (TBM) global distance measure [47]. Jousselmes distance [45] is one of the rational and popular definitions of distance, which is identified based on Cuzzolin’s geometric interpretation of evidence theory [48]. The power set of the frame of discernment space and a distance and vectors are defined with the BPA as a particular case of vectors [45]. Jousselme’s distance is defined as

$$d(m_i,m_j)=\sqrt{\frac{1}{2}{({\overrightarrow{m}}_i-{\overrightarrow{m}}_j)}^{T}D({\overrightarrow{m}}_i-{\overrightarrow{m}}_j)}$$

(5)

with $m_i$, $m_j$ being two BPAs under the frame of discernment $\Omega$ matrix. The element in D is defined as $D(A,B)=|A\cap B|/|A\cup B|$, $A,B\in \Omega$, and $\left|A\right|$ represents cardinality. Jousselme’s distance is an efficient tool to quantify the dissimilarity of two BPAs.

Definition 6.

Entropy of Dempster-Shafer theory.

The concept of entropy comes from physics, which is a measure of uncertainty and disorder [49,50]. The Shannon entropy has been widely accepted for uncertainty measurement (or information measurement) in information theory [51]. However, the uncertainty estimation of BPAs of the Dempster-Shafer theory of evidence still needs trial and error. Since the first definition of a BPA in the evidence theory was given by Höhle in 1982 [52], many definitions of entropy of the Dempster-Shafer theory have raised, for instance, the definitions proposed by Smets [53], Yager [54], Nguyen [55], Dubois and Prade [56], Deng [57], and so on. However, these definitions are still imperfect. For example, Deng entropy has some limitations when the propositions are of the intersection. Thus, several methodologies have been applied for Deng entropy modification [58,59]. Recently, Jiroušek and P. Shenoy proposed a new definition, in which five of the six listed properties of entropy are satisfied [60]. Whether there exists a definition that satisfies the six properties is still an open issue, but the proposed entropy in [60] is acceptable and could be regarded as near-perfect. As a result, we use the definition of entropy of the Dempster-Shafer theory in the literature [60] for uncertainty estimation in this paper. For the frame of discernment defined in $\Omega$ where $x\in \Omega$ and A is a focal element, the entropy of the BPA m is defined as follows:

$$H(m)=H_s(Pl\_P_m)+H_d(m)=\sum _{x\in \Omega }Pl\_P_m(x)log(\frac{1}{Pl\_P_m(x)})+\sum _{A\in 2^{\Omega }}m(A)log(|A|)$$

(6)

where the first part is employed to measure conflict [60,61], and $Pl\_P_m(x)$ is defined as the plausibility transform [60,62], where

$$Pl\_P_m(x)=\frac{P{l}_m(x)}{{\sum }_{x\in \Omega }(P{l}_m(x))}$$

(7)

The second part in Equation (6) can be regarded as non-specificity of the BPA m [56]. That is to say, the uncertainty of the Dempster-Shafer theory of evidence can be captured from two aspects, namely the conflicts between exclusive elements in set $\Omega$ and the non-specificity uncertainty. Both components are on the scale $[0,log(|\Omega |)]$, thus, the maximum entropy of a BPA is $2log(|\Omega |)$.

Example 1.

An example of the Dempster-Shafer theory of evidence is given as follows. Suppose an animal stands far away from us, perhaps a cat or a dog. Then the frame of discernment is presented as $\Omega =\{cat,dog\}$, and three passers-by show their opinions. Their opinions are shown as

1. 

$m_1(Cat)=0.6$, $m_1(Dog)=0.3$, $m_1(Cat,Dog)=0.1$

2. 

$m_2(Cat)=0.4$, $m_2(Dog)=0.4$, $m_2(Cat,Dog)=0.2$

3. 

$m_3(Cat)=0.1$, $m_3(Dog)=0.4$, $m_3(Cat,Dog)=0.5$

In terms of evidence distance, we have the following calculation process:

• $\overrightarrow{m_1}=\{Cat,Dog,(Cat,Dog)\}=(0.6,0.3,0.1)$. Similarly, $\overrightarrow{m_2}=(0.4,0.4,0.2)$, $\overrightarrow{m_3}=(0.1,0.4,0.5);$
• $\mathrm{D}=\begin{array}{c}Cat\\ Dog\\ \left(Cat,Dog\right)\end{array}\begin{array}{c}\begin{array}{ccc}Cat& Dog& \left(Cat,Dog\right)\end{array}\\ \left[\begin{array}{ccc}1& 0& 0.5\\ 0& 1& 0.5\\ 0.5& 0.5& 1\end{array}\right]\end{array}$
• $(\overrightarrow{m_1}-\overrightarrow{m_2})=(0.2,-0.1,-0.1);$
• $d(m_1,m_2)=\sqrt{\frac{1}{2}{(\overrightarrow{m_1}-\overrightarrow{m_2})}^{T}D(\overrightarrow{m_1}-\overrightarrow{m_2})}=0.158$. In a similar way, $d(m_1,m_3)=0.361$ and $d(m_2,m_3)=0.212.$

The three passers-by are all not one hundred percent sure what the animal is. Nevertheless, we may study their degrees of uncertainty, respectively. Let us take the first witness as an example.

• $Pl\_P_m(Cat)={\displaystyle \frac{P{l}_m(Cat)}{{\sum }_{x\in \Omega }(P{l}_m(x))}}=$${\displaystyle \frac{0.6+0.1}{0.6+0.1+0.3+0.1}}=$$\frac{7}{11}$. In the same manner, $Pl\_P_m(Dog)=\frac{4}{11};$
• Thus, H($m_1$)$=\frac{7}{11}lo{g}_2(\frac{7}{11})$$+\frac{4}{11}lo{g}_2(\frac{4}{11})+$$0.6\ast log2(|Cat|)+0.3\ast log2(|Dog|)+$$0.1\ast log2(|(Cat,Dog)|)=1.046.$ In the same way, H($m_2)=1.2,$ and H($m_3)=1.47.$ As we can see, the testimony given by the third passer-by is the most vague and uncertain.

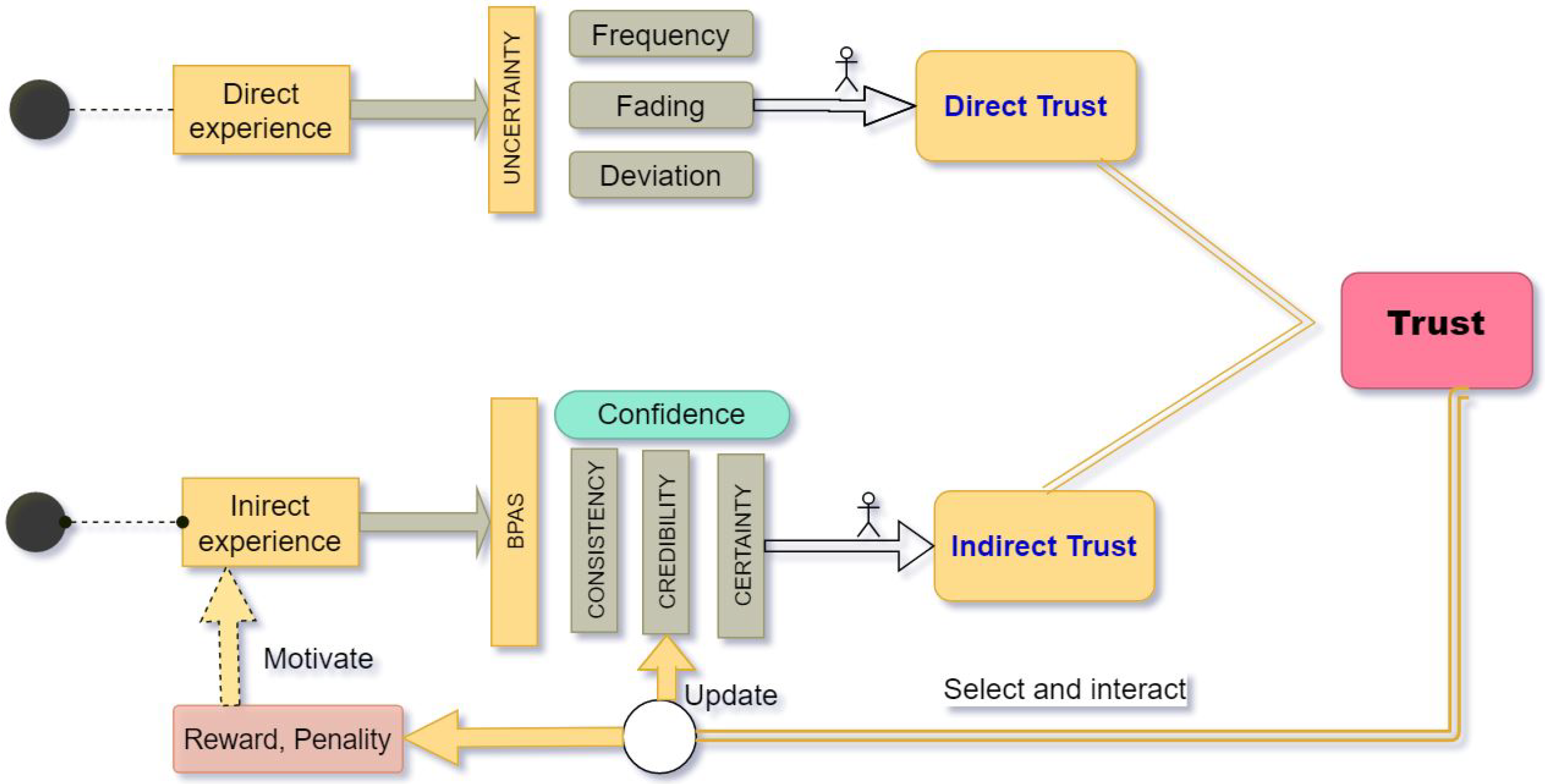
4. Proposed Trust Model

This section presents the trust model for trust estimation in MASs, where agents’ behaviors might differ over time. The proposed method relies on direct trust learned from direct experience and indirect reputation by integrating all indirect experience provided by third-party agents (witness). We study the confidence of witnesses and then combine both direct trust and indirect reputation. In more detail, the direct satisfaction statement based on interactive feedback is first illustrated, mainly emphasizing that recent interactions are more prominent by assigning higher weight. In this way, the proposed method is fitting for dynamic trust estimation. The uncertainty that stems from randomness, incomplete information, and inefficient interactions is then addressed, and the Dempster-Shafer theory of evidence is employed to represent direct trust. We then studied the confidence of individual evidence to determine indirect reputation. Subsequently, direct trust and indirect reputation are combined, and we reach the resource provider’s trustworthiness. The agent with the highest trust value is selected to raise interactions. The credibility of witnesses is updated by the interactive feedback and the average evaluation after the interaction. Finally, credits are reassigned to witnesses, with which they are able to purchase information for trustee evaluations. In this way, information providers are motivated to present accurate information. For simplicity, the detailed processes are shown in Figure 1, and some related parameters are listed in

Table 2. Explanation of main variables.

$c_i$	The resource customer agent $c_i$
$s_i$	The resource supplier agent $s_i$
$w_k$	The information provider (witness) $w_k$
$Scu{r}_{ij}(t)$	The evaluation of the tth interaction
$S_{ij}(t)$	The satisfaction degree before the tth interaction
${\mu }_{ij}(t)$	The relationship between evaluation and current satisfaction
$f{q}_{ij}(R)$	The uncertainty factor
$\Omega =\{T,nT\}$	The frame of discernment
$m_{ij}^d$	The direct evidence
$m_{ij}^{ind}$	The indirect evidence
$Conf(c_i,w_k)$	The confidence degree of $w_k$ from the perspective of $c_i$
$Dis(m_{kj}^{ind})$	The distance of $m_{kj}^{ind}$ in the group of L witness
$Sim(m_{kj}^{ind})$	The similarity of $m_{kj}^{ind}$ in the group of L witness
$Cred(c_i,w_k)$	The credibility value of $w_k$ from the perspective of $c_i$
$Cer(m_{kj})$	The certainty of $w_k$

.

4.1. Direct Trust

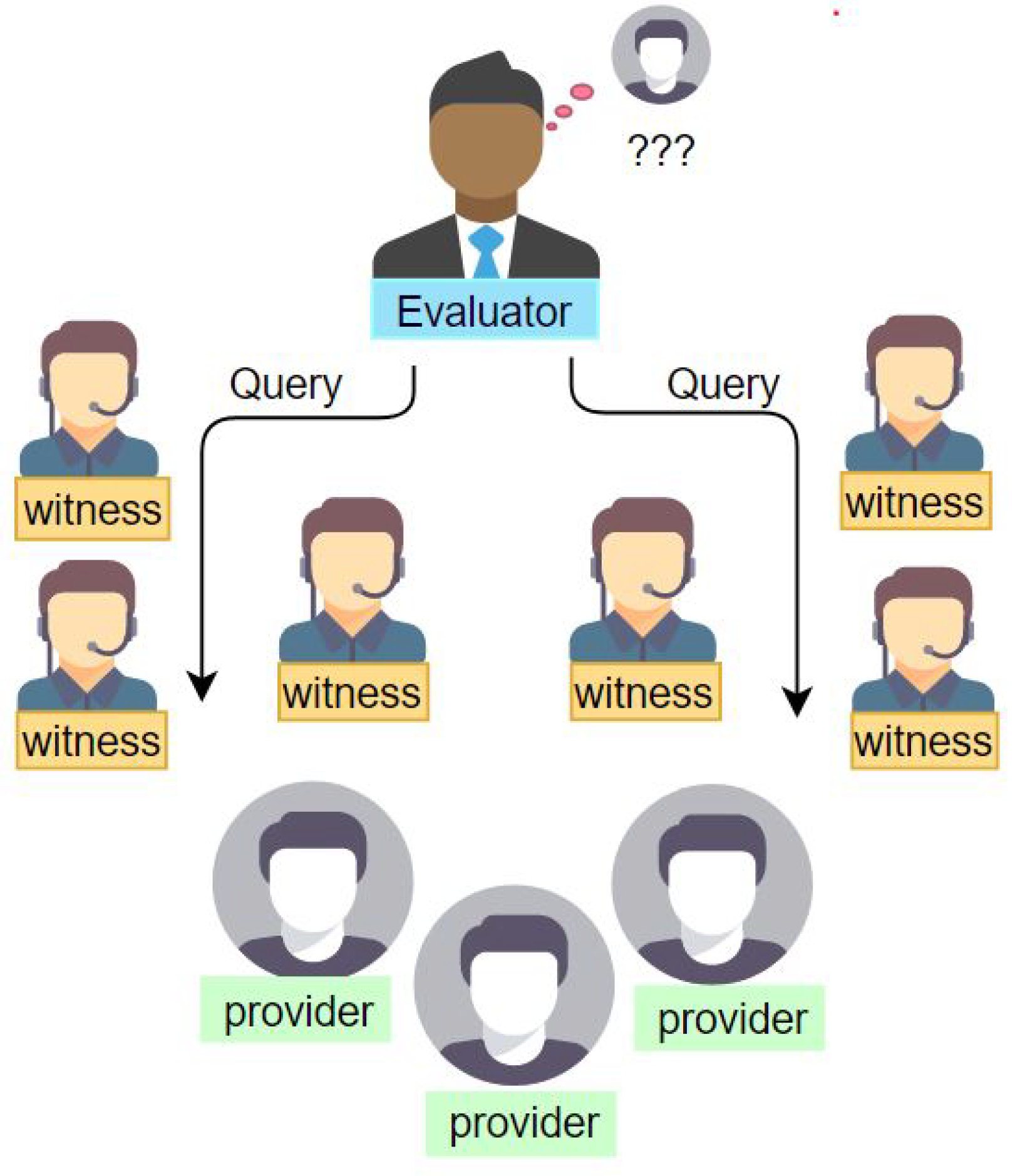
Direct trust is a performance prediction for the next interaction of the selected agent based on previous interaction feedback. The obtained interactive feedback could be binary, i.e., a success or a failure, or any real number in the range $[0,1]$ indicating that the received service is satisfying. This real number can also be interpreted as the trustworthiness of the information or service provider. For the sake of clarity, the service requester is represented by service client agent $c_j$, the service provider is modeled as service provider agent $s_j$, and those who present information to help evaluate the performance are represented as witness agent $w_k$. As is shown in Figure 2, the client agent (evaluator) $c_i$ estimates the trustworthiness of the resource providers $s_j$ according to its direct experience and the indirect reputation provided by the witness $w_k$.

After interactions, each service client updates the corresponding satisfaction degree for each service provider according to its current degree of compensation and the feedback outcome. Of the previous literature, they average all the evaluations to obtain the ultimate satisfactory degree. In [27], an evidence theory-based trust model, two parameters are employed to classify evaluations into trust, uncertainty, and distrust, and the medium evaluations are appointed as uncertainty. It could work, but we argue that recent interactions in dynamic MASs should significantly affect the final assessment, and many causes can result in uncertainty, including medium evaluation as well as conflict evaluations. Subsequently in the literature [2,9], assigning higher weights to the freshest interactions seems reasonable. From our perspective, uncertainty caused by randomness, incomplete information, and the environment is inevitable and should be taken into account in dynamic MASs. Moreover, clients could not have sufficient interactions with one fixed agent all over time. Therefore, uncertainty caused by the number and frequency of interactions and the deviation between current trust and performance will be adopted to generate direct trust.

Let T mean that the service client agent considers the service provider agent to be trustworthy. Accordingly, $nT$ indicates that the supplier agent to be untrustworthy. Thus, the frame of discernment is represented by $\Omega =\{T,nT\}$. When $c_i$ needs to appraise the performance of $s_j$, $S_{ij}(t)$ and $Scu{r}_{ij}(t)$ are employed to represent the satisfaction before the tth interaction and of the tth interaction, respectively. The satisfaction is updated as follows:

$$S_{ij}(t+1)={\mu }_{ij}(t)S_{ij}(t)+(1-{\mu }_{ij}(t))Scu{r}_{ij}(t)$$

(8)

As noted above, $Scu{r}_{ij}(t)$ indicates the current interactive feedback, which could be any number in the range of $[0,1]$, namely,

$$Scu{r}_{ij}(t)=\left\{\begin{array}{c}1,c_i\mathrm{is}\mathrm{completely}\mathrm{satisfied}\mathrm{with}{s}_j;\hfill \\ 0,c_i\mathrm{is}\mathrm{completely}\mathrm{unsatisfied}\mathrm{with}{s}_j;\hfill \\ v\in (0,1);\mathrm{others}.\hfill \end{array}\right.$$

(9)

In Equation (8), it is challenging to decide an appropriate value of ${\mu }_{ij}(t)$. In the literature [2], a forgetting factor is adopted. However, the assignment is suitable for the beta reputation system. In [24], they believe that weight is related to interactive times and frequency. Das et al. hold that ${\mu }_{ij}(t)$ should be dependent on the accumulated deviation [32]. From our perspective, we suppose that ${\mu }_{ij}(t)$ should mainly be determined by the current performance deviation. That is to say, we pay much attention to its previous performance if agents act stably. If agents perform differently with their actual property frequently to hide their performance, the evaluation should play a more important role in the final estimation. Usually, ${\mu }_{ij}(t)$ is close to 0, for instance, ${\mu }_{ij}(t)=0.1$, indicating that most agents consistently react, which is rational and intuitive in practical life. In this paper, we define ${\mu }_{ij}(t)$ as follows:

$${\mu }_{ij}(t)=\frac{exp(1)}{exp(|S_{ij}(t)-Scu{r}_{ij}(t)|-1)+exp(1)}$$

(10)

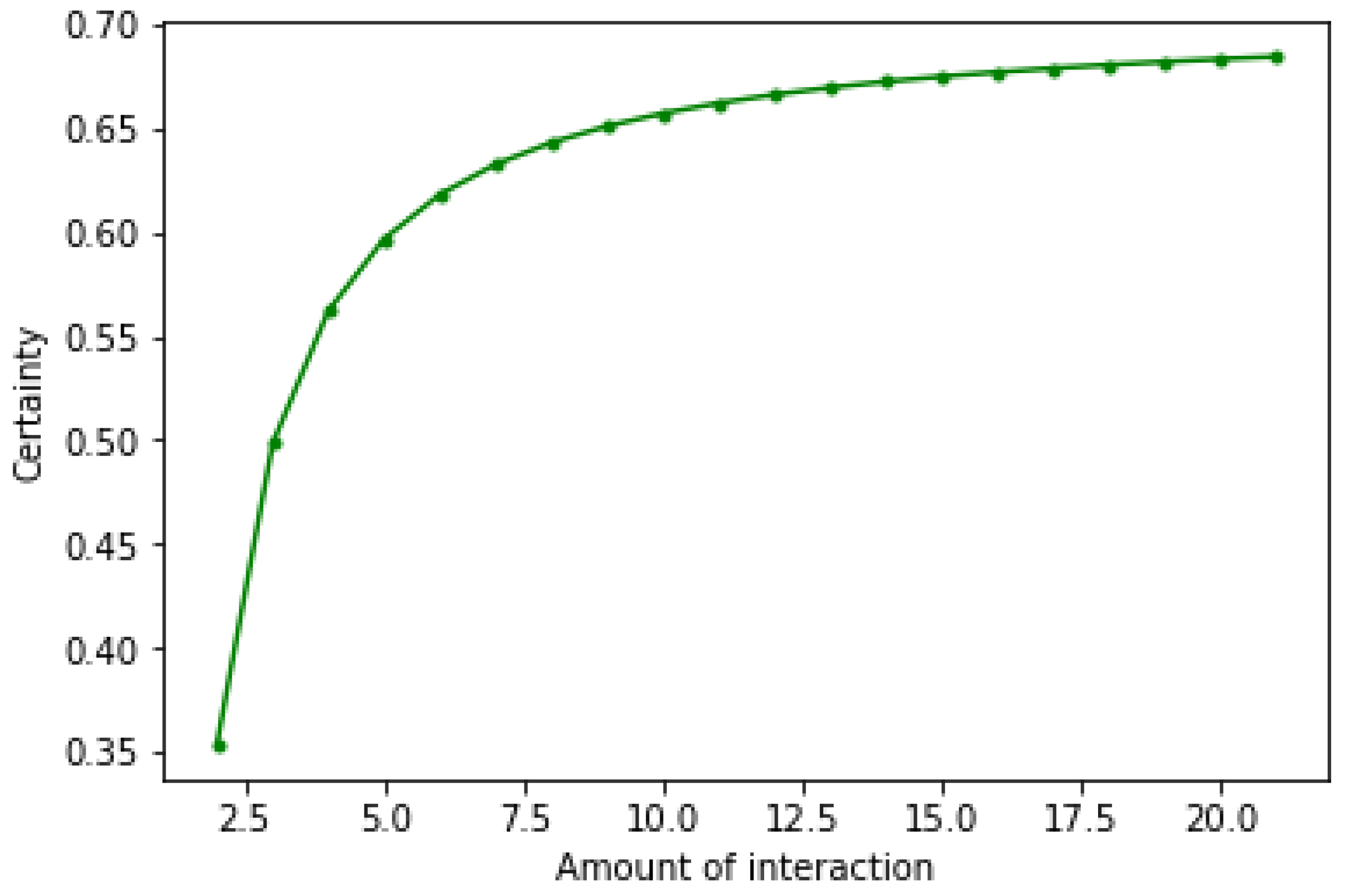
Much uncertainty is involved when generating the evidence due to incomplete information, the interactive frequency, and randomness. A frequency factor $f{q}_{ij}(t)$ is defined to show the uncertainty of $c_i^{\prime }s$ direct experience in the last period, and it is defined as

$$f{q}_{ij}(t)=1-{[\frac{2\ast \lambda }{\pi }\ast atan({\kappa }_{(i,j)})]}^2$$

(11)

where ${\kappa }_{(i,j)}$ shows the amount of interaction between $c_i$ and $s_j$ in the last period considered. The value of $\lambda$ is influenced by the interaction type and the willingness to trust others; it is usually close to 1. As displayed in Equation (11), uncertainty caused by the amount of interaction, incompleteness, and randomness is described, and the uncertainty decreases to 0.2 when two agents have at least eight interactions. As a result, the generated BPAs can be represented as follows:

$$\left\{\begin{array}{c}{m}_{ij}^d(T)=S_{ij}(t)\ast f{q}_{ij}(t)\hfill \\ m_{ij}^d(nT)=(1-S_{ij}(t))\ast f{q}_{ij}(t)\hfill \end{array}\right.$$

(12)

Then $m_{ij}^d(T,nT)=1-(m_{ij}^d(T)+m_{ij}^d(nT))$, the direct experience can also be rewritten as $bp{a}_{ij}^d=$$(m_{ij}^d(T),$$m_{ij}^d(nT),$$m_{ij}^d(T,nT))$.

4.2. Indirect Reputation

In the last subsection, we discussed how to measure direct trust according to interactive feedback. The inevitable factor, perceived as uncertainty caused by low interactive frequency, randomness, or incomplete information, is addressed during trust estimation. In this subsection, we focus on indirect reputation management. In some studies, agents only use direct trust if they have direct experience; otherwise, the agent would demand indirect reputations. Some literature employs only direct trust if it is available; otherwise, it would then demand indirect reputations. From our perspective, we have to make full use of both direct trust and indirect reputation for trust estimation, especially in dynamic and distributed MASs. However, it is challenging to rely on the received information directly for the following reasons:

• Some agents might be dishonest;
• A group of agents can conspire to be deceptive;
• Some agents might have incorrect or insufficient information;
• Agents may be uncertain about their provided information;
• Agents might be used for deception.

Accordingly, the trust evaluator needs to have confidence in each piece of the collected information. We, therefore, determine the indirect reputation from the following aspects.

• The estimated trust from the witness’ experience: This aspect could be modeled with the same method as direct trust. The framework of the Dempster-Shafer theory of evidence is adopted to capture its direct trust from the perspective of the information provider (witness).
• Evidence consistency: As explained, both witnesses and service providers might present misleading information. For instance, the client $c_i$ trusts the witness $w_k$. However, $w_k$ does not have sufficient testimony about the service provider $s_j$, or $w_k$ presents false information deliberately because of a conflict of interest. Under those circumstances, the quality of its received information makes great sense. The conflict is applied to identify the differences between evidences, and—contrary to the differences–the similarities between received evidences could be adopted to judge the quality of the provided information.
• The credibility of witnesses: This factor is measured by a real number in the range of $[0,1]$. We initialize it to a fixed number indicating how much the witness can be trusted. Subsequently, it is updated interaction by interaction by the interactive feedback. The credibility of close to 1 shows that it is reliable. Otherwise, the witness is of low trustworthiness, and interaction should be avoided. In this way, a group of agents no longer has the opportunity to conspire to deceive.
• Certainty of a witness: This factor plays a large role in interaction-based trust estimation among MASs. For instance, agent A trusts agent B completely. However, it is questionable to trust agent B if B is uncertain of its evidence to agent C. In this paper, we believe that certainty is dependent on evidence, and we refine certainty from the received evidence from the entropy perspective. We assume that trusted, witness-provided, good-quality, high-certainty evidence makes a greater contribution to trust estimation.

We use $(m_{kj}^d(T),$$m_{kj}^d(nT),$$m_{kj}^d(T,nT))$ to present the direct trust of the service provider agent $s_j$ from the perspective of the witness $w_k$. As is asserted in the previous part, agents should have a rational confidence in the received information. In our opinion, evidence availability changes accompanying confidence. Low-confidence evidence has a smaller effect on the final decision. Simultaneously, evidence with high confidence has a more critical role in the final decision-making. We assume that the confidence of the received information $(m_{kj}^d(T),$$m_{kj}^d(nT),$$m_{kj}^d(T,nT))$ is represented by $Conf(c_i,w_k)$, then the received information is revised by the degree of confidence as follows:

$$\begin{array}{c}{m}_{ij}^{ind}(T)=m_{kj}^d(T)\ast Conf(c_i,w_k);\hfill \\ m_{ij}^{ind}(nT)=m_{kj}^d(nT)\ast Conf(c_i,w_k);\hfill \end{array}$$

(13)

where $m_{ij}^{ind}(T,nT)=1-m_{ij}^{ind}(T)-m_{ij}^{ind}(nT)$. Here, $m_{ij}^{ind}(T)$ shows the trust evaluation of the agent $s_j$ from the service client agent $c_i$’ perspective according to the information provided by the witness agent $w_k$. As defined, the discounted parts are interpreted as uncertainty. It is logical as if the provided information is not convincing, and more information is assigned as uncertainty. Thus, more information is required to eliminate the uncertainty. After modification, Dempster’s combination rule is used to merge all the evidence.

However, it is not easy to decide an appropriate value of confidence, especially in a dynamic environment. In the literature [28], they assign weights to witnesses representing their credibility. Certainty is also adopted to capture confidence [15]. However, it is not enough to consider these aspects separately to decide confidence. From our perspective, we have to tell the consistency of the obtained information, as we believe that agents may not have enough interactions. At the same time, even if an agent has interacted with the target many times, its performance might diversify. In addition, in the reviewed work, we rarely find that consistency, credibility, and certainty have been integrated to determine confidence. As a result, to provide a near-perfect trust estimation model, consistency, credibility, and certainty are studied for confidence estimation in this paper.

4.2.1. Evidence Consistency

Distance suggests how far two objects are away from each other in practical life. The distance of BPAs shows the conflicts or differences between two BPAs. The shorter distance means that the two BPAs are more likely to support the same target (service provider). For trust estimation models in MASs, we adopt average distance to capture the consistency of some evidence. Assume that the demander received BPAs from L different witnesses $w_k$, each of which is represented by $m_{kj}^d$. As a result, the consistency (the difference) between these pieces of evidence is explored below. First, the average distance of $m_{kj}^d$ is represented by $Dis(m_{kj}^d)$, which is defined as

$$Dis(m_{kj}^d)=\frac{{\sum }_{p=1,p\ne k}^{L}d(m_{kj}^d,m_{pj}^d)}{L-1}$$

(14)

where $d(m_{kj}^d,m_{pj}^d)$ indicates the distance of $m_{kj}^d$ and $m_{pj}^d$, and $Dis(m_{kj}^d)$ represents the average distance to the evidence provided by the witness $w_k$, which also expresses its conflict or difference in the group of L evidence. Obviously, the distance between two pieces of evidence falls in the range $[0,1]$ in this paper. At the same time, we claim that the opposite of difference is similarity. Consequently, we can express the similarity by the following operation:

$$Sim(m_{kj}^d)=1-Dis(m_{kj}^d)$$

(15)

where $Sim(m_{kj}^d)$ represents the consistency towards the service provider $s_j$ from the perspective of the witness $w_k$ in the group of L witnesses.

4.2.2. Credibility of Individual Witnesses

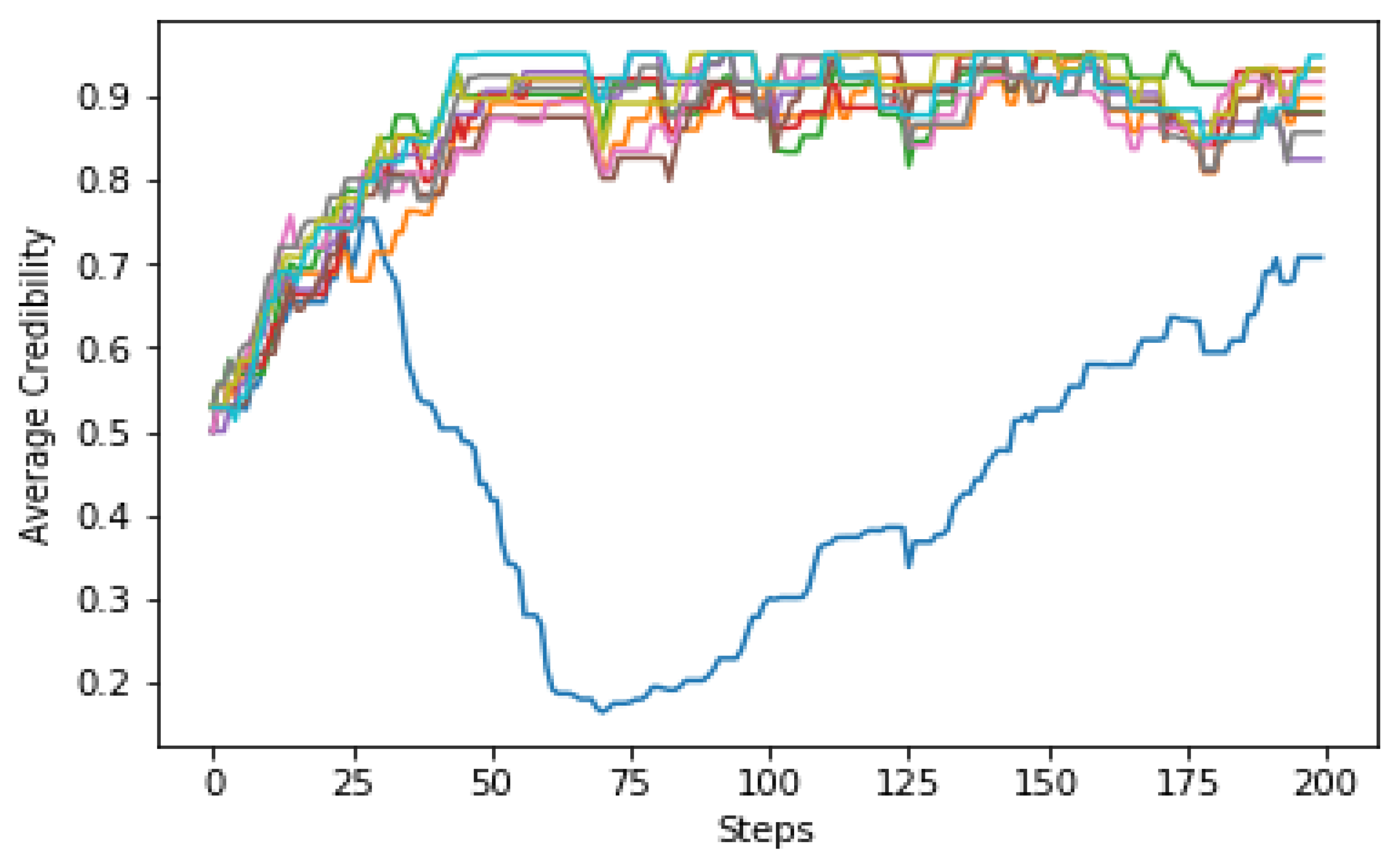
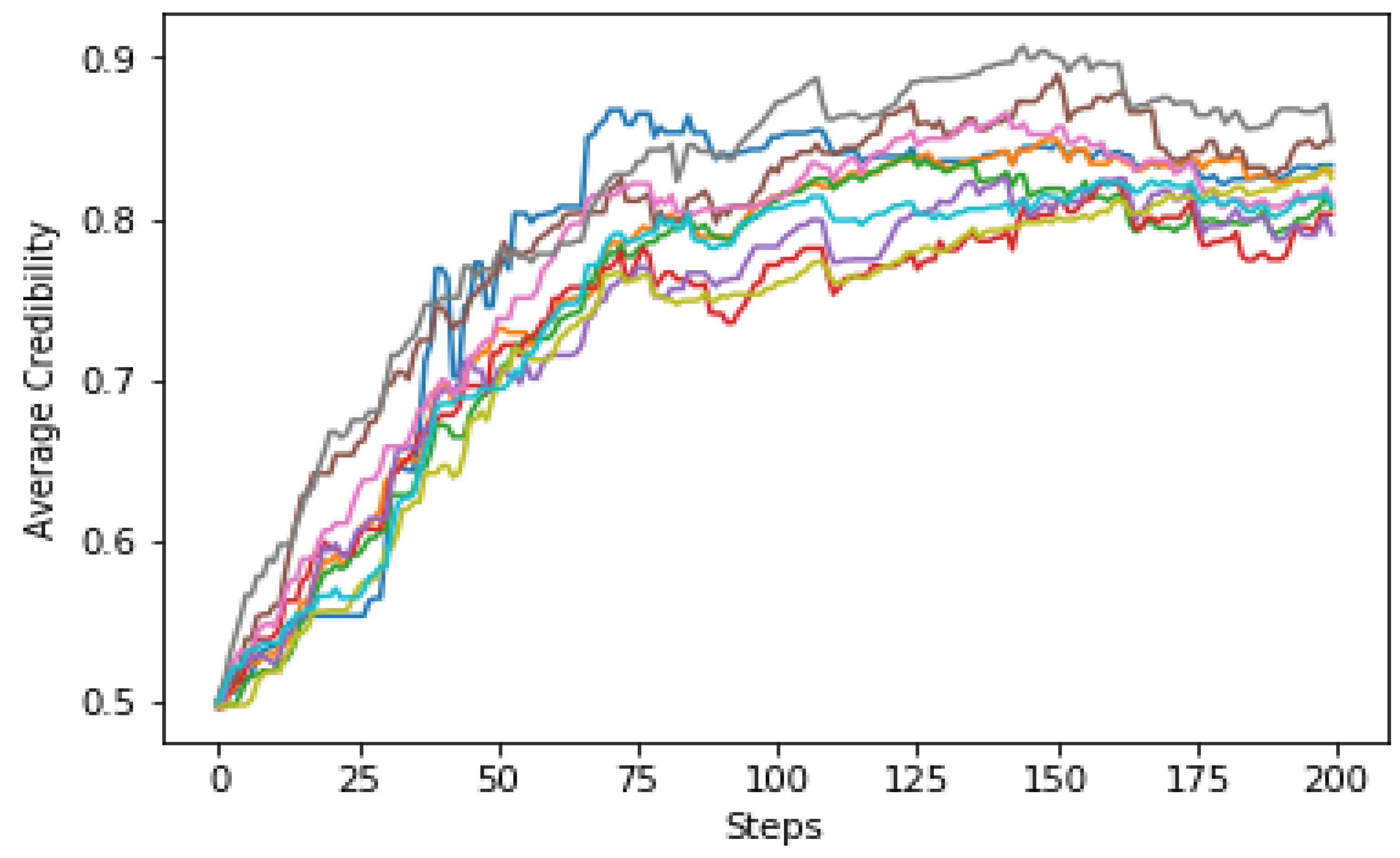
In this subsection, a detailed analysis of the credibility of individual witnesses in MASs is carried out. For a group of witnesses $w_1$, $w_2,\dots$, $w_k$ …$w_L$, they provide testimony to the resource client $c_i$ if $c_i$ urges them to evaluate the trustworthiness of the resource provider $s_j$. From the perspective of $c_i$, to rely on the witness or not is a thought-provoking question. Thus, the agent’s credibility is adopted to indicate how much the witness is reliable. In this paper, we force the witness credibility to be in the range $[0,1]$, and the value is initialized to 0.5 if no cooperation has occurred. As interactions go by, the credibility is updated according to the interactive feedback.

It is necessary to explain how credibility is updated. Of the previous Dempster-Shafer theory based trust estimations models, the value of credibility decreases over interactions all the time if the witness is found lying in [63]. This model works under the assumption that all agents are acting in a constant way. In addition, never forgiving an agent and providing it a second chance also seems irrational. In the literature [29], credibility is learned mainly from two aspects, namely, positive feedback and negative feedback. That is to say, rewards are expressed to all agents when positive feedback is reached, whereas all agents are punished when negative feedback is collected. However, some witnesses may have opposing attitudes when positive feedback is raised, and so it is the same when negative feedback is received. Thus, the credibility of these witnesses needs to be updated separately. What is more, it is sometimes questionable to update the value only according to the current interactive feedback, especially in dynamic systems. Individual reliability has a great influence on indirect reputation. We consider the credibility $Cred(c_i,w_k)$ of the witness $w_k$ from the perspective of $c_i$ when generating indirect reputation. More details about learning from the experience to renew personal credibility are discussed in Section 4.4.

4.2.3. Model Certainty

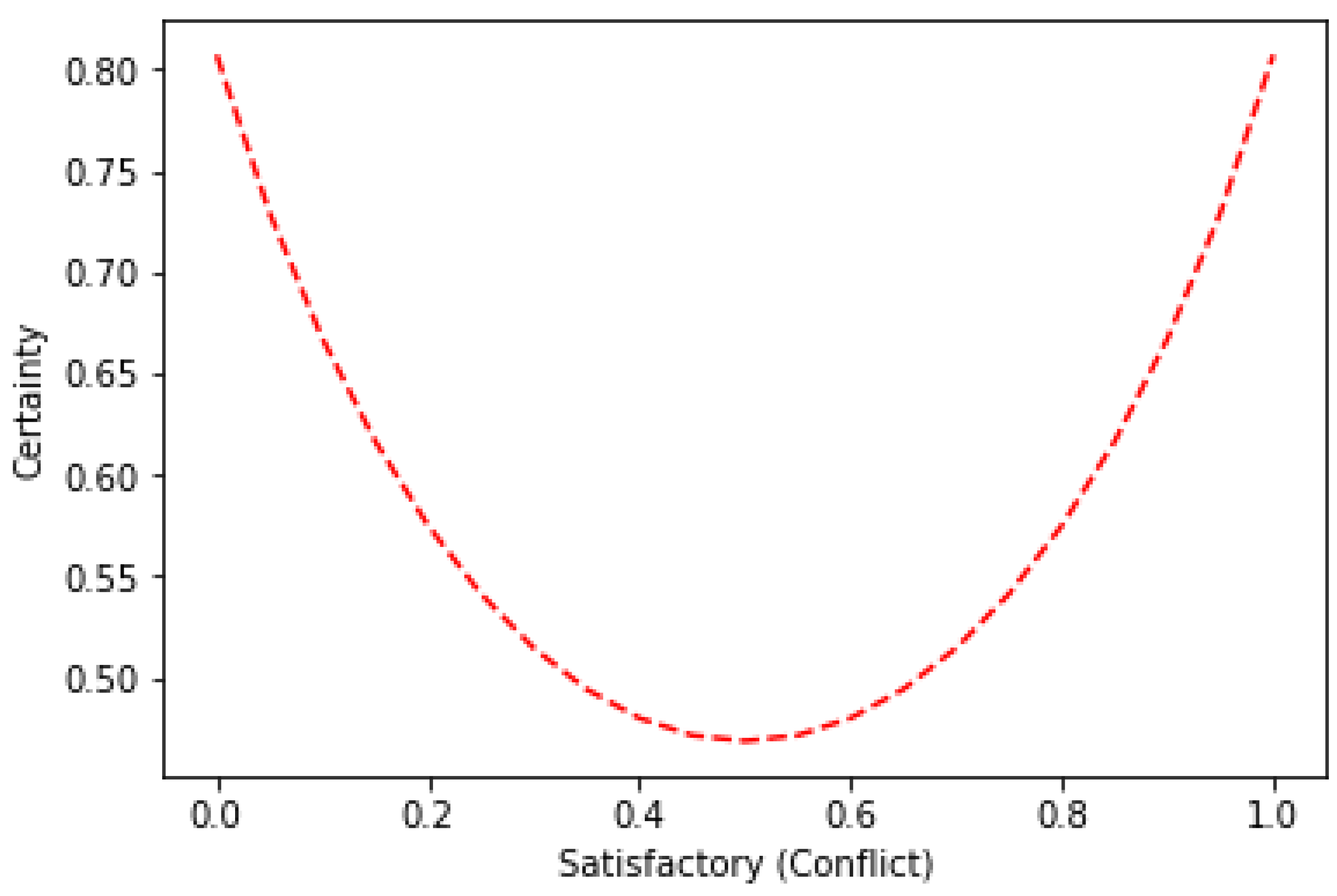
The witness’s certainty also counts for trust estimation in MASs. It is stressed that uncertainty caused by the lack of certainty and complete information is imperative when generating BPAs. Thus, certainty is independent of evidence (BPAs). From our perspective, certainty comes from two perspectives.

• First, certainty decreases as the extent of conflict increases in the evidence (we manage certainty by the ratio of positive and negative observations, namely, trust and distrust). Therefore, evidence certainty decreases as the ratio of positive and negative interactions increases.
• Second, certainty decreases as uncertain information increases. That is to say, evidence certainty increases if $m(T,nT)$ decreases.

At the same time, we wish the value of certainty to fall in the $[0,1]$ range. Due to the listed reasons, the entropy of the Dempster-Shafer theory of evidence is an ideal tool for uncertainty measurement.

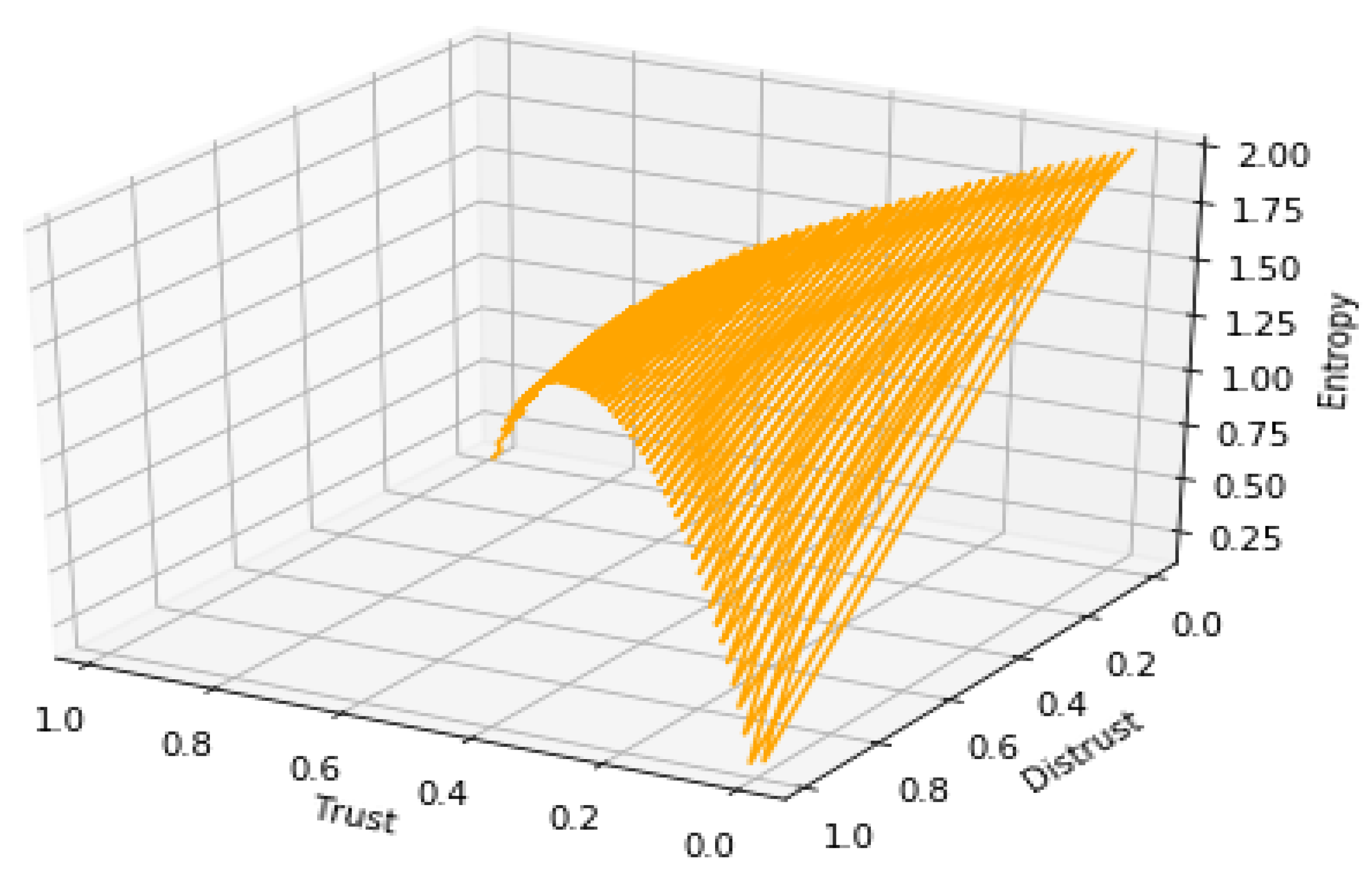
Many definitions of entropy have been proposed for the space of the Dempster-Shafer theory of evidence, for instance, Deng entropy [57] and Dubois and Prade’s definition [56]. In this paper, we adopt the entropy definition presented by Radim and Prakash [60]. The main reasons are that five of the six listed properties are satisfied, which could be regarded as near-perfect in some perspectives. Moreover, the entropy given by Radim and Prakash is designed from two components. The first component is designed to measure conflicts in the BPAs, and the second is used to measure non-specificity in BPAs, which fits for the main reasons of uncertainty in this paper. As explained, we believe that uncertainty yields from the conflict of positive and negative interaction, and a lack of information could also result in uncertainty. For the frame of discernment defined in this paper, i.e., $\Omega =\{T,nT\}$, we have $m(T)=x$, $m(nT)=y$ and $m(T,nT)=1-x-y$, which is under the conditions of $0\le x\le 1$, $0\le y\le 1$, and $0\le 1-x-y\le 1$. The relation between the entropy [60] is presented in Figure 3.

As is shown, the uncertainty is in the range of $[0,2\ast log2|\Omega \left|\right]$. Thus, we define the certainty of the information $m_{kj}$,

$$Cer(m_{kj}^d)=\frac{2-H(m_{kj}^d)}{2}$$

(16)

For example, a BPA is given as $(1,0,0)$ or $(0,1,0)$, then the witness is one hundred percent confident in the evidence. However, the witness is one hundred percent uncertain towards its judgments if the evidence is (0, 0, 1).

4.2.4. Model Indirect Reputation

In this subsection, we explain how to learn the final indirect reputation. As explained, indirect reputation consists of two aspects, namely, the quality evaluation, which is based on performance, and the confidence of the witness. Three sub-factors determine the value of confidence, i.e., the consistency of the provided information (Equation (15)), the credibility of agents (Section 4.2.2), and the certainty (Equation (16)). These three sub-factors are used to revise the generated evidence and $Conf(c_i,w_k)$ in Equation (13). Here, we use $Conf(c_i$, $w_k{)}_t,$$Sim{(m_{kj})}_t,$$Cred{(c_i,w_k)}_t$, and $Cer{(m_{kj})}_t$ to represent the value of confidence, the consistency, the credibility, and the certainty for pretreatment of the tth interaction, respectively. Detailed definition is given as follows:

$$\begin{array}{c}Conf{(c_i,w_k)}_t=Sim{(m_{kj})}_t\ast Cred{(c_i,w_k)}_t\ast [{(Cer{(m_{kj})}_t)}^{|∆|}]\hfill \end{array}$$

(17)

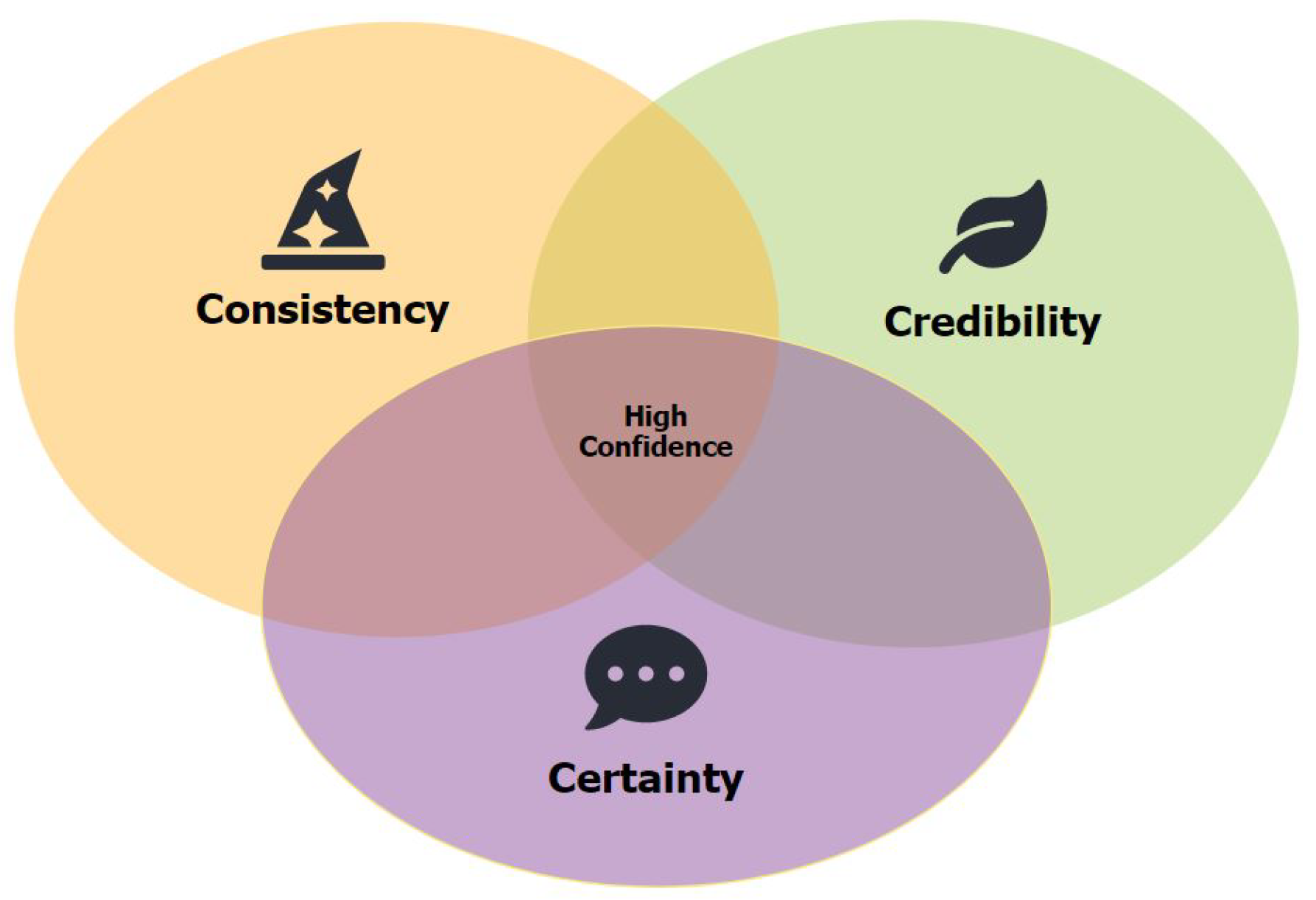
where $∆=min\{0,Sim{(m_{kj}^{dir})}_t\ast Cred{(c_i,w_k)}_t-\frac{1}{L}\sum (Sim{(m_{kj}^{dir})}_t\ast Cred{(c_i,w_k)}_t)\}$ is the smaller value between 0 and the difference of confidence obtained from consistency and credibility. In more detail, the confidence of a piece of evidence provided by the witness is directly proportional to the credibility of a witness, quality, and certainty of the evidence. In terms of certainty, as defines, the confidence $Conf{(c_i,w_k,s_j)}_t$ of the evidence provided by the witness $w_k$ decreases with the certainty $Cer{(m_{kj}^{dir})}_t$ if its credibility $Cred{(c_i,w_k)}_t$ and quality $Sim{(m_{kj}^{dir})}_t$ are below the average level, which is calculated by $Sim{(m_{kj}^{dir})}_t\ast Cred{(c_i,w_k)}_t-\frac{1}{L}\sum (Sim{(m_{kj}^{dir})}_t\ast Cred{(c_i,w_k)}_t)$. Otherwise, the confidence is determined by only the credibility and quality. That is to say, the resource customer agent is more confident in the good-quality indirect experience provided by credibility agents, as presented in Figure 4. Those experiences that originate from unreliable agents must be discounted and are no longer reliable. After modification, agents’ indirect reputations are fused by Dempster’s combination rule, shown in Equation (4).

4.3. Model Overall Trust

In this section, we demonstrate how to model the overall value of trust. The overall evaluation of the service provider $s_j$ from the perspective of the service client $c_i$ derives from two parts, namely direct trust and indirect reputation. In general, a client trusts itself more compared to the information provided by third-party agents. At least, agents do not have self-conception. However, a client agent should better trust others if a system is unstable. Thus, the pretreatment of direct trust and indirect reputation proposed in [64] is adopted; Equation (18) shows the detailed processes. In the equation, $\psi$ indicates the weight of direct trust, and $1-\psi$ corresponds to the indirect reputation. The value of $\psi$ depends totally on the stability in the MASs; a small $\psi$ indicates agents’ performances often change. Generally, $\psi >(1-\psi )$, we use $m_{ij}^{pre}$ to represent the pretreated BPA, then we have,

$$\begin{array}{c}{m}_{ij}^{pre}(T)=\psi m_{ij}^d(T)+(1-\psi )m_{ij}^{ind}(T)\hfill \\ m_{ij}^{pre}(nT)=\psi m_{ij}^d(nT)+(1-\psi )m_{ij}^{ind}(nT)\hfill \\ m_{ij}^{pre}(T,nT)=1-m_{ij}^{pre}(T)-m_{ij}^{pre}(nT)\hfill \end{array}$$

(18)

After the pretreatment, Dempster’s combination rule is applied to combine $(m_{ij}^{pre}(T),$$m_{ij}^{pre}(nT),$$m_{ij}^{pre}(T,nT))$ one time as [64] stated. The client agent, therefore, can receive the final evaluation of the service provider agent. Subsequently, the resource client selects one of the most reliable service providers to increase interactions. The interactive feedback outcome is achieved after the interaction, which could be either binary results (either success or failure) or an evaluation score in the range $[0,1]$. In the following section, we describe how personal credibility is updated.

4.4. Update Credibility

We first have to distinguish the viewpoint of the witness agent $w_k$ on whether it stands with the service provider agent $s_j$ before updating the corresponding credibility. The evaluation of $s_j$ from the perspective of $w_k$ is represented by ($m_{kj}^d(T),$$m_{kj}^d(nT),$$m_{kj}^d(T,nT))$, where $m_{kj}^d(T)$ indicates that $w_k$ believes that $s_j$ is reliable and $m_{kj}^d(nT)$ represents that the resource provider is untrustworthy. The expression $m_{kj}^d(T,nT)$ is used to show the uncertainty caused by delay, interactive frequency, and incomplete information. It is essential to highlight that uncertainty does not mean knowing anything; it could be reassigned to trust or distrust according to Equation (7), which is represented as follows:

$$\begin{array}{c}Pl\_P_m(T)={\displaystyle \frac{P{l}_m(T)}{P{l}_m(T)+P{l}_m(nT)}}\hfill \\ Pl\_P_m(nT)={\displaystyle \frac{P{l}_m(nT)}{P{l}_m(T)+P{l}_m(nT)}}\hfill \end{array}$$

(19)

A value of $Pl\_P_m(T)$ greater than 0.5 symbolizes that the service provider is reliable from the perspective of the witness $w_k$. Otherwise, the witness $w_k$ implies that the service provider $s_j$ is untrustworthy. Hence, an agent’s credibility needs to be updated by the difference between the provided information and the interactive feedback outcome. Generally, the interactive outcome is represented by a success $(1,0,0)$ or a failure $(0,1,0)$ if the binary evaluation system is employed; otherwise $(s,1-s,0)$. As is emphasized, agents in MASs might act unstably. Thus, the obtained incorrect information is probably caused by two conditions: the witness is dishonest, or the service provider intentionally presents a different quality of service. As a result, a client needs to investigate the consistency to update the credibility, and the following four cases are defined to conduct the operation.

• If the interactive feedback is positive:

  case 1:$Pl\_P_m(T)\ge 0.5,$

  $\hspace{1em}Cred{(c_i,w_k)}_{t+1}=Cred{(c_i,w_k)}_t\ast (1+\upsilon D_k);$

  case 2:$Pl\_P_m(T)<0.5,$

  $\hspace{1em}Cred{(c_i,w_k)}_{t+1}=Cred{(c_i,w_k)}_t\ast (1-\upsilon D_k);$

• If the interactive feedback is negative:

  case 3:$Pl\_P_m(T)\ge 0.5,$

  $\hspace{1em}Cred{(c_i,w_k)}_{t+1}=Cred{(c_i,w_k)}_t\ast (1-\upsilon D_k);$

  case 4:$Pl\_P_m(T)<0.5,$

  $\hspace{1em}Cred{(c_i,w_k)}_{t+1}=Cred{(c_i,w_k)}_t\ast (1+\upsilon D_k).$

The expression $D_k$ is the feedback difference, which can be calculated from two aspects. First, its testimony and actual feedback outcome. For instance, the evaluation of service provider $s_j$ given by witness $w_k$ is represented by $(m_{kj}^d(T),m_{kj}^d(nT),m_{kj}^d(T,nT)),$ and the first aspect is represented by

$$D_k^1=d(m_{kj}^d,bpa(outcome))$$

(20)

where $d(m_{kj}^d,bpa(outcome))$ indicates the differences between the provided testimony and the feedback. It could also be interpreted as a consequence of relying on the received information.

The second aspect is the conflict of the evidence in the group of L evidences. From our perspective, it is necessary to emphasize these differences, especially in distributed MASs with deceptive agents where agents may deliberately react to hide their actual attributes. Thus, the second aspect is familiar with the definition with Equation (15), which can be illustrated as follows:

$$D_k^2=\frac{{\sum }_{p=1,p\ne k}^{L}d(m_{kj}^d,m_{pj}^d)}{L-1}.$$

(21)

In summary, $D_k$ is updated with the equation as follows, where $\zeta$ indicates the weight of the difference of its evaluation and the feedback. In general, $\zeta >0.7$ if multiagents do not change their behaviors frequently.

$$D_k=\zeta \ast D_k^1+(1-\zeta )\ast D_k^2.$$

(22)

4.5. Incentives

One of the significant challenges in MASs involving deceptive agents is to motivate agents to bestow accurate information. In this paper, we are inspired by the credit mechanism to achieve this operation. Each of the agents in MASs has a fixed number of credits, no matter whether it acts as a resource client, a witness, or a resource provider, which are administered and displayed by a blackboard. However, credits only make sense when an agent acts as a resource client or a witness. A witness is only allowed to contribute its testimony if the resource client has credits. Simultaneously, a witness might receive or lose credits according to the interactive feedback of the resource client. As a resource client, an agent can no longer solicit others for any testimonies once it runs out of credits because it acts as a witness. Of course, it has the opportunity to encourage information by presenting convincing information and accumulating credits.

We suppose that gaining or losing credits is affected by interactive feedback. The specific amount is determined by its original credit and the confidence value decided by credibility value and consistency. In order to explain the credit mechanism in detail, we apply $C{R}_i$ to represent the credit of agent $c_i$. We force the value to be in the range $[0,2]$, and it is initialized to 1. It is capable of demanding information unless $C{R}_j$ is bigger than the threshold, for example, $C{R}_j>0.2$. After the interaction, the credits of all witnesses are updated as follows:

• If the interactive feedback matches the testimony, then

  $$C{R}_i=C{R}_i[1+Cred(c_i,w_k)\ast Cer(c_i,w_k)]$$
• If the interactive feedback does not match the testimony, then

  $$C{R}_i=C{R}_i[1-Cred(c_i,w_k)\ast Cer(c_i,w_k)]$$

It is necessary to explain what “match” means here. Namely, the witness supports the resource provider if the feedback was a success and the other way around. We set two bounds, as the witness is not allowed to accumulate or lose too many credits in a dynamic MASs. A high-credit agent loses credits rapidly if it keeps lying. Another advantage of our trust estimation model is that another “second chance” mechanism is not required. As soon as a dishonest agent reaches the minimum credit level, it understands that it can no longer demand information for trust estimation. Thus, to maximize its own social welfare, it has to provide honest information to gain credit.

5. Simulation

In order to examine the performance of the proposed model, it is tested using simulation experiments from the following aspects. First, we have to see if the BPA generation approach is sensitive to an unexpected performance change. After that, we check that the entropy-based certainty approach runs correctly and rationally. Finally, the assigned credibility method in the proposed method is compared to previous work to examine its efficiency for trust estimation.

5.1. Evidence Generation

The proposed model aims to maintain the trust of agents, in which agents can react differently over time. That is to say, both resource provider agents and information provider agents (witnesses) can decide to move from genuine to malicious or the other way around, as stated in Section 1. As a result, when an agent switches its performance deliberately, the proposed method enables agents to notice the agility difference and take sharp responses. This part mainly examines if the resource client agent can react sharply, facing an unstable resource provider agent, namely, to investigate the efficiency of the proposed direct trust generation approach.

We fix one resource provider agent and one resource client agent in the experiment. Each round, the resource client agent solicits the resource provider agent for some resources, and, correspondingly, the resource provider agent contributes its resources cooperatively. In addition, concerning the resource provider agent, we also fix the probability of distributing satisfied resources to the decimal number of $P_s$$(P_s\in [0,1])$, which is unknown to the resource client agent. After a fixed number of interactions, for example, $N_{i1}$, the resource provider agent decides to go from genuine to malicious (or from malicious to genuine). Thus, we fix the probability of distributing satisfied resources to $1-P_s$ correspondingly.

In each round, the client agent employs the transaction feedback to estimate the trust of the resource provider, and the transaction feedback could be a success if a randomly generated number is smaller than $P_s$. Otherwise, interaction feedback is a failure. As a comparison, we compared to [65], as they map the evidence $(r,s)$ to the trust represented by $(\frac{r}{r+s+1},\frac{s}{r+s+1},\frac{1}{r+s+1})$ in terms of the absolute error; here, r and s indicate the number of success interactions and failed interactions, respectively. We pay much attention to the estimated value of trust in the proposed method when performance has changed. Figure 5 shows the accumulation of absolute errors (five rounds starting with $N_{i1}$) due to the resource provider changing its performance.

As we can see, the accumulative absolute errors obtained by the proposed method are smaller than the $\frac{r}{r+s+1}$ in Figure 5, no matter whether 10 or 100 rounds are conducted. That is to say, the proposed method has a sharp perception of the sudden change of the resource providers. This improvement enables agents to manage varying performance in a dynamic MAS.

Nonetheless, some issues have to be stressed in this experiment. First, we fixed the number of resource provider agents and resource client agents to one that also fits any other number of agents. We simplify the number of agents because we want to check the performance facing sudden changes. Second, the proposed method generally acts well when the probability of presenting high-quality services is high or low (0.7 and 0.9). However, if the resource provider agent acts averagely (for example, $P_s=0.5$), the estimated trust by [65] may have a better performance because it seems to be no different when the agent decides to go from malicious ($P_s=0.5$) to genuine ($1-P_s=0.5$). As a comparison, we run the test 1000 times, and we set $P_s=0.5$ and $N_{i1}=10$. We say it is a win if the accumulated five-round absolute error by the proposed method is smaller than that of $\frac{r}{r+s+1}$ starting with $N_{i1}$. We received an average of 0.47 for winning the comparison, and the method in [65] wins by a tiny margin. However, the proposed method wins with 0.96 and 0.999 if $P_s=0.7$ and $P_s=0.9$, respectively. Nevertheless, rational agents tend to cooperate with the well-performing resource provider agents rather than the averagely performing agents in practical life. Thus, this is why we focus on 0.1, 0.3, 0.7, and 0.9 to present satisfying resources in the test. In the next part, we discuss evidence certainty from the perspective of entropy.

5.2. Manage Trust Certainty with Entropy

In Section 4.1, we explained that satisfaction is primarily determined by evidence consisting of positive and negative feedback (or the evaluation) and fluctuation. We utilize the satisfactory degree of $S_{ij}$ to represent the performance, which could also be interpreted as the number of positive and negative feedback represented by r and s, respectively. The related evaluation is employed to represent trust with the Dempster-Shafer theory of evidence (Equations (8) and (11)). Much uncertainty caused by randomness, incompleteness, uncertainty, and dynamic environment has been addressed. This direct trust is generally shared with the third-party resource clients to help trust estimation. However, it is essential to decide the certainty of the received or presented evidence. In this paper, we understand certainty with the entropy of the Dempster-Shafer theory of evidence.

In previous work, some literature assumes that certainty is independent of evidence [15], and a third-party agent provides evidence as well as the relevant certainty towards the evaluation. In terms of the evidence $(r,s)$, [65] map this evidence to a trust represented by $(\frac{r}{r+s+1},\frac{s}{r+s+1},\frac{1}{r+s+1})$, and $\frac{1}{r+s+1}$ is designated as uncertainty. Yu and Singh used two parameters in the range of 0 and 1 to model all evidence (evaluations) to positive, negative, or neutral by the Dempster-Shafer theory of evidence [27], and neutral is regarded as uncertainty. However, it fails to embody that conflicting evidence (the amount of positive or negative interaction) increases uncertainty. Furthermore, the amount of interaction also has no impact on certainty. Subsequently in [20,66], certainty is a statistical measure defined on a probability–certainty density function. However, this transformation from evidence to trust neglects implementing an overall analysis of uncertainty caused by a fading factor, lacking information, incompleteness, and randomness. In addition, the work listed above is on the condition that trustees have stable performance. We transform the evidence to trust, providing an overall evaluation appropriate for dynamic agents’ trust estimation, and the certainty of the evidence is well-studied thanks to the entropy definition. We reveal that the certainty estimated with entropy fits well with the general properties listed in Section 4.2.3; more details are expressed in the following subsections.

5.2.1. Certainty Rises with Increasing Experiences under Fixed Conflict

Assuming that agent $a_i$ perceives evidence with the fixed satisfactory degree $S_{ij}$ towards agent $a_j$, we can ascertain how evidence certainty varies with an increasing amount of interaction. Logically, evidence certainty grows with increasing interaction. For example, compare 3 positive feedback instances out of 5 with 12 positive feedback instances out of 20, and we recognize that the satisfactory degree $S_{ij}$ is the same $(\frac{3}{5}=\frac{12}{20}=0.6)$ in both cases. Nevertheless, the certainty in the second case is intuitively greater than the first one. Definition 12 defines the generated BPAs, and Equation (16) is employed to calculate the certainty with the entropy of the Dempster-Shafer theory of evidence. We have certainty of 0.60 from $(3,2)$, and as a comparison, certainty of 0.69 for $(12,8)$. In more detail, Figure 6 indicates how certainty changes with an increasing amount of interaction (x-axis: from 0 to 20) and the fixed satisfaction $S_{ij}=0.5$.

As displayed in Figure 6, certainty increases with the amount of interaction when the satisfaction degree is fixed to 0.5, and it reaches a fixed value of 0.7 with sufficient interaction. Next, we check how certainty changes with increasing conflict under a fixed amount of interactions.

5.2.2. Certainty Rises with Increasing Conflict under Fixed Experience

Under the condition of a fixed interaction amount $(r+s)$, another characteristic of certainty is that the certainty degree differs from the satisfaction, which is also imperative. For instance, two agents have interacted ten times, and the feedback $(10,0)$ is indeed more specific (certain or confident) than that of $(5,5)$. Thus, certainty increases when the satisfactory degree approaches 1 or approaches 0, and it decreases when the satisfactory degree approaches 0.5. Figure 7 displays the relevant result.

We consider four interactions conducted between agent $a_i$ and agent $a_j$, and the number of positive feedback increases from 0 to 4 (the amount of negative feedback decreases from 4 to 0).

Table 3. Certainty computed by different approaches for different satisfactory degrees with a fixed amount of interactions at 4.

	$(4,0)$	$(3,1)$	$(2,2)$	$(1,3)$	$(0,4)$
Yu and Singh [27]	0	0	0	0	0
Jøsangsang et al. [65]	$0.8$	$0.8$	$0.8$	$0.8$	$0.8$
Wang and Singh [20,66]	$0.54$	$0.35$	$0.29$	$0.35$	$0.54$
Proposed entropy-based approach	$0.69$	$0.62$	$0.59$	$0.62$	$0.69$

shows the certainty calculated by Yu and Singh [27], Jøsangsang et al. [65], and Wang and Singh [20,66].

5.2.3. Comparison and Discussion

Here, we discuss trust certainty from the perspective of entropy of evidence. The previous literature studied certainty from the observed trust, namely, the amount of positive or negative feedback. For instance, ref. [20,66] analyzed certainty from the perspective of probability–certainty density function [65], and the estimated certainty was employed to generate evidence. That is to say, a piece of trust represented by belief, disbelief, and the unknown should derive from the amount of positive and negative feedback, and the estimated uncertainty will be employed to obtain the trust of the unknown. We provide another perspective to make use of certainty; we first analyzed multiple conditions that result in uncertainty, including lacking certainty, randomness, incompleteness, and varying performances. BPAs could represent this observation according to the Dempster-Shafer theory of evidence. However, how much we could rely on (or trust) the generated evidence when making decisions is a great challenge, and one of the significant aspects is the certainty of the evidence estimated by entropy.

Shannon entropy [61] is a well-known information-theoretic measure of uncertainty that is based on a discrete probability distribution over a finite set of alternatives. However, entropy is said to be inappropriate for certainty estimation of the observed evidence represented by the binary event $(r,s)$ [20,66]. From one aspect, Shannon entropy’s value ranges from 0 to ∞, which does not fit our intuition. From another aspect, the confidence placed in a probability estimation is required. Finally, the defined Shannon entropy cannot be employed to capture the probability estimation’s uncertainty represented by binary events (positive and negative feedback). In this paper, we used entropy to estimate the certainty of the observed evidence represented by BPAs, and this certainty is an essential part of making full use of BPAs. First, entropy models bits of missing information, which can also be interpreted as the information provided by the evidence, and more information conveyed by the evidence should be more valuable. Second, the estimated entropy value is in the range of 0 to 1, which can be employed to exhibit the evidence’s certainty. Last but most importantly, in our opinion, the uncertainty of a trust derived from two events $(r,s)$ consists of two main aspects: the conflict between each judgment (conflict between r and s) and the uncertain part of the judgment (assigned to uncertainty). Then the entropy definition (Definition 6) [60] is designed to capture the certainty of BPAs from these two aspects that fit well to learn uncertainty. Furthermore, as exhibited in this section, the comparison results have proved the two essential qualities of certainty. That is, certainty rises with increasing experiences beyond a fixed conflict (Section 5.2.1), and uncertainty rises with the increasing conflict under a fixed amount of interactions (Section 5.2.2). Thus, the entropy is appropriate for measuring the uncertainty of the generated evidence by the Dempster-Shafer theory of evidence.

5.3. The Overall Trust Model

In this section, a simulation test is designed to estimate the proposed trust model in cloud manufacturing for service provider selection. The test raises interactions between different cloud manufacturing agents, and each interaction would evaluate the different cloud manufacturing providers and filter with which agent to interact.

The simulation is assumed to have $Wnum$ cloud manufacturing client agents and $Pnum$ cloud manufacturing provider agents. Once the interaction is launched, each client first interacts with each of the providers and collects and records the feedback three times. This information will later be used as evidence and shared with other information demanders. Simulation returns tell how to utilize our model, and the system can adjust to fluctuations in the information providers’ behavior.

At the beginning of the simulation, all cloud manufacturing clients are assumed to be honest. That is to say, once the other cloud manufacturing client agents demand recommendations, an honest agent would contribute whatever it has to the demander to help it make correct decisions. However, after several interactions $Cn1$ (for example, 30 interactions), some of the agents (for example, the client agents $a_1$ and $a_2$) become malicious and become entirely dishonest in sharing information. In other words, they would present excellent evaluations of the bad-performance agents, and vice versa. By using the proposed method, the malicious information providers are recognized, and their average credibility decreases gradually, which means that their contribution or recommendation will less affect the final decision. Although these malicious agents are always providing recommendations, a rational decision maker would never trust or rely on the recommendations to make decisions. After a while (for example, at $Cn2$ rounds and $Cn2=70$), the malicious agents decide to become normal and contribute honest information again. When it decides to change its performance, its average credibility increases and their contributions are more influential. Simulation results and figures are discussed in detail in the following paragraph.

Table 4. Parameters in the simulation.

Parameters	Value	Explanation
$Wnum$	10	Number of cloud manufacturing client agents
$Pnum$	25	Number of cloud manufacturing provider agents
$Snum$	7	Number of selected agents to share information
$Cnum$	3	Number of selected provider agents to conduct interactions
$Cn1$	30	From when some agents become malicious
$Cn2$	70	From when the malicious return to being honest
Rounds	200	Total round

explains the detailed parameters in the simulation. As we can see, there are 10 resource client agents and 25 service provider agents. All agents act honestly in the first 30 rounds $(Cn1=30)$. From round 30, some agents become dishonest and share complete incorrect evidence, and later they become honest again $(Cn2=70)$. Each round, a client agent might decide to initiate interaction with a provider with a probability of $50\%$. One of the ten client agents is appointed as the evaluator each round, and seven agents $(Snum=7)$ are selected to share their information, and the evaluator might be included in the information providers; $Cnum$ best-evaluated service providers are selected to carry interactions. The evaluation process is conducted 200 times, and each of the evaluations is managed ten times. We find the same results, and Figure 8 is used to show the results of the clients’ average credibility.

Figure 8 shows the average credibility of the cloud manufacturing service clients, and one of which, defined as $a_1$, coloured in blue, changes its performance from honest to malicious or the other way around, in round $Cn1$ and $Cn2$, respectively. The agent’s credibility is updated at interaction 30 $(Cn1=30)$, where it is redefined as a malicious information provider. As a result, we can recognize that its average credibility from other clients’ perspectives is degraded and, therefore, rational information demanders decrease the confidence towards the provided information. Forty rounds later, that malicious agent reverts to being honest and restarts telling the truth. As a result, its credibility is gradually rebuilt, and the other agents begin to trust its recommendations. However, we also find that the average credibility decreases quickly (in approximately 40 rounds, it decreases from 0.75 to 0.15) and increases very slowly (it takes approximately 130 rounds to increase from 0.15 to 0.7), reflecting the fact that trust is easy to lose and hard to achieve.

In more detail, we find that only one cloud manufacturing agent out of ten information provider agents has changed its performance in round 30; that is to say, most agents also provide correct information to facilitate making the right decisions. As explained, some trust estimation models assume that most information providers are honest and present correct information [2]. As a result, in round 30, we force five honest cloud manufacturing agents to become malicious and begin sharing incorrect information. Figure 9 shows the result. As is shown, the average credibility of the five agents (coloured in dark blue, pink, red, purple and light green all decreased from round 30 and increased at round 70. That is to say, a rational evaluator can distinguish honest information providers, and if they keep telling an untruth, the information providers would no longer be trustworthy. However, if they give correct information, their provider information would become valuable again.

As a comparison, in terms of applying the Dempster-Shafer theory of evidence to trust estimation in a system of multiagents, ref. [28,29] take personal credibility into consideration. However, in [28], we do not discuss if the BPAs generation is appropriate, especially in a dynamic and open MAS; we focus on how the weight of the third-party agents is updated. As explained, the weight is updated by $w_i^{{}^{\prime }}=\theta \ast w_i$, where $w_i$ is the agent’s weight, and $\theta <1$. Thus, the credibility of third-party agents decreases gradually. As a result, it seems inappropriate in an open and dynamic system. In [29], the agents’ weight is defined as increasing gradually to one if positive feedback is received; on the contrary, the weight decreases linearly for negative feedback. Although evidence consistency, as well as evidence certainty, are not considered in this literature, we also simulate it in the same test as explained in Table 4. Figure 10 indicates the average credibility of each information provider from the other perspective. As we can see, even if agent $a_1$ (coloured in blue) chose to present dishonest information from round 30 to round 70, its average credibility increased. That is to say, no evaluator has recognized this cheater. The main reason for receiving increasing average credibility is that most honest agents share correct information that has helped the decision maker select the well-evaluated service provider. As a comparison, Figure 11 shows the average credibility change when the five agents (coloured in dark blue, pink, red, purple and light green) are set to vary their performance in round 30 and round 70.

As we can see in Figure 11, all agents’ average credibility decreased from round 30 to round 70. That is to say, in this period, the evaluator can barely select well-performing service providers and it can also barely recognize dishonest information providers.

6. Conclusions

Introducing trust into the MASs for decision making eliminates many of the untrustworthy agents and significantly improves decision-making efficiency. In this paper, we proposed a trust estimation model in MASs, and the main contributions can be summarized from the following aspects. First, direct trust addresses uncertainty caused by many factors, and it enables agents to react quickly to unexpected changes in performance. Next, we introduced rational confidence in the received testimony in three aspects: consistency, which reflects the quality of the evidence; credibility, which indicates its reliability according to its previous experience; and certainty of the testimony estimated from the perspective of entropy. In addition, we used a credit mechanism to incentivize agents to share truthful information. These aspects are indispensable for trust estimation in dynamic MASs with deceptive and unstable agents. Simulation results show that: (1) the proposed direct trust has quick intuition regarding agents’ different performances, which fits dynamic MASs properly; (2) the entropy-based certainty evaluation is correct and reasonable; (3) the proposed approach is efficient in dynamic trust management in MASs. Simulations in some industrial applications are conducted to show its efficiency. The proposed method also has limitations. We assume that the agent will maintain the same attitude towards all agents. That is, if an agent is honest, it will act honestly with all agents. In addition, we compare our approach with the previous literature separately. Some actual implementation of the cases may also be beneficial. In future work, we will improve this aspect and use the trust model in cloud manufacturing.